Linkage Effects and Analysis of Finite Sample Errors in the HapMap

Abstract

The HapMap provides a valuable resource to help uncover genetic variants of important complex phenotypes such as disease risk and outcome. Using the HapMap we can infer the patterns of LD within different human populations. This is a critical step for determining which SNPs to genotype as part of a study, estimating study power, designing a follow-up study to identify the causal variants, ‘imputing’ untyped SNPs, and estimating recombination rates along the genome. Despite its tremendous importance, the HapMap suffers from the fundamental limitation that at most 60 unrelated individuals are available per population. We present an analytical framework for analyzing the implications of a finite sample HapMap. We present and justify simple approximations for deriving analytical estimates of important statistics such as the square of the correlation coefficient r² between two SNPs. Finally, we use this framework to show that current HapMap based estimates of r² and power have significant errors, and that tag sets highly overestimate their coverage. We show that a reasonable increase in the number of individuals, such as that proposed by the 1000 genomes project, greatly reduces the errors due to finite sample size for a large proportion of SNPs.

Introduction

The development of the HapMap [1] has ushered in the genome wide association era of human genetics and a tremendous number of studies have reported associations to novel genes for a variety of complex diseases [2,3,4]. These genome wide association studies have been made possible by two recent developments. The first is the development of high throughput genotyping technology enabling the simultaneous genotyping of hundreds of thousands of single nucleotide polymorphisms (SNPs) from an individual at a reasonable cost. The second is the development of the HapMap which provides genotype information for the majority of common SNPs in panels from four populations. Although it is still prohibitively expensive to genotype all common polymorphisms in an association study, linkage disequilibrium (LD) or correlation between SNPs allows association studies to genotype a subset of the SNPs referred to as ‘tag’ SNPs [5]. Association to a phenotype at an ungenotyped SNP can be detected if a nearby correlated SNP is one of the tag SNPs [6]. The HapMap allows us to infer the patterns of LD between SNPs.

The most relevant measure of LD between two SNPs to the statistical power of an association study is r², the square of the correlation coefficient between the two SNPs. As shown in Pritchard and Przeworski [6], to achieve the equivalent power of detecting an association at an SNP with N individuals requires N/r² individuals at a neighboring marker. Using this insight, the standard approach to choosing tag SNPs is to select a subset of the SNPs which have an r² > 0.8 with the remaining SNPs [7]. A SNP that is correlated with a tag SNPs with an r² > 0.8 is referred to as being ‘captured’. The development of the current generation of commercial genotyping products have been strongly motivated by this notion and tag SNPs are chosen to capture as many of the common HapMap SNPs as possible.

In addition to aiding in the design of genome wide association studies, the HapMap genotypes allow us to estimate study power for a given disease model. Recent imputation methods [8, 9] have demonstrated how to further improve study power with the HapMap data by estimating allele frequencies of untyped variants. The HapMap genotypes have also been used to estimate recombination rates across the genome, search for regions under natural selection, and locate structural variations such as deletions and inversions.

Despite its tremendous importance as a resource, the HapMap suffers from the fundamental limitation that it is based on at most 60 unrelated individuals or 120 chromosomes per population. Current methods which use the HapMap effectively assume that the HapMap has infinitely many individuals and that the observed correlation patterns are the true correlation patterns. In reality, the HapMap is not a large enough sample to accurately measure the LD patterns between SNPs. This limitation has significant implications for association studies. First, many of the SNPs which are believed to be captured by tag sets developed using the HapMap are in fact not well captured, but only appear to be captured in the HapMap due to sampling bias. For these SNPs, even very large association studies will not detect associations. Second, the estimates of r² are very inaccurate which leads to inaccurate estimates of the power of association studies. Several groups have previously pointed out this limitation [10] and have performed empirical studies exploring this and the related issue of the transferability of tag SNPs to different populations [11,12,13]. Finally, the linkage structure is used by imputation methods to estimate frequencies of untyped SNPs in association studies. Their accuracy is necessarily tied to that of the HapMap.

In this paper, we present an analytical framework for analyzing the implications of a finite sample HapMap. We observe that most of the error in the estimates of correlation patterns stems from the difficulty in estimating conditional probabilities from small samples. We present and justify simple approximations for obtaining confidence intervals for r² estimates from the HapMap and verify our confidence intervals through simulations using both the HapMap and Welcome Trust Case Control Consortium data [2] (WTCCC). We show how the current HapMap may perform very poorly for estimating the power of an association study at certain SNPs.

Consider a case control study in which 5,000 cases and 5,000 controls are genotyped on 500,000 independent SNPs, and the causal variant has a relative risk 1.5 and minor allele frequency of 0.05. If the causal variant is genotyped directly the study has a power of 93.1% to detect an association at that variant. If the causal variant is not genotyped, but has an r² of 0.8 with a nearby tag SNP, then the study has a power of 55% to detect an association due to the causal variant. Using our framework, we show that approximately 8.2% of the SNPs with a minor allele frequency of 0.05 and an observed r² of 0.8 in the HapMap have a true r² below 0.5. The power to detect an association is only 2.7% for these SNPs, yet using the HapMap we believe the power is 55%. In order to better ground our results in an actual association study context, we extend this analysis using the WTCCC [2] data and show that many of the SNPs in these studies may be affected by finite sample errors in the HapMap. In addition, we show that procedure of selecting tag SNPs is upwardly biased and results in an overestimation of power.

While larger reference sets such as the 1000 genomes project are being proposed to catalogue rare human variation, it is not appreciated how these reference sets will profoundly affect our ability to detect common variation involved in human disease. In addition to providing a highly valuable fine grained picture of low frequency SNPs and a more extensive list of SNPs human populations, these additions to the HapMap reference panels will help resolve many of the issues illustrated in the above examples. To estimate how large of a sample we need to collect in order to avoid these problems we examine confidence intervals around ‘captured’ SNPs with an r² of 0.8. As the sample size or MAF of a SNP increases, the confidence interval for r² will tighten. If a SNP's 95% confidence interval is greater than 0.1 or equivalently that the probability that r² < 0.7 is less than 2.5% we are confident that the estimated r² is close to the true r². The current HapMap cannot provide a bound this tight even for SNPs with MAF 0.5. Increasing the HapMap to 238 individuals would achieve this confidence interval for SNPs with MAF as low as 0.2, and increasing it to 502 individuals would provide for SNPs with MAF as low as 0.1. In order to have a tight confidence interval for low frequency SNPs with MAF of 0.05, 1042 individuals are needed.

Material and Methods

Case Control Studies

In a typical association study, individuals are collected from two populations, a case population consisting of individuals with a disease and a control population consisting of individuals without the disease. The populations differ along the phenotype of interest but individuals are carefully selected so that they are otherwise members of the same population. Each individual in the study is genotyped on a set of tag SNPs such as those on the Affymetrix and Illumina high throughput genotyping platforms. SNPs with alleles that cause an alteration in risk for the phenotype potentially occur in different frequencies in the cases and controls. These causal SNPs may not be included in the set of tag SNPs. It is the primary objective of a case control study to identify these causal polymorphisms.

Suppose that there is a tag SNP A and a causal SNP B in a case control study with N/2 cases and N/2 controls. We denote the frequency of the minor allele of SNP A in the cases, controls, and entire population as p⁺_A, p^–_A, and p_A respectively. We denote p_a = (1 – p_A) as the frequency for the major allele of SNP A and use p_B, p_b for the equivalent frequencies over SNP B. ${\stackrel{‸}{\text{p}}}_{\text{B}}$ and ${\stackrel{‸}{\text{p}}}_{\text{A}}$ denote the observed frequencies of SNP B and SNP A in the collected samples respectively.

Consider a case control study in which we genotype the causal SNP B directly. We compute the following statistic S_B

$$S_B=\frac{{\stackrel{‸}{\text{p}}}_{\text{B}}^{+}-{\stackrel{‸}{\text{p}}}_{\text{B}}^{-}}{\sqrt{2/N}\sqrt{{\stackrel{‸}{\text{p}}}_{\text{B}}\left(1-{\stackrel{‸}{\text{p}}}_{\text{B}}\right)}}\sim \mathcal{N}\left(\frac{\left({\text{p}}_{\text{B}}^{+}-{\text{p}}_{\text{B}}^{-}\right)\sqrt{\mathcal{N}}}{\sqrt{2{\text{p}}_{\text{B}}\left(1-{\text{p}}_{\text{B}}\right)}},1\right)=N\left({\lambda }_{\text{B}}\sqrt{N},1\right)$$ (1)

S_B measures the difference in the frequency of SNP B in the cases ($\stackrel{‸}{\text{p}}$⁺_B) and the controls ($\stackrel{‸}{\text{p}}$^–_B) in the collected sample normalized such that the variance is 1. We refer to λ_B√N as the non-centrality parameter (NCP) for SNP B. In the null hypothesis p⁺_B = p^–_B and λ_B√N is 0. In the alternative hypothesis p⁺_B ≠ p^–_B and λ_B√N is the mean of the distribution of S_B. The NCP λ√N is a function of study size, disease model, SNP minor allele frequency (MAF), and is the fundamental measure of study power. Power is calculated from the NCP and significance threshold (α) as

$$\mathcal{P}\left(\alpha ,\lambda \sqrt{N}\right)=\Phi \left({\Phi }^{-1}\left(\alpha /2\right)+\lambda \sqrt{N}\right)+1-\Phi \left({\Phi }^{-1}\left(1-\alpha /2\right)+\lambda \sqrt{N}\right)$$ (2)

where Φ(x) is the standard normal cumulative distribution function and Φ^–1(x) is the standard normal quantile function. Fixing α (e.g. 0.05), the power is solely a function of the NCP.

Indirect Association

In general we do not expect the causal variant SNP B to be amongst the set of genotyped tag SNPs, but instead rely on the correlation or LD between proximal tag SNPs and the causal variant to discover the association. Consider a case control study in which the causal variant SNP B is not genotyped but is near a tag SNP A. If SNP A is in strong enough LD with SNP B, and the study is sufficiently powered, it may be possible to detect a significant difference in the frequencies of SNP A between the cases and controls due to its correlation with the causal variant SNP B.

In this section we derive the NCP and power for SNP A given that SNP B is causal. This relies on the conditional probability of observing the minor allele at SNP A given that the minor allele at SNP B is observed. This is denoted p_A∣B = p_AB/p_B, where p_AB is the frequency of the haplotype made from minor alleles of both SNPs A and B. The conditional probability of observing the minor allele of SNP A given an observation of the major allele of SNP B is similarly denoted p_A∣b. It is a standard assumption of association studies that, if SNP B is causal then the conditional probability p_A∣B is equal in the cases and controls. Formally, p_A∣B = p⁺_A∣B = p^–_A∣B and p_A∣b = p⁺_A∣b = p^–_A∣b. Note that p⁺_B∣A ≠ p^–_B∣A if p⁺_B ≠ p^–_B under this assumption.

The frequencies of SNP A can be written in terms of the conditional probabilities and the frequency of SNP B. The frequency in the cases is p⁺_A = p⁺_A∣Bp⁺_B + p⁺_A∣b(1 – p⁺_B) and the frequency in the controls is p^–_A = p^–_A∣Bp^–_B + p^–_A∣b(1 – p^–_B). Combining these two equations, the difference in frequency of the genotyped SNP A between the cases and controls is expressed in terms of the conditional probabilities and the frequency of the causal SNP B as p⁺_A – p^–_A = p_A∣B(p⁺_B – p^–_B) + p_A∣b(1 – p⁺_B − 1 + p⁻_B) = (p_A∣B – p_A∣b) (p⁺_B – p^–_B).

We can now derive the NCP for SNP A which will in turn give the power for SNP A in terms of the NCP of SNP B and the conditional probabilities following the derivation of Pritchard and Przeworski, 2001 [6].

$$\begin{array}{c}{S}_A=\frac{{\stackrel{‸}{\text{p}}}_{\text{A}}^{+}-{\stackrel{‸}{\text{p}}}_{\text{A}}^{-}}{\sqrt{2/N}\sqrt{{\stackrel{‸}{\text{p}}}_{\text{A}}\left(1-{\stackrel{‸}{\text{p}}}_{\text{A}}\right)}}\sim N\left({\lambda }_A\sqrt{N},1\right)\\ {\lambda }_A\sqrt{N}=\frac{{\text{p}}_{\text{A}}^{+}-{\text{p}}_{\text{A}}^{-}}{\sqrt{2/N}\sqrt{{\text{p}}_{\text{A}}\left(1-{\text{p}}_{\text{A}}\right)}}=\left({\text{p}}_{\text{A}|\text{B}}-{\text{p}}_{\text{A}|\text{b}}\right)\frac{{\text{p}}_{\text{B}}^{+}-{\text{p}}_{\text{B}}^{-}}{\sqrt{2/N}\sqrt{{\text{p}}_{\text{A}}\left(1-{\text{p}}_{\text{A}}\right)}}\\ =\left({\text{p}}_{\text{A}|\text{B}}-{\text{p}}_{\text{A}|\text{b}}\right)\frac{{\text{p}}_{\text{B}}^{+}-{\text{p}}_{\text{B}}^{-}}{\sqrt{2/N}\sqrt{{\text{p}}_{\text{A}}\left(1-{\text{p}}_{\text{A}}\right)}}\frac{\sqrt{{\text{p}}_{\text{B}}\left(1-{\text{p}}_{\text{B}}\right)}}{\sqrt{{\text{p}}_{\text{B}}\left(1-{\text{p}}_{\text{B}}\right)}}\\ =\left({\text{p}}_{\text{A}|\text{B}}-{\text{p}}_{\text{A}|\text{b}}\right)\sqrt{\frac{{\text{p}}_{\text{B}}\left(1-{\text{p}}_{\text{B}}\right)}{{\text{p}}_{\text{A}}\left(1-{\text{p}}_{\text{A}}\right)}}{\lambda }_B\sqrt{N}\end{array}$$ (3)

The correlation coefficient

$$r_{AB}=\left({\text{p}}_{\text{A}|\text{B}}-{\text{p}}_{\text{A}|\text{b}}\right)\sqrt{\frac{{\text{p}}_{\text{B}}\left(1-{\text{p}}_{\text{B}}\right)}{{\text{p}}_{\text{A}}\left(1-{\text{p}}_{\text{A}}\right)}}$$

between SNP A and SNP B relates λ_A and λ_B and is algebraically equivalent to the standard form of

$$r_{AB}=\frac{p_{AB}-{\text{p}}_{\text{A}}{\text{p}}_{\text{B}}}{\sqrt{{\text{p}}_{\text{A}}\left(1-{\text{p}}_{\text{A}}\right){\text{p}}_{\text{B}}\left(1-{\text{p}}_{\text{B}}\right)}}$$

Equation (3) above shows that the NCP at SNP A is a function of r_AB and the NCP at SNP B, λ_A√N = r_ABλ_B√N. Finally, we can express the power at SNP A if SNP B is causal as:

$$\mathcal{P}\left(\alpha ,{\lambda }_A\sqrt{N}\right)=\mathcal{P}\left(\alpha ,r_{AB}{\lambda }_B\sqrt{N}\right)$$ (4)

As expected, the higher the correlation between the SNPs, the greater the power of using the tag SNP as a proxy for the causal variant.

Estimating Correlation Variance from the HapMap

The HapMap data do not provide the exact frequencies or conditional probabilities of the SNPs in a population, but is commonly used to estimate these quantities as well as the correlation coefficient between SNPs, the NCP, and study power under a given disease model. The finite sample size of each of the HapMap populations introduces a source of error into each of these estimates. In the previous section we derived the NCP for the causal SNP given a tag SNP. Here we extend this derivation to calculate the mean and variance of the NCP and the correlation coefficient assuming a finite reference sample. The variance of the correlation coefficient found in this section uses a simplifying assumption and is therefore denoted σ_S. A more complex estimate is derived in the next section.

We derive an approximation for the correlation coefficient between SNPs A and B.

$${\stackrel{‸}{r}}_{AB}^H\sim \mathcal{N}\left(r_{AB},{\sigma }_s^2\right)$$ (5)

$${\sigma }_s\equiv var\left({\stackrel{‸}{r}}_{AB}^H\right)=\left(\frac{{\text{p}}_{\text{A}|\text{B}}^{\text{H}}\left(1-{\text{p}}_{\text{A}|\text{B}}^{\text{H}}\right)}{N_B^H}+\frac{{\text{p}}_{\text{A}|\text{b}}^{\text{H}}\left(1-{\text{p}}_{\text{A}|\text{b}}^{\text{H}}\right)}{N_b^H}\right)\frac{{\text{p}}_{\text{B}}^{\text{H}}\left(1-{\text{p}}_{\text{B}}^{\text{H}}\right)}{{\text{p}}_{\text{A}}^{\text{H}}\left(1-p_A^{\text{H}}\right)}$$ (6)

where superscript H denotes values over the HapMap data N^H and denotes the number of chromosomes in the HapMap. p^H_B denotes the true frequency of the minor allele SNP B in the HapMap population. The observed frequency of the minor allele of SNP B in the HapMap samples is denoted by $\stackrel{‸}{\text{p}}$^H_B. The true and observed conditional probabilities are p^H_A∣B and $\stackrel{‸}{\text{p}}$^H_A∣B respectively, and N^H_B = $\stackrel{‸}{\text{p}}$^H_BN^H is the number of chromosomes with the minor allele.

To derive an approximation for the variance of r^H_AB in equation 5 we begin with the derivation of the distribution for the estimate of the NCP at SNP A. Assuming normal approximations:

$$\begin{array}{l}{\stackrel{‸}{\text{p}}}_{\text{A}|\text{B}}^{\text{H}}\sim \mathcal{N}\left({\text{p}}_{\text{A}|\text{B}}^{\text{H}},\frac{{\text{p}}_{\text{A}|\text{B}}^{\text{H}}\left(1-{\text{p}}_{\text{A}|\text{B}}^{\text{H}}\right)}{N_B^H}\right)\hfill \\ {\stackrel{‸}{\text{p}}}_{\text{A}|\text{b}}^{\text{H}}\sim \mathcal{N}\left({\text{p}}_{\text{A}|\text{b}}^{\text{H}},\frac{{\text{p}}_{\text{A}|\text{b}}^{\text{H}}\left(1-{\text{p}}_{\text{A}|\text{b}}^{\text{H}}\right)}{N_b^H}\right)\hfill \\ {\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}\sim \mathcal{N}\left({\text{p}}_{\text{B}}^{\text{H}},\frac{{\text{p}}_{\text{B}}^{\text{H}}\left(1-{\text{p}}_{\text{B}}^{\text{H}}\right)}{N^H}\right)\hfill \\ {\stackrel{‸}{\text{p}}}_{\text{b}}^{\text{H}}\sim \mathcal{N}\left({\text{p}}_{\text{b}}^{\text{H}},\frac{{\text{p}}_{\text{b}}^{\text{H}}\left(1-{\text{p}}_{\text{b}}^{\text{H}}\right)}{N^H}\right)\hfill \end{array}$$ (7)

The estimates of the conditional probability are based on far fewer observations than the estimates of the frequency, thus the variance of the estimates of the conditional probabilities are much larger than the variance of the estimates of the allele frequencies.

In order to use the HapMap data for power estimation we make several assumptions about the relation between our case, control, and HapMap populations. The fundamental assumption of the HapMap is that the SNP frequencies conditional on a causal SNP in case and control samples are equal to the conditional frequencies in the HapMap. That is,

$${\text{p}}_{\text{A}|\text{b}}={\text{p}}_{\text{A}|\text{b}}^{+}={\text{p}}_{\text{A}|\text{b}}^{-}={\text{p}}_{\text{A}|\text{b}}^{\text{H}}=\frac{P_{Ab}^H}{p_{\text{b}}^{\text{H}}}.$$

Under these assumptions, we can estimate the NCPs using the estimates of the conditional probabilities and allele frequencies directly from the HapMap. Using these terms we define the NCP $\stackrel{‸}{\lambda }$^H_A in terms of the empirical conditional probabilities and frequencies in the HapMap, and the true NCP λ_B:

$${\stackrel{‸}{\lambda }}_A^H\sqrt{N}\equiv \left({\stackrel{‸}{\text{p}}}_{\text{A}|\text{B}}^{\text{H}}-{\stackrel{‸}{\text{p}}}_{\text{A}|\text{b}}^{\text{H}}\right)\sqrt{\frac{{\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}\left(1-{\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}\right)}{{\stackrel{‸}{\text{p}}}_{\text{A}}^{\text{H}}\left(1-{\stackrel{‸}{\text{p}}}_{\text{A}}^{\text{H}}\right)}}{\lambda }_B\sqrt{N}$$ (8)

In our estimate, the term λ_B√N is considered a constant because we are interested in the relative strength of the association at the tag SNP compared to the strength at the causal SNP. Under this assumption, the only observed values appearing in the equation for the NCP are HapMap SNP frequencies and conditional probabilities.

We make the simplifying assumption that the empirical frequency ${\stackrel{‸}{\text{p}}}_{\text{A}}^{\text{H}}$ is close to the true frequency p^H_A relative to the much larger variance in the estimates of conditional probability. This allows us to derive a simple estimate for the error due to the finite sample.

$${\stackrel{‸}{\lambda }}_A^H\sqrt{N}\sim \mathcal{N}\left({\lambda }_A\sqrt{N},{\sigma }_{\lambda \hspace{0.17em}A}^{2\hspace{0.17em}H}\right)$$ (9)

$${\sigma }_{\lambda A}^{2H}=\left(\frac{{\text{p}}_{\text{A}|\text{B}}^{\text{H}}\left(1-{\text{p}}_{\text{A}|\text{B}}^{\text{H}}\right)}{{\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}{N}^H}+\frac{{\text{p}}_{\text{A}|\text{b}}^{\text{H}}\left(1-{\text{p}}_{\text{A}|\text{b}}^{\text{H}}\right)}{\left(1-{\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}\right)N^H}\right)\frac{{\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}\left(1-{\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}\right)}{{\stackrel{‸}{\text{p}}}_{\text{A}}^{\text{H}}\left(1-{\stackrel{‸}{\text{p}}}_{\text{A}}^{\text{H}}\right)}{\lambda }_B^{2}N$$ (10)

Although there is additional variance due to the assumption that empirical frequency ${\stackrel{‸}{\text{p}}}_{\text{A}}^{\text{H}}$ is close to the true frequency p^H_A, the Results section shows experimentally that simulation of NCPs from linked SNPs are surprisingly close to the derived distribution. We will derive a more sophisticated estimate by dropping this assumption below.

The correlation coefficient is commonly used to measure the strength of SNP A to serve as a proxy for SNP B. We showed above that the decrease in power due to using SNP A as a proxy for SNP B is directly proportional to the correlation coefficient. The NCP and the correlation coefficient can be used together to measure study power. Using the fact that λ_A√N = r_ABλ_B√N and equation (9) above we derive mean and variance of ${\stackrel{‸}{r}}_{AB}^H$

$$var\left({\stackrel{‸}{r}}_{AB}^H\right)\approx \left(var\left({\stackrel{‸}{\text{p}}}_{\text{A}|\text{B}}^{\text{H}}+{\stackrel{‸}{\text{p}}}_{\text{A}|\text{b}}^{\text{H}}\right)\right)\frac{{\text{p}}_{\text{B}}^{\text{H}}\left(1-{\text{p}}_{\text{B}}^{\text{H}}\right)}{{\text{p}}_{\text{A}}^{\text{H}}\left(1-{\text{p}}_{\text{A}}^{\text{H}}\right)}$$ (11)

our experiments validate the assumptions of this approximation with experimental simulation.

Estimating Correlation Variance with the Delta Method

The above ‘simple’ estimate for the variance of the correlation coefficient σ_S assumes that the minor allele frequency is accurately estimated from the data. However, when the frequency of one of the SNPs is very low, this assumption no longer holds. In order to accurately estimate the distribution of ${\stackrel{‸}{r}}_{AB}^H$ we employ the delta method [14] and derive variance σ_Δ. We let $x={\stackrel{‸}{\text{p}}}_{\text{AB}},\hspace{0.17em}y={\stackrel{‸}{\text{p}}}_{\text{B}}^{\text{H}}$, and $z={\stackrel{‸}{\text{p}}}_{\text{A}}^{\text{H}}$ and rewrite the formula for the correlation coefficient in terms of x, y, z.

$$f={\stackrel{‸}{r}}_{AB}^H=\left(\frac{x}{y}-\frac{z-x}{1-y}\right)\left(\frac{\sqrt{y-y^2}}{\sqrt{z-z^2}}\right)$$ (12)

We compute the variance covariance matrix ∑ for x, y, z with σ_xx = p_AB(1 - p_AB), σ_yy = p_B(1 - p_B), σ_zz = p_A(1 - p_A), σ_xy = p_AB(1 - p_B), σ_xz = p_AB(1 - p_A), σ_yz = p_AB - p_Ap_B.

$$\sum =\left(\begin{array}{lll}{\sigma }_{xx}\hfill & {\sigma }_{xy}\hfill & {\sigma }_{xz}\hfill \\ {\sigma }_{yx}\hfill & {\sigma }_{yy}\hfill & {\sigma }_{yz}\hfill \\ {\sigma }_{zx}\hfill & {\sigma }_{zy}\hfill & {\sigma }_{zz}\hfill \end{array}\right)$$ (13)

We compute the gradient of f:

$${\Delta }^T=\left(\frac{\partial f}{\partial x}\hspace{0.17em}\frac{\partial f}{\partial y}\hspace{0.17em}\frac{\partial f}{\partial z}\right)$$ (14)

Finally, the variance is estimated as:

$${\sigma }_{\Delta }\equiv var\left({\stackrel{‸}{r}}_{AB}^H\right)=var\left(f\right)={\Delta }_{\mu }^T\Sigma {\Delta }_{\mu }$$

where Δ_μ is the gradient evaluated at the means of x, y, z. The Results section demonstrates that the ‘delta method’ estimate is accurate over low frequency SNPs with experimental simulation.

Overestimation of r² in Tagging

We showed above that the finite sample size of the HapMap results in error for the estimation of r_AB between SNP A and SPN B but this estimate is unbiased. However, when selecting tags to genotype, since the goal is to choose the smallest subset of SNP which cover as many of the remaining SNPs as possible, the HapMap estimates of the correlation are significantly biased. This bias is compounded by the overestimation described by Bhangale et. al. [15] that is observed when SNPs are eximaned in addition to those contained in the HapMap.

Consider the 3 SNPs, A, B, C, where we are choosing one of A or B to serve as a proxy for SNP C. We will select the SNP which has a stronger correlation with SNP C. For this example, suppose that the correlations coefficients r_AC and r_BC are positive since exchanging major and minor alleles will flip the sign. Using the HapMap will result in estimates of these correlations with variances σ_AC, σ_BC and means r^H_BC and r^H_BC with expected values close to the true correlation. The estimated coverage of SNP C is the max of the empirical measurements of the correlation coefficients in the HapMap

$$max\left({\stackrel{‸}{r}}_{AC}^H,{\stackrel{‸}{r}}_{BC}^H\right)=\frac{{\stackrel{‸}{r}}_{AC}^H+{\stackrel{‸}{r}}_{BC}^H}{2}+\frac{|{\stackrel{‸}{r}}_{AC}^H+{\stackrel{‸}{r}}_{BC}^H|}{2}.$$

We show that this maximum is

$$max\left({\stackrel{‸}{r}}_{AC}^H,{\stackrel{‸}{r}}_{BC}^H\right)=max\left(r_{AC}^H,r_{BC}^H\right)+bias\left(r_{AC}^H,r_{BC}^H\right)$$

and we prove that the term bias(r^H_AC, r^H_BC) is always positive.

To calculate the expectation of this maximum we note that ${\stackrel{‸}{r}}_{AC}^H$ and ${\stackrel{‸}{r}}_{BC}^H$ are normally distributed random variables. The term

$$\frac{{\stackrel{‸}{r}}_{AC}^H+{\stackrel{‸}{r}}_{BC}^H}{2}$$

will have expected value

$$\frac{r_{AC}^H+r_{BC}^H}{2}.$$

The expected value of the other term is more complicated due to the absolute value. We let

$${\sigma }^2=\frac{{\sigma }_{AC}^2+{\sigma }_{BC}^2}{4}$$

and

$$\mu =\frac{r_{AC}^H-r_{BC}^H}{2}.$$

The expected value of

$$\frac{|{\stackrel{‸}{r}}_{AC}^H-{\stackrel{‸}{r}}_{BC}^H|}{2}$$

is:

$$\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\left|x\right|e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx=\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\left|x\right|e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx$$ (17)

$$+\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\mu e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx+\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\mu e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx$$ (18)

Let

$$u=\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}$$

and rewrite the integrals as:

$$\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_0^{\infty }\left(x-\mu \right)e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx+\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{-\infty }^0-\left(x-\mu \right)e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx+\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_0^{\infty }\mu e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx+\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{-\infty }^0-\mu e^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}}dx$$ (19)

$$=\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{\frac{{\mu }^2}{2{\sigma }^2}}^{\infty }{\sigma }^2{e}^{-u}du+\frac{1}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{\int }_{-\infty }^{\frac{{\mu }^2}{2{\sigma }^2}}-{\sigma }^2{e}^{-u}du+\mu \left(1-\Phi \left(-\frac{\mu }{\sigma }\right)\right)-\mu \Phi \left(-\frac{\mu }{\sigma }\right)$$ (20)

The expectation of the entire max is:

$$\frac{r_{AC}^H+r_{BC}^H}{2}+\frac{2{\sigma }^2}{\sqrt{{\sigma }^2}\sqrt{2\pi }}{e}^{-\frac{{\mu }^2}{2{\sigma }^2}}+\mu \left(1-2\Phi \left(-\frac{\mu }{\sigma }\right)\right)$$ (21)

The function μ(1 − 2Φ(−μ/σ)) = − μ(1 − 2Φ(−(−μ)/σ)) because it is symmetric about 0 with respect to μ, and we substitute |μ| for μ and recall that

$$\mu =\frac{r_{AC}^H-r_{BC}^H}{2}:\frac{r_{AC}^H+r_{BC}^H}{2}+\frac{2\sigma }{\sqrt{2\pi }}{e}^{-\frac{{\mu }^2}{2{\sigma }^2}}+\left|\mu \right|\left(1-2\Phi \left(-\frac{\left|\mu \right|}{\sigma }\right)\right)$$ (22)

$$max\left(r_{AC}^H,r_{BC}^H\right)+2\sigma \left({\Phi }^{\prime }\left(\frac{\mu }{\sigma }\right)-\frac{\left|\mu \right|}{\sigma }\Phi \left(-\frac{\left|\mu \right|}{\sigma }\right)\right)$$ (23)

The expected maximum is

$$max\left({\stackrel{‸}{r}}_{AC}^H,{\stackrel{‸}{r}}_{BC}^H\right)=max\left(r_{AC}^H,r_{BC}^H\right)+2\sigma \left({\Phi }^{\prime }\left(\frac{\mu }{\sigma }\right)-\frac{\left|\mu \right|}{\sigma }\Phi \left(-\frac{\left|\mu \right|}{\sigma }\right)\right)$$ (24)

and the bias in the expectation is therefore:

$$2\sigma \left({\Phi }^{\prime }\left(\frac{\mu }{\sigma }\right)-\frac{\left|\mu \right|}{\sigma }\Phi \left(-\frac{\left|\mu \right|}{\sigma }\right)\right)$$ (25)

We show that the bias is positive by proving the following lemma:

$$\text{For}\hspace{0.17em}x\ge 0,\hspace{0.17em}x\Phi \left(-x\right)\le {\Phi }^{\prime }\left(x\right)={\Phi }^{\prime }\left(-x\right):x\Phi \left(-x\right)=x{\int }_{-\infty }^{-x}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}dt$$ (26)

$$\le {\int }_{-\infty }^{-x}-t\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}dt$$ (27)

$$=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}={\Phi }^{\prime }\left(x\right)$$ (28)

$$x\Phi \left(-x\right)\le {\Phi }^{\prime }\left(x\right)={\Phi }^{\prime }\left(-x\right)$$ (29)

$$\frac{\mu }{\sigma }\Phi \left(-\frac{\mu }{\sigma }\right)\le {\Phi }^{\prime }\left(\frac{\mu }{\sigma }\right)={\Phi }^{\prime }\left(-\frac{\mu }{\sigma }\right)$$ (30)

$$2\sigma \left({\Phi }^{\prime }\left(\frac{\mu }{\sigma }\right)-\frac{\left|\mu \right|}{\sigma }\Phi \left(-\frac{\left|\mu \right|}{\sigma }\right)\right)\ge 0$$ (31)

Thus the bias is positive and the expected estimate of the maximum will always be greater than the actual maximum.

Results

Increasing Sample Size

Increasing the size of the HapMap samples will reduce the variance of statistics calculated over the data. Currently a SNP is considered covered by a tag SNP if the r² between the SNP and the tag is greater than 0.8. However, this fails to take into account the minor allele frequency of the SNPs in question, and hence the uncertainty of the HapMap's estimate of the correlation. We derive two analytical distributions for the correlation coefficient and non-centrality parameter in the context of an association study using a finite data set such as the HapMap. The first approximation for correlation coefficient is named σ_S and is a simple approximation which assumes estimates of conditional probability have higher variance than estimates of MAF. The second approximation is named σ_Δ and uses the delta method to avoid this assumption. Our derivations show that SNPs with low minor allele frequencies have a high variance in the estimated correlation coefficient compared to SNPs with higher minor allele frequencies. For example A SNP with MAF 0.05 has a 10.2% chance of having a true r² < 0.8 if its estimated r² is 0.9, while a SNP with MAF 0.15 has only a 1.1% chance.

We use our analytical estimates to produce confidence intervals for the correlation coefficient in order to address this issue and ensure that SNPs we estimate to be captured by a tag set are not missed due to errors from finite sample size. We examine the 95% confidence interval of 0.1 to measure the coverage of tag SNPs. For SNPs with an empirical r² of 0.8 this is the probability that r² < 0.7 is less than 2.5%. For correlation coefficients that fall in this confidence interval, we are confident that the estimated r² is close to the true r². In a sample the size of the HapMap, a tag SNP with MAF of 0.15 requires an estimated r² of 0.95 to lie in this confidence interval, while a tag SNP with MAF 0.3 requires only an estimated r² of 0.91. SNPs with lower minor allele frequencies require higher values of estimated r² before they can be considered good proxies.

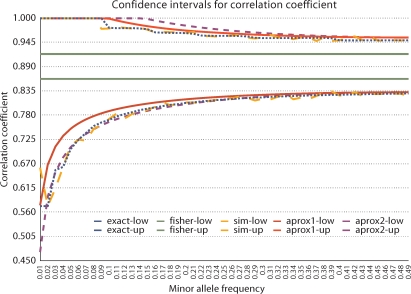
For SNPs in the current HapMap, the sample size is so low that even for SNPs of very high minor allele frequency, we cannot be sure if their true r² falls within a 95% confidence interval of 0.1. We computed the number of chromosomes needed for accurate calculation of r² values near 0.8 over a range of minor allele frequencies using our simple approximation for the variance of the correlation coefficient. Figure 1 shows this approximation is accurate for estimation of the lower bound of a confidence interval. For minor allele frequencies between 0.05 and 0.5 we calculated the number of chromosomes needed to get a variance of 0.0008689 for SNPs with an r² of 0.8. This is the variance required such that the empirical r² has an 95% confidence interval of 0.1. As seen in figure 2, we would need to extend that HapMap to 1003 chromosomes if we wanted accurate estimates of r² for SNPs with minor allele frequency of 0.1. The 1000 genomes project will provide almost twice as many haplotypes as this greatly reducing the error due to finite sample size for a large proportion of SNPs.

Fig. 1.

The 95% confidence intervals for SNPs with r² = 0.8 and N = 200 chromosomes over a range of minor allele frequencies. Confidence intervals are reported for the exact distribution (exact), simulated empirical estimated (sim), Fisher's estimate for correlation coefficients (fisher), our delta methods based estimate (approx1), and our simple estimate (approx2). Our approximations are accurate especially at higher minor allele frequencies.

Fig. 2.

Number of chromosomes required for estimates of correlation coefficient to fall within a 95% confidence interval of 0.1. As the minor allele frequency decreases the number of chromosomes required for accurate estimation increases. Note that the current HapMap is not able to accurately estimate correlation coefficients for any minor allele frequency at its current size.

Effects of Finite Sample Size on Correlation and Power

Figure 3 shows the error in estimation of the correlation coefficient due to the finite size of the HapMap. For a range of MAFs 120 correlated pairs of genotypes are generated 10,000 times and their empirical r² is used to compute the average value of r² in the simulation. The simulations are run with a true value of r² = 0.8. SNPs with low minor allele frequency are much less accurate in determining r² compared to high frequency SNPs. In the context of choosing tag SNPs or follow up SNPs for a case control association study, large numbers of strong tags will have poorly estimated correlation, and many SNPs estimated to have r² > 0.8 will have much weaker true LD.

Fig. 3.

Histogram of empirical estimates of the correlation coefficient from a finite sample of 120 pairs of correlated data. The true value of the correlation coefficient is 0.8. The data are simulated such that both SNPs have minor allele frequency 0.05, 0.1, 0.2, or 0.4. The distributions for SNPs with higher minor allele frequency (c, d), are more tightly clustered and symmetric around 0.8. The distribution for SNPs with low minor allele frequency (a, b), are very wide due to the high variance of the correlation coefficient for such SNPs.

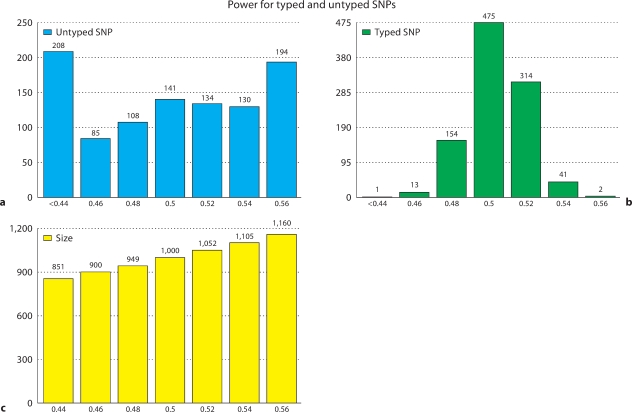
The effect of finite sample size on power estimation is measured by comparing power estimates at genotyped SNPs and untyped SNPs based on simulation over a finite data set. This technique for estimating power is common practice as in the methods of [8, 16]. Case control panels of 1000 cases and 1000 controls are generated from 120 chromosomes with a causal SNP minor allele frequency of 0.1 and relative risk chosen such that the power is exactly 50%. The process is repeated 1000 times and the power computed. This entire power estimation process is then repeated 1000 times and the power of each simulation is recorded as shown in figure 4. This estimate of power at a typed SNP is compared to estimating power at an untyped SNP by repeating the experiment above with a correlated SNP with r² = 0.8 and minor allele frequency of 0.1. Power is measured at the correlated marker and case control status is generated by the original marker. Figure 4 shows the power is more accurately estimated at the typed than untyped SNP. The loss in accuracy is due in large part to the finite sample size of the data in the simulation. We calculated the expected number of individuals required to achieve a range of powers between 44 and 56% in the untyped case and included this histogram in figure 4 for reference. Almost 20% of the untyped SNPs have power overestimated by 6%, which is equivalent to having another 160 individuals in the study.

Fig. 4.

Histograms of power for 1000 simulations of case control studies where the causal SNP is typed (b) or untyped (a). Simulated case control studies were generated by sampling from 120 chromosomes to achieve 1000 cases and 1000 controls. The estimated minor allele frequency of the SNPs were 0.1 and the estimated r² between the typed and untyped SNPs was 0.8. Each of the 1000 power estimates is calculated from 1000 simulated case control studies. The relative risk is chosen such that the simulations at typed and untyped SNPs both have an expected 50% power. The error in power estimation is much higher for the untyped case and leads to severe over and under estimation problems. A histogram of the number of individuals to needed achieve power between 44 and 56% in the untyped simulation is included for reference (c).

We further examine the issue of power estimation by using the WTCCC data [2] and our analytical estimate of power. First we created a set of tag SNPs by selecting all WTCCC SNPs that passed quality control and are found in the HapMap. Then, for each SNP in the HapMap, we found the best tag SNP in our tag set in terms of r². This best tag approach is commonly used to estimate study power. Given a disease model and study size, the power at a HapMap SNP is estimated using its best tag. Given a study size of 2400 cases and 2400 controls, similar to the WTCCC study size, a relative risk of 1.5, and Bonferroni correction factor based on 400,000 SNPs, we measured the probability that the true power of detecting an association at each SNPs was at least 10% less than the estimated power under our simple analytical estimate of the distribution of correlation. We found that over 10% of SNPs have a power at least 10% lower than that estimated under best tag. For example, if the study estimated power for detecting a SNP was 90%, there is a 10% chance that the power is actually ≤81% of detecting that SNP.

Effects of Sample Size on Coverage

Suppose that two SNPs had true correlation coefficients 0.75, but due to the finite size of the HapMap had a variance of 0.01. Then the expected value of the estimated coverage of the third SNP is 0.8. As the number of SNPs considered increases this problem gets worse, and so current estimates of coverage are highly inflated. There exist many different algorithms for selecting tag SNPs which will each potentially result in different levels of estimated coverage. We examine the two SNP case because it is a subproblem used in many tagging algorithms that try and optimize on an r² criterion. In practice the maximization is over many more SNPs and the inflation is therefore even worse. We compared our analytical estimates of this inflation to empirical estimates of the maximum correlation coefficient of 3 SNPs over a range of minor allele frequencies and values of r². The minor allele frequency ranges from 0.1 to 0.5 in increments of 0.1 and the r² ranges from 0.5 to 0.9 in increments of of 0.1. The number of individuals is fixed at 60. The average error did not exceed 0.006 and is therefore accurate.

We use the WTCCC data [2] to examine the inflation of r² in real genotype data. First, we selected 60 individuals from the control population of the WTCCC data set at random. For each SNP in the data set, we found the best r² to that SNP amongst the the 300 most proximal SNPs (i.e. the best tag). We then repeated this procedure with 1000 individuals from the WTCCC control population to measure the overestimation in r² in this population. The results are shown in figure 5. Although the WTCCC SNPs are much less dense than the HapMap there was still significant inflation in the r² values when only 60 individuals are used to estimate r². This is due to the higher variance of the correlation when the sample size is smaller. Amongst SNPs with minor allele frequency between 0.2 and 0.3 over 15% of SNPs have an estimated r² 0.3 greater in the smaller sample size.

Fig. 5.

Overestimation of r² due to finite sample size. We measured r² for the best tag of each SNP in the WTCCC data using 60 then 1000 control individuals. We then measured the difference between these to values. The images show the a histogram over the percentage of SNPs with a given difference in r². In all ranges of minor allele frequency the values of r² over 60 individuals were significantly higher than with 1000 individuals. The difference is greatest amongst the SNPs with minor allele frequency 0.2–0.3. This is most likely due to the greater number of SNPs with minor allele frequency in the range, and hence appearing in the maximization term.

Validation of Analytical Results

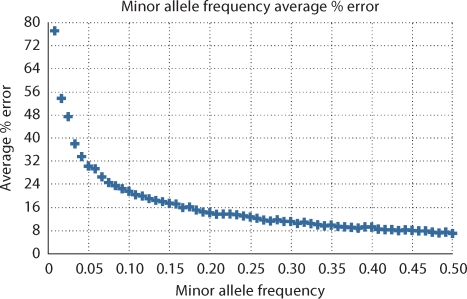
We examine the error in empirical estimates of minor allele frequency and conditional probability due to the finite sample size of the HapMap. Sets of correlated binary random variables were simulated to represent SNP genotypes. In the case of the CEU and YRI HapMap populations, there are 60 unrelated individuals or equivalently 120 chromosomes drawn independently from the population. For a range of MAFs we sample 120 binomial random variables and compute the empirical minor allele frequency $\stackrel{‸}{\text{p}}$_A and the % error ∣$\stackrel{‸}{\text{p}}$_A – p_A∣/p_A. This process is repeated 1000 times to get the average estimated minor allele frequency and the average % error. Figure 6 shows the results of this simulation.

Fig. 6.

The average % error in empirical estimates of minor allele frequency when the sample size is the size of the HapMap. Minor allele frequency error is measured for a given value of MAF by sampling 120 binomial random variables with that MAF and and calculating the % error. This process is repeated 1000 times to get the average error.

We apply a similar procedure to measure the average error in conditional probability estimates due to the finite sample size of the HapMap. We sample 120 pairs of SNPs with a given conditional probability, compute empirical estimates of the frequency and conditional probability from the simulated data, and measure the error. To compute the average error, this process is repeated 1000 times. Figure 7 shows the average error of the conditional probability when the first sampled SNP has a minor allele frequency of 0.05, 0.15, 0.25.

Fig. 7.

The average % error in empirical estimates of conditional probability when the sample size is equivalent to the size of the HapMap. The x-axis shows the true conditional probability, and the y-axis shows the average % error in samples drawn from that distribution 1000 times. Values are given for simulations where the minor allele frequency is 0.05, 0.15, and 0.25. The errors for conditional probability are significantly higher than those for minor allele frequency as shown in figure 6 and contribute greater to the error in estimates of more complicated statistics such as the correlation coefficient and the NCP.

Although these distributions are well known, they are included to demonstrate the substantially larger error of the conditional probability compared to the minor allele frequency. This is due to the lower number of expected observations of the haplotype made from two minor alleles. Consider the case of two SNPs with minor allele frequency 0.1 and conditional probability 0.5. In the HapMap we expect 12 chromosomes with the minor allele for each SNP, but only 6 where both SNPs have the minor allele. Small changes in the sample will therefore have a much larger effect on conditional probability than on minor allele frequency. Our analytical derivations of the distribution of r and NCP given in the Materials and Methods section rely on this relative accuracy of MAF compared to conditional probability. We show empirically that for most values of MAF, our assumption is valid and our estimates are accurate.

We examine the effect of this assumption on our analytical estimates of the mean and variance of the correlation coefficient by sampling correlated binomial random variables and comparing their distribution to the analytical ones we derived. For a range of correlation coefficients and MAFs, 120 pairs of variables were sampled. This was repeated 1000 times to get a mean and variance for the correlation coefficient. Table 1 shows the results. Our analytical predictions of the mean and variance are very close to the results of empirical simulation demonstrating that our approximations are valid. The simple analytical estimate that assumes a correct minor allele frequency estimate is not as accurate for low minor allele frequencies. However, the analytical method based on the delta method accurately estimates mean and variance even for low minor allele frequencies.

Table 1.

Pairs of correlated genotypes were sampled from a distribution with a given correlation coefficient and minor allele frequency as noted in the r² and MAF columns, respectively

r2	MAF	(ινσερτ εϑθατιον)	σΔ	sS	(ινσερτ εϑθατιον)	(ινσερτ εϑθατιον)
0.1	0.1	0.138	0.135	0.143	0.003	0.004
0.1	0.3	0.094	0.093	0.094	0.001	0.001
0.1	0.5	0.087	0.087	0.087	0.001	0.001
0.2	0.1	0.136	0.134	0.146	0.002	0.010
0.2	0.3	0.088	0.089	0.091	0.001	0.003
0.2	0.5	0.080	0.082	0.082	0.001	0.001
0.4	0.1	0.126	0.120	0.137	0.006	0.011
0.4	0.5	0.072	0.071	0.071	0.001	0.001
0.8	0.1	0.071	0.069	0.085	0.002	0.014
0.8	0.3	0.046	0.045	0.048	0.002	0.001
0.8	0.5	0.042	0.041	0.041	0.001	0.001
0.9	0.1	0.050	0.048	0.061	0.001	0.011
0.9	0.3	0.033	0.032	0.034	0.002	0.000
0.9	0.5	0.029	0.029	0.029	0.001	0.001

120 pairs are generated and their empirical correlation coefficients (ινσερτ εϑθατιον) are measured. This process is repeated 1000 times to get the mean and standard deviations of the distribution of the correlation coefficient. We compute the same values using the analytical methods described in the Materials and Methods section to estimate the error in the analytical methods.σ_Δ and $|\stackrel{‸}{\sigma }-{\sigma }_{\Delta }|$ are the estimates of standard deviation and the error in the estimate for the delta method-based estimate respectively. σ_S and $|\stackrel{‸}{\sigma }-{\sigma }_S|$ are the equivalent measurements for the simple analytical estimate. The error is higher for SNPs with low minor allele frequency due to the assumption of a correct minor allele frequency.

We used the genotypes from the Welcome Trust Case Control Consortium [2] in order to examine possible deviations in real genotype data as opposed to the sampled binomial random variables. We computed the correlation coefficient for randomly selected pairs of SNPs using 3008 available individuals. Then, we subsampled random collections of 120 genotypes 10,000 times and computed the mean and variance of these subsets correlation coefficients. Similarly to the case for simulations using binomial random variables, the analytical methods derived in the Materials and Methods section is highly accurate, with an average error of less than 0.001 in estimating the variance. We chose two SNPs rs2381104 and rs4819534 and repeated the experiment with a variety of sample sizes. The results are shown in table 2.

Table 2.

The standard deviation of the correlation coefficient computed over SNPs rs2381104 and rs4819534 in the control population of the welcome trust case control consortium study [2] computed over a range of sample sizes (N)

N	$\stackrel{‸}{\sigma }$	σΔ	crS	$|\stackrel{‸}{\sigma }-{\sigma }_{\Delta }|$	$|\stackrel{‸}{\sigma }-{\sigma }_S|$
60	0.142	0.134	0.153	0.009	0.011
120	0.097	0.095	0.108	0.003	0.011
180	0.079	0.077	0.088	0.002	0.010
240	0.068	0.067	0.077	0.001	0.009
300	0.060	0.060	0.069	0.001	0.008
360	0.055	0.055	0.063	0.000	0.008
420	0.052	0.051	0.058	0.001	0.006
480	0.047	0.047	0.054	0.000	0.007
540	0.045	0.045	0.051	0.000	0.006
600	0.042	0.042	0.048	0.000	0.006

The empirical standard deviation is denoted $\stackrel{‸}{\sigma }$. σΔ and $\left|\stackrel{‸}{\sigma }-{\sigma }_{\Delta }\right|$ are the estimates of standard deviation and the error in the estimate for the delta-method based estimate respectively. σ_S and $\left|\stackrel{‸}{\sigma }-{\sigma }_S\right|$ are the equivalent measurements for the simple analytical estimate. The HapMap sample size of 120 has a much higher high variance for this SNP than the larger sample sizes. The errors are similar to those for simulated binomial random variables, and demonstrate that the assumption of correct minor allele frequency does not affect the accuracy of the analytical values for SNPs when the minor allele frequency is not low.

The analytical estimates derived in the Materials and Methods section assume that the distribution of the correlation coefficient is normal. However genotype data are discrete and the correlation coefficient is discrete. The distribution is therefore not normal and moves further from a normal distribution as r² approaches 1 or the minor allele frequency approaches 0. We measure the utility of our analytical estimates by measuring confidence intervals for the distribution of the correlation coefficient. We estimated the confidence interval for a range of minor allele frequencies when the true r² = 0.8 and N = 200 chromosomes. First we generated all possible contingency tables for pairs of SNPs and measured their probability with Fisher's exact test. This gave us the exact distribution of correlation and exact confidence intervals. Second, we simulated pairs of correlated binomial random variables and recorded their correlation. The 95% confidence intervals were estimated from 10,000 rounds of simulation. Third, we used Fisher's estimate for confidence intervals of the correlation coefficient. The Fisher estimate was not designed for this setting, and does not depend on the minor allele frequency. It is included for reference. Finally, we used our analytical estimates to generate the 95% confidence intervals. Figure 1 shows the results. Surprisingly, the simpler estimate is a more accurate estimate of the lower bound for lower minor allele frequencies. The two estimates converge as the minor allele frequency increases. This is due to the deviation from the normality assumption when minor allele frequency is low. The simpler estimate overestimates the variance (table 1) for low minor allele frequencies in such a way that it more accurately estimates the true confidence intervals.

Discussion

In summary, we derived analytical distributions for the correlation coefficient and non-centrality parameter in the context of an association study design using a finite data set such as the HapMap. We showed via extensive simulation over real and generated data that our distributions very closely followed the true distributions of these statistics in the same context. This permits quick and accurate examination of the effect of sample size on these commonly used measures, and gives the first exploration on the central data set in genome wide association studies (i.e. the HapMap).

Throughout the paper we used a 95% confidence interval of 0.1 and an r² threshold of 0.8. Although somewhat arbitrary, they served as a means to ground the results in a familiar setting. The analytical estimates we derived in this study allow quick and accurate examination of alternative thresholds.

We used our analytical distributions to examine the error of current estimates of LD and power based on the current HapMap. We found that the HapMap at its current size does not provide enough data for accurate estimation of these central statistics. The variance is especially high for SNPs with low minor allele frequency. This error has impact in the field of human disease genetics, especially for researchers conducting genome wide association studies.

In the design phase of an association study, the appropriate number of individuals to achieve desired power cannot be accurately estimated with the current sample for certain SNPs. Although the effect is small for well covered SNPs recent evidence has shown that genome coverage is much worse than currently estimated [15]. This is further hindered by the overestimate of LD in the Affymetrix and Illumina genotyping platforms. We showed that selecting SNPs with maximal r² to find a tag set is heavily upwardly biased. That is, the expected empirical r² under such a procedure is significantly higher than the true r². The current high throughput genotyping platforms utilized hundreds of thousands of such maximizations in selecting their tag SNPs, and therefore, the true average correlation coefficient of these platforms is likely much lower than found by measurement over the HapMap data. This also produces overestimates in power, since the NCPs are linked to r² as described in the Materials and Methods section.

During the analysis phase of an association study, one may select SNPs for follow up based on LD to the tag SNPs found to be significant. The strength of this LD is commonly measured from the HapMap data. As show in figure 3, these estimates have very high variance, and it would not be surprising to have strongly linked SNPs with reported r² < 0.5, or weakly linked SNPs with reported r² > 0.8. Thus, one may incorrectly choose to genotype SNPs without strong LD, and miss SNPs that do have strong LD. Our analytical estimates provide a simple way of estimating errors due to finite sample size so that future association studies may avoid these type of errors.

The HapMap has also been used to estimate global significance levels for genome wide association studies. The finite size of the HapMap as evidenced by the high variance of r² will lead to observed long range LD even though it does not exist. This reduces the effective number of hypotheses being tested, and therefore alters the global significance level for association. Long range LD has also been examined in the HapMap data [17]. Our findings suggest that at least some of the long range LD is expected due to the size of the HapMap.

Increasing the size of the HapMap will improve its utility to researchers working on discovering the genetics basis of human disease. A larger HapMap, such as that proposed by the 1000 genomes project, will address all of the issues described above and provide a foundation for the new and growing high throughput sequencing technology. While genome wide association studies are well powered for common diseases with causes due to common variants, sequencing can examine rare variants. We demonstrated clearly that statistics for SNPs with low minor allele frequency have the greatest variance. If the community decides to make a similar investment for sequence based studies as they did for genotype based studies, a significantly larger number of individuals must be collected.

Table 3.

The overestimation of r² in SNP tagging when taking the maximum of two tag SNPs to cover a third

MAF	r2	mâx	max	err
0.1	0.5	0.595	0.588	0.006
0.1	0.7	0.780	0.781	0.001
0.1	0.9	0.951	0.954	0.003
0.2	0.5	0.566	0.564	0.002
0.2	0.7	0.761	0.760	0.002
0.2	0.9	0.940	0.938	0.001
0.3	0.5	0.561	0.557	0.005
0.3	0.7	0.751	0.751	0.001
0.3	0.9	0.933	0.935	0.002
0.4	0.5	0.549	0.552	0.003
0.4	0.7	0.751	0.747	0.004
0.4	0.9	0.930	0.931	0.001
0.5	0.5	0.547	0.550	0.003
0.5	0.7	0.749	0.746	0.003
0.5	0.9	0.931	0.931	0.000

We generated correlated triples of binomial data such that two tag SNPs had the same minor allele frequency and were associated with a third SNP at the same level of r². 1000 samples of 120 triples were used to estimate the empirical maximum of two SNPs (mˆax), and compared to our analytical formula for the maximum of two SNPs (max). The error (err) is the absolute difference between the empirical and analytical estimates. The inflation of coverage is very significant and suggests that estimates of power based on the best tag for each SNP in the HapMap are overly generous.