Modeling hepatitis C virus kinetics: the relationship between the infected cell loss rate and the final slope of viral decay

Abstract

Background

Patients infected with hepatitis C virus (HCV) who respond to treatment with interferon-α plus ribavirin exhibit biphasic or triphasic viral load declines. While the rapid first phase is indicative of the effectiveness of therapy in blocking viral production, ε, the slope of the final phase, λ, i.e., the second phase in biphasic declines and the third phase in triphasic declines, depends on the infected-cell loss rate, δ. Further, in standard models λ is approximately εδ, when the viral-clearance rate c>>δ as has been previously estimated.

Methods

The relationship among ε, δ, λ and the baseline fraction of HCV-infected hepatocytes, π, was investigated in a model that includes proliferation of hepatocytes.

Results

We find that λ is not proportional to ε but rather obeys complex relationship that can lead to dramatic increases in estimates of δ as ε increases. In particular, when ε<99%, λ moderately underestimates δ in patients with a small π, whereas δ may be up to 10-fold larger than λ in patients with a large π. Interestingly, when ε>99%, δ~λ, regardless of π.

Conclusions

Our results indicate that under therapy achieving <2 log reduction in viral load (ε<99%), previously estimated δ values may represent only a minimal estimate of the infected-cell loss rate. Moreover, combining interferon-α with new antiviral agents to achieve ε>99% should allow for a more accurate estimate of δ in HCV-RNA kinetic studies. This may be important when using viral kinetics to estimate the impact of the immune response on viral elimination and the attainment of sustained virological response.

Approximately 200 million persons are infected with hepatitis C virus (HCV) worldwide and 20% – 30% will likely progress to cirrhosis [1]. Antiviral therapy consisting of pegylated interferon-α (PEG-IFN) and ribavirin achieves sustained virologic response rates (SVR) of ~50% in patients with HCV genotype-1 [2, 3]. There is a compelling need to better understand HCV infection and antiviral therapy in order to optimize the use of interferon-α (IFN) and ribavirin as well as new agents that are in development.

Mathematical models of HCV infection indicate that the final slope of HCV-RNA decay represents the rate of infected cell loss, δ, when the drug effectiveness, ε, is close to 1 [4-6]. However, in models that incorporate the possibility of de-novo hepatocyte infection during therapy or infected cell proliferation this may not be the case as both de novo infection and proliferation of infected cells during therapy reduce the rate of infected cell loss. Therefore, determining the conditions needed in order to estimate, with confidence, δ from the final slope of HCV-RNA decay is the main goal of this communication. To accomplish this goal we explore the relationship among drug effectiveness, the final phase decay slope, the loss rate of infected cells, and the fraction of hepatocytes that are HCV infected at the start of therapy (π) in the context of a kinetic model that allows proliferation of uninfected and infected hepatocytes [5]. The equations describing the dynamics of HCV infection and treatment in this model involve uninfected hepatocytes (T), infected hepatocytes (I) and virus (V), are

$$\begin{array}{c}\frac{dT}{dt}=s+r_T(1-\frac{T+I}{T_{\max }})-d_{T}T-(1-\eta )\beta VT\hfill \\ \frac{dI}{dt}=(1-\eta )\beta VT+r_{I}I(1-\frac{T+I}{T_{\max }})-\delta I\hfill \\ \frac{dV}{dt}=(1-\epsilon )pI-cV.\hfill \end{array}$$ (1)

Uninfected (T) and infected hepatocytes (I) can proliferate with maximum proliferation rates r_T and r_I, respectively, under the control of a homeostatic process in which proliferation shuts down as the total number of hepatocytes, irrespective of whether they are infected or not, approaches a maximum number T_max [7]. Uninfected hepatocytes are also produced by differentiation from precursors at a constant rate s [8], die at rate d_T per cell and are infected with rate constant β. Infected hepatocytes are lost at rate δ per cell. HCV is produced at rate p per infected cell and is cleared at rate c per virion. The efficacy of treatment in blocking virion production and reducing new infections is described by two parameters, ε and η, respectively. For example, a treatment efficacy in blocking virion production of 90% corresponds to ε=0.90. One can combine the drug efficacies into a single term for overall drug effectiveness, ε_tot, where 1 – ε_tot = (1 – η) (−1ε) . However, as explained in the Online Supplementary Material, we make the conservation assumption that η=0 and therefore ε_tot=ε, while ε_tot>ε if η>0. The model’s steady states before and after HCV infection and the baseline fraction of hepatocytes that are HCV-infected, π, are given in the Online Supplementary Material.

We recently introduced the notion of critical drug efficacy, ε_c, for the treatment of HCV [5] and hepatitis B virus [9] analogous to previous efforts in the field of human immunodeficiency virus treatment [10, 11]. For the model given by Eq. (1)

$${\epsilon }_c=1-\frac{c(\delta T_{\max }+r_I({\stackrel{‒}{T}}_0-T_{\max }))}{p\beta T_{\max }{\stackrel{‒}{T}}_0},$$ (2)

where T‾₀ represents the level of uninfected hepatocytes before infection [5,9]. The critical drug efficacy is defined such that if ε ≥ε_c, virus levels continually decline on therapy ultimately leading to eradication, whereas if ε<ε_c viral loads initially decline but ultimately they stabilize at a new steady state despite continued therapy. As shown in sections 2.4 and 3.3 of [4], when ε >ε_c, after an initial rapid first phase viral decline that depends on c and ε (Fig. 1; [6]), and possible transient dynamics such as a shoulder phase (Fig. 1), the viral load ultimately declines in a final phase with slope

$$\lambda =\delta W$$ (3)

where

$$W=[1-\frac{1}{\delta }(\frac{(1-\epsilon )p\beta {\stackrel{‒}{T}}_0}{c}+r_I(1-\frac{{\stackrel{‒}{T}}_0}{T_{\max }}))].$$

One can show that 0 < W < 1, because of the condition ε >ε_c [4]. Thus when ε >ε_c, λ<δ.

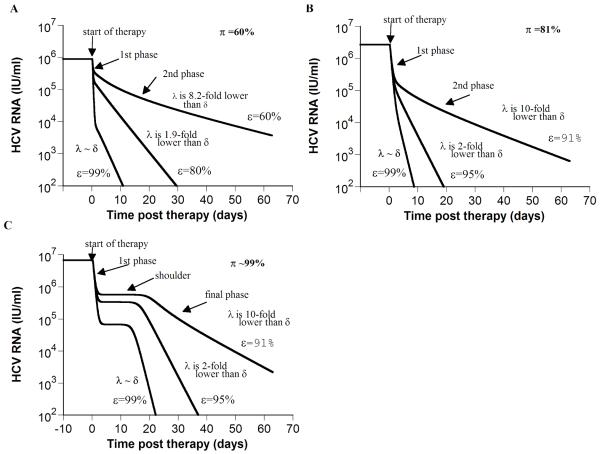
Figure 1. Model predictions of HCV RNA kinetics during successful treatment (ε >ε_c).

If the total drug efficacy, ε, is higher than the critical drug efficacy, ε_c, our model, which includes hepatocyte proliferation [5], predicts two HCV RNA kinetic patterns: biphasic (A and B) and triphasic (C). Using Eq. 3 and parameter values of each in-silico patient, we calculated the theoretical final viral decay slope, λ. In addition, we directly measured from the final phase the viral decline slope (λ_estimated) via linear regression of the kinetic data. When ε is low (i.e., 60% in (A) or 91% in (B and C)), λ ranged from 10-fold to 8-fold lower than δ, and λ_estimated = 0.06, 0.08 and 0.12 day⁻¹, respectively. Whereas when ε =99% λ is close to δ, and λ_estimated = 0.46, 0.85 and 0.84 day⁻¹ in A, B and C, respectively. Note the strong dependence of the final phase slope, λ_estimated, on effectiveness, ε,. e.g., in (B) λ_estimated increases from 0.08 day⁻¹ to 0.85 day⁻¹as ε increases from 91% to 99%. The calculated baseline percentage of hepatocytes that are HCV-infected, π (see Online Supplementary material), is 12%, 90% and 99% in (A), (B) and (C), respectively. Parameter values in (A) are T_max = 7.3 × 10⁶ cells ml⁻¹; d_T = 3.5 × 10⁻³ day⁻¹; δ = 0.47 day⁻¹; β = 5.7 × 10⁻⁷ ml virions⁻¹ day⁻¹; c = 6.0 day⁻¹; p = 1.5 virions cell⁻¹ day⁻¹; r_T = 3.0 day⁻¹; r_I = 0.7 day⁻¹; s = 1 cell day⁻¹ ml⁻¹;ε_c = 55%. With these parameter values T₀ =7.3 × 10⁶ cells ml⁻¹, T̄ =2.4 × 10⁶ cells ml⁻¹, Ī =3.6 × 10⁶ cells ml⁻¹, V̄ =5.95 log₁₀ IU/ml. For both (B) and (C), T_max = 9.8 × 10⁶ cells ml⁻¹; d_T = 1.34 × 10⁻² day⁻¹; δ = 1.0 day⁻¹; β = 8.3 × 10⁻⁷ ml virions⁻¹ day⁻¹; c = 2.4 day⁻¹; p = 2.9 virions cell⁻¹ day⁻¹; r_T = 3.0 day⁻¹; s = 1 cell day⁻¹ ml⁻¹; ε_c = 89.9%, T₀ =9.8 × 10⁶ cells ml⁻¹. As previously explained [5], if we increase the infected cell replication rate – here from r_I = 0.7 day⁻¹ (used in (B)) to r_I = 2.3 day⁻¹ - a shoulder phase emerges in (C). In (B) and (C), T̄ =4.9 × 10⁵ and 0.23 cells ml⁻¹, Ī = 2.2 × 10⁶ and 5.6 × 10⁶ cells ml⁻¹, V̄ = 6.4 and 6.8 log₁₀ IU/ml, respectively.

We examined the relationship among the drug effectiveness, ε, the theoretical final phase slope, λ, δ, and the baseline fraction of infected cells, π, for 1,000 “in-silico” patients with viral kinetic parameters chosen at random within biologically realistic ranges (Online Supplementary Material). We found that when ε<99%, larger π is associated with up to ~10-fold inaccurate estimates of δ (Figs. S1A and S1B). That is, with weak drug effectiveness, HCV production from infected cells slows the decline of HCV RNA and therefore λ represents only a minimal estimate of δ. Further, high π tends to be generated when β, i.e. viral infectivity, is high and/or proliferation of infected cells is high, and hence high π may indicate patients in whom high de-novo infection is occurring during low efficacy treatment. However, when ε>99%, λ/δ is close to 1 irrespective of π (Fig. S1D and S1E). We illustrate our findings for 3 in-silico patients (Fig. 1). In addition, when ε>99% one can estimate δ with good accuracy directly from the final phase viral decline slope (λ_estimated) via linear regression of the kinetic data for both biphasic and triphasic declines (Fig. 1).

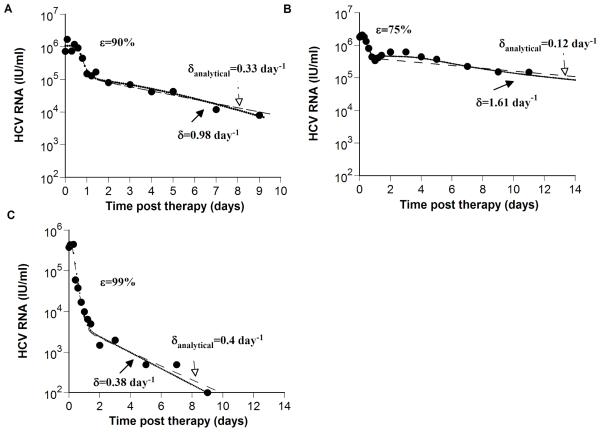
Previous models for HCV dynamics during antiviral therapy do not account for proliferation of both uninfected and infected hepatocytes (see review [12]). Moreover, to explain the biphasic viral decline observed over a short period of time (14 days), Neumann et al. [6] assumed that the target cell population remained constant. This approximation allowed them to solve the biphasic viral decay analytically (Eq. 5 from Neumann et al. [6]). This solution was used to estimate the infected cell loss rate (termed here δ_analytical), as well as other model parameters. We compared (Fig. 2) δ_analytical and δ obtained from fitting the model presented here (Eq. 1) to HCV-RNA decays measured in three patients from Neumann et al [6]. This analysis shows that by including hepatocyte proliferation (Eq. 1), the three patients may have up to approximately 10-fold faster infected cell loss rates than previously estimated by Neumann et al [6] (Figs. 2A-C), thus confirming our in-silico patient analysis. In particular, patient 1B (Fig. 2B) appears to have a triphasic-like decay pattern and analyzing this data with the model presented here (Eq. 1), gives a δ significantly higher than δ_analytical. Interestingly, the ratio δ_analytical/δ gets closer to 1 with higher drug effectiveness, ε (Table 1), as suggested by our analysis of the 10,000 in-silico patients.

Figure 2. Comparison of estimates of δ obtained from models with and without hepatocyte proliferation.

To show that previous estimates of the HCV-infected cell loss rate, δ_analytical, obtained using the Neumann et al. model that does not include hepatocyte proliferation [6], may underestimate δ we examined experimental data (●) of three patients from Neumann et al [6]: (A) patient 3F, (B) patient 1B, and (C) patient 3D. The analytical solution for V(t), i.e., Eq. (4) in Neumann et al. [6], is plotted (dashed lines) using the values given in Table 1 of Neumann et al. [6], for the delay time before viral decay begins, t₀, the interferon-α effectiveness, ε, the viral clearance rate constant, c, and the infected loss rate constant, δ_analytical. Then, we fitted our model (Eq. 1; dotted lines) to the same HCV RNA data (●) with t₀, ε, and c held fixed at the values estimated by Neumann et al. [6], i.e., for (A), (B) and (C), respectively c = 5.8, 6.4 and 6.0 day⁻¹; t₀ = 0.58, 0.33 and 0.21 days, and ε = 0.90, 0.75 and 0.99. In addition, we set T_max = 7.5 × 10⁶ ml⁻¹; d_T = 3.5 × 10⁻³ day⁻¹, s=1 cell ml⁻¹ day⁻¹ and r_T = 3.0 day⁻¹ for all patients and found the best-fit values and corresponding confidence intervals for the parameters p, r_I, β and δ for each patient as explained in Methods. The baseline percentage of hepatocytes that are HCV-infected, π, (see Online Supplementary Material), was estimated as 91%, 99% and 6% in (A), (B) and (C), respectively. Parameter values estimated in (A), (B) and (C), are shown in Table 1. It should be noted that using the F-test or Akaike’s information criterion to compare the fitting results of the analytical model and the extended model with additional parameters describing proliferation we found that there is no statistical support for the extended model (not shown).

Table 1. Parameter estimates obtained by fitting the model to the patient data shown in Figure 2.

Patients (Figure 2)	IFN-α effectiveness in blocking virion production [dose of daily IFN-α] ε (%)	Estimated HCV- infected cell loss rate from Neumann et al. (6) †analytical ± error* (1/day)	Estimated HCV- infected cell loss rate estimated using model that includes hepatocyte proliferation (Eq. 1) δ (1/day) [95% CI]	δanalytical/δ	Estimated baseline percentage of hepatocytes that are HCV- infected** π(%)	HCV-infected cell proliferation rate constant rI (1/day) [95% CI]	Viral production rate p (virions/cell/day) [95% CI]	Viral infection rate β (10−7 mL/virions/day) [95% CI]
A	90% [15 mIU]	0.33 ± 0.03	0.98 [0.43 – 3.1]	0.33	91%	1.2 [0.47 – 3.7]	2.6 [1.2 – 7.9]	17.6 [1.5 – 27.8]
B	75% [5 mIU]	0.12 ± 0.02	1.61 [0.41 – 4.0]	0.08	99%	2.4 [1.5 – 4.8]	5.0 [2.3 – 10.5]	10.6 [1.8 – 13.4]
C	99% [15 mIU]	0.40 ± 0.05	0.38 [0.29 – 0.78]	1.05	6%	0.2 [5.7e-5 – 50]	4.3 [1.7 – 4.7]	0.76 [0.64 – 1.1]

^*Error refers to a 68% confidence interval calculated by a bootstrap method, see (6) for details.

^**π = I‾/T‾(+I‾) , where an over bar denotes a baseline value (calculated by Eq. S2).

Fitting standard models for HCV infection to patients’ HCV-RNA data during treatment with (PEG)-IFN alone or in combination with ribavirin (see review[12]) showed that the estimated infected cell loss rate (δ) is highly variable – from <0.01 day⁻¹ [6] up to 0.49 day⁻¹ [13] (corresponding to infected cells half-lives of ~1.4 days to >70 days). The mean effectiveness of high-daily dose interferon-α (with or without ribavirin), ε, in genotype-1 infected patients, is dose-dependent, ranging from approximately 79% to 99.7% [6]. With PEG-IFN plus ribavirin therapy, the average effectiveness ε is approximately 67%±30% [14] and in HCV/HIV coinfected patients the median weekly average effectiveness of PEG-IFN plus ribavirin was 48% with an interquartile range of 31% [15]. Thus, ε<99% is typical. Above we showed that by including proliferation of uninfected and infected hepatocytes in a model [5], the final phase slope may underestimate δ by as much as 10-fold under low interferon-α efficacies (ε<99%; Figs. 1 and 2). However, when the initial viral drop is greater than 2 log (ε>99%), such as can be achieved with new and highly potent antiviral agents [16], we predict that the final phase slope is close to δ regardless, of π (Fig. S1).

The typical drop of HCV RNA under treatment is biphasic [12]. According to our recent predictions [5], patients who exhibit a biphasic HCV-RNA decay during treatment have a lower percentage of hepatocytes that are HCV-infected, π. Interestingly, while Agnello et al. [17] showed that a high percentage (3% to 83%) of hepatocytes harbor negative-strand HCV RNA (i.e., HCV replicative intermediates) both in HCV-infected patients and chimpanzees, others [18] have found only a low percentage (4% to 25%) in patients with HCV. If indeed, the majority of patients in whom a biphasic pattern is observed have a small π then according to our results (Fig. S1), the estimated HCV-infected cell loss rate, δ_analytical, obtained using the analytical model [6], with ε <99% is close to the actual one (e.g., Fig. 1A, B and 2C) and can reliably be used. It should be noted that in treated patients with ε<99%, better assays to measure the percentage of HCV-infected hepatocytes are needed to estimate the infected cell loss rate with confidence.

A recent report by Neumann et al. [19] indicates that in patients treated with PEG-IFN plus telaprevir, ε>99% and the second-phase slope is significantly higher than previous estimates with (PEG)-IFN alone (or in combination with ribavirin). Our findings (cf., Fig 1) are consistent with this observation and provide a basis for understanding why the second-phase slope in patients treated with new, highly potent antiviral agents is higher than under the standard (PEG)-IFN (with or without ribavirin) therapy.

We have shown that in patients with treatments achieving ε > 99% the final phase slope can be used to accurately estimate the infected cell loss rate. In order to access the role of the immune response in eliminating virally-infected cells accurate estimates of δ are required. Our work shows how these estimates should be attained.