Abstract
The aims of this study were to present a method for developing a path analytic network model using data acquired from positron emission tomography. Regions of interest within the human brain were identified through quantitative activation likelihood estimation meta-analysis. Using this information, a “true” or population path model was then developed using Bayesian structural equation modeling. To evaluate the impact of sample size on parameter estimation bias, proportion of parameter replication coverage, and statistical power, a 2 group (clinical/control) × 6 (sample size: N = 10, N = 15, N = 20, N = 25, N = 50, N = 100) Markov chain Monte Carlo study was conducted. Results indicate that using a sample size of less than N = 15 per group will produce parameter estimates exhibiting bias greater than 5% and statistical power below .80.
Neuroscientists in the field of human functional brain mapping use imaging modalities such as positron emission tomography (PET), transcranial magnetic stimulation (TMS), and functional magnetic resonance imaging (fMRI) to indirectly detect neural activity simultaneously occurring in various regions across the entire brain through metabolic and blood-oxygenation measures. The neural activity occurring within these anatomical regions of interest (ROIs) and their associated causal pathways provide a framework for modeling the covariance structure within the collective system. During data acquisition, the brain is repeatedly imaged while the individual is presented with stimuli or required to perform a task. Spatial variations in signal intensity across the acquired neuroimages reflect differences in brain activity during the presented stimuli or task performance. Statistical analysis of this functional neuroimaging data attempts to establish relationships between the location of activated brain regions and the particular aspect of cognition, perception, or other type of brain functioning being manipulated by the task or stimuli. Generally, this process proceeds by transformation of the data into matrix format with subsequent analyses conducted according to the general linear model (Friston, Holmes, et al., 1995; Holmes, Poline, & Friston, 1997).
Establishing these function–location relationships and uncovering areas of functional dissociation within the cortex has been a primary focus of research, but more investigators are progressing from simple identification of network nodes toward studying the interactions between brain regions. The aim is to understand how sets and subsets of networks function as a whole with the intent of accomplishing specific cognitive goals. Previous studies have analyzed both correlational and covariance structures between brain regions, and techniques for applying structural equation modeling (SEM) to neuroimaging data to investigate connections between brain regions have been under development since 1991 (McIntosh & Gonzales-Lima, 1991, 1994; McIntosh et al., 1994).
Initial application of SEM techniques to functional neuroimaging data was limited to a handful of researchers with advanced statistical backgrounds. In recent years, interest in SEM has increased due to improvements in and accessibility of commercial software and an unavoidable pressing need for the development of methods to test network models and investigate effective connectivity between neuroanatomical regions. Previous studies have applied SEM methods to PET and fMRI data as a means to investigate simple sensory and action processing, such as vision (McIntosh et al., 1994), audition (Gonçalves, Hall, Johnsrude, & Haggard, 2001), and motor execution (Zhuang, LaConte, Peltier, Zhang, & Hu, 2005), as well as higher order cognitive processing, such as working memory (Glabus et al., 2003; Honey et al., 2002), language (Bullmore et al., 2000), and attention (Kondo, Osaka, & Osaka, 2004), and multiple sclerosis (Au Duong et al., 2005). The analytic strategies that researchers conducting these studies have used either posited starting path models a priori based on a single theory alone and then proceeded in a confirmatory manner or an exclusively Bayesian approach to generate optimally weighted network models using little or no prior information. Two shortcomings of these previous studies are that the analytic strategies lack the ability to distinguish from multiple other equally plausible network models, and they did not consider the impact of sample size and its effect on statistical power and parameter estimation bias. To address these issues, we present a two-step approach that uses quantitative activation likelihood estimation (ALE) meta-analysis (Brown, Ingham, Ingham, Laird, & Fox, 2005; Turkeltaub, Guinevere, Jones, & Zeffiro, 2002) for identification of ROIs specific to our research problem in combination with Bayesian SEM to generate a highly informed network model. After model development, we examined issues that previous SEM-based neuroimaging studies have failed to address: sample size, statistical power, and parameter estimation bias. Given that the cost of data acquisition in functional imaging research is very high (e.g., approximately $3,000 per participant), the question of the requisite sample size necessary to model the neural system in a statistically valid and reliable manner is crucial to the ongoing conduct of this work.
The overall aim of functional brain mapping is to determine where and how various cognitive and perceptual processes are controlled in the normal and abnormal (diseased) human brain. In discussing the need for a comprehensive cognitive ontology, Price and Friston (2005) detailed a clear argument for the need for sophisticated network analysis tools. Because there are an immeasurably large number of thought processes that control cognition, perception, action, and interoception, and a finite number of brain regions involved in carrying out these processes, these regions must interact in a highly complex and organized fashion. Determining and characterizing these interactions is a natural and obvious application of SEM. There are advantages to applying SEM to data acquired in human functional brain mapping. For example, in contrast to other fields that utilize SEM methods, such as psychometrics, SEM of functional neuroimaging data involves the analysis of variables that represent actual cortical regions in the brain and path coefficients that reflect actual anatomical and functional connections between these regions. The connections between regions model the interregional covariances between physically remote brain regions. Because researchers know that these regions do not operate independently of each other, SEM or path analysis offers the distinctive ability to model the interrelationships of neural networks. An additional advantage of applying SEM methods to functional neuroimaging data lies in the characteristics of the data itself. Whereas raw neuroimaging image data can demonstrate significant nonnormal characteristics such as skewness and kurtosis, the derived imaging data used in SEM analyses are highly parametric and exhibit a high degree of measurement stability or reliability. This is due to extensive preprocessing procedures such as realignment, spatial normalization, and smoothing techniques (Ashburner & Friston, 1997; Friston, Ashburner, et al., 1995).
In this study, we present a two-step approach for developing a path analytic model using functional imaging data (i.e., PET data were acquired from normal participants or those exhibiting speech dysfunction while performing a reading task) representing regions of interest within the human brain. We then evaluated the impact of sample size on statistical power and parameter estimation bias on the model. The paradigm of speech production was chosen because it represents an extremely rich area of human brain mapping research and one in which the observed results are highly consistent, although highly distributed throughout the brain. Early PET research focused on determining the neural correlates of speech, a language attribute that is uniquely human and thus of great interest to the neuroscientific community (Bookheimer, Zeffiro, Blaxton, Gaillard, & Theodore, 1995; Petersen, Fox, Posner, Mintun, & Raichle, 1988; Price et al., 1994). Indeed, enough research has been published on the neural correlates of speech production to warrant not one but several quantitative meta-analyses of the overt reading paradigm (Brown et al., 2005; Fiez & Petersen, 1998; Fox et al., 2001; Turkeltaub et al., 2002).
The selection of suitable regions of interest and neural pathways in the human brain given the amount of information available to researchers is a challenging task. To meet this challenge, we used quantitative ALE meta-analysis (Brown et al., 2005; Turkeltaub et al., 2002) and Bayesian SEM to develop a “true” or population-based ROI model of speech production based on findings from previous studies. Next, to examine the issues of sample size, statistical power, and parameter estimation bias (i.e., robustness and accuracy), we conducted a Markov chain Monte Carlo (MCMC) simulation study. Additionally, we examined the sensitivity of the model to detect statistical differences in the structural regression weights and intercepts between clinical and normal participants across the sample size conditions. Although the underlying causal mechanisms of the neural correlates of speech in clinical and normal participants was not the focus of this study, we believe that the ability of the analytic strategy to detect statistical differences in structural regression weights and intercepts between these groups provides a potentially powerful analytic tool to aid researchers in their work.
METHOD
Data Acquisition and Participants
The data for this study included PET images from a previous study examining the neural substrates of stuttering (Fox et al., 1996). Data included 10 male participants diagnosed with chronic developmental stuttering (M age = 32.2 years, age range = 21–46 years) and 10 male healthy control participants who were normally fluent (M age = 32.3 years, age range = 22–55 years). All participants gave informed consent according to the approved procedures of the Institutional Review Boards of the University of Texas Health Science Center at San Antonio and the University of California, Santa Barbara. All participants were scanned while they performed three tasks: eyes-closed rest (rest), unaccompanied overt paragraph reading of a text passage (solo), and overt paragraph reading while accompanied by a fluent audio recording of the same paragraph (chorus). Paragraphs for both the solo and chorus conditions were presented on a video display suspended above the participants, approximately 14 in. from the eyes. In the chorus condition, a recording of a nonstutterer reading the same passage was also presented via an earphone inserted into the left ear. Each 40-sec condition was imaged three times in all participants (each participant reading the same text passage on three separate trials); each participant underwent nine PET scans in a counterbalanced order.
PET imaging was performed with a General Electric (Milwaukee, WI) 4906 camera. Brain blood flow was measured with H215O (half-life 123 sec), administered intravenously. Reading commenced at the moment of tracer injection and was stopped after 40 sec of acquisition. Task-induced changes in neural activity were detected as changes in the regional tissue uptake of 15O-water (Fox & Mintun, 1989; Fox, Mintun, Raichle, & Herscovitch, 1984). To optimize spatial normalization of the PET images, anatomical magnetic resonance imaging (MRI) data were acquired for each participants on a 1.9 Tesla Elscint Prestige (Haifa, Israel) using a high-resolution 3D Gradient Recalled Acquisitions in the Steady State (GRASS) sequence: repetition time (TR) = 33 msec, echo time (TE) = 12 msec, flip angle = 60°, voxel size = 1 mm3, matrix size = 256 × 192 × 192, acquisition time = 15 min.
Image Preprocessing and Analysis
Each individual PET scan image was globally normalized by value-normalizing to whole brain mean activity and scaling to an arbitrary mean of 1,000 (Fox, Mintun, Reiman, & Raichle, 1988; Friston et al., 1990; Raichle, Martin, Herscovitch, Mintun, & Markham, 1983). The interscan and intrasubject movement was assessed and corrected in all PET images using the Woods algorithm (Woods, Mazziotta, & Cherry, 1992, 1993). PET and magnetic resonance images were spatially normalized relative to the Talairach and Tournoux (1988) standard brain template using the algorithm of Lancaster et al. (1995). Locations of brain activation were expressed as millimeter coordinates referenced to the anterior commissure as origin, the right, superior, and anterior directions being positive. Data were averaged across trials within each of the three conditions and within the two patient groups, and grand-mean images for solo and chorus conditions were compared to rest for stutterers and controls. Group mean subtraction images (solo–rest and chorus–rest) were converted to Z score images (statistical parametric images of Z scores).
Eight ROIs were extracted from this analysis based on ALE meta-analysis of previously conducted studies corresponding to areas of high brain activation during speech production: left and right primary motor cortex (LM1 and RM1), left and right rolandic operculum (LRO and RRO), left and right auditory cortex (LAUD and RAUD), supplementary motor area (SMA), and cingulate cortex (CING). The coordinates for these regions in Talairach space are presented in Table 1. In an ALE meta-analysis, groups of foci are pooled for convergence in location. This method was created by Turkeltaub et al. (2002), modified by Laird, McMillian, et al. (2005), and has been used with increasing frequency to provide insight on varying patterns of activation across studies in the human brain mapping literature (Fox et al., 2005; Grosbras et al., 2005; Laird, Fox, et al., 2005; McMillian, Laird, Witt, & Meyerand, 2007; Owen, McMillian, Laird, & Bullmore, 2005; Price & Friston, 2005).
TABLE 1.
Region of Interest (ROI) Coordinates
| Brain Region | X | Y | Z |
|---|---|---|---|
| Left primary motor cortex (LM1) | −46 | −10 | 40 |
| Right primary motor cortex (RM1) | 54 | −10 | 36 |
| Left rolandic operculum (LRO) | −54 | −8 | 20 |
| Right rolandic operculum (RRO) | 54 | −8 | 20 |
| Supplementary motor area (SMA) | 4 | −2 | 58 |
| Cingulate cortex (CING) | −6 | 8 | 40 |
| Left auditory cortex (LAUD) | −56 | −14 | 4 |
| Right auditory cortex (RAUD) | 56 | −26 | 2 |
Note. Networks nodes were selected from the image data obtained from healthy control participants. The center of mass of each ROI is presented here as a stereotactic coordinate in a standard brain template in Talairach space (Talairach & Tournoux, 1988). The ROIs extended 5 mm in each direction from the center of mass. Positron emission tomography counts of regional cerebral blood flow were averaged from the voxels in the ROIs from the rest, solo, and chorus conditions from each of the three repeated trials.
Data Screening and Development of Region of Interest Variables
A total of 180 observations across 10 participants (3 trials or repeated measurements × 3 imaging conditions × 10 participants × 2 groups: 1 clinical and 1 control) in 8 ROIs constituted the raw data matrix for both the clinical and control groups. In both groups, there were no missing data points in the matrices and the assumption of univariate and multivariate normality was found to be tenable according to univariate z statistics (± 1.96) and Mardia’s (1970) multivariate criteria.
Prior to deriving the composite ROI variables, we examined the data according to the following psychometric and statistical criteria: (a) autoregressive properties of the three trials or repeated measurements for each ROI averaged across scan condition, (b) the interaction effect between scan condition and trial within each ROI, and (c) the measurement and structural properties of each ROI by specifying eight separate correlated-error measurement models. First we examined the autoregressive properties of the three repeated measurements for each ROI by fitting general Markov and stationary Markov (lag-2 and lag-3 time effects) models as a function of each successive measurement within each respective ROI, plus a random error component (Arbuckle, 1996; Wothke, 2000). Because the general Markov and stationary Markov models are hierarchically nested, chi-square difference tests were conducted for each ROI to determine the existence of a lag-2 or lag-3 time effect. In all eight ROIs, the stationary Markov model was rejected, indicating the presence of a lag-1 time effect across the successive measurements. Based on the results of these tests, aggregated composite variables were created (Bagozzi & Edwards, 1998) using the three correlated measurements obtained for each ROI using a weighting scheme that incorporated the lag-1 time effect.
Second, to examine the interaction between scan condition and trial within each ROI, eight univariate analyses of variance were conducted. No statistical interaction between scan condition and trial was observed for either the clinical or control groups.
Finally, we examined the measurement and structural properties for each ROI by regressing each region on the three repeated measurements (averaging over scan conditions) for a particular region. For the eight regions of interest, each measurement model exhibited excellent fit to the data. In each ROI, we screened the data based on the recommendation of Hoyle and Kenny (1999), that prior to deriving the ROI composite variables, the reliability coefficients of each of the ROI composites should be equal to or greater than .90. Hoyle and Kenny (1999, p. 202) noted that this screening step is particularly critical in composite variable path analytic models that include mediator variables and sample sizes of less than 100 to minimize the impact of measurement error on parameter estimates and statistical power.
After screening and evaluating the requisite assumptions for using an aggregated composite variable path analytic approach, our derivation of the ROI variables proceeded by adhering to the conventions presented in McDonald (1996). McDonald’s criteria for using composite variables within the SEM framework are (a) the variables are “random” (e.g., in this study the data captured using PET scans were obtained from participants in a true experimental setting), (b) a random composite variable is a function (e.g., an optimally weighted sum in this case) of component random variables if and only if each of its components is observable, and (c) each of the ROI composite variables is represented as a “block.” An observed (composite) variable approach, rather than a latent variable approach, was used in this study for the following reasons. First, we were limited to three measurements on each ROI for only 10 participants in each study group. Second, because the ROIs of interest are existing anatomical structures within the human brain, an observed variable approach is logical and provided a parsimonious approach to our model development. Third, the process for investigating and modeling the correlated structure of the three repeated measurements on each participant was more parsimonious. Finally, the reliability of each ROI composite variable was greater than .90, thereby making any gains by correcting for attenuation of measurement error using a latent variable approach negligible.
Population Model Development Using Bayesian SEM
The history and development of Bayesian statistical methods are substantial and closely related to frequentist statistical methods. In fact, Gill (2002) noted that the fundamentals of Bayesian statistics are older than the current dominant paradigms. In some ways, Bayesian statistical thinking can be viewed as an extension of the traditional (i.e., frequentist) approach, in that it formalizes aspects of the statistical analysis that are left to uninformed judgment by researchers in classical statistical analyses. In the Bayesian modeling approach, researchers view any unknown quantity (e.g., parameter) as random and these quantities are assigned a probability distribution (e.g., normal, Poisson, multinomial, geometric, etc.) that provides the impetus for generating a particular set of data at hand. In this study, our unknown population parameters were modeled as being random and then assigned to a joint probability distribution. In this way, we were able to summarize our current state of knowledge regarding the model parameters. At present, the sampling-based approach to Bayesian estimation provides a solution for the random parameter vector θ by estimating the posterior density or distribution of a parameter. This posterior distribution is defined as the product of the likelihood function (accumulated over all possible values of θ) and the prior density of θ (Lee & Song, 2004). The process of Bayesian statistical estimation approximates the posterior density or distribution of say, y, p(θ|y) ∝ p(θ)L(θ|y) where p(θ) is the prior distribution of θ, and p(θ|y) is the posterior density of θ given y. This expression exemplifies the principle that updated knowledge results from combining prior knowledge with the actual data at hand. Finally, Bayesian sampling methods do not rely on asymptotic distributional theory and therefore are ideally suited for investigations in which small sample sizes are common (Ansari & Jedidi, 2000; Dunson, 2000; Scheines, Hoijtink, & Boomsma, 1999).
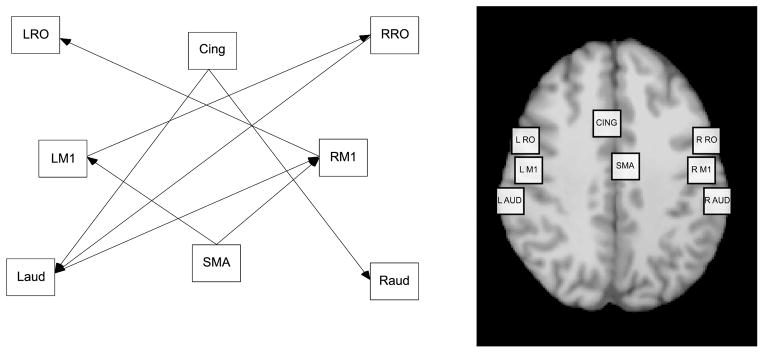
Development of our ROI population model proceeded by specifying the scheme of relations among the ROIs within the brain, as presented in Figure 1. The ROIs used in Figure 1 were selected based on the results of ALE meta-analysis of previous studies investigating the neural correlates of speech. The direction and scheme of the paths illustrated in Figure 1 were posited based on a theoretically plausible neural activation network scheme derived from ALE meta-analysis and then verified by conducting a Bayesian SEM specification search algorithm.
FIGURE 1.
Region of interest path model.
The model in Figure 1 served as the baseline for Bayesian estimation of the model parameters using the MCMC methodology (i.e., Metropolis–Hastings algorithm) and Gibbs sampling (Geman & Geman, 1984). The estimation process proceeded by using centered parameterization, allowing the composite ROI variables to have free intercepts and variances and diffuse (noninformative) uniform priors for the vector of parameters, including the variance components. Although the conceptual design of our path model (i.e., ROIs and regression paths) was informed by ALE meta-analysis, we used a noninformative normal prior distribution for structural regression weights and variance components to prevent the possible introduction of parameter estimation bias due to potential for poorly selected priors (Jackman, 2000; Lee, 2007, p. 281). We followed guidelines offered by Raftery and Lewis (1992) in determining the selection of the number of MCMC burn-in iterations with respect to establishing the convergence criteria for the joint posterior distribution of the model parameters. Based on a review of convergence diagnostics, we selected a burn-in sample of N = 1,000 and the convergence criterion for acceptable posterior distribution summary estimates of parameters was set at 1.001. Additionally, we examined the posterior distribution by evaluating time series and autocorrelation plots to judge the behavior of the MCMC convergence. In both instances, the plots revealed no abnormalities regarding the performance of the MCMC method. Bayesian estimation (incorporating the MCMC algorithm) of the model parameters was conducted using the Bayesian SEM facility in the Analysis of Moment Structures 6.0 (AMOS; Arbuckle, 2005) computer program. Table 2 provides the means, standard deviations, and lower and upper 95% credible intervals for the standardized regression weights estimated for the baseline population model.
TABLE 2.
Posterior Summary of Bayesian Estimates (N = 100,000 Analysis Samples)
| Control |
Clinical |
|||||||
|---|---|---|---|---|---|---|---|---|
| Credible Interval |
Credible Interval |
|||||||
| Regression Path | M | SD | 95% LL | 95% UL | M | SD | 95% LL | 95% UL |
| LRO ← RM1 | .45 | 0.15 | 0.05 | 0.65 | .54 | 0.12 | 0.29 | 0.76 |
| LAUD ← CING | .38 | 0.13 | 0.11 | 0.65 | .18 | 0.18 | −0.16 | 0.54 |
| RAUD ← CING | .22 | 0.19 | −0.19 | 0.60 | .41 | 0.15 | 0.10 | 0.70 |
| RRO ← LM1 | .22 | 0.38 | −0.56 | 0.98 | .54 | 0.09 | 0.34 | 0.72 |
| LM1 ← SMA | .13 | 0.11 | −0.09 | 0.35 | .36 | 0.17 | 0.02 | 0.69 |
| RM1 ← SMA | .39 | 0.15 | 0.08 | 0.71 | .53 | 0.15 | 0.22 | 0.84 |
| LAUD ← RRO | .62 | 0.18 | 0.25 | 1.00 | .30 | 0.12 | 0.06 | 0.54 |
| RM1 ← LAUD | .41 | 0.22 | −0.06 | 0.82 | .14 | 0.14 | −0.13 | 0.42 |
Note. Mean is an estimate obtained by averaging across the random samples produced by the Markov chain Monte Carlo procedure. SD is analogous to the standard deviation in maximum likelihood estimation. LL = lower limit; UL = upper limit; LRO = left rolandic operculum; RM1 = right primary motor cortex; LAUD = left auditory cortex; CING = cingulate cortex; RAUD = right auditory cortex; RRO = right rolandic operculum; LM1 = left primary motor cortex; SMA = supplementary motor area.
Monte Carlo Study
MCMC-based simulation provides an empirical basis that allows researchers to observe the behavior of a given statistic or statistics across a particular number of random samples. A particular strength of conducting an MCMC simulation in this study is that we can examine specific methodological questions that otherwise would be either impossible or restrictively expensive to answer. Our simulation investigation focused on examining the impact of sample size on the accuracy (i.e., parameter estimation bias) and statistical power of the model to recover the baseline parameter estimates for the control and clinical groups. Accordingly, we proceeded by generating data for the variables in our model using a multivariate normal distribution for each of the following six sample sizes for both clinical and control groups: (a) N = 10, (b) N = 15, (c) N = 20, (d) N = 25, (e) N = 50, and (f) N = 100. This 6 (sample size) × 2 (group) design resulted in 12,000 data sets each of size 1,000. For all simulations, the internal Monte Carlo facility within Mplus version 4.2 was used to derive maximum likelihood parameter estimates with robust standard errors (i.e., the MLR option; Muthén & Muthén, 2005, p. 268). Parameter estimates derived from the baseline model for each respective study group then served as the population starting values.
RESULTS
Table 3 provides a summary of the fit statistics obtained from the 1,000 MCMC simulations across each level of sample size by control and clinical groups. At a sample size of N = 10, for both groups, the chi-square was rejected at the α = .001 level, indicating that the model did not display acceptable fit to the data. Across sample size levels of N = 15 and greater, for both groups the chi-square was not rejected at the α = .05 level, indicating an acceptable level of overall fit of the model to the data. Furthermore, at sample sizes of N = 25 and larger, both groups displayed acceptable root mean squared error of approximation (RMSEA) point estimates (.08 or less) as recommended by Steiger (1990); however, examination of the 95% confidence intervals (CIs) reveals the possibility that, in the population, RMSEA values of greater than .08 can exist at samples sizes below 100.
TABLE 3.
Monte Carlo Fit Statistics Summary
| Sample Size | χ2 | df | p | AIC | BIC | RMSEA | RMSEA 95% CI |
|---|---|---|---|---|---|---|---|
| Control group | |||||||
| 10a | 43.54 | 18 | < .001 | 1,021.59 | 1,027.94 | 0.35 | 0.0–.52 |
| 15 | 28.92 | 18 | .05 | 1,622.49 | 1,537.25 | 0.17 | 0.0–.37 |
| 20 | 25.07 | 18 | .12 | 2,158.73 | 2,114.90 | 0.12 | 0.0–.28 |
| 25 | 22.75 | 18 | .20 | 2,695.33 | 2,655.81 | 0.08 | 0.0–.22 |
| 50 | 20.04 | 18 | .33 | 5,378.90 | 5,353.14 | 0.04 | 0.0–.13 |
| 100 | 19.08 | 18 | .38 | 10,748.41 | 10,736.79 | 0.03 | 0.0–.08 |
| Clinical group | |||||||
| 10a | 44.68 | 18 | < .001 | 1,022.67 | 1,029.02 | 0.36 | 0.0–.52 |
| 15 | 28.25 | 18 | .06 | 1,529.70 | 1,480.46 | 0.17 | 0.0–.34 |
| 20 | 25.07 | 18 | .12 | 2,038.86 | 1,995.03 | 0.12 | 0.0–.28 |
| 25 | 23.09 | 18 | .18 | 2,543.73 | 2,504.21 | 0.08 | 0.0–.23 |
| 50 | 20.25 | 18 | .32 | 5,076.53 | 5,050.77 | 0.04 | 0.0–.13 |
| 100 | 18.47 | 18 | .42 | 10,139.80 | 10,128.19 | 0.02 | 0.0–.08 |
Note. AIC = Akaike Information Criterion; BIC = Bayes Information Criterion; RMSEA = root mean squared error of approximation.
Indicates that the fit of the model was rejected at a sample size of N = 10 across 1,000 replication trials.
Table 4 provides the true population parameters and the MCMC-generated average parameter estimates across replications by each level of sample size for the control and clinical groups. At a sample size of N = 10, for the normal group, three out of eight path loadings displayed parameter estimation bias of greater than 5%, and one out eight paths displayed an estimation bias greater than 10%. Specifically, in the normal group, a pattern of estimation bias greater than 5% was observed for the CING to RAUD, SMA to LM1, and SMA to RM1 paths at a sample size of N = 10. In the clinical group, N = 10 sample size, one out of eight paths (i.e., CING to LAUD) displayed parameter estimation bias greater than 5%. Across sample sizes of N = 15 or greater for both groups, no more than two parameter estimates presented a level of bias greater than 3%. Specifically, in the clinical group, a pattern of estimation bias greater than 3% was observed for the CING to LAUD path at a sample size of 25 or smaller. Alternatively, in the control group, a pattern of estimation bias greater than 3% was observed for the LM1 to RRO path at all sample size conditions.
TABLE 4.
Parameter Estimates and Estimation Bias of Path Loadings by Sample Size
| Path | Sample Size |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 |
15 |
20 |
||||||||||
| Contl | Pop | Clin | Pop | Contl | Pop | Clin | Pop | Contl | Pop | Clin | Pop | |
| LRO ← RM1 | .45 | .45 | .56 | .54 | .45 | .45 | .54 | .54 | .45 | .45 | .54 | .54 |
| LAUD ← CING | .37 | .38 | .19b | .18 | .37 | .38 | .19a | .18 | .38 | .38 | .19a | .18 |
| RAUD ← CING | .24b | .22 | .40 | .41 | .22 | .22 | .41 | .41 | .22 | .22 | .41 | .41 |
| RRO ← LM1 | .26c | .22 | .54 | .54 | .23a | .22 | .54 | .54 | .21a | .22 | .54 | .54 |
| LM1 ← SMA | .14b | .13 | .36 | .36 | .13 | .13 | .36 | .36 | .14a | .13 | .36 | .36 |
| RM1 ← SMA | .41b | .39 | .52 | .53 | .38 | .39 | .53 | .53 | .39 | .39 | .53 | .53 |
| LAUD ← RRO | .61 | .62 | .30 | .30 | .61 | .62 | .30 | .30 | .62 | .62 | .30 | .30 |
| RM1 ← LAUD | .41 | .41 | .14 | .14 | .40 | .41 | .14 | .14 | .41 | .41 | .14 | .14 |
| Path |
Sample Size |
|||||||||||
|
25 |
50 |
100 |
||||||||||
| Contl | Pop | Clin | Pop | Contl | Pop | Clin | Pop | Contl | Pop | Clin | Pop | |
| LRO ← RM1 | .45 | .45 | .55 | .54 | .45 | .45 | .55 | .54 | .45 | .45 | .54 | .54 |
| LAUD ← CING | .38 | .38 | .17a | .18 | .38 | .38 | .17a | .18 | .38 | .38 | .18 | .18 |
| RAUD ← CING | .21a | .22 | .41 | .41 | .21a | .22 | .41 | .41 | .21a | .22 | .41 | .41 |
| RRO ← LM1 | .21a | .22 | .54 | .54 | .23a | .22 | .54 | .54 | .23a | .22 | .54 | .54 |
| LM1 ← SMA | .14 | .13 | .36 | .36 | .13 | .13 | .36 | .36 | .13 | .13 | .36 | .36 |
| RM1 ← SMA | .39 | .39 | .53 | .53 | .39 | .39 | .53 | .53 | .39 | .39 | .53 | .53 |
| LAUD ← RRO | .62 | .62 | .30 | .30 | .62 | .62 | .30 | .30 | .62 | .62 | .30 | .30 |
| RM1 ← LAUD | .41 | .41 | .14 | .14 | .40 | .41 | .15 | .14 | .40 | .41 | .14 | .14 |
Note. Contl = control group Monte Carlo estimates; Clin = clinical group Monte Carlo estimates; Pop = population parameters; LRO = left rolandic operculum; RM1 = right primary motor cortex; LAUD = left auditory cortex; CING = cingulate cortex; RAUD = right auditory cortex; RRO = right rolandic operculum; LM1 = left primary motor cortex; SMA = supplementary motor area.
Bias greater than 3%.
Bias greater than 5%.
Bias greater than 10%.
Table 5 provides the average standard errors across 1,000 replications, estimates of statistical power, and the 95% coverage proportions obtained from the MCMC analyses by level of sample size. In Tables 3 and 4, at all control and clinical group sample sizes, parameter estimates of path loadings flagged as having a bias of greater than 3%, 5%, and 10% are displayed. Table 5 provides the standard errors of parameter estimates, statistical power, and the proportion of replications for which the 95% CI contains the true population parameter. At a sample size of N = 25 participants per group or less, in both groups, statistical power dropped below .80 in five out of eight paths.
TABLE 5.
Standard Errors and Statistical Power for Parameter Estimates of Path Loadings by Sample Size
| Path | Sample Size |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 |
15 |
20 |
||||||||||||||||
| Contl | 1 – β | 95% CI | Clin | 1 – β | 95% CI | Contl | 1 – β | 95% CI | Clin | 1 – β | 95% CI | Contl | 1 – β | 95% CI | Clin | 1 – β | 95% CI | |
| LRO ← RM1 | .15 | .76 | .81 | .25 | .60 | .81 | .13 | .85 | .86 | .21 | .67 | .87 | .11 | .95 | .91 | .19 | .78 | .90 |
| LAUD ← CING | .14 | .70 | .80 | .38 | .22 | .80 | .16 | .82 | .92 | .32 | .16 | .89 | .14 | .92 | .90 | .19 | .38 | .92 |
| RAUD ← CING | .20 | .34 | .80 | .31 | .35 | .80 | .17 | .31 | .90 | .26 | .38 | .88 | .15 | .34 | .90 | .23 | .47 | .88 |
| RRO ← LM1 | .46 | .15 | .88 | .27 | .65 | .87 | .37 | .13 | .91 | .18 | .80 | .91 | .33 | .13 | .92 | .16 | .88 | .92 |
| LM1 ← SMA | .14 | .24 | .87 | .39 | .21 | .88 | .11 | .26 | .92 | .32 | .25 | .92 | .09 | .33 | .92 | .27 | .29 | .92 |
| RM1 ← SMA | .16 | .68 | .84 | .34 | .40 | .82 | .13 | .75 | .90 | .28 | .50 | .90 | .12 | .88 | .91 | .24 | .56 | .91 |
| LAUD ← RRO | .19 | .79 | .82 | .26 | .30 | .84 | .16 | .92 | .90 | .21 | .34 | .89 | .14 | .97 | .90 | .19 | .38 | .92 |
| RM1 ← LAUD | .22 | .49 | .84 | .30 | .19 | .83 | .18 | .57 | .90 | .25 | .15 | .88 | .16 | .69 | .90 | .21 | .14 | .91 |
| Path |
Sample Size |
|||||||||||||||||
|
25 |
50 |
100 |
||||||||||||||||
| Contl | 1 – β | 95% CI | Clin | 1 – β | 95% CI | Contl | 1 – β | 95% CI | Clin | 1 – β | 95% CI | Contl | 1 – β | 95% CI | Clin | 1 – β | 95% CI | |
| LRO ← RM1 | .10 | .96 | .91 | .16 | .88 | .91 | .07 | 1.00 | .93 | .12 | .98 | .94 | .05 | 1.00 | .94 | .08 | 1.00 | .95 |
| LAUD ← CING | .12 | .13 | .91 | .17 | .42 | .91 | .06 | 1.00 | .95 | .18 | .19 | .94 | .06 | 1.00 | .94 | .08 | 0.91 | .94 |
| RAUD ← CING | .14 | .92 | .92 | .21 | .50 | .92 | .10 | 0.56 | .94 | .15 | .75 | .94 | .07 | 0.86 | .94 | .10 | 0.97 | .94 |
| RRO ← LM1 | .29 | .74 | .92 | .14 | .94 | .92 | .21 | 0.23 | .93 | .10 | 1.00 | .94 | .14 | 0.32 | .94 | .07 | 1.00 | .96 |
| LM1 ← SMA | .08 | .35 | .92 | .25 | .33 | .92 | .06 | 0.58 | .96 | .17 | .53 | .94 | .04 | 0.85 | .94 | .12 | 0.80 | .94 |
| RM1 ← SMA | .10 | .91 | .90 | .22 | .66 | .90 | .07 | 1.00 | .94 | .15 | .91 | .94 | .05 | 1.00 | .94 | .11 | 1.00 | .94 |
| LAUD ← RRO | .12 | .99 | .91 | .17 | .42 | .91 | .09 | 1.00 | .95 | .12 | .68 | .94 | .06 | 1.00 | .94 | .08 | 0.91 | .94 |
| RM1 ← LAUD | .15 | .74 | .90 | .20 | .14 | .90 | .10 | 0.95 | .95 | .14 | .19 | .93 | .07 | 1.00 | .93 | .10 | 0.29 | .95 |
Note. Contl = control group Monte Carlo estimates; Clin = clinical group Monte Carlo estimates; 1 – β = power of statistical power to recover population parameters; 95% CI = proportion of replications for which the 95% confidence interval contains the true population parameter value; LRO = left rolandic operculum; RM1 = right primary motor cortex; LAUD = left auditory cortex; CING = cingulate cortex; RAUD = right auditory cortex; RRO = right rolandic operculum; LM1 = left primary motor cortex; SMA = supplementary motor area.
Finally, the tenability of the model to detect statistical differences between the groups related to their structural regression (path) weights and structural intercepts (means) yielded positive results. Simultaneous estimation of the model with both clinical and normal participants at sample size conditions of N = 15 or greater provided evidence that the modeling approach was sensitive to detecting statistical differences between the clinical and normal groups of participants. Specifically, differences at p < .001 were observed in the structural regression weights and structural intercepts between the clinical and normal participants at a sample size of N = 15 participants per group and greater.
DISCUSSION AND CONCLUSIONS
The aims of this study were to develop and test a path analytic model using functional imaging data representing regions of interest within the human brain, and to evaluate the performance of the model (i.e., parameter estimates, standard errors, and statistical power) across different sample size conditions. Using ALE and Bayesian SEM, we developed a baseline model that exhibited excellent fit to the empirical data in both the normal and clinical groups. Using our baseline model, we then evaluated the performance of the model in both groups using a Monte Carlo simulation study. Specifically, we examined the impact of sample size on the performance of the model to recover baseline model parameter estimates with an acceptable level of statistical power (.80 or greater) and with a minimal level (< 3%) of parameter estimation bias.
At a sample size of N = 10, in the normal group, three of eight path loadings displayed biased parameter estimates at a level greater than 5%, and one of the eight paths displayed a parameter estimation bias of greater than 10%. In the clinical group, at a sample size of N = 10, one of the eight path loadings displayed a parameter estimation bias of greater than 5%. This information is particularly important to the neuroscience community involved in functional imaging research in which the cost of data acquisition and analysis is high (e.g., approximately $3,000 per participant) and participant sample sizes are often below N = 20. At a sample size of N = 15, for both normal and clinical groups, only one out of eight path loadings displayed a bias in parameter estimation greater than 3%. Furthermore, in the N = 15 sample size condition, the proportion of replication trials for which the 95% CI contained the true population parameters and associated standard errors ranged from 86% to 96% (i.e., 860–960 replication samples). Importantly, statistical power was observed as being below .80 (i.e., between .15 and .79) in all eight estimated regression weights (representing paths) for both groups in the sample size (N = 10) condition. Statistical power was observed as being below .80 in five out of the eight estimated paths for the control group and seven out of eight for the clinical group in the sample size (N = 15) condition. Statistical differences (p < .001) were observed in ROI neural activity in the network and within the ROIs for the structural regression weights and structural intercepts between the clinical and normal participants at sample size conditions of N = 15 participants per group and greater.
We have presented a two-step analytic approach for modeling effective connectivity among anatomic regions within the human brain using data acquired using PET. Importantly, the results of methodological-oriented neuroimaging analytic studies such as ours are of interest to the neuroscience community, in which the ongoing conduct of imaging research is crucial to an increased theoretical and applied understanding of neural systems, yet the cost of conducting such work is very high. The aims of our study were (a) to provide researchers with a highly informed approach to model the human neural system that uses ALE meta-analysis and Bayesian SEM, and (b) to evaluate the derived model regarding the impact of different sample size conditions on statistical power and parameter estimation bias. Importantly, the results from this research will aid researchers in developing informative models and most important, for planning appropriately for adequate sample sizes to ensure reliable and valid results. Our findings illustrate that the ALE/SEM-based approach performed well at sample sizes as small as N = 15 for both speech-impaired and normal participants. Below a sample size of N = 15, statistical power dropped substantially below .80 in seven out of eight regression weights (i.e., statistical power ranged from a low of .15 to a high value of .79 at a sample size of N = 10 in both groups), and parameter estimation bias increased above 5% in seven out of eight paths, and above 10% in 1 out of 10 paths in the clinical group. Based on these findings, we do not recommend using sample sizes less than 15 participants per analytic group. Although the primary aims of our study did not include examining the sensitivity of the model to detect statistical differences between the normal and clinical groups, we believe that the ability of the modeling approach to detect statistical differences in structural regression weights and intercepts between these groups provides a potentially powerful analytic tool to aid researchers in their work.
In summary, the two-step approach of using ALE meta-analysis and Bayesian SEM to develop a path model for investigating the effective connectivity of neural systems in humans appears to be a viable strategy at sample sizes as small as N = 15 participants per group. Ultimately, we believe that the results of our work will aid neuroscientists and cognitive researchers in designing SEM-based studies to evaluate and test complex network models using dynamic neuroimaging data.
Contributor Information
Larry R. Price, Texas State University–San Marcos
Angela R. Laird, University of Texas Health Science Center at San Antonio, Research Imaging Center
Peter T. Fox, University of Texas Health Science Center at San Antonio, Research Imaging Center
Roger J. Ingham, Department of Speech and Hearing Sciences, University of California–Santa Barbara
References
- Ansari A, Jedidi K. Bayesian factor analysis for multilevel binary observations. Psychometrika. 2000;64:475–496. [Google Scholar]
- Arbuckle JL. Full information estimation in the presence of incomplete data. In: Marcoulides GA, Schumacker RE, editors. Advanced structural equation modeling: Issues and techniques. Mahwah, NJ: Lawrence Erlbaum Associates, Inc; 1996. pp. 243–277. [Google Scholar]
- Arbuckle JL. AMOS version 6.0 [Computer program] Chicago: SPSS; 2005. [Google Scholar]
- Ashburner J, Friston KJ. Spatial transformation of images. In: Frackowiak RSJ, Friston KJ, Frith C, Dolan R, Mazziotta JC, editors. Human brain function. New York: Academic Press; 1997. pp. 43–58. [Google Scholar]
- Au Duong MV, Boulanouar K, Audoin B, Treseras S, Ibarrola D, Malikova I, et al. Modulation of effective connectivity inside the working memory network in patients at the earliest stage of multiple sclerosis. Neuroimage. 2005;24:533–538. doi: 10.1016/j.neuroimage.2004.08.038. [DOI] [PubMed] [Google Scholar]
- Bagozzi R, Edwards J. A general approach for representing constructs in organization research. Organizational Research Methods. 1998;1(1):45–87. [Google Scholar]
- Bookheimer SY, Zeffiro TA, Blaxton T, Gaillard WD, Theodore WH. Regional cerebral blood flow during object naming and word reading. Human Brain Mapping. 1995;3:93–106. [Google Scholar]
- Brown S, Ingham RJ, Ingham JC, Laird AR, Fox PT. Stuttered and fluent speech production: An ALE meta-analysis of functional neuroimaging studies. Human Brain Mapping. 2005;25:105–117. doi: 10.1002/hbm.20140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Horwitz B, Honey G, Brammer M, Williams S, Sharma T. How good is good enough in path analysis? Neuroimage. 2000;11:289–301. doi: 10.1006/nimg.2000.0544. [DOI] [PubMed] [Google Scholar]
- Dunson DB. Bayesian latent variable models for clustered mixed outcome. Journal of the Royal Statistical Society B. 2000;6:355–366. [Google Scholar]
- Fiez JA, Petersen SE. Neuroimaging studies of word reading. Proceedings of the National Academy of Science USA. 1998;95:914–921. doi: 10.1073/pnas.95.3.914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT, Huang A, Parsons LM, Xiong JH, Zamarippa F, Rainey L, et al. Location-probability profiles for the mouth region of human primary motor-sensory cortex: Model and validation. Neuroimage. 2001;13:196–209. doi: 10.1006/nimg.2000.0659. [DOI] [PubMed] [Google Scholar]
- Fox PT, Ingham RJ, Ingham JC, Hirsch TB, Downs JH, Martin C, et al. A PET study of the neural systems of stuttering. Nature. 1996;382:158–161. doi: 10.1038/382158a0. [DOI] [PubMed] [Google Scholar]
- Fox PT, Laird AR, Fox SP, Fox M, Uecker AM, Crank M, et al. BrainMap taxonomy of experimental design: Description and evaluation. Human Brain Mapping. 2005;25:185–198. doi: 10.1002/hbm.20141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT, Mintun MA. Noninvasive functional brain mapping by change-distribution analysis of averaged PET images of H215O tissue activity. Journal of Nuclear Medicine. 1989;30:141–149. [PubMed] [Google Scholar]
- Fox PT, Mintun MA, Raichle ME, Herscovitch P. A noninvasive approach to quantitative functional brain mapping with H2(15)O and positron emission tomography. Journal of Cerebral Blood Flow Metabolism. 1984;4:329–333. doi: 10.1038/jcbfm.1984.49. [DOI] [PubMed] [Google Scholar]
- Fox PT, Mintun MA, Reiman E, Raichle ME. Enhanced detection of focal brain responses using inter-subject averaging and change-distribution analysis of subtracted PET images. Journal of Cerebral Blood Flow Metabolism. 1988;8:642–653. doi: 10.1038/jcbfm.1988.111. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Ashburner J, Frith C, Poline JB, Heather JD, Frackowiak RSJ. Spatial registration and normalization of images. Human Brain Mapping. 1995;3:165–189. [Google Scholar]
- Friston KJ, Frith CD, Liddle PR, Dolan RJ, Lammertsma AA, Frackowiak RSJ. The relationship between global and local changes in PET scans. Journal of Cerebral Blood Flow Metabolism. 1990;10:458–466. doi: 10.1038/jcbfm.1990.88. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Poline JB, Grasby PJ, Williams SCR, Frackowiak RSJ, et al. Analysis of fMRI time series revisited. Neuroimage. 1995;2:45–53. doi: 10.1006/nimg.1995.1007. [DOI] [PubMed] [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Gill J. Bayesian methods: A social and behavioral sciences approach. Boca Raton, FL: Chapman-Hall; 2002. [Google Scholar]
- Glabus MF, Horwitz B, Holt JL, Kohn PD, Gerton BK, Callicott JH, et al. Interindividual differences in functional interactions among prefrontal, parietal, and parahippocampal regions during working memory. Cerebral Cortex. 2003;13:1352–1361. doi: 10.1093/cercor/bhg082. [DOI] [PubMed] [Google Scholar]
- Gonçalves MS, Hall DA, Johnsrude IS, Haggard MP. Can meaningful effective connectivities be obtained between auditory cortical regions? Neuroimage. 2001;14:1353–1360. doi: 10.1006/nimg.2001.0954. [DOI] [PubMed] [Google Scholar]
- Holmes AP, Poline JB, Friston KJ. Characterizing brain images with the general linear model. In: Frackowiak RSJ, Friston KJ, Frith C, Dolan R, Mazziotta JC, editors. Human brain function. New York: Academic Press; 1997. pp. 59–84. [Google Scholar]
- Honey GD, Fu CHY, Kim J, Brammer MJ, Croudace TJ, Sucking J, et al. Effects of verbal working memory load on corticocortical connectivity modeled by path analysis of functional magnetic resonance imaging data. Neuroimage. 2002;17:573–582. [PubMed] [Google Scholar]
- Hoyle R, Kenny D. Sample size, reliability, and statistical tests of mediation. In: Hoyle R, editor. Statistical strategies for small sample sizes. Thousand Oaks, CA: Sage; 1999. pp. 197–219. [Google Scholar]
- Jackman S. Estimation and inference via Bayesian simulation: An introduction to Markov chain Monte Carlo. American Journal of Political Science. 2000;44:375–404. [Google Scholar]
- Kondo H, Osaka N, Osaka M. Cooperation of the anterior cingulate cortex and dorsolateral prefrontal cortex for attention shifting. Neuroimage. 2004;23:670–679. doi: 10.1016/j.neuroimage.2004.06.014. [DOI] [PubMed] [Google Scholar]
- Laird AR, Fox PM, Price CJ, Glahn DC, Uecker AM, Lancaster JL, et al. ALE meta-analysis: Controlling the false discovery rate and performing statistical contrasts. Human Brain Mapping. 2005;25:155–164. doi: 10.1002/hbm.20136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, McMillian KM, Lancaster JL, Kochunov P, Turkeltaub PE, Pardo JV, et al. A comparison of label-based review and ALE meta-analysis in the Stroop task. Human Brain Mapping. 2005;25:6–21. doi: 10.1002/hbm.20129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster JL, Glass TG, Lankipalli BR, Downs H, Mayberg H, Fox PT. A modality-independent approach to spatial normalization of tomographic images of the human brain. Human Brain Mapping. 1995;3:209–223. [Google Scholar]
- Lee SY. Structural equation modeling: A Bayesian approach. New York: Wiley; 2007. [Google Scholar]
- Lee SY, Song XY. Bayesian model comparison of nonlinear structural equation models with missing continuous and ordinal data. British Journal of Mathematical and Statistical Psychology. 2004;57:131–150. doi: 10.1348/000711004849204. [DOI] [PubMed] [Google Scholar]
- Mardia KV. The effect of non-normality on some multivariate tests and robustness to non-normality in the linear model. Biometrika. 1970;58:105–121. [Google Scholar]
- McDonald R. Path analysis with composite variables. Multivariate Behavioral Research. 1996;31:239–270. doi: 10.1207/s15327906mbr3102_5. [DOI] [PubMed] [Google Scholar]
- McIntosh AR, Gonzalez-Lima F. Structural modeling of functional neutral pathways mapped with 2-deoxyglucose: Effects of acoustic startle habituation on the auditory system. Brain Research. 1991;547:295–302. doi: 10.1016/0006-8993(91)90974-z. [DOI] [PubMed] [Google Scholar]
- McIntosh AR, Gonzalez-Lima F. Structural equation modeling and its application to network analysis in functional brain imaging. Human Brain Mapping. 1994;2:2–22. [Google Scholar]
- McIntosh AR, Grady CL, Ungerleider LG, Haxby JV, Rapoport SI, Horwitz B. Network analysis of cortical visual pathways mapped with PET. Journal of Neuroscience. 1994;14:655–666. doi: 10.1523/JNEUROSCI.14-02-00655.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillian KM, Laird AR, Witt ST, Meyerand ME. Self-paced working memory: Validation of verbal variations of the n-back paradigm. Brain Research and Brain Research Review. 2007;1139:133–142. doi: 10.1016/j.brainres.2006.12.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthén LK, Muthén BO. M plus version 4.2 [Computer program] Los Angeles: Muthén & Muthén; 2005. [Google Scholar]
- Owen AM, McMillian KM, Laird AR, Bullmore E. N-back working memory paradigm: A meta-analysis of normative functional neuroimaging. Human Brain Mapping. 2005;25:46–59. doi: 10.1002/hbm.20131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen SE, Fox PT, Posner MI, Mintun M, Raichle ME. Positron emission tomographic studies of the cortical anatomy of single word reading. Nature. 1988;331:385–389. doi: 10.1038/331585a0. [DOI] [PubMed] [Google Scholar]
- Price CJ, Friston KJ. Functional ontologies for cognition: The systematic definition of structure and function. Cognitive Neuropsychology. 2005;22:262–275. doi: 10.1080/02643290442000095. [DOI] [PubMed] [Google Scholar]
- Price CJ, Wise RJ, Watson JD, Patterson K, Howard D, Frackowiak RS. Brain activity during reading: The effects of exposure duration and task. Brain. 1994;117:1255–1269. doi: 10.1093/brain/117.6.1255. [DOI] [PubMed] [Google Scholar]
- Raftery AE, Lewis SM. How many iterations of the Gibbs sampler? In: Bernardo J, Berger J, Dawid AP, Smith AFM, editors. Bayesian biostatistics. Vol. 4. Oxford, UK: Oxford University Press; 1992. pp. 641–649. [Google Scholar]
- Raichle ME, Martin MRW, Herscovitch P, Mintun MA, Markham J. Brain blood flow measured with intravenous H215O: II. Implementation and validation. Journal of Nuclear Medicine. 1983;24:790–798. [PubMed] [Google Scholar]
- Scheines R, Hoijtink H, Boomsma A. Bayesian estimation and testing of structural equation models. Psychometrika. 1999;64:37–52. [Google Scholar]
- Steiger JH. Structural model evaluation and modification: An interval estimation approach. Multivariate Behavioral Research. 1990;25:173–180. doi: 10.1207/s15327906mbr2502_4. [DOI] [PubMed] [Google Scholar]
- Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain. Stuttgart, Germany: Thieme; 1988. [Google Scholar]
- Turkeltaub PE, Guinevere FE, Jones KM, Zeffiro TA. Meta-analysis of the functional neuroanatomy of single-word reading: Method and validation. Neuroimage. 2002;16:765–780. doi: 10.1006/nimg.2002.1131. [DOI] [PubMed] [Google Scholar]
- Woods R, Mazziotta J, Cherry S. Rapid automated algorithm for aligning and reslicing PET images. Journal of Computer Assisted Tomography. 1992;16:620–633. doi: 10.1097/00004728-199207000-00024. [DOI] [PubMed] [Google Scholar]
- Woods R, Mazziotta J, Cherry S. MRI-PET registration with automated algorithm. Journal of Computer Assisted Tomography. 1993;17:536–546. doi: 10.1097/00004728-199307000-00004. [DOI] [PubMed] [Google Scholar]
- Wothke W. Longitudinal and multigroup modeling with missing data. In: Little TD, Schnabel KV, Baumert J, editors. Modeling longitudinal and multilevel data. Mahwah: Lawrence Erlbaum Associates, Inc; 2000. pp. 219–240. [Google Scholar]
- Zhuang J, LaConte S, Peltier S, Zhang K, Hu X. Connectivity exploration with structural equation modeling: An fMRI study of bimanual motor coordination. Neuroimage. 2005;25:462–470. doi: 10.1016/j.neuroimage.2004.11.007. [DOI] [PubMed] [Google Scholar]