On the Tightness of Knots in a Polymer Chain

Abstract

It was predicted recently that sufficiently complex knots on a linear wormlike chain can have a metastable size, preventing their spontaneous expansion. We tested this prediction via computer simulations for 7₁ and 10₁₅₁ knots. We calculated the equilibrium distributions of knot size S for both knots. By using the umbrella sampling we were able to obtain the distributions over a wide range of S values. The distributions were converted into the dependencies of knot free energy on S. The obtained free energy profiles have no pronounced local minima, so there are no metastable knot sizes for these knots. We also performed Brownian dynamics simulation of 7₁ knot relaxation that started from a very tight knot conformation. The simulation showed that knot expansion is a fast process compared to knot displacement along the chain contour by diffusion.

I. INTRODUCTION

Over the last 4 decades knots in polymer chains were a subject of numerous theoretical and experimental studies (see refs. [1, 2] for reviews). In particular, a few theoretical studies addressed the questions related to knot tightness in the long chains. It was found that with high probability knots are localized in a relatively small portion of the circular chains [3–5]. The localization increases the total entropy of the circular chains since the conformational restrictions for the entire chain are reduced if the knot is localized. For linear polymer chains topology is not strictly defined, since any kind of entanglement can be removed by continuous deformation of these chains without passing the chain segments through one another. However, if a knot is sufficiently compact compared to the total chain length, its topology can be specified unambiguously. Such compact conformations of knots can be obtained experimentally if a knotted linear chain is stretched [6, 7]. Diffusion of knots along stretched DNA molecules have been studied both experimentally and by computer simulation [7–9]. It seems natural to suggest, however, that if the stretching force applied to the chain ends is eliminated, the knot will expand and eventually disappear, since this unknotting would decrease the bending energy of the chain and increase its conformational freedom. Thus, it was quite unexpected when two theoretical studies concluded that the lifetime of compact knots in long polymer chains with free ends can be very large. Dommersnes et al. showed that unscreened electrostatic interaction between the segments of a flexible linear polymer can prevent a tight knot from expansion [10]. Using computer simulation they found that such tight knots can diffuse along the polymer over a long distance without any signs of expansion. In this case the long-range electrostatic interaction makes the total electrostatic energy of a polymer lower if the knot preserves a tight conformation [10]. Grosberg and Rabin concluded that such diffusion should take place in a much more general case, for sufficiently complex tight knots in an uncharged wormlike chain [11]. A similar idea lies in the base of these two studies. On one hand, tightening a knot increases the elastic (and electrostatic, in the case of a charged polymer) energy and decreases the entropy of the chain segments constituting the knot. Clearly, these factors should promote knot expansion. On the other hand, the free energy of the entire chain can be reduced by knot compaction since other segments of the chain will have more conformational freedom and smaller elastic/electrostatic energy. Thus, in principle, knot expansion can be prevented by a free energy barrier and compact conformations of the knot may become metastable. Theoretical analysis by Grosberg and Rabin showed that entropic gain of the entire chain from a tight conformation of the knot may exceed the increase of bending energy associated with knot tightening [11]. Their conclusion was based, however, on a scaling analysis and a concept of a tube of a constant diameter surrounding the knotted wormlike chain, which may be not sufficiently accurate for this delicate problem. Therefore, to test the prediction made by Grosberg and Rabin, we decided to search for a metastable state of knots on a linear wormlike chain by computer simulations. The results of our computational analysis are presented in this paper.

II. METHODS OF SIMULATIONS

DNA Model

The polymer model used in the Monte Carlo simulations represents a discrete analog of the wormlike chain. It also accounts for the excluded volume of the chain segments. The model chain composed of n persistence lengths is represented by a chain of kn rigid segments that are cylinders of equal length, l, where k is a computational parameter. The bending elastic energy of the chain, E_b, is computed as

$$E_b=\frac{1}{2}{\mathrm{k}}_{\mathrm{B}}Tg{\displaystyle \sum _{i=1}^{\mathit{\text{kn}}-1}{\mathrm{\theta }}_i^2},$$ (1)

where the summation extends over all the joints between the elementary segments, θ_i is the angular displacement of segment i + 1 relative to segment i, g is the bending rigidity constant, and k_BT is the Boltzmann temperature factor. The bending rigidity, g, is directly related to the chain persistence length, a:

$$g=a/l.$$ (2)

The volume interaction between the chain segments was taken into account via their diameter, d (see ref. [8] for details).

The polymer model used for the Brownian dynamics (BD) simulation is very similar to the one described above [12–14]. It was described in detail in our recent publications [8, 15].

Simulation procedure

The simulation of equilibrium properties was based on the Metropolis Monte Carlo procedure (described in detail in ref. [16]). The chain topology was checked at each step of the Metropolis procedure by calculating the Alexander polynomial, Δ(t) , for t = −1 and t = −2 [17]. Hundreds of millions of elementary moves were needed to obtain the equilibrium properties of the knots with accuracy sufficient for the goals of the current study.

To simulate the equilibrium distribution of knot size, P(S) , over a wide range of knot sizes, we used the method of umbrella sampling [18]. In this method an artificial biasing potential is added to the chain elastic energy to sample a particular range of the distribution. The potential, H(S) , was specified by the equation

$$\mathrm{H}(S)=\gamma S,$$ (3)

where γ is a coefficient. Changing the value of γ , we were able to simulate the biased probability distributions for different ranges of S. The values of γ have to be chosen so that the biased distributions have sufficient overlapping: we used γ of 0, 0.15, 0.65, 1, 2, 5. The simulated distributions were combined to obtain the unbiased P(S) [19].

BD simulations were based on the standard 2nd order algorithm [20]. The hydrodynamic interaction between the chain subunits was not taken into account in the majority of the simulation. The timestep in the simulation was equal to 400 ps.

Determination of the knot size

Through our simulations we define the knot size as the length of the shortest subchain containing this knot. To calculate the knot size we projected the chain conformation to a plane that is parallel to the direction of the extending force (although the force was used only for preparing the initial conformation in the BD simulation), simplified the knot diagram (see below), and used the first and the last intersections on the projection as the boundaries of the knot contour. The length of the knot contour was calculated over the projections to 20 different planes parallel to the extending force, and the shortest length was considered as the knot size, S.

Since in some of the chain conformation a flanking chain occasionally formed trivial intersections on a projection, we performed a preliminary simplification of the knot projection. We removed all the trivial intersections, which may erroneously increase the calculated knot size (Fig. 1). This simplification was performed on the table of crossings for the projection as was suggested in ref. ([21]).

Figure 1.

The trivial crossings on a knot projection, which are eliminated by the projection simplification procedure.

The elimination procedure was performed iteratively on the table of crossings until the inspection of all crossings brought no more simplifications. An example of knot size determination based on this procedure is shown in Fig. 2.

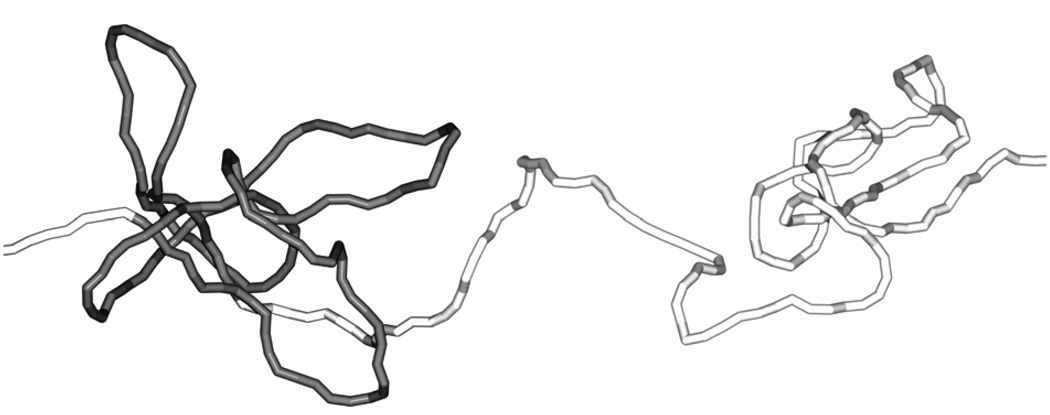
Figure 2.

Calculation of the knot size. After eliminating all of the trivial crossings the entire right coiled part of the chain conformation was disentangled. A part of the chain contour which was determined by our algorithm as the knot is marked by the dark tone.

Through all the simulations in this study each tail of the knot was at least 4 persistence lengths long. Since equilibrium properties of a knot cannot go beyond the chain correlation length, we consider this condition on the length of the knot tails to be sufficient.

III. RESULTS

To study the expansion of knots we always started from their compact conformations, which were obtained by applying a stretching force to the ends of the wormlike chain. The tightness of the knots on the stretched chain depends on the dimensionless force, f = Fa / k_BT (where a is the chain persistence length and F is the stretching force), and the volume interaction between the chain segments. The majority of our simulation results were obtained for one chosen value of the second virial coefficient of the intersegment interactions, B. In the Monte Carlo simulations we used the discrete wormlike chain consisting of the rigid cylinders of a particular diameter, d. The chosen value of d corresponded to the effective diameter of the double-stranded DNA under physiological ionic conditions, often used in experimental studies of polymer topological properties. Under these conditions, when the concentration of sodium ions is close to 0.2 M, the effective diameter of the double helix is approximately 10 times smaller than its persistence length, a [22]. In the Brownian dynamics simulation the hard core potential was replaced by the Debye-Hückel potential, which gives the same value of B as the chosen hard core potential [23, 24]. In a separate simulation, which we wanted to start from a tighter knot, we reduced the chain diameter to 0.02a.

The discrete wormlike chain of the rigid cylinders, used in the Mote Carlo simulation, has k cylinders per persistence length, a, and approximates the continuous wormlike chain. Obviously, the approximation of the wormlike chain by the discrete model improves when k increases. On the other hand, larger values of k slow down the simulation substantially. The minimum value of k that provides an accurate approximation for the wormlike chain depends on the conformational property of interest and should be determined case by case (see ref. [16] for review). We performed such investigation for the stretched knotted polymer chains. The maximum value of f which we used here was equal to 100 for the chain diameter of 0.1a and 250 for d of 0.02a.. An equilibrium set of conformations for the polymer chain stretched by these forces were simulated for two knots of different complexity, 7₁ and 10₁₅₁, used in this study (Fig. 3).

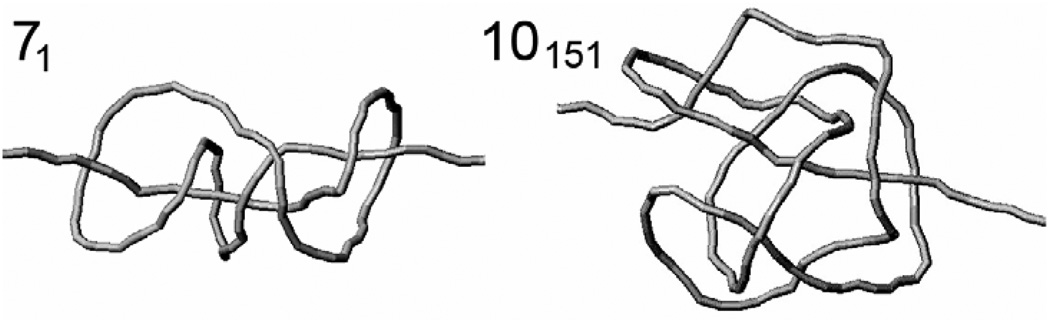
Figure 3.

Knots 7₁ and 10₁₅₁, which were used in this study. The relatively compact conformations of knots shown in the figure are due to the stretching force of 0.5 pN applied to the ends of the model chain. The actual chains used in the simulation had much longer flanks which were cut in the figure.

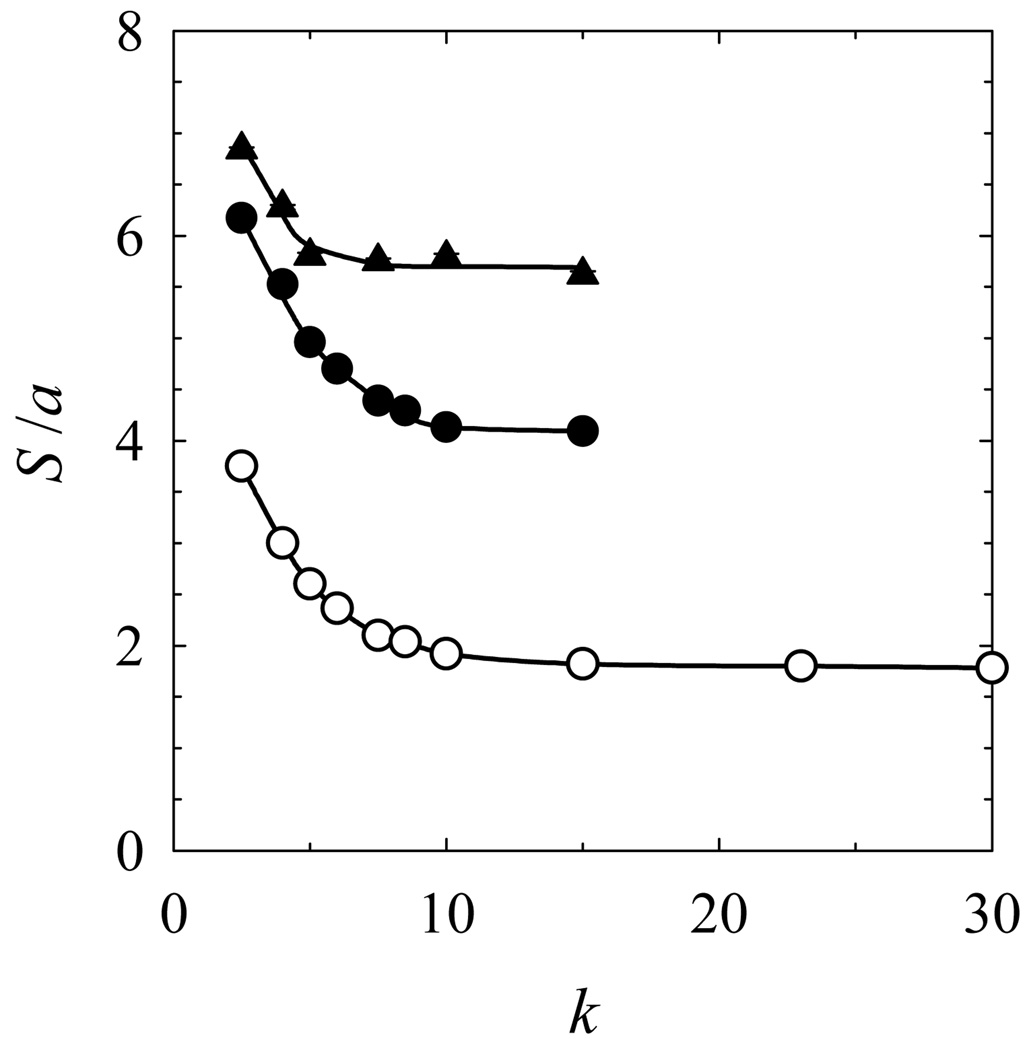
Under this force the knots are very tight, so their length to diameter ratio only slightly exceeds the corresponding minimum values, p [25]. We see from Fig. 4 that the extension for both knots does not change if k is larger than 10. Since even smaller values of k provide good approximation of the wormlike chain at lower stretching forces [26], we used this value of k throughout all of the simulations in this study.

Figure 4.

Approximation of the wormlike chain by its discrete analog. The average sizes of two knots obtained under the stretching force of 100 (filled symbols) and 250 (open symbols) are plotted for knots 7₁ (circles) and 10₁₅₁ (triangles) as a function of the number of straight segments constituting the persistence length of the discrete wormlike chain, k. The data shows that even for this stretching force the limiting properties of the knots are obtained for k equal 10.

Equilibrium size of knots under the stretching force

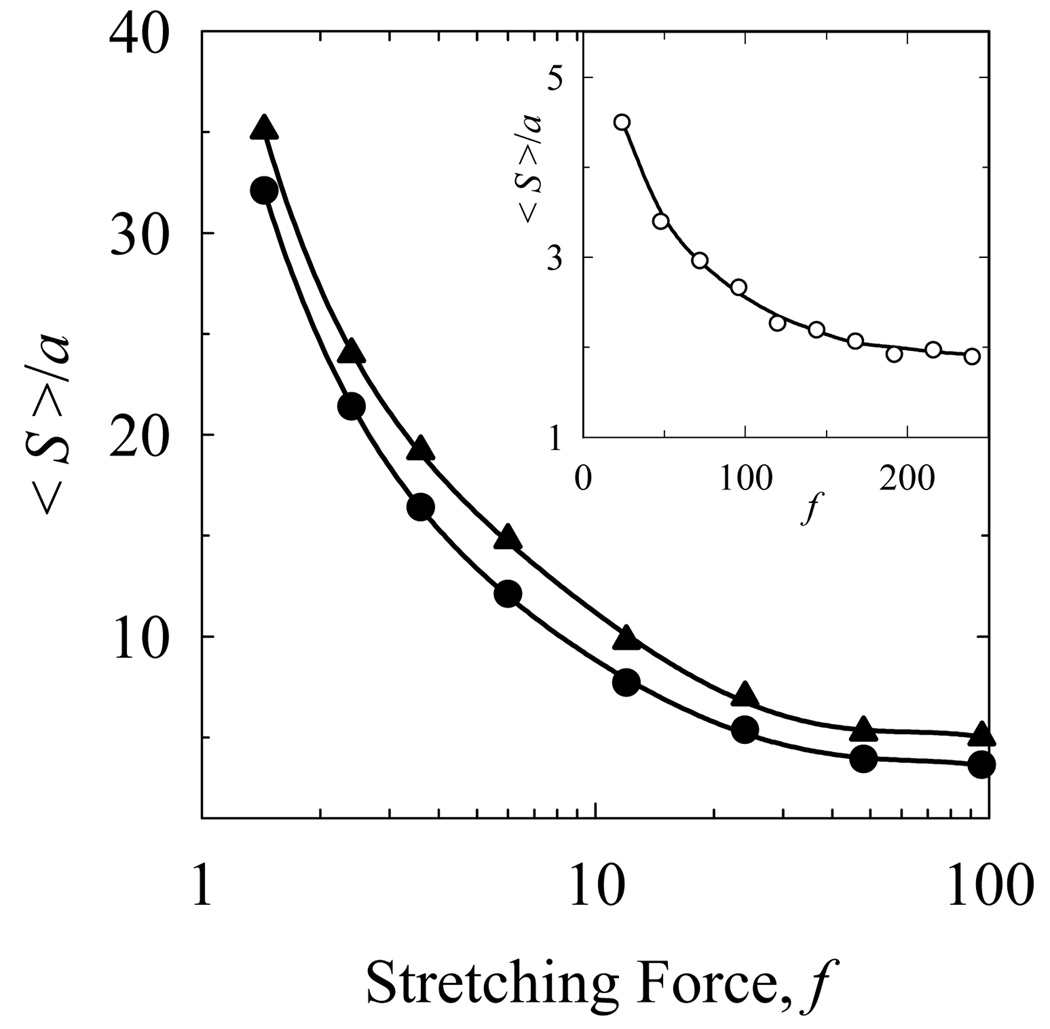
It was predicted that the dependence of the equilibrium knot size on f could be non-monotonic, if a metastable state of the knot exists [11]. To test the prediction we simulated the distributions of knot conformations stretched by force applied to the chain ends. Since identical distributions for a particular value of force were obtained both by extension from a smaller size of the knot and by tightening from a larger size, we believe that the shown average sizes of knots, 〈S〉, correspond to the thermodynamic equilibrium. The simulated values of S over a range of stretching forces are shown in Fig. 5. One can see from the figure that for both knots the average size increases monotonically when the force diminishes. According to the theoretical prediction the metastable state should correspond to a knot size smaller than ap [11]. At force of 0.05 pN the values of 〈S〉 / a for both knots exceed p, which is close to 31 and 40 for knots 7₁ and 10₁₅₁, correspondingly [25]. Clearly, the simulation revealed only monotonic dependences of S on f (Fig. 5). It cannot be excluded, however, that a metastable size of the knots was not detected in the Monte Carlo simulation of the equilibrium ensembles of the chain conformations for the chosen set of the stretching force. Therefore, in the next section we addressed the existence of the metastable knot size directly.

Figure 5.

Average sizes of knots 7₁ (circles) and 10₁₅₁ (triangles) under dimensionless stretching force f applied to the chain ends. The data were obtained by the Monte Carlo simulations of equilibrium ensembles of chain conformations for d of 0.1a (main plot) and 0.02a (insert). Statistical error of the calculations is smaller or close to the size of the symbols.

Free energy of knots as a function of their size

We calculated the free energy of the knotted chain as a function of the knot size, G(S) , for knots 7₁ and 10₁₅₁. Our approach was based on the simulation of the equilibrium distribution of S, P(S), which is directly related to G(S) :

$$G(l_k)=-{\mathrm{k}}_{\mathrm{B}}T\text{ ln }P(S).$$ (4)

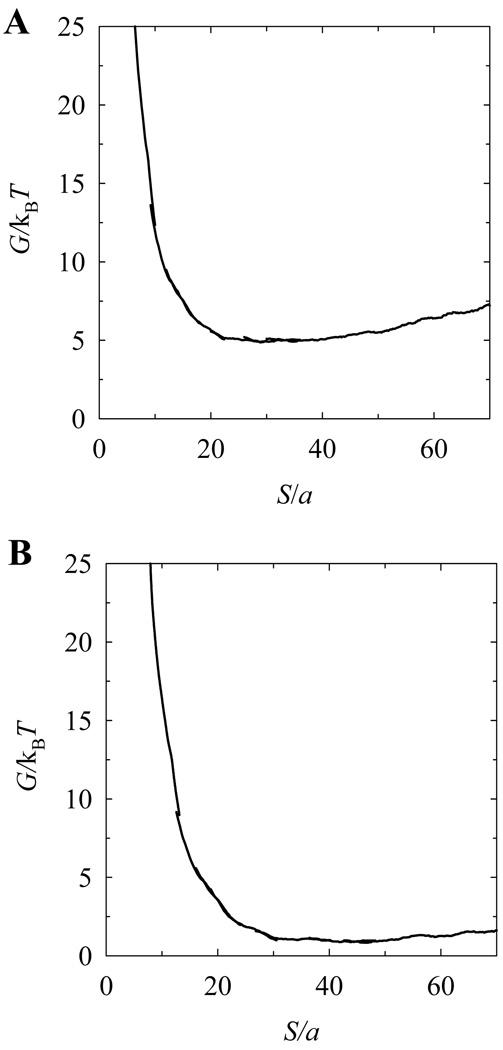
According to our Monte Carlo simulation, knot size always increases when the stretching force diminishes (see Fig. 5). Therefore, to restrict the distribution by a finite range of S, we calculated P(S) , and, correspondingly, G(S) , for the chains extended by a small stretching force (0.05 pN). To cover a large range of S values we used the umbrella sampling (see Methods) [18]. The functions G(S) obtained in this way for knots 7₁ and 10₁₅₁ are shown in Fig. 6. We see from the figure that there is no free energy minimum for S < ap for either of the investigated knots. The broad minimum of G(S) at S > ap is due to the stretching force applied to the chain ends. Since the additional stretching force only slightly increases G(S) when S increases, it cannot eliminate a local minimum of G(S) if such a minimum exists in the absence of the stretching force. Thus, our Monte Carlo simulation shows that there are no metastable sizes for knots 7₁ and 10₁₅₁ in the range of S less than ap, where it was predicted [11].

Figure 6.

The free energy of knots 7₁ and 10₁₅₁ as a function of their sizes, S. The linear chain containing a chosen knot was stretched by a small force of 0.05 pN. The umbrella sampling was used in the Monte Carlo simulation to obtain G(S) over the wide range of S (see Methods). The broad minimum of G(S) seen for both knots is due to the small stretching force (of 0.05 pN) applied to the chain ends.

Dynamics of knot expansion

It is interesting to investigate how fast the knot expansion occurs in the absence of the stretching force. To address this question we performed a Brownian dynamics simulation of the process. As tested in the DNA studies, the method provides an accurate quantitative description of large-scale dynamic properties of the wormlike chain [16]. To save computational time we did not account for hydrodynamic interaction between chain segments in the current simulation. However, our estimations showed that accounting for the hydrodynamic interaction makes the relaxation process a few times faster (data not shown). Therefore, accounting for the hydrodynamic interaction would not essentially change a semi-quantitative picture presented below.

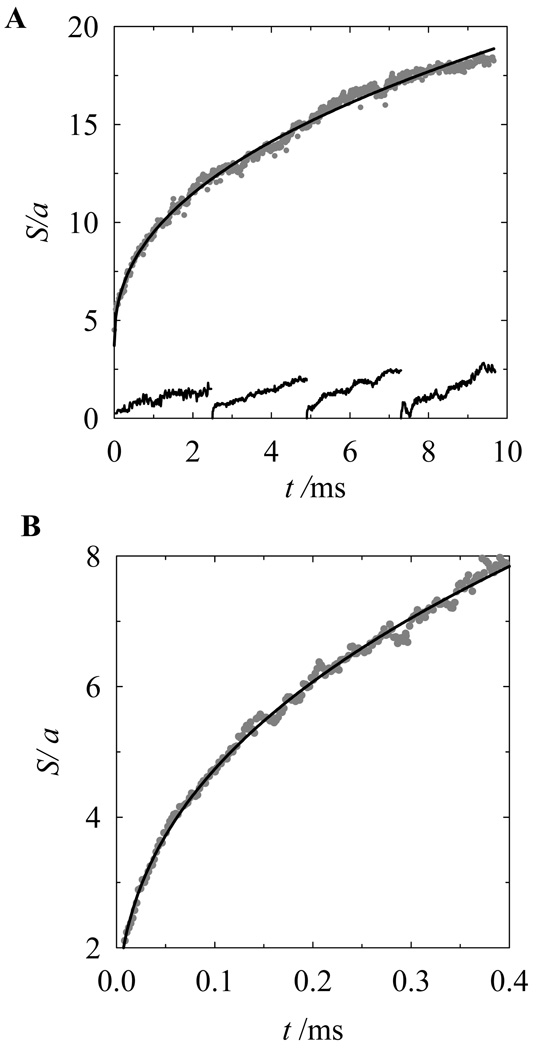
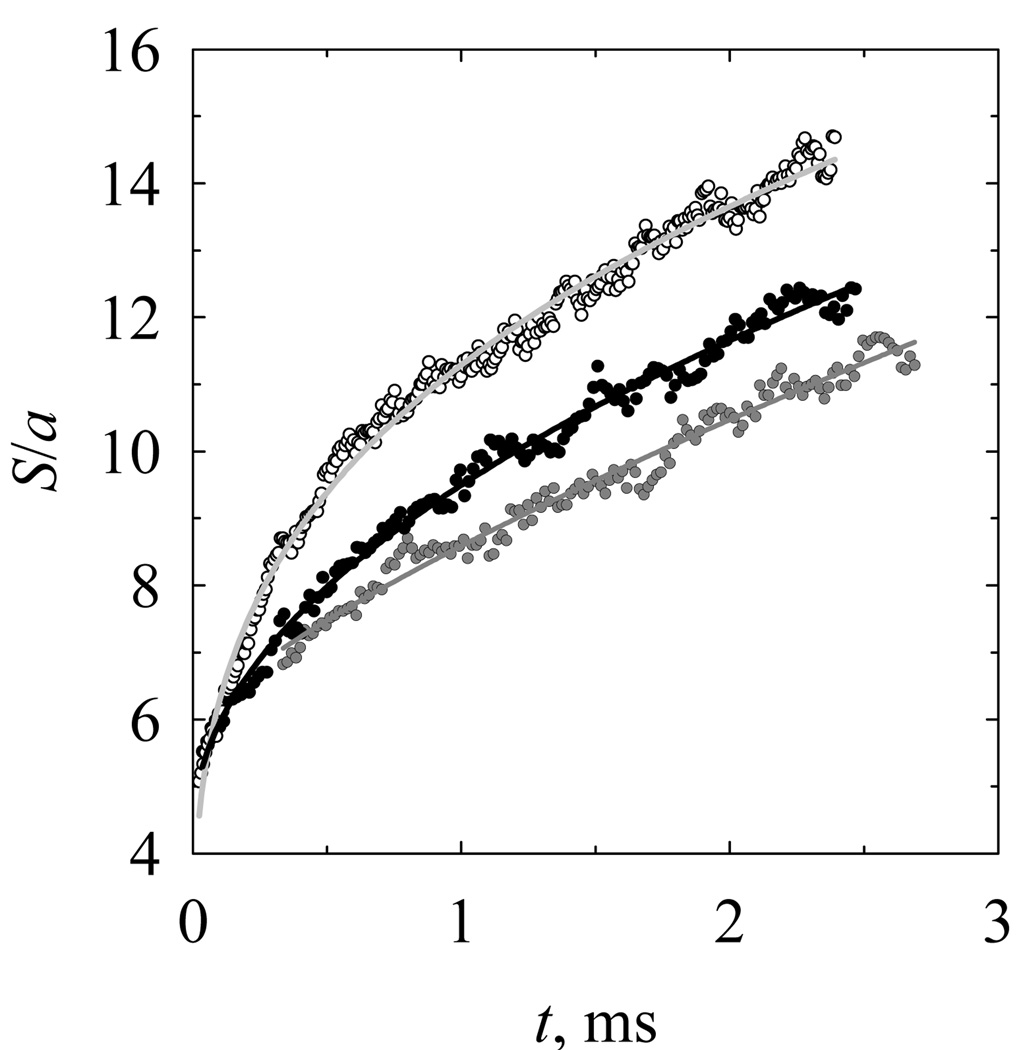
For the current simulation, the initial compact conformations of knots with stretched flanking subchains were created by the Monte Carlo simulation in the presence of the stretching force, which was adjusted to obtain an equilibrium set of conformations with a chosen average knot size. There was no stretching force during the Brownian dynamics simulation of knot relaxation. Kinetics of the 7₁ knot expansion is presented in Fig. 7. This expansion kinetics was obtained by combining the simulations started from four different sizes of the initial conformation. It was not possible to extend the simulation of the knot expansion beyond each of the shown time spans because coiled conformations of the flanking chain compromise the calculation of the knot size. Each of the four spans of knot expansion shown in Fig. 7 represents the average over 28 independent trajectories. We also found that the rate of knot expansion depends on the length of the flanking chains. This is illustrated in Fig. 8, which shows the results of three sets of simulations performed for chains of different lengths. In this simulation the initial conformations were obtained under the same stretching force, and the knot was located at the chain center. This dependence of the knot expansion on the chain length is understandable, if we take into account that the total relaxation time of the chain increases with its length, and earlier or later the knot expansion involves the entire chain.

Figure 7.

Brownian dynamics simulation of knot expansion. (A) The shown dependence of 7₁ knot size on time was obtained by combining four spans of the expansion 2.5 ms each. The initial conformations for each span were obtained by applying a proper stretching force to the chain ends. The simulation corresponds to the chain effective diameter of 0.1a. The average displacements of the knot center of mass over the time spans are shown at the button of the plot. (B) Initial expansion of very tight conformation of 7₁ knot created by the stretching force of 250. The simulation corresponds to the chain effective diameter of 0.02a.

Figure 8.

Dependence of the knot expansion rate on the total length of the chain. The BD simulation results were obtained for knots 7₁ and chain length of 40 (open circles), 60 (black circles), and 80 (grey circles) persistence lengths. The initial conformations of the chains were obtained by applying a 4 pN stretching force to the chain ends.

We compared the rate of knot expansion with the diffusion of its center. At the bottom of Fig. 7A we showed the root mean square of the displacement of the knot center of mass (also averaged over 28 independent trajectories) during each of the four spans of expansion. One can see from the figure that the diffusion rate is slower or comparable to the rate of knot expansion.

Discussion

This study was inspired by a striking prediction that there should be a metastable size of a complex knot that prevents its expansion in the linear uncharged wormlike chain [11]. Of course, the prediction should be equally valid for electrically charged, but strongly screened polyelectrolytes, like double-stranded DNA molecules in moderate and high salt concentration. The theoretical analysis, however, was based on a semi-quantitative treatment of the problem, and, therefore, its computational testing was highly desirable. We performed such testing in this study. Of course, there are some limitations in our simulations as well. First, we considered a discrete wormlike chain. We showed, however, that the chosen discretization is sufficient for modeling the properties of knots in the wormlike chain. Second, we performed the simulations for only two randomly chosen knots, 7₁ and 10₁₅₁. The theoretical prediction, however, should be equally valid for all sufficiently complex knots, and the chosen knots satisfy the criteria of complexity suggested in ref. [11].

Our data showed no traces of metastable states, which could prevent the knot expansion on the linear chain. We found that for both knots the average knot size monotonically decreases when the stretching force applied to the chain ends increases, contrary to the theoretical prediction. We calculated the free energy of the knotted chain as a function of the knot size, and found that for both knots the free energy decreases monotonically when the knot size increases. Finally, using Brownian dynamics simulation, we showed that the rate of 7₁ knot expansion is comparable with the rate of its displacement by diffusion. If we assume that this result is applied to other knots of comparable complexity, we should conclude that knot expansion is a fast process. We think that the data obtained in this study strongly argue against the existence of a metastable size of complex knots on the linear wormlike chain.