Abstract
Determination of copy number variants (CNVs) inferred in genome wide single nucleotide polymorphism arrays has shown increasing utility in genetic variant disease associations. Several CNV detection methods are available, but differences in CNV call thresholds and characteristics exist. We evaluated the relative performance of seven methods: circular binary segmentation, CNVFinder, cnvPartition, gain and loss of DNA, Nexus algorithms, PennCNV and QuantiSNP. Tested data included real and simulated Illumina HumHap 550 data from the Singapore cohort study of the risk factors for Myopia (SCORM) and simulated data from Affymetrix 6.0 and platform-independent distributions. The normalized singleton ratio (NSR) is proposed as a metric for parameter optimization before enacting full analysis. We used 10 SCORM samples for optimizing parameter settings for each method and then evaluated method performance at optimal parameters using 100 SCORM samples. The statistical power, false positive rates, and receiver operating characteristic (ROC) curve residuals were evaluated by simulation studies. Optimal parameters, as determined by NSR and ROC curve residuals, were consistent across datasets. QuantiSNP outperformed other methods based on ROC curve residuals over most datasets. Nexus Rank and SNPRank have low specificity and high power. Nexus Rank calls oversized CNVs. PennCNV detects one of the fewest numbers of CNVs.
INTRODUCTION
Copy number variants (CNVs) are duplications, insertions or deletions of chromosomal segments that are ≥1 kb (1,2). Multiple experimental techniques can detect CNVs, including bacterial artificial chromosome (BAC) arrays, paired end mapping, fluorescent in situ hybridization, representational oligonucleotide microarray analysis (ROMA) and whole genome single nucleotide polymorphism (SNP) arrays (3). Due to increased use of genome wide association (GWA) studies, SNP arrays with sufficiently high-density (>300 K SNPs) have become a convenient tool for studying CNVs. Accurate CNV detection in SNP arrays requires sophisticated algorithms or statistical methods. The accuracy of CNV boundaries derived from SNP arrays is influenced by multiple factors such as the robustness of the statistical method, batch effects, population stratification and differences between experiments (4; http://www.goldenhelix.com/Downloads/login.html?product=SVS&view=./Events/recordings/wgacnv2008/wgacnv2008.html). Experimental validation is therefore important to confirm the accuracy of CNVs derived from SNP array platforms.
To date, several detection methods are available for identifying CNVs from genome-wide SNP array data. Most were initially developed for array comparative genomic hybridization (aCGH) platforms. The statistical models underlying these approaches include hidden Markov models (HMMs) (5,6), segmentation algorithms (7,8), t-tests and standard deviations (SDs) of the log R ratio (9). While these free or commercial programs are available for detecting CNVs from SNP arrays, a thorough comparison of these methods, particularly, the recently developed ones, has not been conducted. The most recent comprehensive survey of the performance of CNV detection methods was performed in 2005, in which Lai et al. (10) tested 11 methods using receiver operating characteristic (ROC) curves and found that segmentation algorithms performed consistently well. However, a few nonsegmentation methods proposed recently such as the QuantiSNP (5) and PennCNV (6) programs were not included. Furthermore, although utilization of high-density SNP arrays to infer CNVs is increasing, the application of these methods on real data is in its infancy. Many practical considerations need further exploration, such as the determination of optimal parameters for each method, parameter setting impact on CNV detection and CNV size, and method adjustments with various CNV sizes, signal levels and signal variations.
In this study, we compared seven frequently used CNV detection methods: circular binary segmentation (CBS) (8), CNVFinder (9), cnvPartition, gain and loss of DNA (GLAD) (7), Nexus segmentation methods Rank and SNPRank, PennCNV (6) and QuantiSNP (5) for the following aspects: (i) optimal parameter settings for each method; (ii) sensitivity, specificity, power and false positive rates of each calling algorithm and (iii) conditions where a method failed to call correct boundaries and where a method detected different CNV sizes.
MATERIALS AND METHODS
Datasets
We used both genome wide SNP arrays and simulated data (described later) to evaluate the performance of these CNV detection methods. The SNP array data were obtained from the GWA study of the Singapore cohort study of the risk factors for Myopia (SCORM). SCORM is a longitudinal cohort designed to evaluate the environmental and genetic risk factors for myopia in Singapore Chinese schoolchildren. A total of 1979 school children from Grades 1–3 in Singapore were followed up yearly by ophthalmologists and optometrists, who measured refractive error, keratometry, axial length, anterior chamber depth, lens thickness and vitreous chamber depth. Buccal samples were collected from 1875 children (aged 8–12 years), in which 1116 samples from Chinese participants were genotyped using Illumina HumanHap 550 and 550 Duo BeadArrays. The study protocol was approved by the Institutional Review Boards of the National University of Singapore and the Singapore Eye Research Institute.
In this study, we analyzed the following three subsets of SNP arrays from the SCORM GWA study: (i) a training dataset of 10 unrelated control samples (five males and five females) from the 550 nonduo chips who had no myopia or hyperopia (emmetropic, spherical equivalent between −0.50 and +0.50 diopters in both eyes) and had the highest genotyping quality (call rate ≥0.98); (ii) a pilot dataset of 16 SNP arrays generated from different sources of DNA specimens from five individuals, all with buccal, whole genome amplified buccal and saliva-derived DNA samples, in which one individual also had an array genotyped from the blood-derived DNA sample; (iii) an analysis dataset of 100 unrelated emmetropic control samples independent from the training dataset that had high-genotyping quality (call rate ≥ 98%), SD of the log R ratio distribution <0.3 and high correlation with at least 95% of the total analysis samples (Pearson correlation coefficient >0.75). Throughout this work, SNPs located within the CNV boundaries detected by each detection method are referred as CNV SNPs.
We used the training dataset to standardize parameter settings for each method. To confirm the optimal parameters chosen by the normalized singleton ratio (NSR) described below, two additional 10 sample datasets were constructed from emmetropic individuals: one chosen from 550 duo chips with the same criteria as the training dataset above and one chosen from samples of moderate genotyping quality (rank 51–60 of 112) regardless of gender or chip type. The optimal parameter setting derived from the training dataset was applied to both the pilot and analysis datasets. The pilot dataset was used to compare the performance of each CNV detection method using different DNA sources. The analysis dataset was used to draw conclusions for the performance of each method. The outcomes from the SCORM CNV data were then evaluated in a simulated dataset.
CNV detection methods
The underlying statistical models for the seven CNV detection methods evaluated in this study differ by varying degrees. The primary raw data used for detecting CNVs from SNP arrays are the SNP intensity measured by log R ratios. Some methods also used B allele frequencies to enhance detection. CBS (8), Nexus 4.1 Rank and Nexus 4.1 SNPRank (http://www.biodiscovery.com) use the same segmentation algorithm that recursively divides chromosomes into segments of common intensity distribution functions, but CBS has no inherent method of determining segment significance while Nexus uses an unknown equation to compute segment significance (Dr Soheil Shams, CSO of Biodiscovery, Developer of Nexus, personal communication). GLAD uses a version of adaptive weights smoothing to build segments by adding neighboring SNPs to the existing set of SNPs in the segment. The QuantiSNP (5) and PennCNV (6) programs use different HMMs. The PennCNV program uses the combined log R ratio and B allele frequency, while the QuantiSNP program treats them independently. The PennCNV program generates a hidden state for copy neutral loss of heterozygosity (LOH) and uses each population-based B allele frequency of the SNP to infer CNVs, while the QuantiSNP program uses a fixed rate of heterozygosity for each SNP. The CNVFinder (9) program uses experimental variability, termed SDe, in the log R ratio distribution. The cnvPartition program implemented in the Illumina BeadStudio software uses an undocumented method of CNV detection.
The experimental platforms for which the CNV detection methods were developed also differ. Several methods were developed for CGH of various types: CBS for BACs and ROMA, GLAD for BACs, PennCNV and Nexus for Agilent and Nimblegen platforms and CNVFinder for whole genome tile path. Nexus and PennCNV were also developed for Illumina and Affymetrix SNP arrays. CNVFinder was also developed for Affymetrix SNP arrays. cnvPartition and QuantiSNP were developed for Illumina SNP arrays.
Optimization of method parameters
We propose using the NSR as a summary metric for determining the optimal parameter setting for each method. The NSR is defined as
where pu is the proportion of unique CNV SNPs (i.e. the proportion of the number of CNV SNPs found in only one sample of the dataset), and µCS is the average number of CNV SNPs called per sample. The NSR hypothesizes that CNV SNPs called in only one sample are more likely to be false positives than CNV SNPs that are called in multiple samples, thus the smaller the NSR, the better the method. Since types of parameters vary among CNV detection methods, the parameters adjusted in this optimization study included the following: SD for CBS, SDe for CNVFinder, confidence for cnvPartition, smoothed segment log R ratio for GLAD, segment threshold for Nexus, confidence and CNV length in SNPs for PennCNV and log Bayes Ratio and CNV length in SNPs for QuantiSNP.
Comparative statistics
The SNP intensity data (log R ratios) were obtained from the Illumina BeadStudio 3.1 program. To compare the characteristics and quality of these CNV detection methods, we used three reference datasets from public databases: CNVs from SNP studies in the Database of Genomic Variants (DGV; http://projects.tcag.ca/ variation) (3) (7950 CNVs; 99 645 CNV SNPs); the set of HapMap CNVs in Asian populations reported by Redon et al. (11) (5753 CNVs; 25 799 CNV SNPs) and the subset of all experimentally confirmed CNVs from Redon et al. (11) (275 CNVs; 4984 CNV SNPs).
For each CNV detection method, the CNV results for the tested dataset (e.g. SCORM dataset) were compared to the reference dataset for each sample. Assuming that all CNVs in the reference datasets are true, the sensitivity, specificity and kappa statistics were computed from the CNV results for all datasets. Since some CNV detection methods such as Nexus cannot correctly handle CNVs in chromosomes X or Y, these chromosomes and the mitochondrial genome were excluded from the analyses.
Accounting for CNV SNPs and CNVs detected in multiple methods
The performance of the seven CNV detection methods was evaluated at both SNP and CNV levels. The CBS, cnvPartition, Nexus Rank and SNPRank, PennCNV and QuantiSNP programs produced CNV boundaries directly, providing the start and end base pair map locations for the CNV detected. The CNVFinder and GLAD programs directly designated the gain or loss of information of each CNV SNP rather than indicating CNV boundaries. For these latter two methods, we defined a CNV as three or more consecutive CNV SNP calls and excluded regions with one or two CNV SNP calls from the analysis.
Correlation between chips
We computed pair-wise Pearson correlations among a set of 20 samples, in which 10 samples were randomly chosen from each BeadArray platform to evaluate sample quality and effects caused by differences between the HumanHap 500 and 500 Duo arrays (Supplementary Table S1). Pearson correlation tests were also conducted on all emmetropic individuals in the SCORM dataset, and samples with pair-wise correlation values <0.75 with more than five other samples were excluded in the three SCORM subsets presented here.
Receiver operating characteristic curve residuals
Methods at optimal parameters were compared by using both ROC curves and ROC curve residuals, the distances from a point on the ROC curve to the diagonal line of y = x for each method. The residuals are calculated using the equation:
The largest ROC curve residuals are optimal.
Simulated datasets
Simulated CNV data were generated to compare the power, false positive rates and boundary calling properties of the CNV detection methods. cnvPartition data were unable to be simulated because of the limitations of data input into BeadStudio. We compared the parameter settings based on the optimal ROC curve residual and on the optimal NSR. Exactly matched boundary calling refers to the CNV region reported by the detection method having the same starting and ending SNPs as the one predesignated in the simulation.
For the simulations mimicking Illumina arrays, we directly used the log R ratio data in the SCORM sample to generate the log R ratio of non-CNV SNPs rather than generating from a given distribution. Among samples in the training and analysis datasets, we chose one sample with mean log R ratio of −0.01 and SD of 0.15, which is the average log R ratio and SD of total samples of these two datasets. We randomly sampled a log R ratio from this sample to assign to the non-CNV SNPs in the simulated datasets.
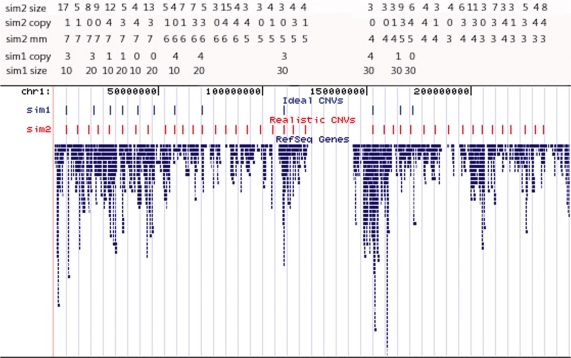
Two sets of Illumina simulations were conducted to generate the log R ratio of the CNV SNP. In simulation 1, we assigned CNVs to the positions shown in Figure 1, mimicking chromosome 1. The CNV at each position was assigned a specific copy number (0, 1, 3 or 4) and size (10, 20 or 30 SNPs). The log R ratio of each CNV SNP was equal to a random number drawn within the interval designated for each CNV: −2 ± SD for 0 copy CNVs, −1 ± SD for one copy CNVs, 0.585 ± SD for three copy CNVs and 1 ± SD for four copy CNVs, where we prespecified both copy number, SD (0.1–0.3 of the base log R ratio) and the length (number of SNPs) at each CNV location (Figure 1).
Figure 1.
Positions of simulated copy number variants with University of California Santa Clara genome browser (http://genome.ucsc.edu/cgi-bin/hgGateway) tracks on chromosome 1. The copy number (sim1 copy, sim2 copy), the size of copy number variant (sim1 size, sim2 size) and the frequency of copy number variant detection method (sim2 mm) were designated at each location for simulations 1 and 2.
In simulation 2, CNVs were designed to reflect CNVs detected in the SCORM samples, from those detected by all seven methods (highest number of replicated CNVs) to those detected by three methods (moderate number of replicated CNVs). First, all CNVs to be simulated were spaced every 1000 SNPs apart as shown in Figure 1. We then designated the copy number of the CNV (sim2 copy: 0, 1, 3 or 4), the frequency of the detection methods that detected the same CNV (sim2 mm: 3–7) and CNV length in SNPs (sim2 size: 3–17) at each CNV location (Figure 1). Second, we created a pool of CNVs from the analysis dataset of SCORM, which were detected by three to seven of the methods tested herein and computed the mean and SD of each CNV. Finally, at each CNV location, we randomly chose a CNV from the pool that had the same copy number, frequency of the detection methods and CNV size as designated in Figure 1. At each CNV location, we simulated the same numbers of CNV SNPs with log R ratio of each SNP randomly drawn from the interval of mean ± SD. For each simulation, 100 replicates were generated.
A neutral simulation was designed as a platform independent test of CNV detection methods. Log R ratios of all SNPs were initially assigned by drawing from a normal distribution with mean 0 and SD 0.25, which is between the Illumina and Affymetrix SDs of datasets used in this study. Forty-eight CNVs, 12 for each of copy numbers 0, 1, 3 and 4 were created by replacing initial log R ratios with log R ratios from the CNV distribution as detailed in Supplementary Table S2. CNVs were placed every 1000 SNPs. For each sample, each CNV was given a random size of 3–15 SNPs and was randomly placed at one of 48 locations. B allele frequencies were randomly assigned from a range of 0–0.07 for AA, 0.52–0.68 for AB and 0.89–1 for BB, where all genotypes are equally likely. SNP positions were spaced randomly from 1–10 000 bp. Since QuantiSNP and PennCNV calls are dependent on platform data, SNP names from Illumina HumanHap 550 chromosomes 18–22 were used.
A simulation based on Affymetrix 6.0 chip data was designed using log R ratio and B allele frequency data generated by PennCNV-Affymetrix (6) from Gene Expression Omnibus (GEO) (12) dataset GSE13372 (13). Log R ratios of all SNPs were initially assigned by drawing from a normal distribution with mean and SD equal to the mean of these two statistics in the GSE13372 samples. Forty CNVs, 10 for each of copy numbers 0, 1, 3 and 4 were created. First, a CNV detected by PennCNV within the GSE13372 dataset was randomly selected. Second, log R ratios were generated by drawing from a normal distribution with the mean and SD of the randomly selected CNV from the GEO dataset (Supplementary Table S3). CNV position and size and B allele frequency were assigned as in the neutral simulation. CNVs were placed every 1000 SNPs. SNP positions were spaced randomly from 1 to 5000 bp to model Affymetrix 6.0 chip density. Since QuantiSNP only works on Illumina data, chromosome 1 SNP names from Illumina HumanHap 550 were used for QuantiSNP, the PennCNV Illumina HMM and Nexus Rank and SNP Rank. Affymetrix SNP names were tested on the PennCNV gw6 and agre HMMs.
RESULTS
Optimization of method parameters
The minimum NSR was observed for parameter settings of 1 SD for the CBS program, (6, 5, 4 and 2 SDe) for the CNVFinder program, 0 confidence for the cnvPartition program, α = 0.001 for the GLAD program, 1 SNP length for the PennCNV program, significance threshold = 0.01 for the Nexus Rank and Nexus SNPRank programs and L = 2 000 000 for the QuantiSNP programs using the training dataset (Table 1). These optimal parameters also lead to maximum ROC curve residuals for all but CBS. ROC residuals were calculated using our Asian HapMap CNV database. The same parameter settings were also observed as optimal for the analysis dataset and the large majority of parameter-DNA source combinations in the pilot dataset by ROC curve residuals (Tables 2 and 3). In simulation 1, the optimal parameters for ROC curve residuals are typically maximal at more conservative parameters than NSR optimal parameters, because NSR optimized parameters decreased specificity without increasing sensitivity (Supplementary Table S4). In all other simulations, sensitivity continued to increase more quickly than 1-specificity, and so optimal parameters concluded by NSR and ROC curve residuals agree with those concluded for the training dataset except for Nexus Rank (Supplementary Table S4). Overall, almost all datasets confirm the validity of the NSR as a metric in choosing optimal parameters.
Table 1.
Results of NSR optimization search on the training datasets
| Method | Parameters | CNV SNPs per Sample | Unique CNV SNPs | NSR | ROC residual |
|---|---|---|---|---|---|
| CBS | 1 standard deviation | 275 | 0.8050 | 0.00293 | 0.00284 |
| 3 standard deviations | 270 | 0.8135 | 0.00302 | 0.00325 | |
| 4 standard deviations | 265 | 0.8169 | 0.00309 | 0.00316 | |
| 5 standard deviations | 130 | 0.9158 | 0.00707 | 0.00079 | |
| CNVFinder | SDe = 6, 4, 4, 2 | 630 | 0.8476 | 0.00135 | 0.0016 |
| SDe = 7, 5, 4, 2 | 446 | 0.8907 | 0.00200 | 0.00114 | |
| SDe = 8, 7, 6, 5 | 258 | 0.9037 | 0.00350 | 0.00061 | |
| cnvPartition | Confidence >0 | 195 | 0.8187 | 0.00420 | 0.00257 |
| Confidence >5 | 193 | 0.8185 | 0.00425 | 0.00253 | |
| Confidence >10 | 186 | 0.8167 | 0.00440 | 0.00249 | |
| GLAD | Default | 262 | 0.7245 | 0.00276 | 0.00208 |
| Segment log R > |0.3| | 243 | 0.7476 | 0.00307 | 0.00186 | |
| Segment log R > |0.4| | 192 | 0.7724 | 0.00402 | 0.00111 | |
| Nexus Rank | Threshold <0.01 | 10 126 | 0.8696 | 8.588E–5 | 0.00481 |
| Threshold <0.001 | 2041 | 0.9385 | 0.00046 | 0.00349 | |
| Threshold <0.0001 | 540 | 0.9137 | 0.00169 | 0.00312 | |
| Nexus SNPRank | Threshold <0.01 | 235 | 0.7862 | 0.00335 | 0.00288 |
| Threshold <0.001 | 206 | 0.7816 | 0.00380 | 0.00272 | |
| Threshold <0.0001 | 185 | 0.7889 | 0.00426 | 0.00246 | |
| PennCNV | All CNV calls | 271 | 0.7909 | 0.00292 | 0.00284 |
| SNPs >1 | 248 | 0.7677 | 0.00310 | 0.00282 | |
| QuantiSNP | L = 2000000 | 332 | 0.8793 | 0.00265 | 0.00313 |
| L = 3000000 | 314 | 0.8423 | 0.00268 | 0.00311 | |
| L = 4000000 | 283 | 0.7978 | 0.00282 | 0.00308 | |
| Log Bayes ≥0 | 311 | 0.8312 | 0.00267 | 0.00308 | |
| Log Bayes ≥2.5 | 268 | 0.8111 | 0.00303 | 0.00299 | |
Table 2.
Number of CNV SNPs and ROC curve residuals for each DNA type in the pilot dataset
| Method | Parametera | Measureb | Buccal | Saliva | Blood | Amplified Buccal |
|---|---|---|---|---|---|---|
| CBS | 1 SD | CNV SNPs | 391 | 209 | 688 | 51 404 |
| ROC residual | 0.0024 | 0.0009 | −8.3E–5 | 0.0217 | ||
| 4 SD | ROC residual | 0.0024 | 0.0009 | −5.9E–5 | 0.0217 | |
| CNVFinder | 6,4,4,2 SDe | CNV SNPs | 336 | 371 | 218 | 2032 |
| ROC residual | 0.0007 | 0.0007 | 0.0008 | 0.0063 | ||
| 7,5,4,2 SDe | ROC residual | 0.0005 | 0.0005 | 0.0007 | 0.0038 | |
| cnvPartition | Confidence >0 | CNV SNPs | 329 | 212 | 410 | 4900 |
| ROC residual | 0.0018 | 0.0012 | 0.0013 | 0.0166 | ||
| Confidence >5 | ROC residual | 0.0018 | 0.0012 | 0.0013 | 0.0167 | |
| GLAD | All calls | CNV SNPs | 135 | 157 | 646 | 7667 |
| ROC residual | 0.0011 | 0.0010 | −0.0009 | 0.0121 | ||
| Smoothed µ > |0.3| | ROC residual | 0.0011 | 0.0010 | 0.0011 | 0.0122 | |
| Nexus Rank | Threshold = 1E–2 | CNV SNPs | 29 843 | 54 662 | 57 186 | 285 812 |
| ROC residual | 0.0057 | 0.0098 | −0.0573 | 0.0096 | ||
| Threshold = 1E–4 | ROC residual | 0.0026 | 0.0029 | 0.0014 | 0.0170 | |
| Nexus SNPRank | Threshold = 1E–2 | CNV SNPs | 592 | 1528 | 2717 | 85 646 |
| ROC residual | 0.0016 | 0.0008 | −0.0003 | 0.0217 | ||
| Threshold = 1E–4 | ROC residual | 0.0011 | 0.0008 | −0.0003 | 0.0216 | |
| PennCNV | SNPs ≥1 | CNV SNPs | 278 | 411 | 382 | 6 663 |
| ROC residual | 0.0016 | 0.0016 | 0.002 | 0.0201 | ||
| SNPs ≥2 | ROC residual | 0.0016 | 0.0016 | 0.0019 | 0.0142 | |
| Confidence >2 | ROC residual | 0.0016 | 0.0016 | 0.0019 | 0.0144 | |
| QuantiSNP | L = 2M | CNV SNPs | 468 | 739 | 568 | 36 200 |
| ROC residual | 0.0026 | 0.0022 | 0.0029 | 0.0267 | ||
| L = 2M; LBF >0 | ROC residual | 0.0025 | 0.0021 | 0.0023 | 0.0235 |
aBold text designates NSR optimal parameter results for each method.
bCNV SNPs are given as number per sample.
Table 3.
ROC curve residuals used to optimize parameters on the analysis dataset
| Method | Parameter | DGV ROC residual | HapMap Asian ROC residual | HapMap confirmed ROC residual |
|---|---|---|---|---|
| CBS | 5 SD | 4.41E–4 | 6.91E–4 | 0.0020 |
| 3 SD | 4.99E–4 | 8.22E–4 | 0.0023 | |
| 1 SD | 9.62E–4 | 0.00172 | 0.0035 | |
| CNVFinder | 8,7,6,5 SDe | 1.85E–4 | 2.56E–4 | 8.36E–4 |
| 7,5,4,2 SDe | 3.76E–4 | 5.10E–4 | 0.0015 | |
| 6,4,4,2 SDe | 6.46E–4 | 9.03E–4 | 0.0024 | |
| cnvPartition | Confidence >10 | 6.98E–4 | 0.00146 | 0.0026 |
| Confidence >5 | 7.21E–4 | 0.00148 | 0.0027 | |
| Confidence >0 | 7.33E–4 | 0.00153 | 0.0028 | |
| GLAD | Smoothed µ >|0.4| | 5.04E–4 | 7.99E–4 | 0.0022 |
| Smoothed µ >|0.3| | 5.87E–4 | 9.59E–4 | 0.0024 | |
| Default | 6.78E–4 | 0.00107 | 0.0026 | |
| Nexus Rank | Threshold 1E–4 | 0.00313 | 0.00307 | −0.00293 |
| Threshold 1E–3 | 0.00432 | 0.00386 | −0.00816 | |
| Threshold 1E–2 | 0.00744 | 0.00578 | −0.03105 | |
| Nexus SNPRank | Threshold 1E–4 | 8.95E–4 | 0.00128 | 1.23E–4 |
| Threshold 1E–3 | 0.00106 | 0.00147 | 1.69E–4 | |
| Threshold 1E–2 | 0.00122 | 0.00174 | 1.79E–4 | |
| PennCNV | Confidence >17.5 | 7.35E–4 | 0.00131 | 0.0025 |
| Confidence >10 | 9.01E–4 | 0.00155 | 0.0030 | |
| SNPs ≥ 1 | 9.65E–4 | 0.00166 | 0.0032 | |
| QuantiSNP | Log Bayes >10 | 9.23E–4 | 0.00159 | 0.0030 |
| Log Bayes >2.5 | 0.0012 | 0.00196 | 0.0038 | |
| L = 2E6 | 0.0015 | 0.00228 | 0.0043 |
Maximal ROC curve residuals are optimal and indicated in bold.
The number of CNV SNPs detected at optimal parameters was typically 150–350 per sample, with cnvPartition calling the fewest. Nexus Rank, however, called by far the most CNV SNPs per sample, over 10 000. Even so, it also had the best ROC residual of all methods (Table 1). QuantiSNP had double the number of CNV SNPs of most methods and also had good NSR and ROC statistics. GLAD had the lowest proportion of unique CNV SNPs (0.72), and QuantiSNP had the highest proportions (0.88). Optimal NSR parameters were identical for all methods over three training datasets varying in chip type and genotype rate.
Method performance for multiple DNA sources
Table 2 summarizes the average number of CNV SNPs per sample and ROC curve residuals for each method at NSR optimal and suboptimal parameters for four DNA types in the pilot dataset. As with the training dataset, the Nexus algorithms overcalled CNV SNPs with as many as three (SNPRank) to 100 (Rank) times the number of calls of other methods (Table 2). The number of SNPs of the Nexus CNVs in the saliva data was small compared to the size of other methods’ CNVs, especially GLAD and cnvPartition, which were more than double the size of the Nexus CNVs. The pattern across DNA types was similar between Nexus and other methods. Amplified buccal DNA consistently showed the highest number of CNV SNPs (2032–225 597) across all methods in comparison to other DNA types (135–39 759). The excessive number of CNV calls in amplified buccal DNA caused bias of the ROC curve residuals, resulting in it having the best performance across all methods. The relationship between the number of CNV and CNV SNP calls in the pilot dataset is found in Table 4. If amplified buccal DNA is disregarded because of overcalling, the ROC residuals were best in blood-derived DNA samples in half of the methods. Overall, the performance of DNA from saliva, blood and buccal swabs was comparable in terms of the number of CNV SNP calls and the value of the ROC curve residuals, which is consistent with the observation of genotype call rates (data not shown).
Table 4.
The relationship between CNV SNPs and CNVs
| CBS | CNVFinder | cnvPartitiona | GLAD | Nexus rank | Nexus SNPRank | PennCNV | QuantiSNP | |
|---|---|---|---|---|---|---|---|---|
| Pilot CNV SNPs | 1046 | 1855 | 1060 | 785 | 273 311 | 7640 | 2055 | 3694 |
| Pilot CNVs | 127 | 210 | 64 | 62 | 42 468 | 1405 | 405 | 369 |
| Pilot SNPs/CNV | 8.24 | 8.83 | 16.56 | 12.66 | 6.44 | 5.44 | 5.07 | 10.01 |
| Analysis CNV SNPs | 35 650 | 119 780 | 18 520 | 32 300 | 3 179 600 | 43 370 | 29 560 | 70 190 |
| Analysis CNVs | 5680 | 13 110 | 1380 | 1520 | 544 410 | 1960 | 6030 | 29 560 |
| Analysis SNPs/CNV | 6.28 | 9.14 | 13.42 | 21.25 | 5.84 | 22.13 | 4.90 | 8.22 |
| Sim 1 CNV SNPs | 24 249 | 47 549 | N/A | 24 370 | 28 178 | 24 059 | 24 080 | 24 825 |
| Sim 1 CNVs | 1319 | 5084 | N/A | 1368 | 1448 | 1202 | 1266 | 1256 |
| Sim 1 SNPs/CNV | 18.38 | 9.35 | N/A | 17.81 | 19.46 | 20.02 | 19.02 | 19.77 |
| Sim 2 CNV SNPs | 21 225 | 21 077 | N/A | 19 209 | 23 037 | 20 564 | 21 066 | 23 041 |
| Sim 2 CNVs | 3587 | 2921 | N/A | 3144 | 2320 | 3346 | 3337 | 3696 |
| Sim 2 SNPs/CNV | 5.92 | 7.22 | N/A | 6.11 | 9.93 | 6.15 | 6.31 | 6.23 |
aN/A is used here because cnvPartition was not evaluated in the simulations.
Method performance by analysis dataset at optimal parameters
The Nexus Rank algorithm again overcalled CNV SNPs (31 796 per sample), and the cnvPartition program detected the least number of CNV SNPs (185 per sample) with at least 40% fewer calls than other methods (Supplementary Table S5). The segmentation methods CBS and GLAD had similar call numbers. The HMM-based PennCNV and QuantiSNP algorithms had divergent CNV SNP call detection numbers (average 295.6 vs. 701.9 CNV SNPs, respectively). Call numbers were correlated to sensitivity, specificity and kappa. Given this correlation, GLAD and CNVFinder did not perform as well as expected for sensitivity, specificity and kappa given their number of CNV SNP calls (Supplementary Table S5). CNVs from GLAD and SNPRank (21 and 22 SNPs long) were four times as big as PennCNV (5 SNPs long) on average. Rank and CBS CNVs were also small at an average of 6 SNPs per CNV. Further details on the relationships between CNVs and CNV SNPs are in Table 4.
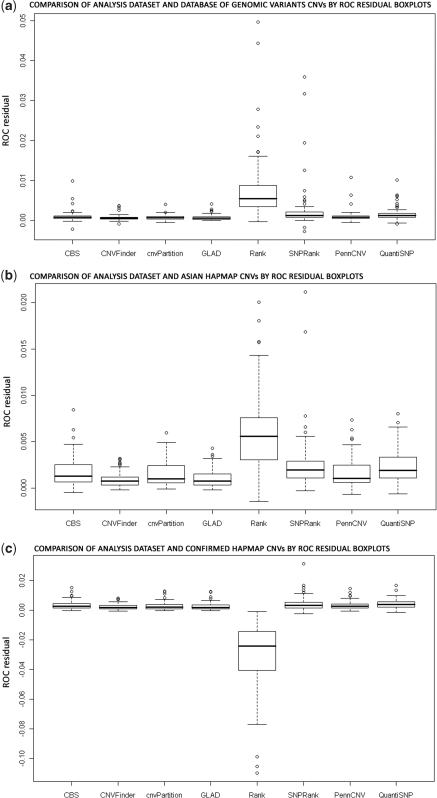
Nexus Rank, QuantiSNP and Nexus SNPRank were the top three programs on our DGV and HapMap Asian CNV databases (ROC residuals 0.0058, 0.0023 and 0.0017, respectively, on the HapMap Asian database) (Table 3, Figure 2). However, Rank falls to the bottom rank in the HapMap Confirmed database. The high ROC curve residuals in the Nexus algorithms were primarily due to overcalling CNVs, which results in sensitivity increasing more quickly than 1-specificity (Table 3). Nexus Rank and CNVFinder had wide distributions of residuals, demonstrating a lot of sample-to-sample variation. The SD of Rank’s sensitivity and specificity distributions were approximately equivalent (0.045 and 0.04, respectively), indicating that the primary factor in the variance is the number of CNV calls per sample. When the total number of CNV calls was fixed to the same level for these methods, we observed smaller ROC curve residuals for the Nexus programs than that of the QuantiSNP and CBS programs (data not shown).
Figure 2.
Boxplots for ROC curve residual from comparison of CNVs in the analysis dataset and three CNV databases. (a) CNVs from SNP studies in the Database of Genomic Variants were used to compute sensitivity and 1-specificity. (b) CNVs from Asian samples in HapMap from Redon et al. (11) were used. (c) Experimentally confirmed CNVs in all HapMap samples from Redon et al. (11) were used.
Method performance by simulation 1 at optimal parameters
Ranking by ROC curve residual
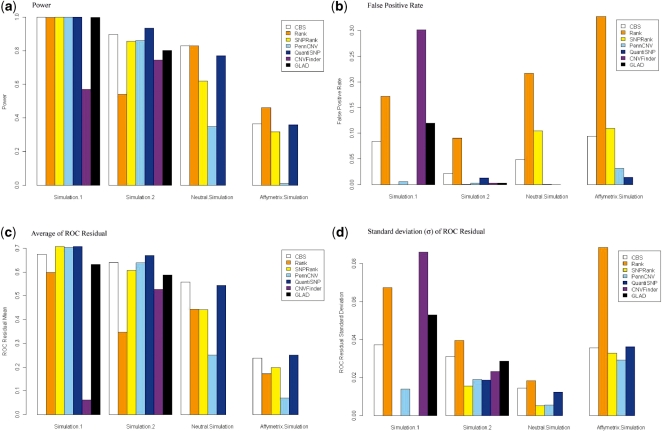
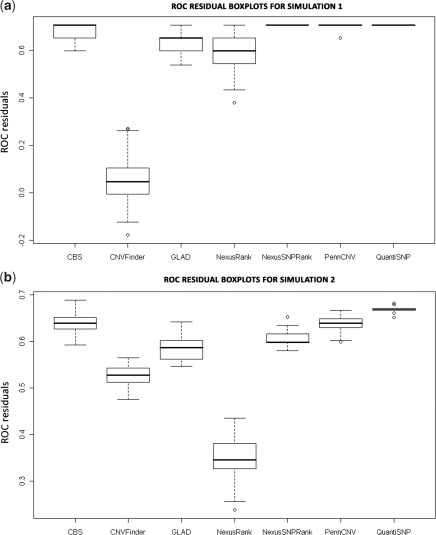
Parameters other than those displayed in Supplementary Tables S4 and S6 were tested. Parameters displayed reflect ROC optimal parameters for simulation 1, NSR optimized parameters or parameters with measurable differences from the optimal parameter. Methods ranked from first to last using CNVs were as follows: QuantiSNP and Nexus SNPRank, PennCNV (average ROC residual = 0.707), PennCNV (0.703), CBS (0.675), GLAD (0.631), Nexus Rank (0.598) and CNVFinder (0.061) (Figure 4c; Supplementary Table S4). The interquartile ranges (IQRs) of the highest ranking methods: CBS, Nexus SNPRank, PennCNV and QuantiSNP have the highest ROC residuals and are overlapping (Figure 3a). These methods also displayed comparable sensitivity and specificity rates. Power and false positive rates differed between the CNV and CNV SNP levels, and so ROC values and rankings also differed (Figure 4; Supplementary Table S6).
Figure 4.
Performance comparison of CNV detection methods using simulated data. (a) power, (b) false positive rate, (c) mean of ROC curve residuals for 100 simulated samples and (d) standard deviation of ROC residuals for 100 simulated samples. CNVFinder and GLAD were not tested on the Neutral and Affymetrix simulations and so do not appear in these graphs.
Figure 3.
Boxplots of ROC curve residual from simulated data for each method. (a) ROC residuals from simulation 1. (b) ROC residuals from simulation 2.
Power and false positive rate
For this simulation, all methods but CNVFinder showed similar power to detect predesignated CNVs, with power greater than 99.8% under the NSR optimal parameter setting for each method (Figure 4a; Supplementary Table S4). False positive CNV calls varied greatly from 0 in the QuantiSNP and SNPRank programs to 296 in the CNVFinder program, which translates to a range of false positive rates from 1.65E–5 to 0.006. CNVFinder, GLAD and Nexus Rank had high false positive rates at both the CNV and CNV SNP levels, while CBS had a high rate (0.08) at the CNV level alone (Figure 4b; Supplementary Tables S4 and S6). At the CNV SNP level, ROC residual rankings were different primarily due to different rankings of false positive rates for the methods. Additionally, the computation of ROC at the CNV SNP level allowed ROC residuals to remain high despite relatively large numbers of false positive CNV SNPs, for example, in CNVFinder. Unlike the analysis of SCORM SNP array data, the total number of CNVs detected by each method displayed minimal variance in this simulated dataset except for the CNVFinder method, which detected the highest number of false positive CNVs under the NSR optimal parameter setting.
Failure in CNV detection
Method performance was impaired by simulated CNV size and copy number at parameters that are stricter than NSR optimal. CBS did not detect any three copy CNVs at a strict setting of 5 SD. CNVFinder was impaired in detecting three copy CNVs at stricter settings than optimal. PennCNV had a weakness in detecting the simulated 10-SNP duplication CNVs but not the simulated 20- or 30-SNP CNVs. Nexus Rank and SNPRank had no significant failures in detection using the attempted parameters. However, the previous version of these algorithms (4.0) had failures in detecting the simulated 10-SNP CNVs (data not shown). In that version, when a stringent significance threshold of 1E–8 was applied, neither Nexus method detected 10-SNP CNVs. The PennCNV method failed to detect 10-SNP CNVs with copy numbers of three or four.
CNV boundary calling
The average size of CNVs detected by Nexus Rank was 3 SNPs larger than simulated, which is consistent with the specificity and kappa statistics observed in the real data. GLAD and CBS had the most accurate CNV boundaries (>99 and >98%, respectively), though CBS called a CNV with large variation as half its simulated size 6% of the time. PennCNV and QuantiSNP had a relatively low percentage of exact boundary calling (80 and 60%, respectively), but the miscalled boundary was only one SNP longer most of the time (70 and 75%, respectively). On average, CNVFinder CNVs had half the expected size in SNPs, while GLAD and CBS CNVs were 2 SNPs smaller than expected. Data on the relationship between the numbers of CNV and CNV SNP calls in simulations 1 and 2 are located in Table 4.
Method performance by simulation 2 at optimal parameters
Ranking by ROC curve residual
ROC curve residuals were computed at both the CNV and CNV SNP levels. By this measure at the CNV level, the top four methods in order were as follows: QuantiSNP (0.67), CBS (0.640), PennCNV (0.638) and Nexus SNPRank (0.606) (Figure 4a; Supplementary Table S4). QuantiSNP, CBS, PennCNV and SNPRank have the same ranking at the CNV SNP level as well. For the distributions of CNV-based ROC curve residuals, QuantiSNP’s IQR was highest and did not overlap any other IQR. The IQRs of CBS and PennCNV were next highest and only overlap each other (Figure 3b). The low-ROC curve residuals for Nexus Rank were most likely due to excessive overcalling that resulted in low specificity (Supplementary Table S4). QuantiSNP still ranked first based on the ROC curve residuals derived from CNV SNPs. Overall, QuantiSNP, CBS and PennCNV were considered to be the top three methods from the analyses of CNVs and CNV SNPs (Supplementary Tables S4 and S7).
Power and false positive rate
QuantiSNP, CBS and PennCNV were also the top three methods ranked by power and had moderate false positive rates in the analyses of both CNVs and CNV SNPs (Figure 4a and b; Supplementary Tables S4 and S7). These methods demonstrated good power, ranging from 0.86 to 0.94 for CNVs and 0.90 to 0.95 for CNV SNPs, and good false positive rates (maximum rate = 0.022 for CNVs and 2.83 × 10−4 for CNV SNPs). In contrast, at the CNV level, Nexus Rank and SNPRank had moderate power (e.g. 0.8 and 0.86, respectively), and Rank had a high false positive rate (0.47). The CNVFinder program had the lowest power for both CNV and CNV SNPs (0.75 and 0.76, respectively), but the false positive rate was smaller than Nexus Rank (e.g. 0.003 versus 0.47). A stricter parameter setting alleviated the high-false positive rate of Nexus Rank, but power was also significantly decreased.
Failure in CNV detection
Method performance was impaired by at least one of three aspects of the simulated CNVs: number of methods detecting the real CNV based on the simulation (sim2 mm), copy number (sim2 copy) and number of SNPs (sim2 size) specified in Figure 1. The number of detection methods in the real data did not greatly impact the performance of all methods. Only CBS showed the trend of missing CNVs with three copies for those modeled by three to four detection methods, with a missing rate of >50%. The copy number probably had the greatest impact on the performance of each method. The GLAD program was impaired in detecting three copy CNVs with a relatively low-detection rate of 45%, in comparison with 91% for detecting four copy CNVs. The CNVFinder program was impaired in detecting three copy CNVs with a low-detection rate of 25%, while 84% of four copy CNVs was detected. Nexus SNPRank had a detection rate of 72% of three copy CNVs, while 98% of four copy CNVs was detected. Small CNV sizes were generally harder to detect by most methods. For instance, the Nexus Rank, PennCNV and QuantiSNP programs were compromised detecting three to four SNP CNVs with a wide range of detection rates: 8% for 3-SNP CNVs by Nexus Rank, 76% for 3-SNP CNVs, 81% for 4-SNP CNVs by PennCNV and 82% for 4-SNP CNVs by QuantiSNP. As for impaired boundary calling, on average, Rank CNVs were 4 SNPs longer than expected and CNVFinder was one SNP longer.
Method performance by neutral and affymetrix simulations at optimal parameters
These simulations were conducted to test the methods on other SNP platforms. Methods with at least moderate ranking in the previously discussed datasets—CBS, Nexus Rank and SNPRank, PennCNV and QuantiSNP—were tested. Optimal parameters for the methods were consistent with the NSR optimized methods in both analyses, except for Nexus Rank. Ranking by ROC, power and false positive rates is largely consistent with Illumina-based simulations and real data. QuantiSNP and CBS are the top two methods, with QuantiSNP first rank by ROC residual in the Affymetrix simulation and CBS first rank in the neutral simulation (Figure 4; Supplementary Table S4). In the neutral simulation, which had CNVs with larger variation than the other simulations (Supplementary Table S2), QuantiSNP often had CNVs more than twice the simulated size, because it bridged the simulated CNV with nearby SNPs that had log R ratios that deviated from the mean in the same direction as the simulated CNV. PennCNV and SNPRank had low power in both analyses, with PennCNV having much lower power than SNPRank, which had power 4 or 15% lower than QuantiSNP (Affymetrix and Neutral simulations, respectively). Rank had the highest power, but also had the highest false positive rate, and so it did not have the highest ROC residual (Figure 4; Supplementary Table S4). Of the three HMMs tested on Affymetrix simulations, PennCNV’s agre HMM had the highest ROC residual (Supplementary Table S4).
DISCUSSION
We present a systematic evaluation of seven current methods for detecting CNVs from genome wide SNP chips on real Illumina data and on simulated Illumina, Affymetrix and platform-independent data. Consistent method performance across platforms gives evidence that the results of this study can be extended to multiple SNP-based platforms. While the goal was to determine an optimal CNV detection method for real data applications, we also present an analytical algorithm for detecting CNVs from SNP arrays. We recommend using a subset of samples with high-quality genotype call rates as a training dataset to determine the best parameter setting for a CNV detection method before analyzing the full dataset. Our study demonstrated that the NSR can serve as a good summary metric to determine the optimal parameters, even for a limited sample size of 10. When multiple detection methods were applied to the same dataset, our study showed that ROC curve residuals, which use sensitivity and specificity, can be a good summary statistic to determine the performance of each method. Through the evaluation of real SNP arrays and simulated data, we conclude that the QuantiSNP program outperformed other methods by the evaluation measures (ROC curve residuals and NSR) used in this study. Two segmentation methods, the Nexus Rank and SNPRank programs, are ranked next to QuantiSNP. However, deficits of these two methods were also observed as discussed below.
The top ranking performance of the QuantiSNP program was consistent in real and simulated datasets that were examined in this study. The fact that QuantiSNP was designed for Illumina data may give it an advantage in Illumina-based simulations and our real data. However, its performance characteristics are consistent in the neutral and Affymetrix simulation datasets. Over all datasets, QuantiSNP ranked by ROC curve residuall and NSR were generally higher than other methods. The number of CNV SNP calls was average, unlike the Nexus program, which often overcalled CNV SNPs. Simulation studies showed that QuantiSNP had the highest statistical power in simulation 2 to detect CNVs (93.5%) and CNV SNPs (95.4%) (Supplementary Tables S4 and S7). Although its false positive rate was not the least among all methods, the rate was small (0.013 for CNVs and 2.83 × 10−4 for CNV SNPs, simulation 2). In other simulations, although power was not as high as Nexus Rank, QuantiSNP had a low false positive rate while Rank did not, and so it had a higher ROC residual. We did not observe any major weaknesses in CNV detection or boundary calling for the QuantiSNP program in the Illumina or Affymetrix simulations, but high amounts of variation in log R ratio distributions cause real CNVs to merge with regions of noise, creating CNVs larger than simulated especially for simulated CNVs of 10-15 SNPs. The Nexus Rank method also had larger CNVs with larger variation, averaging two SNPs larger than the model in simulation 2 and one SNP larger than the model in simulation 1.
Both the CBS and Nexus programs are based on segmentation methods and have similar rankings in terms of performance. The CBS program had strong boundary calling, but had trouble detecting CNVs that were detected by the majority of CNV detection methods. The Nexus Rank and Nexus SNPRank programs are two commercially available segmentation algorithms that are well-documented and user-friendly for CNV analyses and provide visualization of the results in a biological context. While our evaluation indicators such as NSR and ROC curve residuals were promising for the Nexus methods, there are concerns about these methods. Rank’s ROC residuals were inflated by the abundant number of calls as reflected in simulation 2 with a false positive rate of 44% at the CNV level and in the analysis dataset with the lowest specificity of all methods. Rank also has boundary calling problems, with most CNVs called 1–2 SNPs too long and 3–4 SNP CNVs called as 6–7 SNP CNVs. Both Nexus methods have difficulty achieving sufficient power at moderate false positive rates. For example, in simulation 2 and the neutral and Affymetrix simulations, SNPRank can only achieve moderate power while Rank only has high power with a high false positive rate.
The correlation between the results at the CNV and CNV SNP levels are influenced by the boundary calling properties of the method and by the statistical properties of the specificity calculation at the two levels. For example, in simulation 1, QuantiSNP’s inaccuracies in boundary calling give a moderately high-false positive rate at the CNV SNP level, while at the CNV level there are zero false positives. This is one factor contributing to QuantiSNP’s different optimal parameters for the two levels. The second factor is the specificity calculation. For example, because a single false positive CNV has more impact than a single false positive CNV SNP on both false positive rate and sensitivity, Rank’s overabundant CNV calls made the optimal parameter for CNV SNPs (1E–3) less stringent than the one for CNVs (1E–4).
Is there an inherent advantage for QuantiSNP, because it was developed for Illumina SNP arrays, while CBS, GLAD and CNVFinder were developed for other platforms? A definite answer cannot be given here, because testing on real data from multiple platforms was not done here. QuantiSNP could have this advantage, but there are other possibilities. One possibility is that methods developed for SNP array data, like HMMs, are more sophisticated than the methods developed for other platforms, like segmentation and SD-based methods, which would indicate that the advantage of QuantiSNP is method based instead of platform based. Another possibility is that the inherent quality of QuantiSNP, regardless of platform or method type, is higher than that of other methods. There is evidence that the latter is true. First, CBS ranks higher than PennCNV in the analysis, simulation 2, Affymetrix simulation and neutral simulation datasets. This shows that not all HMM methods are superior to segmentation methods like CBS and Nexus. Furthermore, this shows that methods not developed for SNP arrays can outperform methods created for SNP arrays. Second, CBS both has good performance in this SNP array study, and it also had the best performance in the Lai et al. 2005 (10) CGH study, giving additional evidence for platform-independent ranking performance.
The PennCNV program is a HMM-based algorithm like the QuantiSNP program and is probably the most frequently used program for CNV studies in recent publications (14–16). This is in part due to the user-friendly design of the program and free access to users. However, our evaluation ranked the performance of PennCNV at the intermediate level. Simulation 2 showed that the PennCNV program has moderate power. However, its low false positive rate is a promising aspect. The NSR and ROC curve residuals were moderate on real data. It generally detects less CNVs than other methods except cnvPartition in the analysis dataset. It also has some trouble detecting small CNVs (three to four SNP CNVs), which is exacerbated by using stricter than optimal parameters used in our study. These observations serve as good references for the application of PennCNV.
In tuning parameters, the NSR is a more straightforward measure than using ROC curves. It is database independent and does not require the calculation of multiple statistics. As a database independent measure, the NSR does not have to take into account CNV database issues such as limited CNV studies in certain populations, largely unknown CNV population frequencies, and the fact that studies without dense marker spacing call a higher number of CNVs relative to real CNV counts. For instance, we found very low sensitivity between our population and the corresponding ethnic population in the Database of Genomic Variants (3). This is largely due to the large number of CNVs and the lack of CNV validation in DGV. The NSR is robust to the tested Illumina SNP array platforms, to gender bias, and to genotyping quality levels, since it was minimal at the same parameters on multiple values of these characteristics of the training dataset. Our study showed that the same conclusion can be drawn based on NSR and ROC curve residuals, which validates the usage of the NSR. In comparing method quality, the NSR overcomes the correlation between the number of CNV calls and sensitivity, specificity and kappa, which allows every method to be set at any parameter setting.
Since datasets vary in their log R ratio SDs, B allele frequency distributions and other factors, there is no single parameter setting for all datasets. Therefore, the determination of parameter setting for a CNV detection method can be a challenge. Without a priori knowledge, one may choose the default setting of the program, which may not be optimal. In this study, we proposed to standardize the parameters in a small subset of samples before the full analysis. Since half of the methods tested take at least 15 minutes per sample, it is important to find a technique that requires an initial few samples to test multiple parameter settings in order to find the optimal parameters. On the other hand, this strategy should be able to ensure that the optimal parameter setting determined in the training dataset is also optimal for the full dataset. The method used in this study accomplishes both goals. In our real data example, 10 training samples were sufficient to find the same optimal parameters as those found for the analysis dataset of 100 samples. As a secondary confirmation of optimal parameters on a training dataset, the ROC curve residual can be used with the NSR to determine if the two metrics agree. Overall, the NSR and the ROC curve residuals can provide good guidance for tuning parameters to the optimal level.
Although blood-derived DNA is considered the best choice for genotyping, not all studies can obtain blood samples, particularly for studies involving child subjects. Our analysis of DNA types on the pilot dataset concluded that buccal, saliva and blood DNA samples were comparable in CNV detection thus, these DNA sources are adequate for CNV detection. However, this conclusion may be limited to this set of small pilot samples that were selected because of known high genotype call rates. The only DNA type that showed poor performance for CNV detection by all methods was the amplified buccal DNA, as has been seen in previous studies (17,18). All methods detected too many CNV SNPs in the amplified buccal DNA compared to other DNA types (∼10 times as many), even though genotype call rates were still above 98%. Therefore, amplified buccal DNA was determined to be unreliable for CNV detection, possibly due to the large variation in the log R distribution of these samples (data not shown).
This comparison is limited in that: more parameters could be tested, especially less conservative parameters than were found to be optimal; marker density of the one million marker array will provide more accurate CNV detection and may alter relative outcomes among the methods; and there are many new methods not tested in this study. However, many more parameters were run than are shown here, and optimal parameters were often the least conservative parameter available to the method. Also, increased marker density is not likely to change the core characteristics of the methods found in this study or to radically change the rankings of the methods tested. For example, weakness in detecting CNVs with few SNPs and in boundary calling conditions should not change with an increase in marker density. Finally, this study can be used as a template for easy future studies of the many new CNV detection methods that are available now and in the future.
In summary, the utility of determining CNVs from SNP arrays usually occurs in two steps: (i) determine the genome location, and number and size of the CNVs and (ii) relate these CNVs with phenotypes of interest using methods such as association analyses. The detection of CNVs plays an important role in the final conclusion of the study. Among the seven methods evaluated in this report, we conclude that the QuantiSNP program outperformed the other methods. We also presented the limitations of each method in terms of failure of CNV detection. The NSR can be used as a valid evaluation parameter of method quality in CNV detection methods. Use of the NSR and a training dataset as demonstrated herein serves as a valid template for determining optimal parameter setting for the method of choice prior to the full data analysis.
Web resources
Database of Genomic Variants, http://projects.tcag.ca/variation/.
Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/.
Redon databases, http://www.nature.com/nature/journal/v444/n7118/full/nature05329.html.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
US National Institute of Health/National Eye Institute (1R21-EY-019086-01 to Y.-J.L.); Singapore BioMedical Research Council 06/1/21/19/466 to S.-M.S.; Singapore Tissue Network. Funding for open access charge: US National Institute of Health/National Eye Institute (1R21-EY-019086-01 to Y.-J.L).
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank all the individuals and families who participated in the SCORM study. They also thank the clinical staff for helping with recruitment and the laboratory staff at the Genome Institute of Singapore for performing the genotyping. They thank Dr Ioannis Ragoussis for allowing us trial use of the QuantiSNP program. They also thank Dr Elizabeth Hauser for her valuable suggestions to improve this manuscript.
REFERENCES
- 1.Itsara A, Cooper GM, Baker C, Girirajan S, Li J, Absher D, Krauss RM, Myers RM, Ridker PM, Chasman DI, et al. Population analysis of large copy number variants and hotspots of human genetic disease. Am. J. Hum. Genet. 2009;84:148–161. doi: 10.1016/j.ajhg.2008.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Feuk L, Carson AR, Scherer SW. Structural variation in the human genome. Nat. Rev. Genet. 2006;7:85–97. doi: 10.1038/nrg1767. [DOI] [PubMed] [Google Scholar]
- 3.Iafrate AJ, Feuk L, Rivera MN, Listewnik ML, Donahoe PK, Qi Y, Scherer SW, Lee C. Detection of large-scale variation in the human genome. Nat. Genet. 2004;36:949–951. doi: 10.1038/ng1416. [DOI] [PubMed] [Google Scholar]
- 4.Jakobsson M, Scholz SW, Scheet P, Gibbs JR, VanLiere JM, Fung HC, Szpiech ZA, Degnan JH, Wang K, Guerreiro R, et al. Genotype, haplotype and copy-number variation in worldwide human populations. Nature. 2008;451:998–1003. doi: 10.1038/nature06742. [DOI] [PubMed] [Google Scholar]
- 5.Colella S, Yau C, Taylor JM, Mirza G, Butler H, Clouston P, Bassett AS, Seller A, Holmes CC, Ragoussis J. QuantiSNP: an objective Bayes Hidden-Markov Model to detect and accurately map copy number variation using SNP genotyping data. Nucleic Acids Res. 2007;35:2013–2025. doi: 10.1093/nar/gkm076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wang K, Li M, Hadley D, Liu R, Glessner J, Grant SF, Hakonarson H, Bucan M. PennCNV: an integrated hidden Markov model designed for high-resolution copy number variation detection in whole-genome SNP genotyping data. Genome Res. 2007;17:1665–1674. doi: 10.1101/gr.6861907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hupé P, Stransky N, Thiery JP, Radvanyi F, Barillot E. Analysis of array CGH data: from signal ratio to gain and loss of DNA regions. Bioinformatics. 2004;20:3413–3422. doi: 10.1093/bioinformatics/bth418. [DOI] [PubMed] [Google Scholar]
- 8.Olshen AB, Venkatraman ES, Lucito R, Wigler M. Circular binary segmentation for the analysis of array-based DNA copy number data. Biostatistics. 2004;5:557–572. doi: 10.1093/biostatistics/kxh008. [DOI] [PubMed] [Google Scholar]
- 9.Fiegler H, Redon R, Andrews D, Scott C, Andrews R, Carder C, Clark R, Dovey O, Ellis P, Feuk L, et al. Accurate and reliable high-throughput detection of copy number variation in the human genome. Genome Res. 2006;16:1566–1574. doi: 10.1101/gr.5630906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lai WR, Johnson MD, Kucherlapati R, Park PJ. Comparative analysis of algorithms for identifying amplifications and deletions in array CGH data. Bioinformatics. 2005;21:3763–3770. doi: 10.1093/bioinformatics/bti611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Redon R, Ishikawa S, Fitch KR, Feuk L, Perry GH, Andrews TD, Fiegler H, Shapero MH, Carson AR, Chen W, et al. Global variation in copy number in the human genome. Nature. 2006;444:444–454. doi: 10.1038/nature05329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Barrett T, Troup DB, Wilhite SE, Ledoux P, Rudnev D, Evangelista C, Kim IF, Soboleva A, Tomashevsky M, Marshall KA, et al. NCBI GEO: archive for high-throughput functional genomic data. Nucleic Acids Res. 2009;37:D885–D890. doi: 10.1093/nar/gkn764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chiang DY, Getz G, Jaffe DB, O’Kelly MJ, Zhao X, Carter SL, Russ C, Nusbaum C, Meyerson M, Lander ES. High-resolution mapping of copy-number alterations with massively parallel sequencing. Nat. Methods. 2009;6:99–103. doi: 10.1038/nmeth.1276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Blauw HM, Veldink JH, van Es MA, Van Vught PW, Saris CG, van der ZB, Franke L, Burbach JP, Wokke JH, Ophoff RA, et al. Copy-number variation in sporadic amyotrophic lateral sclerosis: a genome-wide screen. Lancet Neurol. 2008;7:319–326. doi: 10.1016/S1474-4422(08)70048-6. [DOI] [PubMed] [Google Scholar]
- 15.Glessner JT, Wang K, Cai G, Korvatska O, Kim CE, Wood S, Zhang H, Estes A, Brune CW, Bradfield JP, et al. Autism genome-wide copy number variation reveals ubiquitin and neuronal genes. Nature. 2009;459:569–573. doi: 10.1038/nature07953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Vrijenhoek T, Buizer-Voskamp JE, van d.SI, Strengman E, Sabatti C, van Geurts KA, Brunner HG, Ophoff RA, Veltman JA. Recurrent CNVs disrupt three candidate genes in schizophrenia patients. Am. J. Hum. Genet. 2008;83:504–510. doi: 10.1016/j.ajhg.2008.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fiegler H, Geigl JB, Langer S, Rigler D, Porter K, Unger K, Carter NP, Speicher MR. High resolution array-CGH analysis of single cells. Nucleic Acids Res. 2007;35:e15. doi: 10.1093/nar/gkl1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pugh TJ, Delaney AD, Farnoud N, Flibotte S, Griffith M, Li HI, Qian H, Farinha P, Gascoyne RD, Marra MA. Impact of whole genome amplification on analysis of copy number variants. Nucleic Acids Res. 2008;36:e80. doi: 10.1093/nar/gkn378. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.