Post-translational modifications of amino acid side chains, are crucial in structural biology due to their modulation of signaling pathways in the cell.1 Phosphorylation is the most widely known and well studied form of reversible post-translational modification, playing a key role in signaling mechanisms in diverse cellular processes such as ion channel regulation, metabolism and cell cycle modulation.2 In smooth muscle, phosphorylation of S19 (pS19) on the regulatory light chain (RLC) is required for activation of muscle contraction. The unphosphorylated state of smooth muscle myosin has negligible catalytic activity, while phosphorylation produces as much as a 1000-fold increase in actin-activated ATPase activity3, 4. Electron paramagnetic resonance (EPR) experiments 5 and computational simulations 6 on spin-labeled RLC bound to functional myosin have provided insight into the conformational shifts induced by phosphorylation in the N-terminal phosphorylation domain (PD) of this protein. These studies have shown that, upon phosphorylation, the PD undergoes a disorder-to-order transition. Molecular dynamics (MD) simulations of PD suggest that the interaction between pS19 and the adjacent residue R16 plays a major role in the phosphorylation-induced conformational transitions5. Here we provide a quantitative analysis of the thermodynamic and structural basis of the phosphorylation-induced disorder-to-order conformational transitions of RLC by means of molecular dynamics simulations.
Two independent all-atom MD simulations of phosphorylated and unphosphorylated PD were performed using the program NAMD7 and the CHARMM 27 force field8 with CMAP correction9. SSKRAKAKTTKKRPQRATSNVFAMF, the sequence of PD, was translated into an ideal α-helix, which was used as a starting model. Phosphorylation was assigned to S19. The production runs were carried out for 140 ns using a NPT ensemble with periodic boundary conditions. The free energy change in the phosphorylation-induced disorder-to-order transition was calculated using the MM/PBSA method 10.The entropic contribution to the relative free energy was estimated using the quasi-harmonic approximation11, as discussed in detail in Supporting Information.
Analysis of the trajectories showed that in the absence of phosphorylation, the peptide experienced a loss of α-helical periodicity at positions T9-K11 (Figure 1), with an inherent gain of conformational backbone dynamics (Figure S1A). In contrast, phosphorylation favored α-helical periodicity, populating the ordered state of the peptide (Figure 1, Figure S1B). Moreover, a stable salt-bridge interaction between pS19 and R16 was present in at least 90% of the total time of simulation.
Figure 1.

Decomposition of the free energy of ordering
The trend observed in these MD simulations corresponds to the previously suggested effect of phosphorylation in the ordering of the PD6, with two significant differences in the present study: the absence of a transient π-helix in both unphosphorylated and phosphorylated peptides and the shift of backbone disorder from region K12-Q15 to T9-K11. These differences arise from the use of the CMAP correction in the present study, which has been found to more accurately describe protein backbone motions9. The presence of a stable α-helix is in closer agreement with EPR data5. The existence of a disordered region at T9-K11 correlates well with the presence of P14, which apparently increases the rigidity of the N terminus and disfavors the stability of the backbone hydrogen bond between T10 and P14.
We calculated the free energy change of the phosphorylation-induced disorder-to-order transition (ΔGord) from the MD trajectories (Figure 1). Short- and long-range electrostatic interactions introduced by phosphorylation were found to significantly contribute to the favorable enthalpy of ordering. For instance, the contact minimum free energies of the interaction between phosphoserine and arginine (such as the one observed between pS19 and R16) have been estimated between −4.7 and −10.6 kcal/mol2. The magnitude of the contact minimum free energy depends on the monodentate or bidentate-like geometry. We found a ratio of 2:1 between bidentate and monodentate-like geometry in our simulations, indicating that the contribution of this specific interaction guides the enthalpy of ordering to a deeper energy minimum.
The radius of gyration of cationic residues was computed (except for R16, which will be discussed later) as a measure of sidechain disorder (Figure 2). Convergence in the radius of gyration was achieved after 80 ns of simulation, so only the last 60 ns of simulation were considered for further analysis. Upon phosphorylation, there is a decrease of ~ 2 Å in the radius of gyration, which represents a loss of 20% in the conformational dynamics of the positively charged sidechains.
Figure 2.

Radius of gyration of cationic residues in the PD.
We showed previously that R16 plays an important role in ordering of RLC, due to formation of a salt bridge with pS196. Here we computed the conformational probability of the torsional angle χ of R16 from trajectories (Figure 3). In the unphosphorylated peptide, R16 was significantly populated by an entropically favorable extended conformation (χ=±180°), with χ=+180° and χ=-180° equally populated, indicating that rapid sidechain motions take place on the ns time scale (Figure 3). Upon phosphorylation, the R16 sidechain was constrained by pS19 to an entropically unfavorable conformation (χ≈+70°) (Figure 3B). Populations of χ=±180° were negligible, indicating that phosphorylation induced a significant reduction in conformational freedom.
Figure 3.
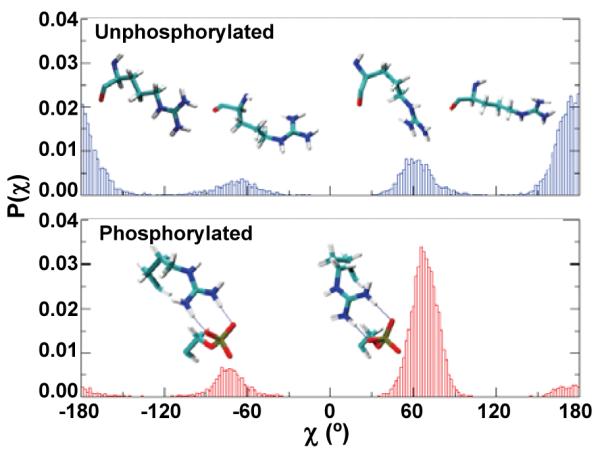
Calculated probabilities of the torsional angle χ of R16.
To further explore the importance of R16 in the disorder-to-order transitions, we performed 140-ns MD simulations of the phosphorylated mutants R16A and R16E, which have been shown to stabilize SMM in the 6S conformation12, 13 and greatly inhibit phosphorylation by MLCK14. Both mutations destabilized the helix substantially compared with the phosphorylated WT peptide (Figure 4, Figure S2), apparently due to the loss of the salt bridge pS19-R16, but also due to the formation of new salt bridges that destabilize the helix.
Figure 4.
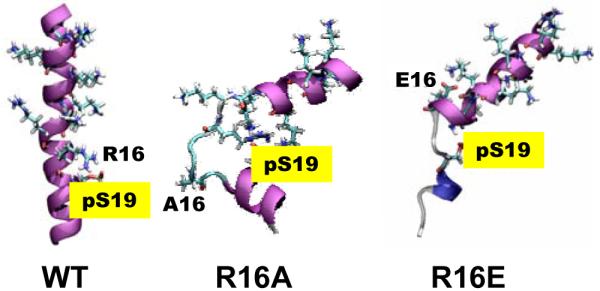
Final MD structures of phosphorylated PD containing R16 mutations (purple: α-helix; blue: 310-helix; cyan: turn; white: coil).
By what mechanism does phosphorylation balance the enthalpy-entropy compensation in the disorder-to-order transition? we calculated a free energy increase of ~6 kcl/mol from the decrease in entropy due to backbone ordering, in good agreement with the estimated entropy of backbone folding in formation of a single helical turn.15 We calculated an additional increase in free energy of ~6 kcal/mol due to loss of conformational entropy of the R16 sidechain. Thus, backbone ordering and the conformational restriction of R16 account for 60% of the total entropic free energy increase (about 20 kcal/mole, Figure 1) upon phosphorylation. Restriction of the motions of positively charged residues also contributed to the overall unfavorable entropy of ordering. Thus electrostatic interactions introduced by phosphorylation make a significant contribution to the total entropy of ordering.
In conclusion, phosphorylation balances the enthalpy-entropy compensation in RLC by favoring the electrostatic contribution to the enthalpy and constraining the conformational dynamics of positively charged residues. Phosphorylation tunes ΔGord by adding a significant constraint to R16, which contributes to the loss of entropy in the disorder-to-order transition. We propose that this balance, keeping ǀΔGordǀ small, serves to ensure that phosphorylation is a reversible switch.
A phosphorylation-induced change in order has also been observed, by EPR16, NMR17, and MD simulation18 in the N-terminal domain of phospholamban; but in that case an order-to-disorder transition was found, due to the formation of a helix-destabilizing salt bridge (as observed for the RLC mutants in Figure S2). We propose that entropically balanced disorder-order transitions are a common theme in phosphorylation-induced conformational shifts involved in cell signaling.
Supplementary Material
Acknowledgements
This work was supported by grants to D.D.T. from NIH (AR32961, AG26160). D.K. was supported by an NIH Training Grant (AR07612) and the Victor Bloomfield Fellowship. Computational resources and support for L.M.E.F. were provided by the Minnesota Supercomputing Institute.
Footnotes
Supporting Information Available: More details on computational methods, results and complete ref 8 are available free of charge via the Internet at http://pubs.acs.org.
References
- (1).Johnson LN, Lewis RJ. Chem Rev. 2001;101:2209–42. doi: 10.1021/cr000225s. [DOI] [PubMed] [Google Scholar]
- (2).Mandell DJ, Chorny I, Groban ES, Wong SE, Levine E, Rapp CS, Jacobson MP. J Am Chem Soc. 2007;129:820–7. doi: 10.1021/ja063019w. [DOI] [PubMed] [Google Scholar]
- (3).Sellers JR. J Biol Chem. 1985;260:15815–9. [PubMed] [Google Scholar]
- (4).Ellison PA, Sellers JR, Cremo CR. J Biol Chem. 2000;275:15142–51. doi: 10.1074/jbc.275.20.15142. [DOI] [PubMed] [Google Scholar]
- (5).Nelson WD, Blakely SE, Nesmelov YE, Thomas DD. Proc Natl Acad Sci U S A. 2005;102:4000–5. doi: 10.1073/pnas.0401664102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Espinoza-Fonseca LM, Kast D, Thomas DD. Biophys J. 2007;93:2083–90. doi: 10.1529/biophysj.106.095802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. J Comput Chem. 2005;26:1781–802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).MacKerell AD, et al. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. (see Supporting Information for complete reference).
- (9).MacKerell AD, Jr., Feig M, Brooks CL., 3rd J Am Chem Soc. 2004;126:698–9. doi: 10.1021/ja036959e. [DOI] [PubMed] [Google Scholar]
- (10).Kollman PA, Massova I, Reyes C, Kuhn B, Huo S, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE., 3rd Acc Chem Res. 2000;33:889–97. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- (11).Andricioaei I, Karplus M. J Chem Phys. 2001;115:6289–6292. [Google Scholar]
- (12).Sweeney HL, Yang Z, Zhi G, Stull JT, Trybus KM. Proc Natl Acad Sci U S A. 1994;91:1490–4. doi: 10.1073/pnas.91.4.1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Ikebe M, Ikebe R, Kamisoyama H, Reardon S, Schwonek JP, Sanders CR, 2nd, Matsuura M. J Biol Chem. 1994;269:28173–80. [PubMed] [Google Scholar]
- (14).Ikebe M, Reardon S, Schwonek JP, Sanders CR, 2nd, Ikebe R. J Biol Chem. 1994;269:28165–72. [PubMed] [Google Scholar]
- (15).Wang J, Purisima EO. J Am Chem Soc. 1996;118:995–1001. [Google Scholar]
- (16).Karim CB, Zhang Z, Howard EC, Torgersen KD, Thomas DD. J Mol Biol. 2006;358:1032–40. doi: 10.1016/j.jmb.2006.02.051. [DOI] [PubMed] [Google Scholar]
- (17).Metcalfe EE, Traaseth NJ, Veglia G. Biochemistry. 2005;44:4386–96. doi: 10.1021/bi047571e. [DOI] [PubMed] [Google Scholar]
- (18).Paterlini MG, Thomas DD. Biophys J. 2005;88:3243–51. doi: 10.1529/biophysj.104.054460. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


