Synthesized Population Databases: A US Geospatial Database for Agent-Based Models

Abstract

Agent-based models simulate large-scale social systems. They assign behaviors and activities to “agents” (individuals) within the population being modeled and then allow the agents to interact with the environment and each other in complex simulations. Agent-based models are frequently used to simulate infectious disease outbreaks, among other uses.

RTI used and extended an iterative proportional fitting method to generate a synthesized, geospatially explicit, human agent database that represents the US population in the 50 states and the District of Columbia in the year 2000. Each agent is assigned to a household; other agents make up the household occupants.

For this database, RTI developed the methods for

• generating synthesized households and persons

• assigning agents to schools and workplaces so that complex interactions among agents as they go about their daily activities can be taken into account

• generating synthesized human agents who occupy group quarters (military bases, college dormitories, prisons, nursing homes).

• In this report, we describe both the methods used to generate the synthesized population database and the final data structure and data content of the database. This information will provide researchers with the information they need to use the database in developing agent-based models.

Portions of the synthesized agent database are available to any user upon request. RTI will extract a portion (a county, region, or state) of the database for users who wish to use this database in their own agent-based models.

Introduction

An agent-based model is a computational model for simulating the actions and interactions of autonomous individuals (hereafter referred to as “agents”) in a network so as to assess their effects on the system as a whole. Agent-based models have been applied to such disparate fields as business (e.g., supply chain optimization,¹ logistics, consumer behavior²), traffic congestion,² infectious agents,^3-6 social and financial policy,⁷ and the human immune system.⁸ In these and other applications, the system of interest is simulated by capturing the behavior of individual agents and their interactions. Agent-based models can be used to test how changes in the behaviors of individual agents will affect the system's overall behavior.

Agent-based models are built on microdata (i.e., data on individual agents), not on aggregated population summary data. Microdata—in which each data element is associated with a specific agent—allow researchers to specify and model important population characteristics and structures, such as family structure, that are derived from data on individuals. For example, microdata on a single household of four would contain information about the age, sex, and relationship of each individual to the household and to each other. This level of detailed structure could not be derived from aggregated population data.

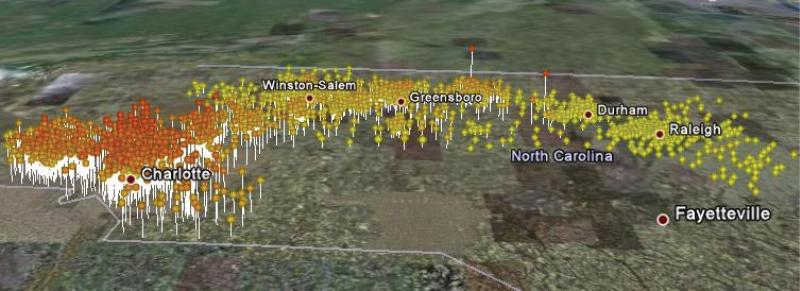
The database described in this report was developed to support the infectious disease models of the Modeling of Infectious Disease Agents Study (MIDAS), funded by the National Institutes of Health (see www.midasmodels.org). These models are used to study the spread of infectious diseases through social contact. Cooley et al.,⁹ for example, used the synthesized population database in a model studying the spread of seasonal influenza in North Carolina. The simulation model predicted the spread of influenza by calculating probabilities of disease spread between individuals represented in the synthesized agent database. The synthesized agent database, along with the associated school and workplace assignments, provided the agents for the model and baseline data about how individuals may come into contact with each other at school or work. Figure 1 illustrates a portion of the model results. Specifically, it shows the percentage of persons who are ill on day 85 of a simulated influenza outbreak in central North Carolina. Yellow dots are low percentages, orange are medium, and red are high. The epidemic is concentrated in the western part of the study area.

Figure 1.

An example of how the synthetic agent database may be used in disease modeling

For models that depend on social interactions, aggregating people into settings that enhance the probability of interpersonal contact is especially important. Close interpersonal contact occurs in a limited number of settings, such as a households, workplaces, schools, or hospitals. The methods reported here result in a georeferenced population of households containing individuals with correct and appropriate age and sex demographics. The result is a synthetic population that reflects the actual population and household family relationships in different areas of the United States. We also developed a separate, related method to generate the locations of group quarters (military bases, college dormitories, prisons, and nursing homes) and their occupants, but it is not the focus of this paper. In addition, the synthetic population does not include the homeless: although the Census Bureau collected some data on the homeless population as part of the 2000 decennial Census, it was not considered a census of the homeless and the data are not reported within the general Census databases used to generate the synthesized population database described here.¹⁰

The synthesized population database contains a record for each household and separate records for each individual in the United States. All individual occupants are identified for any given household. Household characteristics, characteristics of each person, and the link between individuals and the households they belong to are maintained. Figure 2 shows a map of a portion of the geospatial database consisting of an area about 2 miles wide. The black dots represent the synthesized households in this area. The characteristics of a single household (highlighted in blue) are shown, as is the link between the household and its four occupants. The database contains the geographic location, household attributes, and data on the four persons who live in the household. If all of the households in a geospatial area (such as a census tract, county, or state) were aggregated, the resulting synthetic population would be consistent with the census data for that area.

Figure 2.

The integrated spatial and tabular model of the synthesized population database

The remainder of this report describes the conceptual model of the synthesized agent database and the methods we used to generate it. We also summarize the methods used to assign agents to schools, workplaces, and group quarters. Portions of the synthesized agent database are available to any user upon request. RTI will extract a portion (a county, region, or state) of the database for users who wish to use this database in their own agent-based models.

Conceptual Model of the Synthesized Agent Database

The final synthesized database consists of two key database tables: one contains a record representing each household (the Household table), and the other contains a record representing each individual who lives in a household (the Person table), as shown in Figure 2.

Table 1 depicts a portion of the Household table. Here, each record (row) represents a different household. The hh_id is a unique identifier for every household in the United States. “Persons” represents a count of the persons in the household; “hinc” represents the total income of the household; “p18” represents the number of persons in the household less than 18 years of age; and “wif ” represents the number of working people in the family. The “xcoord” and “ycoord” fields contain the location of each household in a standard map projection (Albers equidistant conic projection) and are provided to simplify certain display and measurement functions for users of the data. The “lat” and “long” fields contain the latitude and longitude coordinates, respectively, of the household.

Table 1.

The synthesized agent household database table

hh_id	persons	hinc	p18	wif	xcoord	ycoord	lat	long
490490001011_0	4	66000	l	4	-1330069.28828	272413.77702	40.411208	-111.831806
490490001011_1	2	131250	0	3	-1330092.56251	273035.26643	40.416684	-111.833349
490490001011_10	2	361200	0	3	-1330062.27417	272976.02531	40.416206	-111.832874
490490001011_100	2	33100	0	1	-1331116.29058	272017.25303	40.406062	-111.843207
490490001011_101	5	94900	2	3	-1331164.86933	271631.66868	40.402566	-111.842985
490490001011_102	4	275500	2	2	-1329985.36666	273339.5739	40.41955	-111.832721
490490001011_103	5	138200	3	2	-1331350.99602	271410.89026	40.400318	-111.844704
490490001011_104	6	76400	4	4	-1331160.13135	271513.01796	40.401521	-111.842687
490490001011_105	6	19200	3	3	-1330301.58117	272295.60555	40.409798	-111.834274
490490001011_106	3	55000	1	3	-1331477.84377	271360.72153	40.399675	-111.846081

A portion of the Person table appears in Table 2. In this table, each record represents an individual person, or agent. The “person_id” is a unique identifier for every agent in the US database; “hh_id” contains the unique identifier of the household in which each agent resides; “pnum” is a number assigned to each individual in the household; “age” contains the person's age; “sex” contains the person's sex; and the remaining fields contain additional attributes about each person, such as the school and workplace to which he or she is assigned. The table also contains xcoord, ycoord, lat, and long, as described previously for the household table but not shown here.

Table 2.

The synthesized person database table

person_id	hh_id	pnum	age	sex	school_id	work_id	xcoord	ycoord	lat	long
490490014021_391_1	490490014021_391	1	42	2	<Null>	4904900140100240	-1319560.00475	252560.73722	40.25134	-111.668978
490490014021_391_3	490490014021_391	3	16	1	490081000459	4904900140200163	-1319560.00475	252560.73722	40.25134	-111.668978
490490014021_391_2	490490014021_391	2	17	2	490081000459	<Null>	-1319560.00475	252560.73722	40.25134	-111.668978
490490015011_126_2	490490015011_126	2	17	2	490081000466	<Null>	-1317568.26417	257446.94308	40.297762	-111.655651
490490015011_126_1	490490015011_126	1	42	2	<Null>	4904900150300124	-1317568.26417	257446.94308	40.297762	-111.655651
490490015011_126_3	490490015011_126	3	16	1	490081000466	4904900150300124	-1317568.26417	257446.94308	40.297762	-111.655651
490490015011_229_3	490490015011_229	3	16	1	490081000466	4904900150100067	-1318020.76014	255893.50443	40.283281	-111.657785
490490015011_229_2	490490015011_229	2	17	2	490081000466	<Null>	-1318020.76014	255893.50443	40.283281	-111.657785
490490015011_229_1	490490015011_229	1	42	2	<Null>	<Null>	-1318020.76014	255893.50443	40.283281	-111.657785
490490015011_262_2	490490015011_262	2	17	2	490081000466	<Null>	-1317719.43457	256146.49564	40.28599	-111.654786
490490015011_262_1	490490015011_262	1	42	2	<Null>	4904900170000037	-1317719.43457	256146.49564	40.28599	-111.654786
490490015011_262_3	490490015011_262	3	16	1	490081000466	<Null>	-1317719.43457	256146.49564	40.28599	-111.654786
490490015011_83_1	490490015011_83	1	42	2	<Null>	<Null>	-1317595.33356	255811.66373	40.283209	-111.652664
490490015011_83_2	490490015011_83	2	17	2	490081000466	<Null>	-1317595.33358	255811.66373	40.283209	-111.652664

The two tables are linked with a common identifier (hh_id); records for individuals thus contain the identifier for the household in which they live. We can, therefore, identify all the individuals who constitute a household. This feature is important in infectious disease models because the close proximity and frequent contact among household members increases the likelihood of disease transmission among them.

Methods

This section describes the main processing methods that we developed to generate the synthesized agent database. The overall process includes four steps: (1) generating the basic synthesized households and agents, (2) assigning agents to schools, (3) assigning agents to workplaces, and (4) generating additional agents to reside in group quarters housing.

Generating Synthesized Households and Persons

Household and Individual Data Sources

We used three primary data sources to generate the synthesized agents and households. All three data sources are produced by the US Census Bureau:

• US Census Bureau TIGER Data. The TIGER (Topologically Integrated Geographic Encoding and Referencing) data provide the spatial context for decennial Census data collection.¹¹ TIGER defines, among many other things, the boundaries of states, counties, Census tracts, block groups, and blocks. Census tabulation data are aggregated into these various geographic boundaries. The smallest Census geographic boundary for which the full suite of Census variables (including socioeconomic variables) is available is the Census block group. In addition, the TIGER files include data on boundaries of bodies of water and road networks, which were used in generating the synthesized database.

• Summary File 3 (SF3) Data. The SF3 data contain the demographic variables from the Census, organized and aggregated to many different geographic boundaries.¹² Data variables on population and housing are available in these files.

• Public Use Microdata Sample (PUMS). The PUMS data contain records representing a 5 percent sample of the occupied and vacant housing units in the United States and the people in the occupied units.¹³ These data are actual responses to Census long-form questionnaires and, therefore, retain family structure information. Data on households (including number of persons in the household, number of bedrooms, age of building, access to telephone service, type of heating, mortgage data, and many other variables) are provided. PUMS also provides data on individuals within each household (including age, sex, ethnicity, language spoken, school enrollment, occupation, travel time to work, military service, and many other variables). In addition, the PUMS data set maintains linkages between individuals and households, which allows the household population structure to be brought forward through further analyses.

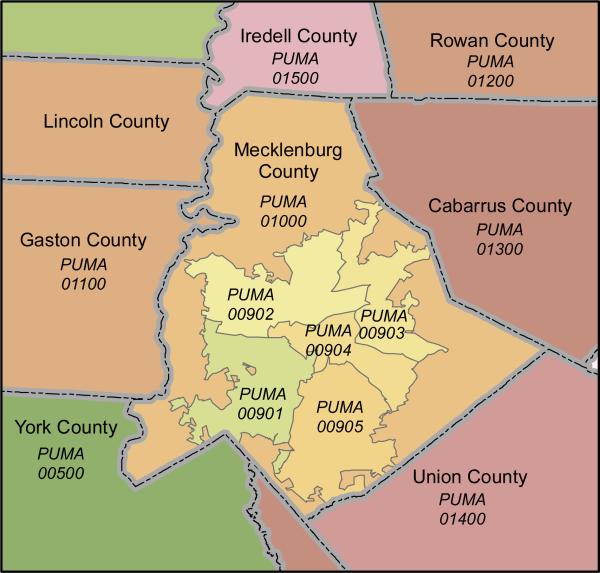
• The PUMS data are available for predefined Census areas known as Public Use Microdata Areas (PUMAs). PUMAs are defined by each state, rather than by the US Census Bureau. The Census Bureau requires that each PUMA contain about 100,000 persons, but otherwise, states have wide latitude to define the shape and extent of each PUMA. PUMAs tend to be relatively small in densely populated areas and relatively large in sparsely populated areas. Figure 3 illustrates the variability of sizes and shapes of PUMAs in Mecklenburg County, North Carolina. Some PUMAs are smaller than counties (as in this case), whereas others encompass multiple counties.

Figure 3.

Public Use Microdata Areas for Mecklenburg County, N.C.

Each PUMA must be associated with a Census block group so that the PUMS household and person records can be explicitly tied to geographic areas containing SF3 summary statistics. RTI generated a cross-walk table defining these associations using standard geographic information system (GIS) spatial overlay techniques.

Synthetic Population Data Processing Methods

Figure 4 provides an overview of the process we used to generate the synthetic population database. This process included two basic activities:

• generating household locations

• generating microdata records for all households.

Figure 4.

Generalized flow chart of the synthetic population data processing

In addition, we also compared the synthetic population to Census counts as a quality control measure.

Generating Household Locations

Each household in the database is represented as a GIS “point feature.” Point features are unique x,y locations containing descriptive tabular attributes. Because no national database of household locations is available, RTI generated point features to represent the location of each household. We determined the number of points generated within each Census block group by the count of households in the block group according to SF3 data. The location within the block group is random, except that we did not place households within bodies of water (lakes, ponds, or large rivers).

Generating Microdata Records for All Households

Because the microdata are available for only 5 percent of US households, we needed to devise a process to replicate the PUMS household data records to generate microdata records for 100 percent of the households represented by the point features described above. We did this using a statistical technique known as iterative proportional fitting (IPF).¹⁴

To carry out the IPF procedures, we used an existing computer program, the Population Generator, developed at Los Alamos National Laboratory as part of the TRANSIMS¹⁵ transportation simulation modeling package. The Population Generator implements a procedure developed by Beckman et al.¹⁴ to generate synthetic populations from the three US Census data sets described above (TIGER, SF3, and PUMS) and the cross-walk table that associates PUMAs with Census block group polygons.

The basic concept of the IPF procedure is as follows: given that the PUMS data contain a 5 percent sample of actual household microdata in a PUMA (made up of many census blocks), and given that aggregated counts of households and their characteristics are summarized at the block group geography in the SF3 data, then a set of PUMS household microdata records can be selected for a PUMA that accurately represent the characteristics of real households in the census block group. The details of the IPF procedure used in the TRANSIMS Population Generator are fully described in Beckman et al.¹⁴

The IPF procedure selects records from the 5 percent sample of households contained in the PUMS data to represent households in a particular Census block group such that, when the assignment process is complete, 100 percent of the known households in a block group are represented. People living in group quarters are not included in the TRANSIMS Population Generator process. Consequently, we used a separate procedure to handle group quarters residents; that process is described in a later section of this report.

The TRANSIMS population generator program was developed to create synthetic households and associated population in major metropolitan areas (where population density is high). The synthesized database we created using the TRANSIMS population generator also includes rural areas and other areas with lower population density. Because TRANSIMS uses specific criteria to assign households to block group areas, we expect the synthetic population to have the best fit for the following population characteristics:

• number of people in the household under age 18

• household income

• household size

• household population

• vehicles available.

Comparing the Synthetic Population to Census Counts

The IPF procedure used to generate microdata for all households attempts to select the most relevant household records from the PUMS sample to construct a set of records for 100 percent of households such that the aggregated household demographics of that 100 percent data set match the original Census block data. However, because the PUMS data are a sample of households, it is not possible to perfectly reconstruct the original Census data attributes while also honoring the actual total household population, household income, number of workers in the family, persons under age 18 years, and vehicles available in each block group.

To measure the difference between the synthesized households and the actual Census aggregated counts, we aggregated the attributes of the synthesized households for Durham County, North Carolina, summarized them by Census block group, and compared them with the original Census aggregated data for each of the 129 Census block groups in Durham County. Table 3 illustrates how the data compare at the county level. The percentage difference in total household population is 0.08 percent; the percentage difference in average household income is 1.52 percent.

Table 3.

Comparison of Census aggregated data and synthesized data for Durham County, N.C.

Data Type	Total Household Population	Average Household Income
Census SF3	213,500	$56,705.85
Synthesized Households	213,325	$55,844.73
Percentage Difference	0.08 percent	1.52 percent

Figure 5 shows the frequency distribution of the total household population comparison, by Census block group. The sizes of synthesized household populations were within 5 percent of the sizes of the Census-reported household populations for about 81 percent (104 of 129) of the block groups

Figure 5.

Frequency distribution of the percentage difference in household population between the synthesized data set and the Census data for Durham County, N.C.

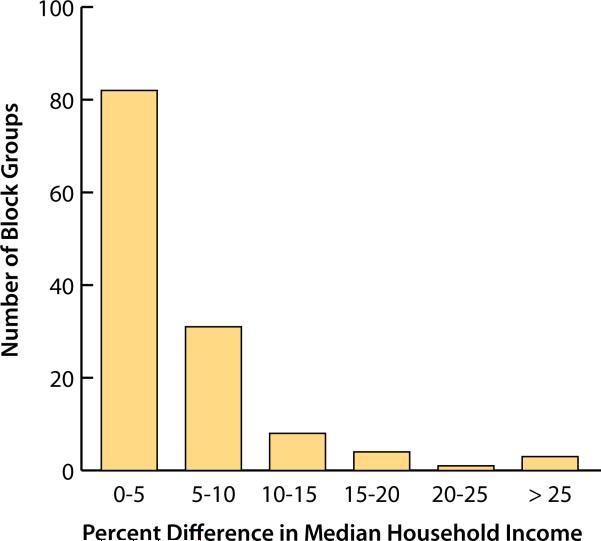
Figure 6 shows the frequency distribution of the household income comparison, by block group, based on median household income. The synthesized median household incomes were within 5 percent of the Census-reported median income for about 64 percent (82 of 129) of the block groups. For two block groups, the difference between the synthesized income and Census income was significantly greater than for the other block groups (difference greater than 75 percent). These two block groups contain the dormitories for Duke University, which the Census categorized as group quarters. Very few households that are not group quarters are located in these two block groups, and the Population Generator was not able to do as good a job selecting a set of synthetic households that match the census SF3 data as for other blocks because it considers only households when performing its selections.

Figure 6.

Frequency distribution of the percentage difference in median household income between the synthesized data set and the Census data for Durham County, N.C.

Assigning Agents to Schools

Infectious disease transmission is known to occur at a higher rate in schools because of the relatively close and sustained contact between students.¹⁶ Therefore, the synthesized agent database must assign school-age individuals to schools to enable modelers to model explicitly the social contacts between agents in school settings.

School Data Sources

RTI used the synthesized agent database described previously, public school data from two sources, and road network information from a third source to assign synthesized school-age children to schools. The three data sources are the following:

• National Center for Education Statistics (NCES) Public School Data for 2005–2006. These NCES data contain a list of public schools for the United States, along with each school's location and grade-by-grade capacity.¹⁷

• Private school data. These data, obtained from a commercial data vendor,¹⁸ contain a list of private and parochial schools and their locations.

• TIGER road network data. These 2000 data (described earlier) from the US Census contain the entire US road network.¹¹

School Assignment Method

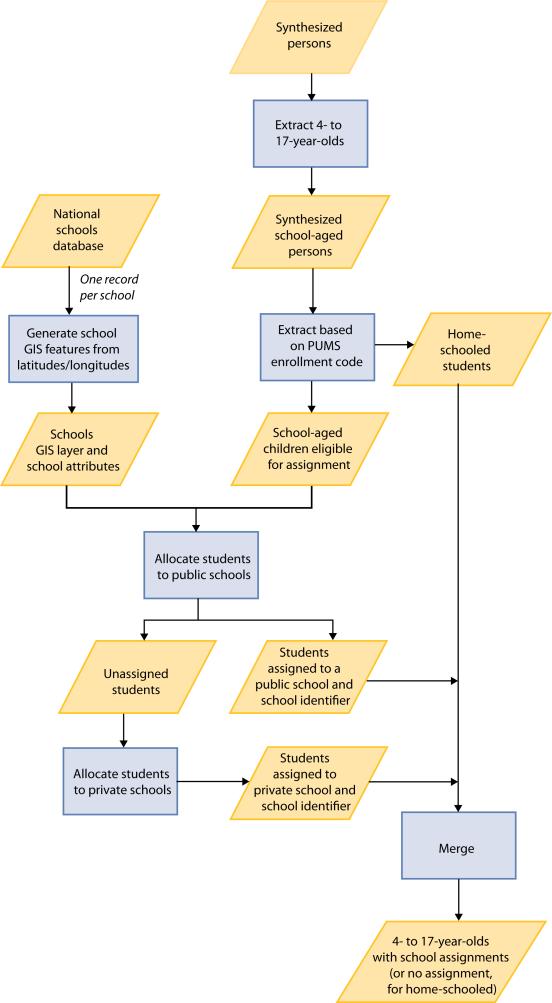
Figure 7 illustrates the data processing steps that we used to assign school-age students to schools.

Figure 7.

Flow chart of the process of assigning school-age children to schools

The PUMS data include a code indicating whether a child is enrolled in public school, private school, or no school. We use those codes to select only children who attend either private or public school for use in the school assignments method described below. Children who do not have a school enrollment code in the PUMS data are not assigned to any school and represent the approximately 2.2 percent of school-age children who are home-schooled.

We used different methods to assign students to public and private schools to reflect the different geographical processes inherent in enrollment decisions for public versus private schools. We determined how many students should be assigned to public or private schools in each area based on codes found in the PUMS data.

The public schools assignment method is based on the assumption that public school students are enrolled at the closest school having adequate capacity. This assumption is necessary because no national data source of school catchment areas exists. Even within school districts, there may be magnet schools, which draw students from throughout a county or city; or there may be busing or other school assignment methods that are not based on distance to schools. However, in the absence of good data on these factors, we believe the minimum distance assumption for school assignments is valid and an appropriate simplification that allows students to be assigned to schools in a nationally consistent manner.

The public school allocation method assigns agents who are of school age (4 to 17 years of age) to public schools. The allocation uses the public-school database from NCES (which contains data on location and enrollment by grade), the synthesized agent database, and the TIGER road network data to perform an assignment that attempts to fill each grade in each school to capacity. The spatial allocation is based on a minimum path algorithm such that available students of a certain grade level will be assigned to the closest school that has capacity for students of that grade level. In a single household, one child could be assigned to a public school, a second to a private school, and a third might be home-schooled. We did not attempt to make the assignments to public, private, or home schools homogeneous within households because of the added complexity and processing that would have been necessary to complete this more complex assignment process.

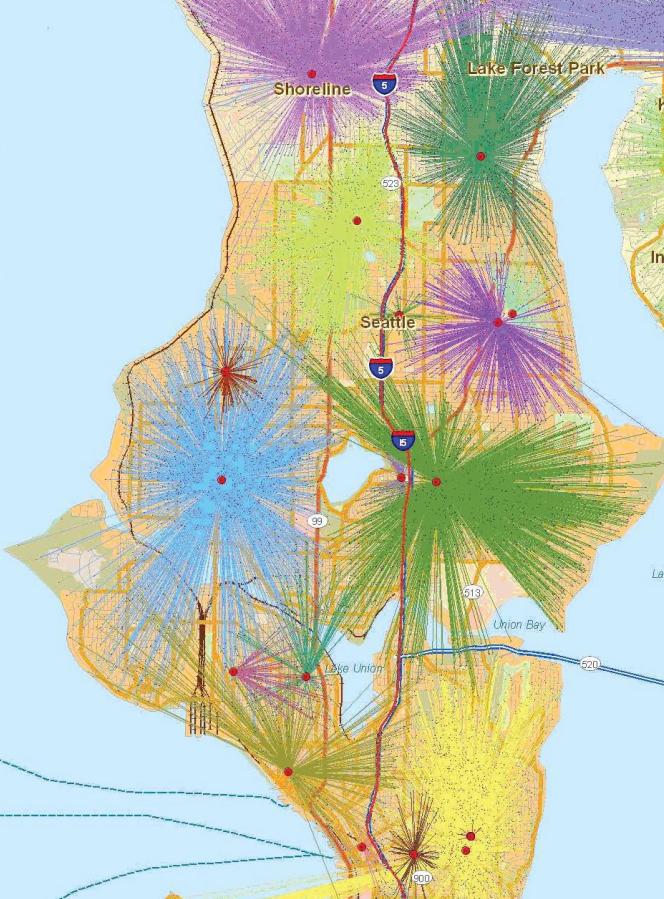
Figure 8 illustrates the spatial distribution of high schools in a portion of Kings County, Washington, and the allocation of high school students from the synthesized agent database to those schools. Each dot on the map represents the location of a high school. For each student assigned to a high school, a line is drawn between the location of the student's household and the high school. The figure illustrates the results after all high school grade assignments have been run. Because the process is run grade by grade, in some cases students seem to be drawn from other schools’ catchments. In effect, each grade has its own catchment, and assignment overlaps result. If a school's grade-by-grade capacity has not been met and unassigned students are available at greater distances, the algorithm will assign those students even if they are closer to a different school, if the closer school's capacity has already been met.

Figure 8.

Allocation of high-school-age synthesized agents to Kings County, Wash., high schools

Public school assignments are done separately for each county. Children who are 4 years old are assigned only to schools that have pre-kindergarten enrollment. Children who are 5 years old are assigned to kindergarten. The remaining children, ages 6 to 17, are assigned to appropriate grades from first grade to twelfth grade. In the absence of school-specific data on actual enrollment, we assume that each school is fully enrolled. Thus, the process continues until all public school positions have been assigned.

After public-school students have been assigned, we implement the private-school assignment method on school-age individuals not assigned to public schools and not reserved as homeschooled. Catchment areas for private schools are broader than for public schools; therefore, the private-school method allows students to be assigned to a private school that is not necessarily in the same county. Because private schools draw students from across county borders, we cannot process these assignments one county at a time, as we did with public-school assignments. Instead, we did private-school assignments one state at a time. This allowed the schools to draw from a more natural distribution of potential students.

Individual choice is a major factor affecting whether students attend private schools and which specific private school they might attend. These factors are difficult to account for in assigning a synthetic population to private schools. We assumed that although distance is important in private school assignments, it is less critical than in public school assignments. Therefore, distance was still the key criteria in assigning students to private and parochial schools, but unlike the public school allocation method, private school students were not constrained to attending the nearest private school with capacity. Instead, students were assigned to private schools using a concentric ring approach.

Table 4 illustrates the size of each concentric ring and our assumptions about the proportion of a private school's enrollment drawn from each ring. These assumptions are the same across the United States, and they have not been validated. Figure 9 illustrates the geographical distribution of students assigned to the twelfth grade for one private school. The distribution closely aligns with the percentages specified in Table 4.

Table 4.

Ring sizes and percent enrollment for private school assignments

Distance	Percentage of School Enrollment
0–10 km (0–6.2 mi)	50%
10–15 km (6.2–9.3 mi)	25%
15– 20 km (9.3–12.4 mi)	25%

Figure 9.

Allocation of 12th-grade synthesized agents to a sample private school

At the end of the allocation process, we may still have non-home-schooled school-age children who have not been assigned to a public or private school. We assume in these cases that our schools databases are incomplete and that these school-age children should be assigned to schools. Thus, we conducted a post-allocation process that assigns remaining unassigned school-age children to the closest school even if the school's capacity has already been met.

Assigning Agents to Workplaces

To identify persons and locations where infectious disease may be transmitted, we need to be able to assign the non-school-age population to workplaces. A brief overview of the workplace assignment methods is provided here; a complete and detailed description will be included in a future methods report.

Workplace Data Sources

We used the following data sources for making workplace assignments:

• US Census Bureau Special Tabulation Product 64 (STP64). STP64¹⁹ provides counts of workers by Census tract of residence and Census tract of work. It therefore provides a useful national data set to guide the assignment of synthesized agents to workplaces.

• Synthesized Population. The synthesized agent database described above was the source of the worker agents to be assigned to workplaces.

• InfoUSA Business Counts. We obtained these 2006 data from InfoUSA via the ESRI Business Analyst GIS product.²⁰ InfoUSA provides data on more than 14 million US businesses, including their location and a count of employees at each workplace. To simplify the assignment process, we summarized these individual workplace records into the following six categories by number of employees: 1–4, 5–24, 25–99, 100–499, 500–4,999, and 5,000+ employees.

Workplace Assignment Method

Figure 10 illustrates the generalized data processing steps followed to assign workers to individual workplaces.

Figure 10.

Flow chart of the process of assigning workers to workplaces

We developed a two-stage method to assign synthesized agents to workplaces. The first stage assigned workers to a Census tract for work. The second stage created individual workplace locations within each Census tract and assigned workers to specific workplaces.

The STP64 data contain a record for each combination of Census tract of residence and Census tract of work for which persons from one Census tract work in the same or another Census tract. We assigned a set of synthesized agents from each Census tract of residence to a Census tract of work as specified by the STP64 data. For example, if the STP64 data indicated that 50 persons living in tract A work in tract B, then 50 agents living in tract A were coded with a work identifier of tract B.

After assigning agents to a Census tract of work, we ran a process to generate specific workplaces that meet the workplace counts and sizes in the InfoUSA data. For each Census tract, we generated a record for each business located within the tract. We also coded these records with a unique identifier that included the Census tract identifier and the size of the business (one of the six categories noted above for number of workers based on the distribution of business sizes from InfoUSA).

The result of this analysis was a workplace identifier for each person assigned to a place of work. The resulting data table contains a record representing each business workplace (along with the number of employees who work there) found in the Census tract. Each workplace is placed at the center of the Census tract for this analysis.

After determining which workers work in each Census tract and generating records for each workplace in each tract, we then assigned the synthesized agents who work in a Census tract to specific workplaces. We used the specified capacity of each workplace to determine how many workers should be assigned to that site.

At the conclusion of the workplace assignment process, we assigned agents to individual workplaces to meet two main criteria: (1) each agent works in the correct tract, as specified in the STP64 data, and (2) each agent is assigned to a workplace such that the distribution and capacity of each workplace within each tract is honored. Agents who work in the same workplace have the same workplace identifier; therefore, developers of agent-based models know explicitly which workers may come into contact with each other based on their workplace assignments. The method does not account for workers working different shifts or for telecommuters.

Generating Group Quarters and Assigning Agents to Them

Because residents of group quarters (college dormitories, prisons, military barracks, nursing homes, and others) make up 2.7 percent of the US population,²⁰ they are important subpopulations for infectious disease research. However, the synthesized agent database described above does not include representations of agents who live in group quarters. Therefore, we created a separate process to generate group quarters agents and assign them to appropriate group quarters locations.

Group Quarters Data Sources

We used four types of primary data sources to generate group quarters data:

• US Census Bureau Summary File 1 (SF1). The SF1 provides counts of group quarters residents by type of group quarters, by block group.²¹ The SF1 provides the number and sex of group quarters populations and breaks out population by sex into the following age groups: under 18 years, 18 to 64 years, and over 64 years.

• Homeland Security Infrastructure Program (HSIP) Database. HSIP is a US Department of Homeland Security geospatial data product that contains, among many other things, locations of prisons, military quarters, colleges and universities, and nursing homes.²²

• Group Quarters Age Distributions. To refine the age data, we needed additional data on the age distributions of group quarters populations for the year 2000. These additional data allow us to generate person records with associated age and sex information. We used several sources, including those from US Department of Justice (DOJ) on prison populations²³ and the US Department of Defense (DoD) on military populations.²⁴

Group Quarters Generation and Assignment Methods

Figure 11 illustrates the generalized procedure for creating the group quarters locations and corresponding synthesized residents.

Figure 11.

Flow chart of the process of creating group quarters locations and assigning residents

The goal of this process was to generate records for group quarters and associated records for the people within each group quarters unit that mimic the synthesized agent data structure (described above) as much as possible to enable the two data sets to be used together with minimal difficulty. The person records do not include all the detailed information in the synthesized household agent database generated from the PUMS data, but they do include sex and age.

We used the location data from HSIP and other sources to generate points reflecting accurate locations for group quarters, where possible. We then assigned the count of residents of that type (e.g., military residents) for a specific block group from the SF1 data to the group quarters points in that block group. Each point, therefore, became a group quarters of a specific type. In some instances, we could not find accurate locations for specific group quarters. When we could demonstrate that it was rare for more than one group quarters of a specific type (e.g., military bases) to occur within a block group, we generated a single point for the group quarters in the block group, located at the geographic center of the block group. We assigned all agents for that type of group quarters in that block group to that point. When necessary, we generated multiple points to represent multiple facilities.

We then refined the age distributions using the additional age data. We used the SF1 data to obtain, for example, the number of males under 18 in the military population; we then used the age distribution of males found in the population for military personnel to assign specific person records for the block group.

Computer Resources, Time Resources, and Scalability

The original iterative proportional fitting procedures that we used were designed to generate data one city at a time. RTI developed automation routines to run these procedures for the entire country on a county-by-county basis. The basic synthesized population database is complete for the entire United States. The processes for generating group quarters and assigning synthesized agents to schools, workplaces, and group quarters are too time-consuming to run for the entire United States at one time. Instead, these processes are run to make assignments on an as-needed basis as requests for synthesized populations for a particular area are received.

The storage size of the final database (even if school, workplace, and group quarters assignments were included for the whole United States) would total less than 50GB of storage disk space. The data are housed in a geospatial database to allow the data to be used in geospatial models and analyses.

Summary and Conclusions

Our US synthesized human agent database provides a realistic agent population for use in agent-based models. We developed the database by combining available national data sets, population-generating techniques, and GIS techniques. Moreover, we developed several custom enhancements, including creating group quarters and assigning agents to schools, workplaces, and those group quarters.

Because of the large input data sets, nationwide processing, and the inherent difficulty in appending county-based and state-based processing into national geospatial databases, we encountered many technical hurdles during production. We applied several quality assurance and quality control processes to check the results as we processed each county and state. For example, we compared maps showing the counts of synthesized persons by Census tract and block group with the aggregated counts provided by the Bureau of the Census. This step ensured that we did not create any holes or gaps in the data.

Future directions for enhancing and improving the database include improving the locations of household point features, developing a process for including race and ethnicity in the iterative proportional fitting technique, and developing updated versions of the database that use newer demographic data provided by the American Community Survey.²⁵

Agent-based models are an increasingly popular tool for analyzing large-scale social systems as varied as disease epidemics, tax policy, and transportation planning. The US synthesized database developed by RTI and described here is available to any researcher who would like to use it in his or her own model. The database is too large to be distributed as a whole, but RTI will extract portions of the database by county or groups of counties and make these extracted subsets available to researchers on request.