On the Impact of Parametric Assumptions and Robust Alternatives for Longitudinal Data Analysis

Summary

Models for longitudinal data are employed in a wide range of behavioral, biomedical, psychosocial, and health-care related research. One popular model for continuous response is the linear mixed-effects model (LMM). Although simulations by recent studies show that LMM provides reliable estimates under departures from the normality assumption for complete data, the invariable occurrence of missing data in practical studies renders such robustness results less useful when applied to real study data. In this paper, we show by simulated studies that in the presence of missing data estimates of the fixed-effect of LMM are biased under departures from normality. We discuss two robust alternatives, the weighted generalized estimating equations (WGEE) and the augmented WGEE (AWGEE), and compare their performances with LMM using real as well as simulated data. Our simulation results show that both WGEE and AWGEE provide valid inference for skewed non-normal data when missing data follows the missing at random (MAR), the most popular missing data mechanism for real study data.

1 Introduction

Models for longitudinal data are employed in a wide range of behavioral, biomedical, psychosocial, and health-care related research studies. One popular modeling paradigm is the latent variable, or random-effect, based approach for addressing correlated responses arising from such study data (Demidenko, 2004; Fitzmaurice et al. 2004; Raudenbush and Bryk, 2002). For example, for continuous response, the linear mixed-effects model (LMM) is one of the most widely used methods for modeling longitudinal data. By using random-effects to account for correlations across multiple within-subject outcomes, the LMM extends the classic multiple linear regression for modeling cross-sectional data to a general longitudinal data setting.

One major drawback of LMM as well as other random-effects based models is their dependence on distribution assumptions for inference. In recent years, many software packages have implemented robust methods to improve the validity of inference in the presence of departures from assumed parametric models. For example, simulation studies of Maas and Hox (2004; 2005) have found that estimates of the fixed-effects, or population parameters, of LMM are quite robust when model errors depart from the assumed normal distribution. However, these simulation studies have all been carried out under complete data. In most real studies, missing data invariably occurs and the robustness of estimates from LMM requires reassessment in the presence of missing data.

In this paper, we show by simulated data that the robustness of fixed-effect estimates of LMM is compromised under non-random missing data when the error term of the model deviates from the normality assumption. To address this key limitation, we investigate the performance of two robust alternatives, the weighted generalized estimating equations (WGEE) and augmented WGEE (AWGEE), for inference for non-normal longitudinal data. In Section 2, we briefly review the parametric LMM and the distribution-free formulation of this model. In Section 3, we discuss inference by the two dueling paradigms under missing data. In Section 4, we use simulated data to compare the performance of the various approaches for fitting non-normal longitudinal data under non-random missing data. In Section 5, we give our concluding remarks.

2 Models for Longitudinal Data

Over the past three decades, studies in biomedical and behavioral sciences have evolved from simple cross-sectional study designs to modern day longitudinal trials. As longitudinal study designs use subjects as their own controls, they provide a unique opportunity to study changes of outcomes of interest over time, causal effects and disease progression, in addition to providing more power for assessing treatment differences. In this section, we briefly review the two most popular approaches for modeling longitudinal data with continuous response.

2.1 Parametric Linear Mixed-effects Model

First, consider a relatively simple longitudinal study design with only two assessments, i.e., the so-called pre-post design. Let n denote the number of subjects and y_it some continuous outcome of interest from the ith subject at time t (= 1, 2). We are interested in modeling the mean response E(y_it) of y_it over time. One popular approach is the linear mixed-effects model (LMM), which for such a pre-post study design, has the simple form:

$$y_{it}={\beta }_0+{\beta }_1{I}_{\{t=2\}}+b_i+{\epsilon }_{it},b_i\sim N(0,{\sigma }_b^2),{\epsilon }_{it}\sim N(0,{\sigma }^2),1\le i\le n,1\le t\le 2,$$ (1)

where I_{·} denotes a set indicator, and N (μ, σ²) denotes a normal with mean μ and variance σ². In the LMM above, since E (y_it) = β₀ + β₁I_{t=2}, β_t represents the (population) mean of y_it at pre-(t = 1) and post-treatment (t = 2) and is known as the fixed or population effect. The latent b_i in (1) accounts for the variation across the individual subjects around the fixed effect or population mean and is known as the random effect.

Let y_i = (y_i1,y_i2)^┬. It then follows from (1) that

$$V=\text{Var}({\text{y}}_i)=\left(\begin{array}{cc}{\sigma }^2+{\sigma }_b^2& {\sigma }_b^2\\ {\sigma }_b^2& {\sigma }^2+{\sigma }_b^2\end{array}\right)=({\sigma }^2+{\sigma }_b^2)C_2(\rho ),$$ (2)

where $\rho ={\sigma }_b^2/({\sigma }_b^2+{\sigma }^2)$ is known as the intraclass correlation (ICC) and C_m (ρ) denotes a m × m compound symmetry correlation matrix with a correlation coefficient ρ. The LMM for the pre-post study design will be used to illustrate the performance of LMM in Section 4.

More generally, the LMM for a longitudinal data with n assessments has the following form:

$$y_{it}={\mathbf{\text{x}}}_{it}^{\top }\beta +{\mathbf{\text{z}}}_{it}^{\top }{\mathbf{\text{b}}}_i+{\epsilon }_i,{\mathbf{\text{b}}}_i\sim N(\mathbf{0},{\mathbf{\sum }}_b),{\epsilon }_i\sim N(\mathbf{0},{\sigma }^2{\mathbf{\text{I}}}_m),1\le i\le n,1\le t\le m,$$ (3)

where x_it = (1, x_i1t …, x_ipt)^┬ (z_it = (1, z_i1t …, z_ilt)^┬) denotes a p × 1 (l × 1) vector of covariates, b_i = (b_i1,…, b_il)^┬ a l × 1 vector of normal random-effect, ε_i = (ε_i1,…, ε_im)^┬ the error term for the model, N (μ, Σ) a multivariate normal with mean μ and variance Σ, I_m the m × m identity matrix. Under (3), we have:

$$V_i=\text{Var}({\mathbf{\text{y}}}_i|{\mathbf{\text{x}}}_i,{\mathbf{\text{z}}}_i)={\mathbf{\text{Z}}}_i{\mathbf{\sum }}_b{\mathbf{\text{Z}}}_i^{\top }+{\sigma }^2{\mathbf{\text{I}}}_m.$$ (4)

By setting ${\mathbf{\text{x}}}_{it}^{\top }={\left(1,I_{\{t=2\}}\right)}^{\top }$ and z_it = 1 in (4), we immediately obtain (2).

Maximum likelihood (ML) is the most popular inference procedure for LMM (Demidenko, 2004; Raudenbush and Bryk, 2002). One major drawback of ML estimate is the dependence on the parametric assumptions; if data does not follow the normality assumptions in (1), model estimates may become biased or inconsistent. In recent years, many packages have adopted the sandwich variance estimate to address this issue (Goldstein, 1995; Rasbash et al., 2000; Raudenbush and Bryk, 2002). In this case, these procedures essentially yield variance estimates equivalent to those from the generalized estimating equations (GEE), which we review next.

2.2 Distribution-free Linear Model

Since the seminal work of Liang and Zeger (1986), the generalized estimating equations (GEE) approach has been widely used as an alternative for modeling longitudinal data. By modeling the marginal mean of the response at each assessment time, GEE eliminates both layers of distribution assumptions for the random effect and error term, thereby providing consistent estimates regardless of data distributions and the complexities of structure of correlated responses.

Within our context, consider the following linear model:

$$\text{E}(y_{it}|{\mathbf{\text{x}}}_{it})={\mu }_{it}={\mathbf{\text{x}}}_{it}^{\top }\mathit{\beta },1\le i\le n,1\le t\le m.$$ (5)

In (5), only the marginal mean at each time t is specified, which models the fixed-effect of LMM in (1) at time t. Under GEE, inference is based on the following score-like vector equation:

$${\mathbf{\text{W}}}_n(\mathit{\beta })=\sum _{i=1}^n{\mathbf{\text{W}}}_{ni}(\mathit{\beta })=\sum _{i=1}^n{\mathbf{\text{G}}}_i({\mathbf{\text{x}}}_i){\mathbf{\text{S}}}_i(\mathit{\beta })=\sum _{i=1}^n{\mathbf{\text{G}}}_i({\mathbf{\text{x}}}_i)({\mathbf{\text{y}}}_i-{\mathit{\mu }}_i)=0,$$ (6)

where μ_i = (μ_il, …, μ_im)^┬, G_i (x_i) is some matrix function of ${\mathbf{\text{x}}}_i=\left({\mathbf{\text{x}}}_{i1}^{\top },\dots ,{\mathbf{\text{x}}}_{im}^{\top }\right)$. If the model in (5) is correct, then the GEE in (6) is unbiased, i.e., E [W_n (β)] = 0, regardless of the choice of G_i (x_i), ensuring the consistency of estimate of β obtained as the solution to (6) (Liang and Zeger, 1986; Diggle et al. 2002). In most applications, G_i (x_i) has the form:

$${\mathbf{\text{G}}}_i({\mathbf{\text{x}}}_i)={\mathbf{\text{D}}}_i{\mathbf{\text{V}}}^{-1}(\alpha ),{\mathbf{\text{D}}}_i=\frac{\partial }{\partial \beta }{\mu }_i,1\le i\le n,$$ (7)

where V (α) denotes a working variance matrix parameterized by α.

The phrase working variance is used to emphasize the fact that V (α) is not necessarily the true variance matrix of y_i. For example, the simplest choice is V =diag_t (Var(y_it)), where diag_t (α_t) denotes a diagonal matrix with α_t on the tth diagonal. In this case, the correlated responses y_it are treated as if they are independent. In addition, there is no parameter associated with this particular working independence model. Another popular choice is the exchangeable or uniform compound symmetry correlation matrix, $V(\alpha )={\text{diag}}_t\left(\sqrt{\text{Var}(y_{it})}\right)C_m(\rho ){\text{diag}}_t\left(\sqrt{\text{Var}(y_{it})}\right)$, where C_m(ρ) denotes a m × m matrix correlation matrix with a common correlation ρ for any pair of the component responses of y_i.

In addition to β, (6) also depends on α, though we have suppressed this dependence to highlight the fact that (6) is the equation for estimating β. Thus, before proceeding with inference about β, α must be estimated (except for the working independence model). Although the consistency of β̂ does not depend on how α is estimated, judicious choices of the type of estimates of α are required to ensure the asymptotic normality of β̂. In particular, if α̂ is $\sqrt{n}$-consistent, β̂ is asymptotically normal with its asymptotic variance Σ_β given by (e.g. Liang and Zeger, 1986; Kowalski and Tu, Chap. 4, 2007):

$${\mathbf{\sum }}_{\beta }={\mathbf{\text{B}}}^{-1}\text{E}\left({\mathbf{\text{G}}}_i{\mathbf{\text{S}}}_i{\mathbf{\text{S}}}_i^{\top }{\mathbf{\text{G}}}_i^{\top }\right){\mathbf{\text{B}}}^{-\top },\mathbf{\text{B}}=\text{E}\left(\frac{{\partial }^{\top }}{\partial \mathit{\beta }}{\mathbf{\text{W}}}_{ni}\left(\mathit{\beta },\mathit{\alpha }\right)\right).$$

A consistent estimate of Σ_β is obtained by substituting consistent estimates in place of the respective quantities above. For example, we can estimate B by $\widehat{\mathbf{\text{B}}}={\sum }_{i=1}^n\frac{{\partial }^{\top }}{\partial \mathit{\beta }}{\mathbf{\text{W}}}_{ni}\left(\widehat{\mathit{\beta }},\widehat{\mathit{\alpha }}\right)/n$. Since moment estimates are $\sqrt{n}$-consistent, α is readily estimated for the working independence and exchangeable correlation models (e.g. Liang and Zeger, 1986).

3 Inference under Missing Data

In longitudinal studies, missing data are inevitable; subjects may simply quit or they may not show up at follow-up visits. We characterize the impact of missing data on model estimates through assumptions or missing data mechanisms, which allow us to ignore the multitude of reasons for missing data and focus on addressing their impact on estimation of model parameters. The missing completely at random (MCAR) assumption models a class of missing data that does not affect model estimates when completely ignored. For example, in a treatment study, missing data resulting from patient's relocation or scheduling conflict falls into this category. However, MCAR is not a plausible model when missing data are associated with treatment interventions such as patients' deteriorated or improved health conditions due to treatment. By modeling the occurrence of missing data as a function of observed responses prior to the assessment point, the missing at random (MAR) assumption addresses this class of treatment related or response-dependent missing data.

Within the longitudinal study setting in Section 2, define a missing (or rather, observed) data indicator as:

$${\mathit{\text{r}}}_{it}=\{\begin{array}{ll}1\hfill & \text{if}{y}_{it}\text{is observed}\hfill \\ 0\hfill & \text{if}{y}_{it}\text{is missing}\hfill \end{array},{\mathbf{\text{r}}}_i={\left(r_{i1},\dots ,r_{im}\right)}^{\top },1\le t\le m,1\le i\le n.$$

We assume no missing data at baseline t = 1 such that r_i1 = 1 for all 1 ≤ i ≤ n. Below, we first briefly review inference for the parametric LMM in (3) and then turn our attention to the distribution-free version in (5).

3.1 Parametric Model

Let y_i = (y_i1, …, y_im)^┬ and ${\mathbf{\text{x}}}_{\mathbf{\text{i}}}={\left({\mathbf{\text{x}}}_{i1}^{\top },\dots ,{\mathbf{\text{x}}}_{im}^{\top }\right)}^{\top }$. Let $y_i^o$ and ${\mathbf{\text{y}}}_i^m$ denote the observed and missing responses, respectively. Under likelihood based parametric inference, we jointly model the response y_i and missing data indicator r_i.

The joint density function, f (y_i, r_i | x_i), can be factored into the product of marginal and conditional distributions:

$$f({\mathbf{\text{y}}}_i,{\mathbf{\text{r}}}_i|{\mathbf{\text{x}}}_i)=f({\mathbf{\text{y}}}_i|{\mathbf{\text{x}}}_i)f({\mathbf{\text{r}}}_i|{\mathbf{\text{y}}}_i,{\mathbf{\text{x}}}_i).$$ (8)

Under MAR, the distribution of r_i depends only on the observed response, ${\mathbf{\text{y}}}_i^o$, and thus:

$$f({\mathbf{\text{r}}}_i|{\mathbf{\text{y}}}_i,{\mathbf{\text{x}}}_i)=f({\mathbf{\text{r}}}_i|{\mathbf{\text{y}}}_i^o,{\mathbf{\text{y}}}_i^m,{\mathbf{\text{x}}}_i)=f({\mathbf{\text{r}}}_i|{\mathbf{\text{y}}}_i^o,{\mathbf{\text{x}}}_i).$$ (9)

It follows from (8) and (9) that:

$$\begin{array}{ll}f({\mathbf{\text{y}}}_i^o,{\mathbf{\text{r}}}_i|{\mathbf{\text{x}}}_i)& =\int f({\mathbf{\text{y}}}_i^o,{\mathbf{\text{y}}}_i^m|{\mathbf{\text{x}}}_i)f({\mathbf{\text{r}}}_i|{\mathbf{\text{y}}}_i^o,{\mathbf{\text{x}}}_i)d{\mathbf{\text{y}}}_i^m\\ & =f({\mathbf{\text{r}}}_i|{\mathbf{\text{y}}}_i^o,{\mathbf{\text{x}}}_i,{\mathit{\text{θ}}}_{\mathit{\text{y}}|\mathit{\text{r}}})\int f({\mathbf{\text{y}}}_i^o,{\mathbf{\text{y}}}_i^m|{\mathbf{\text{x}}}_i)d{\mathbf{\text{y}}}_i^m\\ & =f({\mathbf{\text{y}}}_i^o|{\mathbf{\text{x}}}_i,{\mathit{\text{θ}}}_y)f(r_i|y_i^o,{\mathbf{\text{x}}}_i,{\mathit{\text{θ}}}_{y|r}).\end{array}$$ (10)

If θ_y and θ_y|r are assumed disjoint, then following (10) the log-likelihood based on the joint observations $({\mathbf{\text{y}}}_i^o,{\mathbf{\text{r}}}_i)$ is given by:

$$l(\mathit{\text{θ}})=\sum _{i=1}^{n}log(f({\mathbf{\text{y}}}_i^o|{\mathbf{\text{x}}}_i,{\mathit{\text{θ}}}_{\mathit{\text{y}}}))+\sum _{i=1}^{n}log(f({\mathbf{\text{r}}}_i|y_i^o|{\mathbf{\text{x}}}_i,{\mathit{\text{θ}}}_{y|r}))=l_1({\mathit{\text{θ}}}_y)+l_2({\mathit{\text{θ}}}_{y|r}).$$

Thus, inference about θ_y can simply be based on the log-likelihood l₁ (θ_y).

Most packages provide inference about the parameters of interest θ_y based on maximizing the likelihood function l₁ (θ_y). Under the model assumptions of LMM, estimates are consistent under both MCAR and MAR. When study data fail to follow the parametric assumptions, maximum likelihood estimates are no longer guaranteed to be consistent. We examine bias from such estimates using simulated data in Section 4.

3.2 Distribution-free Model

3.2.1 Weighted Generalized Estimating Equations

In the presence of missing data, we may apply the GEE in (6) to the observed responses, i.e.,

$${\mathbf{\text{W}}}_n(\mathit{\beta })=\sum _{i=1}^n{\mathbf{\text{W}}}_{ni}(\mathit{\beta })=\sum _{i=1}^n{\mathbf{\text{G}}}_i({\mathbf{\text{x}}}_i){\mathbf{\text{R}}}_i{\mathbf{\text{S}}}_i=\sum _{i=1}^n{\mathbf{\text{G}}}_i({\mathbf{\text{x}}}_i){\mathbf{\Delta }}_i\left({\mathbf{\text{y}}}_i-{\mathit{\mu }}_i\right)=0,$$ (11)

where Δ_i = diag_t(r_it). However, the vector estimating equation in (11) is generally biased, i.e., E(W_n(β)) ≠ 0, unless missing data follow the MCAR model. To obtain consistent estimates of β under MAR, we must revise the GEE above.

To illustrate the basic idea for modification, consider the relatively simple, pre-post design, with a homogeneous sample. We are interested in estimating the mean response at pre- and post-assessment, μ = E (y_i) = (E (y_i1), E (y_i2))^┬. By selecting the G_i (x_i) according to (7), it follows from (11) that

$${\mathbf{\text{W}}}_n(\mathit{\mu })=R{(\mathit{\alpha })}^{-1}\left(\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & r_{i2}\hfill \end{array}\right)\left[\sum _{i=1}^n\left(\begin{array}{l}{y}_{i1}-{\mu }_1\hfill \\ y_{i2}-{\mu }_2\hfill \end{array}\right)\right]=\mathbf{0}.$$ (12)

Solving the equations above for μ yields:

$$\widehat{\mathit{\mu }}={\left({\widehat{\mu }}_1,{\widehat{\mu }}_2\right)}^{\top }={\left(\frac{1}{n}\sum _{i=1}^n{y}_{i1},\frac{1}{n_2}\sum _{i=1}^n{r}_{i2}{y}_{i2}\right)}^{\top },n_2=\sum _{i=1}^n{r}_{i2}.$$ (13)

If the missingness of y_i2 depends on y_i1, it is readily checked that E(μ̂₂) ≠ μ₂, implying that μ̂₂ is not a consistent estimate. This is also clear on intuitive grounds. For example, if y_i1 and y_i2 are positively correlated with higher values of y_i1 leading to missing y_i2, μ̂₂ in (13) will be downwardly biased, since it only averages over the observed y_i2 corresponding to lower values of y_i1. In treatment studies, this type of response-dependent missingness often occurs if a patient feels that his/her health condition has improved (or deteriorated) during study and decides not to undergo any additional treatment.

Under MAR, the missingness of y_i2 only depends on y_i1, i.e.,

$${\pi }_{i2}=\text{P}(r_{i2}=1|y_{i1},y_{i2})=\text{P}(r_{i2}=1|y_{i1}).$$

This probability π_i2 selects which y_i2's are to be observed based on the values of y_i1. Thus, each ith subject observed at t = 2 represents a subgroup of 1/π_i2 subjects with the same baseline value y_i1, but unobserved at post-treatment because of the selection process defined by π_i2. By augmenting each observed response y_i2 at t = 2 with the weight function 1/π_i2, we can statistically include the missing responses in the estimation of μ₂ by using a weighted GEE (WGEE):

$${\mathbf{\text{W}}}_n(\mathit{\mu })=\mathbf{\text{R}}{(\mathit{\alpha })}^{-1}\left(\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & \frac{r_{i2}}{{\pi }_{i2}}\hfill \end{array}\right)\left[\sum _{i=1}^n\left(\begin{array}{l}{y}_{i1}-{\mu }_1\hfill \\ y_{i2}-{\mu }_2\hfill \end{array}\right)\right]=\mathbf{0}.$$ (14)

It is readily checked that E(W_n(μ)) = 0, enabling (14) to yield a consistent estimate of μ₂, $\widehat{{\mu }_2}=\left({\sum }_{i=1}^n\frac{r_{i2}}{{\pi }_{i2}}{y}_{i2}\right)/n$ (e.g. Kowalski and Tu, Chap. 4, 2007). We can also directly verify this:

$${\widehat{\mu }}_2=\frac{1}{n}\sum _{i=1}^n\frac{r_{i2}}{{\pi }_{i2}}{y}_{i2}{\to }_p\text{E}\left(\frac{r_{i2}}{{\pi }_{i2}}{y}_{i2}\right)=\text{E}\left[y_{i2}\frac{1}{{\pi }_{i2}}E(r_{i2}|y_{i1},y_{i2})\right]=\text{E}\left[y_{i2}\frac{1}{{\pi }_{i2}}E(r_{i2}|y_{i1})\right]={\mu }_2,$$

where →_p denotes convergence in probability.

By comparing (12) with (14), it is seen that the latter differs from the former only in the definition of Δ_i. By carrying this modification over to a general setting with m assessments, we obtain the WGEE for inference about β for the distribution-free LMM in (5), which is defined by the same vector equation in (11) except for substituting the following modified Δ_i:

$${\pi }_{it}=\text{P}(r_{it}=1|{\mathbf{\text{x}}}_i,{\mathbf{\text{y}}}_i),{\mathbf{\Delta }}_{it}=\frac{r_{it}}{{\pi }_{it}},{\mathbf{\Delta }}_i={\text{diag}}_t({\mathbf{\Delta }}_{it}),1\le t\le m,1\le i\le n.$$ (15)

It is again readily checked that E [G_i (x_i) Δ_iS_i] = 0, ensuring that the WGEE yields consistent estimates of β (e.g. Robins et al. 1995; Kowalski and Tu, Chap. 4, 2007).

To use WGEE, we must know or have estimates of π_it. In some cases, subject dropout is created by study design and π_it are known. For example, in some multi-stage trials, patients can only enter the next stage of the study if they satisfy certain criteria such as response to treatment at the previous stage. However, as noted earlier, in most studies, missing data patterns are defined by a host of factors not directly related to study design. We discuss estimation of π_it for the general setting after introducing another robust approach for the distribution-free LMM.

3.2.2 Augmented Weighted Generalized Estimating Equations

The WGEE discussed in Section 3.2.1 depends on the model for missing data in (15). In most studies, π_it are unknown and must be modeled and estimated. If such a model is misspecified, the WGEE estimate may be inconsistent. In applications, reliable models may also exist for directly relating the missing response to the observed ones and other covariates. The augmented WGEE (AWGEE) is developed to take advantage of this additional source of modeling information to ensure valid inference when the model for π_it may be incorrect (Robins et al., 1995; Tsiatis, 2006).

To illustrate, consider again the pre-post study design. Suppose that we can predict y_i2 directly based on y_i1 using a linear regression:

$$\text{E}(y_{i2}|y_{i1})={\eta }_0+{\eta }_1{y}_{i1},1\le i\le n.$$ (16)

Then, we can estimate μ₂ without using WGEE by ${\stackrel{\sim }{\mu }}_2={\sum }_{i=1}^n\left({\widehat{\eta }}_0+{\widehat{\eta }}_1{y}_{i1}\right)/n$. This new estimate is consistent if (16) is a correct model, since

$${\stackrel{\sim }{\mu }}_2={\widehat{\eta }}_0+{\widehat{\eta }}_1\frac{1}{n}\sum _{i=1}^n{y}_{i1}{\to }_p{\eta }_0+{\eta }_1\text{E}(y_{i1})=\text{E}[\text{E}(y_{i2}|y_{i1})]=E(y_{i2})={\mu }_2.$$

By combining both the prediction model in (16) and the WGEE in (14), we obtain an augmented WGEE to estimate μ as follows:

$${\mathbf{\text{W}}}_n(\mathit{\mu })=\sum _{i=1}^n\mathbf{\text{R}}{(\mathit{\alpha })}^{-1}\left({\mathbf{\Delta }}_i{\mathbf{\text{S}}}_i-{\mathbf{\Delta }}_i^c{\stackrel{\sim }{S}}_i\right),{\mathbf{\Delta }}_i^c={\mathbf{\Delta }}_i-{\mathbf{\text{I}}}_2,$$ (17)

$${\stackrel{\sim }{S}}_i={\left(y_{i1}-{\mu }_1,{\widehat{y}}_{i2}-{\mu }_2\right)}^{\top },{\widehat{y}}_{i2}={\eta }_0+{\eta }_1{y}_{i1}.$$

It is readily checked that $\text{E}\left[{\mathbf{\text{G}}}_{\mathbf{\text{i}}}({\mathbf{\text{x}}}_{\mathbf{\text{i}}})\left({\mathbf{\Delta }}_{\mathbf{\text{i}}}{\mathbf{\text{S}}}_i-{\mathbf{\Delta }}_i^c\stackrel{\sim }{{\mathbf{\text{S}}}_i}\right)\right]=\mathbf{0}$ if either (15) or (18) or both are correct. Thus, the AWGEE above yields consistent estimates of μ if at least one of these models is correct. Further, when both models are correct, the AWGEE estimate from (17) may also be more efficient than the WGEE estimate (Robins et al, 1995; Tsiatis, 2006).

The above is readily extended to a more general setting where the prediction model in (16) also involves other baseline covariates. Let u_i be a set of baseline variables including y_i1 and the prediction model be defined by:

$$\text{E}(y_{i2}|{\mathbf{\text{u}}}_i)={\eta }_0+{\mathbf{\text{u}}}_i^{\top }{\eta }_1,1\le t\le 2,1\le i\le n.$$ (18)

The AWGEE is defined by

$${\mathbf{\text{W}}}_n(\mathit{\beta })=\sum _{i=1}^n{\mathbf{\text{W}}}_{ni}(\mathit{\beta })=\sum _{i=1}^n{\mathbf{\text{G}}}_i\left({\mathbf{\text{x}}}_i\right)\left({\mathbf{\Delta }}_i{\mathbf{\text{S}}}_i-{\mathbf{\Delta }}_i^c{\stackrel{\sim }{S}}_i\right)=\mathbf{0},$$ (19)

where ${\widehat{y}}_{i2}={\eta }_0+{\text{u}}_i^{\top }{\eta }_1$. To ensure consistent estimation for the regression model, we assume a surrogacy-type assumption, [y_i2 | u_i, x_i] = [y_i2 | u_i], where [y_i2 | v_i] denotes the conditional distribution of y_i2 given v_i (e.g. Prentice, 1989; Kowalski and Tu, 2002). Of course, the condition holds if u_i includes x_i. Under the surrogacy condition, $\text{E}[{\mathbf{\text{G}}}_i(x_i)({\mathbf{\Delta }}_i{\mathbf{\text{S}}}_i-{\mathbf{\Delta }}_i^c\stackrel{\sim }{{\mathbf{\text{S}}}_i})]=\mathbf{0}$, if either (15) or (18) or both are correct. Thus, the AWGEE in (15) yields consistent estimates of β if at least one of the missing data models is correct.

Although feasible in principle, it is more complex to implement AWGEE for a general longitudinal study with more than two assessments. For example, for m = 3, we need to consider two missing data patterns when predicting missing y_i3: one with observed y_i1 and y_i2, and the other with observed y_i1 only. The number of prediction models grows rapidly as the frequency of assessments increases. Further, it is more intricate to specify the prediction models than models for the missing response probabilities π_it.

3.2.3 Estimation of Weight Function and Augmented Term

Under MCAR, r_i are independent of x_i and y_i and π_it = P [r_it = 1] = π_t. In this case, π_t are readily estimated by the sample moment: ${\widehat{\pi }}_t=\left({\sum }_{i=1}^n{r}_{it}\right)/n(1\le t\le m)$. In many studies, however, π_it are dependent of either x_i or y_i or both. It is difficult to model π_it as a function of x_i and y_i without imposing some additional assumptions regarding the relationship between them. As in the literature, we focus on the MAR mechanism.

As noted earlier, missing data in longitudinal trials often occur as the result of subject dropout due to deteriorated/improved health conditions and other related conditions, exhibiting the so-called monotone missing data pattern (MMDP). The structured patterns under MMDP make it possible to model π_it in most studies.

Under MMDP, if y_it is observed at time t, then all y_is at all earlier times s (< t) are also observed. Let

$$\begin{array}{l}{\mathbf{\text{H}}}_{it}=\{{\stackrel{\sim }{\mathbf{\text{x}}}}_{is},{\stackrel{\sim }{\mathbf{\text{y}}}}_{is};1\le s\le t-1\},{\stackrel{\sim }{\mathbf{\text{x}}}}_{it}={(x_{i1}^{\top },\dots ,x_{i1(t-1)}^{\top })}^{\top },\\ {\stackrel{\sim }{\mathbf{\text{y}}}}_{it}={(y_{i1},\dots ,y_{i(t-1)})}^{\top },2\le t\le m.\end{array}$$

The subset H_it contains all observed data prior to time t. Under MAR,

$${\pi }_{it}=\text{P}(r_{it}=1|{\mathbf{\text{x}}}_i,{\mathbf{\text{y}}}_i)=\text{P}(r_{it}=1|{\mathbf{\text{H}}}_{it})=\text{P}(r_{it}=1|{\stackrel{\sim }{x}}_{it},{\stackrel{\sim }{y}}_{it}).$$ (20)

Thus, under MMDP and MAR, π_it are a function of observed data only, making it possible to estimate these selection probabilities.

Let p_it = E (r_it = 1 | r_i(t−1) = 1, H_it) denote the one-step transition probability of the occurrence of missing data. Then, by invoking MMDP, it is readily checked that

$${\pi }_{it}=\prod _{s=2}^t{p}_{is},2\le t\le m,1\le i\le n.$$ (21)

Thus, we can estimate π_it by modeling the p_it. Since p_it is the probability of a binary response, we model that using logistic regression:

$$\text{logit}(p_{it}({\alpha }_t))=\text{logit}(\text{E}(r_{it}=1|r_{i(t-1)}=1,{\mathbf{\text{H}}}_{it}))={\mathbf{\xi }}_t^{\top }{\stackrel{\sim }{w}}_{it},2\le t\le m,$$ (22)

where ${\stackrel{\sim }{\mathbf{\text{w}}}}_{it}={\left(1,{\stackrel{\sim }{\mathbf{\text{x}}}}_{it}^{\top },{\stackrel{\sim }{\mathbf{\text{y}}}}_{it}^{\top }\right)}^{\top }$ and ${\stackrel{\sim }{\mathbf{\text{w}}}}_i={\left({\stackrel{\sim }{\mathbf{\text{w}}}}_{i2}^{\top },\dots ,{\stackrel{\sim }{\mathbf{\text{w}}}}_{im}^{\top }\right)}^{\top }$. For each t, we can estimate ξ_t by maximum likelihood or GEE conditional on the observed w̃_it at t − 1 (2 ≤ t ≤ m).

For AWGEE, we again consider the pre-post study design. In this case, we can readily estimate η in (18) using GEE, where $\eta ={({\eta }_0,{\eta }_1^{\top })}^{\top }$. With an estimate η̂, we can predict y_it By using η̂ and ξ̂ = ${\widehat{\mathit{\xi }}}_2^{\top }$, we can construct the AWGEE in (19).

3.2.4 Inference for WGEE and AWGEE Estimates

For inference based on WGEE, let Δ_i, (ξ) be modeled as in (21) and (22). If ξ_t is estimated by GEE or maximum likelihood, $\widehat{\xi }={({\widehat{\xi }}_2^{\top },\dots ,{\widehat{\xi }}_m^{\top })}^{\top }$ is the solution to the following vector estimating equation:

$${\sum }_{i=1}^n{\mathbf{\text{q}}}_i(\mathit{\xi })={\sum }_{i=1}^n{\left({\mathbf{\text{q}}}_{i2}^{\top },\dots ,{\mathbf{\text{q}}}_{im}^{\top }\right)}^{\top }=0,{\mathbf{\text{q}}}_{it}=\frac{\partial }{\partial {\mathit{\xi }}_t}\left\{r_{i(t-1)}\left[r_{it}log(p_{it})-(1-r_{it})log(1-p_{it})\right]\right\}.$$ (23)

Now, let

$$\mathbf{\text{B}}=\text{E}\left(\frac{{\partial }^{\top }}{\partial \mathit{\beta }}{\mathbf{\text{W}}}_{ni}\right),\mathbf{\text{C}}=\text{E}\left(\frac{{\partial }^{\top }}{\partial \mathit{\xi }}{\mathbf{\text{W}}}_{ni}\right),\mathbf{\text{F}}=\text{E}\left(\frac{{\partial }^{\top }}{\partial \mathit{\xi }}{\mathbf{\text{q}}}_i(\mathit{\xi })\right),$$

where W_ni is defined in (11). Then, as shown in Appendix A, under $\sqrt{n}$-consistency of α̂, the WGEE estimate β̂ is asymptotically normal with the asymptotic variance given by

$${\sum }_{\mathit{\beta }}={\mathbf{\text{B}}}^{-1}(\text{Var}({\mathbf{\text{W}}}_{ni})+\mathbf{\Phi }){\mathbf{\text{B}}}^{-\top },\mathbf{\Phi }={\mathbf{\text{CF}}}^{-1}\text{Var}({\mathbf{\text{q}}}_i){\mathbf{\text{F}}}^{-\top }{\mathbf{\text{C}}}^{\top }-\text{E}\left({\mathbf{\text{W}}}_{ni}{\mathbf{\text{q}}}_i^{\top }{\mathbf{\text{F}}}^{-\top }{\mathbf{\text{C}}}^{\top }\right)-{\left[\text{E}\left({\mathbf{\text{W}}}_{ni}{\mathbf{\text{q}}}_i^{\top }{\mathbf{\text{F}}}^{-\top }{\mathbf{\text{C}}}^{\top }\right)\right]}^{\top }.$$ (24)

In (24), Φ accounts for the variability of estimated ξ̂. We can estimate Σ_β by substituting consistent estimates in place of the respective quantities.

For AWGEE inference, we also need to estimate η for the prediction model in (18). Using GEE, the vector estimating equation is given by:

$${\sum }_{i=1}^n{\mathbf{\text{g}}}_i(\eta )={\sum }_{i=1}^n\frac{\partial }{\partial \eta }\left\{r_{i2}\left[y_{i2}-\left({\eta }_0+{\mathbf{\text{u}}}_i^{\top }{\mathit{\eta }}_2\right)\right]\right\}=\mathbf{0}.$$ (25)

Let $\widehat{\phi }={\left({\widehat{\phi }}_1^{\top },{\widehat{\phi }}_2^{\top }\right)}^{\top }$ with ϕ₁ = ξ and ϕ₂ = η. Then, by combining (23) and (25), ϕ̂ can be expressed as the solution to the following joint vector estimating equation:

$${\sum }_{i=1}^n{\mathbf{\text{s}}}_i={\sum }_{i=1}^n{\left({\mathbf{\text{q}}}_i^{\top }({\varphi }_1),{\mathbf{\text{g}}}_i^{\top }({\varphi }_2)\right)}^{\top }=\mathbf{0},{\mathbf{\text{s}}}_i={\left({\mathbf{\text{q}}}_i^{\top }({\varphi }_1),{\mathbf{\text{g}}}_i^{\top }({\varphi }_2)\right)}^{\top }.$$

The AWGEE estimate β̂ is also asymptotically normal under $\sqrt{n}$-consistency of α̂, with the asymptotic variance having the same form as in (24) except for substituting s_i for q_i and redefining $\mathbf{\text{C}}=\text{E}\left(\frac{{\partial }^{\top }}{\partial \phi }{\mathbf{\text{W}}}_{ni}\right)$ and $\text{F}=\text{E}\left(\frac{{\partial }^{\top }}{\partial \phi }{\mathbf{\text{S}}}_i\text{(}\phi \text{)}\right)$. Again, we can estimate the asymptotic variance by substituting consistent estimates in place of the respective parameters.

4 Application

We illustrate our considerations with both real and simulated data. We first present an application to data from a longitudinal study in depression research and then investigate the performance of the approach with small to moderate sample sizes by simulation. In all the examples, we set the statistical significance at α = 0.05. All analyses are carried out using a code we have developed for implementing the proposed approach using the R software platform (Free Software Foundation, 1999). This code is available from the author upon request.

4.1 Real Study

In a study on geriatric depression and associated medical comorbidities for old primary care patients, 744 subjects were enrolled from private practices and University-affiliated clinics in general internal medicine, geriatrics, and family medicine in Monroe County, New York (Lyness et al., 2007). All patients age 65 years and older who presented for care on selected days and were capable of giving informed consent. Enrolled subjects underwent semi-structured interviews, administered by trained raters in the subjects' homes or in research offices at the UR Medical Center. The raters' subject interviews included assessments of cognition, functional status, and psychopathology, the latter including the Structured Clinical Interview for DSM-IV (SCID) (Spitzer et al. 1986). Interviews and chart reviews were conducted at study intake, and again at one- and two-year follow-up time points.

In geriatric research, overall functional disability is of particular importance, as it reflects both the mental and physical health conditions of the individual. Primary measures of overall functional status include the Instrumental Activities of Daily Living (IADL), Physical Self-Maintenance Scales (PSMS), Global Assessment of Functioning (GAF), and the Karnofsky Performance Status Scale (KPSS) (Lawton MP and Brody, 1969, Karnofsky DA and Burchenal JH, 1949, Ware JE, Jr. and Sherbourne CD). For illustration purposes, we analyzed the change of IADL from baseline to one-year follow-up, as this measure assesses instrumental activities such as shopping or using the telephone and is particularly popular in geriatric research. Further, we only included the baseline value as a predictor when modeling the missingness of this outcome as well as the outcome itself at the follow-up using the respective logistic (20) and linear (18) models.

Of the 744 enrolled, 468 completed the IADL at the one-year follow-up. Shown in Table 1 are the estimates of the intercept and slope from the fitted logistic regression for modeling the missingness and the linear regression for modeling the outcome of IADL as a function of its baseline value at the follow-up. The baseline IADL was significant in both models, indicating that it did predict the occurrence of missing IADL as well as the outcome itself at the follow-up. Note that the negative sign of the estimate of the coefficient for baseline IADL in the logistic model indicates that the subjects with lower baseline IADL were more likely to come for assessment at the one-year follow-up. As lower IADL is associated with poorer functioning status, the observed sample at the follow-up visit seemed to be biased towards those with more severe overall functional disability at baseline.

Table 1.

Estimates of parameters of (1) logistic regression for modeling missingness at one-year follow-up, and (2) linear model for predicting IADL at one-year follow-up for the study on geriatric depression and associated medical comorbidities.

Estimates of models for missingness and outcome at one-year follow-up
Predictors	Estimate	Standard error	p-value
Logistic regression for missingness at one year follow-up
Intercept	0.635	0.086	<0.0001
Baseline IADL	−0.0491	0.018	0.007
Linear regression for predicting missing IADA at one year follow-up
Intercept	0.685	0.124	<0.0001
Baseline IADL	1.01	0.03	<0.0001

We fit the LMM in (1) and the distribution-free alternative in (5) to examine the change of IADL from baseline to the one-year follow-up. Shown in Table 2 are the estimates of the intercept β₀ and slope β₁ for the respective models under the different inference procedures. As the estimates of β₁ were positive across the board, the mean IADL increased at the follow-up visit, indicating better functioning status for the old primary care patients in this observational study.

Table 2.

Estimates of parameters of (1) linear mixed-effects model (ML), and (2) distribution-free linear model (GEE, WGEE and AWGEE) for change of IADL from baseline to one-year follow-up for the study on geriatric depression and medical comorbidities.

Estimates of models for change of IADL from baseline to one-year follow-up
Methods	β0 (s.e.)	p-value for β0	β1 (s.e.)	p-value for β1
ML	2.11(0.16)	<0.0001	0.054(0.009)	<0.0001
GEE	2.11(0.15)	<0.0001	0.032(0.014)	0.02
WGEE	2.11(0.15)	<0.0001	0.061(0.016)	0.0002
AWGEE	2.11(0.15)	<0.0001	0.060(0.013)	0.0001

However, the magnitude of the estimate of β₁ did vary substantially — not only between the models, but also across the different procedures within the same distribution-free linear model. The WGEE and AWGEE yielded quite similar estimates, with the latter AWGEE also providing improved efficiency, as indicated by smaller asymptotic standard errors. The GEE performed poorly, with a whopping 50% downward bias, as compared to its counterparts WGEE and AWGEE estimates. For the between-model comparison, the ML estimate of β₁ from the fitted LMM also incurred a downward bias, albeit with a much smaller magnitude relative to the GEE estimate. The downward bias in both cases was consistent with the fact that those assessed at the follow-up visit represented a subgroup with more severe overall functional disability at baseline.

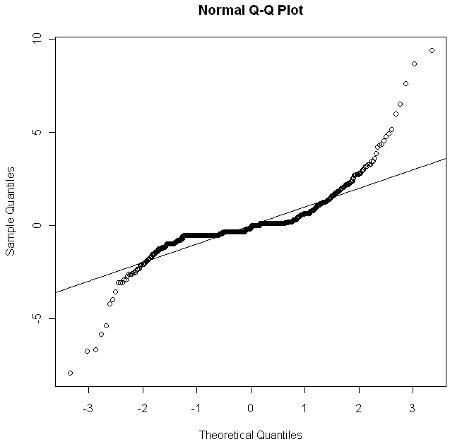
Shown in the Figure is the normal-based Q-Q plot of the conditional residuals obtained from the estimated fixed and random effects for the fitted LMM model (Nobre and Singer, 2007). The plot indicates clearly that the residuals did not follow a normal distribution, which may explain the difference in the estimates of the fixed effects between the parametric (LMM) and distribution-free models (WGEE and AWGEE).

4.2 Simulation Study

Given the discrepant estimates between LMM and WGEE (AWGEE) for the real study data in 4.2, we conducted a simulation study with a pre-post study design to investigate this issue further. We considered two non-normal distributions for the model error term of the LMM: a rescaled central chi-square with one degree of freedom and a uniform between −1 and 1. Since the results are quite similar, we only discuss and report the results from the chi-square-distributed error. To examine the performance of the models under small, moderate and large samples, we performed the simualation study with three sample sizes: n = 50, 100 and 2,000. All simulations were performed with a Monte Carlo sample of 1,000 using the R software (R Development Core Team, 2007).

We considered the pre- and post-treatment design and simulated the outcome according to the LMM in (1) by setting β₀ = β₁ = 1 and ∈_it (t = 1, 2) to follow the rescaled chi-square distribution, $({\chi }_1^2+1)\sqrt{{\sigma }^2/2}$, where ${\chi }_1^2$ denotes a central chi-square with one degree of freedom. We varied ${\sigma }_b^2$ and σ² to control the within-subject correlation $\rho ={\sigma }_b^2/({\sigma }_b^2+{\sigma }^2)$. We assumed no missing data at baseline t = 1 and simulated the missing response at post-treatment t = 2 under MAR according to the following logistic regression:

$$\text{logit}({\pi }_{i2})=\text{logit}(\text{P}(r_{i2}=1|y_{i1}))={\xi }_0+{\xi }_1{y}_{i1},1\le i\le n.$$ (26)

We set ξ₀ = 0.5 and ξ₁ = 1.2 to create about 25% missing response y_i2 at t = 2.

Under (1), it is readily checked that regardless of the distributions for b_i and ∈_it (see Appendix)

$$\text{E}(y_{i2}|y_{i1})={\eta }_0+{\eta }_1{y}_{i1},{\eta }_0={\beta }_0\left(1-\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }^2}\right)+{\beta }_1,{\eta }_1=\rho =\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }^2},1\le i\le n.$$ (27)

The above was used to predict missing y_i2 from y_i1 for AWGEE inference about β as discussed in Section 3.2.4. To study the effect of wrong weight function on WGEE and the robustness of AWGEE in such a scenario, we also estimated π_i2 under an incorrect model by leaving out y_i1 in (26).

We considered the null H₀ : β₀ = β₁, i.e., the mean at post-treatment is twice that at pretreatment. We tested H₀ using the Wald statistic, ${\mathit{\text{Q}}}_n^2=n{\widehat{\mathit{\beta }}}^{\top }{\mathbf{\text{K}}}^{\top }{(\mathbf{\text{K}}{\widehat{\sum }}_{\beta }{\mathbf{\text{K}}}^{\top })}^{-1}\mathbf{\text{K}}\widehat{\mathit{\beta }}$, which has an asymptotic central ${\chi }_1^2$ distribution. We estimated the type I error rate α based on the distribution of $Q_n^2$ from 1, 000 Monte Carlo (MC) replications, $\widehat{\alpha }=({\sum }_{j=1}^{1000}{I}_{\{Q_{nj}\ge q0.95\}})/1000$, where $Q_{nj}^2$ denotes the value of $Q_n^2$ from the jth MC replication and q_0.95 the 95th percentile of ${\chi }_1^2$. The maximum likelihood (ML) inference about β = (β₀,β₁)^┬ for LMM was obtained from the LME procedure in R, while the WGEE and AWGEE estimates for the distribution-free alternative in (5) were computed based on the asymptotic results in Section 3.2.

Shown in Table 3 are the estimates of β and associated asymptotic standard errors averaged over 1,000 MC replications obtained from ML, GEE, WGEE and AWGEE for the respective models, with a within-subject correlation ρ = 0.1 (or ${\sigma }_b^2=2/9$ and σ² = 2). The results confirmed that the baseline mean β₀ is consistently estimated by all four procedures. For β₁, ML yielded consistent estimates for the normal distributed error, but biased estimates under the rescaled ${\chi }_1^2$ error. As expected, GEE estimates were biased under both types of error distributions. Note that in the rescaled ${\chi }_1^2$ error case, the standard errors of these estimates did not increase much, making the upwardly biased estimates yield false significant results in practice.

Table 3.

Averaged estimates of β over 1,000 Monte Carlo replications along with asymptotic standard errors (s.e.) and type I error rates α for sample size 50, 100, 2000, with about 25% missing data at post-treatment based on ML for linear mixed-effects model, and GEE, WGEE and AWGEE for distribution-free linear model, with true β₀ = 1 and β₁ = 1 and within-subject correlation ρ = 0.1.

Methods	Weight Function	Prediction Model	Normal Distribution			Chi-square Distribution
			β0 (s.e.)	β1 (s.e.)	α	β0 (s.e.)	β1 (s.e.)	α
Sample size = 50
ML			1.00(0.21)	0.98(0.30)	0.06	1.00(0.22)	1.10(0.23)	0.07
GEE			1.01(0.21)	1.05(0.31)	0.05	1.00(0.20)	1.05(0.30)	0.05
WGEE	Right		0.99(0.21)	1.00(0.33)	0.08	1.01(0.21)	1.00(0.31)	0.06
	Wrong		1.01(0.21)	1.04(0.31)	0.06	1.00(0.20)	1.04(0.30)	0.06
AWGEE	Right	Right	1.00(0.21)	1.00(0.39)	0.07	1.00(0.21)	1.01(0.38)	0.07
	Wrong	Right	1.01(0.21)	0.99(0.32)	0.08	1.01(0.20)	0.99(0.32)	0.09
	Right	Wrong	0.99(0.21)	1.00(0.40)	0.06	0.99(0.21)	1.00(0.39)	0.06
	Wrong	Wrong	1.01(0.21)	1.05(0.33)	0.07	1.01(0.21)	1.05(0.34)	0.07
Sample size = 100
ML			1.00(0.15)	1.00(0.21)	0.06	1.00(0.15)	1.09(0.17)	0.06
GEE			1.00(0.15)	1.04(0.22)	0.06	1.00(0.15)	1.05(0.22)	0.05
WGEE	Right		1.00(0.15)	1.00(0.23)	0.05	1.00(0.15)	1.00(0.22)	0.06
	Wrong		1.00(0.15)	1.04(0.22)	0.07	1.00(0.15)	1.05(0.22)	0.05
AWGEE	Right	Right	1.00(0.15)	1.00(0.29)	0.04	1.00(0.15)	1.00(0.30)	0.04
	Wrong	Right	1.00(0.15)	1.00(0.23)	0.05	1.00(0.15)	1.00(0.22)	0.06
	Right	Wrong	1.00(0.15)	1.01(0.30)	0.04	1.00(0.15)	1.00(0.30)	0.04
	Wrong	Wrong	1.00(0.15)	1.04(0.24)	0.07	1.00(0.15)	1.06(0.23)	0.07
Sample size = 2000
ML			1.00(0.033)	1.00(0.049)	0.06	1.00(0.035)	1.10(0.038)	0.59
GEE			1.00(0.033)	1.04(0.049)	0.14	1.00(0.033)	1.05(0.049)	0.21
WGEE	Right		1.00(0.033)	1.00(0.054)	0.05	1.00(0.033)	1.00(0.050)	0.05
	Wrong		1.00(0.033)	1.04(0.049)	0.12	1.00(0.033)	1.05(0.049)	0.17
AWGEE	Right	Right	1.00(0.033)	1.00(0.052)	0.05	1.00(0.033)	1.00(0.051)	0.05
	Wrong	Right	1.00(0.033)	1.00(0.048)	0.06	1.00(0.033)	1.00(0.047)	0.06
	Right	wrong	1.00(0.033)	1.00(0.053)	0.05	1.00(0.033)	1.00(0.052)	0.05
	Wrong	Wrong	1.00(0.033)	1.04(0.049)	0.12	1.00(0.033)	1.05(0.048)	0.15

Under the correct weight function, WGEE performed well. When the incorrect constant weight function was used, WGEE yielded biased estimates, while the AWGEE estimates remained close to the true value of β₁ under the correct prediction model. However, AWGEE did not show any significant gain in efficiency; in fact, the estimate of the slope β₁ had a larger standard error under AWGEE than under WGEE across small sample sizes n.

To further investigate the relative efficiency between WGEE and AWGEE, we replicated the above analysis by increasing the within-subject correlation. For example, shown in Tables 4 and 5 are the estimates from one such replicated analysis with ρ = 0.3 (or ${\sigma }_b^2=1$ and σ² = 2 and 0.6 (or ${\sigma }_b^2=1.5$ and σ² = 1), respectively. It is seen that all conclusions above remain the same, except for the relative efficiency between WGEE and AWGEE under the correct weight function and prediction model. As ρ increased to 0.3, AWGEE have smaller standard errors than its counterpart WGEE when n = 2000. At ρ = 0.6, not only did AWGEE show smaller standard errors than WGEE across all sample sizes, their differences also widened as compared to those with ρ = 0.1.

Table 4.

Averaged estimates of β over 1,000 Monte Carlo replications along with asymptotic standard errors (s.e.) and type I error rates α for sample size 50, 100, 2000, with about 25% missing data at post-treatment based on ML for linear mixed-effects model, and GEE, WGEE and AWGEE for distribution-free linear model, with true β₀ = 1 and β₁ = 1 and within-subject correlation ρ = 0.3.

Methods	Weight Function	Prediction Model	Normal Distribution			Chi-square Distribution
			β0 (s.e.)	β1 (s.e.)	α	β0 (s.e.)	β1 (s.e.)	α
Sample size = 50
ML			1.00(0.25)	1.00(0.31)	0.06	1.01(0.24)	1.08(0.32)	0.06
GEE			1.00(0.24)	1.18(0.32)	0.08	1.00(0.24)	1.22(0.33)	0.08
WGEE	Right		0.99(0.25)	1.02(0.36)	0.05	1.02(0.24)	1.00(0.35)	0.04
	Wrong		1.00(0.24)	1.18(0.33)	0.09	1.01(0.24)	1.24(0.32)	0.11
AWGEE	Right	Right	1.00(0.24)	1.01(0.40)	0.04	1.01(0.24)	0.99(0.41)	0.03
	Wrong	Right	1.01(0.24)	0.99(0.35)	0.05	1.02(0.24)	1.00(0.34)	0.05
	Right	Wrong	0.99(0.24)	1.00(0.41)	0.03	1.00(0.24)	1.01(0.41)	0.04
	Wrong	Wrong	1.00(0.24)	1.17(0.34)	0.08	1.01(0.24)	1.21(0.34)	0.10
Sample size = 100
ML			0.99(0.17)	1.01(0.22)	0.07	1.00(0.17)	1.12(0.23)	0.07
GEE			1.00(0.17)	1.19(0.23)	0.15	1.00(0.17)	1.23(0.23)	0.15
WGEE	Right		1.00(0.17)	1.01(0.26)	0.06	1.00(0.17)	1.02(0.25)	0.03
	Wrong		1.00(0.17)	1.20(0.24)	0.13	1.00(0.17)	1.23(0.23)	0.18
AWGEE	Right	Right	1.00(0.17)	0.99(0.28)	0.05	1.00(0.17)	1.00(0.27)	0.04
	Wrong	Right	1.00(0.17)	1.01(0.24)	0.06	1.00(0.17)	0.99(0.25)	0.06
	Right	Wrong	1.00(0.17)	1.01(0.29)	0.05	1.00(0.17)	0.99(0.30)	0.04
	Wrong	Wrong	1.00(0.17)	1.18(0.25)	0.11	1.00(0.17)	1.22(0.25)	0.16
Sample size = 2000
ML			1.00(0.039)	1.00(0.050)	0.06	1.00(0.038)	1.12(0.052)	0.64
GEE			1.00(0.039)	1.20(0.052)	0.97	1.00(0.038)	1.23(0.052)	0.99
WGEE	Right		1.00(0.039)	1.00(0.068)	0.06	1.00(0.039)	1.00(0.059)	0.05
	Wrong		1.00(0.039)	1.20(0.053)	0.95	1.00(0.039)	1.23(0.052)	1.00
AWGEE	Right	Right	1.00(0.039)	1.00(0.055)	0.05	1.00(0.039)	1.00(0.054)	0.06
	Wrong	Right	1.00(0.039)	1.00(0.050)	0.06	1.00(0.039)	1.00(0.050)	0.06
	Right	wrong	1.00(0.039)	1.00(0.057)	0.05	1.00(0.039)	1.00(0.056)	0.05
	Wrong	Wrong	1.00(0.039)	1.19(0.051)	0.94	1.00(0.039)	1.23(0.052)	1.00

Table 5.

Averaged estimates of β over 1,000 Monte Carlo replications along with asymptotic standard errors (s.e.) and type I error rates α for sample size 50, 100, 2000, with about 25% missing data at post-treatment based on ML for linear mixed-effects model, and GEE, WGEE and AWGEE for distribution-free linear model, with true β₀ = 1 and β₁ = 1 and within-subject correlation ρ = 0.6.

Methods	Weight Function	Prediction Model	Normal Distribution			Chi-square Distribution
			β0 (s.e.)	β1 (s.e.)	α	β0(s.e.)	β1(s.e.)	α
Sample size = 50
ML			1.00(0.22)	1.01(0.23)	0.06	1.00(0.22)	1.08(0.24)	0.07
GEE			1.01(0.22)	1.30(0.26)	0.19	1.00(0.22)	1.32(0.25)	0.25
WGEE	Right		1.00(0.22)	1.02(0.29)	0.05	0.99(0.22)	1.04(0.29)	0.04
	Wrong		1.01(0.22)	1.30(0.27)	0.21	1.01(0.22)	1.32(0.25)	0.24
AWGEE	Right	Right	1.00(0.22)	1.01(0.27)	0.06	1.01(0.22)	1.01(0.28)	0.05
	Wrong	Right	1.01(0.22)	0.99(0.26)	0.06	1.00(0.22)	1.02(0.27)	0.06
	Right	Wrong	0.99(0.22)	1.02(0.28)	0.07	1.00(0.22)	0.99(0.28)	0.05
	Wrong	Wrong	1.01(0.22)	1.28(0.27)	0.20	1.01(0.22)	1.30(0.26)	0.22
Sample size = 100
ML			1.00(0.16)	1.00(0.16)	0.06	1.00(0.16)	1.10(0.17)	0.09
GEE			1.00(0.16)	1.30(0.18)	0.36	1.01(0.16)	1.32(0.18)	0.42
WGEE	Right		1.00(0.16)	1.02(0.21)	0.04	1.00(0.16)	1.01(0.21)	0.03
	Wrong		1.00(0.16)	1.29(0.18)	0.35	1.00(0.16)	1.33(0.18)	0.44
AWGEE	Right	Right	1.00(0.16)	1.00(0.18)	0.05	1.00(0.16)	1.00(0.19)	0.04
	Wrong	Right	1.00(0.16)	1.01(0.16)	0.06	1.00(0.16)	1.01(0.16)	0.06
	Right	Wrong	1.00(0.16)	0.99(0.19)	0.05	1.00(0.16)	1.00(0.19)	0.05
	Wrong	Wrong	1.00(0.16)	1.26(0.17)	0.34	1.00(0.16)	1.31(0.16)	0.44
Sample size = 2000
ML			1.00(0.038)	1.00(0.046)	0.06	1.00(0.035)	1.10(0.038)	0.59
GEE			1.00(0.035)	1.30(0.041)	1.00	1.00(0.035)	1.32(0.041)	1.00
WGEE	Right		1.00(0.035)	1.00(0.057)	0.05	1.00(0.035)	1.00(0.054)	0.04
	Wrong		1.00(0.035)	1.30(0.041)	1.00	1.00(0.035)	1.32(0.041)	1.00
AWGEE	Right	Right	1.00(0.035)	1.00(0.043)	0.05	1.00(0.035)	1.00(0.044)	0.05
	Wrong	Right	1.00(0.035)	1.00(0.040)	0.06	1.00(0.035)	1.00(0.040)	0.06
	Right	wrong	1.00(0.035)	1.00(0.043)	0.06	1.00(0.035)	1.00(0.045)	0.05
	Wrong	Wrong	1.00(0.035)	1.27(0.041)	1.00	1.00(0.035)	1.30(0.042)	1.00

5 Discussion

We investigated the two primary modeling strategies for longitudinal continuous response, the linear mixed-effects model (LMM) and the distribution-free linear model, with respect to their performance under missing data, and illustrated our considerations using real as well as simulated study data. Our results show that LMM and the GEE procedure for the distribution-free alternative generally yield biased estimates under MAR when the normality assumption for LMM is violated. Further, as indicated by the simulation results, the standard errors of these estimates do not increase to reflect model misspecification, making inference prone to misleading findings. Thus, when modeling longitudinal data, it is important to test the MCAR assumption as discussed in Section 3.2 before applying any of the models and inference procedures considered. If the null of MCAR is rejected, WGEE and/or AWGEE should be considered, unless there is strong evidence to support the use of the alternative linear mixed-effects model.

Our simulation results also indicate that the gain in efficiency by AWGEE over WGEE depends on the magnitude of the within-subject correlation ρ. Within the context of the particular simulation model considered, AWGEE is less efficient than WGEE for small sample size under small ρ such as 0.1. But, AWGEE edged out WGEE to be a more efficient procedure as ρ increased to 0.6.

Appendix

Under (1), we have

$${\rho }_{\mathit{\text{yb}}}=\text{Corr}(y_{i1},b_i)=\frac{\text{Cov}(y_{i1},b_i)}{\sqrt{\text{Var}(y_{i1})\text{Var}(b_i)}}=\sqrt{\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }^2}}.$$ (28)

Further, the above holds regardless of the distributions for b_i and ∈_it. Now, consider the linear regression

$$b_i={\varphi }_0+{\varphi }_1{y}_{i1}+{\delta }_i,{\delta }_i\sim (0,{\sigma }_{\delta }^2),1\le i\le n,$$

Where $(0,{\sigma }_{\delta }^2)$ denotes a distribution with mean 0 and variance ${\sigma }_{\delta }^2$. It follows from (28) and the relationship between linear regression coefficients and correlation that

$${\varphi }_1={\rho }_{\mathit{\text{yb}}}\sqrt{\frac{\text{Var}(b_i)}{\text{Var}(y_{i1})}}=\sqrt{\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }^2}}\sqrt{\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }^2}}=\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }^2}.$$

Also, since

$$0=\text{E}(b_i)={\varphi }_0+{\varphi }_1\text{E}(y_{i1})={\varphi }_0+{\varphi }_1{\beta }_0,$$

it follows that ${\phi }_0=-{\beta }_0{\sigma }_b^2/({\sigma }_b^2+{\sigma }^2)$.

Under (1) and regardless of the distributions for b_i and ∈_it, we have

$$\text{E}(y_{i2}|y_{i1})={\beta }_0+{\beta }_1+\text{E}(b_i|y_{i1})={\beta }_0+{\beta }_1+{\varphi }_0+{\varphi }_1{y}_{i1}.$$

By substituting the expressions of φ₀ and φ₀ into the above and combining the coefficients, we obtain (27).