Photochemical Reaction Dynamics of the Primary Event of Vision Studied by Means of a Hybrid Molecular Simulation

Abstract

The photoisomerization reaction dynamics of a retinal chromophore in the visual receptor rhodopsin was investigated by means of hybrid quantum mechanical/molecular mechanical (QM/MM) molecular dynamics (MD) simulations. The photoisomerization reaction of retinal constitutes the primary step of vision and is known as one of the fastest reactions in nature. To elucidate the molecular mechanism of the high efficiency of the reaction, we carried out hybrid ab initio QM/MM MD simulations of the complete reaction process from the vertically excited state to the photoproduct via electronic transition in the entire chromophore-protein complex. An ensemble of reaction trajectories reveal that the excited-state dynamics is dynamically homogeneous and synchronous even in the presence of thermal fluctuation of the protein, giving rise to the very fast formation of the photoproduct. The synchronous nature of the reaction dynamics in rhodopsin is found to originate from weak perturbation of the protein surroundings and from dynamic regulation of volume-conserving motions of the chromophore. The simulations also provide a detailed view of time-dependent modulations of hydrogen-out-of-plane vibrations during the reaction process, and identify molecular motions underlying the experimentally observed dynamic spectral modulations.

Introduction

Rhodopsin (Rh) resides in the rod cells of the retina and functions as a photoreceptor for vision. Upon photoabsorption, the receptor binds and activates a G-protein to initiate a signal transduction cascade (1). Rh includes a retinal molecule as a chromophore, the structure of which is schematically depicted in Fig. 1. The retinal molecule consists mainly of a polyene chain with six conjugated double bonds. One end of the polyene chain is covalently attached to a lysine residue of the protein through a protonated Schiff base, and the other end forms a β-ionone ring. A π-π^∗ excitation of the protonated Schiff base retinal is responsible for photoabsorption in the visible wavelength region.

Figure 1.

Chemical structure of the retinal chromophore. The chromophore is covalently bound to Lys²⁹⁶ of the protein via a protonated Schiff base. Dashed lines indicate boundaries between the QM and MM regions in the simulations.

The photoactivation of Rh leading to G-protein binding and subsequent activation of the rod cell is triggered by a photochemical reaction of the retinal chromophore (2,3). In the dark, Rh is in a resting state, with the chromophore bound in an 11-cis conformation in the protein-binding pocket. Absorption of a photon by the chromophore gives rise to photoisomerization around the C₁₁=C₁₂ bond and formation of a strained all-trans conformation, which initiates protein conformational changes resulting in G-protein binding.

The photoisomerization reaction in Rh is known as one of the fastest reactions in nature. Formation of the primary transient photoproduct, photorhodopsin (photo-Rh) (4), is completed within 200 fs (5), followed by relaxation of photo-Rh into a first quasi-stable, intermediate bathorhodopsin (batho-Rh) (6,7). Photoisomerization occurs much more rapidly in the Rh binding pocket than in solution (e.g., 2.5–4 ps in methanol (8)), indicating that the protein environment greatly facilitates the photoreaction. The fast reaction furnishes the receptor with high sensitivity to incoming light by avoiding unfavorable decay of the excited state without the 11-cis to all-trans isomerization.

The isomerization-based mechanism of Rh photoactivation is shared by analogous Rhs found in archae-bacteria (3). It was once thought that these species are a biological rarity; it is now known that archaeal photosynthetic species constitute the largest biological mass in the huge euphotic zone of the deep sea and possibly on Earth, and that they base their light processes on proteorhodopsin, an analog of Rh (9,10). A recent genetic analysis of microbial populations collected en masse in the Sargasso Sea revealed more than 782 new Rh-like photoreceptors (11). Bacteriorhodopsin (bR), an extensively studied archaeal Rh, functions as a light-driven proton pump. In the case of bR, the primary event is photoisomerization of the retinal chromophore from an all-trans form to a 13-cis one. As with Rh, the isomerization reaction occurs more rapidly than in solution, being completed in 240–500 fs (12), and being slightly slower than the reaction in Rh.

Many time-resolved spectroscopic experiments have been carried out in an attempt to elucidate the reaction mechanism (2,3,5,8,12–21). In addition to the determination of kinetic properties, recent advances in ultrafast spectroscopy have made it possible to reveal the characteristic dynamic features of reaction processes, such as molecular vibrations that are synchronous (coherent in a classical mechanics sense) among the proteins excited by photons in an ultrashort pulse (13,18–20). Moreover, in such experiments the isomerization reaction can be controlled optically by shaped excitation pulses, exploiting the quantum coherence of the reaction dynamics (21).

An ultrafast pump-probe experiment by Wang et al. (13) showed an oscillatory spectral modulation of pump probe signals in the Rh photoproduct, which was suggested to originate from an in-phase vibrational motion in the product. The observation implies that the reaction dynamics is fast and synchronous during the entire reaction process, i.e., from photoabsorption to the product formation, even in the presence of strong thermal noise in the surrounding protein environment. In contrast, Ruhman et al. (20) characterized photoproduct formation in bR as incoherent (in a classical mechanics sense) by means of a pump-dump-probe spectroscopic measurement, although synchronous vibrations were observed in the excited state (18,19). The results indicate that the vibrational synchronicity existing in the excited state is lost upon formation of the photoproduct, i.e., upon crossing of the excited-state and ground-state potential energy surfaces. The difference in the kinetic behaviors of Rh and bR may be important with regard to their different underlying enzymatic regulation mechanisms.

A recent time-resolved stimulated Raman experiment with a time resolution of ∼200 fs performed by Kukura et al. (15) revealed remarkable time-dependent frequency shifts of hydrogen-out-of-plane (HOOP) vibrations of the polyene chain of the retinal chromophore during the formation of batho-Rh. On the basis of the experimental findings, the authors proposed a model reaction scheme in which the A₂ HOOP motion at the isomerizing bond immediately after photoabsorption leads to transition to the electronic ground state. However, since the electronic transition is expected to take place faster than the time resolution of the experiment, the proposed A₂ HOOP motion was not directly observed.

The photoisomerization reaction in Rh has been the subject of molecular simulation studies for a long time. Three decades ago, Warshel (22) carried out a reaction dynamics simulation of retinal photoisomerization in Rh. In the simulation, the excited state of the chromophore was described at a semiempirical level of theory and the overall molecular dynamics was described in a modeled protein cavity. The simulation successfully predicted the completion of the photoisomerization reaction within 200 fs and revealed the photoproduct to be a strained all-trans conformation accompanied by a rotation around C₁₅ = N_ζ. The author also proposed that “bicycle pedal” isomerizing motions, i.e., co-rotations around two adjacent double bonds, permit the extremely fast space-conserving isomerization in the binding pocket. Such a semiempirical description for the excited state of the chromophore was also used for simulations of Rh and bR (22–27). After crystallographic structures of Rh and bR were solved, molecular dynamics (MD) simulations for the realistic protein systems were performed (28–31).

It is known from quantum chemical studies of small molecules that, in addition to the rotation of the isomerizing bond, photoisomerization involves rather complex motions, such as large hydrogen motions leading to pyramidalization (32) and hydrogen migration (33). Thus, rather accurate methodologies are required to describe the excited-state dynamics on the complex potential energy surfaces. Fortunately, recent progress in quantum chemistry has enabled investigators to calculate the excited-state potential energy surface of the retinal chromophore or its reduced analogs at the ab initio level of theory (34–36), and MD trajectories of the excited-state processes have been computed “on the fly” by using energy and forces obtained from ab initio quantum chemical calculations at each time step (37–41).

As described above, photoisomerization of retinal is markedly facilitated (i.e., catalyzed) by the protein environments of Rh and bR. When studying these reaction processes, therefore, it is necessary to take into account the effect of the surrounding protein. For that purpose, hybrid quantum mechanical/molecular mechanical (QM/MM) methods have been used in studies of retinal proteins (23,24,42–55). These methods combine QM methods, such as molecular orbital or density functional theories for the reactive moieties, with MM methods based on empirical force fields for the surrounding protein. The QM/MM methodology has been also applied to on-the-fly MD simulation. The photoisomerization dynamics of bR and Rh has been studied by QM/MM calculations with an empirical QM method (23,24), an ab initio QM method based on complete active space self-consistent theory (CASSCF) for a truncated chromophore analog (44), an open-shell Kohn-Sham density functional theory method (53), and an ab initio CASSCF method for an excited-state trajectory in a frozen protein matrix (50).

One advantage of QM/MM MD simulations is that the method enables one to compute straightforwardly, and without imposing empirical assumptions, time-dependent spectroscopic properties, such as the dynamic spectral modulations observed experimentally. For example, a QM/MM simulation of bR (44) succeeded in directly reproducing the experimentally observed dynamic spectral modulations (18,19) and in identifying molecular motions underlying the spectroscopic observations.

In the study presented here, we employed QM/MM MD simulations to investigate the dynamics and kinetics of the photoisomerization reaction in Rh. The trajectories of the entire reaction process from the vertically excited state to the photoproduct, which corresponds to the photo-Rh intermediate state (4) formed in 200 fs (5), were computed. An ensemble of such trajectories at room temperature provides a molecular view of the prominent dynamic and kinetic features of Rh. By comparing retinal motion in the protein with that in vacuo, we were able to elucidate that the fast and coherent photoisomerization dynamics of Rh is attributed to weak perturbation of the photoisomerization dynamics by the protein surroundings, and to dynamic regulation of volume-conserving motions in the electronically excited state. The results illustrate remarkable differences in the catalytic mechanism of the photoisomerization reaction in Rh and bR. We also computed time-dependent frequency shifts of HOOP vibrations during the reaction process in Rh, which shed light on molecular motions underlying the experimentally observed dynamic spectral modulations.

Materials and Methods

In the simulations presented here, we calculated several trajectories using classical and ab initio QM/MM MD methods. Standard classical MD simulations for the electronic ground state at 300 K were carried out to sample initial configurations, from which photochemical reaction trajectories were computed with ab initio QM/MM MD methods. We also calculated photoisomerization trajectories in the presence and absence of the protein to examine the influence of the protein cavity and its thermal fluctuation on the reaction dynamics.

Classical MD simulations

The starting model was constructed from the crystallographic structure of Rh determined by Okada et al. (56). The AMBER94 force field (57) was used for the protein. For the retinal protonated Schiff base, previously determined force-field parameters (43,58) were used. The trajectory was computed with a time step of 0.5 fs. The leap-flog algorithm was employed for integration. No cutoff for Lennard-Jones and Coulombic interactions was assumed. To maintain the overall shape of the protein, harmonic constraints with a force constant of 2.0 kcal/mol Å⁻² were imposed on C_α atoms beyond 12 Å from the chromophore. After minimization, a 2-ns MD equilibration was performed. Continuing the MD simulation, coordinates and velocities were sampled at 50 ps intervals and used to initiate an ensemble of 14 independent excited-state QM/MM MD simulations. For this purpose, 200 fs classical trajectories from the sampled configurations were computed by the velocity Verlet method with a time step of 1.0 fs to set up stable initial configurations for the QM/MM excited-state MD simulations (see below).

We also performed a simulated annealing classical MD simulation for 200 ps after the 2 ns equilibration to obtain a structure at 0 K, which was then refined by an ab initio QM/MM geometry optimization. The computational scheme used for the QM/MM geometry optimization was the same as that described elsewhere (42,59). During the QM/MM optimization, the harmonic constraints on the C_α atoms described above were not imposed.

Ab initio QM/MM MD simulations

The on-the-fly QM/MM MD simulations were carried out for the photoisomerization reaction in a fashion similar (see below) to our earlier investigation of bR (44). Fig. 1 depicts the QM region of the QM/MM simulations. The QM region includes the full polyene chain of the chromophore. The sp³ part of the β-ionone ring of retinal and the protein were treated at the MM level. The link atom approach with addition of hydrogen atoms was employed for chemical bonds at the boundaries between the QM and MM regions. Using the initial structures generated by the MD simulations described above, the excited-state trajectories were started at the state-averaged CASSCF level of theory (60,61). The CAS space includes full valence π-electrons, i.e., 12 electrons in 12 orbitals. Dunning's DZV basis functions (62) were used. The ground and the lowest π-π^∗ excited states were averaged evenly in the CASSCF calculations. The electronic structures were computed with MOLPRO (63). The velocity Verlet method with a time step of 1.0 fs was used for time integration. The MM code, the QM/MM interface, and the MD routine (44) were implemented in the MOLPRO program package.

Once the trajectory encountered the intersection between excited state and ground state, the electronic state solved for the trajectory was switched to the ground-state one, and the trajectory calculation was continued for the ground state at the state-averaged CASSCF level. Here the intersection was defined as the point along the trajectory where the energy difference between excited state and ground state reached its minimum and was <0.012 au (7.5 kcal/mol). The average of the energy differences at the intersection points over the trajectories was 1.8 kcal/mol and is much smaller than the average of the nonadiabatic coupling elements evaluated semiclassically (44), 21.9 kcal/mol, indicating that the two electronic states were strongly mixed at the intersection points. The excess energy upon the transition corresponding to the energy difference between the excited and ground states at the intersection was distributed by increasing the momenta of atoms along the nonadiabatic coupling elements calculated at the intersection (64). The time step of the MD trajectory in the energy-crossing region where the energy difference was <0.010 au was shortened to 0.25 fs.

After the crossing process was completed, when the energy difference between the excited state and the ground state along the ground-state trajectory became sufficiently large (>20 kcal/mol), the trajectory calculation was continued with the state-specific CASSCF method. We note here that force calculation for the state-specific CASSCF wave function does not require solving the coupled perturbed CASSCF equation, which is one of the most time-consuming computational steps in the force calculation for the state-averaged CASSCF wavefunction. Hence the use of the state-specific CASSCF method considerably reduces the computational effort of the simulations. Furthermore, it was often observed in the ground-state trajectories that the state-average description introduced artifacts in the electronic wave function because of energy curve crossings of the S₁ state with a higher excited state at strongly distorted photoproduct conformations. The state-specific treatment naturally solves this difficulty. The ground-state trajectories were then computed for 200 fs.

Using the state-averaged CASSCF method, we also computed an in vacuo trajectory of the QM chromophore, i.e., without the MM parts, for 196.25 fs from a QM/MM optimized geometry of the resting ground state described elsewhere (59) without adding initial velocities.

In previous QM and QM/MM MD studies (24,40,41,44,50), quantum yields of the reaction, i.e., the branching ratio of possible photoproduct conformations, were computed. In the case of Rh, the photoexcitation results either in formation of the photoproduct state with all-trans retinal or in a decay to the initial state with the 11-cis conformation. The branching of the trajectories to the two different states takes place mainly at the energy curve crossing (24,44,65). An evaluation of the quantum yield, however, was beyond the scope of this study because of the very demanding computational cost (see below). The scheme presented here for the energy curve crossing is inappropriate for evaluating the quantum yield of the reaction because the treatment neglects contributions from trajectories surviving in the excited state after passing the curve-crossing region (24,44,65).

These simulations provide representative trajectories for examining the kinetic behavior and spectral modulations, irrespective of the impossibility of calculating the quantum yield. First, the kinetic features are determined mainly by the dynamics before the curve-crossing region, not that at the crossing points, as described below for Rh and shown in a previous study for bR (44). Second, it is not necessary to take into account the paths going back to the initial state, which would be determined by the quantum yield calculation. Note that the trajectories relevant to the experimentally observed spectral phenomena are the reactive ones, not those returning to the initial (11-cis) state, since all of the spectroscopic experiments measured difference spectra (i.e., spectral components that differ from the initial state). Finally, as observed in our previous study of bR (44), the first curve-crossing event after the vertical excitation along each trajectory exclusively leads to the photoproduct without formation of the initial state, and thus gives a major contribution to the reaction photoproduct (24,44,65). The curve-crossing events determined by the scheme presented here are well characterized as the first crossing event, and are consistent with the exclusive formation of the reaction photoproduct.

Although the quantum yield could be computed by alternative methods, such as Tully's surface hopping (TSH) methods (66), the trajectories calculated in this study are too limited in time and number for that purpose because of the high computational cost for the large QM system. For example, the standard TSH scheme requires a much larger number of trajectories to obtain a converged result because the electronic transition event is determined by comparing the transition probability along the trajectory with a random number. The approximate surface hopping method introduced in our previous study of bR (44) also needs longer trajectories in the excited state to achieve convergence. One may consider using the Landau-Zener (LZ) formula (67,68) to evaluate the transition probability at the energy curve crossing; however, the LZ theory is only valid for constant coupling during curve crossing, which is not the case for retinal photoisomerization. As shown in our previous study of bR (44), the nonadiabatic coupling constant exhibits a sharp peak in time at the crossing point, which renders the LZ theory unsuitable.

QM/MM interaction

In this study we adopted an IMOMM-type (mechanical embedding) (69) description of the QM/MM interaction for the on-the-fly MD simulation, instead of a conventional QM/MM method as previously employed for the photoisomerization reaction of bR (44). The two methods differ mainly in the treatment of the electrostatic interactions between the QM and MM regions. In the conventional QM/MM method, electrons of the QM molecules explicitly interact with MM effective point charges of the surrounding protein through one-electron integrals, whereas in the IMOMM-type description the electrostatic interactions between the QM and MM regions are described at the MM level of theory. Thus, in principle, the description of electrostatic interaction in the conventional QM/MM method is more straightforward and therefore more accurate than that in the IMOMM method. Nevertheless, in this case we found that the conventional QM/MM description for the CASSCF wave functions gives rise to an unbalanced energy increase of the S₁ π-π^∗ excited state, whose electronic character is of an ionic B_1u type, relative to the S₂ A_g-like excited state. The unbalanced description of the energy levels of S₁ and S₂ leads to failure in completing the photoisomerization due to transition to the A_g-like state along the trajectories. The trajectory, which is kept in the B_1u-like state, could be computed by a surface-hopping scheme with a three-state averaged CASSCF method. However, the trajectory of the B_1u-like state is largely perturbed by unrealistic curve crossings to the A_g-like state because of a strong mixing of the electronic wave functions.

One could overcome this difficulty by taking into account the dynamic electron correlation by post-CASSCF calculations, because the electron correlation stabilizes the ionic B_1u state more than the A_g one (42,48), suppressing the artificial crossing between those states. Unfortunately, it is too formidable a task to carry out an on-the-fly QM/MM MD simulation with post-CASSCF methods because of their extremely high computational cost. Instead, we approximated the electrostatic interaction between the QM and MM regions by the IMOMM treatment, which lowers the energy level of S₁ relative to that of S₂ and thus cancels the error of the unbalanced description of the energy levels. Although the approximation alters the description of the electrostatic interaction, these approximate trajectories lead to complete photoisomerization events with kinetic properties that are in good agreement with experimental results, as described further below.

The electronic wave function obtained with the approximation is of the gas phase type, i.e., it does not include explicit coupling of the electronic wave functions with the electrostatic field of the protein. Nevertheless, the chromophore-protein interactions, which are important for in situ photoisomerization dynamics, such as the hydrogen bonding and steric interactions found in the previous study of bR (44), are at least qualitatively treated at the MM level. Furthermore, as shown in previous studies (35,50), the dipole moment of the chromophore does not change significantly along the isomerization path before the curve-crossing region, indicating a weak dynamic coupling of the chromophore's electronic redistribution with the electrostatic field of the protein before the curve crossing. Since the kinetic behavior is determined mainly in the region before the curve crossing as described above, the approximation is expected to have only a minor effect on the kinetic behavior. However, in the curve-crossing region, where the chromophore is known to undergo a sudden polarization, the abrupt change of the electronic distribution would affect the reaction dynamics. In fact, as shown in the previous study of bR (44), the curve-crossing probability at the crossing point is largely altered by the sudden polarization. Fortunately, the curve-crossing event is not directly related to reaction kinetics and spectral modulations, the main subject of this study.

Results

The photoisomerization trajectories of Rh at room temperature were computed by ab initio QM/MM MD methods. At t = 0, the trajectories were started with vertically excited chromophores in the S₁ excited state. Through curve crossing to the S₀ (ground) state, the trajectories proceed to the photoproduct state at t = ∼200 fs. The photoproduct is considered to be the photo-Rh state (4), i.e., the experimentally assigned state that forms after 200 fs (2).

The statistical and kinetic behaviors of the reaction were examined for an ensemble of the reaction trajectories in the presence of thermal fluctuation. Vibrational spectra modulations observed in time-resolved Raman spectroscopy (15) were also investigated to identify their molecular origin. The characteristics of the conformational changes of the chromophore in the excited-state part of the simulations are very similar to those observed in an excited-state trajectory at 0 K with a frozen protein environment studied by Frutos et al. (50), despite the very different reaction conditions. We thus only briefly describe the time evolutions of the S₁ and S₀ energy levels and conformational changes along the trajectories in the excited-state part below. Reasons for the similarity of the excited-state trajectories under these different conditions are discussed later. In contrast to the excited-state dynamics, formation of the photoproduct in the ground state after the curve crossing exhibits remarkable dynamic inhomogeneity, as revealed by the trajectory ensemble. Prominent vibrational motions were also found during the formation of the photoproduct.

Reaction dynamics

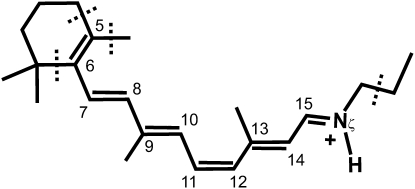
Fig. 2 shows the time evolution of the S₁ and S₀ energy levels of a typical isomerization trajectory (see also Movie S1 in the Supporting Material). At t = 0, the chromophore is vertically excited upon photoabsorption, and the trajectory starts in the S₁ excited state. Immediately after the photoabsorption is completed (t = 10 fs), the S₁ energy level decreases along with a large increase in the S₀ energy. In this initial phase, in-plane relaxation of the bond alternation of the polyene chain in the chromophore takes place, accounting for the changes in the energy levels (50). At the same time, the isomerizing bond begins to rotate away from the cis form. The rotation around the isomerizing bond develops further along the excited-state trajectory and eventually reaches the intersection points at t = 75.75 fs. During the excited-state relaxation, the energy level of the S₁ state decreases gradually, whereas that of the S₀ state increases more steeply. At the intersection point, the energy difference between the two states is small (1.1 kcal/mol), indicating that the electronic transitions occur through the conical intersection, as suggested by previous ab initio molecular orbital studies (34–36). The dihedral angle of the isomerizing bond is almost perpendicular at the intersection point.

Figure 2.

Time evolution of the potential energy of the chromophore along a typical photoisomerization trajectory at 300 K. The dark solid curve before energy crossing at 75.75 fs indicates the potential energy of the excited state along the excited-state trajectory after vertical excitation at t = 0. Dark and light solid curves after the crossing indicate the potential energy of the ground state along the ground-state trajectory computed by state-averaged and state-specific CASSCF methods (see Materials and Methods). The potential energy of the state-specific CASSCF calculation is shifted by a constant to connect to the energy of the state-averaged one at the switching time. Dashed curves show the potential energies of the ground and excited states along the trajectory in the excited and ground states, respectively. Geometries of the chromophore at t = 0, at the crossing point, and in the photoproduct (t = 250 fs) are shown.

After the electronic transition from the excited state at the intersection point, the trajectory proceeds in the ground state. The energy level of the S₀ state largely decreases until t = ∼200 fs, whereas the S₁ energy level quickly increases and separates from the S₀ one. This separation in energy is accompanied by a rotation of the isomerizing bond in the S₀ state from the perpendicular form to the all-trans form. After ∼200 fs, the photo-Rh photoproduct state is considered to have formed.

Statistical and kinetic behaviors

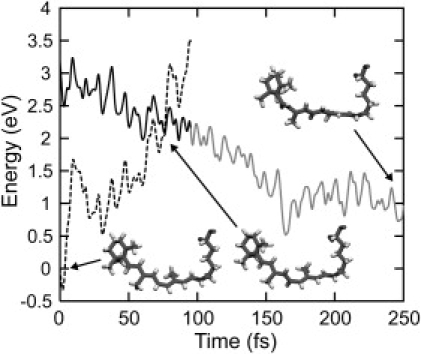
To examine the statistical and kinetic behaviors of the reaction, 14 trajectories were computed from different initial random configurations (see Materials and Methods). Fig. 3 depicts the time evolution of energy differences between the S₀ and S₁ states along the 14 trajectories, which directly corresponds to the time-dependent fluorescence spectrum. The vertical excitation energies at t = 0 are estimated to be ∼3.2 eV. Immediately after the vertical excitation, the energy gap decreases quickly with oscillations attributed to the in-plane stretching motion of the polyene chain (34). After a very short stay (20–60 fs) in a transient state at ∼1.2 eV, all trajectories encounter the electronic transitions to S₀ within 100 fs. The time constant of the decay of the transient excited state is in good agreement with the experimental findings, i.e., ∼50 fs (5,70). The decay observed in the current simulations is slightly faster than that seen in a QM/MM trajectory computed by Frutos et al. (50), presumably because of differences in the treatment of the electronic wave function, the QM/MM interactions, and the inclusion of protein motions.

Figure 3.

Time evolutions of the potential energy gap between the excited state and the ground state along 14 trajectories at 300 K. Gray solid and dashed curves indicate the potential energy gap between the two states along the trajectory in the excited state and the ground state, which correspond to emission and absorption energies, respectively. The energy gaps along a trajectory at 0 K are also indicated by black curves.

As can be clearly seen in Fig. 3, the kinetic behavior in the excited state decay is highly synchronous. All trajectories decay to S₀ within 100 fs, as mentioned above. In addition, the time evolution of the energy gap along the trajectories at 300 K is narrowly distributed and the energy gap stays close to the value seen in the trajectory at 0 K. This indicates that stochastic perturbations to the excited-state dynamics introduced by thermal fluctuation at 300 K are minimal, with the regularity of the isomerization dynamics being largely preserved. Such coherent kinetics of the excited-state decay in Rh is a prerequisite for the synchronous vibration in the photoproduct observed in a pump-probe time-resolved experiment by Wang et al. (13).

It is noteworthy that the kinetic behavior of the isomerization in Rh is in striking contrast to the behavior seen in bR (20,44). In Rh, all trajectories decay synchronously within the first 100 fs to the ground state, whereas the decay events in bR are widely distributed in time, i.e., between 50 and 500 fs, as shown previously by a similar QM/MM MD study (44). This asynchronous kinetic behavior in bR was also identified in a pump-dump-probe time-resolved experiment reported by Ruhman et al. (20).

Bond rotation

After the electronic transition, at the first intersection point, most trajectories (13 out of 14) resulted in the formation of the all-trans configuration, with one proceeding in a bicycle-pedal fashion to the 9-cis configuration through co-rotations around the C₁₁=C₁₂ and C₉=C₁₀ bonds. The dominant formation of the all-trans photoproduct upon the first electronic transition event is due to a momentum of bond rotation toward the all-trans configuration, as shown previously in QM/MM trajectories for bR and Rh (22–24,44,65).

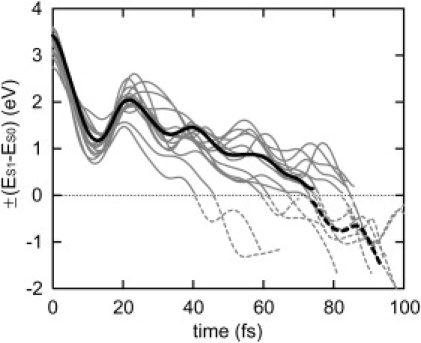
Fig. 4 a depicts the time evolution of dihedral angles along the calculated trajectories. The dihedral angles at the vertically excited state (t = 0), at the energy crossing point (t = 69.75 fs being the mean crossing time), and at the photo-Rh state (t = 250 fs) are depicted in Fig. 4 c along with the geometry of the chromophore. The dihedral angle around the isomerizing bond, C₁₁=C₁₂, changes unidirectionally from −16.5° at t = 0 to −88.3° at the crossing point, reaching −163.5° after the electronic transition to S₀ at t = 250 fs.

Figure 4.

Dihedral angle dynamics. (a) Time evolution of retinal dihedral angles averaged over 13 11-cis→all-trans isomerization trajectories at 300 K. Colored curves indicate the dihedral angles of C₁₁=C₁₂ (red), C₉=C₁₀ (light blue), C₈-C₉ (green), and C₆-C₇ (dark blue); black curves indicate dihedral angles of C₇=C₈, C₁₀-C₁₁, C₁₂-C₁₃, C₁₃=C₁₄, C₁₄-C₁₅, and C₁₅=N_ζ (see text). (b) Time evolution of standard deviations of the mean dihedral angles shown in a. (c) Retinal geometries and means as well as standard deviations (values in parentheses) of the dihedral angles at the moment of vertical excitation time (t = 0), at the mean crossing time (t = 69.75 fs), and in photo-Rh (t = 250 fs). The geometry depicted is taken from the trajectory at 0 K.

Along with the rotation of the isomerizing bond, remarkable torsions around other bonds in the polyene chain develop (Fig. 4, a and c). The C₉=C₁₀ double bond changes its dihedral angle from −190.0° at t = 0 to ∼60.0° at t = ∼100 fs. Such co-rotational behavior of the retinal photoisomerization in Rh was suggested in the bicycle-pedal model proposed by Warshel (22), but in our trajectories the bicycle-pedal torsions developed only transiently. The torsion around C₉=C₁₀ during the isomerization has also been suggested by static potential energy surface calculations for the isomerization in the protein confinement (49), and by classical (28) and QM/MM (50) MD simulations.

Our calculation also shows a large dihedral change of the C₆-C₇ single bond upon photoisomerization, which represents torsion between planes of the polyene chain and the β-ionone ring, respectively. As shown in Fig. 4, a and c, this bond is rather strongly twisted by −51.8° from planarity at t = 0, differing in this regard from the other bonds in the retinal backbone. After photoexcitation, the dihedral angle changes within 50 fs to −30°. The initial rotary motion in the excited state was also observed by Frutos et al. (50). As discussed below, the increase of the dihedral angle in the excited state is partly attributed to a change of the electronic structure upon photoexcitation. The rotation then develops further and the dihedral angle gradually approaches −10° in the photoproduct.

A significant torsion is induced around the C₈-C₉ single bond after the electronic transition to the ground state. The dihedral angle around C₈-C₉ is −180.4° at t = 0; it then undergoes a small change at ∼180° until t = 100 fs and changes then to ∼−210° during photoproduct relaxation. The torsions induced around the C₈-C₉ and C₉=C₁₀ bonds during photoproduct relaxation seem to originate from steric interaction of the 9-methyl group of retinal with the nearby Tyr²⁶⁸.

As shown in Fig. 4 a, some of the other dihedral angles also undergo characteristic changes, although the changes are not large. During photoproduct relaxation, i.e., at t > 100 fs, the dihedral angles of N_ζ=C₁₅, C₁₃=C₁₄, C₁₂-C₁₃, and C₇=C₈ gradually increase to ∼−160°. As discussed previously (28), such small torsions, extended over the polyene chain, play an important role in keeping the overall bent shape of the chromophore, which minimizes steric conflict in the protein cavity after formation of the all-trans conformation. A much smaller torsion around C₁₄-C₁₅ is due to steric interaction of the C₁₄-H₁₄ moiety with a proximal alanine residue, as discussed below.

Fig. 5 a depicts the time evolution of the dihedral angle of the trajectory at 0 K. It is noteworthy that the time evolution averaged over the 13 trajectories at 300 K is similar to that at 0 K computed in this study for the overall reaction process, and by Frutos et al. (50) for the excited-state process in a fixed protein. Thus, thermal fluctuation of the environment does not appear to perturb the conformational dynamics of the chromophore.

Figure 5.

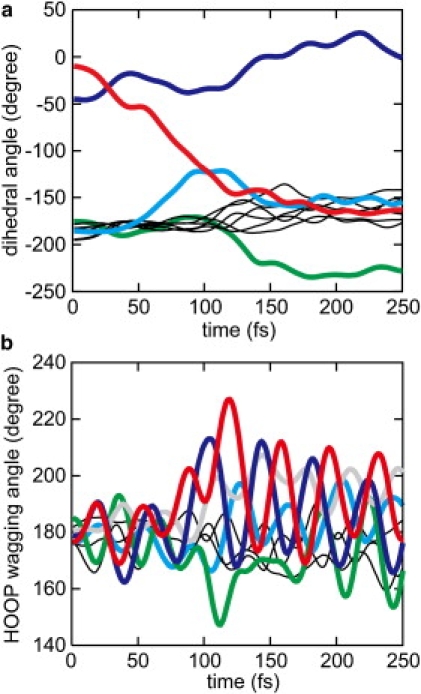
Time evolution of dihedral and HOOP wagging angles along the trajectory at 0 K. (a) Time evolution of the dihedral angles. The color scheme is the same as in Fig. 4. (b) Time evolution of HOOP wagging angles. Colored curves indicate the wagging angles at C₁₀ (red), C₁₂ (dark blue), C₁₁ (green), C₈ (gray), and C₁₄ (light blue), and thin black curves denote those at C₇, C₁₃, and N_ζ.

The time evolution of the root mean-square displacement (RMSD) of the dihedral angle, as shown in Fig. 4, b and c, allows one to assess more precisely the dynamic inhomogeneity of the dihedral angle changes during the isomerization process. The RMSD of the isomerizing bond, C₁₁=C₁₂, which measures 7.4° at t = 0, increases to ∼20° during the photoisomerization process, indicating dynamic inhomogeneity. The inhomogeneity arises mainly from small thermal variation in initial motions at the Franck-Condon region among the individual trajectories, as shown in Fig. S1 in the Supporting Material. Slightly distributed survival times in the Franck-Condon region due to the differences in the initial rotational motions at t = 0 lead to the inhomogeneity. The quick changes of the angles in the crossing region amplify the angular inhomogeneity in this region. Furthermore, vibrational coupling with a HOOP motion may contribute to the inhomogeneity. As shown in Fig. S1, the development of the rotational angle exhibits a small oscillation with a period of ∼40 fs originating from the vibrational coupling with the HOOP motion.

Nevertheless, compared to the 147° change of the C₁₁=C₁₂ dihedral angle, the observed dynamic inhomogeneity is remarkably small, reflecting synchronous dynamics of the rotation around the isomerizing bond. It is noteworthy that the dynamic inhomogeneity in Rh is much smaller than that in bR. It is also remarkable that the RMSD of C₉=C₁₀ increases up to ∼18° in the curve-crossing region, which is much smaller than the average torsion induced in this region, showing a synchronous behavior similar to that of the C₁₁=C₁₂ torsion. The other dihedral angles also exhibit small deviations in the excited state. Overall, the conformational dynamics in Rh's excited state is found to be highly homogeneous.

In contrast to the homogeneous dynamics of the torsions in the excited state, the dynamics at the C₆-C₇ and C₈-C₉ bonds after crossing to the ground state exhibits significant inhomogeneity. The RMSDs of those dihedral angles steeply increase after 150 fs and reach up to ∼40° at t = 250 fs, i.e., two dihedral angles in the photoproduct deviate largely from one another among the trajectories.

HOOP wagging vibrational motion

In addition to the torsional motions, the HOOP wagging vibrational motions undergo significant changes during the isomerization process. Fig. 5 b depicts the time evolution of the HOOP wagging angles in the trajectory at 0 K. In the ground state (t < 0), the HOOP wagging angles slightly deviate from planarity due to the torsions around the dihedral angles described above. Upon photoexcitation at t = 0, the HOOP wagging angles start small oscillations around ∼180°. After crossing to the ground state (t > 80 fs), the HOOP wagging vibrations, especially at C₈, C₁₀, C₁₁, C₁₂, and C₁₄, become strongly excited, and the centers of the vibrational oscillation quickly depart from planarity.

To characterize the change in the HOOP vibrational motions, the time evolution of the HOOP angles was analyzed with the use of a sliding Hunning window function:

$$H(t,t_g)=\frac{1}{2}\left[1-\cos \frac{\pi }{2\alpha }\left(t-t_g\right)\right],$$ (1)

where t_g denotes the time of the window center (i.e., the gate delay time), and α is the full width at half maximum (FWHM) of the window. In this calculation, FWHM was set to 64 fs. The time evolution of the vibrational oscillation was extracted by applying the sliding window along t_g. First, the mean wagging angle in the window, $\overline{\theta }$, was calculated using the formula

$$\overline{\theta }\left(t_g\right)=\frac{{\int }_{-\alpha }^{\alpha }dtH(t,t_g)\theta \left(t\right)}{{\int }_{-\alpha }^{\alpha }dtH(t,t_g)}.$$ (2)

Accordingly, the mean wagging angle reported corresponds to the origin of the vibrational oscillation in the window. The frequency of the vibrational oscillation within the window was then analyzed by Fourier transformation using

$$\begin{array}{c}\tilde{\theta }(\omega ,t_g)={\int }_{-\alpha }^{\alpha }dtH(t,t_g)\Delta \theta \left(t\right)e^{-i\omega t},\\ \Delta \theta \left(t\right)=\theta \left(t\right)-\overline{\theta }\left(t\right).\end{array}$$ (3)

The Fourier components as a function of t_g, $\tilde{\theta }(\omega ,t_g)$, indicate the time evolution of the frequencies of oscillation. Finally, the amplitude of the oscillation within the window, A(t_g), was estimated using

$$A^2\left(t_g\right)={\int }_0^{{\omega }_{\max }}d\omega {\left|\tilde{\theta }(\omega ,t_g)\right|}^2.$$ (4)

The quantities described above were also averaged over the 13 trajectories at 300 K.

Fig. 6 a shows the time evolution of the mean wagging angle, $\overline{\theta }$. As can be clearly seen, the mean wagging angles change drastically during photoisomerization. The mean wagging angle at C₁₀ in the initial ground state before the photoexcitation at t_g = −100 fs is −6°. Upon photoexcitation, the mean wagging angle increases steeply and reaches a maximum deviation from planarity of 17° at t_g = 130 fs. Such a large deviation indicates a strong pyramidalization at the wagging center atom. It is noteworthy that the pyramidalization coincides with the large torsion around C₉=C₁₀, i.e., the adjacent double bond of the polyene chain discussed above (see Fig. 4 a). Thus, the formation of the pyramidal conformation is closely coupled to the torsion of the polyene chain. After reaching its maximum, the mean wagging angle starts to decrease, indicating relaxation from the pyramidal structure.

Figure 6.

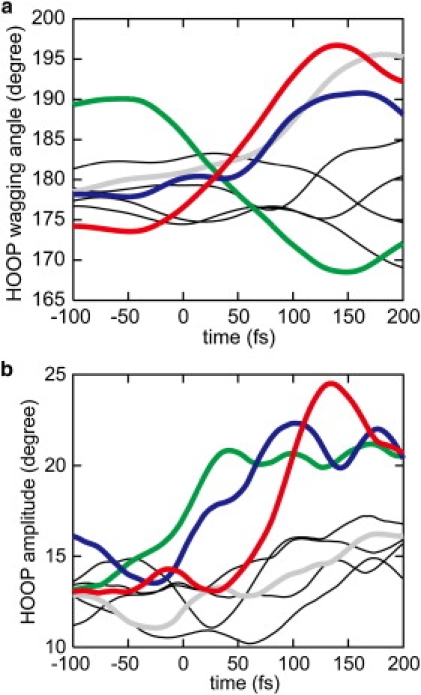
Time evolution of (a) mean angles, $\overline{\theta }\left(t_g\right)$, and (b) amplitudes, A(t_g), of HOOP motions evaluated by means of Eqs. 2 and 4, respectively, averaged over 13 11-cis→all-trans isomerization trajectories at 300 K. The color scheme of the curves is the same as in Fig. 5b, except for the angle at C₁₄, which is indicated by a thin black curve.

The mean wagging angles at C₈ and C₁₂ increase by more than 10° upon photoisomerization. The increases are accompanied by large changes in the dihedral angles around the adjacent bonds, C₈-C₉ and C₁₁=C₁₂, respectively, and are indicative of pyramidalization. Large pyramidalization at C₁₁ is also induced by the isomerizing rotation around C₁₁=C₁₂, although the direction of pyramidalization is opposite to those at the other wagging centers described above. Thus, at t_g = ∼150 fs, the isomerizing bond C₁₁=C₁₂ brings about a large pyramidalization at the two atom centers, with both apexes of the pyramidalization pointing toward the extracellular side. After t = ∼150 fs, the pyramidalization undergoes relaxation similar to that at C₁₀.

Fig. 6 b depicts the time evolution of the amplitude of the wagging oscillation calculated according to Eq. 4. The amplitudes at the C₁₀, C₁₁, and C₁₂ wagging centers increase significantly upon photoisomerization. In the case of the wagging oscillation at C₁₀, the amplitude is ∼13° before photoexcitation at t_g = 0. After photoexcitation, the oscillation stays at similar amplitudes until t_g = 50 fs. Subsequently, the amplitude rises steeply to ∼25° upon crossing to the ground state. Together with the large increase of the mean wagging angle, the deviation of the wagging angle from planarity can reach more than 40° at t_g = 100 ∼150 fs.

In the case of the wagging oscillations at C₁₁ and C₁₂, the amplitudes start to increase from t_g = ∼−50 to t_g = ∼ 0 fs, respectively, i.e., earlier than that at C₁₀. Since the amplitude at t_g is evaluated using a Hunning window function with FWHM of 64 fs, it includes components of the oscillation during a period from t = t_g − 64 fs to t = t_g + 64 fs. The early increases before and around t_g = 0 are therefore attributed to vibrational excitations induced by photoexcitation at t_g = 0, and the vibrational excitations are then intensified after crossing to the ground state. No significant wagging amplitude develops at C₈, although the mean wagging angle greatly increases upon the formation of photoproduct, as shown in Fig. 6 a.

Shift in wagging frequencies

The frequencies of the oscillation are also altered during photoisomerization. Fig. 7 shows the time evolution of the frequencies of the wagging oscillations at C₈, C₁₀, C₁₁, and C₁₂. As can be clearly seen, the frequencies change over time. In particular, the peak of the frequency distribution exhibits a prominent change. For the wagging oscillation at C₁₀, the peak frequency is ∼1000 cm⁻¹ before t_g = 0. Upon photoexcitation, the peak frequency quickly decreases by 100 cm⁻¹ around t_g = 0 and then decreases further and reaches a minimum frequency of ∼800 cm⁻¹ at t_g = ∼120 fs. Subsequently, the peak frequency increases again, reaching 950 cm⁻¹ at t_g = 200 fs. The time evolution of the frequencies at C₁₁ and C₁₂ shown in Fig. 7 exhibits features similar to those described above. The peak frequencies at C₁₁ and C₁₂ gradually decrease by ∼50 cm⁻¹ and ∼100 cm⁻¹, respectively, from t_g = −50 fs to t_g = ∼100 fs, and then increase again. In the case of C₈, although the intensity of the component is rather small compared to the other ones, the peak frequency decreases gradually from ∼1000 cm⁻¹ to 900 cm⁻¹ from t_g = 0 to t_g = 200 fs.

Figure 7.

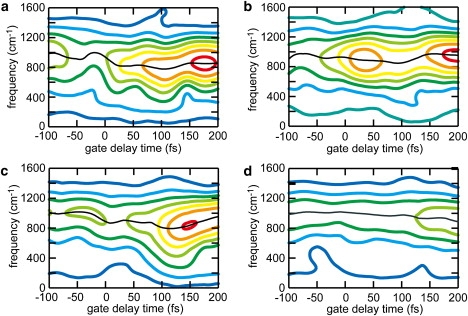
Time evolutions of the frequency spectra ${\left|\tilde{\theta }(\omega ,t_g)\right|}^2$ of the HOOP motions evaluated with Eq. 3 at (a) C₁₂, (b) C₁₁, (c) C₁₀, and (d) C₈. The colors of the contours represent the amplitude (large: red; small: blue) of the frequency components. Black lines trace the peak frequencies along time. Frequency components are interpolated by cubic spline functions.

It is noteworthy that the time-dependent shift of the peak frequency coincides with the change of the mean wagging angle described above (see also Fig. 6 a). The temporal feature of the mean angle at C₁₀, which is the atom pyramidalizing until 130 fs and then relaxing, correlates closely with that of the peak frequency. The formation and relaxation of the pyramidalized conformations at C₁₁ and C₁₂ also coincide with the change of the peak frequencies. In the case of C₈, relaxation from a pyramidal structure is not observed within 200 fs (Fig. 7); accordingly, the peak frequency only decreases in the time region between t = 0 and t = 200 fs.

Discussion

Our simulations of Rh photoexcitation, excited-state dynamics, crossing to the ground state, and relaxation into photoproduct states demonstrate highly homogeneous dynamical features that lead to the remarkably prompt formation of the isomerized photoproduct. The rotation around the isomerizing bond accompanied by coupled torsions around C₉=C₁₀ and C₆-C₇ gives rise to a ∼50 fs decay. The fast dynamics is barely disturbed by thermal fluctuation.

To elucidate the mechanism underlying the homogeneous and highly regulated dynamics of photoexcited Rh, we computed a QM photoisomerization trajectory for the chromophore in the absence of the protein surroundings (see Materials and Methods) from the QM/MM optimized geometry. Fig. 8 shows the time evolution of the dihedral angles of the QM chromophore for the trajectory. One can clearly see that the reaction profile is very similar to that seen in the protein. The rotation around the isomerizing bond develops very quickly, and the trajectory reaches the crossing point at t = 65.75 fs (see also the Supporting Material). Furthermore, the trajectory in the absence of the protein surroundings also exhibits, surprisingly, the characteristic coupled torsions around C₉=C₁₀ and C₆-C₇ observed in the trajectories in the protein. The result implies that the dynamics in the excited state is regulated so as to minimize perturbation of the reaction dynamics by the protein, which is in contrast to a previously proposed mechanism (50) that invokes a steric constraint imposed by the protein for the induction of the torsion around C₉=C₁₀.

Figure 8.

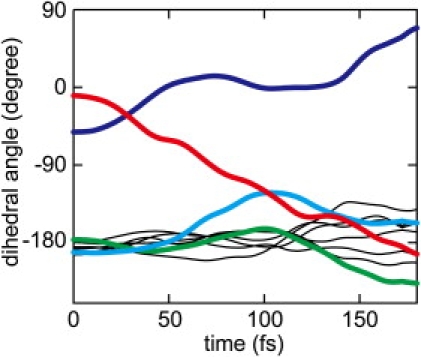
Time evolution of the dihedral angles of the polyene chain along the trajectory in the absence of the protein cavity, i.e., in vacuo. The color scheme is the same as in Fig. 4.

The conformation of the chromophore in the unphotolyzed resting state is significantly distorted, as shown in Fig. 4 c, and thus retinal is prepared for fast isomerization upon photoexcitation. The dihedral angle of the isomerizing bond, C₁₁=C₁₂, deviates by 16.5° from planarity, shifting the vertical excitation structure to facilitate immediate bond rotation. In addition, the C₆-C₇ bond of retinal is strongly twisted by 51.8°. The torsion around C₆-C₇ is stable in the ground state as a result of steric interactions between 5-methyl and 8-H moieties. However, the torsion is destabilized upon photoexcitation because the conjugated single bond increases its double-bond character in the excited state. Accordingly, the bond rotation toward the planar conformation is induced upon excitation, accelerating the isomerization through the coupled rotary motions around C₁₁=C₁₂ and C₆-C₇.

The gas phase trajectory indicates that the reaction dynamics of the chromophore from the distorted structure is intrinsically fast. Hence, the high efficiency of the reaction is retained by reducing the influence of the protein surroundings on the excited-state dynamics. Such a “hands-off” role of the protein in the excited-state dynamics was previously suggested by Weingart et al. (40,41) based on the QM-MD simulation of the isomerization of a truncated chromophore analog in vacuo.

It is noteworthy that the dynamic trajectory path in the excited state deviates remarkably from the static minimum energy path in vacuo. As shown by Olivucci and co-workers (34,35), the gas phase static minimum energy path of retinal analogs does not involve the characteristic coupled torsion around C₉=C₁₀. The molecular conformations at the minimum energy crossing point are kept almost planar, except for that at the isomerizing C₁₁=C₁₂ bond. Thus, the coupled torsional behavior observed in the dynamic trajectory originates from dynamic effects. In contrast, the static minimum energy path in the protein confinement exhibits the coupled torsion around C₉=C₁₀ as shown by Andruniów et al. (49), resembling the dynamic trajectory path described above. Hence, the intrinsic chromophore dynamics regulates the reaction path in the protein to follow the static minimum energy path involving volume-conserving reactions, thereby avoiding unfavorable collision of the isomerizing chromophore with the protein surrounding.

The regulatory mechanism of the reaction dynamics in Rh contrasts with the mechanism found in bR (44). In bR, the isomerization paths after the vertical excitation in vacuo can be diverse, leading to inhomogeneous product conformations, whereas the isomerization reaction in the protein pocket exhibits strict bond selectivity for the formation of the 13-cis product. Thus the protein surroundings in bR play a decisive role in blocking inhomogeneous paths in the excited state and funneling them to the proper product. Blocking and funneling of the reaction paths through the interaction between the chromophore and the protein destroys the synchronicity of the motions of the chromophore in bR, giving rise to the incoherent behavior of the reaction dynamics observed by ultrafast spectroscopy (20) and in QM/MM dynamics simulations (44).

One can interpret the two different types of reaction regulation in Rh and bR in terms of general catalytic mechanisms found in enzymes (71,72). The catalytic activity of an enzyme that reduces the activation energy employs one of two mechanisms. One mechanism reduces the activation energy directly through interactions with the protein surroundings that stabilize the transition state (TS). The second mechanism involves formation of a so-called near attack conformer (NAC) in a pre-TS intermediate state (72). Upon binding of the substrate, the protein surroundings force the substrates to form a NAC such that reactive parts of the substrates are optimally situated for the reaction; even if the protein surroundings do not contribute to reducing the activation energy, the reaction barrier of the overall catalytic process is lowered.

The reaction regulation in bR and Rh can be related to these two mechanisms. In the respective photoisomerization reaction, the electronically excited state is regarded as the TS. In bR, the reaction is regulated in the excited-state process by the protein surroundings that funnel the dynamic reaction paths into the proper photoproduct, i.e., TS stabilization plays a pivotal role. In Rh, the protein surroundings do not strongly perturb the reaction dynamics in the excited state, but the conformation of the chromophore in the resting state is strongly distorted by the protein surroundings, leading to the fast and highly regulated reaction upon photoexcitation.

In contrast to the excited-state process, the chromophore dynamics after crossing to the ground state is greatly perturbed by the protein surroundings in Rh. The steep increases of the standard deviations of dihedral angles around the C₈-C₉ and C₆-C₇ bonds during the formation of the photoproduct after t = 150 fs (Fig. 4 b) indicate dynamic inhomogeneity due to interaction of the chromophore with the protein. It is noteworthy that previous MD simulations (28,29) have shown that large conformational changes of the chromophore take place around the β-ionone half of the chromophore on a nanosecond timescale. The dynamic inhomogeneity around bonds in this half observed in our simulation is considered to be a precursory behavior of the large conformational change in the subsequent relaxation process.

The protonated Schiff base half of the chromophore also establishes a strong interaction with the protein surroundings, which does not manifest itself in the dihedral angles, but rather in a remarkable conformational change of the protein. Fig. 9 depicts the conformational change of helix III in the vicinity of the chromophore seen in the simulation at 0 K (see also Movie S1 in the Supporting Material). The H-C bond at position 14 of the chromophore, which finds itself in a strained conformation in the photoproduct, strongly interacts with Ala¹¹⁷ in helix III and pushes helix III toward the cytoplasmic side.

Figure 9.

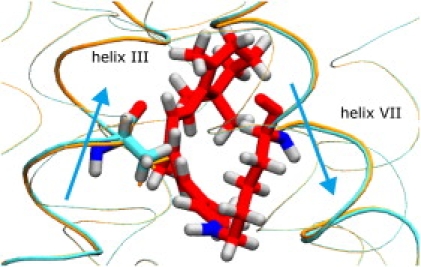
Molecular structures of retinal chromophore (red) and the surrounding protein at t = 250 fs of the trajectory at 0 K, indicating structural changes of the proteins upon formation of photo-Rh. The protein α-helices are depicted in tube representation. Thick tubes correspond to helix III (left) and helix VII (right), which include Ala¹¹⁷ and Lys²⁹⁶ with the chromophore, respectively. The α-helices at t = 0 and t = 250 fs are drawn in orange and cyan, respectively, indicating vertical shifts toward cytoplasmic and extracellular sides (upward and downward, respectively) of helices III and VII. Ala¹¹⁷ at t = 250 fs and t = 0 is depicted in thick and thin orange licorice representations, respectively, showing its upward displacement by the chromophore upon formation of photo-Rh. Light blue arrows indicate the movements of helices III and VII.

The cytoplasmic end of helix III contains so-called CAM residues, which are crucial for G-protein activation; mutations of these residues constitutively activate G-protein. The movement of helix III may therefore be significant for the signaling function of Rh. It appears that, although conformational changes of helix III and the CAM residues are more extended and occur much later during the Rh photocycle, the protein-chromophore interactions that trigger these conformational changes are already established within a picosecond.

The cis-trans conformational change of the chromophore also induces a vertical shift of helix VII toward the extracellular side, as shown in Fig. 9. Helix VII contains Lys²⁹⁶, which connects to the chromophore through the protonated Schiff base. Such vertical shifts of chromophore-binding helices have been also found in other microbial Rhs (43,73–75) and have been suggested to contribute to the photoactivation mechanism commonly utilized by retinal proteins.

It should be noted that the protein movements described here are not realistically described because our simulation does not include a membrane and water environment; however, since the simulations were carried out without harmonic constraints on distant C_α atoms, the movements were not affected by any additional imposed forces. The conformational changes observed in this simulation only illustrate the chromophore-protein interactions established upon photoisomerization reaction. For more accurate and realistic simulations of protein conformational changes due to chromophore-protein interaction, sufficient trajectory samples for a complete simulation system, i.e., a membrane and water environment, would be necessary.

Torsional deformations of the chromophore have been examined by spectroscopic measurements such as resonance Raman and infrared spectra. Although it is difficult to directly detect the torsional vibrations of the polyene chain, the HOOP wagging signals are known to serve as good indicators of the torsional deformations. This study shows that the HOOP wagging motions undergo significant changes along with the torsional deformations during the photoproduct formation, in agreement with observations.

Recently, Kukura et al. (15) experimentally detected time-dependent changes of the HOOP vibrations by ultrafast time-resolved Raman spectroscopy. Their study revealed that the frequencies of the HOOP vibrations of H₁₀, H₁₁, and H₁₂, originally observed at ∼970 cm⁻¹ in the resting state, undergo considerable downshifts to ∼770, ∼810, and ∼760 cm⁻¹, respectively, within the time resolution of the experiment (200 fs) after the photoabsorption. The HOOP frequencies then gradually increase and reach the values of the quasi-stable intermediate, batho-Rh (875, 920, and 850 cm⁻¹), in the next 2 ps. On the basis of these results, the authors proposed that immediately after photoabsorption, a large deformation of the A₂ HOOP at C₁₁ and C₁₂, and not the dihedral rotation around C₁₁=C₁₂, takes place first and leads to the electronic transition to the ground state. The dihedral rotation around C₁₁=C₁₂ to complete the isomerization then follows in the electronically ground state.

As described above, the simulations presented here also show HOOP frequencies at C₁₀, C₁₁, and C₁₂ exhibiting remarkable downshifts until ∼100 fs, and then an increase, which is consistent with the experimental observation; however, the frequency changes occur within a shorter period than the time resolution of the experiment (15). Thus, the time-dependent changes revealed in our simulations are not resolved by the experiment.

In our simulation, the large A₂ HOOP deformation at C₁₁ and C₁₂ that, according to the reaction model of Kukura et al. (15), leads to the electronic transition is not observed. In the excited state, although the mean wagging angles and the HOOP amplitudes are increased to some extent, they are much smaller than the development of the dihedral rotation around the isomerizing bond. Such limited increases of the wagging angles after the vertical excitation were also previously observed in QM/MM simulations (50) questioning the reaction model of Kukura et al. (15). A question then arises: What is the molecular origin of the remarkably large frequency shifts? Our simulations revealed that the HOOP deformations accompanied by the frequency shifts reach their maxima at around t = 150 fs in the photoproduct, not in the excited state. Therefore, they are likely coupled to the torsional distortions of the polyene chain in the photoproduct immediately after the electronic transition to the ground state. We conclude that the excited-state motion leading to the S₁→S₀ electronic transition toward the photoproduct is predominantly the dihedral rotation around the isomerizing bond rather than the A₂ HOOP motion, and that the observed remarkable downshifts of the HOOP frequencies can be attributed to the torsional distortions induced by the dihedral rotation upon photoproduct formation.

Similar to HOOP motions, analysis of relevant torsional modes would provide significant additional insights into the reaction dynamics. Unfortunately, the photoisomerization reaction time (<200 fs) is too short for the sliding-window analysis to obtain sufficient time and frequency resolution of the reactive torsional motion, whose vibrational frequency is expected to be very low compared to HOOP frequencies. In principle, the time dependence of the reactive modes could also be computed by instantaneous normal mode analysis; however, such an analysis requires Hessian matrix calculations along the trajectories, which are not feasible computationally for the large QM system presented here.

Conclusions

The photochemical reaction dynamics in Rh was investigated by means of ab initio QM/MM-MD simulations. An ensemble of reaction trajectories calculated under thermal fluctuation of the entire chromophore-protein complex reveals prominent features of the isomerization dynamics of the retinal chromophore. The excited-state dynamics is found to be homogeneous and synchronous as a result of a remarkably weak interference of the protein surroundings with the intrinsic excited-state reaction dynamics of the chromophore.

The simulations also reveal large vibrational excitations of HOOP modes accompanied by large low-frequency shifts upon photoproduct formation after the S₁→S₀ electronic transition, which are suggested to underlie the HOOP frequency shifts experimentally observed by time-dependent Raman spectroscopy.

Supporting Material

Two movies and four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(08)00071-4.