On the Minimum Description Length Complexity of Multinomial Processing Tree Models

Abstract

Multinomial processing tree (MPT) modeling is a statistical methodology that has been widely and successfully applied for measuring hypothesized latent cognitive processes in selected experimental paradigms. This paper concerns model complexity of MPT models. Complexity is a key and necessary concept to consider in the evaluation and selection of quantitative models. A complex model with many parameters often overfits data beyond and above the underlying regularities, and therefore, should be appropriately penalized. It has been well established and demonstrated in multiple studies that in addition to the number of parameters, a model’s functional form, which refers to the way by which parameters are combined in the model equation, can also have significant effects on complexity. Given that MPT models vary greatly in their functional forms (tree structures and parameter/category assignments), it would be of interest to evaluate their effects on complexity. Addressing this issue from the minimum description length (MDL) viewpoint, we prove a series of propositions concerning various ways in which functional form contributes to the complexity of MPT models. Computational issues of complexity are also discussed.

Introduction

The issue of model complexity is of fundamental importance in the evaluation and selection of statistical models and has received much attention recently in the field of mathematical psychology (see, e.g., Myung, Forstery & Browne, 2000; Myung, 2000; Grünwald, 2000; Myung, Navarro & Pitt, 2006; Pitt & Myung, 2002). Model complexity refers to a model’s inherent flexibility that allows the model to fit diverse data patterns. A model that gives good fit to a wide range of data patterns is more complex than one that can only fit a limited range of data patterns. Generally speaking, the more parameters a model has, the more complex it is.

The relevance of model complexity in model selection has to do with the overfitting phenomenon. The flexibility of a model is a double edged sword. Flexibility allows the model to readily capture the regularities underlying the observed data but also enables it to improve model fit by capitalizing on random noise, which would result in over-fitting the data beyond and above the regularities. Consequently, choosing among models based solely on goodness of fit (i.e., how well each model fits observed data) can lead to misleading conclusions about the underlying process, unless the overfitting effect is appropriately taken into account. This is realized in model selection by defining a selection criterion that trades off a model’s goodness of fit for its simplicity so as to avoid overfitting. The resulting criterion, known as generalizability (or predictive accuracy), quantifies how well a model can predict future, yet unseen, data patterns from the same underlying process that has generated the current data pattern.

Of particular importance in estimating a model’s generalizability is to accurately measure its complexity considering all relevant dimensions of model complexity. This is especially true for multinomial processing tree (MPT) models, for reasons detailed in a later part of this section. MPT modeling is a statistical methodology introduced in the 1980s for measuring latent cognitive capacities in selected experimental paradigms (Batchelder & Riefer, 1980, 1986; Riefer & Batchelder, 1991; Hu & Batchelder, 1994; Hu & Phillips, 1999). MPT models have been successfully applied to modeling performance in a range of cognitive tasks including associative recall, source monitoring, eyewitness memory, hind-sight bias, object perception, speech perception, propositional reasoning, social networks, and cultural consensus (see Riefer & Batchelder, 1988; Batchelder & Riefer, 1999; Erdfelder, Auer, Hilbig, Aßfalg, Moshagen & Nadarevic, 2009, for detailed reviews). The data structure requires that participants make categorical responses to a series of test items, and an MPT model parameterizes a subset of probability distributions over the response categories by specifying a processing tree designed to represent hypothesized cognitive steps in performing a cognitive task, such as memory encoding, storage, discrimination, inference, guessing and retrieval.

To give a concrete example of MPT modeling, consider a source monitoring experiment in which participants, after having studied a list of items from two sources, A and B, are asked to judge the source of a test item as either from A, from B, or new (i.e., stimulus from neither source). MPT models for such experiments typically consist of three distinct trees (Batchelder & Riefer, 1990; Riefer, Hu & Batchelder, 1994; Bayen, Murnane & Erdfelder, 1996), each of which models the hypothetical processes a participant might employ to select a response to a given type of item with three possible responses, A, B, or N. One such model is depicted on the left panel of Figure 1. A distinguishing feature of this one-high-threshold model (1HTM) is that it assumes only thresholds for old items to be correctly detected, with probability D₁ and D₂ for sources A and B, respectively. If an old item is correctly detected as old, a discriminating decision on its source is made and the parameters d₁ and d₂ represent this process for items from sources A and B, respectively. If either the detection or the discrimination process fails, one or more guessing processes involving parameters b, g and a follows. For new items, however, the model assumes no detection process, and instead response selection is determined solely by guessing represented by the parameters b and g. By imposing constraints successively on the model parameters, a hierarchy of sub-models can be derived from the original model. This is shown in the right panel of Figure 1. Likewise, new processes can be added to the original model. For example, the two-high-threshold model (2HTM) as depicted in Figure 2 assumes a separate detection probability D₃ for the new items.

Figure 1.

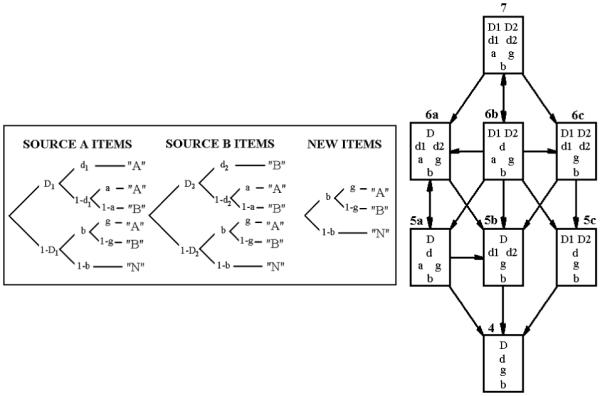
The one-high-threshold (1HT) multinomial processing tree model of source monitoring is shown on the left panel. The parameters are defined as follows: D₁ (detectability of source A items); D₂ (detectability of source B items); d₁ (source discriminability of source A items); d₂ (source discriminability of source B items); a (guessing that a detected but nondiscriminated item belongs to source A category); a (guessing “old” to a nondetected item); g (guessing that a nondetected item biased as old belongs to source A category). The right panel shows a nested hierarchy of eight versions of the model on the left, created by imposing successive constraints on the parameters. In this figure, the model parameters for each model are listed and a directed arrow from one model to another means that the second model is nested in the first. Note this figure combines the nesting relationships shown in both Figures 2 and 3 of Batchelder & Riefer (1990), and some of the nesting relationships are not explicit from the parameter constraints.

Figure 2.

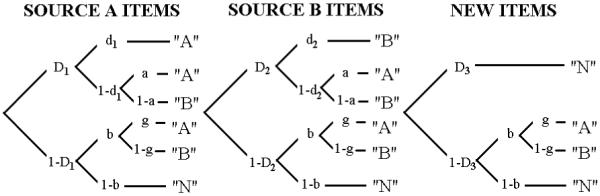
The two-high-threshold (2HT) multinomial processing tree model of source monitoring. Adapted from Bayen, Murnane & Erdfelder (1996, Figure 3). The parameters are defined in the same way as in 1HTM shown in Figure 1, except for the additional parameter D₃ (detectability of new items).

One prominent aspect of these MPT models of source monitoring is that they differ from one another not only in terms of the number of parameters but also in terms of functional form. For example, all three models, 6a, 6b and 6c, in Figure 1 have the same number of parameters (6) but each has different functional form distinct from the others. The same can be said about the three 5-parameter models, 5a, 5b and 5c in the figure. This is also true in general for MPT models and will be discussed in the next section. In addition to these, it is not uncommon that researchers develop and validate various MPT models with processing assumptions represented by different structures (e.g., Chechile, 2004; Bayen, Murnane & Erdfelder, 1996). In selecting among such MPT models, it would be of particular interest to accurately measuring the contributions of model complexity due to functional form, as well as number of parameters. Importance of the former factor in model selection is well documented and demonstrated for models of information integration, retention and categorization (e.g., Myung & Pitt, 1997; Pitt, Myung & Zhang, 2002; Pitt & Myung, 2002), but the issue remains to be explored in the context of MPT modeling.

In this paper we investigate the effects of model structure on the complexity of MPT models. The particular approach we take here is that of minimum description length (MDL; Grünwald, 2000; Grünwald, Myung & Pitt, 2005; Myung, Navarro & Pitt, 2006; Grünwald, 2007). The desirability and success of MDL in addressing model selection problems for various types of cognitive models are well documented (e.g., Lee, 2001; Pitt, Myung & Zhang, 2002; Navarro & Lee, 2004; Lee & Pope, 2006; Myung, Pitt & Navarro, 2007). Importantly, MDL is well suited for the present purpose; among other things, the MDL complexity measure (defined in the next section) not only is theoretically well justified, intuitively interpretable and readily computable, but also, importantly, takes into account both the number of parameters and functional form dimensions of model complexity. In this article, we address the issue of model complexity for this class of models from the standpoint of MDL. The application of MDL to the selection of MPT models is discussed in Wu, Myung & Batchelder (accepted).

The rest of the paper is organized as follows. We first define the class of binary MPT (BMPT) models and show how they can be constructed recursively from elementary decision nodes. A BMPT model, by definition, allows only binary choices at each decision node. Since any MPT model with a single tree¹ can be reparameterized into an equivalent BMPT model (Hu & Batchelder, 1994), it is sufficient to restrict our attention to this class of models. This is followed by a formal definition of MDL and a brief discussion of its statistical properties in relation to the issue of model complexity. The next section presents the main results of our theoretical investigations. Here we prove various propositions regarding MDL complexity of BMPT models. Some of these results are possible because of the recursive nature of the BMPT models. The section followed discusses computational issues of MDL complexity. Finally, the conclusion summarizes and recaps the contributions of the present work.

BMPT Models and MDL

Formal Definition of BMPT Models

Binary multinomial processing tree (BMPT) models are a subclass of MPT models that involve exactly two processing possibilities at each decision node of the tree. The have been defined in details in other papers (e.g. Batchelder & Riefer, 1999; Knapp & Batchelder, 2004; Purdy & Batchelder, in press), so our definition will be succinct and emphasizes some of the properties of the class that turn out to play a role in establishing some of the propositions involving model complexity. Any BMPT model is built out of a set of J > 1 mutually exclusive and exhaustive observable categories, C = {C₁, C₂, ⋯ , C_J}, and a set ϴ of S latent parameters arrayed for convenience in a vector θ = (θ₁, θ₂, ⋯ , θ_S)’. Each parameter θ_s represents the probability of the occurrence, and (1 − θ_s) the non-occurrence, of some latent cognitive event, such as storing an item in memory, retrieving a stored item, guessing a response given imperfect memory, making a particular inference, and the like. The parameters are functionally independent and each is free to vary in (0,1), so the parameter space for the model is given by Ω = {θ ∈ (0, 1)^S}².

Each BMPT model has a structural component and a computational component. The structural component is specified by the assignment of observable categories and latent parameters to the nodes of a full binary tree (FBT). A FBT is a special type of digraph D = (V, R), where V is a full set of nodes, R ⊆ V × V , and (v, v’) ∈ R represents a directed edge from v to v’. In order to define the class of FBTs, we need the concepts of the parents and children of a digraph node. For any node v ∈ V , the set of parents of v is defined as {v’|(v’, v) ∈ R}, and the set of children of v is defined as {v’|(v, v’) ∈ R}. A FBT is a directed graph with a single root node with no parents, a set of terminal nodes with no children (called leaves), and satisfying the properties that every node but the root has exactly one parent and every non-terminal node has exactly two children. In this paper, FBTs are oriented with the root on the left, so every nonterminal node has an upper child and a lower child. The structural component of a BMPT model is completed by specifying the assignment of a parameter (or a fixed number x ∈ (0, 1)) to each nonterminal node and a category to each leaf of the FBT. It is possible to assign a category to more than one leaf and a parameter to more than one nonterminal node. The left panel of Figure 1 exhibits three BMPT models. Note that the root is on the left and the leaves are on the right with their assigned categories. In the first tree, parameter D₁ is written next to the upper child of the root node and its ’complement’, 1 − D₁, is written next to the lower child of this node. By convention this notation is designed to depict the case that the parameter D₁ is assigned to the root node of this FBT. This convention will be explained more fully when we discuss the computational component of a BMPT model.

The computational component of a BMPT model provides the set of probability distributions over the categories of the model in terms of the parameters and numbers assigned to the nonterminal nodes of the model’s FBT. The parameter (or number) assigned to a nonterminal node represents the conditional probability of taking the upper child of this node given this node is reached by prior binary decisions. Starting at the root, a path leading to a leaf is probabilistically selected by a series of binary choices governed by the parameters (or numbers) associated with the nonterminal nodes of the tree.

In general, a BMPT model may have I_j paths (denoted by B_ij, i = 1, 2, ⋯ , I_j) leading to category C_j. Let p_ij(θ) represent the probability of selecting the path B_ij as a function of the parameters θ ∈ Ω. Then the computational rules specify that the probability of category C_j is given by summing all the I_j probabilities,

$$p_j\left(\theta \right)=\sum _{i=1}^{I_j}{p}_{ij}\left(\theta \right)$$ (1)

Further from the computational rules, these path probabilities take a particular form given by (see Hu & Batchelder, 1994, for more details)

$$p_{ij}\left(\theta \right)=c_{ij}\prod _{s=1}^S{\theta }_s^{a_{ijs}}{(1-{\theta }_s)}^{b_{ijs}}$$ (2)

where a_ijs and b_ijs are, respectively, the number of times θ_s and 1 − θ_s that appear on the path B_ij of category C_j, and c_ij is the product of the numbers along the same path or set to unity if there are no numbers along that path. From equations (1) and (2) we can seen that any BMPT model M_J with J categories parametrically specifies a subset of all possible multinomial distributions over the J categories with parameter space {p = (p₁, p₂, ⋯ , p_J)|p_j ≥ 0, Σ_j p_j = 1}.

In the present paper it is assumed that several participants each make categorical responses to the same set of items and that these responses are independent and identically distributed into the J categories of a model. Let n_j be the number of these responses that fall into category C_j, n = (n₁, n₂, ⋯ , n_J) and N = Σ_j n_j. Then from the computational rules in equations (1) and (2), n is distributed as a structured multinomial distribution given by

$$f(\mathit{n}\mid \theta )=\left(\begin{array}{c}\hfill N\hfill \\ \hfill n_1,\cdots ,n_J\hfill \end{array}\right)\prod _{j=1}^J{p}_j^{n_j}\left(\theta \right)$$ (3)

The Fisher information matrix of a BMPT model in terms of the representation of equations (1), (2) and (3) is given in Lemma 2 in the Appendix.

It is particularly important to note the role of the structural component of a BMPT model in this paper. It gives rise to the functional form differences among different BMPT models, which is a central issue in this article. Because the structural component involves more than the structure of the FBT, functional form differences may still arise for BMPT models with the same FBT. In particular, how the categories are assigned to the leaves of th FBT and how the parameters are assigned to the nonterminal nodes may change a model’s functional form. To see the different sources of functional form differences, we note the 1HTM and 2HTM described in Introduction section differ in their tree structures (though they may have the same number of parameters after assuming appropriate constraints), while the functional difference between models 5a and 5b in Figure 1 is entirely due to the different assignment of parameters to the nodes. To avoid possible confusions when referring to identical BMPT models, we use the following definition in this paper.

Definition 1 (functionally identical)

BMPT models are called functionally identical if

1. they share the same FBT structure,

2. the probabilities assigned to the non-terminal nodes of the FBT are subject to the same parametric restrictions.

3. their leaves are combined into categories in the same way.

Two functionally identical BMPT models may have different category sets and parameter sets, but there exist one-to-one mappings between their parameter sets and between their category sets, such that one model becomes the other after its categories and parameters are mapped to those of the other model. Functionally identical models are exactly the same except that they may use different symbols for the categories and parameters.

In addition to its implication on functional form, the structural component of a BMPT model satisfies several recursive properties that are useful in understanding the model complexity properties of BMPT models developed in the next section. First suppose ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ are two BMPT models where some of the categories and some of the parameters may be shared between models. Let p ∈ (0, 1) be a parameter which may or may not be in the parameter set of either model. Then we can construct a new BMPT model, denoted by $p{\mathcal{A}}_1{\mathcal{A}}_2$, by introducing a root node assigned to p and associating ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$, respectively, to the upper and lower children of the new root node. In this new model, the categor set is the union of the category sets of the two component models, and the parameter set is the union of the parameter sets and {p}. In fact Purdy & Batchelder (in press) have shown that all BMPT models can be built up by joining pairs of models in this way starting with elemental BMPT models consisting of a single category. A second recursive property of BMPT models is that one can select one or more categories in a BMPT model $\mathcal{A}$ and replace each of them with another BMPT model, and the result is a BMPT model.³ In this new model, the category set is the union of the category set of $\mathcal{A}$ (with the replaced categories removed) and the category sets of the other BMPT models used to replace the selected categories in $\mathcal{A}$. The first two panels of Figure 6 illustrate these two ways that new BMPT models can be constructed from other BMPT models.

Figure 6.

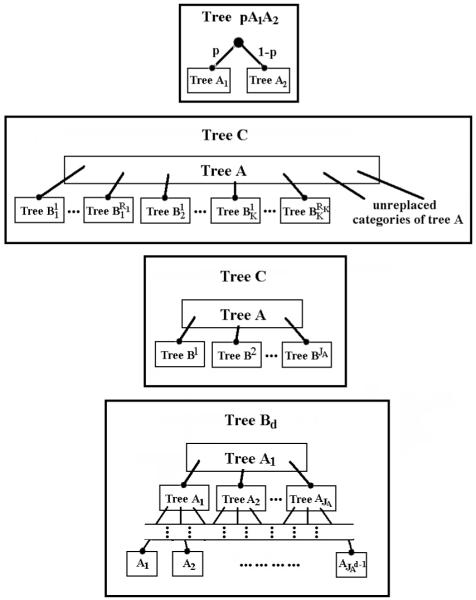
Graphical illustrations of model constructions. The top panel shows the new model constructed in Proposition 4 by joining two trees ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$. The second panel portrays the situation described in Lemma 3 and Proposition 5 and 6, in which some of the categories of $\mathcal{A}$ are replaced by ${\mathcal{B}}_k^r$. In the third panel, a new tree $\mathcal{C}$ is created by replacing every category of tree $\mathcal{A}$ by ${\mathcal{B}}^j$, j = 1, 2, ⋯ , $J_{\mathcal{A}}$, as in Proposition 7. The bottom panel demonstrates how tree ${\mathcal{B}}_{d-1}$ in Proposition 8 is created by adding the same tree structure to every category of itself recursively.

Minimum Description Length

The principle of minimum description length (MDL) originates from algorithmic coding theory in computer science. According to the principle, statistical modeling is viewed as data compression, and the best model is the one that compresses the data as tightly as possible. A model’s ability to compress the data is measured by the shortest code length with which the data can be coded with the help of the model. The resulting code length is related to generalizability such that the shorter the code length, the better the model generalizes (Grünwald, Myung & Pitt, 2005; Grünwald, 2007).

There are currently two implementations of the MDL principle, Fisher Information Approximation (FIA: Rissanen, 1996) and Normalized Maximum Likelihood (NML: Rissanen, 2001). For a model with probability density f(y|θ) and observed data y, they are defined as an additive combination of goodness of fit and model complexity terms:

$$FIA=-LML+C_{\mathrm{FIA}}$$ (4)

$$NML=-LML+C_{\mathrm{NML}}$$ (5)

where

$$LML=\ln f(\mathit{y}\mid \widehat{\theta }\left(\mathit{y}\right))$$

$$C_{\mathrm{FIA}}\left(N\right)=\frac{S}{2}\ln \frac{N}{2\pi }+\ln {\int }_{\Omega }\sqrt{\mid \mathbf{I}\left(\theta \right)}\mid d\theta$$ (6)

$$C_{\mathrm{NML}}\left(N\right)=\ln {\int }_{\chi }f(\mathit{x}\mid \widehat{\theta }\left(\mathit{x}\right))d\mathit{x}$$ (7)

In the above equations, LML standing for the logarithm of the maximized likelihood represents a goodness of fit measure, θ̂ is the maximum likelihood estimator as a function of data, S is the number of parameters, N is the sample size, Ω is the parameter space, $\mathcal{X}$ is the set of all possible samples with sample size N, and I(θ) is the Fisher information matrix (e.g. Casella & Berger, 2001) of sample size one defined as $I{\left(\theta \right)}_{ij}=-\mathrm{E}\left[\frac{{\partial }^2\ln f(x_1\mid \theta )}{\partial {\theta }_i\partial {\theta }_j}\right]$, i, j = 1, ⋯ , S. When data is discrete, as in the case of MPT modeling, the integration in Equation (7) is replaced by summation, with f replaced by the probability mass function. Note that both complexity measures are functions of sample size N. Under each selection method, a smaller criterion value indicates better generalization, and thus, the model that minimizes the criterion should be chosen.

In both FIA and NML, generalizability is measured as a trade-off between goodness of fit and simplicity, thus formalizing the Occam’s razor (Myung & Pitt, 1997). Specifically, both methods share the same goodness of fit measure (i.e., LML) but differ from each other in how complexity is measured, represented by C_FIA and C_NML, respectively. As mentioned earlier, models with the same number of parameters but with different equation forms can differ in complexity. This is called the functional form dimension of model complexity. To illustrate, two psychophysics models in perception, $y\sim \mathrm{N}(a{x}^b,{\sigma }_0^2)$ and $y\sim \mathrm{N}(a\ln (x+b),{\sigma }_0^2)$, may have different complexity values, despite the fact that they both have two parameters a and b.

The NML complexity measure, C_NML in Equation (7), is derived to minimize the extra description length in addition to the amount associated with the predictive distribution with MLE in the worst case of the data(Rissanen, 2001). Note that this complexity term is defined as the logarithm of the sum of maximum likelihoods the model can provide across all possible data (of sample size N) that could potentially be observed in a given experimental design.⁴ Accordingly, a model that can fit well almost every data pattern, human or non-human, would be more complex than another model that fits well a few data patterns but fits poorly other data patterns, thereby nicely capturing our intuition about model complexity.

The FIA complexity measure, C_FIA in Equation (6), is derived as an asymptotic expansion of C_NML with C_NML = C_FIA + o(1) (Rissanen, 1996). C_FIA takes into account the number of parameters (S), the sample size (N) and importantly, functional form captured through the Fisher information matrix (I(θ)). This is unlike two selection criteria most commonly in use, namely, the Akaike Information Criterion (AIC: Akaike, 1973) and the Bayesian Information Criterion (BIC: Schwartz, 1978), neither of which considers functional form. Because of the asymptotic relationship between C_NML and C_FIA, all three dimensions of complexity that C_FIA captures are also represented, though implicitly, in C_NML.

It should be noted that Equation (6) is only applicable for statistically identified⁵ models. If a model is not identified, C_FIA can be taken as that of a statistically equivalent⁶ but identified model.

In what follows, we present results from our theoretical investigation of the properties of C_FIA and C_NML for MPT models and also discuss some computational issues that may arise in practical implementations of these measures.

Theoretical Investigation of MDL Complexity

In this section we prove some important properties of the MDL complexity measures that are valid for the entire class of BMPT models, with a particular focus on the effects of functional form on complexity.

Complexity of Nested and Equivalent Models

In exploring the issue of model complexity for BMPT models, it is useful to note two observations about MDL that apply to any family of models. Our first observation concerns complexity relationship between nested MPT models. If model $\mathcal{A}$ is nested within model $\mathcal{A}$, then the complexity of model $\mathcal{B}$ is no greater than that of model $\mathcal{B}$, or formally, $C_{\mathrm{NML},\mathcal{A}}\le C_{\mathrm{NML},\mathcal{B}}$. This observation is self-evident. If model $\mathcal{A}$ is nested within model $\mathcal{B}$, then the collection of distributions defined by model $\mathcal{A}$ is a subset of that of model $\mathcal{B}$. Consequently, for every data set, the maximum likelihood for model $\mathcal{B}$ would be equal to or smaller than that of model $\mathcal{B}$. Therefore, according to the definition of C_NML in equation (5), model $\mathcal{A}$’s C_NML value is not larger than that of model $\mathcal{B}$. However, it should be noted that the inequality relationship between nested models may not hold for C_FIA because C_FIA is an asymptotic approximation to C_NML. It can sometimes exhibit abnormal complexity order relationships due to the inaccuracy of the approximation (Navarro, 2004), which will be observed later in this paper.

Our second observation concerns models that are statistically equivalent. Because they defined exactly the same set of probability distributions, equivalent models must have the same maximum likelihood for each data set and therefore must generate identical values of C_NML. For C_FIA, because the integral in equation (6) is invariant under reparameterization, equivalent models always have the same C_FIA. The observation that equivalent models have the same complexity implies that model complexity is an intrinsic property of the model, independent of the model’s parameterization and identifiability.

These observations are helpful in understanding the fact that an apparently more complicated model may turn out to have the same or even smaller complexity value than one that looks much simpler. One good example is given by the following proposition concerning two source monitoring models: the two-high-threshold five parameter model (2HTM-5) and the one-high-threshold four parameter model (1HTM-4). Both the 1HTM and 2HTM classes have been described in the Introduction section and they are depicted in Figures 1 and 2 respectively. 1HTM-4 is a restricted 1HTM described in the bottom of the right panel of Figure 1 with constraints D₁ = D₂(≡ D), d₁ = d₂(≡ d) and a = g (denoted by g). 2HTM-5 is a restricted 2HTM assuming all the above constraints as in 1HTM-4 but with one extra parameter D₃ (denoted by D*) for the probability of direct identification of the new items. This model is known to be not identified (e.g. Bayen, Murnane & Erdfelder, 1996).

Proposition 1

The 1HTM-4 and 2HTM-5 models are statistically equivalent.

Proof

We only need to prove 2HTM-5 is nested in 1HTM-4. To distinguish between the parameters in the two models, we use (D̃, D̃*, d̃, b̃, g̃) for parameters of 2HTM-5 and (D, d, b, g) for 1HTM-4. The following set of equations reparameterizes the 2HTM-5 into 1HTM-4.

$$\begin{array}{cc}\hfill g& =\tilde{g}\hfill \\ \hfill b& =\tilde{b}(1-{\tilde{D}}^{\ast })\hfill \\ \hfill D& =\frac{\tilde{b}{\tilde{D}}^{\ast }+\tilde{D}(1-\tilde{b})}{\tilde{b}{\tilde{D}}^{\ast }+(1-\tilde{b})}\hfill \\ \hfill d& =\left(\frac{\tilde{b}{\tilde{D}}^{\ast }+(1-\tilde{b})}{\tilde{b}({\tilde{D}}^{\ast }∕\tilde{D})+(1-\tilde{b})}\right)\tilde{d}\hfill \end{array}$$

It is self evident that for all values of (D̃, D̃*, d̃, b̃, g̃) within [0, 1], the parameters (D, d, b, g) determined by the above equations are always within [0,1].

Because the two models are statistically equivalent, they must have the same complexity, though 2HTM-5 looks more complex by allowing an extra threshold for the new items and assuming an extra parameter. Especially, the well-known result that 2HTM-4 is nested in 1HTM-4 (e.g. Bayen, Murnane & Erdfelder, 1996) is implied by this proposition. Consequently 2HTM-4 actually has smaller complexity than 1HTM-4 though it assumes one more threshold.

Another example concerns BMPT models with inequality constraints. In many cases, theoretical considerations such as the desired order of treatment effects are incorporated into BMPT models as inequality constraints on the parameters. Such a model with inequality constraints is nested in the original model without such constraints and therefore has smaller complexity value. Especially, Knapp & Batchelder (2004) showed that when the inequality constraints are in the form of 0 < θ₁ < θ₂ < ⋯ < θ_k < 1, the BMPT model can be reparameterized into an equivalent BMPT model with the same number of parameters and categories but without inequality constraints. The second BMPT model looks more complex than the original model. It should be noted, however, since the new, unconstrained model is statistically equivalent to the original model with the inequality constraints, the complexity values of the two models are the same, and both are smaller than that of the original model without those constraints. This, again, indicates sometimes a model that looks more complex may turn out to have smaller complexity value than one that looks simpler.

A third example concerns the class of uBMPT models in which different non-terminal nodes are assigned different parameters and different leaves are assigned different categories. For each value of J, there are many different uBMPT models with J categories that may differ greatly in their tree structures. However, Purdy & Batchelder (in press, Proposition 10) has proved that these different models are all statistically equivalent to the multinomial model with J categories and unstructured probabilities. Consequently, all uBMPT models with J categories have the same C_FIA (and C_NML) complexity value, which is also the maximal complexity value for any MPT model with J categories. Thus for the special case of uBMPT models, the shape of the tree does not affect the complexity of the model. The FIA complexity value of uBMPT models is given by $C_{\mathrm{FIA}}=\frac{J-1}{2}\ln \frac{N}{2\pi }+\frac{J}{2}\ln \pi -\ln \Gamma \left(\frac{J}{2}\right)$ (see Rissanen, 1996; Grünwald, Myung & Pitt, 2005, Chapter 16), which is a non-linear function of the number of parameters J due to the presence of ($\ln \Gamma \left(\frac{J}{2}\right)$). In Grünwald, Myung & Pitt (figure 16.3 of 2005, Chapter 16), both C_FIA and C_NML are plotted against J. Both curves are concave, increasing more slowly as J increases, different from the complexity measure in BIC and AIC, which are linear in J.

Complexity of MPT Models with Multiple Trees

As experiments often involve multiple treatments, most MPT models involve multiple trees, each representing a different treatment. Because in these models the sum of category counts in each tree is fixed at the treatment sample size, MPT models with multiple trees cannot be statistically equivalent to any BMPT model. To evaluate the complexity of such models, the following proposition is needed.

Proposition 2

Any MPT model $\mathcal{A}$ with multiple trees ${\mathcal{A}}_k$, k = 1, 2, ⋯ , K, has the same C_FIA value as an MPT model $\mathcal{B}$ with a single tree constructed by joining the ${\mathcal{A}}_k$ ’s by constant multinomial probabilities $c_k=\frac{N_k}{N}$, k = 1, 2, ⋯ , K , where N_k is the sample size for tree ${\mathcal{A}}_k$ and N is the total sample size.

Proof

It follows directly from Lemma 3 in the Appendix that the Fisher information matrix (of sample size one) of $\mathcal{B}$ is given by ${\sum }_{k=1}^K{c}_k{\tilde{\mathbf{I}}}_k$, where ${\tilde{\mathbf{I}}}_k$ denotes the Fisher information matrix of tree ${\mathcal{A}}_k$ extended to include all parameters in the model as defined in Lemma 3. It is evident that the Fisher information matrix of model $\mathcal{A}$ with sample size (N₁, N₂, ⋯ , N_K) is given by ${\sum }_{k=1}^K{N}_k{\tilde{\mathbf{I}}}_k$, so it has the same Fisher information matrix of sample size one. The two models therefore have the same C_FIA value.

This property can be exploited for the computation of C_FIA of models with multiple trees using a program intended for BMPT models, as $\mathcal{B}$ in the proposition can be further reparameterized into a BMPT model. It should be noted that the two models $\mathcal{A}$ and $\mathcal{B}$ as in the proposition in general have different NML complexity values, though their C_NML value must differ at most by o(1) given the asymptotic relationship between C_FIA and C_NML.⁷ Similar to the construction proposed by Hu & Batchelder (1994) in which the ${\mathcal{A}}_k$’s are joined by free parameters instead of fixed probabilities, the construction in Proposition 2 can also be used to obtain MLE as $\mathcal{A}$ and $\mathcal{B}$ gives the same likelihood function of θ.

Effects of Combining Response Categories on Complexity

The following proposition concerns what happens to the complexity of an MPT model when two or more response categories are combined into one.

Proposition 3

Let $\mathcal{A}$ be an MPT model and another MPT model $\mathcal{B}$ is created by combining some of the categories in $\mathcal{A}$, then we have $C_{\mathrm{NML},\mathcal{B}}\le C_{\mathrm{NML},\mathcal{A}}$. The equality holds if and only if the probabilities associated with the to-be-combined categories, say p_k(θ), k ∈ K ⊆ {1, 2, ⋯ , J} satisfy the relationship p_k = c_kp(θ), where c_k are constants not depending on θ. The same conclusion holds for C_FIA if both models are identified.

Proof

Without loss of generality, let K = {1, 2, ⋯ , K}. We first prove the NML part of the proposition. Suppose the probability mass function of the original model is $P_{\mathcal{A}}(\stackrel{‒}{\mathit{n}},\mathit{n}\mid \theta )$ where n = (n₁, n₂, ⋯ , n_K) is the vector of counts in the k categories to be combined, and n‾ = (n_K+1, ⋯ , n_J) includes counts of the rest categories. Denote by 1_K the column vector of K 1’s. Following from the law of total probability, the probability mass function of the new model is $P_{\mathcal{B}}(\stackrel{‒}{\mathit{n}},n_0)={\sum }_{\mathit{n}{1}_{K=n_0}}{P}_{\mathcal{A}}(\stackrel{‒}{\mathit{n}},\mathit{n}\mid \theta )$, where n₀ denotes the count in the new category in $\mathcal{B}$. Summing over both sides of the equation, we have

$$\begin{array}{cc}\hfill C_{\mathrm{NML},\mathcal{A}}& =\sum _{\stackrel{‒}{\mathit{n}}1+n_0=N}\sum _{\mathit{n}1=n_0}{P}_{\mathcal{A}}(\stackrel{‒}{\mathit{n}},\mathit{n}\mid {\widehat{\theta }}_{(\stackrel{‒}{\mathit{n}},\mathit{n})})\hfill \\ \hfill & \ge \sum _{\stackrel{‒}{\mathit{n}}1+n_0=N}\sum _{\mathit{n}1=n_0}{P}_{\mathcal{A}}(\stackrel{‒}{\mathit{n}},\mathit{n}\mid {\widehat{\theta }}_{(\stackrel{‒}{\mathit{n}},n_0)})\hfill \\ \hfill & =\sum _{\stackrel{‒}{\mathit{n}}1+n_0=N}{P}_{\mathcal{B}(\stackrel{‒}{\mathit{n}},n_0\mid {\widehat{\theta }}_{(\stackrel{‒}{\mathit{n}},n_0)})}=C_{\mathrm{NML},\mathcal{B}}\hfill \end{array}$$

where θ̂_(n‾,n) and θ̂_(n‾,n0) denote the MLEs obtained from $P_{\mathcal{A}}$ and $P_{\mathcal{B}}$, respectively, and 1 denotes a column vector of 1’s of appropriate length. The equality holds if and only if

$$\forall \stackrel{‒}{\mathit{n}},\mathit{n}{P}_{\mathcal{A}}(\stackrel{‒}{\mathit{n}},\mathit{n}\mid {\widehat{\theta }}_{(\stackrel{‒}{\mathit{n}},n)})=P_{\mathcal{A}}(\stackrel{‒}{\mathit{n}},\mathit{n}\mid {\widehat{\theta }}_{(\stackrel{‒}{\mathit{n}},n_0)})$$ (8)

or the maximizer of $P_{\mathcal{A}}$ is a function of n through n₀ only. Note $P_{\mathcal{A}}(\stackrel{‒}{\mathit{n}},\mathit{n}\mid \theta )=P_{\mathcal{B}}(\stackrel{‒}{\mathit{n}},n_0\mid \theta )P(\stackrel{‒}{n}\mid n_0,\theta )$. Condition (8) is equivalent to P(n|n₀, θ) does not depend on θ. Further note that $P(\stackrel{‒}{\mathit{n}}\mid n_0,\theta )\propto {\prod }_k{(p_k\left(\theta \right)∕p_0\left(\theta \right))}^{n_k}$, where $p_0\left(\theta \right)={\sum }_{k=1}^K{p}_k\left(\theta \right)$ is the model implied probability of the new category in $\mathcal{B}$, and we can see (8) is equivalent to p_k(θ) = c_kp₀(θ).

For the FIA part of the proposition, we note the Fisher information matrix of model $\mathcal{A}$, ${\mathbf{I}}^{\mathcal{A}}$, is given by $I_{rs}^{\mathcal{A}}={\sum }_j{p}_j^{-1}{P}_{jr}{P}_{js}$, where $P_{js}=\frac{\partial p_j}{\partial {\theta }_s}$ (see Grünwald, Myung & Pitt, 2005, equation 16.4 on p.420). Similarly, that of model $\mathcal{B}$ is given by $I_{rs}^{\mathcal{B}}=p_0^{-1}{P}_{0r}{P}_{0s}+{\sum }_{j=K+1}^J{p}_j^{-1}{P}_{jr}{P}_{js}$. Let a = (a₁, a₂, ⋯ , a_S)’ be an arbitrary vector, and let ${\alpha }_j={\sum }_s{a}_s{P}_{js}$, j = 0, 1, ⋯ , J. We have

$$\begin{array}{cc}\hfill & {\mathit{a}}^{\prime }{\mathbf{I}}^{\mathcal{A}}\mathit{a}=\sum _j{p}_j^{-1}{\alpha }_j^2=\sum _{j=1}^K{p}_j^{-1}{\alpha }_j^2+\sum _{j=K+1}^J{p}_j^{-1}{\alpha }_j^2\hfill \\ \hfill \ge & {\left(\sum _{j=1}^K{P}_j\right)}^{-1}{\left(\sum _{j=1}^K{\alpha }_j\right)}^2+\sum _{j=K+1}^J{p}_j^{-1}{\alpha }_j^2=p_0^{-1}{\alpha }_0^2+\sum _{j=K+1}^J{p}_j^{-1}{\alpha }_j^2={\mathit{a}}^{\prime }{\mathbf{I}}^{\mathcal{B}}\mathit{a}\hfill \end{array}$$ (9)

where the inequality follows from Hölder inequality: ${\left({\sum }_{j=1}^K{\alpha }_j\right)}^2\le \left({\sum }_{j=1}^K{p}_j\right)\left({\sum }_{j=1}^K{p}_j^{-1}{\alpha }_j^2\right)$. In particular, if {u_s|s = 1, 2, ⋯ , S} is a set of eigenvectors of ${\mathbf{I}}^{\mathcal{A}}$, we have

$$\begin{array}{cc}\hfill & \ln \mid {\mathbf{I}}^{\mathcal{A}}\mid =\sum _s\ln \left({\mathit{u}}_s^{\prime }{\mathbf{I}}^{\mathcal{A}}{\mathit{u}}_s\right)\hfill \\ \hfill \ge & \sum _s\ln \left({\mathit{u}}_s^{\prime }{\mathbf{I}}^{\mathcal{B}}{\mathit{u}}_s\right)=\sum _s\ln \left({\mathit{v}}_s^{\prime }{\mathbf{D}}_{\lambda }^{\mathcal{B}}{\mathit{v}}_s\right)=\sum _s\ln \left(\sum _r{\lambda }_r^{\mathcal{B}}{v}_{sr}^2\right)\hfill \\ \hfill \ge & \sum _s\sum _r{v}_{sr}^2\ln {\lambda }_r^{\mathcal{B}}=\sum _r\ln {\lambda }_r^{\mathcal{B}}=\ln \mid {\mathbf{I}}^{\mathcal{B}}\mid \hfill \end{array}$$ (10)

where ${\lambda }_s^{\mathcal{B}}$, s = 1, 2, ⋯ , S, are the eigenvalues of ${\mathbf{I}}^{\mathcal{B}}$, ${\mathbf{D}}_{\lambda }^{\mathcal{B}}$ is a diagonal matrix involving the above eigenvalues, v_s and v_sr are the typical column and the typical element of some orthogonal matrix V, the first inequality follows from (9) and the second inequality follows from the concavity of logarithm function. Now we have proved $\mid {\mathbf{I}}^{\mathcal{A}}\mid \ge \mid {\mathbf{I}}^{\mathcal{B}}\mid$. The FIA inequality $C_{\mathrm{FIA},\mathcal{B}}\le C_{\mathrm{FIA},\mathcal{A}}$ can be established by applying equation (6).

Given $\mid {\mathbf{I}}^{\mathcal{A}}\mid \ge \mid {\mathbf{I}}^{\mathcal{B}}\mid$, a necessary and sufficient condition for the equality sign “=” in the above FIA inequality to hold is $\mid {\mathbf{I}}^{\mathcal{A}}\mid =\mid {\mathbf{I}}^{\mathcal{B}}\mid$, which holds if and only if “=” in (9) holds for all vector a. To see this, on the one hand, if there exists some vector a such that “>” in (9) holds, then “=” in (10) cannot hold because {u_s} is a linear basis, and we must have $\mid {\mathbf{I}}^{\mathcal{A}}\mid >\mid {\mathbf{I}}^{\mathcal{B}}\mid$; on the other hand, if “=” holds in (9) for arbitrary vector a, we must have $\mid {\mathbf{I}}^{\mathcal{A}}\mid =\mid {\mathbf{I}}^{\mathcal{B}}\mid$. Further, we note that “=” in (9) holds if and only if ${\left(p_j\right)}^{-1}\left(p_j^{-1}{\alpha }_j^2\right)={\left(p_j^{-1}{\alpha }_j\right)}^2$ does not depend on j, or $p_j^{-1}{P}_{js}$ P_js does not depend on j for all s, which is equivalent to $\frac{\partial (\ln p_j-\ln p_i)}{\partial {\theta }_s}=p_j^{-1}{P}_{js}-p_i^{-1}{P}_{is}=0$, or p_j(θ) = c_ijp_i(θ), for some constants c_ij not depending on θ.

It should be noted that because equation (6) is used, the identification of both models is required. When either model is not identified, the inequality still holds for the quantity on the right hand side of equation (6), but in this case, the C_FIA value is defined instead as that of an equivalent and identified model, which may not satisfy the inequality.

Figure 3 illustrates the proposition. In the top panel, the model on the right is obtained by combining two categories C₁ and C₂ of the model on the left into a new category C₀. According to the proposition, the resulting model, shown on the right, will have a smaller complexity value than the original one. The two models on the bottom panel of the figure are both equally complex, because the probabilities of two categories C₁ and C₂ of the model on the left are equal (i.e., pq).

Figure 3.

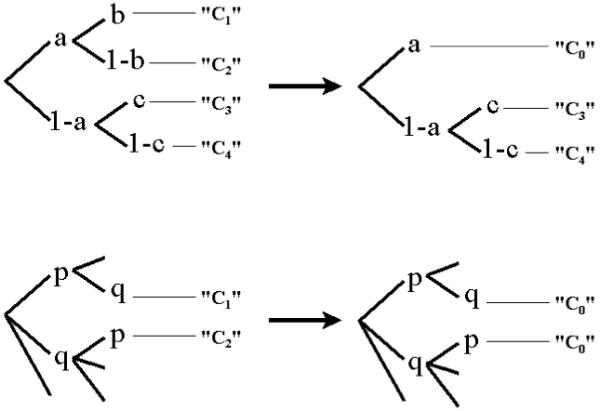
Examples of models created by combining categories.

Figure 4 provides another illustration of Proposition 3, this time for a well studied MPT model of pair-clustering (Batchelder & Riefer, 1986). The pair clustering experiment involves studying a list of two types of items, paired items and singletons, followed by free recall of the list. The model posits three parameters: c, probability of pairs being clustered and stored in memory; r, probability of a stored pair being retrieved from memory; u, probability of a single item being stored and retrieved from memory. Accordingly, response category E₁ indicates recalling adjacently both items of the studied pairs, response category E₂ indicates recalling non-adjacently both items of the pairs, response category E₃ indicates recalling only one item, and so on. Figure 5 shows C_NML and C_FIA curves as a function of sample size for the model (two upper curves). The two trails closely parallel each other, indicating that C_FIA provides a good approximation of C_NML in this case.

Figure 4.

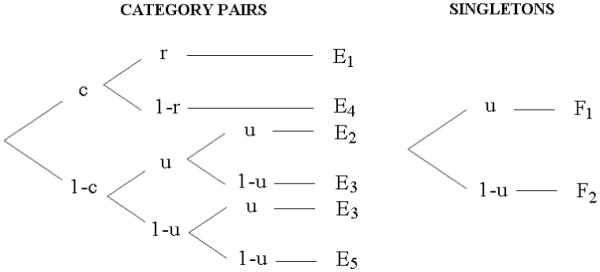
Batchelder and Riefer’s (1999) multinomial processing tree model of pair-clustering. Note the two categories E₄ and E₅ are usually combined in practice as they are not distinguishable in the data.

Figure 5.

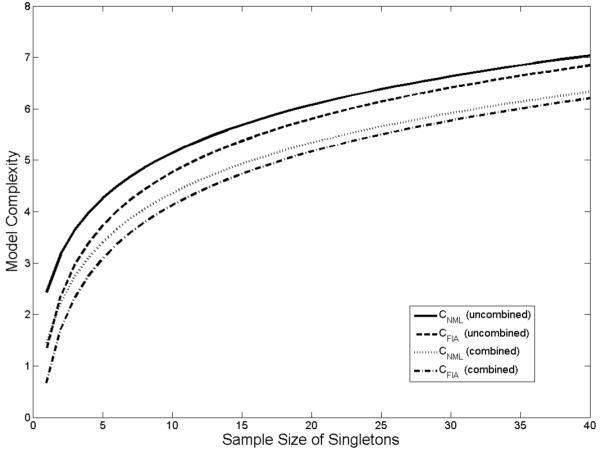
C_NML and C_FIA complexity curves for the model in Figure 4, plotted as a function of the sample size of singletons. The sample size of category pairs are set to be twice that of singletons. The uncombined version of the model assumes five distinct response categories E₁ − E₅ for paired items. In the combined version of the model, the two response categories E₄ and E₅ are combined into one category. Note that all four models have the same number of parameters (3).

Both of categories E₄ and E₅ represent unsuccessful retrieval and as such, cannot be distinguished from each other based on observed responses. It is therefore necessary to combine the two categories into one. What would happen to model complexity if this is done? As shown by the two lower curves in Figure 5, combining the categories has reduced complexity as predicted by Proposition 3. Since the number of parameters (3) remain unchanged, the reduction in complexity must be due to the difference in functional forms between the two models, one uncombined and the other combined.⁸

Effects of Combining Trees on Complexity

As we noted in the section of Formal Definition of BMPT Models, the structural component of BMPT models satisfies two recursive properties. In this section we will exploit these recursive properties and focus on the situation in which two or more BMPT models are combined to form a new BMPT model. We are interested in knowing how model complexity is affected by such operations. All results in this subsection are based on Lemma 3 in the Appendix, which gives the form of Fisher information matrix of combined BMPT models in general. We begin with the simplest situation in which two BMPT models are combined with a single binomial parameter.

Proposition 4

Let ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ be two BMPT models with disjoint parameter sets ϴ₁ and ϴ₂ and disjoint category sets. Suppose $\mathcal{C}=p{\mathcal{A}}_1{\mathcal{A}}_2$ (see the top panel of Figure 6) where p ∉ ϴ₁ ∪ ϴ₂. Then

$$C_{\mathrm{FIA},\mathcal{C}}\left(N\right)=C_{\mathrm{FIA},{\mathcal{A}}_1}\left(N\right)+C_{\mathrm{FIA},{\mathcal{A}}_2}\left(N\right)+\frac{1}{2}\ln \frac{N}{2\pi }+\ln \beta \left(\frac{S_1+1}{2},\frac{S_2+1}{2}\right)$$

where S₁ and S₂ are the number of parameters in model ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$, respectively, and β is the beta function.

This proposition follows directly from Lemma 3 in the Appendix and equation (6). Note that the third and fourth terms of the foregoing equation reflects an increase in complexity due to the binomial parameter p that joins the two trees. If we were to assume that the addition of the binomial parameter independently contributes to overall complexity, an expected increase in complexity would be $\frac{1}{2}\ln \frac{N}{2\pi }+\ln \beta \left(\frac{1}{2},\frac{1}{2}\right)$, the FIA complexity of binomial distribution according to equation (6). Since $\ln \beta \left(\frac{S_1+1}{2},\frac{S_2+1}{2}\right)<\ln \beta \left(\frac{1}{2},\frac{1}{2}\right)$, the complexity of tree $\mathcal{C}$ with (S₁ + S₂ + 1) parameters would be smaller than the sum of complexities of the two individual trees and the binomial model, in contrast to the AIC and BIC complexity measures which are additive in this case.

The above proposition shows that the FIA complexity value is generally not additive and will be less than the sum of all three parts of the model in a very simple situation. In the following proposition, we further pursue this decrease in complexity and present a result in a more general setting.

Proposition 5

Let ${\mathcal{B}}_k^r$, r = 1, 2, ⋯ , R_k, k = 1, 2, ⋯ , K, be ${\sum }_k{R}_k$ BMPT models that satisfy the following condition: for all k, the R_k models ${\mathcal{B}}_k^r$, r = 1, 2, ⋯ ,R_k are functionally identical with identical parameter assignment (and therefore with identical parameter set ϴ_k of S_k parameters and identical complexity value C_FIA,k). In addition, let $\mathcal{A}$ be a BMPT model with parameter set ${ϴ}_{\mathcal{A}}$ and complexity value $C_{\mathrm{FIA},\mathcal{A}}$. Suppose all the $1+{\sum }_k{R}_k$ models have disjoint category sets and the K + 1 parameter sets ${ϴ}_{\mathcal{A}}$, ϴ_k, k = 1, 2, ⋯ , K are disjoint. If a new BMPT model $\mathcal{C}$ is constructed by replacing ${\sum }_k{R}_k$ of $\mathcal{A}$’s categories by the ${\sum }_k{R}_k$ models ${\mathcal{B}}_k^r$ respectively, then we have

$$C_{\mathrm{FIA},\mathcal{C}}\left(N\right)\le C_{\mathrm{FIA},\mathcal{A}}\left(N\right)+\sum _k{C}_{\mathrm{FIA},k}\left(N\right)+\frac{1}{2}\sum _k{S}_k\ln S_k-\frac{1}{2}\left(\sum _k{S}_k\right)\ln \left(\sum _k{S}_k\right)$$

Proof

From Lemma 3 in the Appendix we can see ${\mathbf{I}}^{\mathcal{C}}$ is a block diagonal matrix given by $\mathrm{diag}\{{\mathbf{I}}^{\mathcal{A}},p_1{\mathbf{I}}_1,p_2{\mathbf{I}}_2,\cdots ,p_K{\mathbf{I}}_K\}$, where for any k = 1, 2, ⋯ , K, p_k denotes the total probability of the R_k categories in model $\mathcal{A}$ replaced by ${\mathcal{B}}_k^r$, r = 1, 2, ⋯ , R_k. Taking the determinant, we have $\mid {\mathbf{I}}^{\mathcal{C}}\mid =\mid {\mathbf{I}}^{\mathcal{A}}\mid {\prod }_k\left(\mid {\mathbf{I}}_k\mid p_k^{S_k}\right)$. Apply equation (6), note the parameter sets of the K + 1 models are disjoint, and we have

$$\begin{array}{cc}\hfill \int \mid {\mathbf{I}}^{\mathcal{C}}\left(\theta \right){\mid }^{\frac{1}{2}}d\theta & =\left(\int \mid {\mathbf{I}}^{\mathcal{A}}\left({\theta }_{\mathcal{A}}\right){\mid }^{\frac{1}{2}}\prod _{k}pk{\left({\theta }_{\mathcal{A}}\right)}^{\frac{S_k}{2}}d{\theta }_{\mathcal{A}}\right)\prod _k\int \mid {\mathbf{I}}_k\left({\theta }_k\right){\mid }^{\frac{1}{2}}d{\theta }_k\hfill \\ \hfill & \le \left\{\prod _k{\left(\frac{S_k}{{\Sigma }_j{S}_j}\right)}^{\frac{S_k}{2}}\right\}\left(\int \mid {\mathbf{I}}^{\mathcal{A}}\left({\theta }_{\mathcal{A}}\right){\mid }^{\frac{1}{2}}d{\theta }_{\mathcal{A}}\right)\prod _k\int \mid {\mathbf{I}}_k\left({\theta }_k\right){\mid }^{\frac{1}{2}}d{\theta }_k\hfill \end{array}$$

The inequality follows from the fact that ${\prod }_k{p}_k^{S_k}$ with ${\sum }_k{p}_k\le 1$ reaches its maximum when $p_k=\frac{S_k}{{\sum }_k{S}_k}$. Further taking logarithm of both sides and applying equation (6) completes the proof.

The model constructed in this proposition is described in the second panel of Figure 6. The proposition shows that the complexity of the new model is always less than the sum of those of its parts, and the amount decrease in complexity has a lower bound of $-\frac{1}{2}{\sum }_k{S}_k\ln S_k+\frac{1}{2}\left({\sum }_k{S}_k\right)\ln \left({\sum }_k{S}_k\right)\ge 0$ (this inequality can be verified by both sides).

The following proposition summarizes the same result for NML complexity.

Proposition 6

Assuming the same conditions in Proposition 5 except for the requirement of disjoint parameter sets, we have

$$C_{\mathrm{NML},\mathcal{C}}\left(N\right)\le C_{\mathrm{NML},\mathcal{A}}\left(N\right)+\underset{{\Sigma }_k{n}_k=N}{\max }\sum _k{C}_{\mathrm{NML},k}\left(n_k\right)\le C_{\mathrm{NML},\mathcal{A}}\left(N\right)+\sum _k{C}_{\mathrm{NML},k}\left(N\right)$$

Proof

We only prove the proposition for the case where all categories of model $\mathcal{A}$ are replaced by some ${\mathcal{B}}_k^r$. The other case where some categories of model $\mathcal{A}$ are also categories of model $\mathcal{C}$ can be easily taken care of by allowing some ${\mathcal{B}}_k^r$ be a degenerated tree with no parameter and a single category with category probability 1.

We index the categories of tree $\mathcal{A}$ by $\underset{k}{\overset{r}{}}$, k = 1, 2, ⋯ , K, r = 1, 2, ⋯ , R_k, according to the index of ${\mathcal{B}}_k^r$ attached to it. We also index the counts of tree $\mathcal{C}$ by $n_{kj}^r$, j = 1, 2, ⋯ , J_k, as they are always counts in some tree ${\mathcal{B}}_k^r$. Let $m_k^r={\sum }_{j=1}^{J_k}{n}_{kj}^r$ be the sum of counts of tree ${\mathcal{B}}_k^r$, $o_{kj}={\sum }_{r=1}^{R_k}{n}_{kj}^r$ be the sum of the corresponding counts in category j across the R_k trees ${\mathcal{B}}_k^r$ (r = 1, 2, ⋯ , R_k) and $l_k={\sum }_{r=1}^{R_k}{m}_k^r={\sum }_{j=1}^{J_k}{o}_{kj}$. Vector n involves all counts of $\mathcal{C}$, and ${\mathit{n}}_k^r$ involves all counts that share the same indices $\underset{k}{\overset{r}{}}$. Other vectors such as m, n_kj, n_k and o_k are similarly defined.

We have

$$\begin{array}{cc}\hfill \sum _{\mathit{n}}P(\mathit{n}\mid {\widehat{\theta }}_{\mathit{n}})& =\sum _{\mathit{m}}{P}_{\mathcal{A}}(\mathit{m}\mid {\widehat{\theta }}_{\mathit{n}})\sum _{\mathit{n}\mid \mathit{m}}P(\mathit{n}\mid \mathit{m},{\widehat{\theta }}_{\mathit{n}})\hfill \\ \hfill & \le \sum _{\mathit{m}}{P}_{\mathcal{A}}(\mathit{m}\mid {\widehat{\theta }}_{\mathit{m}}^{\mathcal{A}})\sum _{\mathit{n}\mid \mathit{m}}\prod _k\prod _r{P}_k({\mathit{n}}_k^r\mid m_k^r,{\widehat{\theta }}_{{\mathit{n}}_k}^k)\hfill \end{array}$$ (11)

where $\underset{\mathit{m}}{\Sigma }$ denotes $\underset{{\sum }_{k,r}{m}_k^r=N}{\Sigma }$, $\underset{\mathit{n}}{\Sigma }$ denotes $\underset{{\sum }_{k,r,j}{n}_{kj}^r=N}{\Sigma }$, $\underset{\mathit{n}\mid \mathit{m}}{\Sigma }$ denotes $\underset{{\sum }_j{n}_{kj}^r=m_k^r}{\Sigma }$, and ${\widehat{\theta }}_{{\mathit{n}}_k}^k$ maximizes ${\prod }_r{P}_k({\mathit{n}}_k^r\mid m_k^r,\theta )$. Note the conditional distribution P_k depends only on k but not r since ${\mathcal{B}}_k^r$, r = 1, 2, ⋯ , R_k have the same tree structure and parameter assignment.

To simplify the last term, we note

$$\begin{array}{cc}\hfill \prod _r{P}_k({\mathit{n}}_k^r\mid m_k^r,{\theta }^k)& =\prod _r\left\{\left(\begin{array}{c}\hfill m_k^r\hfill \\ \hfill n_{k1}^r,n_{k2}^r,\cdots ,n_{k{J}_k}^r\hfill \end{array}\right)\prod _{j}p{k}_j{\left({\theta }^k\right)}^{n_{kj}^r}\right\}\hfill \\ \hfill & =\left\{\prod _r\left(\begin{array}{c}\hfill m_k^r\hfill \\ \hfill n_{k1}^r,n_{k2}^r,\cdots ,n_{k{J}_k}^r\hfill \end{array}\right)\right\}\prod _{j}p{k}_j{\left({\theta }^k\right)}^{o_{k_j}}\hfill \\ \hfill & =\frac{\prod _r\left(\begin{array}{c}\hfill m_k^r\hfill \\ \hfill n_{k1}^r,n_{k2}^r,\cdots ,n_{k{J}_k}^r\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill l_k\hfill \\ \hfill o_{k1},o_{k2},\cdots ,o_k{J}_k\hfill \end{array}\right)}{P}_k({\mathit{o}}_k\mid l_k,{\theta }^k)\hfill \end{array}$$

We can see immediately that ${\widehat{\theta }}_{{\mathit{n}}_k}^k={\widehat{\theta }}_{{\mathit{o}}_k}^k$ depends on o_k only. Back to equation (11) we have

$$\begin{array}{cc}\hfill \sum _{\mathit{n}}P(\mathit{n}\mid {\widehat{\theta }}_{\mathit{n}})& \le \sum _{\mathit{m}}{P}_{\mathcal{A}}(\mathit{m}\mid {\widehat{\theta }}_{\mathit{m}}^{\mathcal{A}})\prod _k\sum _{{\mathit{n}}_k\mid {\mathit{m}}_k}\frac{{\prod }_r\left(\begin{array}{c}\hfill m_k^r\hfill \\ \hfill n_{k1}^r,n_{k2}^r,\cdots ,n_{k{J}_k}^r\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill l_k\hfill \\ \hfill o_{k1},o_{k2},\cdots ,o_k{J}_k\hfill \end{array}\right)}{P}_k({\mathit{o}}_k\mid l_k,{\widehat{\theta }}_{{\mathit{o}}_k}^k)\hfill \\ \hfill & =\sum _{\mathit{m}}{P}_{\mathcal{A}}(\mathit{m}\mid {\widehat{\theta }}_{\mathit{m}}^{\mathcal{A}})\prod _k\left\{\sum _{{\mathit{o}}_k}{P}_k({\mathit{o}}_k\mid l_k,{\widehat{\theta }}_{{\mathit{o}}_k}^k)\sum _{{\mathit{n}}_k\mid {\mathit{m}}_k,{\mathit{o}}_k}\frac{{\prod }_r\left(\begin{array}{c}\hfill m_k^r\hfill \\ \hfill n_{k1}^r,n_{k2}^r,\cdots ,n_{k{J}_k}^r\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill l_k\hfill \\ \hfill o_{k1},o_{k2},\cdots ,o_{k{J}_k}\hfill \end{array}\right)}\right\}\hfill \\ \hfill & =\sum _{\mathit{m}}{P}_{\mathcal{A}}(\mathit{m}\mid {\widehat{\theta }}_{\mathit{m}}^{\mathcal{A}})\prod _k\sum _{{\mathit{o}}_k}{P}_k({\mathit{o}}_k\mid l_k,{\widehat{\theta }}_{{\mathit{o}}_k}^k)\hfill \\ \hfill & \le \left\{\sum _{\mathit{m}}{P}_{\mathcal{A}}(\mathit{m}\mid {\widehat{\theta }}_{\mathit{m}}^{\mathcal{A}})\underset{\mathit{l}}{\max }\prod _k\sum _{{\mathit{o}}_k}{P}_k({\mathit{o}}_k\mid l_k,{\widehat{\theta }}_{{\mathit{o}}_k}^k)\right\}\hfill \end{array}$$

in which Lemma 1 in the Appendix has been applied. Taking natural logarithm to both sides completes the proof of the smaller upper bound.

Regarding Proposition 5 and Proposition 6, we have the following remarks. First, if all categories of $\mathcal{A}$ are replaced and all the attached models are statistically equivalent, the upper bound in Proposition 5 becomes $C_{\mathrm{FIA},\mathcal{A}}\left(N\right)+K{C}_{\mathrm{FIA},\mathcal{B}}(N∕K)$ and the smaller upper bound in Proposition 6 becomes $C_{\mathrm{NML},\mathcal{A}}\left(N\right)+K{C}_{\mathrm{NML},\mathcal{B}}(N∕K)$. Second, when sample size is large, C_FIA and C_NML will be close to each other and the bound given by Proposition 5 will be close to the smaller upper bound in Proposition 6. Third, the larger upper bound in Proposition 6 will be achieved only when K = 1 and all categories of model $\mathcal{A}$ were replaced. The same condition would be needed for the lower bound of C_FIA complexity difference in Proposition 5 to be 0. In this case, for both NML and FIA, the complexity of the new model is the sum of those of model $\mathcal{A}$ and ${\mathcal{B}}_1$. This special additive case is summarized in the following proposition.

Proposition 7

Suppose trees $\mathcal{A}$ and ${\mathcal{B}}^j$, j = 1, 2, ⋯ , $J_{\mathcal{A}}$, represent $J_{\mathcal{A}+1}$ BMPT models with disjoint sets of categories. Let the $J_{\mathcal{A}}$ models ${\mathcal{B}}^j$, j = 1, 2, ⋯ , $J_{\mathcal{A}}$ be functionally identical with identical parameter assignment. Suppose the two parameter sets ${ϴ}_{\mathcal{A}}$ and ${ϴ}_{\mathcal{B}}$ are disjoint, and tree $\mathcal{C}$ is created by replacing the $J_{\mathcal{A}}$ response categories of tree $\mathcal{A}$ by the $J_{\mathcal{A}}$ trees ${\mathcal{B}}^j$. Then the complexity of tree $\mathcal{C}$ is equal to the sum of complexities of $\mathcal{A}$ and $\mathcal{B}$, that is, $C_{\mathrm{NML},\mathcal{C}}=C_{\mathrm{NML},\mathcal{A}}+C_{\mathrm{NML},\mathcal{B}}$ and $C_{\mathrm{FIA},\mathcal{C}}=C_{\mathrm{FIA},\mathcal{A}}+C_{\mathrm{FIA},\mathcal{B}}$.

The third panel of Figure 6 illustrates the proposition. Note that the additive-complexity rule of the proposition relies on two conditions: (a) the two models do not share common parameters; and (b) one model is added to every category of the other model. The failure to satisfy either of these conditions invalidates the additivity rule, as has been demonstrated in Proposition 4, 5 and 6. This is in sharp contrast to AIC and BIC viewpoint, in which the complexity is linear in the number of parameters and is therefore always additive.

Now consider the case in which the same tree structure is added recursively to every one of its own categories. The following proposition shows that the complexity increases as a logarithmic function of the total number of layers.

Proposition 8

Let ${\mathcal{A}}_k$ be a collection of functionally identical BMPT models with identical parameter assignment but disjoint category sets. The sequence of trees ${\mathcal{B}}_d$ is constructed as follows:

1. ${\mathcal{B}}_1={\mathcal{A}}_1$, which has $J_{\mathcal{A}}$ categories.

2. ${\mathcal{B}}_{d+1}$ is constructed by replacing the ${\left(J_{\mathcal{A}}\right)}^d$ categories of ${\mathcal{B}}_d$ by ${\mathcal{A}}_k$, k = 1, 2, ⋯ , ${\left(J_{\mathcal{A}}\right)}^d$, respectively.

Then the $C_{\mathrm{FIA},{\mathcal{B}}_d}=C_{\mathrm{FIA},\mathcal{A}}+\frac{S_{\mathcal{A}}}{2}$, where $S_{\mathcal{A}}$ is the number of parameters in tree $\mathcal{A}$.

This proposition follows directly from Lemma 3 in the Appendix. The bottom panel of Figure 6 illustrates the proposition, from which we can see d is the number of layers in ${\mathcal{B}}_d$ formed by the recursive operation as described in the proposition. The significance of this proposition lies in that it enables us to construct two MPT models that have the same number of parameters but differ greatly in their complexity values. From Proposition 8 we can seen that ${\mathcal{B}}_1$ and ${\mathcal{B}}_d$ have the same number of parameters but differ in their complexity by $\frac{S_{\mathcal{A}}}{2}\ln d$. However, they have different numbers of categories and therefore the direct contrast of complexity may not be useful. This can be resolved by constructing another MPT model $\mathcal{C}$ by splitting each category of ${\mathcal{B}}_1$ into ${\left(J_{\mathcal{A}}\right)}^{d-1}$ categories with equal probabilities. Now $\mathcal{C}$ has the same number of categories as ${\mathcal{B}}_d$, but according to Proposition 3, it has the same complexity as ${\mathcal{B}}_1$.

To conclude the present section, the above analytical results on the complexity of BMPT models provide an illuminating understanding of various ways that functional form can contribute to the MDL complexity. For the great majority of MPT models of practical interest, however, the complexity measures C_NML and C_FIA do not usually have analytical form solutions. As such, the complexity must be calculated numerically on computer, to which we now turn our discussion in the following section.

Computational Issues

In this section we discuss practical implementation issues concerning the MDL complexity, which can be non-trivial to compute. Recall that to compute C_NML, one must first obtain the maximized likelihood for all possible data sets of a given sample size. Given the fact that analytic expression for maximum likelihood is generally not available for MPT models, computing C_NML directly would be out of question unless the sample size is small or the models are simple enough to yield the maximum likelihood in analytic form. Given this, the next best thing to do would be computing C_FIA instead. Note that C_FIA represents an asymptotic approximation of C_NML but does not requiring calculating maximum likelihoods. In the rest of the section, we give a Monte Carlo algorithm for computing C_FIA. This algorithm has been implemented using MATLAB and a brief description of the program is available in Wu, Myung & Batchelder (accepted).

A Monte Carlo Algorithm

A key step in computing C_FIA is the evaluation of the integral in Equation (6) via Monte Carlo. The rationale of Monte Carlo integration lies as follows. The integral ${\int }_{\Omega }\sqrt{\mid \mathbf{I}\left(\theta \right)\mid }d\theta$ can be written as the expected value of $h\left(\xi \right)=\sqrt{\mid \mathbf{I}\left(\xi \right)\mid }∕\pi \left(\xi \right)$, where random vector ξ follows a distribution with density π(ξ). Monte Carlo method then approximates the expectation by the sample average $\frac{1}{N}{\sum }_{i=1}^{N}h\left({\xi }_i\right)$, where ξ_i’s are realizations of ξ. Although the choice of density π is arbitrary, different choices of π may lead to different rate of convergence of the sample average to the integral. To choose an appropriate proposal distribution π(ξ), we need the following proposition.

Proposition 9

$\sqrt{\mid \mathbf{I}\left(\theta \right)\mid }<c\prod _{s=1}^S\frac{1}{\sqrt{{\theta }_S(1-{\theta }_s)}}$ for some constant c.

Proof

Consider the matrix I(θ)D(θ), where diagonal matrix D has typical element D_ss = θ_s(1 − θ_s), and the elements in the Fisher information matrix I(θ) is given by Equation (13) in the Appendix. We can see

$${\left(\mathbf{ID}\right)}_{sr}=\sum _{j=1}^J\left\{\sum _{i=1}^{I_j}{p}_{ij}\left(\frac{a_{ijs}}{{\theta }_s}-\frac{b_{ijs}}{1-{\theta }_s}\right)\right\}\left\{\sum _{i=1}^{I_j}\frac{p_{ij}}{p_j}(a_{ijr}(1-{\theta }_r)-b_{ijr}{\theta }_r)\right\}$$

From the expression of p_ij given by (3) we know that for all i, j and s, $\frac{a_{ijs}{p}_{ij}}{{\theta }_s}$ and $\frac{b_{ijs}{p}_{ij}}{1-{\theta }_s}$ are polynomials of the θ_s and are therefore bounded on [0,1]. In addition, p_ij/p_j is also bounded, so (ID)_sr must also be bounded. The proposition follows immediately.

This proposition has two implications. First, it implies that the integral is finite and our Monte Carlo computation is meaningful. Second, it implies that the choice of density $\pi \left(\theta \right)=\prod _{s=1}^S\frac{1}{\pi \sqrt{{\theta }_s(1-{\theta }_s)}}$ would lead to a bounded h(θ) for all MPT models. This is desirable as it gives a finite Monte Carlo standard deviation of the estimate. It should be noted that uniform distribution over [0,1]^S does not generally satisfy this requirement and the convergence of Monte Carlo algorithm can be very slow if π(θ) = 1 is chosen.

Models with Inequality Constraints

For models with inequality constraints on the parameters, the calculation of C_FIA is straightforward: one simply needs to restrict the integral in equation (6) to the restricted parameter space $\tilde{\Omega }\subset \Omega ={(0,1)}^S$. To do this, the algorithm needs to be modified to sample ξ_i’s from the proposal distribution π(θ) restricted to $\tilde{\Omega }$, and the integral needs to incorporate the change in the normalizing constant of the proposal distribution. We have

$${\int }_{\tilde{\Omega }}\sqrt{\mid \mathbf{I}\left(\theta \right)\mid }d\theta ={\int }_{\tilde{\Omega }}h\left(\theta \right)\pi \left(\theta \right)d\theta =\left({\int }_{\tilde{\Omega }}h\left(\theta \right)\tilde{\pi }\left(\theta \right)d\theta \right)\left({\int }_{\tilde{\Omega }}\pi \left(\theta \right)d\theta \right)$$

where $\tilde{\pi }\left(\theta \right)\propto \pi \left(\theta \right)1_{\tilde{\Omega }}\left(\theta \right)$ is the renormalized proposal distribution restricted to $\tilde{\Omega }$ In general, the second term on the right hand side can be easily estimated when sampling from the restricted parameter space using rejection method. This is done in the program described in Wu, Myung & Batchelder (accepted). However, due to the symmetry of the proposal distribution π(θ), for most inequality constraints in practice such as the full or partial order relations on ϴ, this term can be easily computed analytically. A full order of K parameters θ₁ < θ₂ < ⋯ < θ_K reduces the parameter space Ω to its 1/K!. A subset of the parameter space Ω defined by partial orders on ϴ can always be expressed as a union of several subsets, each defined by some full order on a subset of ϴ, and its normalizing constant can be calculated accordingly. For example {θ₁ < θ₂, θ₁ < θ₃} = {θ₁ < θ₂ < θ₃} ∪ {θ₁ < θ₃ ≤ θ₂}, so it reduces Ω to its 2 × 1/3! = 1/3.

In particular, if the original unconstrained model has some symmetry property, the ratio between the constrained and unconstrained integrals can be calculated analytically and a separate run of the Monte Carlo algorithm is not needed. For example, if a BMPT model involves K functionally identical trees representing K experimental treatments and parameters θ₁, θ₂, ⋯ , θ_K are correspondent parameters for the treatments, a treatment effect on θ represented by θ₁ < θ₂ < ⋯ < θ_K would reduce the integral to its 1/K!. However, if treatment effects are expected simultaneously on two parameters, this method would not work as the treatments are no longer symmetric after the placement of one of the effects. For example, if either D₁ > D₂ or d₁ > d₂ is assumed in 1HTM-6c (shown in figure (1)), its model complexity will reduce by ln 2, as the two sources have symmetric role in the model, but the inclusion of both at the same time may not reduce the complexity by 2 ln 2.

Complexity of Source Monitoring Models

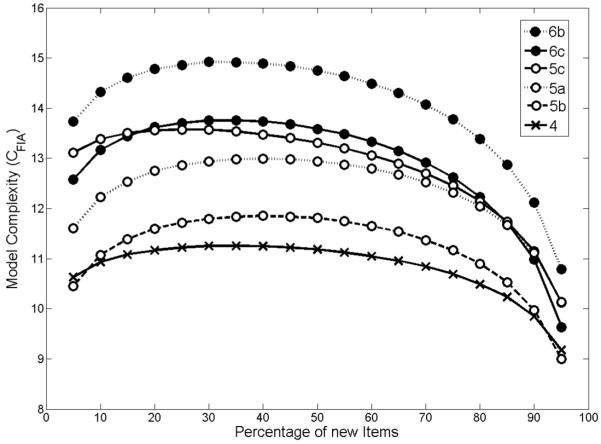
To provide a concrete example of MDL complexity, here we compute C_FIA for some well-known MPT models of source monitoring. The MPT models of source monitoring in Figure 1 (also see Figure 2) are among the most widely studied classes of MPT models in cognitive psychology. Application of MDL-based model evaluation to this class of models is therefore of special interest. C_FIA was computed for the hierarchy of models shown on the right panel of Figure 1. Each model is defined in terms of three tree structures, one for each item type, so three sample sizes (n_A, n_B, n_N) are defined. In a typical source monitoring experiment, the sample sizes for the old items, A or B, are set to be the same (n_A = n_B = n_O/2), and only the ratio of new items to the total number of items (n_N/(n_O + n_N)) varies from experiment to experiment.

Shown in Figure 7 are C_FIA complexity curves for six selected models⁹, plotted as a function of the percentage of new items for the total sample size of n_O + n_N = 1000. The first thing to note in the figure is that complexity is generally ordered according to the number of parameters. The two six-parameter models are the most complex, trailed by the three five-parameter models, and the four-parameter model is the simplest. Also note that among models with the same number of parameters, their complexity values can differ significantly from one another, sometimes even greater than the complexity difference due to the difference in the number of parameters. The case in point is the three models, 4, 5b and 5c. At the 50% value of new items, the complexity difference between model 5c and model 5b is equal to about 1.50, which is greater than the complexity difference (0.62) between models 5b and 4.¹⁰ These results, taken together, again, demonstrate that mode complexity is determined not only by the number of parameters but also importantly, by functional form, and sometimes even more so by the latter.

Figure 7.

C_FIA complexity curves for six source-monitoring models in Figure 1. The total sample size is N = 1000.

Conclusions

Model complexity is an integral and key concept in the evaluation and selection of quantitative models of cognition. In this paper we have explored the issue of model complexity in multinomial process tree (MPT) modeling with a special focus on the effects of tree structure on complexity for MPT models. The particular approach we took in the present investigation is that of minimum description length (MDL). The primary contributions of the present study are a series of Propositions we proved concerning the properties of the MDL complexity of this class of models and a general algorithm for the computation of C_FIA.

Speaking of model complexity, recall that complexity refers to the range of data patterns a model can provide good fits to, in the sense that a complex model fits well a wider range of data patterns than a simpler model. This idea is formalized in the NML complexity measure, C_NML, which is equal to the logarithmic value of the sum of best fits that the model can provide, by varying its parameter values, for all potential data patterns. Here we highlight a few important insights we have gained about complexity of MPT models from our analytic investigations. First of all, according to the NML complexity measure, what matters in measuring a model’s complexity is not the apparent complications of its tree structure (i.e., “functional form”) or the number of its parameters but instead the “size” of the family of probability distributions indexed by the model’s parameters. Second, insofar as the same family of probability distributions are indexed, complexity remains unchanged regardless of how the model is parameterized. Third, if other things are equal, the more distinct response categories a model assumes, generally, the more complex the model is (Proposition 3). Fourth, complexity is, in general, non-additive with respect to combing two or more models of disjoint parameter sets (Proposition 4, 5 and 6). Finally and related, tree structure can significantly contribute to model complexity, sometimes even more than the number of parameters. As an extreme example of this, it is possible to construct two MPT models with the same number of parameters yet with complexity values different greatly, as described in Proposition 8.

A step further beyond the current research is to implement the MDL method to addressing actual model selection problems in the field of MPT modeling, which is described in a separate paper of ours (Wu, Myung & Batchelder, accepted).

On final note. The primary concern of the present study is the issue of complexity for MPT models in MDL based model evaluation. This paper is not, however, advocating that the evaluation of MPT models be made entirely in terms of MDL and its complexity. It is also important to consider other statistical procedures and criteria in model evaluation. For example, null hypothesis significant testing takes a model falsification point of view and thus may be useful to test specific parametric constraints under investigation. By the same token, qualitative, non-statistical criteria of model evaluation such as plausibility and interpretability are equally, if not more, important to get a “holistic view” of a model’s adequacy.

Appendix: Three Lemmas

Here we present three lemmas used in the proofs of prepositions. Lemma 1 gives an equality of combination numbers used in the proof of Proposition 6. Lemma 2 gives the form of Fisher information matrix for BMPT models in standard representation. Lemma 3 gives the form of Fisher information matrix of complex BMPT models in terms of its components by exploiting the recursive property of BMPT models.

Lemma 1

For all non-negative integer N , ${\left\{G^{\left(i\right)}\right\}}_{i=1}^p$, ${\left\{G_j\right\}}_{j=1}^q$ and ${\left\{g_j^{\left(i\right)}\right\}}_{i=1}^p{,}_{j=1}^q$ that satisfy the restriction ${\sum }_i{G}^{\left(i\right)}={\sum }_j{G}_j=N$, the following equality holds:

$$\sum _{\left\{g_j^{\left(i\right)}\mid \begin{array}{c}\hfill {\Sigma }_i{g}_j^{\left(i\right)}=G_j\hfill \\ \hfill {\Sigma }_j{g}_j^{\left(i\right)}=G^{\left(i\right)}\hfill \end{array}\right\}}\frac{\prod _i\left(\begin{array}{c}\hfill G^{\left(i\right)}\hfill \\ \hfill g_1^{\left(i\right)},g_2^{\left(i\right)},\cdots ,g_q^{\left(i\right)}\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill N\hfill \\ \hfill G_1,G_2,\cdots ,G_q\hfill \end{array}\right)}=1$$ (12)

Proof

Suppose N objects belongs to p groups, with G⁽ⁱ⁾ objects in the ith group. Now we would like to randomly re-group all the objects into q groups, with G_j objects in the jth group. Let $g_j^{\left(i\right)}$ be the number of objects that are recruited from the ith original group to the jth new group. Then the fraction in this lemma gives the probability for this particular solution, which, after summed up over all possible solutions, yields 1.

Lemma 2

The Fisher information matrix of a BMPT model with the representation shown in Equations (3),(1) and (2) is given by

$$I_{rs}=-\mathrm{E}\frac{{\partial }^2\ln L}{\partial {\theta }_s\partial {\theta }_r}=\sum _{j=1}^J\frac{1}{p_j}\left\{\sum _{i=1}^{I_j}{p}_{ij}\left(\frac{a_{ijs}}{{\theta }_s}-\frac{b_{ijs}}{1-{\theta }_s}\right)\right\}\left\{\sum _{i=1}^{I_j}{p}_{ij}\left(\frac{a_{ijr}}{{\theta }_r}-\frac{b_{ijr}}{1-{\theta }_r}\right)\right\}$$ (13)

Especially, if every category of the BMPT model includes only a single leaf, its Fisher information matrix is a diagonal matrix given by

$$I_{ss}=\sum _{j=1}^J\sum _{i=1}^{I_j}{p}_{ij}\left(\frac{a_{ijs}}{{\theta }_s^2}+\frac{b_{ijs}}{{(1-{\theta }_s)}^2}\right)$$ (14)

Proof

Equation (13) follows from Grünwald, Myung & Pitt (2005, equation 16.4 on p.420) with the matrix P_js in the equation given by Hu & Batchelder (1994, equation 36 on p.40). When the MPT model is a simple one, its Hessian matrix is given by (Hu & Batchelder, 1994, equation 37 on p.40). Taking expectation of both sides completes the proof of (14).

Lemma 3

Let $\mathcal{A}$ and $\mathcal{B}$ be BMPT models with disjoint sets of categories ${\mathbf{C}}_{\mathcal{A}}$ and ${\mathbf{C}}_{\mathcal{B}}$ and parameter sets ${ϴ}_{\mathcal{A}}$ and ${ϴ}_{\mathcal{B}}$, which need not be disjoint. Consider an BMPT model $\mathcal{C}$ constructed by replacing category C₀ of $\mathcal{A}$ with model $\mathcal{B}$. The Fisher information matrix of $\mathcal{C}$ is given by ${\mathbf{I}}^{\mathcal{C}}={\tilde{\mathbf{I}}}^{\mathcal{A}}+{\tilde{\mathbf{I}}}^{\mathcal{B}}{p}_0^{\mathcal{A}}$, where $p_0^{\mathcal{A}}$ is the implied category probability of C₀ in $\mathcal{A}$, and ${\tilde{\mathbf{I}}}^{\mathcal{A}}$ is the extended Fisher information matrix in which all parameters in $\mathcal{C}$ are included but the entries corresponding to parameters not in model $\mathcal{A}$ are set to 0.

Remarks:

1. This proposition can be easily extended to the case in which k > 1 categories in $\mathcal{A}$ are replaced by trees ${\mathcal{B}}_k$ of disjoint sets of categories.

2. When the two parameter sets are disjoint, ${\mathbf{I}}^{\mathcal{C}}$ is block diagonal and its determinant is given by $\mid {\mathbf{I}}^{\mathcal{C}}\mid =\mid {\mathbf{I}}^{\mathcal{A}}\mid \mid {\mathbf{I}}^{\mathcal{B}}\mid {\left(p_0^{\mathcal{A}}\right)}^{S_{\mathcal{B}}}$, where $S_{\mathcal{B}}$ is the number of parameters in model $\mathcal{B}$.

Proof

It is evident that the probability of category $j\in \mathcal{C}$ (i.e. $C_j\in {\mathbf{C}}_{\mathcal{C}}$) is given by $p_j^{\mathcal{C}}=p_j^{\mathcal{A}}{1}_{\mathcal{A}}\left(j\right)+p_0^{\mathcal{A}}{p}_j^{\mathcal{B}}{1}_{\mathcal{B}}\left(j\right)$. Consequently we have

$$\frac{\partial p_j^{\mathcal{C}}}{\partial {\theta }_s}=\frac{\partial p_j^{\mathcal{A}}}{\partial {\theta }_s}{1}_{\mathcal{A}}\left(j\right)+\frac{\partial p_0^{\mathcal{A}}{p}_j^{\mathcal{B}}}{\partial {\theta }_s}{1}_{\mathcal{B}}\left(j\right)$$

Applying the above equation to equation 16.4 of Grünwald, Myung & Pitt (2005, p.420), we have

$$\begin{array}{cc}\hfill I_{rs}^{\mathcal{C}}& =\sum _{j\in \mathcal{C}}\frac{1}{p_j^{\mathcal{C}}}\frac{\partial p_j^{\mathcal{C}}}{\partial {\theta }_r}\frac{\partial p_j^{\mathcal{C}}}{\partial {\theta }_s}\hfill \\ \hfill & =\sum _{j\in \mathcal{A}-0}\frac{1}{p_j^{\mathcal{A}}}\frac{\partial p_j^{\mathcal{A}}}{\partial {\theta }_r}\frac{\partial p_j^{\mathcal{A}}}{\partial {\theta }_s}+\sum _{j\in \mathcal{B}}\frac{1}{p_0^{\mathcal{A}}{p}_j^{\mathcal{B}}}(p_j^{\mathcal{B}}\frac{\partial p_0^{\mathcal{A}}}{\partial {\theta }_r}+p_0^{\mathcal{A}}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_r})(p_j^{\mathcal{B}}\frac{\partial p_0^{\mathcal{A}}}{\partial {\theta }_s}+p_0^{\mathcal{A}}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_s})\hfill \\ \hfill & =\sum _{j\in \mathcal{A}-0}\frac{1}{p_j^{\mathcal{A}}}\frac{\partial p_j^{\mathcal{A}}}{\partial {\theta }_r}\frac{\partial p_j^{\mathcal{A}}}{\partial {\theta }_s}+\sum _{j\in \mathcal{B}}\frac{p_j^{\mathcal{B}}}{p_0^{\mathcal{A}}}\frac{\partial p_0^{\mathcal{A}}}{\partial {\theta }_r}\frac{\partial p_0^{\mathcal{A}}}{\partial {\theta }_s}+\sum _{j\in \mathcal{B}}\frac{\partial p_0^{\mathcal{A}}}{\partial {\theta }_r}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_s}+\sum _{j\in \mathcal{B}}\frac{\partial p_0^{\mathcal{A}}}{\partial {\theta }_s}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_r}+\sum _{j\in \mathcal{B}}\frac{p_0^{\mathcal{A}}}{p_j^{\mathcal{B}}}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_r}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_s}\hfill \end{array}$$

We note $\underset{j\in \mathcal{B}}{\Sigma }{p}_j^{\mathcal{B}}=1$ and $\underset{j\in \mathcal{B}}{\Sigma }\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_r}=0$, and the above equation can be simplified as

$$I_{rs}^{\mathcal{C}}=\sum _{j\in \mathcal{A}}\frac{1}{p_j^{\mathcal{A}}}\frac{\partial p_j^{\mathcal{A}}}{\partial {\theta }_r}\frac{\partial p_j^{\mathcal{A}}}{\partial {\theta }_s}+p_0^{\mathcal{A}}\sum _{j\in \mathcal{B}}\frac{1}{p_j^{\mathcal{B}}}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_r}\frac{\partial p_j^{\mathcal{B}}}{\partial {\theta }_s}={\tilde{\mathbf{I}}}^{\mathcal{A}}+{\tilde{\mathbf{I}}}^{\mathcal{B}}{p}_0^{\mathcal{A}}$$