Effects of heartbeat and respiration on macaque fMRI: implications for functional connectivity

Abstract

The use of functional magnetic resonance imaging (fMRI) in non-human primates is on the increase. It is known that the blood-oxygen-level-dependent (BOLD) signal varies not only as a function of local neuronal energy consumption but also as a function of cardiac and respiratory activity. We mapped these cyclic cardiac and respiratory artifacts in anesthetized macaque monkeys and present an objective analysis of their impact on estimates of functional connectivity (fcMRI). Voxels with significant cardiac and respiratory artifacts were found in much the same regions as previously reported for awake humans. We show two example seeds where removing the artifacts clearly decreased the number of false positive and false negative correlations. In particular, removing the artifacts reduced correlations in the so called resting state network. Temporal band-pass filtering or spatial smoothing may help to reduce the effects of artifacts in some cases but are not an adequate replacement for an algorithm that explicitly models and removes cyclic cardiac and respiratory artifacts.

1 Introduction

Recent years have seen an increase in the number of fMRI studies using anesthetized as well as awake macaque monkeys (e.g., Logothetis et al., 1999; Essen et al., 2001; Brewer et al., 2002; Tsao et al., 2003; Pinsk et al., 2005; Vincent et al., 2007; Hadj-Bouziane et al., 2008). Such studies provide a unique opportunity to bridge the gap between invasive single cell electrophysiology in monkeys and non-invasive fMRI methods in humans. Vincent et al. (2007) were recently able to show that measures of functional connectivity yield meaningful results even in anesthetized monkeys. This finding amplifies the potential range of applications of monkey imaging.

The BOLD signal is modulated by several physiological artifacts such as fluctuations in breathing rate and amplitude as well as pulsatile and respiratory motion. It is still a mater of debate to what extent measures of functional connectivity represent such artificial processes (for reviews see Rogers et al., 2007; Auer, 2008). The current study focuses exclusively on blood volume, blood oxygenation, and motion artifacts with a fixed phase relation to the cardiac and respiratory cycle. These artifacts will be referred to as cyclic physiological artifacts or simply cyclic artifacts. Cyclic artifacts have long been known to affect human BOLD signals (e.g., Hu et al., 1995; Biswal et al., 1996; Glover and Lee, 1995; Mitra et al., 1997; Lowe et al., 1998; Dagli et al., 1999; Glover et al., 2000; Raj et al., 2001; Lund, 2001a; Lund et al., 2006; Harvey et al., 2008). Despite the current interest in monkey fMRI, cyclic artifacts of this species have not been quantified.

The detection and removal of cyclic artifacts may be of great importance for fcMRI, especially when using long TRs (Mitra et al., 1997; Lowe et al., 1998; Lund, 2001a; Cordes et al., 2001; Maldjian, 2001; Rogers et al., 2007; Auer, 2008). Lund (2001a) has argued that with long TR’s cyclic artifacts may be aliased into lower frequency bands which are typically used for fcMRI. Further, Lowe et al. (1998) has shown that the spatial specificity of fcMRI is reduced when using long TR’s, the most likely cause being aliased cyclic artifacts. However, despite the potential impact of cyclic artifacts on fcMRI and the availability of tools to remove them (e.g., RETROICOR, Glover et al., 2000), a large number of studies do not make use of this possibility (for a review of clinical studies see Auer, 2008).

One reason for this might be that so far, no study has actually compared standard whole-brain connectivity maps before and after removal of cyclic artifacts. Previous studies which have analyzed cyclic artifacts (e.g., Glover et al., 2000; Lund et al., 2006; Harvey et al., 2008), only show maps of the affected regions (susceptibility maps). However, the fact that two voxels are both affected by cardiac artifacts, does not automatically imply that they will have correlated artifacts. For example, if the artifact a₁ follows the sine of the cardiac cycle in one voxel, a₁ = sin(φ), and the cosine of the cardiac cycle in another region, a₂ = cos(φ), they are effectively uncorrelated. Also, it is important to consider differences in slice-time acquisition which will cause different voxels to be sampled at different phases of the cardiac and respiratory cycle. Depending on the average phase shift introduced by the difference in slice-timing, two voxels with identical dependence on cardiac and respiratory activity may show significant positive, negative or no correlation.

Further, standard fcMRI preprocessing steps typically involve explicit as well as implicit spatial low-pass filtering. Artifacts in adjacent slices are not necessarily sampled in a similar phase of the artifact, thus introducing high spatial frequencies perpendicular to the slice-orientation. Thus, spatial smoothing may reduce the amplitude of the cyclic artifacts to a larger degree than other signals. In summary, the relation between susceptibility maps on the one, and fcMRI maps on the other is not immediately obvious and merits empirical investigation.

The present study has two primary goals. First, it provides a quantitative assessment of cyclic artifacts in macaque monkeys, analogous to previous studies in humans (Glover et al., 2000; Cordes et al., 2001; Lund et al., 2006; Harvey et al., 2008). Second, it analyses the effects of removing cyclic artifacts on standard whole-brain functional connectivity maps of anesthetized macaques. We find that, indeed, cyclic artifacts quantitatively affect estimates of functional connectivity and may lessen our ability to detect and quantify functional networks.

2 Materials and Methods

2.1 Imaging

Three adult male macaque monkeys (macaca mulatta, 7–10 kg) were scanned under light isoflurane anesthesia (0.8–1.1%, spontaneous ventilation) on a 3T Philips scanner. The monkeys were scanned in the supine position while head motion was restrained by padding placed between the head and the headcoil. In the initial phase of the anesthesia, resting state T2*-weighted functional images were acquired (TR=2000 ms, TE=25 ms, flip-angle=72 deg, FOV: 192mm×160mm×50mm, 96×96×25 2 mm³ isotropic voxels, 400 volumes per series). Slices were acquired with the standard Philips ventral to dorsal interleaved sequence. Subsequently, under deeper anesthesia, T1-weighted structural images were taken (256×256×100 1mm³ isotropic voxels).

2.2 Physiological measures

During functional scans, cardiac activity was derived from peripheral blood oxygenation measured with a pulse-oximeter placed on one of the monkey’s toes. The spontaneous respiratory activity was monitored by measuring end-tidal CO₂-concentration. These signals, i.e., the cardiac signal C(t) and the respiratory signal R(t) were sampled and digitized at a rate of 200 Hz and saved alongside the slice triggers from the scanner.

Following Hu et al. (1995) and Glover et al. (2000) we defined the phase of the cardiac signal φ_C by the following equation:

$${\phi }_C(t)=2\pi (t-t_{\mathit{pre}})/(t_{\mathit{post}}-t_{\mathit{pre}})$$

Here t_pre and t_post are the two local maxima in peripheral blood oxygenation preceding and following t. Hence, φ_C advances at a steady pace within each cardiac cycle. The rate of change of φ_C differs between cycles of different duration. In contrast to Glover et al. (2000) we used the same method to derive an estimate of phase of the respiratory cycle, φ_R (see section 2.3 for details).

To detect the local maxima of C(t) and R(t), we first filtered out high frequencies using Gaussian kernels with a standard deviation of 25 and 200 ms for C and R, respectively. Subsequently, we calculated time derivatives of the signals by subtracting a lagged version of the same signal:

$$dx/dt[n]=\nu {\delta }_t\ast (x[n]-x[t-\nu ])$$

Here δ corresponds to the temporal resolution, in our case 1/200 and ν to the lag which was chosen as 1 and 2 for C and R, respectively. Local maxima were detected when the sign of the derivative switched from positive to negative.

2.3 Artifact removal

In the present study we used harmonic or trigonometric regression (e.g., Mardia, 1972) to detect and remove cyclic cardiac and respiratory artifacts. Briefly, the method assumes that the raw BOLD signal is the result of neuronally driven changes in BOLD and artificial changes in BOLD related to cardiac and respiratory activity, respectively:

$$B_{\mathit{raw}}(t)=B_N(t)+B_C(t)+B_R(t)$$

Further, it is assumed that both B_C and B_R are functions of the phase of the cardiac and respiratory cycle, respectively:

$$\begin{array}{l}{B}_C(t)=a_C[{\phi }_C(t)]\\ B_R(t)=a_R[{\phi }_R(t)]\end{array}$$

Here a_C and a_R describe the effect of an average cardiac or respiratory cycle on BOLD as a function of phase. In order to visualize a_C and a_R we plot the raw BOLD activity B_raw not as a function of time, but as function of the current phase φ_C(t) and φ_R(t), respectively (see supplementary Figures S1b&c and S2b&c, respectively). The functions a_C and a_R can be estimated in several ways. In the present paper we used harmonic regression to fit a subset of orthogonal basis functions to the data. The functions we fit consist of a constant offset plus the first N Fourier components:

$$a_{C/R}[\phi ]={\alpha }_0+\sum _{\omega =1}^N{\alpha }_{\omega }sin[\omega {\phi }_{C/R}]+{\beta }_{\omega }cos[\omega {\phi }_{C/R}]$$

Thus, for each of the two artifacts the entire model is determined by 1 + 2N parameters. In the present paper we used N = 6, unless stated otherwise. To remove the artifact we subtracted the estimated artifact from the raw data.

$$B_{\mathit{clean}}(t)=B_{\mathit{raw}}(t)-a_C[{\phi }_C(t)]-a_R[{\phi }_R(t)]$$

The standard harmonic regression which we used here is highly similar to the RETROICOR method described by Glover et al. (2000). RETROICOR differs from standard harmonic regression in its treatment of the respiratory artifacts. The respiratory artifact is thought to arise from apparent motion caused by changes in bulk susceptibility in the lungs (Raj et al., 2001). Hence, the artifact is supposed to depend not only on the phase of the respiratory cycle, but also on the amplitude. RETROICOR treats this dependency by introducing a different estimate of phase (see Glover et al., 2000, for details). We decided not to use this alternative estimate of phase for two reasons. First, we observed very little variability in the amplitude of the respiratory cycles. Thus, our method and RETROICOR, produce virtually identical estimates of phase with correlation coefficients on the order of .975. Second, if amplitudes do vary, the RETROICOR phase estimate will have discontinuities in phase space (supplementary Figure 3, top panel). This will cause the sine-regressors to have discontinuities in the time domain (supplementary Figure 3, bottom panel) which do not match the continuous nature of the respiratory artifact.

It is important to note that harmonic regression does not assume constant frequency of the cardiac and respiratory signals. However, it does implicitly assume that the functions a_C and a_R are constant over the time- and frequency range of the cardiac and respiratory signals during data acquisition. Deviations from this assumption will cause the model to underestimate the amount of variance caused by cardiac and respiratory artifacts.

We used standard statistical methods to describe the model fit. F values were calculated as the fraction of the sums of squares of the model SSQ_mod and the sums of squares of the residuals SSQ_res normalized with the respective degrees of freedom, $F=\frac{{\mathit{SSQ}}_{\mathit{mod}}}{d{f}_{\mathit{mod}}}\frac{d{f}_{\mathit{res}}}{{\mathit{SSQ}}_{\mathit{res}}}$. The model was considered to provide a significant fit to the data if the F-value exceeded the 0.95-quantile of an F distribution with the corresponding degrees of freedom. The percent variance explained (%Var) was calculated as 1 minus the fraction of the sums of squares of the residuals and the sums of squares of the original data, $\%\mathit{Var}=1-\frac{{\mathit{SSQ}}_{\mathit{res}}}{{\mathit{SSQ}}_{\mathit{raw}}}$. For fixed degrees of freedom (as was the case here) there is a simple relation between the F-values and the percent variance explained: the percent variance explained corresponds to the fraction of the F-value and the sum of the F-value and the fraction of the degrees of freedom, $\%\mathit{Var}=F/(F+\frac{{df}_{\mathit{res}}}{{df}_{\mathit{mod}}})$. In the current case, with 13 − 1 = 12 numerator and 394 − 12 − 1 = 381 denominator degrees of freedom the critical F-value (see above) corresponds to 1.78. This F-value, in turn, corresponds to 5.3% variance explained.

2.4 Preprocessing

For all runs we used two different preprocessing protocols, one of which used the phase-regression method. The leading 6 volumes were removed to avoid onset non-stationarities. A functional reference volume was drawn halfway through the scan ((400−6)/2=197). All the voxels with intensity values in the lower 5-percentile in any of the 394 volumes were masked out.

The following steps were executed only if the phase-regression method was applied. Using FSL’s math routine (fslmaths, Smith et al., 2004) the shortened and masked series was highpass-filtered with a cutoff wavelength of 400 s. From the highpassed data we estimated and removed cardiac and respiratory artifacts with the phase-regression method described above. The removed artifacts were stored for further analysis. The previously removed low frequency components were added to the artifact-free data to make the two data sets with and without the artifacts identical in every other aspect.

From here on the two preprocessing pipelines were identical. FSL’s motion correction algorithm (mcflirt, Jenkinson et al., 2002) was used to register all volumes to the reference functional volume. Typically, the motion was small, well below the dimensions of a single voxel (2mm³). FSL’s slicetime-correction algorithm (slicetimer, Smith et al., 2004) was used to correct for differences of slice-time acquisition between different slices of a volume. Finally, using FSL’s linear registration tool (flirt, Jenkinson et al., 2002) this data-set was registered to a global reference volume which corresponded to the first high-contrast functional volume of the fourth run of the session.

Functional images and statistical maps from different animals were registered into a common space by a two-step procedure. First, the brain-extracted global functional reference volume was registered to the brain-extracted structural volume. Second, the structural images of all animals were registered in a standardized space. The standardized space was created by co-registering and averaging structural volumes of four previously scanned macaque monkeys and aligning the resulting mean structural image along the anterior- to posterior commissure line.

Brain voxels were determined from the high-resolution structural images using FSL’s brain extraction tool (bet, Smith et al., 2004). Output of the brain extraction tool was corrected by hand in some difficult cases. These maps were registered to the low-resolution functional imaging space and served as masks for the detection of brain voxels (see below).

2.5 Functional connectivity

Functional connectivity was calculated for anatomically defined seed regions in several temporal waveband bands and with different amounts of spatial smoothing. The preprocessed time-series were demeaned and normalized by their standard deviation. Mean BOLD activity of all previously determined brain voxels was regressed out using FSL’s linear regression tool (fsl glm, Smith et al., 2004). This data was filtered with four Gaussian kernels with a standard deviation of 1 or 2 mm, respectively (fslmaths, Smith et al., 2004). The resulting 4D-volumes, including the original one without spatial smoothing, were filtered with a 400 sec temporal highpass (fslmaths, Smith et al., 2004) in order to remove low-frequency drift. In addition, we created a bandpassed version of the data by filtering with a 20 sec lowpass. The proprocessing gave rise to 3 (spatial filters) × 2 (temporal filters) × 2 (cyclic artifact removal) = 12 4D-Volumes for each original run.

To calculate functional connectivity of a seed region to the rest of the brain we averaged activity in this region and correlated it separately to the activity of all brain voxels. This procedure was repeated for all runs of the animal in question. For each voxel this rendered a set of 6 to 8 correlation values, depending on the number of functional runs acquired for this animal. These values were transformed using Fischer’s z-transformation and fed into a one-sample t-test. The resulting t-maps were corrected for multiple comparisons using a two-sided cluster criterion with a t-value cutoff of 2.3 and a critical cluster value of 0.05 (cluster, Smith et al., 2004).

3 Results

3.1 Heart and breathing rate

Before describing the cardiac and respiratory artifacts in detail we briefly report the properties of the cardiac and respiratory signals. For all monkeys, the average cardiac cycle was around 550 ms, slightly larger than a quarter of the TR. (monkey C: 565 ms ± 7; monkey L: 537 ms ± 3; monkey P: 598 ms ± 12). An average respiratory cycle was around 2 s, on the order of magnitude of the TR (monkey C: 1935 ms ± 75; monkey L: 2025 ms ± 67; monkey P: 2675 ms ± 88). In addition, we analyzed the variability of heart and breathing rate over the course of an individual run. For individual runs, the range of cardiac cycle durations, i.e., the longest cycle minus the shortest cycle, was 32 ms (monkey C: 32 ms± 3; monkey L: 34 ms± 10; monkey P: 31 ms± 4). The range of respiratory cycle durations, i.e., the duration of the longest cycle minus the duration of the shortest cycle, was 344 ms on average (monkey C: 241 ms± 107; monkey L: 360 ms± 155; monkey L: 432 ms± 35).

3.2 Cardiac artifacts

For all three monkeys a large number of voxels had significant cardiac artifacts (see Figure 1a and 2a). Supplementary Figure S1 shows the cardiac artifact for an example voxel in the anterior cingulate. The bulk of voxels with cardiac artifacts was found close to the major arteries, such as the basilar artery and Circle of Willis, as well as the anterior, middle, and posterior cerebral arteries. Voxels around major veins seemed to be less affected. However, voxels around the superior sagittal sinus did show significant cardiac artifacts.

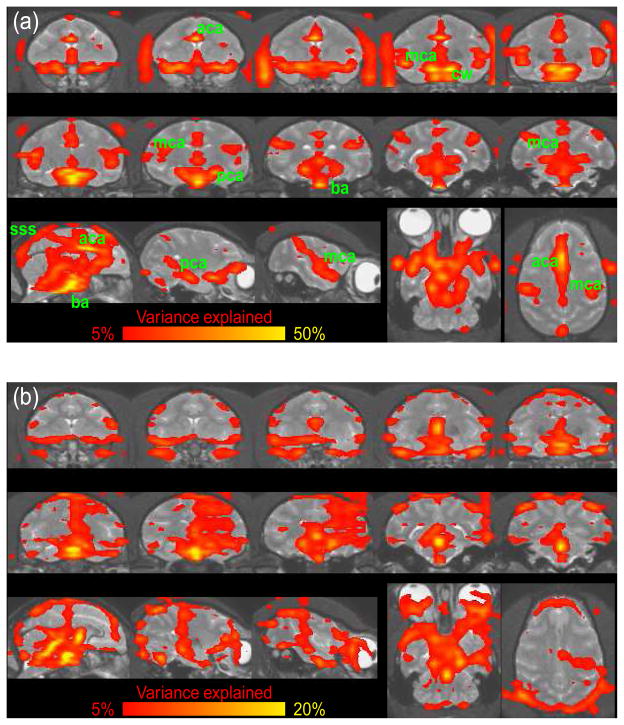
Fig. 1.

Cardiac (a) and Respiratory Artifact (b) from one macaque monkey. Data were averaged over 8 runs of 400 volumes each. Regions with significant cyclic artifacts are overlaid on the individual T1-weighted structural image. The colors correspond to the percent variance explained by the harmonic regression. Note the different scales of the color bar for the cardiac and respiratory artifacts. (a) Regions with significant artifacts can be found around major vessels. The basilar artery (ba), anterior (aca), medial (mca) and posterior (pca) cerebral arteries can clearly be distinguished. Veins seem to cause less artifacts but the superior sagital sinus (sss) is clearly visible. Arteries outside the brain such as the opthalmic artery are also visible. (b) Part of the respiratory artifacts are caused by breathing related apparent motion.

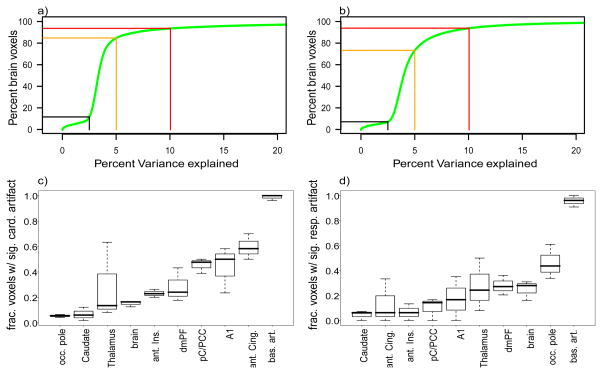
Fig. 2.

Empirical distribution function of percent variance explained (a) by cardiac and (b) respiratory artifacts. All brain voxels of all three monkeys aggregated. Black, orange and red line denote the values of the distribution function for 2.5, 5 and 10% variance explained. (c) Cardiac and (d) respiratory artifacts in different brain regions. Artifacts are quantified as the fraction of voxels with significant artifacts. occ. pole: occipital pole, aIC: anterior insular cortex, dmPF: dorsomedial prefrontal cortex, A1: primary auditory cortex, pC/PCC: posterior cingulate and posterior cuneal cortex (resting-state seed), ant. Cing.: anterior cingulate, bas. art.: basilar artery, brain: all voxels assigned to neither of the specific regions.

The most affected brain regions are (1) the ventral base of the cerebrum including the frontal pole of the temporal lobe, hypothalamus, para-hippocampal cortex, and the entire brain stem, (2) the entire medial wall of the two hemispheres including anterior and posterior cingulate, and (3) regions in the fold of the sylvian fissure including the insula and auditory cortex (see Figure 1a and 2c). This is likely to be due to the proximity of these regions to major vessels. Note that apart from the fourth ventricle, the other ventricles are not affected by the cardiac artifact.

3.3 Respiratory artifacts

For all three monkeys a large number of voxels had significant respiratory artifacts (see Figure 1b, and 2b). Supplementary Figure S2 shows the respiratory artifact for an example voxel in the fourth ventricle. Voxels with significant respiratory artifacts were more common than voxels with significant cardiac artifacts. Part of the respiratory artifacts seemed to arise from breathing-related motion as opposed to breathing-related changes in blood oxygenation. To test this hypothesis we performed FSL’s motion correction (mcflirt, Jenkinson et al., 2002) on the estimated artifact. For all three monkeys we found small but highly consistent breathing related motion in the anterior-posterior and, with smaller amplitude, the ventro-dorsal direction. A study by Raj et al. (2001) concludes that analogous effects in humans are apparent motion caused by changes in bulk susceptibility in the lungs.

3.4 Spectral analysis of cardiac and respiratory artifacts

To determine the temporal properties of the artifacts we compared power spectra of the uncorrected and corrected data sets. We selected voxels with significant artifacts and calculated the mean power spectra of these voxels for the uncorrected and the corrected time-series. Figure 3 shows the fraction of the corrected and uncorrected power spectra which corresponds to 1 minus the percent variance explained for the temporal waveband in question.

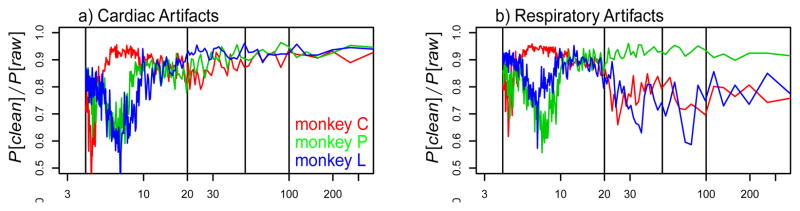
Fig. 3. Spectral analysis.

Fraction of remaining power after removal of the cardiac (a) and respiratory artifacts (b). Different colors correspond to the three different animals. Data are averaged over all runs and voxels with significant cardiac (a) and respiratory artifacts (b). Note that most of the artifacts are in the waveband below 10 s. However, some of the respiratory artifacts are in the waveband between 20 and 300 s. The differences between the animals are due to different cardiac and respiratory frequencies which cause an aliasing of the artifacts into different wavebands

Cardiac artifacts were mainly found in wavelengths below 10 s (see Figure 3a). In contrast, respiratory artifacts were observed also with longer wavelengths (see Figure 3b). It is important to note that these differences are not an intrinsic property of the two signals, because the observed wavelength depends on the aliasing of the artifacts. The aliased frequency is determined by the difference between TR and the average duration and variability of the cardiac or respiratory cycle (e.g., Glover et al., 2000; Lund, 2001a; Kiviniemi et al., 2005). Aliasing into low frequency bands is especially likely to occur if the TR and duration of the artifactual cycle are very similar. In line with this, we find an aliasing of the respiratory artifact into long wavelengths for monkeys C and L who have respiratory cycles of 1935 and 2025 ms, respectively, but not for monkey P with a respiratory cycle of 2675 ms (see Figure 3b).

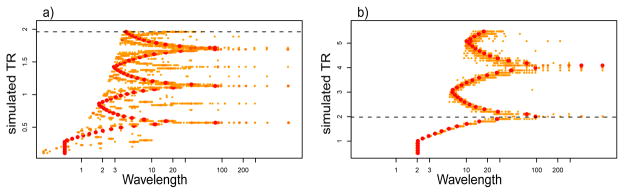
We simulated the effect of different TRs on the aliasing of the cardiac and respiratory artifacts. To do so, we used the estimated artifact a_c(φ_c) of a strongly affected voxel, and determined the phase of the cardiac artifact φ (n) = φ (n * TR) for a variety of different TRs. Then, we calculated the power spectra of the simulated artifacts a_c[φ_c(n * TR)] for all choices of TR. The results in Figure 4a show that for a TR of 2 seconds (dotted line), the cardiac artifacts are aliased mainly into very short wavebands. In contrast, the respiratory artifacts are aliased to a wavelength of roughly 100 s. Furthermore, the simulation shows that for some choices of TR the cardiac artifacts can be expected in wavelengths well above 10 s. In such cases, low-pass filtering the data will not remove the cardiac artifacts.

Fig. 4. Aliasing of (a) cardiac and (b) respiratory activity as a function of simulated TRs.

Normalized color coded power spectra for cardiac and respiratory activity of a random run sampled at different simulated TRs. Large red dots denote wavelengths with maximal power, smaller orange dots denote wavelengths which are affected to a lesser degree. For TRs shorter than half the length of the average cycle (Nyquist frequency; 0.25s for cardiac and 1s for respiratory activity) the frequency analysis detects the power in the correct waveband. Longer TRs lead to an aliasing of the physiological activity into lower wavelengths. Note the large systematic change of the aliased wavelengths as a function of TR. For a TR of 2 sec (dotted line) the predictions from the simulation match the data, i.e., cardiac artifacts are found mainly in a short wavelengths while respiratory artifacts are also found with longer wavelengths.

3.5 Functional connectivity

The previous results have shown that a large fraction of voxels have significant cardiac and respiratory artifacts. In the following we will test how these artifacts affect functional connectivity maps. The impact of the cyclic artifacts was assessed by comparing results from three conditions. As a baseline we use the highpassed data set from which merely slow linear drifts had been removed. Results form this data set were compared to two artifact removal methods, the harmonic regression algorithm as well as the standard lowpass method.

Example 1: basilar artery seed

To test whether cyclic artifacts may affect fcMRI maps we selected a region which is highly affected by cyclic artifacts. The susceptibility maps suggest that the basilar artery can be considered such a worst case scenario. Selecting the basilar artery as a seed-region has several advantages. First, under the assumption that there are no residual gray-matter voxels in the seed, we can assume that all observed correlations are not neuronally driven and hence artificial. Thus, to a first approximation, the improvement of the fcMRI maps can be quantified as the reduction in the number of voxels with a significant correlation. Second, in the event that we do find voxels with artificial correlations, it will serve as a benchmark test for the effectivity of the artifact removal method. If the method works, we would expect at least some of those correlations to disappear.

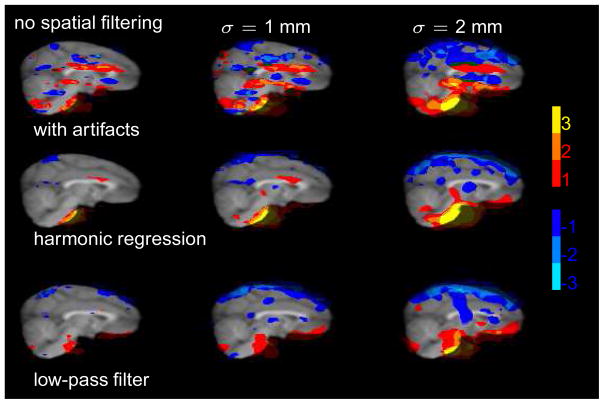
Figure 5 shows the results of the fcMRI analysis for the basilar artery seed. For the data with the artifacts (top row) we find a large number of voxels with significant positive or negative correlations to the seed region. These artificial correlations are most pronounced for moderate spatial filtering, but can also be observed for no or strong spatial filtering. A closer inspection reveals a very prominent spatial pattern which consists of alternating stripes of positive and negative correlations. The orientation of the stripes is parallel to the slice-orientation. We suggest that the pattern is due to differences in slice-time acquisition δ_t which amount to an average phase shift δ_φ of the cardiac cycle between two voxels in different slices. Because the artifact as a function of phase is similar for most voxels a₁(φ) ≃ a₂(φ), this shift determines the sign and magnitude of correlation ρ(a₁, a₂) between observed artifacts of two voxels in different slices, ρ (a₁, a₂) ≃ ρ (a₁(φ), a₁(φ + δ_φ)).

Fig. 5.

Functional connectivity of the basilar artery seed. The different columns correspond to different amounts of spatial smoothing. The color code displays the number of animals with significant positive (red to yellow) and negative (dark to light blue) correlations to the seed region. A large fraction of the artificial correlations (top row) is removed by both the harmonic regression technique and the low-pass filter. It is important to note that the low-pass filter method works only if the cyclic artifacts are aliased into the corresponding waveband as happened to be the case here. The alternating horizontal stripes of positive and negative correlation are most likely due to differences in slice-time acquisition.

The bulk of these artificial correlations disappears after removing the cyclic artifacts (middle row, see Table 1 for details). This is a clear indication that (1) cyclic artifacts may affect fcMRI maps and (2) that the harmonic regression algorithm clearly reduces the impact of the artifacts. The alternating stripes of positive and negative correlations which can be observed in the data set with the artifacts disappear almost completely. These findings suggest that after removal of the artifacts the fcMRI maps reflect random spurious correlations as would be expected from any statistical method.

Table 1.

Percent voxels with significant positive and negative correlation to the basilar artery seed region.

	monkey L	monkey P	monkey C
with artifacts	6.3/7.7 %	9.2/10.6 %	5.3/6.3 %
without artifacts	1.7/1.9 %	2.8/3.7 %	3.9/5.5 %
low-passed	2.0/1.6 %	9.4/2.8 %	3.7/4.3 %

In the current case, the artifacts are removed just as effectively by standard low-pass filtering (third row). It is important to note that the low-pass filtering works if and only if the artifacts happen to be aliased into the high frequency range. While this happened to be the case for the cardiac artifacts in the present case (see Figure 3), this is not the rule. As we show above, the cyclic artifacts may be aliased into any waveband (see Figure 4). In such a case, the low-pass method will be ineffective and render the same artificial fcMRI maps as the highpassed data (top row).

Example 2: resting state network

A recent study has reported a network of correlated brain areas in anesthetized macaques (Vincent et al., 2007). The described network consisted of 4 regions which showed strong similarity to the so called ’resting state’ or ’default’ network previously described for awake human subjects (Raichle et al., 2001; Fox et al., 2005; Damoiseaux et al., 2006): the posterior cingulate/precuneal cortex (pC/PCC), the dorsal medial prefrontal cortex (dmPFC), lateral temporoparietal cortex (lTPC) and posterior parahippocampal cortex (pPHip). It is noteworthy that all of these regions are close to major vessels (pC/PCC and dmPFC are near the anterior cerebral artery; lTPC is near the middle cerebral artery; pPHip near the posterior cerebral artery, see also Figure 6c). Thus, the resting state network is optimally suited to test whether correlated cardiac artifacts can affect fcMRI of a realistic seed region, i.e., the pC/PCC.

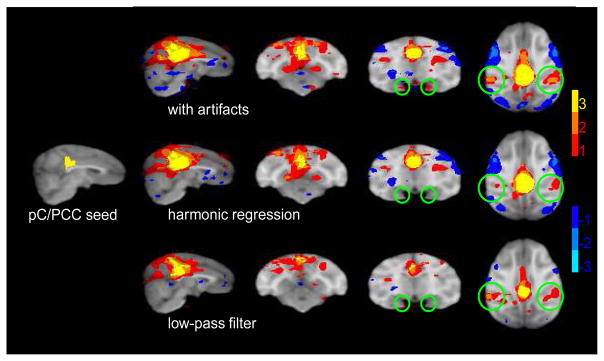
Fig. 6. ’Resting state’ network.

fcMRI maps for a seed in the posterior cingulate/precuneal cortex (leftmost panel). Conventions as in Figure 5. Regions with significant correlations were found in the lateral temporo-parietal cortex and posterior parahippocampal cortex (top row). In contrast to previous fcMRI studies, no correlations were found in the dorso-medial prefrontal cortex. The number of voxels with significant correlations in the lateral temporo-parietal cortex and the posterior parahippocampal cortex was reduced by the harmonic regression method (middle row) and to a lesser degree by the low-pass filtering (bottom row).

Using moderate spatial filtering (σ =1 mm) we found correlations in brain areas which partially resemble the ones described by Vincent et al. (2007). Significant positive correlations were found mainly in the lTPC (see Figure 6 top row). Significant positive correlations were less consistent in pPHip and completely absent in the dmPFC. Despite the differences, these results were sufficient to test whether the observed correlations in the lTPC were affected by cyclic artifacts. Indeed, after removal of the artifacts the number of voxels with positive correlations in lTPC and and pPHip was clearly reduced (Figure 6 middle row). This suggests that even for realistic seed-regions like the pC/PCC, fcRMI maps may be affected by cyclic artifacts.

As for the basilar artery seed, we expected the low-pass method to be just as effective in the current case. However, the low-passed data revealed the same pattern of positive correlations in lTPC as the highpassed data (Figure 6 bottom vs. top row). This seems to suggest that in this case the low-pass method was less effective at removing the cyclic artifacts. There is an alternative explanation for this finding: assume that there are two independent sources which give rise to the positive correlations in lTPC, one artificial source linked to the cyclic artifacts, and another source which probably reflects correlated neuronal activity. Removing the cyclic artifacts reduced the number of positive voxels by removing the artifacial source of correlation. The residual correlations of neuronal origin were lost because of uncorrelated noise. The low-pass filter removed not only the cyclic artifacts (which happened to be aliased to this waveband) but also a big amount of the uncorrelated noise. Hence, by removing both correlated and uncorrelated artifacts the correlations of putatively neuronal origin are now able to reach significance.

4 Discussion

Cardiac and respiratory artifacts were mapped in lightly anesthetized macaque monkeys. The artifacts were found to have a spatially and temporally nonuniform effect on BOLD signals. The spatial distribution of the artifacts was similar to that previously described for awake humans (Glover et al., 2000; Cordes et al., 2001; Lund et al., 2006; Harvey et al., 2008). The bulk of the cardiac artifacts were found close to major vessels. Respiratory artifacts were mainly found in regions with a high spatial derivative as found, for example, at the fringes of the brain, and could be explained by breathing-related (apparent) motion. Depending on the rate as well as the variability of the respiratory and cardiac cycle, the corresponding artifacts were aliased into a wide range of temporal wavebands (Biswal et al., 1996; Glover et al., 2000; Lund, 2001a; Lund et al., 2006). In cases where the artifacts are aliased to wavebands typically used for fcMRI (~10/20 - 400 s), they will have a profound impact on fcMRI maps if the seed region is affected by the artifacts. These findings complement studies showing that the removal of cyclic artifacts improves the quality of statistical inferences for standard fMRI GLM analyses (Harvey et al., 2008; Lund et al., 2006).

4.1 Necessary, sufficient and modulating conditions

Our results show that under certain conditions the removal of the cyclic cardiac and respiratory artifacts may have a profound impact on fcMRI. In the following we describe the factors that determine whether cyclic artifacts will cause artificial correlations.

Spatial restrictions

Two voxels may show artificial correlations only if both of them are affected by the artifact. Thus, if the seed region itself is not affected then the entire fcMRI map will not be affected. If the seed region is affected, there is a chance that other affected voxels may show artificial positive or negative correlations (see Figure 5 and 6).

Temporal restrictions

Our results and our simulations show that cardiac and respiratory artifacts can be aliased into a variety of different wavebands (see Figure 3 and 4; also refer to citations Biswal et al., 1996; Glover et al., 2000; Lund, 2001a; Lund et al., 2006). The aliased wavelength is determined by the TR and the cardiac/respiratory frequency. The artifacts will affect fcMRI only if they are aliased into the waveband used for fcMRI. Typical choices of TR and values of cardiac/respiratory frequency can easily lead to an aliasing into wavelengths from 10/20 to 400 s which are typically used for fcMRI. Thus, adequate temporal filtering may reduce the effects of artifacts in some cases, but it is not a reliable substitute for an algorithm that measures and removes the artifact.

Spatial smoothing

Due to differences in slice-time acquisition, the artifacts in different slices of a volume are sampled during different phases of the artifact. Such differences in acquisition time may introduce high spatial frequencies in the direction perpendicular to the slices. The presence of high spatial frequencies is determined by the mean difference in the phase of the artifacts for adjacent slices. If the difference is large i.e., close to π, the artifacts will have high spatial frequency content perpendicular to the slices. In such a case any kind of spatial smoothing will attenuate the artifacts. Spatial smoothing may occur explicitly as part of the standard preprocessing routine or implicitly during motion correction and registration. Another source of spatial smoothing comes from the averaging of activity of all voxels in the seed region. Thus, if the seed region spans several slices, averaging the activity may cancel out a considerable fraction of the artifact. However, even with explicit spatial smoothing, motion correction and a seed region spanning several slices, cardiac and respiratory artifacts still had a significant effect on our fcMRI maps (see Figures 5 and 6). Thus, spatial smoothing may reduce the effects of the artifacts sometimes, but they are no substitute for an actual artifact removal algorithm.

Slice acquisition time and slice orientation

If spatial and temporal restrictions for the presence of artifacts are met, fcMRI maps will be affected by the artifacts. The precise pattern of artificial correlations is determined by seemingly unrelated parameters such as slice-timing and slice orientation. The average difference in slice acquisition time between voxels in the seed region and the voxel in question will determine the sign and magnitude of the artificial correlations. The slice-orientation will determine the slice acquisition time between a voxel and the average voxel in the seed region. Taken together the two parameters determine the spatial pattern of the artificial correlation in affected brain regions (see top row in Figure 5)

4.2 Resting state network

We investigated the effects of cyclic artifacts on fcMRI of the PC/PCC, a well studied brain region which has been implicated to play an important role in the so called resting-state network. We found significant positive correlations in the lTPC as previously described for anesthetized macaque monkeys (Vincent et al., 2007). However, correlations in the pPHip and dmPFC were less reliable or completely absent. Comparing the results before and after removal of the artifacts we conclude that correlations in the lTPC and the pPHip may be overestimated if cyclic artifacts are not removed. However, our results are in line with the assumption that a significant part of the correlations between PC/PCC and lTPC were not caused by cyclic artifacts. This is in line with a previous study which showed that the correlations in the resting state network are not not due to changes in blood oxygenation caused by slow fluctuations in breathing rate or depth (Birn et al., 2006). In summary, our findings clearly outline the necessity to include sophisticated artifact removal algorithms such as RETROICOR into the standard fcMRI preprocessing pipeline even when using realistic seed regions which are only moderately affected by cyclic artifacts.

4.3 Comparison of artifact removal methods

Our data show that, as predicted by Lund (2001a), standard low-pass filtering does not adequately remove artificial correlations from fcMRI data. In the present paper we used harmonic regression to remove the cyclic cardiac and respiratory artifacts. A number of alternative methods with different advantages and requirements have been suggested in the literature (e.g., Hu et al., 1995; Biswal et al., 1996; Mitra et al., 1997; Josephs et al., 2001; Glover et al., 2000; Frank et al., 2001; Lund, 2001b; Thomas et al., 2002; Lund et al., 2006). A review of most of these methods is provided in Lund et al. (2006). It was beyond the scope of our study to systematically compare the effectivity of these methods. All of these methods have been shown to remove significant fractions of the artifacts. Our results suggest that either one of them will help reduce the number of false positive correlations.

5 Conclusions

Our results show that standard preprocessing steps which include spatial and temporal low-pass filtering are not sufficient to exclude artificial correlations in studies of functional connectivity, unless the TR is short enough to prevent aliasing. The precise spatial pattern of artificial correlations depends on the interaction of a number of factors such as TR, cardiac frequency, respiratory frequency, slice-timing and slice orientation. These intricate interactions may give rise to spatial patterns of artificial correlations which are hard to distinguish from patterns of neuronally driven correlations.