CHARACTERIZATION OF THE BINDING OF SULFONYLUREA DRUGS TO HSA BY HIGH-PERFORMANCE AFFINITY CHROMATOGRAPHY

Abstract

Sulfonylurea drugs are often prescribed as a treatment for type II diabetes to help lower blood sugar levels by stimulating insulin secretion. These drugs are believed to primarily bind in blood to human serum albumin (HSA). This study used high-performance affinity chromatography (HPAC) to examine the binding of sulfonylureas to HSA. Frontal analysis with an immobilized HSA column was used to determine the association equilibrium constants (K_a) and number of binding sites on HSA for the sulfonylurea drugs acetohexamide and tolbutamide. The results from frontal analysis indicated HSA had a group of relatively high affinity binding regions and weaker binding sites for each drug, with average K_a values of 1.3 (± 0.2) × 10⁵ M⁻¹ and 3.5 (± 3.0) × 10² M⁻¹ for acetohexamide and values of 8.7 (± 0.6) × 10⁴ and 8.1 (± 1.7) × 10³ M⁻¹ for tolbutamide. Zonal elution and competition studies with site-specific probes were used to further examine the relatively high affinity interactions of these drugs by looking directly at the interactions that were occurring at Sudlow sites I and II of HSA (i.e., the major drug binding sites on this protein). It was found that acetohexamide was able to bind at both Sudlow sites I and II, with K_a values of 1.3 (± 0.1) × 10⁵ and 4.3 (± 0.3) × 10⁴ M⁻¹, respectively, at 37°C. Tolbutamide also appeared to interact with both Sudlow sites I and II, with K_a values of 5.5 (± 0.2) × 10⁴ and 5.3 (± 0.2) × 10⁴ M⁻¹, respectively. The results provide a more quantitative picture of how these drugs bind with HSA and illustrate how HPAC and related tools can be used to examine relatively complex drug-protein interactions.

1. Introduction

Sulfonylureas are a group of drugs used to treat type II diabetes (i.e., adult onset or non-insulin dependent diabetes). These drugs stimulate acute insulin release from the beta cells of pancreatic islet tissue [1]. Tolbutamide and acetohexamide are two common “first-generation” sulfonylurea drugs (see Figure 1) [1–3]. These agents have been widely used since the introduction of tolbutamide in 1956 [2,4]. All sulfonylureas bind tightly to serum proteins, with human serum albumin (HSA) being the main protein that is believed to be involved in these interactions [2].

Figure 1.

Structures of acetohexamide and tolbutamide.

HSA is the most prevalent plasma protein [5,6]. This protein is composed of a single peptide chain and has a typical concentration in blood of 35–50 mg/ml (i.e., 0.6–0.7 mM) [5–9]. HSA is known to act as a transport protein that binds to a wide variety of compounds, including many drugs, hormones, bilirubin, and fatty acids [5–8]. In this role, HSA and its interactions with drugs can have a strong influence on the free concentrations of drugs in plasma [6,7,10] and the pharmacologic and pharmacokinetic properties of a drug [5–8,11]. For instance, this binding can affect drug adsorption, distribution, metabolism and excretion [5,12].

Previous studies have been conducted to investigate the binding of both acetohexamide [4,13–15] and tolbutamide [3,13–19] to HSA using equilibrium dialysis, dynamic dialysis, equilibrium gel filtration, fluorescence quenching, ultrafiltration, isothermal titration calorimetry, heteronuclear 2-D NMR, and reversed-phase liquid chromatography. However, the binding constants that have been obtained in these studies have ranged by almost ten-fold for both acetohexamide (i.e., 0.4 to 4.1 × 10⁵ M⁻¹) [4,15] and tolbutamide (0.4 to 3.0 × 10⁵ M⁻¹) [15–20]. It is also not yet apparent as to whether one or several major sites on HSA are involved in these interactions [4,16–18].

This current report will use the method of high-performance affinity chromatography (HPAC) to obtain more detailed information on the identity and strength of the binding sites on HSA for acetohexamide and tolbutamide. This method has previously been used to examine the binding of HSA to many other drugs and small solutes, such as coumarins [20–22], indoles [23], carbamazepine [20,24,25], ibuprofen and benzodiazepines [22,26]. Immobilized proteins used in HPAC have also been shown to give good qualitative and quantitative agreement with proteins in solution. For instance, the binding constants, displacement and allosteric interactions seen between various solutes on immobilized HSA columns have been shown in numerous studies to be good models for the behavior observed for soluble HSA (e.g., see review in Ref. [27] and references cited therein). The benefits of HPAC over traditional methods like ultrafiltration and equilibrium dialysis include its use of smaller amounts of sample, its speed, its better reproducibility and precision, and its ease of automation [27–29].

The combined use of HPAC with frontal analysis (i.e., frontal affinity chromatography) and immobilized HSA columns will first be used in this study to estimate the total number of binding sites and association equilibrium constants of acetohexamide and tolbutamide with HSA. Zonal elution and competition with site-selective probe compounds for HSA will then be used to examine the binding of these two sulfonylurea drugs at the major binding regions for drugs on this protein (i.e., Sudlow site I and II) [30,31]. The results will be compared to previous observations made in the literature and should provide a more complete picture of how these drugs bind with HSA and are transported by this protein in the circulation. This work will also be used to illustrate how HPAC and several tools available in this method (e.g., equations for examining multi-site interactions or allosteric effects) [26] can be utilized to examine relatively complex drug-protein interactions.

2. Theory

2.1 Frontal analysis

In these studies, frontal analysis was used to estimate the association equilibrium constants (K_a) and the number of binding sites of this drug with HSA by using HPAC and columns that contained immobilized HSA. This was done by measuring the binding capacity of this column (m_L) as the concentration of acetohexamide that was applied to the column was varied. Some typical breakthrough curves that were obtained in these experiments are shown in Figure 2. If fast association/dissociation kinetics are present for the binding of the applied analyte with the immobilize protein (i.e., as is typically present during drug-HSA interactions), the central position of the resulting breakthrough curve can be related to K_a, m_L, and the applied concentration of the analyte [A] [27,28]. For an analyte that binds to only a single type of site within the column, the following equations can be used to describe this relationship [24,27].

$$\frac{1}{m_{\mathit{\text{Lapp}}}}=\frac{1}{(K_a{m}_L[\mathrm{A}])}+\frac{1}{m_L}$$ (1)

or

$$m_{\mathit{\text{Lapp}}}=\frac{m_L{K}_a[\mathrm{A}]}{(1+K_a[\mathrm{A}])}$$ (2)

In these equations, m_Lapp is the apparent moles of analyte required to saturate the column at a particular concentration. Eqn. (1) indicates for a system with a single type of binding site that a plot of 1/m_Lapp versus 1/[A] should provide a linear relationship from which the values of K_a and m_L can be determined from the slope and intercept. If multi-site binding is present, such a plot should approach a linear response at low concentrations (i.e., high values for 1/[A]) and give a curved response and negative deviations at high analyte concentrations (i.e., low values for 1/[A]), as illustrated in Figure 3.

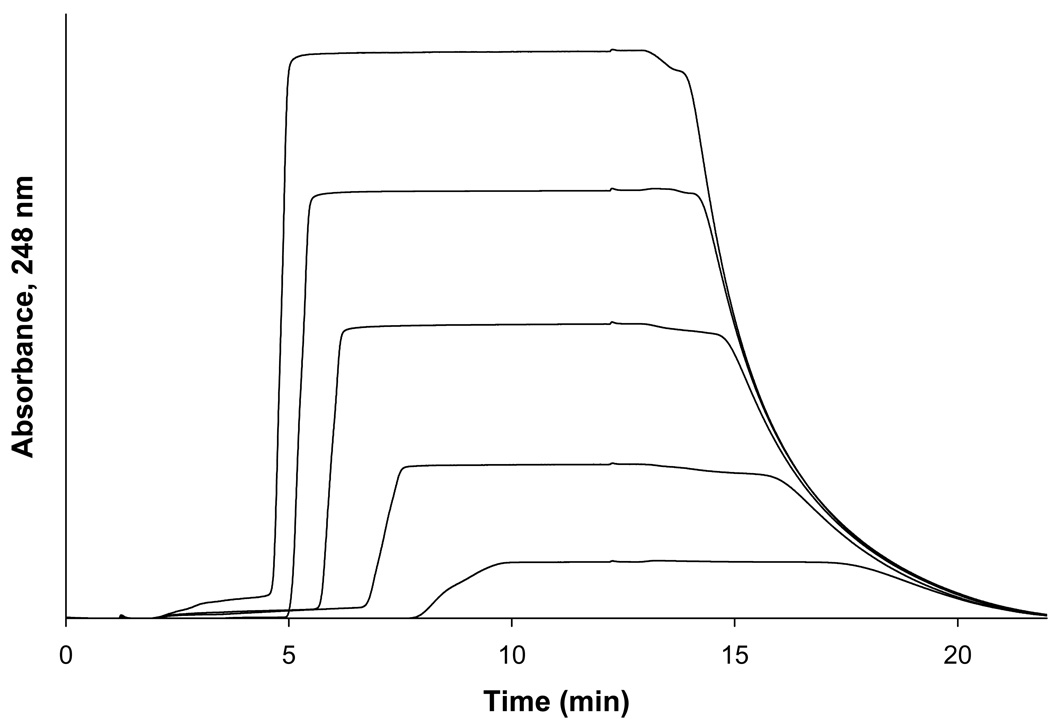
Figure 2.

Breakthrough curves for acetohexamide on an immobilized HSA column at applied concentrations (from left to right) of 10, 7.5, 5, 2.5, and 1 µM. Alternative detection wavelengths were used for some of the higher concentrations of analyte solutions to maintain a linear response in absorbance versus concentration during these studies, as described in the Experimental Section. Other conditions are given in the text.

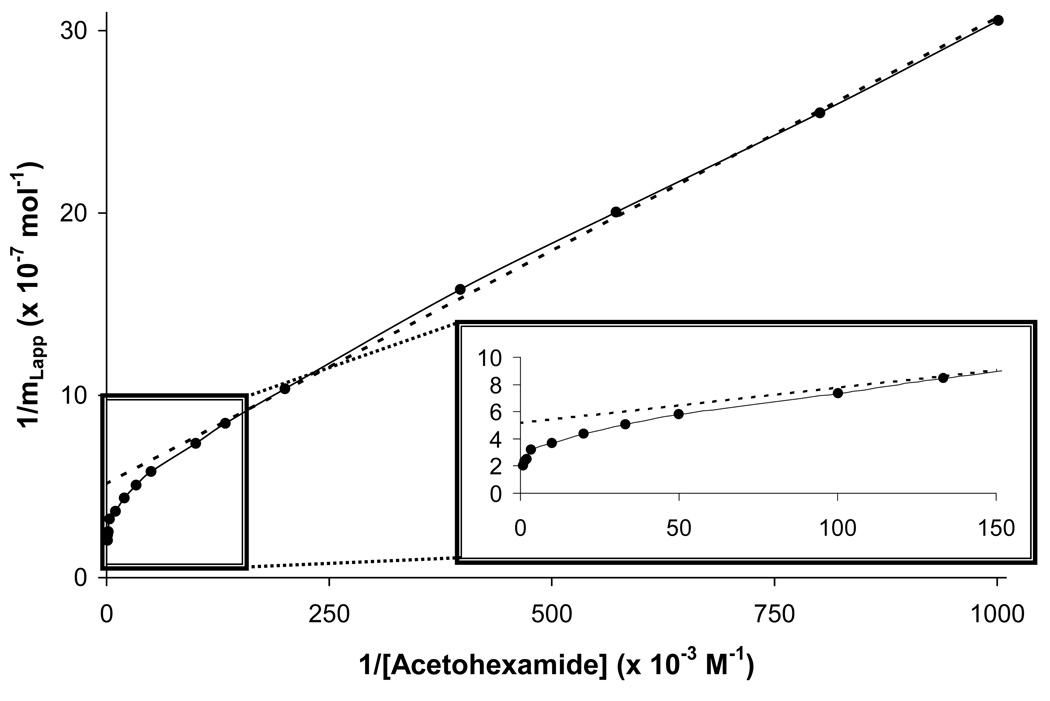
Figure 3.

A double-reciprocal plot for frontal analysis studies examining the binding of acetohexamide to an immobilized HSA column. When comparing this response to the linear relationship that is predicted by Eqn. (1), it was apparent that negative deviations occurred at high analyte concentrations (i.e., low values of 1/[A]), indicating that multiple binding regions for acetohexamide were present. The dashed line shows the linear response that was obtained for the data at relatively low analyte concentrations (i.e., high 1/[A] values), which can still be used in such a case to estimate the association equilibrium constant for the highest affinity binding sites in such a system.

In the case of multi-site binding, Eqn. (1) can be expanded to allow for more than one class of binding sites. For example, a system containing two binding sites would have the following relationship [24,27],

$$\frac{1}{m_{\mathit{\text{Lapp}}}}=\frac{1+K_{a1}[\mathrm{A}]+{\beta }_2{K}_{a1}[\mathrm{A}]+{\beta }_2{K}_{a1}^2{[\mathrm{A}]}^2}{m_{\mathit{\text{Ltot}}}\{({\alpha }_1+{\beta }_2-{\alpha }_1{\beta }_2)K_{a1}[\mathrm{A}]+{\beta }_2{K}_{a1}^2{[\mathrm{A}]}^2\}}$$ (3)

where K_a1 is the association equilibrium constant for the binding site with the highest affinity (L₁) and α₁ is the fraction of all binding regions that make up the high affinity binding sites (i.e., α₁ = m_L1,tot/m_Ltot). The term β₂ is the ratio of the association equilibrium constants for any lower affinity site (e.g., K_a2) versus the highest affinity site, where β₂ = K_a2/K_a1 and 0 < K_a2 < K_a1. Eqn. (3) can also be written in a non-reciprocal form, as given below [24,27].

$$m_{\mathit{\text{Lapp}}}=\frac{m_{L1}{K}_{a1}[\mathrm{A}]}{(1+K_{a1}[\mathrm{A}])}+\frac{m_{L2}{K}_{a2}[\mathrm{A}]}{(1+K_{a2}[\mathrm{A}])}$$ (4)

Using this latter equation (i.e., which represents a bi-Langmuir binding model) it is possible to find both K_a and m_L values for an analyte by plotting m_Lapp versus [A], from which the values of the individual association equilibrium constants and binding capacities for each site can be obtained by non-linear regression, as illustrated in Figure 4. Although Eqn. (3) would be expected to produce a non-linear response throughout a broad range of concentrations, it is known at low analyte concentrations that a linear response can still be observed even for a system with multi-site binding, as demonstrated by the following equation [32].

$$\underset{[\mathrm{A}]\to 0}{\text{lim}}\frac{1}{m_{\mathit{\text{Lapp}}}}=\frac{1}{m_{\mathit{\text{Ltot}}}({\alpha }_1+{\beta }_2-{\alpha }_1{\beta }_2)K_{a1}[\mathrm{A}]}+\frac{{\alpha }_1+{{\beta }_2}^2-{\alpha }_1{{\beta }_2}^2}{m_{\mathit{\text{Ltot}}}{({\alpha }_1+{\beta }_2-{\alpha }_1{\beta }_2)}^2}$$ (5)

Eqn. (5) indicates that a linear relationship will be approached even for a multi-site system for a plot of 1/m_Lapp versus. 1/[A] at low analyte concentrations, or high values for 1/[A]. The values of m_Ltot and K_a1 in this relationship will now be a function of the relative amount of each type of binding site in the column and their relative affinities for the analyte, as described by the terms α₁ and β₂ in the Eqn. (5). However, it has also been shown in previous theoretical studies that the ratio of the intercept versus slope for this plot can still be used to provide a good estimate of K_a1 (i.e., the association equilibrium constant for the highest affinity sites) [32].

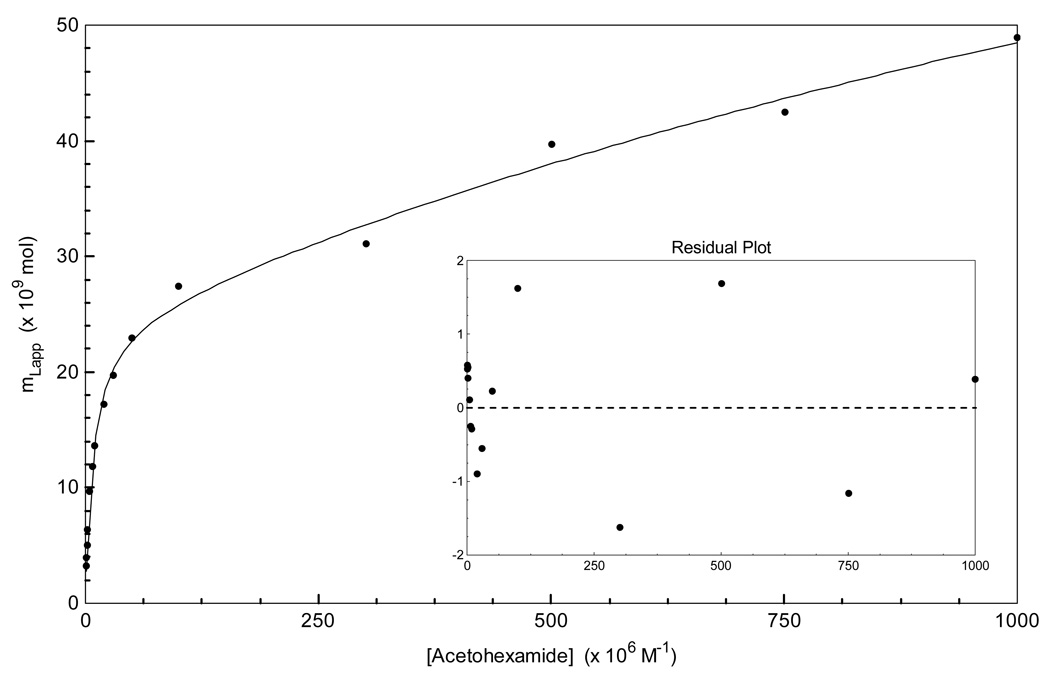
Figure 4.

Non-linear regression of the acetohexamide frontal analysis data using a two-site binding model, as described by Eqn. (4). The data used in this plot were the same as utilized for the double-reciprocal plot in Figure 3.

2.2 Zonal elution

Competition studies using zonal elution were performed to determine the specific binding regions on HSA that were interacting with each of these tested drugs. In this technique a mobile phase containing a known concentration of competing agent ([I]) was applied to the column while a small plug of analyte was injected onto the column (see Figure 5). The retention time for the analyte was then measured and used to calculate the retention factor (k), where k = (t_R – t_M)/t_M, t_R is the retention time of the injected solute’s peak, and t_M is the retention time of a non-retained solute (e.g., sodium nitrate). The results are examined by making a plot of 1/k versus [I]. The following equation predicts that such a plot will give a linear response if A and I compete at a single type of site on the immobilized protein and I has no other types of binding sites with the column [27,28].

$$\frac{1}{k}=\frac{K_{\mathit{\text{aI}}}{V}_M[\mathrm{I}]}{K_{\mathit{\text{aA}}}{m}_L}+\frac{V_M}{K_{\mathit{\text{aA}}}{m}_L}$$ (6)

In this equation, K_aA and K_aI are the association equilibrium constants for the analyte and the competing agent, respectively, at their site of competition and V_M is the void volume. According to Eqn. (6), if a plot of 1/k versus [I] is linear, the association equilibrium constant for I at the site of competition can then be calculated from the ratio of the slope versus the intercept of this plot. This is a useful tool in that it can allow information to be obtained on site-selective interactions and local association equilibrium constants for analytes that may have multiple binding sites to an immobilized ligand [27].

Figure 5.

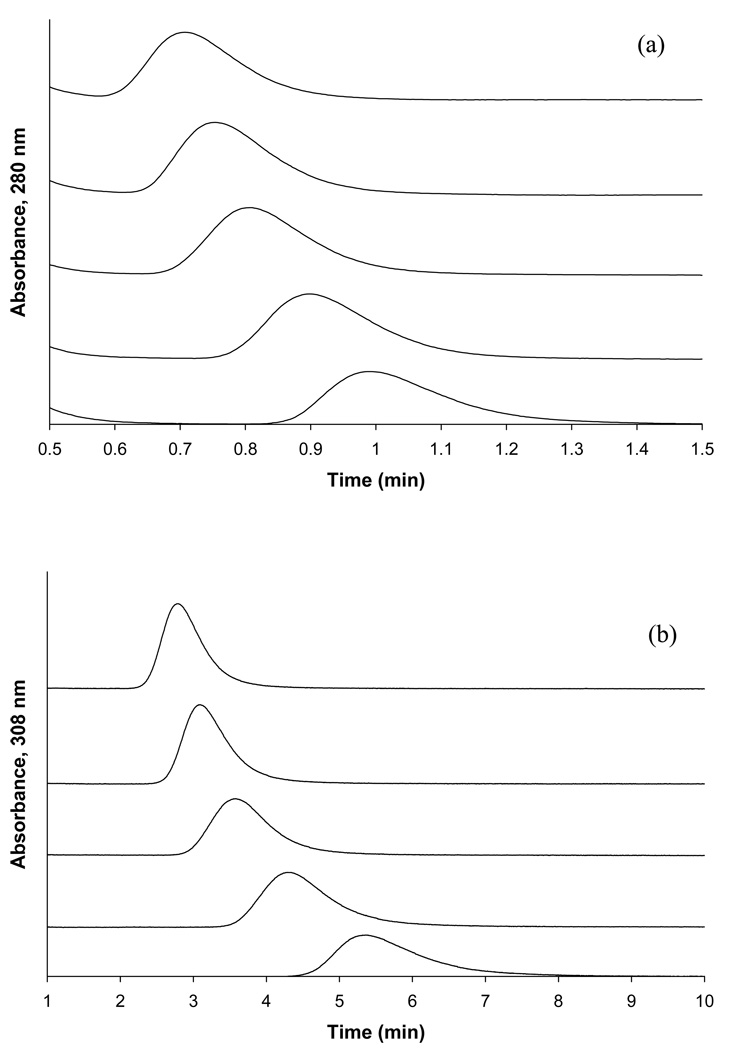
Competition studies based on zonal elution for the injection of (a) L-tryptophan or (b) R-warfarin as site-selective probes onto HSA columns and in the presence of various concentrations of tolbutamide in the mobile phase. The concentration of tolbutamide in these examples (from left to right) was 20, 15, 10, 5, or 1 µM. The injected concentration of each probe, L-tryptophan and R-warfarin, was 5 µM and the injection volume was 20 µL. Other conditions are given in the text.

Deviations from linearity in a plot made according to Eqn. (6) can occur if competition occurs between A and I at multiple binding sites, as is demonstrated in Eqn. (7) for a two-site system [33].

$$\frac{1}{k}=\frac{V_m(1+K_{\mathrm{I}1}[\mathrm{I}]+{\gamma }_2{K}_{\mathrm{I}1}[\mathrm{I}]+{\gamma }_2{K_{\mathrm{I}}}^2{[\mathrm{I}]}^2}{m_{\mathit{\text{Ltot}}}{K}_{a1}\{({\alpha }_1+{\beta }_2-{\alpha }_1{\beta }_2)+K_{\mathrm{I}1}[\mathrm{I}]({\gamma }_2{\alpha }_1+{\beta }_2-{\alpha }_1{\beta }_2)\}}$$ (7)

In this relationship, K_a1 is the association equilibrium constant for the injected analyte binding to the highest affinity site of the ligand and K_I1 is the association equilibrium constant for the competing agent at that site. The terms α₁ again represents the fraction of active sites in the column that is due to the high affinity binding sites, and β₂ is again the ratio of the association equilibrium constant for the lower affinity site vs. the highest affinity region (β₂ = K_a2/K_a1). The term γ₂ in this equation is similar to β₂ but now represents the ratio of the association equilibrium constant for the competing agent at the site with the lower affinity for the injected analyte vs. the highest affinity for the injected analyte (γ₂ = K_I2/K_I1). At reasonably high values of [I], the response of Eqn. (7) will approach a linear relationship, which is described by Eqn. (8).

$$\underset{[I]\to \infty }{\text{lim}}\frac{1}{k}=\frac{V_m{K}_{I1}[I]{\gamma }_2}{m_{\mathit{\text{Ltot}}}{K}_{a1}({\gamma }_2{\alpha }_1+{\beta }_2-{\alpha }_1{\beta }_2)}+\frac{V_m({\beta }_2+{\alpha }_1{\gamma }_2^2-{\alpha }_1{\beta }_2)}{m_{\mathit{\text{Ltot}}}{K}_{a1}{({\gamma }_2{\alpha }_1+{\beta }_2-{\alpha }_1{\beta }_2)}^2}$$ (8)

In this relationship, the slope and intercept are now a function of the relative amount and affinity of each binding site (as described by the terms α₁, β₂, and γ₂) as well as the values for V_m, K_a1 and m_Ltot. However, it has been demonstrated in theoretical studies that the use of the slope versus intercept ratio from this linear region can still be used to provide a reasonable estimate of K_I1 in a system with multisite interactions [33].

Another possible source for deviations from linearity in a plot made according to Eqn. (6) is if some allosteric effects are present during the binding of A and I to an immobilized ligand [27]. The previous equation has been developed to describe such an interaction when A and I bind to two separate, but allosterically-linked sites when a trace amount of A is injected into a mobile phase containing a fixed concentration of I [34].

$$\frac{k_0}{k-k_0}=\frac{1}{{\beta }_{I\to A}-1}\times \left(\frac{1}{K_{\mathit{\text{IL}}}[\mathrm{I}]}+1\right)$$ (9)

In this equation, k is retention factor observed for the injected analyte A, [I] is the mobile phase concentration of I, and K_IL is the association equilibrium constant for the binding of I to the immobilized ligand L. Other terms in this equation include k₀, which is the retention factor for A in the absence of any competing agent, and β_I→A, which is the coupling constant for the allosteric interaction, as given by β_I→A= K_aL,/K_aL (where K_aL is the initial association equilibrium constant for A with L, and K_aL’ is the association equilibrium constant for A with I after I has been bound to L, also resulting in a change in the binding of A to L). Eqn. (9) predicts that a plot of k₀/(k – k₀) will give a linear relationship for a simple allosteric interaction, where the intercept is equal to 1/(β_I→A − 1) and the slope is 1/[(β_I→A − 1) K_IL]. From the slope and intercept it is possible to determine the values of β_I→A and K_IL. A value of β_I→A>1 will occur if positive allosteric effects are present between I and A and a value of 0 < β_I→A< 1 will occur if negative allosteric effects are taking place. If β_I→A is equal to zero, then direct competition is taking place between I and A, while a value of one for β_I→A indicates that there is no effect of I on A as these agents bind to L.

3. Experimental

3.1 Reagents

The acetohexamide, tolbutamide (≥ 99.9 %), warfarin (≥ 97%), and L-tryptophan (98%) were purchased from Sigma-Aldrich (St. Louis, MO, USA). The buffer salts and HSA (essentially fatty acid free, ≥ 96%) were also obtained from Sigma-Aldrich. The pH 7.00 and pH 10.00 buffers used for pH meter calibration were purchased from Fisher Scientific (Pittsburg, PA, USA). The Nucleosil Si-300 (7 micron particle diameter, 300 Å pore size) was from Macherey-Nagel (Düren, Germany). Reagents used in the bicinchoninic acid (BCA) protein assay were from Pierce (Rockford, IL, USA). All solutions were made using water obtained from a NANOpure system (Barnstead, Dubuque, IA, USA). Prior to use, all aqueous solutions were filtered through a 0.20 µm GNWP nylon membrane from Millipore (Billerica, MA, USA).

3.2 Apparatus

The chromatographic system consisted of a DG-2080-53 three-solvent degasser, two PU-2080 isocratic HPLC pumps, a UV-2075 absorbance detector, and a AS-2055 autosampler (Jasco, Tokyo, Japan), along with a Rheodyne Advantage PF 6-port valve (Cotati, CA, USA). A Jasco CO-2060 column oven was used to control the column temperature. All of the chromatographic components were controlled through EZChrom Elite software v3.2.1 (Scientific Software, Inc., Pleasanton, CA, USA) via Jasco LC Net hardware. In-house programs written in Labview 5.1 (National Instruments, Austin, TX, USA) were used to determine the analyte breakthrough times in the frontal analysis experiments. PeakFit 4.12 (Jandel Scientific Software, San Rafael, CA, USA) was used to determine the peak central moments in the zonal elution studies.

3.3 Methods

Nucleosil Si-300 silica was modified to produce diol silica by using a previously-published procedure [35]. This diol silica was then used to immobilize HSA by the Schiff base method, also according to previous methods [21,36]. A control support was made in the same manner without any added HSA. A small amount of the HSA immobilized support and the control support was dried overnight in a vacuum oven, and a bicinchoninic acid (BCA) assay was used to determine the final protein content of this material. This assay was performed in triplicate using soluble HSA as the standard and the control support as the blank. The amount of immobilized HSA was estimated to be 38 (± 3) mg/g silica, or approximately 600 (± 30) nmol HSA/g silica. Separate 2.0 cm × 2.1 mm ID stainless steel columns containing either the HSA silica or the control support were downward slurry packed with the silica at 3000 psi (20.7 MPa) using pH 7.4, 0.067 M potassium phosphate buffer as the packing solution. These columns were stored in pH 7.4, 0.067 M potassium phosphate buffer at 4 °C when not in use. Experiments were performed over a period of eleven months and over the course of less than 500 sample applications or injections; similar HSA columns have been shown to maintain good stability in drug binding studies under these conditions [37].

All aqueous solutions of samples and competing agents were prepared using pH 7.4, 0.067 M potassium phosphate buffer to mimic physiological conditions in serum. The pH of this buffer was set and adjusted to within 0.01 pH units by using a pH meter calibrated with pH 7.00 and 10.00 standard buffers. This pH was found to vary by less than 0.05 units over the course of several months under the experimental conditions used in this study. The pH 7.4, 0.067 M phosphate buffer was also used as the application and regeneration buffer during the frontal analysis and zonal elution studies (note: no elution buffer was needed in this work because the drugs and competing agents that were applied to the HSA columns could later be eluted under isocratic conditions by this same buffer). All solutions were filtered through a 0.2 µm nylon filter and degassed under vacuum for at least 15 min prior to use. A flow rate of 0.5 ml/min was used throughout this work for sample application and injection. This flow rate has been shown in previous work to obtain reproducible binding capacities and retention factors for other drugs or small solutes on similar HSA columns [38]. During frontal analysis, the application of either the pH 7.4, 0.067 M phosphate buffer or the desired drug solution was made by alternating between these solutions through the use of a six-port valve. The application of samples in the zonal elution experiments was controlled through the autosampler and was carried out by using an injection volume of 20 µL. Three to four repetitions were performed per sample concentration.

Frontal analysis studies were performed by first equilibrating the HSA column in the presence of pH 7.4, 0.067 M potassium phosphate buffer at 37 °C. A switch was then made from this buffer to the same buffer that also contained a known concentration of the analyte of interest, which included fifteen concentrations of acetohexamide ranging from 1 to 1000 µM, and nine concentrations of tolbutamide ranging from 1 to 200 µM (Note: although sulfonylureas are weak acids with pK_a values in the range of 5.2–6.2, less than a 0.05 pH change in the pH 7.4 buffer was seen for even the highest concentrations of acetohexamide and tolbutamide that were examined in this study). Once the analyte had saturated the column and created a breakthrough curve, the system was switched back to applying only the pH 7.4 buffer to elute the retained analyte from the column. Elution of the analyte was monitored using a UV/Vis detector, with the wavelength of detection being adjusted at high concentrations to ensure that a linear change in signal with concentration was always present. Acetohexamide was monitored at 248 nm for applied concentrations of 1–20 µM and at 315 nm for concentrations of 30–1000 µM. Tolbutamide was monitored at 250 nm for all of its applied concentrations. These runs were performed in triplicate on both the HSA column and the control column. Breakthrough times were determined using the equal area method [27] and were corrected for non-specific binding to the support by subtracting the values for the control column for those measured on the HSA column at each given concentration of the analyte (e.g., interactions with the support made up 33% of the total binding noted for 1 µM tolbutamide and 21% for 1 µM acetohexamide on the HSA columns, but a correction for these non-specific interactions could be effectively made in this manner, as demonstrated for other analytes in previous studies with HSA columns) [20–22]. The resulting data were analyzed according to various binding models, as described in Section 4. Linear regression was performed using Microsoft Excel 2003 (Microsoft Corporation, Redmond, WA, USA). Non-linear regression was carried out using DataFit 8.1.69 (Oakdale Engineering, PA, USA).

The competitive binding, zonal elution studies were performed using R-warfarin and L-tryptophan as the injected agents. These compounds have been shown in the past to bind to Sudlow sites I and II, respectively, and are often used as probes in drug-binding studies [30,31]. Due to the limited stability of L-tryptophan in aqueous solution (e.g., due to oxidation), all L-tryptophan solutions were made fresh daily. Such solutions have been shown to be sufficiently stable under such conditions for use in binding studies in HPAC (i.e., a reported usable lifetime of 2 days at 25°C under normal laboratory lighting or 9 days in the dark at 4°C) [23]. Injections of 20 µL 5 µM R-warfarin or L-tryptophan were made onto a column equilibrated with a mobile phase that contained a known concentration of the drug of interest. The solute concentration of 5 µM that was used in this work has been in found in previous experiments to provide linear elution conditions on HSA columns similar to those used in this study [23,39]. The analyte in the mobile phase (acetohexamide or tolbutamide) was applied at concentrations that ranged from 0 to 20 µM. These studies were performed at 37 °C on both the HSA and control columns. A pH 7.4, 0.067 M potassium phosphate buffer was used as the mobile phase and to prepare all solutions of the injected analytes and competing agents. The elution of R-warfarin and L-tryptophan was monitored at 308 and 280 nm, respectively. The central moments of the resulting peaks were determined by using PeakFit v.4.12 and an exponentially-modified Gaussian curve fit. The resulting values were used along with the measured void time of the system, as determined by injecting 20 µL of 20 µM sodium nitrate (i.e., a non-retained solute on HSA columns), to obtain the retention factors for each probe compound. Sodium nitrate was monitored at 205 nm.

4. Results and Discussion

4.1 Frontal analysis studies using acetohexamide

From the breakthrough curves that were obtained for acetohexamide (see examples in Figure 2), double-reciprocal plots were first made of 1/m_Lapp versus 1/[A] and compared to the responses predicted by Eqns. (1) and (3). Some curvature was noted at high analyte concentrations (i.e., low values for 1/[A]), indicating that more than one type of binding site was present for acetohexamide on HSA (Figure 3). In addition, a linear response was approached at high values of 1/[A], as predicted by Eqn. (5). By using the best-fit line to the linear region of this data set (as occurred at 1–10 µM acetohexamide, n = 7), an estimate of 2.0 (± 0.1) × 10⁵ M⁻¹ was obtained for the association equilibrium constant for the highest affinity sites (K_a1) in this system with an m_L value of 1.9 (± 0.1) × 10⁻⁸ mol.

The frontal analysis data for acetohexamide were also examined by using a non-reciprocal plot. Figure 4 shows the results that were obtained when these results were compared to the best-fit response predicted by Eqn. (4) for a two-site binding model. Using a two-site model, acetohexamide was found to have a relative high affinity group of sites with an average K_a of 1.3 (± 0.2) × 10⁵, as well as a group of low affinity sites with an average K_a of 3.5 (± 2.9) × 10² M⁻¹. The corresponding best-fit values of m_L for these sites were 2.4 (± 0.1) × 10⁻⁸ and 9.3 (± 5.5) × 10⁻⁸ mol, respectively. The result for the high-affinity binding site in this two-site model showed good agreement with the estimate of K_a made for the high affinity site using the linear region of Figure 3 when this previous plot was examined according to Eqn. (5).

For the sake of comparison, the acetohexamide data in the non-linear plot given in Figure 4 were also analyzed directly according to a one-site binding model. As expected for the results in Figures 3 and 4, the two-site model gave a higher correlation coefficient versus the one-site model (i.e., r = 0.998 versus 0.964 for n = 15) and a smaller sum of the square of the residuals (i.e., 1.2 × 10⁻¹⁷ versus 2.2 × 10⁻¹⁶). In addition, a residual plot that was prepared for the fit of these data to a two-site model appeared to give only random variations about the predicted best-fit response, while the residuals for the one-site fit followed a non-random pattern. All of these results indicated that acetohexamide was binding to HSA through at least two general groups of sites: a set of high affinity regions and a set of low affinity regions. This conclusion fits with the fact that many sulfonylurea drugs are known to bind to more than one binding site on HSA and bovine serum albumin (BSA) (e.g., as noted when using equilibrium dialysis methods to examine the binding of acetohexamide) [4,40]. This overall result also gave good agreement with previous ultrafiltration studies performed at pH 7.4 and 37°C with soluble HSA, which identified a general group of high affinity sites on HSA for acetohexamide (K_a1 = 5.9 (± 1.9) × 10⁴ M⁻¹) and a group of lower affinity sites (K_a2 = 3.4 (± 3.3) × 10³ M⁻¹) [41].

A comparison of the measured binding capacities with the known protein content of the column, 1.78 (± 0.09) × 10⁻⁸ mol HSA, indicated that each of the two groups of binding sites actually involved more then one region of interaction for acetohexamide with HSA. For example, the best-fit value of m_L for the high affinity sites represented a relative activity of 1.35 (± 0.08) mol acetohexamide/HSA, which suggested that at least two regions contributed to this group of interactions (e.g., this might correspond to two sites each with relative activities of 0.55–0.8, as is often seen with HSA columns) [41]. In the same manner, the weak affinity sites had a binding capacity that gave a relative activity of 5.2 (± 3.1) mol/mol HSA, a result which was similar to results that have been obtained when examining the non-specific binding regions for other drugs with this protein [41].

Based on the binding capacity data, an attempt was made to re-examine the frontal analysis data to test the fit of an expanded form of Eqns. (1) and (4) to a three-site (tri-langmuir) binding model to see if any distinction could be made between multiple high affinity sites. At first glance, this three-site model appeared to give a reasonable fit to the data. The correlation coefficient (r = 0.998) was comparable to that of the two-site model and the sum of the square of the residuals was slightly smaller (i.e., 9.2 × 10⁻¹⁸ versus 1.2 × 10⁻¹⁷). However, the best-fit parameters for the three-site model had high levels of uncertainty associated with them (see Table 1). This greater uncertainty indicated that, if more than one type of high affinity sites were present, the difference in the binding parameters for these sites could not be reliably determined by using the frontal analysis results alone.

Table 1.

Binding parameters obtained by frontal analysis for acetohexamide with HSA^a

	One-Site Model	Two-Site Model	Three-Site Model
Ka1 (M−1)	2.0 (± 0.1) × 105,b	1.3 (± 0.2) × 105	3.6 (± 5.9) × 105
mL1 (mol)	1.9 (± 0.1) × 10−8,b	2.4 (± 0.1) × 10−8	9.0 (± 15.4) × 10−8
Ka2 (M−1)		3.5 (± 3.0) × 102	4.9 (± 6.5) × 104
mL2 (mol)		9.3 (± 5.5) × 10−8	1.9 (± 1.3) × 10−8
Ka3 (M−1)			4 (± 39) × 101
mL3 (mol)			5 (± 44) × 10−7
Correlation coefficient	0.964c	0.998	0.998
Sum of residuals squared	2.2 × 10−16,c	1.2 × 10−17	9.2 × 10−18

^aAll of these parameters are for data obtained at pH 7.4 and 37 °C. The values in parentheses represent a range of ± 1 S.D (n = 15), as based on regression using Excel and the linear region of a plot made according to Eqn. (1) for a single-site model or the standard error as calculated by DataFit for a fit made according Eqn. (4) for a two-site or a similar expanded expression for a three-site model.

^bThe K_a1 and m_L1 values given for the one-site model were estimated from the linear region of a plot made according to Eqns. (1) or (5).

^cThe correlation coefficient and sum of residuals squared given for the one-site model are for a fit of the entire data set to Eqn. (2).

4.2 Frontal analysis studies using tolbutamide

Frontal analysis studies with tolbutamide were conducted in the same fashion as the work described for acetohexamide in Section 4.1 to estimate the total the number of binding sites and affinities of this drug with HSA. When these tolbutamide results were examined according to a double-reciprocal plot, deviations at high analyte concentrations (or low values of 1/[A]) were again seen, indicating that multiple binding sites were present (data not shown). When the linear region of this plot was analyzed according to Eqn. (5), the estimate obtained for K_a of the high affinity sites was 8.2 (± 0.4) × 10⁴ M⁻¹ with a corresponding m_L value of 2.4 (± 0.1) × 10⁻⁸ mol (r = 0.999, n = 6).

These data were next examined by using non-reciprocal plots and fits to both one-site and two-site models according to Eqns. (2) and (4). Using a single-site model, this type of regression gave a K_a value of 4.7 (± 0.4) × 10⁴ M⁻¹ and an m_L of 3.2 (± 0.1) × 10⁻⁸ mol. Fitting the data to a two-site model, tolbutamide had a K_a value for its major binding site of 8.7 (± 0.6) × 10⁴ M⁻¹ and a value of 8.1 (± 1.8) × 10³ M⁻¹ for the second set of binding sites; the corresponding m_L values for tolbutamide at these sites were 2.0 (± 0.1) × 10⁻⁸ and 1.8 (± 0.1) × 10⁻⁸ mol, respectively. This model gave a correlation coefficient of 0.999 with randomly distributed residuals and a sum of the square of the residuals of 4.3 × 10⁻²⁰, (versus values of r = 0.998 and 3.9 × 10⁻¹⁸ for the fit of the one-site model). The K_a estimated for the high affinity binding site when using either model were within the range of 0.4 to 3.0 × 10⁵ M⁻¹ that has been reported in the literature for this interaction [15–20].

The binding capacities estimated for these sites were compared to the protein content of the HSA column. A relative activity of 1.12 (± 0.08) mol tolbutamide/mol HSA was calculated for the higher affinity binding sites. Given the fact that not all of the binding sites on HSA are probably active [41], this last result suggested but was not conclusive evidence that more than one group of binding sites was involved in these particular interactions (Note: the presence of multiple binding sites in this case will be examined further in Section 4.4). The lower affinity regions gave a relative activity of 1.01 (± 0.08) mol tolbutamide/mol HSA. This latter result indicated that only a few regions on HSA were taking part in these weaker interactions.

The use of a three-site model was also attempted for tolbutamide but gave results similar to those for acetohexamide. The sum of the square of the residuals decreased slightly in going from the two-site to three-site model (i.e., decreasing from 4.3 × 10⁻²⁰ to 2.9 × 10⁻²⁰), but the correlation coefficient of 0.999 was comparable to that found for the two-site binding model (see Table 2). The variations in many of these parameters were again quite large, which indicated that if more than two groups of sites were present they could not be differentiated with just the frontal analysis data.

Table 2.

Binding parameters obtained by frontal analysis for tolbutamide with HSA^a

	One-Site Model	Two-Site Model	Three-Site Model
Ka1 (M−1)	8.2 (± 0.4) ×104,b	8.7 (± 0.6) × 104	1.1 (± 0.9) × 105
mL1 (mol)	2.4 (± 0.1) × 10−8,b	2.0 (± 0.1) × 10−8	1.3 (± 2.0) × 10−8
Ka2 (M−1)		8.1 (± 1.7) × 103	2.6 (± 6.5) × 104
mL2 (mol)		1.8 (± 0.1) × 10−8	1.7 (± 0.6) × 10−8
Ka3 (M−1)			5 (± 149) × 102
mL3 (mol)			4 (± 97) × 10−8
Correlation Coefficient	0.998c	0.999	0.999
Sum of residuals squared	3.9 × 10−18,c	4.3 × 10−20	2.9 × 10−20

^aAll of these parameters are for data obtained at pH 7.4 and 37 °C. The values in parentheses represent a range of ± 1 S.D (n = 9), as based on regression using Excel and the linear region of a plot made according to Eqn. (1) for a single-site model or the standard error as calculated by DataFit for a fit made according Eqn. (4) for a two-site or a similar expanded expression for a three-site model.

^bThe K_a1 and m_L1 values given for the one-site model were estimated from the linear region of a plot made according to Eqns. (1) or (5).

^cThe correlation coefficient and sum of residuals squared given for the one-site model are for a fit of the entire data set to Eqn. (2).

4.3 Zonal elution studies using acetohexamide

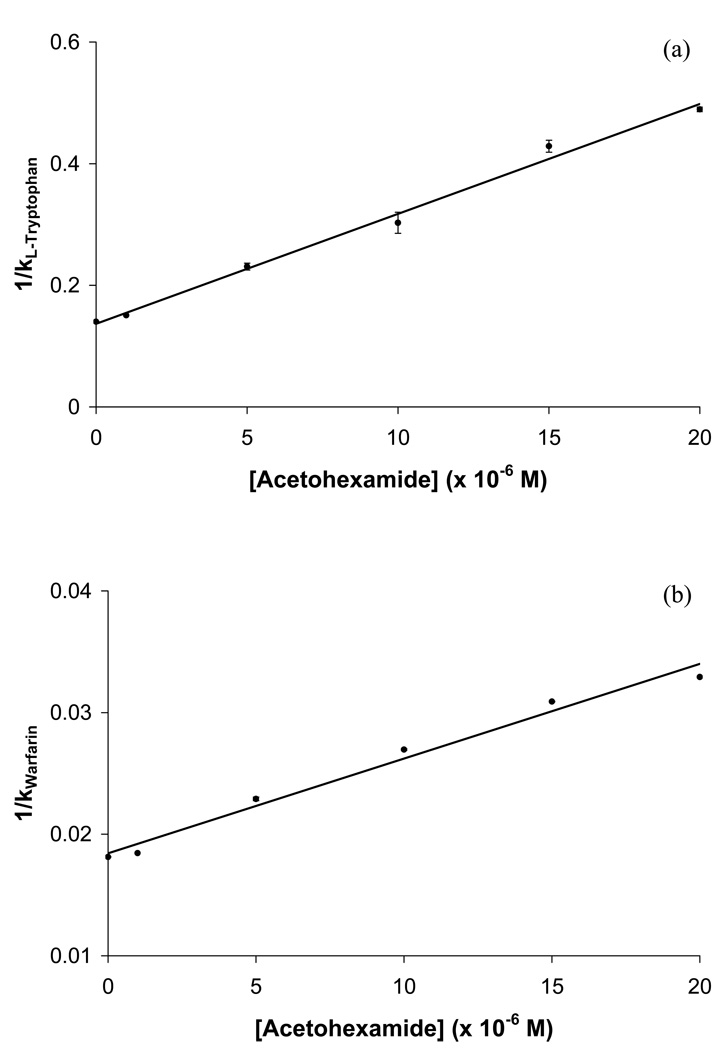
Competition studies using zonal elution were next performed to determine the specific binding regions on HSA that were interacting with each of these tested drugs. In the competition studies that were conducted in this study, R-warfarin was used as a site-selective probe for Sudlow site I and L-tryptophan was used as a site-selective probe for Sudlow site II, as employed in previous studies examining the binding of HSA with other drugs and solutes [21,23,24,39]. It was found in these experiments when using acetohexamide as the competing agent that plots of 1/k versus [I] gave a linear response for the injection of both R-warfarin and L-tryptophan (see Figure 6), with correlation coefficients of 0.991 and 0.996, respectively (n = 6), when fit to Eqn. (6).

Figure 6.

Plots of 1/k versus [Acetohexamide] for competition studies performed by zonal elution using (a) L-tryptophan or (b) R-warfarin as site-selective probes injected onto HSA columns in the presence of various concentrations of acetohexamide as a competing agent. The equations for the best-fit lines in these plots are as follows: (a) y = 18,100 (± 800) x + 0.137 (± 0.009), with a correlation coefficient of 0.996 (n = 6); and (b) y = 780 (± 50) x + 0.0184 (±0.0006), with a correlation coefficient of 0.991 (n = 6). The error bars represent a range of ±1 S.D. (Note: some of the ranges represented by these error bars are small and not easily visible on the scale employed for this plot).

The predicted value of k (as calculated by taking the inverse of the intercept) for R-warfarin when no acetohexamide was present in the mobile phase was 54.3 (± 1.7), which showed good agreement with the actual measured value of 55.1 (± 0.1). The retention factor for L-tryptophan when no competing agent was present in the mobile phase was 7.13 (± 0.02), while the predicted value was 7.31 (± 0.47). The relative difference in retention factors between the predicted value (i.e., as obtained from the best-fit intercept) and the actual value (i.e, k when no competing agent was present in the mobile phase) was only 1.6% for R-warfarin and 2.4% for L-tryptophan showing little difference between predicted and actual values. The agreement of these results was a further indication that acetohexamide had direct competition with both R-warfarin and L-tryptophan, indicating that acetohexamide also had binding to both Sudlow sites I and II of HSA. It was possible to use the best-fit lines to the plots in Figure 6 along with Eqn. (6) to determine the site-specific association equilibrium constants for acetohexamide at Sudlow sites I and II. The K_a values that were obtained through this process were 4.2 (± 0.3) × 10⁴ M⁻¹ and 1.3 (± 0.1) × 10⁵ M⁻¹, respectively. It was noted that the K_a value found by this approach for Sudlow site II was similar to that for the highest affinity site when using a two-site model to examine the frontal data.

4.4 Zonal elution studies using tolbutamide

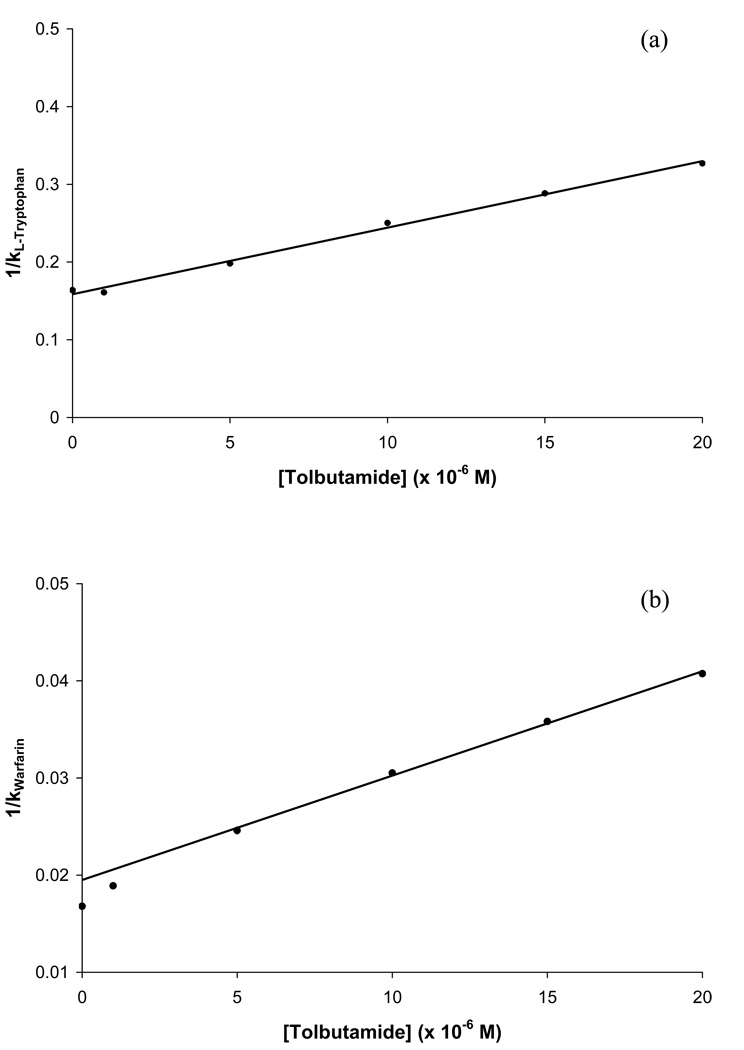
Competition studies in zonal elution experiments were also carried out for tolbutamide. The results that were obtained when injections of L-tryptophan were made in the presence of tolbutamide are shown in Figure 7(a). The resulting plot of 1/k versus [Tolbutamide] gave a linear relationship with a correlation coefficient of r = 0.998 (n = 6). This result indicated that direct competition was taking place between tolbutamide and L-tryptophan at Sudlow site II. By using Eqn. (6) to analyze this plot (see Table 3), it was determined that the association equilibrium constant for tolbutamide at this site was 5.3 (± 0.2) × 10⁴ M⁻¹, which was similar to the value calculated for the high-affinity binding site of tolbutamide with HSA when using frontal analysis.

Figure 7.

Plots of 1/k versus [Tolbutamide] for competition studies performed by zonal elution using (a) L-tryptophan or (b) R-warfarin as site-selective probes injected onto HSA columns in the presence of various concentrations of tolbutamide as a competing agent. The equations for the best-fit lines shown in these plots are as follows: (a) y = 8400 (± 300) x + 0.157 (± 0.003), with a correlation coefficient of 0.998 (n = 6); (b) y = 1070 (± 30) x + 0.0194 (± 0.0004), with a correlation coefficient of 0.999 (n = 4). Error bars representing a range of ±1 S.D. are included in this plot but the corresponding ranges are small and not easily visible on the scale employed for this plot).

Table 3.

Binding parameters obtained by zonal elution and competition studies for acetohexamide and tolbutamide with HSA^a

	Association equilibrium constant Ka (M−1)
Drug	Sudlow Site I	Sudlow Site II
Acetohexamide	4.2 (± 0.4) × 104	1.3 (± 0.1) × 105
Tolbutamide	5.5 (± 0.2) × 104,b	5.3 (± 0.2) × 104

^aAll of these parameters are for data obtained at pH 7.4 and 37 °C. The values in parentheses represent a range of ± 1 S.D., as found by conducting error propagation with the standard deviations of the best-fit linear parameters determined by using Excel and a plot prepared according to Eqn. (6).

^bSome curvature was noted at low competing agent concentrations in a plot prepared according to Eqn. (5) when examining the competition of R-warfarin with tolbutamide. The linear region of this plot was used to obtain the result given here, based on behavior predicted by Eqn. (8).

The plot of 1/k versus [Tolbutamide] that was generated when R-warfarin was the injected probe compound is shown in Figure 7(b). This plot appeared to be linear at high tolbutamide concentrations but did have some deviations from linearity at tolbutamide concentrations below 5 µM. One way this behavior may be produced is if some competition were present between R-warfarin and tolbutamide at both Sudlow site I and at a few of the weaker affinity regions for tolbutamide on HSA. For instance, the behavior seen in Figure 7(b) is predicted by Eqn. (7) for the multi-site competition of an analyte A with a competing agent I for two groups of binding sites in the column. However, Eqn. (8) also predicts that the response of such a plot will approach a linear relationship at reasonably high values of [I]. Based on previous theoretical studies the slope versus intercept ratio from this linear region can be used to estimate of K_I1 in a system with multisite interactions. A linear fit was made to the data for tolbutamide and warfarin in Figure 7(b) at tolbutamide ranging from 5–20 µM. This approach gave an estimate for K_I1 of 5.5 (± 0.2) × 10⁴ M⁻¹, which would represent the binding of tolbutamide at its highest affinity site of competition with R-warfarin. This value was similar to the value calculated for the high-affinity binding site when using frontal analysis, and direct binding by tolbutamide at Sudlow site I was consistent with previous information reported in the literature [3,30]. It is interesting to note that this value is also quite close to the association equilibrium constant that was determined for tolbutamide at Sudlow site II. This latter observation explains why a two-site model using only a single group of higher affinity sites plus a group of weaker affinity sites appeared to give a good fit in the frontal analysis work described for tolbutamide with HSA in Section 4.2. Even when the results of these zonal studies were combined with the previous frontal analysis data, no further distinction between the interactions of tolbutamide at the two proposed high affinity sites could be made when using the overall binding isotherm because of the similarity in these values. This behavior demonstrates the value of using both frontal analysis and site-selective competition studies in zonal elution to examine such interactions.

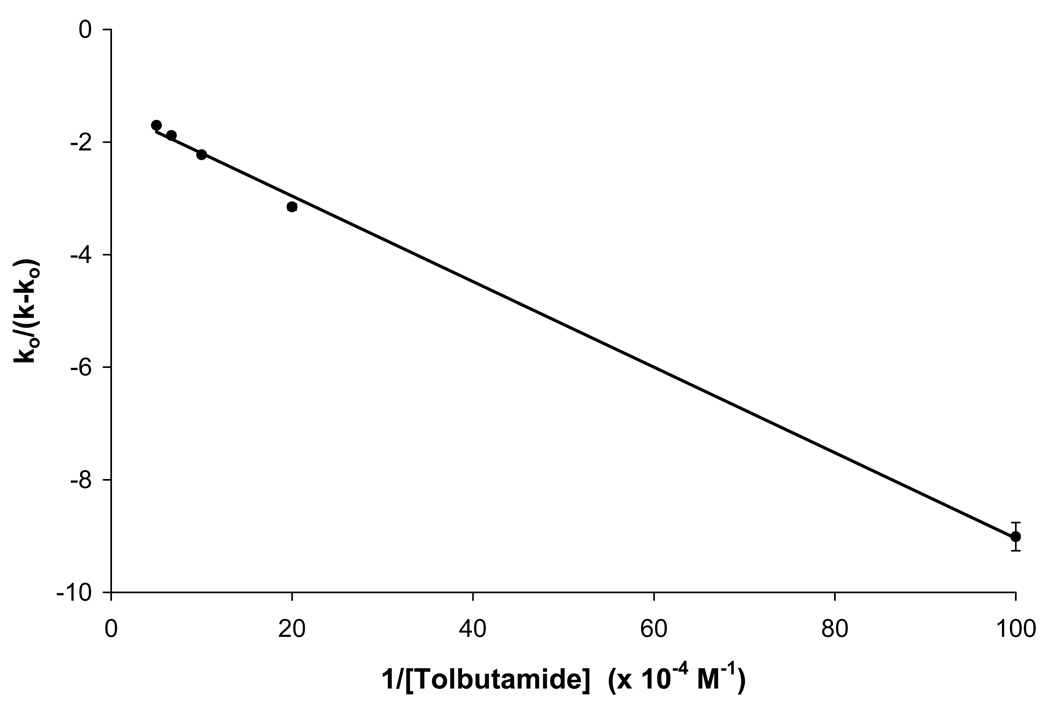
Another possible explanation for the deviations from linearity that were noted in Figure 7(b) is that some allosteric effects were occurring between R-warfarin at Sudlow site I and some other region that was interacting with tolbutamide. This possibility was explored by preparing a plot of k₀/(k-k₀) versus 1/[I] according to Eqn. (9). The result that was obtained is shown in Figure 8. This plot appeared to have a good correlation coefficient for a linear fit (r =0.999, n = 5); however, some curvature did appear to be present in this plot. If these deviations were ignored, a β_I→A value of 0.31 (± 0.02) would be obtained for the coupling constant, which would represent a negative allosteric effect for tolbutamide on the binding of R-warfarin at Sudlow site I. The value of K_IL that would be obtained from the same fit is 1.9 (± 0.1) × 10⁵ M⁻¹ for the binding of tolbutamide to HSA. This latter result is similar to some previously reported values for the binding of tolbutamide with HSA [15–18], but is higher than the K_a value for the high affinity site that was determined in this current work when using frontal analysis. Based on these observations, the curved behavior noted for the plot in Figure 8, and the results that were obtained for acetohexamide, it was concluded that a multi-site model was a more likely explanation than allosteric interactions for the curvature seen in Figure 7(b).

Figure 8.

Change in the retention of R-warfarin in the presence of tolbutamide during zonal elution studies, as examined according to Eqn. (9). The best-fit line shown in this plot is described by the equation y = {7.60 (± 0.17) × 10⁻⁶} x − 1.44 (± 0.08) and had a correlation coefficient of 0.999 (n = 5). The error bars represent a range of ±1 S.D. (Note: the ranges represented by some of these error bars are small and not easily visible on the scale employed for this plot).

5. Conclusion

These studies showed that frontal studies and zonal studies compliment each other as a means for gleaning a better understanding of the overall binding of drugs such as sulfonylureas to proteins like HSA. Using frontal analysis alone, it was initially determined that acetohexamide was interacting with HSA at two general classes of binding sites, including a set of higher affinity regions and a group of weaker affinity regions. The use of more detailed competitive binding studies and zonal elution studies indicated that acetohexamide was binding with relatively high affinity to both Sudlow sites I and II. It was also possible through these measurements to obtain site-selective equilibrium constants for these interactions (1.3 (± 0.1) × 10⁵ and 4.3 (± 0.3) × 10⁴ M⁻¹) and to combine the zonal elution and frontal analysis data to further refine the overall binding model and estimates of the weak affinity interactions of acetohexamide with HSA.

Tolbutamide was also determined by frontal analysis to bind with HSA at both high affinity and lower affinity regions. Zonal elution studies and work with site-selective probes indicated that the high affinity interactions probably involved binding at both Sudlow sites I and II, with interactions that were quite similar in strength. The K_a values estimated for tolbutamide at Sudlow sites I and II were 5.5 (± 0.2) × 10⁴ and 5.3 (± 0.2) × 10⁴ M⁻¹, respectively, and were again used with the frontal analysis results to refine a model for describing the overall binding of this drug to HSA. This study demonstrates that using both frontal analysis and zonal elution can be extremely valuable in obtaining a good quantitative description of how drugs such as sulfonylureas are interacting with HSA. Future studies will look at other drugs in this class, including second- and third-generation sulfonylureas. The same approach should also be useful when employing HPAC to examine other complex drug-protein interactions.