Population Pharmacokinetics of Micafungin in Neonates and Young Infants

Abstract

Micafungin is an echinocandin with potent activity against Candida spp. Hematogenous Candida meningoencephalitis (HCME) is a frequent complication of disseminated Candida infection in premature infants. A preclinical model of HCME suggests that micafungin may be an effective agent for this syndrome, but relatively high weight-based dosages are required. This prompted the further study of the safety and pharmacokinetics (PK) of micafungin in infants. Here, we describe the population pharmacokinetics of micafungin in 47 infants with a proven or presumptive diagnosis of disseminated candidiasis, who received 0.75, 1.5, 3, 7, 10, and 15 mg/kg of micafungin. The drug was infused daily, and samples were taken in the first dosing interval and at steady state. Serum concentrations were measured using high-performance liquid chromatography (HPLC). Data were modeled using an allometric pharmacokinetic model using a three-fourths scaling exponent for clearance and parameters normalized to a 70-kg adult. Drug exposures were estimated using Monte Carlo simulation. Optimal sampling times were determined using D-optimal design theory. The fit of the allometric model to the data was highly acceptable. The pharmacokinetics of micafungin were linear. The weight-normalized estimates of clearance and volume of distribution approximated those previously described for adults. The original population parameter values could be recapitulated in the Monte Carlo simulations. A dosage of 10 mg/kg/day resulted in 82.6% of patients with areas under the concentration-time curve (AUCs) that are associated with near-maximal decline in fungal burden within the central nervous system (CNS).

The echinocandins are high-molecular-weight, water-soluble, semisynthetic fungal derivatives with activity against Candida and Aspergillus spp. (7). The pharmacokinetics (PK) and clinical efficacy for members of this class have been investigated in infants, older children, and adults (10, 11, 17). Micafungin is licensed for treatment of invasive fungal infections in children in the European Union and Japan, as well as parts of Asia.

Premature infants are at increased risk of invasive fungal infections because of the relative immaturity of innate and adaptive immunological defenses (4, 9). Disseminated candidiasis in this patient population differs from that in adults because of a propensity for involvement of the central nervous system (CNS) (1). The syndrome of hematogenous Candida meningoencephalitis (HCME) is difficult to diagnose and is frequently clinically silent. This syndrome is associated with neurological injury that manifests as moderate-to-severe cerebral palsy, blindness, deafness, and low cognitive and/or motor developmental performance scores. Adequate treatment requires the timely administration of a safe and potent antifungal agent that penetrates the CNS. Unfortunately, however, there are few safe and effective compounds that fulfill these criteria.

The first micafungin pharmacokinetic trial with infants studied 0.75 to 3 mg/kg (11) and was designed to identify dosages that result in systemic drug exposure comparable to that for adults being treated for disseminated candidiasis. The echinocandins were not originally thought to be effective compounds for the treatment of infections within the CNS because of the aqueous solubility and relatively large molecular weight common to these compounds (circa. 1,200). Subsequently, however, an in vivo-to-clinical bridging study of HCME suggested that human infant dosages of >9 mg/kg micafungin may be required for successful treatment (12). Because these dosages were significantly in excess of those that had been studied, the conclusions of this preclinical study were qualified by a requirement to demonstrate the safety and linear pharmacokinetics of higher dosages (12). Recently, the safety and noncompartmental pharmacokinetics of micafungin at 7, 10, and 15 mg/kg have been reported (3, 18). Here, we model the entire clinical pharmacokinetic data set for micafungin in infants and demonstrate that the population pharmacokinetics are linear in the range of 0.75 to 15 mg/kg. Furthermore, we demonstrate that the dosage of 10 mg/kg would achieve near-maximal decline in fungal burden within the CNS of most infants.

(This work was presented in part at the 49th Interscience Conference of Antimicrobial Agents and Chemotherapy, San Francisco, CA, 2009 [14].)

MATERIALS AND METHODS

Patient population and pharmacokinetic data.

This analysis used data for 47 infants receiving micafungin at 0.75 to 15 mg/kg and enrolled in three clinical trials. The study design, safety, and noncompartmental pharmacokinetic analyses have been reported elsewhere (3, 11, 18). In these studies, infants with suspected or proven disseminated candidiasis received micafungin intravenously (i.v.) over 30 min or 1 h every 24 h. Serum samples were drawn throughout the first dosing interval and/or at steady state. The concentration of micafungin was measured using high-performance liquid chromatography (HPLC), as described in the individual publications (3, 11, 18).

Pharmacokinetic modeling.

On the basis of previous population pharmacokinetic modeling for a range of compounds in neonates and children (including micafungin) (13, 21), an allometric model was used. The two differential equations that described this system were as follows:

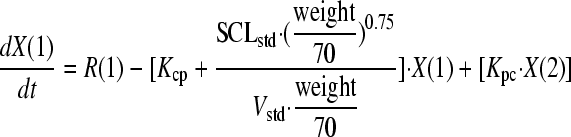(1a)

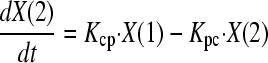(1b)

where X(1) and X(2) represent the amount of micafungin (milligrams) in the central (c) and peripheral (p) compartments, respectively. R(1) represents the rate of infusion of drug into the central compartment (milligrams/hour [not milligrams/hour/kg]).

SCL_std and V_std represent the normalized estimates for clearance and volume, respectively, for a 70-kg individual. K_cp and K_pc are the first-order intercompartmental rate constants.

All population PK modeling was performed using the Big version of the population pharmacokinetic program Nonparametric Adaptive Grid (BIG NPAG). The data were weighted by the inverse of the estimated assay variance. The Bayesian estimates for each individual infant's pharmacokinetic parameters were obtained using the “population of one” utility within BIG NPAG. The predictive power of the model was assessed using measures of bias and precision, and the fit of the model to the data was assessed by a visual inspection and the coefficient of determination of the regression of observed-versus-predicted values after the Bayesian step.

Monte Carlo simulations were performed using the simulation module of the pharmacokinetic program ADAPT II (5). The mean parameter values and their associated variances used for these simulations were obtained from the output of the population pharmacokinetic analysis. Micafungin was administered to each infant on a mg/kg basis. A subroutine within ADAPT II (provided by David D'Argenio and available from the corresponding author) enabled the dosage (mg/kg) to be multiplied by the simulated weight (kg) so that each simulated individual received an absolute dosage of micafungin (mg), as would occur in clinical practice. This process provided the best approximation of a clinical setting, in which physicians plan micafungin dosing in terms of mg/kg, but ultimately allowed for an absolute dosage of drug to be administered to each patient. Both normal and log-normal parameter distributions were explored and discriminated on the basis of their ability to recapitulate the original parameter means and their distribution.

A 9,999-patient Monte Carlo simulation was performed for a population receiving 8, 10, and 12 mg/kg. These dosages were chosen because they encompassed dosages predicted to be associated with near-maximal antifungal effect within the CNS of infants with HCME on the basis of an in vivo-to-clinical bridging study (12). In that study, we observed near-maximal antifungal effect in rabbits receiving 8 mg/kg, which corresponded to an area under the concentration-time curve from 0 to 24 h (AUC_0-24) of ∼166.5 mg·h/liter; this has been used to bridge experimental findings and clinical practice. In the simulations, the AUC_0-24 at steady state was calculated for each simulated infant by the use of integration.

The MIC of the challenge strain of Candida albicans was 0.125 mg/liter. Therefore, the pharmacodynamic target was an AUC/MIC ratio of 1,332 (166.5 divided by 0.125). The fraction of simulated patients receiving micafungin at 10 mg/kg that achieved this value was determined for MICs in the range 0.007 to 0.5 mg/liter. An expectation for therapeutic success for the population was obtained by multiplying the target attainment rate for each MIC value by the fraction of the C. albicans population with that MIC. Data for the latter were obtained from the work of Pfaller et al. (16).

Optimal sampling times.

Optimal sampling times were determined using the SAMPLE module within the pharmacokinetic program ADAPT 5 (6). The support points and their associated probabilities from the population pharmacokinetic solution were obtained from the multiple model file from the output of NPAG. This file contains the support points that are a summary of the overall population pharmacokinetic solution and contain the individual sets of parameter values that describe the behavior of drug within the population. Each set of support points has an associated probability that indicates the proportion of the population that is described by that set of parameters (those sets of parameters that describe more “common” patients are more probable, whereas those points that are less probable describe the “outliers” within the population). The micafungin assay variance structure was used in the estimation process. Consistent with classical optimal design theory, the number of sampling points for each set of parameter values (i.e., each support point) is the same as the number of system parameters. In this case, each support point yielded 4 sampling times, corresponding to the four model parameters to be estimated (i.e., SCL_std, V_std, K_cp, and K_pc, as defined in equations 1a and 1b, above).

To obtain optimal sampling times for infants receiving micafungin, the method originally described by Tam et al. (19) was used. A dosage of 10 mg/kg was administered to each support point. Optimal sampling times were obtained for 0.5- and 1.5-kg patients (the absolute values for clearance and volume at each support point were calculated for 0.5- and 1.5-kg infants). These weights were chosen because they encompassed the majority of the original population of 47 infants. As each of the 4 sampling times for each support point was determined, it was multiplied (weighted) by the probability associated with that support point before being plotted on a histogram with 15-min increments throughout the dosing interval.

RESULTS

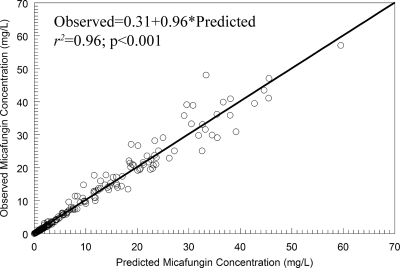
The allometric model provided an excellent fit to the pharmacokinetic data. The observed-versus-predicted values are shown in Fig. 1. A linear regression of these values had an intercept and slope that approximated zero and 1, respectively. The coefficient of determination was 0.96. The mean weighted error (a measure of bias) and bias-adjusted mean weighted squared error (a measure of precision) were −0.111 and 1.11, respectively. The estimates for the means, medians, and standard deviations for the parameter values from the population pharmacokinetic analysis are shown in Table 1.

FIG. 1.

The observed-versus-predicted values from the allometric population pharmacokinetic model after the Bayesian step.

TABLE 1.

The estimates for the means, medians, standard deviations, and coefficients of variation for each parameter from the population pharmacokinetic model

Parameter	Vstd (liters/70 kg)	SCLstd (liters/h/70 kg)	Kcp (h−1)	Kpc (h−1)	Wta
Mean	10.300	1.080	11.780	7.800	1.297
Median	8.020	0.760	11.180	3.280	1.210
SD	4.030	0.926	7.350	9.310	0.513
Coefficient of variation (%)	39.140	85.540	62.410	119.320

^aWt, weight.

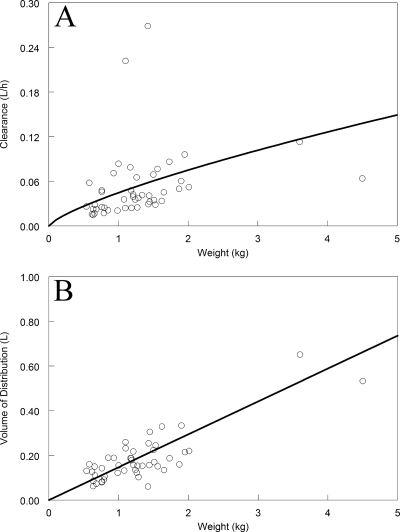
The Bayesian estimates for clearance and volume of distribution are shown in Fig. 2. The absolute estimates for clearance and volume progressively increased with increasing weight. Of note, for the Bayesian estimates of clearance, there were three “outliers”: two infants had very rapid clearances, whereas one larger infant had a low estimate for clearance.

FIG. 2.

The Bayesian estimates for absolute estimates for clearance (A) and the volume of distribution (B) for each of the 47 neonates. The solid line represents the fit of the model to the data.

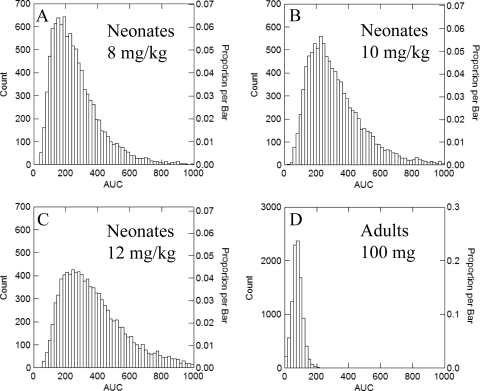
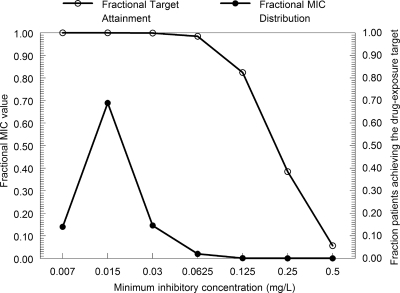
The original parameter values (means and distributions) for the 47 infants could be recapitulated with a log-normal distribution for each parameter in the Monte Carlo simulations. The expected AUC_0-24 values at steady state for infants receiving 8, 10, and 12 mg/kg in comparison to adults receiving 100 mg are shown in Fig. 3. The simulations showed a broader spread of AUCs compared with those for adults (Fig. 3). The proportion of the simulated patients receiving 8, 10, and 12 mg/kg with an AUC of <166.5 mg·h/liter was 29.3, 17.4, and 10.5%, respectively. The target attainment rates as a function of the MIC are shown in Fig. 4. All neonates receiving 10 mg/kg had an AUC/MIC ratio of at least 1,332 for MICs of 0.007 to 0.0625 mg/liter. Progressively fewer neonates achieved the pharmacodynamic target with isolates with MICs of 0.125 mg/liter and higher. The overall expectation for attainment of the pharmacodynamic target for the whole population was 99.56%. While therapy may be more likely to fail for patients with these more-resistant isolates, this did not have an appreciable impact on the overall success because these resistant isolates represent a small proportion of the microbial population.

FIG. 3.

Monte Carlo simulations for 9,999 patients receiving micafungin. (A) Neonates receiving 8 mg/kg; (B) neonates receiving 10 mg/kg; (C) neonates receiving 12 mg/kg; (D) adults receiving 100 mg. The simulations in panel D were performed using the mean population parameter estimates from Gumbo et al. (10).

FIG. 4.

Target attainment rates as a function of the MIC. The distribution of MICs for Candida albicans is shown (solid circles). The target attainment rates for the 9,999 simulated neonates for each MIC value is represented by open circles. Target attainment rates fall dramatically with MICs of >0.0625 mg/liter.

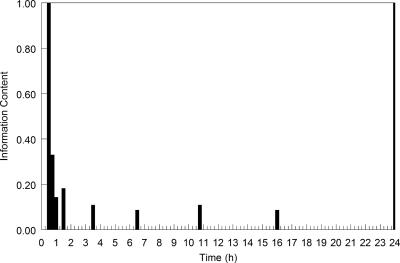
The optimal sampling times for infants weighing 0.5 and 1.5 kg are shown in Fig. 5. As can be seen, each support point demanded a sampling time at the end of the infusion, and the majority also required a sample to be taken immediately prior to the administration of the next dose (i.e., a trough micafungin concentration). The timing of the second and third samples was variable. The majority of these optimal sampling times fell in the first 1 to 3 h of the dosing interval.

FIG. 5.

Optimal sampling times for neonates weighing 0.5 and 1.5 kg receiving micafungin at 10 mg/kg.

DISCUSSION

Micafungin is an echinocandin that has been investigated for treatment of infants, children, and adults with invasive fungal infections. This compound exhibits linear pharmacokinetics and can be used without dosage adjustment for patients with renal impairment and moderate hepatic impairment. Results from 47 infants with a mean ± standard deviation (SD) weight of 1.3 ± 0.5 kg (range, 0.54 to 4.5 kg) suggest that micafungin exhibits linear pharmacokinetics for dosages of 0.75 to 15 mg/kg. The use of a scaling exponent to estimate clearance does not imply nonlinear pharmacokinetics in infants but reflects the fact that many physiological phenomena, such as basal metabolic rate, heart rate, and respiratory rate, do not exhibit a relationship that is directly proportional to size. In this study, as previously, we chose to model clearance using a three-fourths scaling exponent. The underlying biological reasons for this are discussed in detail elsewhere and reflect inherent constraints posed on the structure and optimal function of progressively larger organs (20). An advantage of estimating values for clearance and the volume of distribution that are normalized for a 70-kg person is that these values derived for infants should approximate values obtained for adults. Indeed, the estimates for the normalized parameters V_std and SCL_std in this study are concordant with parameter estimates obtained for adults (10). The mean values for clearance for infants normalized to a 70-kg person and adults are 1.08 and 1.17 liters/h, respectively, whereas the values for the volume of distribution are 10.30 and 10.43 liters, respectively.

Clinical studies of adults have suggested that an appropriate dosage of micafungin is 100 to 150 mg/day and that the clinical responses with these dosages compare favorably with those with licensed dosages of caspofungin (i.e., 70-mg loading dose followed by 50 mg/day) (15). This adult micafungin dosage is approximately 2 mg/kg. An in vivo-to-clinical bridging study suggests that higher weight-based dosages of micafungin are required for infants with disseminated candidiasis in whom infection within the CNS is present or assumed (12). A micafungin AUC_0-24 of 166.5 mg·h/liter in a rabbit model of HCME is associated with near-maximal reduction in the fungal burden in the brain. While only a single strain was studied, this model provides useful preclinical information that can be bridged to human neonates. Monte Carlo simulations suggest that an infant dosage of 10 mg/kg results in a satisfactorily high proportion of the simulated population exceeding this level of drug exposure.

A potentially important consideration for the use of micafungin in neonates is the recently identified high concentrations of the micafungin metabolite M5 that have been observed with neonates. This metabolite does not have any seemingly meaningful antifungal activity or known safety issues identified in studies performed to date, including those of 12 neonates and young infants dosed at 15 mg/kg for 4 or 5 days. However, further pharmacokinetic and toxicological studies are currently being undertaken prior to the commencement of a phase III clinical trial with neonates and young infants. The safety of these higher dosages of micafungin has been examined as a component of recently completed pharmacokinetic escalation studies (2, 18). To date, there has been no evidence of increased toxicity. Clearly, however, more information is required before these dosages can be widely advocated, and this is planned as a component of further clinical studies.

There are two principal reasons that a higher weight-based dose is required for infants compared with adults. First, higher systemic drug exposures are required to achieve effective drug concentrations within the CNS (i.e., to “drive” drug into the CNS). Second, while absolute estimates of clearance in infants are lower than those in adults (0.05 versus 1.17 liters/h, respectively), the weight-adjusted clearances are, in fact, higher (0.043 versus 0.017 liters/h/kg for infants and adults, respectively), meaning that higher weight-based dosages are required to achieve comparable systemic AUCs.

The use of D-optimal design theory provides a way that the minimum number of maximally informative sampling times can be identified to ensure that PK parameters can be estimated in an efficient and unbiased manner (8). Sampling times with a low information content may result in an inability of estimation processes to achieve convergence or the attainment of biased parameter estimates. The application of optimal design theory to infants is highly relevant because of the difficulties in obtaining multiple blood samples. These results can be used in clinical trial design in which adjunctive pharmacokinetic data are also required. High-quality prospectively collected data enable efficient and robust estimates of drug exposure in individual patients (using Bayesian estimation techniques) that then enable measures of drug exposure (e.g., AUC/MIC ratio) to be linked with clinically relevant outcome measures (e.g., survival and neurodevelopmental impairment). This process will also facilitate the further refinement of experimental models that can then be used to address future clinically pertinent questions pertaining to HCME.