Estimation of the Initial Viral Growth Rate and Basic Reproductive Number during Acute HIV-1 Infection

Abstract

During primary infection, the number of HIV-1 particles in plasma increases rapidly, reaches a peak, and then declines until it reaches a set point level. Understanding the kinetics of primary infection, and its effect on the establishment of chronic infection, is important in defining the early pathogenesis of HIV. We studied the viral dynamics of very early HIV-1 infection in 47 subjects identified through plasma donation screening. We calculated how fast the viral load increases and how variable this parameter is among individuals. We also estimated the basic reproductive ratio, the number of new infected cells generated by an infectious cell at the start of infection when target cells are not limiting. The initial viral doubling time had a median of 0.65 days with an interquartile range of 0.56 to 0.91 days. The median basic reproductive ratio was 8.0 with an interquartile range of 4.9 to 11. In 15 patients, we also observed the postpeak decay of plasma virus and found that the virus decay occurred at a median rate of 0.60 day⁻¹, corresponding to a half-life of 1.2 days. The median peak viral load was 5.8 log₁₀ HIV-1 RNA copies/ml, and it was reached 14 days after the virus was quantifiable with an assay, with a lower limit of detection of 50 copies/ml. These results characterize the early plasma viral dynamics in acute HIV infection better than it has been possible thus far. They also better define the challenge that the immune response (or therapeutic intervention) has to overcome to defeat HIV at this early stage.

During primary infection, the number of human immunodeficiency virus type 1 (HIV-1) particles in plasma increases rapidly, reaches a peak, and then declines until it reaches a set point level (i.e., a quasi-steady state) (3, 26). Often, the peak in viral load coincides with the first appearance of an acquired immune response. Thus, early HIV infection can be seen as a race between the immune system and the virus (4). It has been suggested, based on the macaque model with simian immunodeficiency virus (SIV) infection, that early viral expansion is somewhat homogeneous across subjects, but the viral load set point varies by orders of magnitude (14). However, studies with SIV also suggest that the early events during viral expansion, i.e., before the peak, are important in defining the viral load set point later in infection (14).

Thus, improved knowledge of the very early expansion of HIV-1 will be beneficial for our understanding of primary infection and its effect on the establishment of chronic infection. Moreover, if the immune system primed by a vaccine could respond quickly enough to HIV, perhaps it would be possible to prevent infection. However, all but the recombinant canarypox-gp120 vaccine, used in the RV144 trial in Thailand (23), have failed to provide protection, and the immune response generated by T-cell-based vaccines has been described as “too little, too late” (1, 5, 24). Here, we characterize the early events in infection and the prepeak expansion of HIV-1 to better understand the biology of infection.

We examine longitudinal viral load data from 47 frequent plasma donors who became HIV positive during the course of their plasma donations. Thus, this data set includes samples in which virus was absent or below the limit of detection of the assay used, as well as viral loads at very early times postexposure with HIV. From this data, we quantify the rate of viral expansion during primary HIV infection. Previously, Fiebig et al. (8, 9) analyzed some aspects of early viral load expansion, the existence of viral blips, and the timing of HIV-1 marker expression, defining the stages for early infection (9). Here, we extend these analyses to characterize in detail the expansion of the virus and its basic reproductive ratio, R₀. In the context of host viral dynamics, R₀ is a measure of whether a virus can establish infection (12). It specifically measures how many cells a single infected cell will infect when there is no target cell limitation. If R₀ is less than 1, on average an infected cell will infect less than 1 susceptible cell, and the infection will die out. If R₀ is greater than 1, on average an infected cell will infect more than 1 susceptible cell, and generally the infection will spread (25).

R₀ for HIV infection in humans has been estimated previously in smaller data sets. Little et al. (15) used both viral load and CD4⁺ T-cell count data to find R₀ for four individuals whose infection was identified within a couple of weeks of exposure. Stafford et al. (27) estimated R₀ from viral load data obtained from 10 primary infection patients, again identified within a few weeks of infection. Our work differs from these previous studies in that we analyzed a much larger number of patients and the viral load data that we analyzed encompassed the earliest stages of infection, in most cases before the viral load was even detectable. By contrast, both Little et al. (15) and Stafford et al. (27) analyzed data obtained primarily near or after the peak in viral load.

MATERIALS AND METHODS

Patient data: plasma donor panels.

Two sets of archived plasma donor samples (n = 51) were obtained from Zeptometrix (Buffalo, NY) and Seracare (Milford, MA). The Zeptometrix plasma data set was originally collected by Alpha Therapeutic Corporation (Los Angeles, CA) from August 1996 through December 1998, and the Seracare plasma data set was collected from Boston Biomedica (West Bridgewater, MA) from June 1984 through October 1994. At both collection sites, each patient donated 600 to 800 ml of plasma, which was frozen to −20°C or less within 8 h. The plasma samples were stored up to 2 months and then sent in pools of 512 to be serologically screened for HIV. Donors who were HIV positive were notified and deferred from subsequent donation. HIV-positive samples were aliquoted and refrozen at −20°C. Aliquoted samples of plasma donors were reanalyzed with a Roche Amplicor HIV-1 reverse transcriptase (RT)-PCR assay by Quest Diagnostics (Lyndhurst, NY), with a lower limit of quantification of 50 HIV-1 RNA copies/ml. The data are fully anonymous, without any possibility of linking them back to the original donors.

Definition and calculation of R₀.

We used a target cell-limited model of HIV infection, which has been shown to capture the dynamics of primary infection (19, 21, 27), to analyze the plasma donor samples. In a target cell-limited model, viral growth depends on the availability of target cells, and the death of infected cells occurs at a constant rate, δ, consistent with death due to viral cytopathic effects. While an immune response may also contribute to infected cell death, we assume that any innate response is approximately constant and included in the death rate (δ), whereas an acquired response is most likely absent during the early stages of infection before the viral load peak (10, 13). This model can be summarized by the following equations:

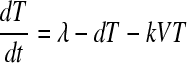(1)

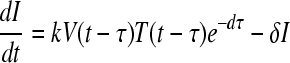(2)

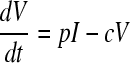(3)

where T is the target cell density, I is the productively infected cell density, V is the HIV-1 RNA concentration, λ is the rate of target cell generation, d is the target cell death rate, k is the rate constant for infection, δ is the death rate of infected cells, p is the rate of virus production from one infected cell, and c is the virion clearance rate constant. Here, we also assume that, after a virion infects a cell, there is a time delay, τ, before that cell produces virus, i.e., τ represents the length of the eclipse phase of the viral life cycle (7, 20). The term e^−dτ is the probability that a cell will not die during the eclipse phase of length τ (11, 17, 18). Here, for simplicity we have assumed that a cell that is infected but not yet producing virus dies at rate d, equal to that of an uninfected cell (see equation 1). In this way, productively infected cells are the result of infection events that occurred τ time units ago, assuming that the infected cells survive to the present time (e^−dτ).

While R₀ can be formally calculated from the model equations (25), the following is an intuitive derivation. Each infected cell produces virus at rate p. While producing virus, infected cells live, on average, for time 1/δ. Thus, on average, each infected cell produces a total of p/δ virions. Because virus is cleared at rate c per virion, each virion survives on average for time 1/c. During this time, before target cells become limiting, each virion on average infects kT₀e^−dτ/c cells, where T₀ is the preinfection target cell density and e^−dτ is the probability that the cell will not die before becoming productively infected and producing any virus. Thus, the total number of cells productively infected by the p/δ virions released from 1 infected cell is determined by R₀ = pkT₀e^−dτ/δc. From equation 1, the preinfection steady-state target cell density, T₀, is λ/d. This gives the following expression for R₀:

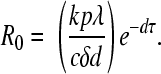(4)

Viral load expansion rate and R₀.

Estimating R₀ from equation 4 requires having enough data to estimate all seven parameters in this equation. Stafford et al. (27), who analyzed data collected over the first 80 to 100 days of infection, used this approach. Since plasma donation was stopped once individuals were identified as HIV positive, our data sets tend to have frequent early samples but limited data after the peak viral load. We can use these data to find R₀ by an alternative approach that first estimates the viral expansion rate, r, which can be found from consecutive measurements of the viral load. In early HIV infection, before the peak in viral load, we assume that the total number of uninfected target cells, T₀, is approximately constant and equal to λ/d. Thus, in early infection, the target cell-limited model is reduced to equations 2 and 3, with T being equal to T₀. In this case, one finds that to a good approximation the viral load initially increases exponentially, and V(t) ≃ V₀ e^rt, where r, the initial viral load expansion rate, is the dominant (i.e., largest) solution of the equation r² + (c + δ)r + (δc − kpT₀e^−rτ) = 0 (17). Using the definition of R₀ from equation 4 and the equation T₀ = λ/d, this becomes r² + (c + δ)r + δc(1 − e^−rτR₀) = 0. Solving for R₀, one finds

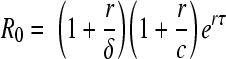(5)

If c is large compared to r, then

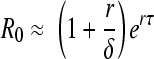(6)

Estimates of c made during chronic infection suggest that c is ∼23 day⁻¹ (22). Below, we shall show that r is ∼1.1 day⁻¹, and thus, if virion clearance is also rapid in acute infection, as has been shown in rhesus macaques (30), c ≫ r is a good assumption and equation 6 can be used to estimate R₀ from the observed initial viral expansion rate, r. Equation 6 tells us that for the same observed initial expansion rate, r, the longer the delay, τ, the larger the estimated R₀. One way to understand this result is that the longer the delay before viral production begins, the slower the virus would be expected to expand. Thus, to match a given observed expansion rate, r, the larger R₀ needs to be to offset the longer delay. A reasonable estimate for the value of τ in vivo is 24 h (7, 16a), which is also in agreement with in vitro data (2), and we will use this value to calculate R₀.

Estimates of r, δ, and R₀.

The value of R₀ depends on the values of r, δ, and τ. For all patients, we calculated r by two methods. In the first, the two viral load measurements defining the highest viral expansion rate were used. We refer to this value of r as r_max. In the second, all available viral loads for each patient, from the minimum or the last point at the lower limit of detection to the peak viral load, were used. The data set was then analyzed using a linear mixed-effects model in which the individual expansion rates varied around a group expansion rate (see below for details). We call this group expansion rate r_g. The first method of finding r gives the highest observed viral expansion rate, r_max, for each patient. The second method includes more data points for statistical accuracy and also models the expansion rate in the context of a group, which given the sparse data allows one to make better estimates for the whole population.

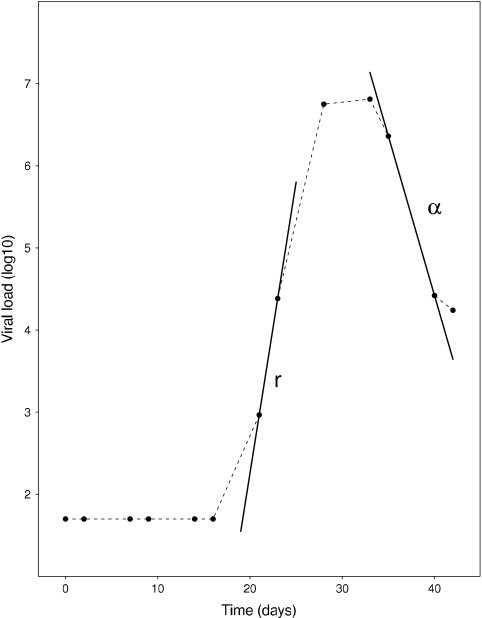
In the target cell-limited model where c ≫ δ, the virus concentration, V(t), and the density of productively infected cells, I(t), quickly become equilibrated, i.e., they become proportional to each other. Thus, after the peak, the viral load and infected cells should decay at the same rate and the observed rate of viral decay from the peak, α, can be used as an estimate of the net loss rate of infected cells. This net rate of infected cell loss, α, will underestimate the true infected cell death rate, δ, since continuing viral infection will create new infected cells (6, 15, 19). As one can see from equation 6, using α as an estimate of δ when calculating R₀ will result in a higher R₀ than would be found by using the true value of δ. The parameters r and α, and how they relate to the viral load profile, are shown in Fig. 1.

FIG. 1.

Schematic of the calculation of the viral expansion rate, r, and the postpeak decay, α.

Mixed-effects models.

To analyze the kinetics of primary infection, the natural definition of time t = 0 is the time of infection. However, the time of infection is not available for the current data set involving plasma donors. Thus, we arbitrarily define the time origin as the time that the subject's viral load first reached the limit of detection, 50 cp/ml, and call it t₅₀. This definition allows us to align the viral load data of all the patients to a common reference time point. This parameter is estimated by the best fit of a model defining the exponential growth of the early viral load. Because many subjects have sparse measurements during the initial increase in viral load, we fit a linear mixed-effects model, which borrows information across subjects while estimating both the population average and subject-specific parameters (29). To account for censoring at the assay detection limit, a full likelihood-based algorithm is used to estimate the mixed-effects model (28).

The mixed-effects model estimation was performed after two preprocessing steps. First, we removed subjects who did not have enough viral load data in the early phase of infection. Five subjects were removed. Patient 9019 (P9019), P9028, P9075, and P12007 had more than 2 weeks between the last negative and first positive HIV-1 measurement, resulting in great uncertainty about their early viral kinetics, and PRB940 had only one data point before the viral load peak, which is not enough for reliable estimation of the viral kinetic parameters. Second, for the 42 subjects with data during the eclipse phase of infection, viral loads within the upswing (exponential expansion) phase were selected to estimate the time origin. Let t_50,i denote the time origin and {ỹ_ij, t̃_ij, j ∈ U_i} denote a collection of observations that are within the upswing window U_i for each subject i. The upswing window is determined such that (i) the enclosed viral loads have a significant exponential increase and (ii) the maximum viral load and the last value at the limit of detection are included. That is, for each subject, we fitted a series of linear regressions to the viral load data in between the last censored value and the observed maximum value. The data points corresponding to the largest window that permitted a significant expansion were used for each subject. We then fitted a mixed-effects model to the log₁₀-transformed data: log₁₀ ỹ_ij = α + (β + b_i)(t̃_ij − t_50,i) + e_ij, (b_i, t_50,i)^T ∼ N(0, Σ), and e_ij ∼ N(0, 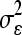), where Σ denotes the variance-covariance matrix of (b_i, t_50,i)^T and e_ij are independent and identically distributed random errors.

Statistics.

Results are presented as medians and interquartile ranges (IQR) to better reflect the unknown distribution of the underlying measurements. However, for completeness, we have also presented means and standard deviations, as specified in the text.

RESULTS

Early infection data sets.

We obtained HIV viral load data from the plasma of 51 donors. The viral loads were measured by an RT-PCR assay with a lower limit of detection of 50 copies/ml. Two donors (P6242 and P9078) were discarded from our analysis because they had only HIV-1-negative samples, and two more (P9014 and P9017) were also discarded because they were caught too late in this early phase, showing only viral load decline. In addition, five other patients who did not have enough data before the peak viral load were not included in the mixed-effects model analysis (see Materials and Methods).

There was a median of 10 data points for each analyzed donor, with infection estimated to occur at a median of 21 days after the first collection date. There was a median interval of 5 days between the last sample below the lower limit of quantification and the first measurement above detection. A median of 4 data points was available after HIV-1 was detectable.

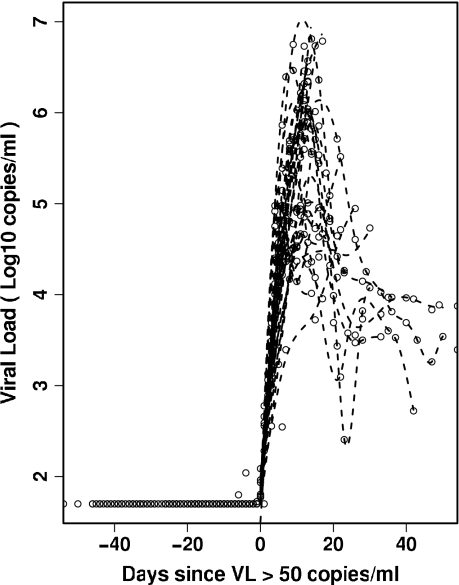
A better idea of the variation in the viral load profiles at these early times postinfection can be seen in Fig. 2, where we plot the viral loads of all the patients with a common time origin, t₅₀ (see Materials and Methods). Many of the viral load expansion profiles exhibit similar growth rates and seem to peak at about 10⁶ copies/ml, approximately 10 to 15 days after t₅₀.

FIG. 2.

Profile of the initial viral load (VL) for all patients aligned at the beginning of viral expansion.

Expansion rate/doubling time.

This data set includes a large collection of plasma samples obtained before and soon after HIV-1 RNA is detectable and thus presents a unique opportunity to directly estimate very early viral expansion rates. In order to obtain an estimate of the viral load expansion rate, we used two methods. In the first, we found the maximum slope between any two data points before the viral load peak. Using this method, we found the median r_max to be 1.06 day⁻¹ (IQR, 0.76 to 1.2 day⁻¹) and the corresponding doubling time was 0.65 days (IQR, 0.56 to 0.91 days) (Table 1). The second method involved using a linear mixed-effects model in which all the patient data obtained during the viral load increase were analyzed at once as a group (see Materials and Methods) (28). We found the group expansion rate (average ± standard deviation) to be 1.09 ± 0.18 day⁻¹, and the doubling time was 0.66 ± 0.14 days (Table 1). Thus, the two methods gave very consistent estimates for the expansion rate of HIV in early infection.

TABLE 1.

Estimates of the expansion rate and the basic reproductive ratio by the two methods used^a

Patient ID	rmax	t2	α	t1/2	R0	R0*	rg	t2g	R0g
P1001	0.72	0.96	NA	NA	4.53	NA	1.12	0.62	8.86
P1006	1.51	0.46	NA	NA	16.02	NA	1.46	0.47	14.95
P1011	1.24	0.56	NA	NA	10.69	NA	1.16	0.60	9.39
P1018	0.53	1.30	NA	NA	3.23	NA	0.62	1.12	3.78
P1026	1.24	0.56	1.18	0.59	10.70	7.10	1.21	0.57	10.22
P1055	1.52	0.46	0.42	1.63	16.27	20.99	1.46	0.47	14.96
P12007	0.45	1.52	NA	NA	2.78	NA	NA	NA	NA
P12008	1.63	0.42	0.89	0.78	19.13	14.45	1.29	0.54	11.54
P6240	1.06	0.65	0.47	1.46	8.04	9.35	1.05	0.66	7.84
P6243	1.00	0.69	0.19	3.59	7.30	16.85	1.07	0.65	8.21
P6244	1.22	0.57	NA	NA	10.28	NA	1.13	0.61	9.01
P6246	1.15	0.61	0.74	0.93	9.19	7.98	0.98	0.71	7.08
P6247	1.23	0.56	NA	NA	10.55	NA	1.05	0.66	7.94
P6248	0.88	0.79	NA	NA	6.00	NA	0.95	0.73	6.67
P63215	1.27	0.54	NA	NA	11.20	NA	1.17	0.59	9.61
P63521	1.86	0.37	0.60	1.15	26.37	26.06	1.12	0.62	8.87
P63753	1.27	0.55	0.93	0.75	11.08	8.38	1.12	0.62	8.85
P9010	0.91	0.76	0.21	3.38	6.32	13.60	0.94	0.74	6.61
P9011	0.77	0.90	NA	NA	4.94	NA	1.12	0.62	8.82
P9012	1.11	0.63	NA	NA	8.66	NA	0.91	0.76	6.28
P9013	1.23	0.56	NA	NA	10.52	NA	1.27	0.54	11.23
P9016	0.98	0.71	NA	NA	7.03	NA	0.94	0.74	6.56
P9018	0.95	0.73	NA	NA	6.72	NA	1.00	0.69	7.32
P9019	0.27	2.61	NA	NA	1.89	NA	NA	NA	NA
P9020	1.05	0.66	NA	NA	7.96	NA	1.09	0.64	8.39
P9021	1.07	0.64	NA	NA	8.22	NA	1.09	0.64	8.41
P9022	1.11	0.63	NA	NA	8.65	NA	1.12	0.62	8.79
P9023	1.31	0.53	NA	NA	11.82	NA	1.18	0.59	9.73
P9024	1.08	0.64	NA	NA	8.33	NA	0.97	0.72	6.91
P9025	0.76	0.92	NA	NA	4.83	NA	0.82	0.84	5.42
P9026	0.52	1.33	NA	NA	3.16	NA	1.12	0.62	8.89
P9028	0.36	1.92	NA	NA	2.31	NA	NA	NA	NA
P9029	0.63	1.10	NA	NA	3.86	NA	1.12	0.62	8.78
P9030	1.17	0.59	NA	NA	9.54	NA	1.11	0.63	8.65
P9031	0.48	1.44	NA	NA	2.93	NA	0.57	1.22	3.46
P9032	0.92	0.75	0.37	1.87	6.39	8.75	1.01	0.69	7.38
P9034	1.48	0.47	NA	NA	15.34	NA	1.44	0.48	14.50
P9075	0.37	1.87	NA	NA	2.35	NA	NA	NA	NA
P9077	1.02	0.68	0.51	1.36	7.49	8.29	1.05	0.66	7.92
P9079	1.41	0.49	0.77	0.90	13.71	11.50	1.39	0.50	13.42
PRB931	0.58	1.20	NA	NA	3.52	NA	1.12	0.62	8.80
PRB939	0.93	0.75	NA	NA	6.46	NA	1.06	0.66	8.00
PRB940	0.52	1.33	0.94	0.74	3.17	NA	NA	NA	NA
PRB943	1.78	0.39	0.60	1.16	23.57	23.57	1.34	0.52	12.42
PRB951	1.10	0.63	NA	NA	8.60	NA	1.09	0.63	8.45
PRB952	1.11	0.62	0.22	3.14	8.69	18.30	1.12	0.62	8.77
PRB957	0.83	0.84	NA	NA	5.44	NA	0.98	0.71	7.06
Mean	1.01	0.83	0.60	1.56	8.63	13.94	1.09	0.66	8.78
SD	0.37	0.45	0.30	1.01	5.30	6.30	0.18	0.14	2.54
Median	1.06	0.65	0.60	1.16	8.04	12.55	1.11	0.62	8.71
Q25	0.76	0.56	0.40	0.84	4.88	8.47	1.00	0.60	7.33
Q75	1.24	0.91	0.83	1.75	10.62	17.94	1.15	0.69	9.30

^aR₀, basic reproductive ratio calculated using r_max, median viral decay of 0.60 day⁻¹, and a τ of 1 day. R₀* is the R₀ for patients with an individually estimated α. R_0g, basic reproductive ratio calculated from group analyses, α of 0.60 day⁻¹, and a τ of 1 day. ID, patient identification number; r_max, maximal individual expansion rate; t₂, doubling time; α, decay rate for patients with data postpeak; t_1/2, half-life postpeak; r_g, expansion rate from group analysis; t_2g, doubling time from group analysis; Q25 and Q75, first and third quartiles, respectively; NA, not available.

Time to viral load peak and profile shape.

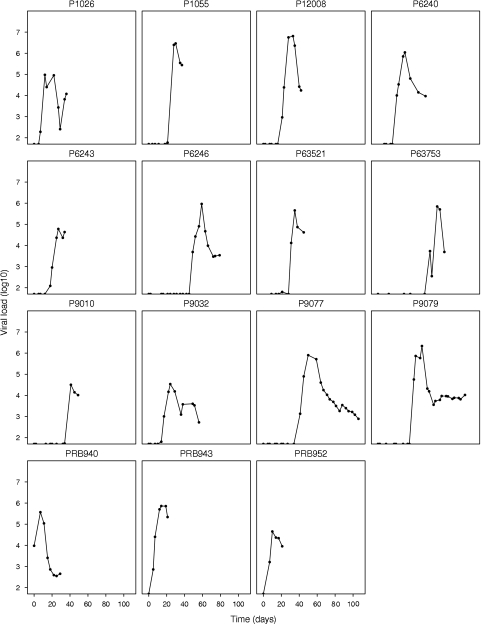
In 15 patients (P1026, P1055, P6240, P6243, P6246, P9010, P9032, P9077, P9079, P12008, P63521, P63753, PRB940, PRB943, and PRB952), we could observe the viral load peaking and then starting to decline, since they had at least two data points postpeak (Fig. 3). For these patients, the median time between the last measurement below the lower limit of detection, 50 HIV RNA copies/ml, to the maximum measured viral load was 14 days (IQR, 10.5 to 14 days). The median peak viral load for these patients was 5.8 log RNA copies/ml, with an IQR of 4.7 to 6.0 log RNA copies/ml. Estimates of the r_max, α, R₀, and half-life of the virus during its postpeak decline in these patients are listed in Table 1.

FIG. 3.

Early viral load profiles for the 15 patients who showed a viral peak and postpeak decay. The data for these patients were used to estimate the postpeak decay rate of the virus.

Viral decay/half-life.

Since we have no data on the rate of decline of infected cells, we estimated the productively infected cell death rate, δ, by the viral load decay rate postpeak, α (Fig. 1). Most patients do not have data for a period of time long enough to show viral decay. However, for the 15 patients who showed a viral load peak, the median viral load decay rate was 0.60 day⁻¹, with an IQR of 0.40 to 0.83 day⁻¹ (Table 1). The corresponding median viral load half-life was 1.2 days.

Estimates of R₀.

For all patients, we calculated R₀ using the estimated median viral decay rate of 0.60 day⁻¹ noted above. For those patients who had enough data to estimate the viral decay rate (Fig. 3), we also calculated R₀ using their individually determined value of α.

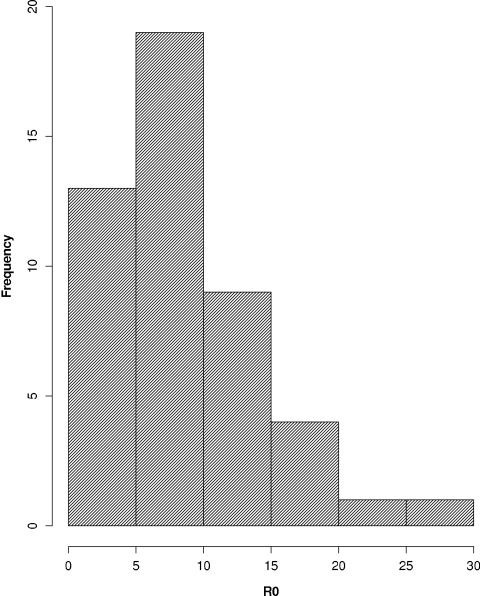
The median R₀ found with the highest expansion rate, r_max, for each individual patient, the median individual decay rate of 0.60 day⁻¹, and an eclipse time of 1 day was 8.0 (IQR, 4.9 to 11) (Table 1). A histogram of the distribution of R₀ values is shown in Fig. 4. Using the average expansion rate from the group analysis, r_g, the decay rate of 0.60 day⁻¹, and an eclipse time of 1 day gave an R_0g of 8.8 ± 2.5.

FIG. 4.

Histogram of R₀ calculated from the highest expansion rate in each of the 47 patients studied.

In the subset of patients who showed a viral load peak and subsequent decay, the individual maximal expansion and decay rates resulted in higher R₀ values, with a median R₀ of 13 (IQR, 8.5 to 18).

DISCUSSION

Here, we analyzed the viral load profiles of 47 patients in very early HIV-1 infection. This is a unique data set that allows the observation and measurements of viral load during primary infection, even before the initial peak in viral load. Our main objective was to determine R₀, the basic reproductive ratio. For the whole population, based on a mixed-effects model, we obtain an estimated R_0g of 8.8 if we assume that the eclipse phase of viral infection is 24 h (7, 16a). In addition, our results also give an idea of how variable R₀ is in the human population. Seventy-five percent of the individuals in our sample have an R₀ of <11, but a few individuals could have a basic reproductive ratio of >20. Whether this is just a random distribution, or whether it represents individuals with specific susceptibility to infection, cannot be ascertained from this data set. In any case, these results seem to indicate that a reduction in R₀ of 10- to 20-fold, say, by vaccine-induced immunity, could drive R₀ below 1 and lead to prevention of HIV infection in a majority of HIV-exposed individuals. Moreover, our estimate for the net loss rate of infected cells (α = 0.60 cells day⁻¹) is significantly lower than that obtained by drug treatment during chronic infection, i.e., δ = 1.0 cells day⁻¹ (16). This could be because, later in infection, an acquired immune response develops that contributes to this loss. If this is the case, then this effect mimicked by a vaccine could reduce R₀ to about 5. Alternatively, this difference could be due to ongoing viral infection, which would affect our estimate of α but not δ. If we use an δ of 1.0 cell day⁻¹, the median R₀ would be 6 even in early infection, before the development of acquired immunity, consistent with the prior analysis of Stafford et al. (27).

A question that remains is what is occurring in patients prior to the time at which their viral load exceeds the lower limit of detection and hence prior to the time the virus starts to grow exponentially. In the study by Fiebig et al. (8), viral blips occurring before this time were reported, and it may be that the viral load fluctuates before full viral infection sets in, as suggested by stochastic models of infection (J. E. Pearson, P. Krapivsky, and A. S. Perelson, submitted for publication). If this is the case, there may be a window of opportunity, before the virus starts to grow uncontrollably, where an intervention (e.g., vaccine) could be effective even if it cannot lower R₀ 10- to 20-fold. Indeed, our estimates of R₀ are only valid once the virus starts to grow exponentially; before that, viral blips may indicate localized small bursts of viral production with an R₀ below or near 1. More experimental data using more-sensitive assays at these extremely early times would be needed to understand these aspects of the viral dynamics.

Two other studies have analyzed the value of R₀ in the setting of HIV-1 infection. Stafford et al. (27) analyzed 10 patients, who were only identified and fitted a model similar to that given by equations 1 to 3. In this way, they obtained estimates for the parameters of the model and were able to calculate R₀ using expression (4). They found a median R₀ of 5.7, with a range between 2.8 and 11.0. These values are lower than those found in the current study. This is most likely due to late identification of the subjects, when viral load growth decelerates as the virus nears the peak. Indeed, using their data to calculate the maximum expansion rate, r_max, as we did here, we found a mean r_max of 0.13 day⁻¹, much lower than ours. On the other hand, calculating the decay rate from the peak for their subjects, we found an α of 0.48 day⁻¹, just slightly lower than ours.

The other study, by Little et al. (15), calculated R₀ in only four patients and used a method analogous to the one in the current study, i.e., calculating R₀ based on the initial expansion rate of the virus. However, for three patients, viral load measurements were collected only within days of the peak, potentially reflecting a reduced rate of expansion as the viral load growth slows before the peak. Thus, those authors attempted to infer the initial expansion rate by correcting the observed expansion rate, taking into account the slowed expansion due to target cell loss (15). With this correction, the average expansion rate found was 2.0 day⁻¹, which is much higher than the expansion rate found here. Without the correction, their expansion rate was 0.85 day⁻¹, slightly lower than our median of 1.06 day⁻¹. The R₀ value calculated also depended on the correction for target cells; it was calculated by multiplying the R₀ value obtained from the observed expansion rate by the fold decrease in CD4⁺ T cells calculated by the ratio of the assumed preinfection value of 1,000 RNA cells/μl (the true value being unknown in that study) and the first measurement at presentation. For the four patients, they found R₀ values of 23, 34, 7, and 12, averaging to 19.3. Our data, including many more patients with much better early sampling, allowed us to calculate an R₀ that is lower than that found by Little et al. (15). The discrepancy could be due to either the correction factors introduced by Little et al. (15) or perhaps some bias in patient selection. The latter could arise since patients were identified because they were symptomatic (15). Interestingly, in that study, they estimated the viral decline from the peak (α) in eight subjects and found an α of 0.3 day⁻¹, lower than in the present study.

It is interesting to compare our results to those found in macaques, which are often used as a prototypic model of HIV infection for vaccine studies. Nowak et al. (19) found the expansion rate r for 12 macaques infected with SIVsmE660. The average r for the group was 2.20 day⁻¹, similar to that found by Little et al., with a doubling time of 0.32 days. In the study by Nowak et al. (19), the decay after the peak viral load occurred with a mean rate of 0.52 day⁻¹, with a range from 0.18 to 0.86 day⁻¹ (half-life of 1.33 days). These values are very similar to the values we found here. Due to the large estimated value of r, Nowak et al. estimated a mean R₀ of 36.5, with a range of 5.4 to 68, using an eclipse phase duration of 1 day (19). This value, like the expansion rate r, is much greater than our highest R₀ values. The specific strain of SIV or the macaque model may account for the difference. Also, these differences may indicate that a vaccine that works in macaques has to pass a more stringent test, from the point of view of reducing viral growth, than that needed for humans.

Overall, we were able to provide an estimate for R₀ and for its variation across infected individuals, based on very early viral load data postinfection. According to our analysis, HIV has an R₀ with an interquartile range between 5 and 11, with most patients having an R₀ close to 8 (see histogram of R₀ in Fig. 4). Thus, in order to prevent chronic infection in a majority of patients, an early infection intervention, such as a vaccine, must be about 90% effective in reducing viral growth.