Transient release kinetics of rod bipolar cells revealed by capacitance measurement of exocytosis from axon terminals in rat retinal slices

Abstract

Presynaptic transmitter release has mostly been studied through measurements of postsynaptic responses, but a few synapses offer direct access to the presynaptic terminal, thereby allowing capacitance measurements of exocytosis. For mammalian rod bipolar cells, synaptic transmission has been investigated in great detail by recording postsynaptic currents in AII amacrine cells. Presynaptic measurements of the dynamics of vesicular cycling have so far been limited to isolated rod bipolar cells in dissociated preparations. Here, we first used computer simulations of compartmental models of morphologically reconstructed rod bipolar cells to adapt the ‘Sine + DC’ technique for capacitance measurements of exocytosis at axon terminals of intact rod bipolar cells in retinal slices. In subsequent physiological recordings, voltage pulses that triggered presynaptic Ca²⁺ influx evoked capacitance increases that were proportional to the pulse duration. With pulse durations ≤100 ms, the increase saturated at ∼10 fF, corresponding to the size of a readily releasable pool of vesicles. Pulse durations ≥400 ms evoked additional capacitance increases, probably reflecting recruitment from additional pools of vesicles. By using Ca²⁺ tail current stimuli, we separated Ca²⁺ influx from Ca²⁺ channel activation kinetics, allowing us to estimate the intrinsic release kinetics of the readily releasable pool, yielding a time constant of ∼1.1 ms and a maximum release rate of 2–3 vesicles (release site)⁻¹ ms⁻¹. Following exocytosis, we observed endocytosis with time constants ranging from 0.7 to 17 s. Under physiological conditions, it is likely that release will be transient, with the kinetics limited by the activation kinetics of the voltage-gated Ca²⁺ channels.

Introduction

Chemical synaptic transmission occurs when docked vesicles in the presynaptic terminal fuse with the plasma membrane and release neurotransmitter onto postsynaptic receptor channels. Ribbon synapses, found in neurons that convey visual, auditory and electrosensory signals (review by Sterling & Matthews, 2005), constitute a special subclass of chemical synapses that can sustain high rates of exocytosis (Heidelberger et al. 1994; von Gersdorff et al. 1996). The vesicles docked at the plasma membrane of a ribbon synapse are thought to represent the readily releasable pool of vesicles (Mennerick & Matthews, 1996; von Gersdorff et al. 1996). The dynamics of vesicular cycling have been studied in great detail by capacitance measurements from the large presynaptic terminals of goldfish retinal bipolar cells, both from isolated terminals in dissociated preparations (e.g. Heidelberger et al. 1994) and from isolated terminals in retinal slices (e.g. Palmer et al. 2003a,b;). However, our knowledge of the rod bipolar ribbon synapse in the mammalian retina is considerably more limited. The main reason for this is the difficulty of performing whole-cell recordings from axon terminals of mammalian rod bipolar cells in situ (Veruki et al. 2006). An additional complicating factor is that the passive membrane properties of rod bipolar cells cannot generally be adequately described by a single-compartment model (Oltedal et al. 2007, 2009; see also Mennerick et al. 1997; Palmer et al. 2003b). With branching cells that cannot be described as simple resistor–capacitor (RC) circuits, capacitance measurements may still be feasible, but require careful morphological analysis and modelling (Hallermann et al. 2003; Kushmerick & von Gersdorff, 2003). Here we have adapted the ‘Sine + direct current’ (‘Sine + DC’) technique, originally developed for cells that can be described as a single electrical compartment (Lindau & Neher, 1988; Gillis, 1995), for capacitance measurements at axon terminals of rod bipolar cells in situ.

Rod bipolar cells are presynaptic to AI and AII amacrine cells. Whereas rod bipolar cells display a predominantly sustained visual response (Dacheux & Raviola, 1986; Euler & Masland, 2000), AII amacrine cells display an enhancement of the transient response component (Nelson, 1982; Dacheux & Raviola, 1986). It was recently proposed, on the basis of dual recordings from synaptically connected rod bipolar cells and AII amacrine cells, that the enhanced transient response of AII amacrines is caused by the presynaptic release of a relatively small number of readily releasable vesicles and that the release kinetics of rod bipolar cells are inherently transient (Singer & Diamond, 2003, 2006). However, there are some important limitations of studying transmitter release by recording postsynaptic currents (e.g. Sun & Wu, 2001; Wölfel & Schneggenburger, 2003). For example, saturation and desensitization of postsynaptic receptors can give rise to a non-linear relationship between presynaptic release and postsynaptic currents and the time course of depletion of a vesicle pool can be wrongly estimated. In addition, endocytosis cannot be measured directly by recording postsynaptic currents. We therefore decided to extend previous studies of transmitter release from rod bipolar cells by applying presynaptic capacitance measurements to recordings from the axon terminals of rod bipolar cells in situ, with a specific focus on estimating the size and release kinetics of a readily releaseable pool of vesicles.

Previous capacitance measurements of exocytosis from rod bipolar cells have been limited to recordings from dissociated retina preparations (Pan et al. 2001; Zhou et al. 2006). In this study, we first used computer simulations of morphologically reconstructed rod bipolar cells to optimize and validate capacitance measurements with axon terminal recordings. Then, we used patch-clamp recordings from rod bipolar axon terminals in acute retinal slices and obtained evidence for a readily releasable pool of vesicles with capacitance ∼10 fF. The pool could be released with a time constant of ∼1.1 ms, corresponding to a maximum release rate of 2–3 vesicles (release site)⁻¹ ms⁻¹.

Methods

Retinal slice preparation

General aspects of the methods have previously been described in detail (Oltedal et al. 2007). Albino rats (4–7 weeks postnatal) were deeply anaesthetized with isoflurane in oxygen and killed by cervical dislocation (procedure approved under the surveillance of the Norwegian Animal Research Authority). Retinal slices were cut by hand with a curved scalpel blade at a thickness of ∼50 to ∼150 μm. The slices were visualized (Axioskop 2 FS, Zeiss) with a ×60 water immersion objective (0.9 NA; Olympus) and infrared differential interference contrast (IR-DIC) videomicroscopy. Recordings were carried out at room temperature (22–25°C).

Solutions and drugs

The extracellular perfusing solution was continuously bubbled with 95% O₂–5% CO₂ and had the following composition (in mm): 125 NaCl, 25 NaHCO₃, 2.5 KCl, 2.5 CaCl₂, 1 MgCl₂, 10 glucose, pH 7.4 (osmolarity ∼300 mosmol l⁻¹). Recording pipettes were filled either with intracellular solution A (in mm): 125 CsCl, 8 NaCl, 1 CaCl₂, 5 EGTA, 10 Hepes, 15 tetraethylammonium chloride (TEA-Cl), 4 MgATP, 0.5 NaGTP (osmolarity ∼315 mosmol l⁻¹) or with intracellular solution B (in mm): 125 caesium methanesulfonate (CsCH₃SO₃), 10 TEA-Cl, 8 NaOH, 1 CaCl₂, 5 EGTA, 10 Hepes, 4 MgATP, 0.3 NaGTP, biocytin (1 mg ml⁻¹) (osmolarity ∼300 mosmol l⁻¹). Each intracellular solution also contained Lucifer yellow (1 mg ml⁻¹) and pH was adjusted to 7.3 with CsOH. Cs⁺-based internal solutions with addition of TEA-Cl were used to block K⁺ currents and permit measurement of Ca²⁺ currents in some experiments. We did not employ additional blocking agents that might interfere with vesicle release (cf. Keen & Hudspeth, 2006). In some recordings, however, we observed that presynaptic Ca²⁺ currents could be contaminated by slowly activating, outward K⁺ currents. With 5 mm EGTA and 1 mm CaCl₂, the free concentration of EGTA will be about 4 mm and the free concentration of Ca²⁺ will be about 20 nm (see Supplemental material, available online only). This may inhibit some of the recruitment and release of slower vesicle pools, but should not affect release of the readily releaseable pool that is the primary focus of the present study. Solution A was used in initial experiments where we wanted to study exocytosis isolated from endocytosis by utilizing the inhibitory effect of high internal chloride on endocytosis (Hull & von Gersdorff, 2004). In later experiments, where we intended to measure endocytosis in addition to exocytosis, we used solution B with lower internal chloride. Because we could not find any evidence for a difference between the two solutions with respect to exocytosis, we have combined the results when reporting such measurements. Theoretical liquid junction potentials (the potential of the extracellular solution relative to that of the intracellular solution) were calculated to be +3.3 mV and +9.2 mV for intracellular solutions A and B, respectively (JPCalcW; Molecular Devices, Sunnyvale, CA, USA). Membrane holding potentials (V_hold) were automatically corrected for the liquid junction potential on-line.

Drugs were added directly to the extracellular solution used to perfuse the slices and were present throughout all recordings. The concentrations of drugs were as follows (μm; supplier Tocris Bioscience, Bristol, UK, unless otherwise noted): 10 bicuculline methchloride, 1 strychnine (Research Biochemicals Inc., Natick, MA, USA), 50 (1,2,5,6-tetrahydropyridin-4-yl)methylphosphinic acid (TPMPA), and 50 dl-threo-β-benzyloxyaspartic acid (TBOA). Solutions were either made up freshly for each experiment or were prepared from concentrated aliquots stored at −20°C. TEA-Cl and CsCl were added to the extracellular solution at 20 and 1 mm, respectively, with TEA-Cl replacing an equivalent concentration of NaCl. Both TEA-Cl and CsCl were present throughout all recordings.

Electrophysiological recording and data acquisition

Patch pipettes were pulled from thick-walled borosilicate glass (outer diameter, 1.5 mm; inner diameter, 0.86 mm). Electrodes were coated with Parafilm (American National Can; Greenwich, CT, USA) to reduce their capacitance and were heat-polished before use. In addition, the fluid level both in the recording chamber and in the pipette was kept low to minimize the electrode capacitance. The open-tip resistance of the pipettes ranged from ∼5 to ∼12 MΩ when filled with either intracellular solution (mean ±s.e.m., 6.9 ± 0.2 MΩ; n= 49). Whole-cell voltage-clamp recordings from rod bipolar cell axon terminals or somata (Oltedal et al. 2007) were performed with an EPC9-dual amplifier controlled by PatchMaster software (HEKA Elektronik, Lambrecht/Pfalz, Germany). After establishing GΩ-seals, currents caused by the recording electrode capacitance (C_fast) were automatically measured and neutralized by the amplifier. The C_fast was 3.8 ± 0.1 pF (range 3.0–7.4 pF) and the mean C_fast time constant was 1.00 ± 0.03 μs (range 0.8–1.8 μs; n= 49). After breaking into the cell, currents caused by the cell membrane capacitance (C_slow) were partially neutralized by the amplifier. Between periods with capacitance measurements, cells were voltage clamped at V_hold=−60 mV. Pipette pressure was monitored continuously with a digital manometer (Sigmann Elektronik, Hüffenhardt, Germany) and manually adjusted to a slighty negative level (−0.7 mbar; Heidelberger et al. 2002; Hull & von Gersdorff, 2004).

The on-line estimate of R_s by the PatchMaster software is based on fitting the capacitive current decay with a single-exponential function and consistently overestimates R_s in axon terminal recordings (Oltedal et al. 2007). To avoid this problem, we estimated R_s off-line from capacitive current transients evoked by 10 mV hyperpolarizations (15 ms duration), with the C_slow capacitance neutralization disabled. In this way, R_s was monitored regularly throughout a whole-cell recording. R_s in axon terminal recordings was 96 ± 6 MΩ (n= 45) and R_s in soma-end recordings was 20 ± 3 MΩ (n= 4). At a holding potential of −60 mV the mean holding current was −7.5 ± 1.0 pA (n= 49). The membrane resistance (R_m), estimated from the steady-state current at the end of the 10 mV hyperpolarizing voltage pulses, was 6.4 ± 0.7 GΩ for axon terminal recordings (n= 45) and 3.6 ± 1.0 GΩ for soma-end recordings (n= 4). When we sampled other current responses, the C_slow capacitance neutralization circuitry was enabled and signals were low-pass filtered with a corner frequency (−3 dB) between 1/5 and 1/3 of the inverse of the sampling interval (10–200 μs; depending on protocol).

When we investigated the frequency dependence of activation of voltage-gated currents, we used a time-varying voltage stimulus described by a ZAP-function (impedance (Z) amplitude profile (AP)):

(1)

where a is the peak amplitude, and b, c and d are empirically assigned constants (Puil et al. 1986). The values of these constants were chosen to obtain waveforms with amplitudes ±15 and ±30 mV (relative to V_hold) and frequencies ranging from ∼5 Hz to ∼2.5 kHz. Each waveform had a duration of 1 s, with constant voltage segments (200 ms duration) added at the beginning and end. Before using a waveform as a stimulus, it was temporally reversed, such that the highest frequencies preceded the lowest frequencies. To subtract leak and capacitive currents, we generated leak subtraction stimuli by multiplying the amplitude of each original stimulus waveform by 1/4. The average leak response (n= 10 repetitions) was multiplied by 4 and subtracted from the response evoked by the original stimulus. When we recorded voltage-gated currents evoked by square-wave voltage pulses, leak and capacitive currents were subtracted by standard P/N protocols (for details, see figure legends).

Capacitance measurements in physiological recordings

Capacitance measurements were obtained with the ‘Sine + DC’ technique (Lindau & Neher, 1988; Gillis, 1995) as implemented in PatchMaster software in combination with the EPC9 amplifier. For each of the sine wave frequencies used in the experiments, we calibrated phase and attenuation values manually by using the 6 pF capacitance of the MC-9 model cell circuit (HEKA Elektronik). To confirm that a correct calibration had been obtained, we reduced the setting of C_fast by 1, 3, or 5 pF and applied the stimulus protocols used for the physiological experiments. The magnitude with which C_fast had been reduced was accurately predicted at all sine wave frequencies tested (except for a slight drop at 10 kHz), indicating that the calibration procedure and the phase setting were both correct.

During capacitance measurements, the C_slow capacitance neutralization circuitry was transiently disabled. We applied sine wave voltage stimuli with frequency (f_c) ranging from 100 Hz to 10 kHz and amplitudes of ±15 or ±30 mV relative to V_hold. For a sine wave stimulus with frequency f_c, the current signal was low-pass filtered (analog 3- and 4-pole Bessel filters in series) with a cut-off frequency of 2f_c and sampled at a frequency of 10f_c. After sampling, the current signal was processed by the lock-in extension of PatchMaster to obtain estimates of membrane capacitance (C_m), membrane conductance (G_m; inverse of R_m) and series conductance (G_s; inverse of R_s) with a temporal resolution of one data point per sine wave cycle. Because G_m in rod bipolar cells can be very low, with noise causing some measurement points to be very close to zero, R_m can become correspondingly large (infinity, if G_m happens to be zero). In the figures we have therefore plotted G_m instead of R_m, and to be internally consistent, we also plotted G_s instead of R_s. The reversal potential (E_rev) of the DC (direct current; steady state) (I_DC) was by default set to 0 mV. We verified, through simulations and off-line re-calculations with E_rev=−55 mV, that the results obtained for C_m were independent of the exact value of E_rev when it ranged between 0 and −60 mV (see Results). Stimulus-evoked changes in C_m (ΔC_m), R_m (ΔR_m) and R_s (ΔR_s) were calculated as the difference between the mean of each parameter during a 400 ms period before the stimulus and the mean value during a 400 ms period (for stimulus durations <400 ms) or a 1000 ms period (for stimulus durations ≥400 ms) after the stimulus. The standard depolarizing stimulus applied to a rod bipolar cell was a pulse from V_hold to −10 mV. This has been reported to evoke a maximal EPSC amplitude in postsynaptic AII amacrine cells (Singer & Diamond, 2003). Depolarizing stimuli were applied at intervals of ∼30 s, presumably sufficient to recover from potential paired-pulse depression of release (Wan et al. 2008). Before and after the depolarizing voltage pulse, the membrane potential was held constant (without sine wave modulation) for 25 ms. To investigate endocytosis, we obtained low-resolution measurements of C_m by averaging measurements repeated at 2 Hz (2 kHz sine wave stimulation for 100 ms). In experiments where we obtained baseline estimates of C_m, G_m and G_s at a series of sine wave stimulus frequencies (100 Hz to 10 kHz), each data point was calculated as the mean of one or two 100 ms periods.

General statistical analysis and data presentation

Data were analysed with FitMaster (HEKA Elektronik) and IGOR Pro (WaveMetrics, Lake Oswego, OR, USA). Data are presented as means ±s.e.m. (n= number of cells). Statistical analyses with comparisons between or within groups were performed using Student's two-tailed t test (unpaired or paired as stated). Correlations were analysed with Spearman's rank order correlation test. Differences were considered statistically significant at the P < 0.05 level. The number of individual traces included in the averaged current traces in the figures are stated for each case.

Imaging

Each cell was filled with Lucifer yellow and after the recording, fluorescence microscopy allowed visualization of the cell's full morphology. For some cells, fluorescence images at a series of focal planes were acquired with a digital CCD camera (CoolSnap ES; Photometrics/Roper Scientific, Tucson, AZ, USA) controlled by RSImage (Photometrics/Roper Scientific) running under Windows XP. During image acquisition, exposure to UV light was controlled by an electronic shutter (Uniblitz VCM-D1, Vincent Associates, NY, USA), thereby minimizing the total exposure time. Subsequently, the images were assembled in a montage to reveal the cell's morphology and digital manipulation was used to improve visualization of the morphological characteristics (ImageJ version 1.37v, W. S. Rasband, US National Institutes of Health, Bethesda, MD, USA, http://rsb.info.nih.gov/ij/ or Adobe Photoshop 7.0, Adobe Systems).

Computer simulations

Computer simulations were performed with NEURON (version 6.1.2) running under Mac OS X (10.4 and 10.5) (Carnevale & Hines, 2006). All simulations were run with a variable time step with absolute tolerance set to 0.0001. For analysis, data were imported to IGOR Pro. In the simulations, an idealized single-electrode voltage clamp (SEClamp; taken from the standard repertoire of NEURON point processes) was connected to a specific compartment of a morphologically reconstructed rod bipolar cell with the following passive membrane parameters (for details, see Oltedal et al. 2009): cytoplasmic resistivity (R_i) = 190 Ω cm, specific membrane capacitance = 1.07 μF cm⁻², and specific membrane resistance (R_m) = 20.8 kΩ cm². The morphological and passive membrane parameters of this cell were close to and representative of the averages of a group of reconstructed rod bipolar cells (for details, see Oltedal et al. 2009). In the simulations, we varied the theoretical value of R_s for the SEClamp (R_s(theory)) to examine the effects of uncompensated R_s on the capacitance measurements. E_rev of the leak current (e_pas) was set to −60 mV. Spatial discretization (compartmentalization) was implemented by applying the d_lambda rule (Carnevale & Hines, 2006). Briefly, the alternating current (AC) length constant at 100 Hz (λ₁₀₀) was calculated for each section and the number of segments (nseg) in each section was adjusted such that the length of each segment was smaller than a fraction d_lambda of λ₁₀₀. The fraction was set by the adjustable parameter d_lambda= 0.01 for all simulations. Before each simulation run, the model was initialized to steady state (Carnevale & Hines, 2006).

To simulate an increase in capacitance, we increased either the diameter or the specific membrane capacitance of a restricted part of the axon terminal. For analysis of the capacitance of the computer model, we applied a sine wave voltage stimulus using an SEClamp point process located at a specific compartment of the rod bipolar cell. The temporal resolution of the stimulus was 1 μs, the amplitude was ±15 mV relative to V_hold and f_c ranged from 100 Hz to 10 kHz. First, we determined the phase of the sine wave stimulus by fitting it with the function,

(2)

where A is the amplitude, α is the phase, and 2πf_c is equivalent to the angular frequency (ω). Second, we determined the real and imaginary components of the current response (in phase and 90 deg out of phase with the voltage stimulus, respectively) by fitting it with the function,

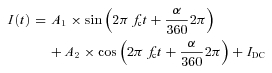(3)

where A₁ is the amplitude of the real component, A₂ is the amplitude of the imaginary component, and α is the phase (determined by eqn (2)). C_m, R_m and R_s were calculated from A₁, A₂ and I_DC, according to eqn (28) in Gillis (1995). By default, E_rev for I_DC was set to −60 mV, corresponding to E_rev (e_pas) of the leak current.

Results

When standard capacitance measurement techniques are extended to handle morphological structures with arbitrary geometry that cannot be represented by a simple, electrically equivalent RC circuit, it is necessary to carefully validate the method (Hallermann et al. 2003; Kushmerick & von Gersdorff, 2003). In our case, the goal was to quantify the capacitance increase that is expected to result from exocytosis of transmitter vesicles at the ribbon synapses located at the axon terminals of rod bipolar cells and to perform such measurements directly from axon terminals of intact cells in slices. In principle, there are two recording approaches available, either soma-end or terminal-end recordings (Fig. 1). In neither case can a rod bipolar cell be modelled as a simple, one-compartment RC circuit (Oltedal et al. 2007). In our experiments, we followed the approach taken by Hallermann et al. (2003) in their capacitance measurements of exocytosis at mossy fibre boutons in the hippocampal slice preparation. We started by simulating capacitance increases at the axon terminal of a computer model of a rod bipolar cell, previously physiologically characterized and morphologically reconstructed (Oltedal et al. 2009). We applied the ‘Sine + DC’ technique (Lindau & Neher, 1988; Gillis, 1995) for quantifying the capacitance increase via either terminal-end or soma-end recordings and evaluated the accuracy of the results obtained with each recording configuration. Based on these results, we decided that terminal-end recording was the optimal technique for capacitance measurements. Finally, with electrophysiological recordings from rod bipolar axon terminals in in vitro slices, we validated the sine wave stimulus parameters and characterized the magnitude and release kinetics of the readily releasable pool of synaptic vesicles.

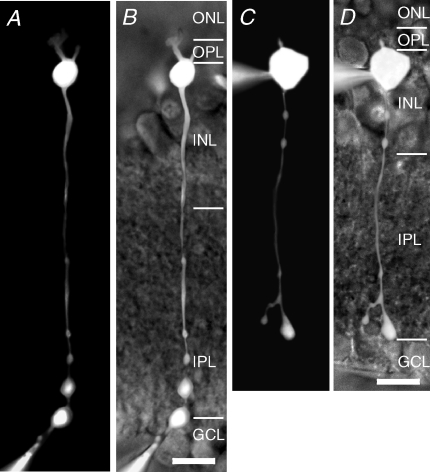
Figure 1. Rod bipolar cells in the rat retina recorded from the axon terminal or the soma.

A, composite fluorescence digital micrograph of a rod bipolar cell filled with Lucifer yellow from a recording pipette placed at the axon terminal. The micrograph was generated by assembling a series of images taken with epifluorescent illumination at different focal planes. B, micrograph in A overlaid on an infrared micrograph to show the position of the cell in the retinal slice. The retinal layers are indicated by abbreviations (ONL, outer nuclear layer; OPL, outer plexiform layer; INL, inner nuclear layer; IPL, inner plexiform layer; GCL, ganglion cell layer). Scale bar: 10 μm (A and B). C, composite fluorescence digital micrograph of a rod bipolar cell filled with Lucifer yellow from a recording pipette placed at the soma (generated as in A). D, micrograph in C overlaid on an infrared micrograph to show the position of the cell in the retinal slice. The retinal layers are indicated by abbreviations (as in B). Scale bar: 10 μm (C and D).

Soma-end versus terminal-end recordings for capacitance measurement of exocytosis from rod bipolar cells in situ

Using computer simulations to increase the capacitance at the axon terminal of a morphologically reconstructed rod bipolar cell (Fig. 2), we asked a series of related questions with respect to our ability to quantify both the baseline capacitance (C_m) and the capacitance increase (ΔC_m) following exocytosis. First, what are the differences between the results obtained with soma-end versus terminal-end recordings? Second, how does the frequency of the sine wave stimulus influence capacitance measurements? Finally, how do changes in R_s influence the measurements of C_m and ΔC_m?

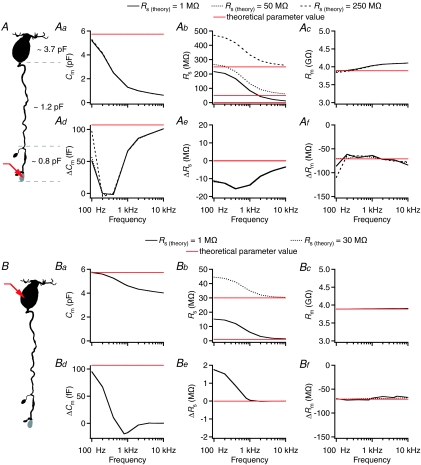
Figure 2. Performance of the ‘Sine + DC’ technique for measuring capacitance of rod bipolar cells and capacitance increase at the axon terminal with computer simulations of either terminal-end or soma-end recording.

A, shape plot of morphologically reconstructed rod bipolar cell (for details, see Oltedal et al. 2009) used for computer simulations. Red arrow indicates position of idealized single-electrode voltage clamp (SEClamp) connected to an axonal ending where a capacitance increase was simulated (grey). The total capacitance of the soma-dendritic, axonal and axon terminal compartments (demarcated by dashed grey lines) as indicated in the plot. Aa–c, estimates of total capacitance (C_m; Aa), series resistance (R_s; Ab), and total membrane resistance (R_m; Ac) as a function of sine wave stimulation frequency (100 Hz to 10 kHz) for three different values of R_s (R_s(theory); 1, 50 and 250 MΩ). Here and later, theoretical parameter values indicated by red horizontal lines. Ad–f, estimates of changes in capacitance (ΔC_m; Ad), series resistance (ΔR_s; Ae), and membrane resistance (ΔR_m; Af) after increasing the membrane capacitance of an axonal ending by 107 fF (corresponding to an increase in surface area of 10 μm² with specific capacitance 1.07 μF cm⁻²). Estimates indicated as a function of sine wave stimulation frequency (100 Hz to 10 kHz) for three different values of R_s (R_s(theory); as for Aa–c). B, as in A, but with SEClamp (red arrow) connected to soma. Ba–c (as in Aa–c) and Bd–f (as in Ad–f), SEClamp connected to soma, two different values of R_s (R_s(theory); 1 and 30 MΩ). In all simulations the sine wave voltage stimulus amplitude was ±15 mV (from V_hold=−80 mV).

We first addressed the question concerning sine wave frequency. For a simple RC circuit, one can calculate a range of useful stimulus frequencies (cf. eqn (52) in Gillis (1995)), but this approach is not feasible for more complicated morphological structures that cannot be described by a single-compartment equivalent electrical circuit. Thus, we systematically evaluated the accuracy of estimates of C_m, R_m and R_s for a range of sine wave frequencies (100 Hz to 10 kHz) and for different theoretical values of R_s (R_s(theory)) with terminal-end recordings. The morphologically reconstructed rod bipolar cell used for the simulations had a total membrane capacitance (C_m(theory)) of ∼5.7 pF and a membrane resistance (R_m(theory)) of ∼3.9 GΩ. The entire range of sine wave frequencies was tested for three different values of R_s (1, 50 and 250 MΩ). As illustrated in Fig. 2Aa, the estimate of C_m depended strongly on sine wave frequency, with increasing frequency causing progressive underestimation of C_m, but with no effect of different values of R_s. The sine wave frequency had a strong influence on the estimate of R_s, with increasing overestimation for decreasing frequency values (Fig. 2Ab), and a moderate influence on the estimate of R_m, with increasing overestimation for increasing frequency values (Fig. 2Ac). The different values of R_s(theory) had almost no effect on the estimates of R_m (Fig. 2Ac).

We next evaluated the performance of the ‘Sine + DC’ technique with respect to detecting an increase in capacitance at the axon terminal, using the same stimuli and conditions as above. The increased capacitance (ΔC_m(theory)) was simulated as an increase in the membrane surface area of 10 μm², corresponding to an increase of 107 fF. The accuracy, defined as ΔC_m/ΔC_m(theory), was highest for the very lowest frequency tested and for a range of frequencies between 1 and 10 kHz (Fig. 2Ad). Because rat rod bipolar cells cannot be adequately described by a single-compartment equivalent electrical circuit (Oltedal et al. 2007), it is expected that an increase in capacitance will evoke correlated (parallel or antiparallel) changes in the resistive circuit parameters R_m and/or R_s (Gillis, 1995; see also Hallermann et al. 2003). Confirming this, we observed cross-talk between ΔC_m and ΔR_s, with the increase of C_m accompanied by an apparent decrease of R_s (Fig. 2Ae). In contrast, the decrease of R_m (Fig. 2Af) could be fully explained by the reduction expected by the addition of 10 μm² of membrane with ion channel density identical to the rest of the cell membrane. When we increased C_m by increasing the specific membrane capacitance, no correlated change of R_m could be detected (data not shown).

We then evaluated the accuracy of estimates of C_m, R_m and R_s with soma-end recordings from the same rod bipolar cell used above (Fig. 2B). The same range of sine wave frequencies (100 Hz to 10 kHz) was applied with two different values of R_s (1 and 30 MΩ). The estimates for C_m, R_s and R_m were influenced by the sine wave frequency in a qualitatively similar, but less pronounced, way as for terminal-end recordings (Fig. 2Ba–c). However, the performance of soma-end recording, with respect to detecting an increase of capacitance at the axon terminal, was very different from that of terminal-end recording, with a sharp drop in accuracy when the stimulus frequency was higher than 100 Hz (Fig. 2Bd). As for terminal-end recordings, we observed cross-talk between ΔC_m and ΔR_s (Fig. 2Be) and the observed reduction of R_m corresponded to the reduction expected for an increase of the surface area (Fig. 2Bf).

These results suggested that when the goal is to detect a capacitance increase at the axon terminal with high accuracy, one should either use soma-end recordings with low sine wave frequency (100 Hz; Fig. 2Bd) or terminal-end recordings with high sine wave frequency (≥2 kHz; Fig. 2Ad). As described later, the use of very low frequencies confers a higher risk of activating voltage-gated conductances when the sine-wave amplitude is increased in order to increase the signal-to-noise ratio, arguing against the use of soma-end recordings. For terminal-end recordings, there are at least two problems potentially associated with the use of high frequencies. First, very high frequencies can give rise to increased noise (Gillis, 1995). Second, very high frequencies can isolate the axon terminal ending carrying the recording pipette, and thereby prevent detection of a capacitance increase taking place at a neighbouring axon terminal ending (cf. Hallermann et al. 2003; their Fig. 2D). Based on the simulation results, we propose that a sine wave frequency of 2 kHz represents a reasonable compromise between these opposing relationships. Specifically, we observed that with 2 kHz, the value of C_m was ∼1 pF (Fig. 2Aa, similar to the value for the axon terminal compartment (∼0.8 pF; see Fig. 2A). In the following, we further evaluated the performance of the ‘Sine + DC’ technique with a 2 kHz sine wave stimulus.

Detecting capacitance increases at different locations in rod bipolar axon terminals

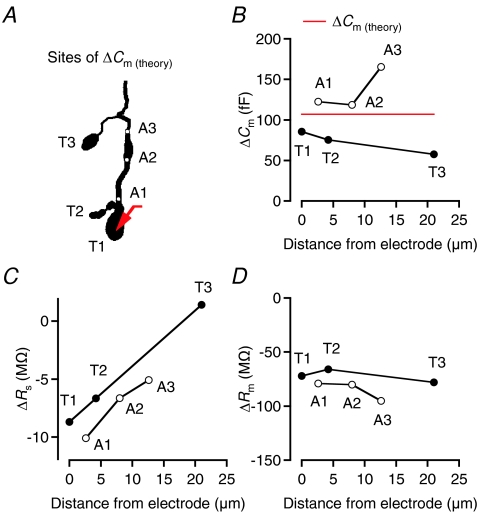
Rod bipolar cells in situ typically have 2–3 axon terminal endings (average 2.4) in stratum 5 of the inner plexiform layer (Oltedal et al. 2009). To evaluate the ability of the ‘Sine + DC’ technique to detect capacitance increases occurring at different locations in the axon terminal, we simulated increased surface area (ΔC_m(theory)= 107 fF) at either of the three axon terminal endings of the rod bipolar cell (T1–T3; Fig. 3A). In each case, the recording electrode (SEClamp) was located at the larger terminal ending (T1; Fig. 3A). The distance from the recording electrode to each of the terminals ranged from 0 to ∼20 μm. As illustrated in Fig. 3B, ΔC_m decreased with increasing distance between the recording electrode and the site of capacitance increase (T1, T2, or T3). If the site of capacitance increase was located in the axon (A1–A3; Fig. 3A), rather than in the terminal endings, the ‘Sine + DC’ technique consistently overestimated the capacitance increase (Fig. 3B). For all but the most distal site of capacitance increase, ΔR_s was negative, but the magnitude of ΔR_s decreased with increasing separation between the recording electrode and the site of capacitance increase (Fig. 3C). ΔR_m was negative, with little influence from the site of capacitance increase (Fig. 3D). This analysis should not be taken to suggest that exocytosis takes place independently at the different terminal endings of a rod bipolar cell in situ. The computational analysis only addressed the question concerning the ability of the ‘Sine + DC’ technique to detect capacitance increases occurring at different distances from the recording electrode. It is currently unknown to what extent release can occur independently at different terminals under physiological conditions.

Figure 3. Accuracy of ΔC_m estimates as a function of location of capacitance increase investigated by computer simulation.

A, shape plot of morphologically reconstructed rod bipolar cell used for computer simulations (same cell as in Fig. 1). Red arrow indicates position of idealized single-electrode voltage clamp (SEClamp) connected to one of the axonal endings (T1) of the axon terminal. ΔC_m of 107 fF (corresponding to an increase in surface area of 10 μm² with specific capacitance 1.07 μF cm⁻²) simulated at three different axonal endings (T1–T3) or three different positions in the axon terminal (A1–A3; indicated by white circles). ΔC_m estimated by 2 kHz sine wave stimulation (±15 mV from V_hold=−80 mV). B–D, estimates of ΔC_m (B), ΔR_s (C) and ΔR_m (D) as a function of location of capacitance increase, indicated as distance between the electrode (located at T1) and the location of capacitance increase.

Frequency-dependent activation of voltage-gated Ca²⁺ currents

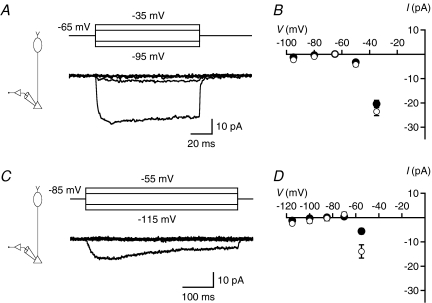
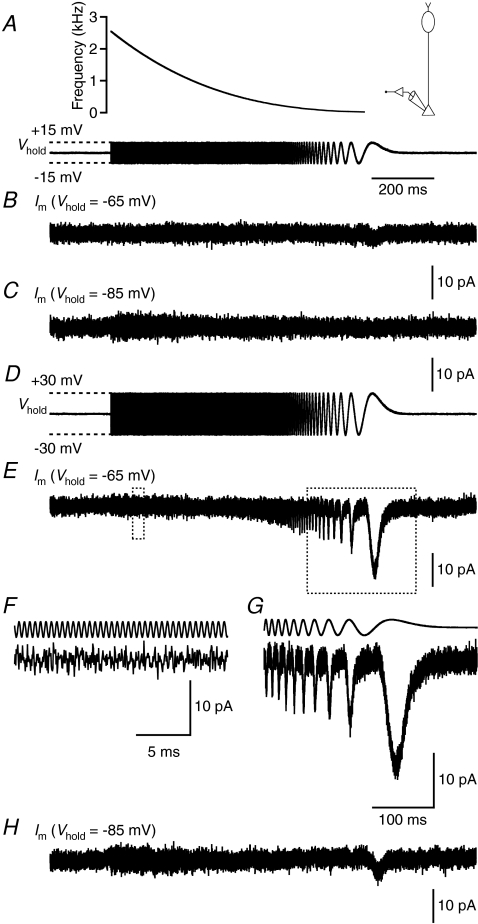
The most effective way to increase the signal-to-noise ratio of measurements of ΔC_m is to increase the peak-to-peak amplitude of the sine wave stimulus (Lindau & Neher, 1988; Gillis, 1995), but it is important that the stimulus does not activate voltage-gated currents. Rat rod bipolar cells express a T-type Ca²⁺ current with activation threshold between −70 and −60 mV and an L-type Ca²⁺ current with activation threshold between −50 and −40 mV (de la Villa et al. 1998; Protti & Llano, 1998; Satoh et al. 1998; Hartveit, 1999; Pan, 2000; Pan et al. 2001). On this background, we considered two different holding potentials (−65 and −85 mV) and two different stimulus amplitudes relative to V_hold (±15 and ±30 mV). At V_hold=−65 mV, the T-type Ca²⁺ current should be largely inactivated and depolarization either to −50 mV (+15 mV) or to −35 mV (+30 mV) activated a sustained current (peak amplitude −4.2 ± 0.8 and −24 ± 2 pA, respectively; n= 17; Fig. 4A and B), most likely an L-type Ca²⁺ current. Short hyperpolarizing pulses to −80 or −95 mV evoked no detectable currents (Fig. 4A and B). At V_hold=−85 mV, the T-type Ca²⁺ current is not inactivated, and depolarization to −55 mV (+30 mV) activated an inward current with both transient and sustained components (peak amplitude −14 ± 3 pA; n= 6; Fig. 4C and D), most likely a mixture of T- and L-type Ca²⁺ currents. Depolarization to −70 mV (+15 mV), and short hyperpolarizing pulses to −100 or −115 mV, evoked no detectable currents (Fig. 4C and D). We did not observe an effect of proton release from exocytosis on the Ca²⁺ currents illustrated in Fig. 4, most likely because the corresponding protocols were run relatively late in the recordings, after rundown of transmitter release. The inhibition of Ca²⁺ current is observed routinely in goldfish bipolar cells (Palmer et al. 2003a) and can be observed in recordings from axon terminals of rat rod bipolar cells as well (e.g. Veruki et al. 2006).

Figure 4. Voltage-gated Ca²⁺ currents recorded at rod bipolar axon terminals.

A, currents (lower panel) activated by ±15 and ±30 mV depolarizing (to −50 and −35 mV) and hyperpolarizing (to −80 and −95 mV) voltage pulses from V_hold=−65 mV (upper panel). Notice larger-amplitude inward current activated by depolarization to −35 mV and lower-amplitude inward current activated by depolarization to −50 mV. Subtraction of leak and capacitive currents performed by standard P/N protocol (leak pulse amplitude 1/4 of original stimulus amplitude, 10 leak pulses; A and C). Recording configuration indicated in left diagram (A and C). B, current–voltage (I–V) relationships for Ca²⁺ currents (as in A; n= 17 cells) measured at peak (open symbols) or at steady state (filled symbols; average of last 50 ms of response). Data points represent mean ±s.e.m. (B and D). C, currents (lower panel) activated by ±15 and ±30 mV depolarizing (to −70 and −55 mV) and hyperpolarizing (to −100 and −115 mV) voltage pulses from V_hold=−85 mV (upper panel). Notice larger-amplitude inward current activated by depolarization to −55 mV. D, I–V relationships for Ca²⁺ currents (as in C; n= 6 cells) measured at peak (open symbols) or at steady state (filled symbols; average of last 250 ms of response).

These results demonstrated that voltage-gated Ca²⁺ currents can be activated by 30 mV depolarizations from −65 and −85 mV, and by 15 mV depolarization from −65 mV. To examine how the frequency of a sine wave stimulus could influence the activation of these voltage-gated Ca²⁺ currents, we designed a 1 s long ZAP stimulus where the frequency was ramped from a maximum of ∼2.5 kHz to a minimum of ∼5 Hz (Fig. 5A; see Methods). A ±15 mV ZAP stimulus applied at V_hold=−65 mV activated a low-amplitude, inward current when the frequency fell below ∼20 Hz (2/4 cells; Fig. 5B). When the same stimulus was applied at V_hold=−85 mV, no current was activated (Fig. 5C; n= 4). A ±30 mV ZAP stimulus (Fig. 5D) applied at V_hold=−65 mV activated a larger-amplitude, inward current when the frequency fell below ∼150 Hz (4/4 cells; Fig. 5E–G). When the same stimulus was applied at V_hold=−85 mV, an inward current was activated when the frequency fell below ∼20 Hz (2/4 cells; Fig. 5H). These results suggested that a sine wave stimulus of 2 kHz, with an amplitude of either ±15 or ±30 mV, can be applied at a V_hold of both −65 and −85 mV with little risk of activating voltage-gated currents. In the majority of our subsequent recordings, we employed a frequency of 2 kHz and an amplitude of ±15 mV. The moderate increase in noise that sometimes occurred during a ZAP stimulus (Fig. 5C) was most likely caused by imperfect subtraction of leak and capacitive currents.

Figure 5. Voltage-gated currents activated by ZAP stimuli in rod bipolar axon terminal recordings.

A, ZAP stimulus (lower trace) with amplitude ±15 mV from V_hold. Instantaneous frequency of ZAP stimulus (∼2.5 kHz to ∼5 Hz; calculated as the inverse of the intervals defined by the V_hold-crossing time points) indicated by function in upper panel. Recording configuration indicated in right diagram. Scale bar for time also applies to all current traces except F and G. B and C, currents evoked by ZAP stimulus in A at V_hold=−65 mV (B) and V_hold=−85 mV (C) (after subtracting leak and capacitive currents). Notice low-amplitude, inward currents at V_hold=−65 mV (evoked when stimulus frequency fell below ∼20 Hz), but absence of voltage-activated currents at V_hold=−85 mV. D, ZAP stimulus (as in A) with amplitude ±30 mV from V_hold. E, current evoked by ZAP stimulus in D at V_hold=−65 mV (after subtracting leak and capacitive currents). Notice increasing activation of voltage-gated current with each depolarizing stimulus cycle when the stimulus frequency dropped below ∼150 Hz. Epochs demarcated by dotted rectangles are displayed at higher temporal resolution in F (left rectangle) and G (right rectangle). F and G, discrete epochs of the current trace in E (lower traces), together with corresponding parts of the ZAP stimulus (upper traces). H, current evoked by ZAP stimulus in D at V_hold=−85 mV (after subtracting leak and capacitive currents). Notice activation of voltage-gated current when the stimulus frequency dropped below ∼20 Hz.

Capacitance measurements from rod bipolar cells in retinal slices

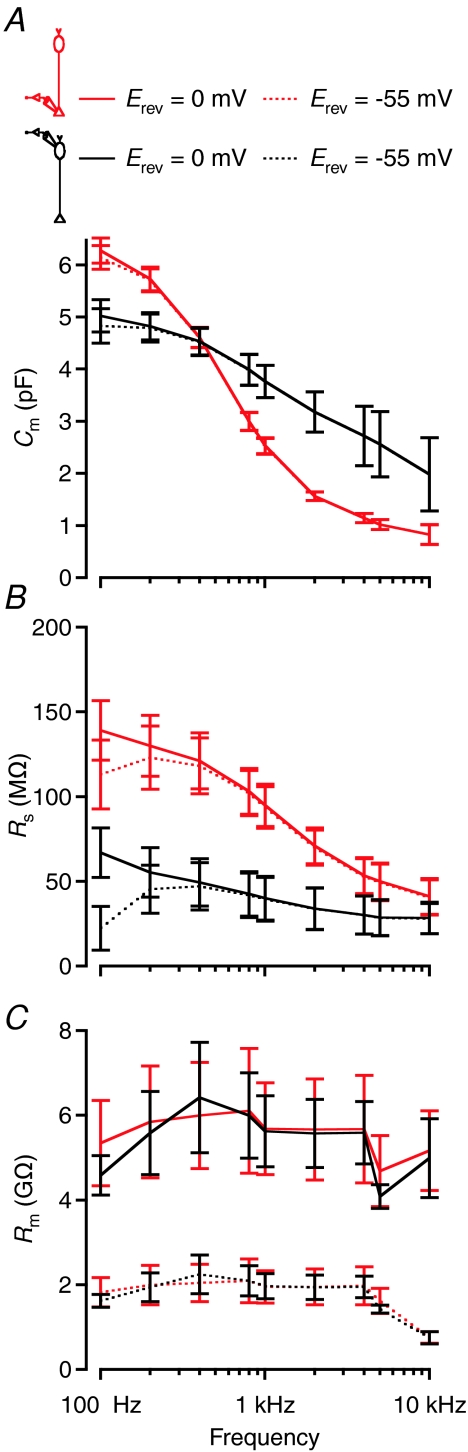
We next investigated the degree of similarity between capacitance measurements based on computer simulations (Fig. 2) and capacitance measurements based on physiological recordings of morphologically intact rod bipolar cells in slices (V_hold=−85 mV; Fig. 1). Similar to the computer simulations, increasing the sine wave frequency from 100 Hz to 10 kHz reduced the estimates for C_m (Fig. 6A) and R_s (Fig. 6B). The estimates for R_m, however, showed no systematic dependence on frequency (Fig. 6C). These relationships were observed both for terminal-end and soma-end recordings, and the qualitative differences between the two recording modes were similar to those observed for equivalent computer simulations (Fig. 6A–C). The original measurements were based on the default value for E_rev of I_DC (0 mV; see Methods). If we re-calculated the estimates with a more realistic value for E_rev (−55 mV), there was almost no change in the results for C_m (Fig. 6A) and R_s (Fig. 6B). As expected, the estimates for R_m were reduced, but with no systematic dependence on frequency (Fig. 6C). Occasionally, we also recorded from isolated terminals in stratum 5 of the inner plexiform layer (most likely separated from the axon during preparation of the slices). As expected for a round structure, we observed no dependence on frequency for estimates of C_m (data not shown).

Figure 6. Performance of the ‘Sine + DC’ technique for measuring capacitance of rod bipolar cells with either terminal-end or soma-end recording and the influence of the sine wave frequency.

A–C, estimates of total capacitance (C_m; A), series resistance (R_s; B), and total membrane resistance (R_m; C) as a function of sine wave stimulation frequency (100 Hz to 10 kHz). Recording configurations indicated in top diagrams. Terminal-end recordings indicated by red lines (n= 3 cells) and soma-end recordings indicated by black lines (n= 3 cells). Data points represent mean ±s.e.m. Sine wave amplitude ±15 mV from V_hold=−85 mV. The continuous lines represent results obtained for setting E_rev for I_DC to 0 mV and the dotted lines represent results obtained for setting E_rev to −55 mV. For each stimulus frequency used, manual calibration of the patch-clamp amplifier was performed with an external capacitance. All measurements were obtained within ∼3 min of establishing the whole-cell recording configuration.

We consider it unlikely that the influence of sine wave frequency on the estimates for C_m and R_s (Fig. 6A and B) resulted from properties of the instrumentation as such. This contrasts with the suggestion made by Zhou et al. (2006). First, we manually calibrated the phase and attenuation values for all sine wave frequencies employed in the measurements and found no frequency dependence of estimates for the capacitance of an electronic model cell circuit. Second, the frequency dependence was very similar to the results obtained with computer simulations using a morphologically reconstructed rod bipolar cell (Fig. 2).

Depolarization-evoked increase of capacitance is Ca²⁺ dependent and reflects exocytosis

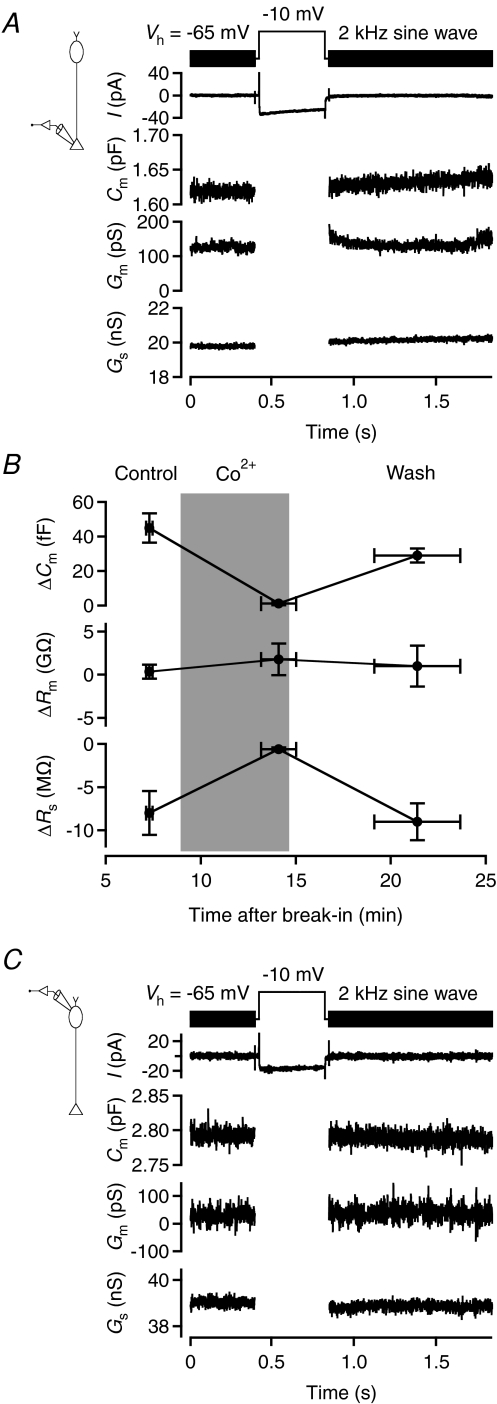
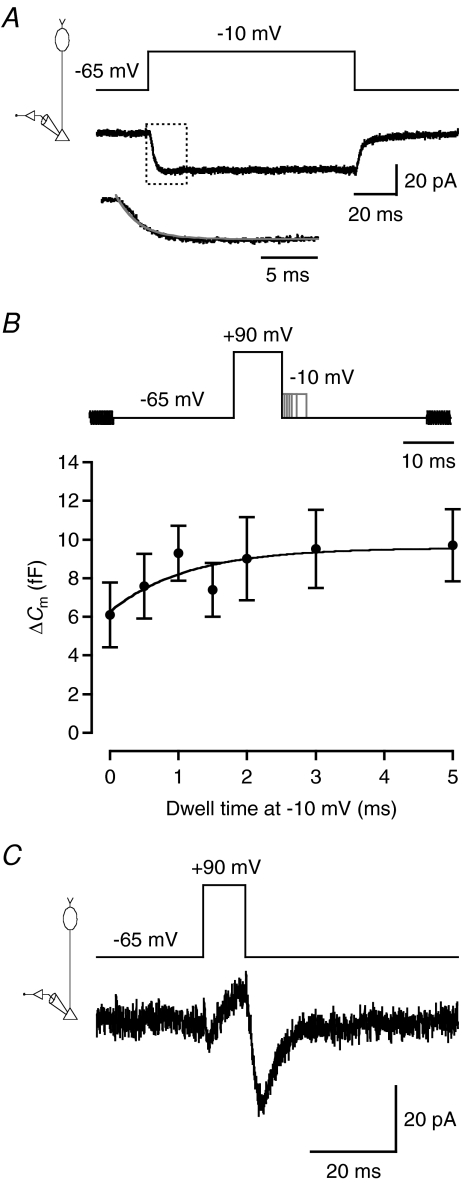
To study depolarization-evoked increase of capacitance caused by exocytosis at rod bipolar axon terminals, we applied 400 ms voltage pulses from −65 mV (V_hold) to −10 mV. The capacitance was measured using 2 kHz sine wave stimuli (±15 mV relative to V_hold), applied before and after the voltage pulse. For the cell illustrated in Fig. 7A, the voltage pulse evoked an inward current and an associated increase of capacitance. The mean C_m before the depolarization was 1618 fF and the mean C_m after the depolarization was 1632 fF (averaged over a 1 s period), corresponding to a ΔC_m of 14 fF (mean ΔC_m= 17.4 ± 2.8 fF; n= 6 cells; three trials for each cell). For the same cells, ΔR_s was −1.0 ± 0.4 MΩ and ΔR_m was 165 ± 234 MΩ. The ΔC_m obtained with 2 kHz sine wave stimulation (15.6 ± 2.7 fF) was similar to that found with 4 kHz stimulation (16.8 ± 2.1 fF; n= 3 cells; P= 0.82; paired t test), consistent with the results from computer simulations. Because the C_m trace in Fig. 7A drifted slowly upwards after the depolarizing pulse, we checked whether the range of data points used for measurement were critical for the estimate of ΔC_m. When the first 200 ms of the C_m trace after the depolarizing pulse was eliminated from measurement, there was a significant, albeit small, difference in ΔC_m (18.1 ± 2.9 fF versus 17.4 ± 2.8 fF; P= 0.03; paired t test), suggesting that the exact duration over which C_m was averaged was of little practical importance for the results.

Figure 7. Measuring exocytosis-evoked capacitance increase in axon terminal recordings of rod bipolar cells in retinal slices.

A, sine wave stimulation (2 kHz; ±15 mV from V_hold=−65 mV; top) before and after a 400 ms step depolarization to −10 mV to activate voltage-gated Ca²⁺ current and Ca²⁺-dependent exocytosis. Recording configuration indicated in left diagram. Notice inward current (no leak subtraction) evoked by the depolarization (for illustration purposes, the current evoked by the sine wave stimulus itself has been strongly low-pass filtered). For each sine wave cycle, one data point was obtained for cell capacitance (C_m), cell membrane conductance (G_m), and series conductance (G_s). Notice that the increase in C_m is accompanied by an increase in G_s, but no overall change in G_m. B, changes in capacitance (ΔC_m), membrane resistance (ΔR_m), and series resistance (ΔR_s) evoked by depolarization from V_hold=−65 to −10 mV (1 s duration) in rod bipolar axon terminal recordings (n= 4 cells). Measurements obtained in the control condition (‘Control’), during replacement of Ca²⁺ with Co²⁺ in the extracellular solution (‘Co²⁺’) and after washout of Co²⁺ (‘Wash’). Data points show mean ±s.e.m. and for each cell 2–4 trials were averaged for each of the three conditions. Period with Co²⁺ indicated by grey background which shows nominal times of solution changes. Notice that the increase in C_m, as well as the accompanying apparent decrease in R_s, was reversibly blocked by Co²⁺. C, as in A, but with results for soma-end recording. There is a small reduction in the average value of C_m after the depolarizing stimulus, but no consistent change in G_m or G_s. Recording configuration indicated in left diagram.

A series of observations suggested that the capacitance increase was caused by exocytosis occurring at the axon terminal. First, if the capacitance increase was caused by exocytosis, one would expect a larger ΔC_m with a longer stimulus duration. Confirming this, when we increased the duration of the voltage pulse from 400 to 1000 ms, ΔC_m increased to 61.5 ± 8.9 fF (n= 6 cells; three trials for each cell; P= 0.0008; unpaired t test). Second, if the capacitance increase was caused by Ca²⁺-dependent exocytosis, it should be eliminated by blocking voltage-gated Ca²⁺ channels. Confirming this, when we replaced Ca²⁺ in the extracellular solution with Co²⁺, the depolarization-evoked ΔC_m was reduced from 44.9 ± 8.4 fF in the control condition to 1.3 ± 1.0 fF during Co²⁺ (n= 4 cells; Fig. 7B). After washout of Co²⁺ (and wash-in of Ca²⁺), ΔC_m recovered to 64% of control values (28.7 ± 4.0 fF; Fig. 7B). Estimates of R_m were not influenced by Co²⁺ (Fig. 7B). Interestingly, the negative ΔR_s associated with a positive ΔC_m in the control condition was eliminated by Co²⁺ and recovered after washout of Co²⁺ (Fig. 7B). Finally, if the capacitance increase is caused by exocytosis in the axon terminal region, it should be undetectable with a 2 kHz sine wave stimulus in soma-end recordings (cf. Fig. 2Bd). Confirming this, in soma-end recordings there was no difference between C_m before and after a 400 ms voltage pulse to −10 mV (ΔC_m=−3.4 ± 2.2 fF; n= 4 cells; Fig. 7C).

Time course of exocytosis and detection of distinct vesicle pools

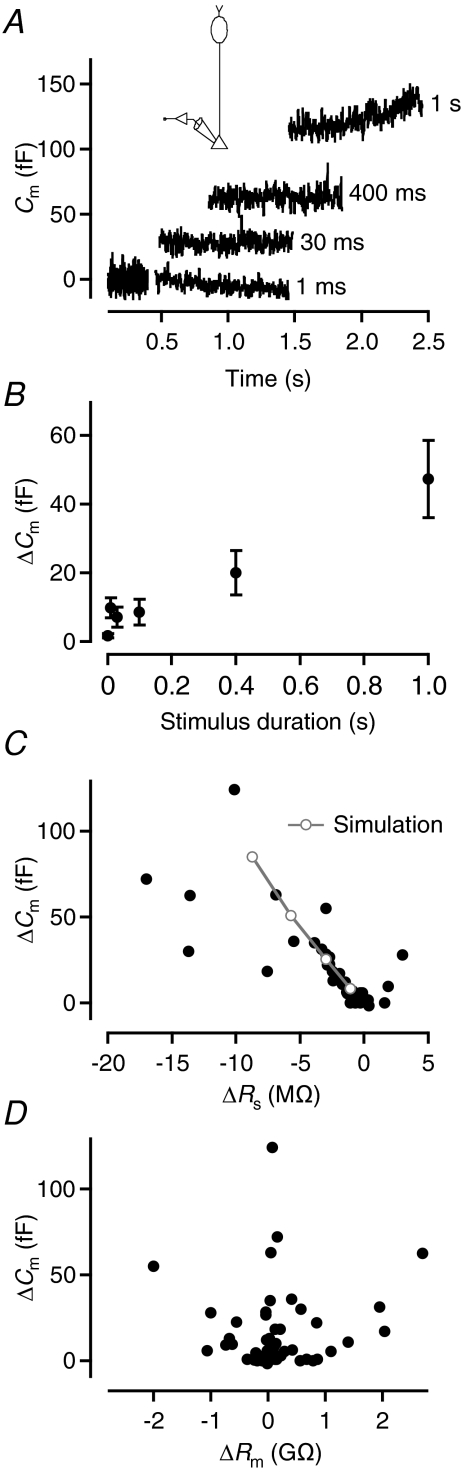
The saturation of capacitance responses and the observation of kinetically distinct components of capacitance responses predict the existence of distinct pools of synaptic vesicles (von Gersdorff & Matthews, 1999). To investigate the kinetics of capacitance increase at rod bipolar axon terminals, we applied depolarizing stimuli (from −65 to −10 mV) with durations ranging from 1 to 1000 ms. An example of the increase in C_m obtained with increasing pulse durations can be seen in Fig. 8A. With a pulse duration of 1 ms, ΔC_m was ∼0 (mean 1.7 ± 0.7 fF; n= 9 cells; Fig. 8B). When we increased the pulse duration to 10, 30 and 100 ms, ΔC_m plateaued at 9–10 fF (Fig. 8B). However, when we further increased the pulse duration to 400 and 1000 ms, ΔC_m again increased (Fig. 8B). A linear fit to the data points at 100, 400 and 1000 ms indicated a capacitance increase of ∼43 fF s⁻¹. A slow upward drift of the C_m trace after the 1 s depolarizing pulse (Fig. 8A) was observed for 3/9 cells and could be an indication of copious asynchronous release after a strong stimulus (cf. von Gersdorff et al. 1998; Singer & Diamond, 2003). Because it was not a consistent observation, we did not investigate this further. The plateau observed for pulse durations ≤100 ms suggested depletion of a readily releasable pool of vesicles, while the additional increase seen for 400 and 1000 ms pulses suggested recruitment of vesicles from an additional pool. We did not attempt to deplete this additional pool by increasing the pulse duration beyond 1000 ms. That the readily releasable pool could be depleted with pulse durations ≤10 ms suggested that the release kinetics could be limited by the activation kinetics of the Ca²⁺ channels themselves (Mennerick & Matthews, 1996; Singer & Diamond, 2003). Accordingly, instead of attempting to resolve the kinetics by applying additional pulses with durations between 1 and 10 ms, we examined the kinetic properties of release by using Ca²⁺ tail current stimuli (see below).

Figure 8. Increasing the duration of depolarization increases the magnitude of the capacitance increase (ΔC_m).

A, superimposed, baseline-subtracted capacitance traces (low-pass filtered at 100 Hz) before and after variable duration depolarization to −10 mV (durations as indicated; ∼30 s interpulse interval). Diagram (inset) indicates recording configuration. Capacitance measured with 2 kHz sine wave stimulus (±15 mV from V_hold=−65 mV; A–D). B, capacitance increase (ΔC_m) as a function of stimulus duration (1, 10, 30, 100, 400 and 1000 ms; depolarization to −10 mV from V_hold=−65 mV). Notice saturation of ΔC_m for stimulus durations ≤100 ms. Data points represent mean ±s.e.m. (n= 9 cells; B–D). C, relationship between ΔC_m and apparent change of R_s (ΔR_s; filled circles). Notice negative correlation. For comparison between results from physiological recordings and computer simulations, the plot also includes data points (open circles connected by grey lines) from simulations as in Fig. 2A, but for four different values of ΔC_m(theory), corresponding to surface area increase of 1, 3, 6, or 10 μm² at axon terminal ending T1. D, relationship between ΔC_m and ΔR_m. Notice lack of correlation.

In the experiments using different pulse durations, we found a correlation between the increase of capacitance (ΔC_m) and the apparent decrease in series resistance (ΔR_s; Spearman's R=−0.80; P < 0.001; Fig. 8C). This was consistent with our results from simulations of capacitance increases (Fig. 2Ba) and previous observations for mossy fibre boutons (Hallermann et al. 2003). There was no correlation between ΔC_m and ΔR_m (Spearman's R= 0.11; P= 0.42; Fig. 8D).

The release kinetics of a readily releasable pool of vesicles is limited by Ca²⁺ channel activation kinetics

To measure the activation kinetics of voltage-gated Ca²⁺ channels, we applied voltage steps from −65 to −10 mV. For the cell illustrated in Fig. 9A, the voltage step evoked a sustained, inward current with an activation phase well described by a single-exponential function with time constant (τ_act) of 2.4 ms. The mean τ_act was 1.6 ± 0.2 ms (n= 12 cells). Because pulse durations ≤10 ms seemed sufficient to deplete a readily releasable pool of vesicles, it may not be possible to adequately measure the kinetics of release with variable-duration voltage pulses from −65 to −10 mV. An alternative strategy for kinetic measurements is to separate the influx of Ca²⁺ from the activation of the Ca²⁺ channels (Mennerick & Matthews, 1996; von Gersdorff et al. 1998). We used a stimulus protocol that first depolarized the cell to +90 mV to maximally activate the Ca²⁺ channels. Because of the strong depolarization, the driving force for Ca²⁺ will be minimal with insignificant Ca²⁺ influx. The cell was then repolarized to −10 mV, to maintain the Ca²⁺ channels in a state with high open probability and minimal inactivation (Fig. 9A), while the instantaneous increase in driving force will evoke a strong Ca²⁺ influx. Finally, the cell was stepped back to −65 mV, leading to deactivation of the Ca²⁺ channels and termination of Ca²⁺ influx. By varying the time at which the cell was held at −10 mV, we could vary the duration and amount of Ca²⁺ influx.

Figure 9. Estimating the release kinetics for the readily releasable pool of vesicles in rod bipolar cells.

A, voltage-gated Ca²⁺ current (lower traces) evoked by a 100 ms depolarization from V_hold=−65 to −10 mV (upper trace). Recording configuration indicated in left diagram (A and C). Notice absence of inactivation at −10 mV. The current trace is the average of five trials. Subtraction of leak and capacitive currents performed by standard P/N protocol (leak pulse amplitude −1/5 of original stimulus amplitude, 14 leak pulses). The activation phase of the current is displayed at higher temporal resolution in the lower trace (corresponding to dotted rectangle in the main current trace) and a single-exponential fit has been overlaid (grey line). B, relationship between ΔC_m and duration of depolarization at −10 mV (‘dwell time’; 0, 0.5, 1, 1.5, 2, 3, or 5 ms) after conditioning depolarization to +90 mV (10 ms; top panel). Depolarization to +90 mV evokes maximum open probability of voltage-gated Ca²⁺ channels with minimal Ca²⁺ influx, whereas stepping the membrane potential back to −10 mV evokes immediate Ca²⁺ influx caused by the increased driving force with minimal closure of Ca²⁺ channels. Capacitance measurement with 2 kHz sine wave stimulus (±15 mV from V_hold=−65 mV) before and after depolarizing stimulus (top panel). Data points represent mean ±s.e.m. (n= 12 cells; B and C). Data points have been fitted with a single-exponential function plateauing at ∼10 fF (τ= 1.1 ms). C, relatively slow deactivation of Ca²⁺ tail current (lower trace) following repolarization to −65 mV after 10 ms voltage pulse to +90 mV (upper trace). The current trace is the average of three trials. Subtraction of leak and capacitive currents performed by standard P/N protocol (leak pulse amplitude −0.13 of original stimulus amplitude, 14 leak pulses).

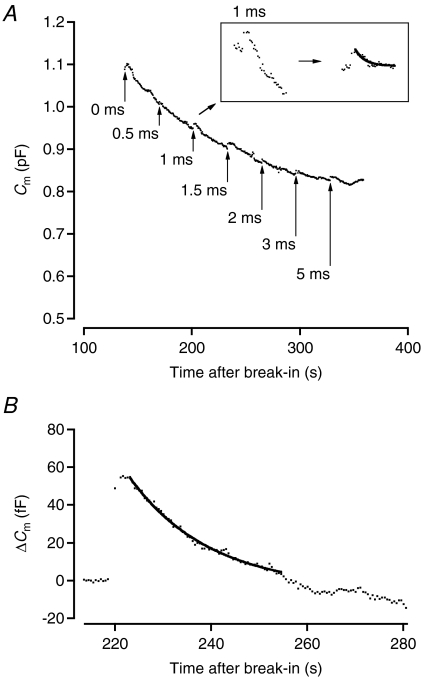
To measure the release kinetics of the readily releasable pool of vesicles, we combined the stimulus protocol described above with sine wave stimuli to measure the capacitance increase (Fig. 9B). We used 10 ms pre-pulses to +90 mV, followed by repolarization to −10 mV for 0–5 ms, followed by repolarization to −65 mV (Fig. 9B). With increasing dwell time at −10 mV, ΔC_m gradually increased from a minimum of 6.1 ± 1.7 fF (for 0 ms duration), to a plateau where ΔC_m saturated at ∼10 fF for the longest pulse durations (Fig. 9B). The increase of ΔC_m, as a function of dwell time at −10 mV, was fitted with a single-exponential function with a time constant of 1.1 ms (Fig. 9B), faster than the Ca²⁺ channel activation time constant at −10 mV (see above). This supported the idea that with a standard depolarizing stimulus, e.g. from −65 to −10 mV, the activation kinetics of the Ca²⁺ channels limit the release kinetics of the readily releasable pool of vesicles. The plateau at ∼10 fF was similar to the plateau observed for capacitance increases after depolarization from −65 to −10 mV (Fig. 8B).

The minimum ΔC_m of 6.1 fF, observed for a dwell time of 0 ms at −10 mV, corresponds to influx of Ca²⁺ during the Ca²⁺ tail current evoked by stepping the membrane potential directly from +90 to −65 mV (Fig. 9B). In goldfish bipolar cells, the Ca²⁺ tail current evoked by a similar stimulus deactivates with a time constant of 118 μs, too fast to evoke Ca²⁺ influx that is sufficient for exocytosis and a measurable ΔC_m (Mennerick & Matthews, 1996). Our observation of a significant minimum ΔC_m could be explained by slower deactivation kinetics of the Ca²⁺ tail current in rat rod bipolar cells compared to goldfish bipolar cells. This hypothesis was supported by experimental observations. For the cell illustrated in Fig. 9C, the deactivation kinetics, corresponding to the time course of the inward Ca²⁺ tail current evoked by a 10 ms depolarization to +90 mV, followed by repolarization to −65 mV, were well described by a single-exponential function with time constant (τ_deact) of 4.1 ms (mean τ_deact= 5.8 ± 0.9 ms; n= 12 cells). This suggests that relatively slow deactivation kinetics of the Ca²⁺ tail current lead to a measurable minimum of Ca²⁺ influx. This phenomenon limited our ability to fully resolve the kinetics corresponding to release of the first few femtofarads of the readily releasable pool. Taken together, these results suggested that vesicle release displays a very transient time course, probably corresponding to a limited supply of readily releasable vesicles, and that the kinetics of release, under normal conditions, are limited by the Ca²⁺ channel activation kinetics.

Endocytosis of the readily releasable pool of vesicles

To measure the rate of endocytosis of the readily releasable pool of vesicles, we constructed an average C_m trace for the cells stimulated with the protocol in Fig. 9B (n= 12 cells). The cells were stimulated with depolarizing stimuli at 30 s intervals and baseline C_m was monitored with 100 ms sine wave stimuli applied every 0.5 s. For each cell, each data point was the mean C_m calculated from a 100 ms epoch. From the average C_m trace illustrated in Fig. 10A, it can be seen that there is a gradual decrease in baseline C_m during the recording, apparently unrelated to the transient changes of C_m following each discrete stimulus pulse. A similar decrease has been observed for goldfish bipolar cells (e.g. Hull & von Gersdorff, 2004). The transient decrease following each stimulus pulse corresponds to endocytosis of the readily releasable pool of vesicles. We measured the kinetics of endocytosis by fitting a single-exponential function to each transient decay phase of the average C_m trace (Fig. 10A, inset; after subtracting out the downward baseline drift of the capacitance; cf. Hull & von Gersdorff (2004)). The time constant ranged from ∼0.7 to ∼8 s, with longer time constants obtained for longer-duration stimuli. We also measured the kinetics of endocytosis following 1 s depolarizations from −65 to −10 mV. For seven cells, each with ΔC_m≥ 30 fF (average 45.7 ± 5.6 fF) and identifiable endocytosis, fitting of the average capacitance trace with a single-exponential function gave a time constant of ∼17 s (Fig. 10B). We also observed a delay in the onset of endocytosis of ∼3.7 s from the end of the depolarizing stimulus used to evoke exocytosis (cf. Wan et al. 2008).

Figure 10. Transiently increased exocytosis is followed by transient increase of endocytosis.

A, total membrane capacitance followed as a function of time throughout whole-cell rod bipolar axon terminal recording. The trace represents the average time course for 12 cells recorded with identical stimulus protocols. Capacitance measurement points updated at 2 Hz. For each cell, each data point represents the mean value obtained for a 100 ms sine wave stimulus (2 kHz), except immediately before and after each depolarizing stimulus where the sine wave stimulus durations were 400 and 1000 ms, respectively. Arrows indicate time points where depolarizing stimuli were applied (as in Fig. 9, duration as indicated). Notice transient increase of C_m, corresponding to exocytosis, and transient decay of C_m, corresponding to endocytosis, after each depolarizing stimulus. Transient changes in C_m are overlaid on a slow, monotonic decrease of C_m during whole-cell recording. Inset shows magnified section of the trace, corresponding to the capacitance increase evoked by a 1 ms depolarization and the subsequent capacitance decrease resulting from endocytosis. Left trace shows raw data points and right trace shows data points after correction for downward baseline drift with overlaid single-exponential fit to decay phase. B, baseline-subtracted capacitance measurements before and after a 1 s depolarizing stimulus from −65 to −10 mV. The data points were updated at 2 Hz and represent the average time course for 7 cells recorded with identical stimulus protocols. For each cell, each data point represents the mean value obtained for a 100 ms sine wave stimulus (2 kHz), except immediately before and after the depolarizing stimulus where the sine wave stimulus durations were 400 and 1000 ms, respectively. Notice transient increase of C_m, corresponding to exocytosis, followed by slower decay of C_m, corresponding to endocytosis, after the depolarizing stimulus. Notice delay in onset of endocytosis. The data points have been overlaid with a single-exponential fit to the decay phase.

Discussion

We have established a method for high-resolution, time-resolved capacitance measurements of exocytosis from presynaptic rod bipolar axon terminals in rat retinal slices. Using this method, we obtained evidence for the existence of a readily releasable pool of vesicles with a capacitance of ∼10 fF that could be released with a time constant of ∼1.1 ms. Under normal conditions, it is likely that the kinetics of release will be determined by the activation kinetics of the voltage-gated Ca²⁺ conductance. Several of the processes investigated here are likely to be strongly influenced by temperature and our quantitative estimates would most likely be different if the experiments had been carried out at typical mammalian body temperatures (e.g. Ca²⁺ current activation kinetics, maximum vesicle release rate). It is important to point out, however, that previous studies, with which we compare our estimates, were also performed at room temperature.

As we will demonstrate, our estimates of the size and release kinetics of the readily releasable pool of vesicles agree very well with those obtained by dual recording of synaptically connected rod bipolar and AII amacrine cells (Singer et al. 2004; Singer & Diamond, 2006). It is therefore useful to stress the advantages of presynaptic capacitance measurements over postsynaptic current recordings, both general and with specific reference to rod bipolar cells. First, capacitance measurements avoid potential problems related to non-linearities caused by receptor saturation and desensitization. Second, they can yield direct estimates of endocytosis. Third, capacitance measurements avoid problems related to divergence and convergence in the synaptic contacts between rod bipolar and AII amacrine cells (Strettoi et al. 1990, 1992). The presence of divergence means that recording postsynaptic currents may not capture exocytosis from all the terminals of a rod bipolar cell. The presence of convergence means that heterogeneity and variability among synaptic contacts and postsynaptic receptors may confound analysis based on dual recording of a specific pair of cells. This can be important given the relatively high frequency of spontaneous release from rod bipolar cells (e.g. Veruki et al. 2003).

General methodological considerations

Rat rod bipolar cells can be adequately modelled as a two-compartment equivalent electrical circuit (Oltedal et al. 2007), similar to bipolar cells in goldfish retina (Mennerick et al. 1997). Because sine wave techniques for capacitance measurements were originally developed for cells that can be described as single-compartment RC circuits (Lindau & Neher, 1988; Gillis, 1995), we evaluated the performance of the ‘Sine + DC’ technique with a range of stimulus parameters for both terminal-end and soma-end recordings using computer simulations of a morphologically reconstructed rod bipolar cell with realistic physiological parameters (Oltedal et al. 2009). This approach is similar to that used by Hallermann et al. (2003) for mossy fibre boutons and several of our results are comparable to theirs. First, the accuracy of ΔC_m measurements increases with increasing sine wave frequency. Second, positive ΔC_m is correlated with apparent negative ΔR_s. A negative ΔR_s is obtained when the site of capacitance increase is located within a distance of 10–20 μm from the recording electrode. Third, with a 2 kHz sine wave stimulus, the accuracy of ΔC_m for a theoretical increase of ∼100 fF was ∼0.8. In our simulations, we found that a frequency of 2 kHz represented a reasonable compromise between the conflicting goals of achieving the highest possible accuracy of ΔC_m measurements at the axonal ending carrying the recording electrode and achieving high accuracy of ΔC_m measurements at neighbouring terminal endings. These results support the general applicability of the modelling approach pioneered by Hallermann et al. (2003) and provide an additional example of how capacitance measurements can be extended from cells with simple and compact geometry to more general classes of neurons and nerve terminals (Hallermann et al. 2003; Kushmerick & von Gersdorff, 2003).

Terminal-end versus soma-end recordings for measuring ΔC_m occurring at the axon terminal

Computer simulations suggested that high accuracy measurements of ΔC_m occurring at the axon terminal could also be obtained with soma-end recordings, provided that very low sine wave frequencies (≤100 Hz) were used. We decided against soma-end recordings for measurements of ΔC_m for the following reasons. First, recordings with a ZAP stimulus suggested that for a given sine wave amplitude, the risk of activating voltage-gated Ca²⁺ channels increased with decreasing sine wave frequency and could potentially become a problem for the low frequencies required for soma-end recordings. To compensate for this by reducing the sine wave amplitude would decrease the signal-to-noise ratio of the measurements. Second, low sine wave frequencies can by themselves increase the noise (Gillis, 1995). A detailed discussion of the use of soma-end recordings is included in the online Supplemental material.

Synaptic vesicle pools of rod bipolar cells

We estimated the size of the readily releasable pool as ∼10 fF. Despite the methodological differences, our result compares favourably with an indirect estimate for acutely isolated mouse rod bipolar cells (4–10 fF; Wan et al. 2008). With a conditioning depolarization to +90 mV, we could separate Ca²⁺ influx from Ca²⁺ channel activation and estimate the release kinetics of the readily releasable pool of vesicles with a time constant of ∼1.1 ms. We cannot exclude, however, that the true time constant is even smaller, because a Ca²⁺ tail current stimulus alone depleted ∼60% of the readily releasable pool. This limited our ability to fully resolve the true time course of the initial release process. Another interpretation of these experiments is that release actually occurred with slower kinetics, involving the period (25 ms) between the end of the voltage stimulus and the beginning of the sine wave stimulus. However, the release kinetics inferred from paired recordings between synaptically connected rod bipolar cells and AII amacrine cells demonstrate that a Ca²⁺ tail current stimulus evokes an EPSC with a rise time of ∼0.7 ms, suggesting rapid presynaptic release (Singer & Diamond, 2003).

Our data suggest that exocytosis will display two distinct kinetic components during sustained Ca²⁺ influx. An initial rapid release, presumably corresponding to the readily releasable pool, saturates at ∼10 fF and can be depleted with ≤10 ms sustained depolarization at −10 mV. This estimate can be compared to previous estimates of the size of the readily releasable pool and morphological measurements of synaptic vesicles. First, using paired recordings between rat rod bipolar cells and AII amacrine cells, Singer & Diamond (2006) estimated that the readily releasable pool corresponded to seven vesicles per active zone. With an average number of 36 ribbons per rod bipolar cell (Singer et al. 2004), we can calculate a total number of ∼250 docked vesicles for the readily releasable pool. Second, if we assume that the diameter of synaptic vesicles in rat rod bipolar cells is within the range reported for vesicles in goldfish bipolar cells, it will be between 29 nm (von Gersdorff et al. 1996) and 36 nm (Lagnado et al. 1996). With a specific membrane capacitance of 1 μF cm⁻², this yields a readily releasable pool of 6.6–10.2 fF. Our estimate of ∼10 fF is close to the upper limit of this range. Singer & Diamond (2006) also concluded that the Ca²⁺ tail current after a 10 ms depolarization to +90 mV evoked release of 54% of the readily releasable pool. This corresponds very well with our measurements, where a similar stimulus evoked a mean ΔC_m of 6.1 fF, or 60% of our estimate of the readily releasable pool. For the goldfish bipolar neuron, a limited pool of fast releasing vesicles has been well characterized (e.g. Mennerick & Matthews, 1996; reviewed in Heidelberger et al. 2005). It was recently demonstrated that the size of this vesicle pool is sensitive to the EGTA concentration in the patch pipette (Coggins & Zenisek, 2009). We did not explore the sensitivity of the readily releasable pool to different concentrations of EGTA. However, our results demonstrated faster release kinetics when exocytosis was evoked by Ca²⁺ tail currents, consistent with a model in which multiple Ca²⁺ channels that open simultaneously enhance the rate of vesicle release (cf. Coggins & Zenisek, 2009).

With a 1 s depolarization to −10 mV, we obtained a ΔC_m of 50–60 fF. This compares well with an estimate obtained via postsynaptic recording (Singer & Diamond, 2006) for the steady-state refilling rate during sustained synaptic release of ∼50 Hz (0.53 vesicles ms⁻¹ (10 synapses)⁻¹). With an average of 36 ribbons per rod bipolar cell (see above), a 1 s depolarization would evoke release of ∼2050 vesicles (50 vesicles at each of 36 ribbons plus 250 vesicles from the readily releasable pool). Assuming that the effect of endocytosis can be neglected during the depolarizing pulse, this would correspond to a ΔC_m of 54–83 fF (for the range of vesicle diameters indicated above). Importantly, both our estimate of 50–60 fF, and the estimate of 50–80 fF derived from the results of Singer & Diamond (2006), exceed the number of tethered vesicles. With an average number of 36 ribbons per rod bipolar cell (Singer et al. 2004), seven docked vesicles per active zone, and a ratio between tethered and docked vesicles of 5:1 (Sterling & Matthews, 2005), the number of tethered vesicles can be calculated as ∼1250. This suggests that with sustained depolarization vesicles are recruited from a pool of non-tethered vesicles.

Functional implications of transient vesicular release

The results based on capacitance measurements presented in our study support the view that the release kinetics of rod bipolar cells are inherently transient (Singer & Diamond, 2003). Because we used pharmacological agents to block GABA and glycine receptors, as well as presynaptic glutamate transporters (Veruki et al. 2006), the transient release cannot be explained by synaptic feedback. After release of the readily releasable pool of vesicles, the capacitance increased approximately linearly with pulse duration at a rate of ∼43 fF s⁻¹. This combination of transient and sustained release seems sufficient to account for the transient and sustained components seen in the EPSC during sustained presynaptic depolarization in recordings of synaptically connected pairs of rod bipolar cells and AII amacrine cells (Singer & Diamond, 2003; Veruki et al. 2003, 2006) and is similar to observations made for goldfish bipolar cells (Mennerick & Matthews, 1996).

An interesting question concerns the amount of Ca²⁺ influx and number of vesicles released by a single photon response in a rod bipolar cell. The excitatory conductance corresponding to a single photon event could evoke a substantial depolarization (Field & Rieke, 2002), potentially sufficient to evoke release of the readily releasable pool. This could correspond to the feedforward gain control reported for the rod bipolar → AII amacrine synapse (Dunn & Rieke, 2008), but interaction with other presynaptic conductances could shift the transmission characteristics from transient to sustained (Snellman et al. 2009).

From the time derivative of the release function estimated in Fig. 9B, we estimate a maximal capacitance increase of ∼2.9 fF ms⁻¹, corresponding to a release rate of 2–3 vesicles (release site)⁻¹ ms⁻¹ (assuming 36 ribbons per axon terminal). It is possible, however, that artificially slow deactivation kinetics for the Ca²⁺ tail current might have confounded our estimate (see online Supplemental material). If so, the maximal release rate could be even higher. Nevertheless, our estimate corresponds reasonably well with that of Singer et al. (2004) obtained for postsynaptic recording from AII amacrine cells (∼4 vesicles (release site)⁻¹ ms⁻¹). Although these estimates by themselves do not provide evidence for a specific mechanism of release, it is of interest to note that such high rates of release at individual active zones could lend support to recent physiological (Singer et al. 2004; Singer, 2007) and morphological (Matthews & Sterling, 2008) evidence for multivesicular release at bipolar axon terminals.

Glossary

Abbreviations

AC

alternating current

DC

direct current

RC

resistor–capacitor

SEClamp

single-electrode voltage clamp

ZAP

impedance (Z) amplitude profile (AP)

Author contributions

L.O. and E.H. designed the research; L.O. performed the experiments, E.H. contributed analytical tools; L.O. analysed data, L.O. and E.H. interpreted data, wrote the paper, and approved the final version of the paper. The experiments were done in the Department of Biomedicine, University of Bergen.

Supplemental material

Supplementary Material

Supplementary Figure 1.

Supplementary Figure 2.

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors