Field Effects in the CNS Play Functional Roles

Abstract

An endogenous electrical field effect, i.e., ephaptic transmission, occurs when an electric field associated with activity occurring in one neuron polarizes the membrane of another neuron. It is well established that field effects occur during pathological conditions, such as epilepsy, but less clear if they play a functional role in the healthy brain. Here, we describe the principles of field effect interactions, discuss identified field effects in diverse brain structures from the teleost Mauthner cell to the mammalian cortex, and speculate on the function of these interactions. Recent evidence supports that relatively weak endogenous and exogenous field effects in laminar structures reach significance because they are amplified by network interactions. Such interactions may be important in rhythmogenesis for the cortical slow wave and hippocampal sharp wave–ripple, and also during transcranial stimulation.

Introduction

The electrical field produced by neural activity is commonly viewed as a measure of that activity rather than as a mechanism for influencing it. However, an influence can be exerted when currents associated with an extracellular field (Ve) cross a region of cell membrane. In that case, the transmembrane potential, Vm, differs from the intracellular potential (Vi) and instead equals the difference Vi − Ve (Furukawa and Furshpan, 1963; Faber and Korn, 1989) (Figure 1). This notion is straightforward and is based upon first principles, and thus, so called field effects or ephaptic interactions, are well known to be theoretically feasible (Arvanitaki, 1942; Katz and Schmitt, 1942). However, they are most often treated as being of negligible magnitude and to be nonspecific. Indeed, a current generated across the membrane of one neuron will produce a field that decays with distance and may affect all points at a fixed distance equally. On this basis, it is difficult to imagine how an electrical field effect might be useful in neural computations involving neurons interconnected with discrete and plastic synapses. Rather, field effects, when recognized, are usually associated with dysfunction in neural circuits brought on by hypersynchrony, for example. They are thought to contribute to epileptic activity (Jefferys and Haas, 1982; Haas and Jefferys, 1984; Traub et al., 1985a,b; Jefferys, 1995; Dudek et al., 1998; Bikson et al., 2003; Grenier et al., 2003; Fox et al., 2004; Haglund and Hochman, 2005; Jiruska et al., 2010) and to crosstalk between demyelinated axons (Rasminsky, 1980) in multiple sclerosis (Smith and McDonald, 1999), and in trigeminal neuralgia (Love and Coakham, 2001; Prasad and Galetta, 2009).

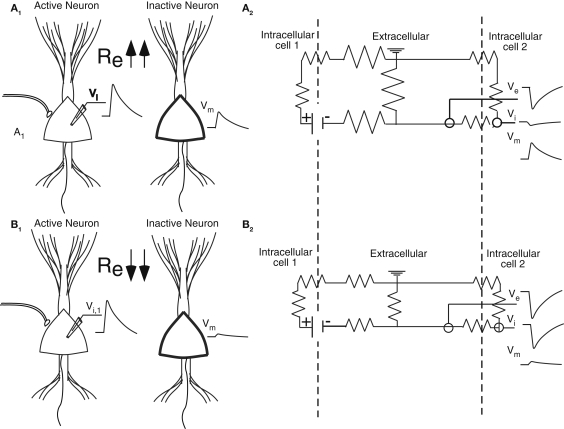
Figure 1.

(A1, B1) An EPSP in the soma of the left neuron produces a depolarization (Vm) in the soma of the right inactive neuron (thick line). The extracellular resistance (Re) is larger in (A) than in (B). Because the resistance is higher, more current is channeled across the membrane of the cell to the right in (A) and the field effect is bigger. (A2, B2) The equivalent circuit, with the dotted line representing the membranes, demonstrates how the magnitude of the field effect depends upon the relative values of the intracellular, transmembrane, and extracellular resistances. The transmembrane potential in cell 2 (Vm) is calculated as the difference between the extracellular potential (Ve) and the intracellular potential (Vi).

There is an alternative view, namely that field effects are not epiphenomena, but are specialized forms of neurotransmission that in some cases are known to mediate computations in neural circuits. Until recently, evidence for field effects in the CNS, which depend upon structural features, such as the orientation and proximity of neurons, as well as the uniformity, anisotropy, and impedance in the extracellular medium, was restricted to a few systems, most notably that of the teleost Mauthner cell (Furukawa and Furshpan, 1963; Korn and Faber, 1975; Weiss et al., 2008). However, recent reports of functional field effect interactions in the mammalian brain suggest that they are more common than previously accepted and are also shaped by the temporal dynamics of neural activity especially when relatively homogeneous populations of neurons are synchronously active (Bracci et al., 1999; Grenier et al., 2003; Vreugdenhil et al., 2005; Foffani et al., 2007; Frohlich et al., 2009; Anastassiou et al., 2010). That is, when the dipoles produced by a group of individual neurons are similarly oriented in space, neuronal population activity that is synchronous or coherent in phase produces a larger field and a more powerful effect. Here, we review the recent work on field effects in the context of their functional roles in neuronal communication, rather than in pathology. As previously, new results with the M-cell system provide insights not otherwise accessible at the single cell level.

Fields Generated by Neural Activity and the Principles of Field Effect Interactions

Electrical field effects are generated when extracellular currents associated with electrical activity of the dendrites, soma or axon of one or more neurons are sufficiently large that they are channeled across the membranes of adjacent inactive neurons. These effects are greatest when the extracellular resistance is high, a condition which favors the flow of current along an alternative parallel pathway. Figure 1 illustrates the case of two neighboring neurons with similar orientations, typical of many cortical structures. The difference between the two examples is that the extracellular resistance is higher in Figure 1A than Figure 1B. In both, an EPSP in Figure 1A is associated with an inward current at the soma and, because of charge conservation, outward currents at the dendrites. The field in the somatic region will be negative and, as noted above, the field effect will be greater in Figure 1A because more current will be channeled across the somatic membrane of the inactive cell on the right. Geometry also plays a role, as polarization along the longitudinal axis of a pyramidal neuron results in a dipole and an open field with currents and associated field effects detectable far from the generator (Holt and Koch, 1999; Gold et al., 2006). In contrast, in radially symmetric neurons, such as stellate cells, somatic polarization produces a closed field, and an extracellular potential restricted to the space within the range of the dendrites (Bishop and O'Leary, 1942; Lorente de No, 1947).

Recently, the extracellular fields produced by action currents of neurons with complex geometries have been estimated with multicompartment models and line source approximations using Coulomb's law extended to three-dimensional conducting media (Holt and Koch, 1999). Results from these simulations demonstrate that the type and distribution of ion channels outweighs dendritic morphology in determining the spatial orientation and amplitude of the field generated by an action potential in modeled CA1 pyramidal neurons (Gold et al., 2006, 2007), and that close to the axon hillock field potentials can be several millivolts in magnitude, which may be strong enough to influence conduction at a node of Ranvier in a neighboring axon via a field effect (Holt and Koch, 1999).

The importance of extracellular resistivity in determining how an electric field produced by a neuron(s) affects its neighbor, as illustrated in Figure 1, has also been demonstrated experimentally. Tissue swelling, which occurs during pronounced neuronal population activity (Autere et al., 1999), increases the extracellular resistivity, and increases the strength of field effects in hippocampal slices (Fox et al., 2004). Notably, the administration of furosemide and mannitol, two agents that act by different mechanisms to prevent tissue swelling, suppresses epileptic activity in human cortex, perhaps by reducing field effect interactions (Haglund and Hochman, 2005).

Another consideration is the superposition principle, that the fields produced by individual neurons spatially summate in space. On this basis, the orientation of neurons is a critical factor governing field effect interactions. If multiple neurons are oriented in a parallel laminar orientation, such as pyramidal neurons in the neocortex and hippocampus, the electrical fields produced by synaptic currents can be additive, and an inactive neuron oriented in parallel with these neurons will experience depolarizations and hyperpolarizations of spatially separated regions due to interneuronal current flow.

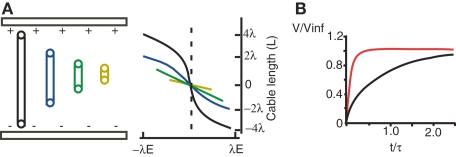
A key factor in discerning the functional consequences of a field effect interaction is the electrotonic properties of the neurons affected (Chan and Nicholson, 1986; Tranchina and Nicholson, 1986; Anastassiou et al., 2010). Cable and multicompartment simulations have proved helpful for investigating these relationships, particularly the simple case of a cylinder with passive membrane properties in a constant or spatially inhomogenous field. When the length of the cylinder is greater than the space constant (λ) the maximum polarization at the sealed ends approaches a constant value of λ multiplied by the magnitude of the electric field (Chan and Nicholson, 1986; Figure 2A). If however this length is less than λ the polarization is decreased and is more linearly related to the position along the cylinder. When the cylinder is in an oscillatory spatially inhomogenous field oriented along the dendro-somatic axis, the transmembrane polarization is maximized if the electronic length of the cylinder exceeds the distance between periodic values of field strength, or in other words the spatial frequency of the field. Also, polarization is strongest when the diameter of the cylinder is relatively large (Anastassiou et al., 2010).

Figure 2.

Spatiotemporal properties of field effects. (A) Cylinders of varying electrotonic length (colors) in a uniform electric field (E). The membrane polarization along the cable depends on the cable's electrotonic length. Adapted from Chan and Nicholson (1986). (B) Extra- (red) and intracellular (black) stimulation of a passive sphere results in a different time course of membrane polarization. Adapted from Cartee and Plonsey (1992).

In such simulations the transients across the membrane have a more rapid rate of rise than when current is injected intracellularly (Figure 2B) (Cartee and Plonsey, 1992; Svirskis et al., 1997a,b; Vigmond et al., 1997; Anastassiou et al., 2010). The reason is that with field stimulation each line of the field crosses the membrane in both directions and the total net charge on the membrane capacitance is zero at all times. In this case, the kinetics of the transient are due to the redistribution of charge and hence are proportional to the intracellular and extracellular conductivities.

These spatial and temporal properties of constant field polarization have been experimentally verified in isolated neurons (Svirskis et al., 1997a), and hippocampal slices using electrophysiological recordings, voltage sensitive dyes (Bikson et al., 2004), and cell reconstructions (Radman et al., 2009). Both models and experiments show that electrotonic properties dictate how specific types of neurons will respond to an applied field or a field occurring in vivo.

Electrical Inhibition in Sensorimotor Integration in the M-Cell System

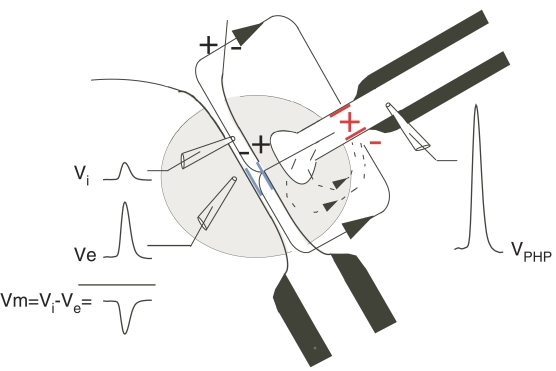
The teleost M-cell system that initiates the C-start escape behavior has served as the prototype for demonstrating field effects in vivo (Furukawa and Furshpan, 1963). Monosynaptic inputs from ipsilateral inner ear afferents have mixed electrotonic and chemical excitatory synapses on the M-cell lateral dendrite (Pereda et al., 2004) and also have electrotonic synapses on interneurons which inhibit the M-cells. The inhibitory interneurons release glycine and also inhibit the M-cells via a field effect (Korn and Faber, 1975, 2005). The latter occurs in a specialized region called the axon cap, with an extracellular volume resistivity that is approximately ninefold greater than the surrounding medium (Korn and Faber, 1975; Weiss et al., 2008). The axon cap surrounds the M-cell axon hillock and is penetrated by the unmyelinated axons of the feed-forward inhibitory interneurons (Figure 3). Action currents in these axons flow passively out at the terminals in the axon cap and some current flows inward across the M-cell axon hillock due to the high resistance of the axon cap, this inward current produces a significant hyperpolarization of the M-cell, i.e., the M-cell is electrically inhibited.

Figure 3.

Illustration of the electrical inhibition mediated by impulses in interneurons that inhibit the M-cell. Inward currents generated at the excitable heminode, or last node of Ranvier (red) of the inhibitory interneurons cell‘s myelinated axon (black) flow passively out at the terminal and other unmyelinated portions in the cap and inward across the membrane of the axon hillock (blue) of the M-cell. A region of high extracellular resistance (gray area), the axon cap, reduces extracellular currents returning to the heminode or last node of Ranvier within the cap (arrow with dashed line) and directs the current across the membrane of the M-cell.

We investigated the functional role of this electrical inhibition, using loud sounds to simulate a predatory strike. The auditory stimulus elicits synchronized action potentials in as many as 20 or more inhibitory interneurons, and the resulting action currents coincide with and counteract the sound evoked monosynaptic electrotonic excitation of the M-cell (Weiss et al., 2008). The amplitude of this electrical inhibition was ∼30–40% the size of the electrotonic excitation, and it was strong enough to prevent the M-cell from reaching threshold. Functional inhibition was confirmed by showing that the same sound could elicit an M-spike when the electrical inhibition was neutralized by a cathodal current pulse produced by a second electrode in the axon cap. Furthermore, since a single M-spike initiates the C-start behavior by activating neural networks in the spinal cord (Korn and Faber, 2005) and sound evoked electrical inhibition coincides with the M-spike in ∼45% of trials in free swimming fish (Weiss et al., 2008), we concluded that electrical inhibition regulates the behavioral threshold.

The functional role of the electrical inhibition is best understood in the context of the extremely short utilization time of the M-cell, as little as 400 μs, which serves to ensure survival by triggering a rapid escape (Catania, 2009). Within this very short interval two important computations must take place. First, in order to determine whether an escape is warranted, the M-cell system must determine if the auditory stimulus is salient, as would be the case if it were produced by an attacking predator. Second, in order for the escape to be directed away from the sound source its location must be identified and the appropriate left or right M-cell activated. Experimental results (Oda et al., 1998; Weiss et al., 2009) and neural simulations (Guzik et al., 1999) support the notion that these computations involve excitatory-inhibitory integration. Therefore, electrical inhibition, in complementing the electrotonic excitation, minimizes the escape latency while preserving the functionality of the neural circuit.

A similar type of electrical inhibition may occur between basket cells and Purkinje cells in the cerebellar cortex (Korn and Axelrad, 1980). However, electrical inhibitory synapses are less efficient than classical chemical synapses, because a higher portion of the current flows extracellularly (Bennett, 1968). If electrical inhibition in the cerebellar cortex is indeed a reality, presumably only conditions in which a substantial number of inhibitory fibers are synchronously active will result in a meaningful inhibition.

Electrical Interactions at Chemical Synapses: Variations on a Theme

In addition to the concept of electrical synapses involving field effect transmission, there are suggestions that fields can modify chemical synaptic transmission, for example, by clearing negatively charged glutamate molecules from the cleft by electrodiffusion (Sylantyev et al., 2008) or by influencing voltage gated channels involved in exocytosis (Voronin et al., 1999; Kasyanov et al., 2000; Voronin, 2000; Kamermans et al., 2001; Kamermans and Fahrenfort, 2004; Fahrenfort et al., 2009).

Voronin and colleagues concluded that, at synapses in visual cortex and hippocampus, synaptic currents may be directed across the membrane of the pre-synaptic cell because of the high intra-cleft resistance resulting in a positive feedback loop (Voronin et al., 1999; Kasyanov et al., 2000; Voronin, 2000). A similar mechanism has been proposed to occur in Type I hair cells (Goldberg, 1996) and in synapses in the electrosensory system of Gymnarchus (Carr, 2004; Matsushita and Kawasaki, 2005).

It has been postulated that a synaptic field effect mediates feedback between horizontal cells and cones in the retina (Kamermans and Fahrenfort, 2004). This feedback may contribute to establishing the center-surround organization of bipolar cells and ganglion cells (Kamermans et al., 2001; Kamermans and Fahrenfort, 2004; Fahrenfort et al., 2009). In this case, it is thought that currents flowing into the horizontal cell at one cone-horizontal cell synapse passively flow out through gap junction hemichannels localized to another cone-horizontal cell synapse. The current is then directed across the pre-synaptic membrane of the cone and influences the opening of voltage gated calcium channels. Modeling studies suggest, however, that this proposed mechanism requires revisions since according to an equivalent circuit model this inhibition is of minimal amplitude, performs better in the dark, and is more effective in mediating positive rather than negative feedback (Dmitriev and Mangel, 2006) but see rebuttal by Fahrenfort et al. (2009).

Field Effects in the Hippocampus and Neocortex Associated with Synchronous Activity

Whereas in the example of the M-cell, sizeable field effects can be generated by, or exerted on a single neuron, in the cortex and hippocampus tens of thousands of neurons per cubic millimeter of brain have multiple generators, such as chemical synapses and active conductances, that produce intercellular currents that are pooled together. The local field potential (LFP) results from the sum of these intercellular currents and contains structure that correlates with attention, perception, movement, and memory (for example see, Wehr and Laurent, 1996; Buzsaki, 2002; Perez-Orive et al., 2002; Pesaran et al., 2002; Mehring et al., 2003; Womelsdorf et al., 2006; Fries et al., 2007). The LFP is estimated to represent a region with a radius of 100–250 μm in which neurons may share some common inputs and computational features (Katzner et al., 2009; Xing et al., 2009). On this basis, it is popular to regard the LFP as a sign of the underlying synchronous dynamics and computations in the neurons that produce the currents with which the LFP is associated. Here we instead ask whether currents associated with the LFP can influence neural dynamics and participate in neural computation via field effects (Jefferys, 1995; Bullock, 1997).

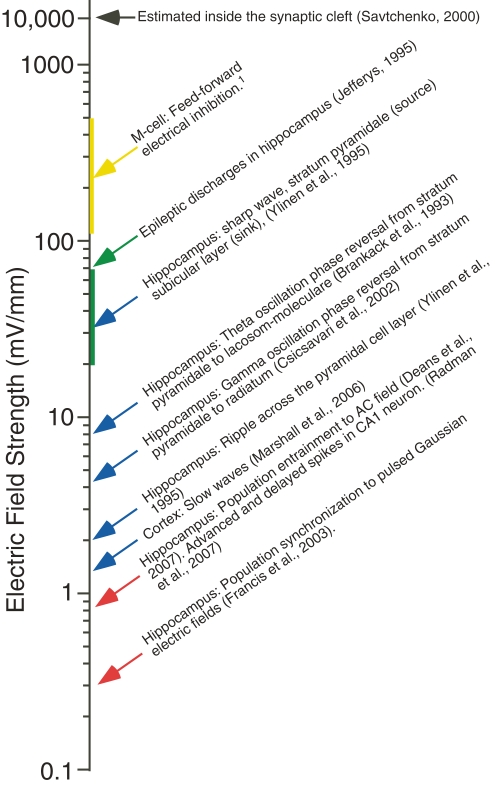
One obstacle to investigating the influence of the electric field associated with the LFP is that it is technically challenging to experimentally manipulate the fields, to test for effects on network function because of the complex spatial structures of endogenous fields and the filtering characteristics of brain tissue (Bédard et al., 2004; Logothetis et al., 2007). With this shortcoming in mind, one experimental approach has been to measure the threshold electric field strength at which field effects are induced in vitro in hippocampus and cortex, and compare it to electric field strength measured in vivo (Figure 4) (Francis et al., 2003; Fujisawa et al., 2004; Deans et al., 2007; Radman et al., 2007; Frohlich et al., 2009). These studies have found that extremely weak fields (<0.5 mV/mm) are capable of significantly modulating activity at the network and single cell level.

Figure 4.

A comparison of the strength of endogenous electric fields with that of exogenous fields shown to alter spike timing in vitro. Approximate strength of endogenous electrical fields resulting from normal activity in the cortex and hippocampus (blue arrows), as well as the in the M-cell system (yellow arrow, vertical line indicates range). The approximate field strength of epileptic discharges (green arrow and vertical line). Spike timing in hippocampal slices (red arrows) is altered by exogenous fields that are considerably weaker in strength.

In one such study hippocampal slices were bathed in high K⁺ to elicit spontaneous seizure-like activity. This spontaneous activity could be entrained to an exogenous pulsed electric field produced by parallel plate electrodes oriented perpendicular to the somadendritic axis of area CA1 (Figure 2A). The threshold for inducing this entrainment, in area CA1, was ∼295 μV/mm (Francis et al., 2003), far lower than many extracellular field gradients evident in vivo (Figure 4). In a similar study, hippocampal slices were bathed in kainate to elicit spontaneous activity in the beta and gamma frequency ranges (Deans et al., 2007). In the presence of an AC field as small as 1 mV/mm, oriented as described above, the peak of the spontaneous oscillation frequency shifted from the spontaneous frequency to the frequency of the applied field, ∼50 Hz, or its subharmonic.

These effects are remarkable considering that applied uniform DC fields alter the transmembrane potential in individual neurons by 0.18 mV/mm, and AC fields are even less effective (Deans et al., 2007). One explanation is that the small influence that a field effect exerts across a large population of laminar neurons is amplified by network interactions between the affected neurons (Purpura and McMurtry, 1965). For example, in spontaneously firing interconnected neurons a field effect may induce small changes in spike timing (Radman et al., 2007; Anastassiou et al., 2010) that can increase synchronicity in excitatory chemical synaptic transmission thereby significantly impacting network dynamics (Fujisawa et al., 2004). Theoretically, this amplification would be maximized by a network configuration of laminarly arranged neurons interconnected by chemical synapses, and also if spike timing in this network is sufficiently synchronous to generate strong fields (Figure 5). Although, this amplification also occurs in more complex network structures such as in the hippocampus (Francis et al., 2003; Fujisawa et al., 2004; Deans et al., 2007) and when ongoing spiking is relatively random (Francis et al., 2003).

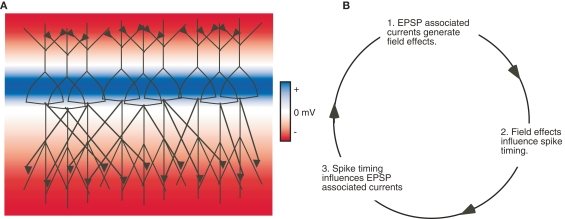
Figure 5.

Field effects can be amplified by network interactions involving chemical synapses. (A) An illustration of pyramidal neurons arranged in a parallel laminar orientation interconnected by excitatory chemical synapses on the apical and basal dendrites. Colors indicate the extracellular potential resulting from synaptic activity in the apical and basal dendrites in this network. (B) Field effects associated with the EPSPs in the network are amplified by affecting spike timing and consequently chemical synaptic transmission. Note this amplification can theoretically occur within diverse network architectures.

Evidence for a role of field effects in rhythmogenesis in cortex and hippocampus

Several studies support the notion that endogenous fields are involved in generating and maintaining neural oscillations (Bracci et al., 1999; Grenier et al., 2003; Park et al., 2005; Richardson et al., 2005; Vreugdenhil et al., 2005; Foffani et al., 2007; Frohlich et al., 2009). DC fields with intensities comparable to those of endogenous fields (<1 mV/mm) can accelerate the neocortical slow wave oscillation associated with deep sleep (Steriade et al., 1993), by uniformly depolarizing the soma of layer 5 pyramidal neurons and decreasing the time spent in the down state. Similarly, amplitude matched AC sine waves (<1 Hz), and waves identical to those recorded in vivo, can entrain and amplify the slow oscillation (Frohlich et al., 2009).

Field effects have also been implicated in rhythmogenesis in tetanus-induced gamma oscillations recorded in hippocampal slices. In this case intercellular action currents entrain pyramidal neurons to fire at gamma frequency (Bracci et al., 1999; Vreugdenhil et al., 2005). Paroxysmal events with characteristics of high-frequency oscillations in the neocortex may be generated by a similar mechanism and may also involve slow shifts in the transmembrane potential via field effect interactions (Grenier et al., 2003).

The sharp wave–ripple complex described in area CA1 of the hippocampus (O'Keefe and Nadel, 1978) may involve field effect interactions as well (Buzsaki et al., 1992). First, the synaptic currents generated on the apical dendrites of pyramidal neurons by Schaffer collateral activation during the sharp wave could influence the timing of dendritic spikes in neighboring neurons (Anastassiou et al., 2010). Second, the pooled currents that contribute to the high-frequency ripple, thought to be generated by perisomatic GABAergic synapses (Buzsaki et al., 1992; Ylinen et al., 1995; Klausberger et al., 2003, 2004), or in part by gap junctions (Draguhn et al., 1998; Traub and Bibbig, 2000; Maier et al., 2002; Nimmrich et al., 2005; Roopun et al., 2010), could promote neuronal discharges during the trough of the ripple oscillation (Buzsaki et al., 1992; Ylinen et al., 1995; Chrobak and Buzsaki, 1996) via field effect interactions (Bikson et al., 2003; Foffani et al., 2007; Jiruska et al., 2010). In support of this hypothesis, hippocampal slices from epileptic rats with a lower tissue resistivity at the somatic layer of area CA3 due to sclerosis exhibit smaller amplitude field effects and abnormal high-frequency ripples (Foffani et al., 2007). The frequency of the ripple is thought to increase because of a desynchronization between individual cell activation and the network oscillation.

If in fact field effects do mediate the sharp wave–ripple complex they may be involved in determining the pattern of pyramidal cell activation that is transferred to entrorhinal cortex (Chrobak and Buzsaki, 1996) and neocortex (Siapas and Wilson, 1998; Sirota et al., 2003; Girardeau et al., 2009; Wierzynski et al., 2009). It is unclear if this interaction could be computationally advantageous as opposed to a form of crosstalk, since the functional topographical organization of the hippocampus is still not entirely established (Jung et al., 1994; Redish et al., 2001; Maurer et al., 2005; Kjelstrup et al., 2008; Lubenov and Siapas, 2009).

Nevertheless, field effects are ideal to mediate synchronization of fast oscillations, such as paroxysmal events and the sharp wave–ripple complex, since temporal constraints imposed by membrane capacitance are reduced (Figure 2B) (Cartee and Plonsey, 1992; Svirskis et al., 1997a; Anastassiou et al., 2010). For example, modeling demonstrates that, due to a field effect, an action potential in one pyramidal neuron is transmitted to a neighboring pyramidal cell as a biphasic spikelet, lasting 1–2 ms (Vigmond et al., 1997). Similar spikelets can also result from action currents conducted across gap junctions between pyramidal neurons in the hippocampus (Bennett and Pereda, 2006; Mercer et al., 2006). Field effects may be able to mediate neurotransmission even more rapidly, and consequently also participate in fast rhythmogenesis (Stacey et al., 2009).

Field effects and computations in single neurons

While the aforementioned studies provide preliminary evidence that field effects influence network dynamics in the hippocampus and neocortex, evidence for a computational role in these structures is lacking. In this context the example of the Mauthner cell may be instructive. There integration of field effect inhibition with chemical and electrotonic excitation defines the threshold of activation and consequently the performance of the corresponding C-start behavior. Whether or not field effects play a similar role for the diverse computations performed by single hippocampal and neocortical neurons is unknown.

The influence of field effects on spike timing in single neurons has been described (Radman et al., 2007; Anastassiou et al., 2010) and underlies the described network effect in Figure 5 (Fujisawa et al., 2004). When an intracellular current ramp is applied to CA1 pyramidal neurons in the presence of a DC field or an AC field in the gamma frequency band the spikes produced by the ramp are advanced or delayed by the applied field (Radman et al., 2007). Similarly, spatially inhomogenous theta and sharp wave fields, derived from in vivo experimental data, were found to influence excitability and influence spike timing in simulated cortical pyramidal neurons, particularly in the apical dendrites (Anastassiou et al., 2010). Whether such effects are also important in a computational context in single neurons depends on the strength of the field, the pattern of the synaptic activity, and the nature of the computation in question.

One potential computational mechanism that could involve field effect interactions is spike-phase coding. This involves converting the excitatory drive in individual neurons in to a phase value relative to the LFP (O'Keefe and Recce, 1993; Hopfield, 1995; Fries et al., 2007; Jacobs et al., 2007; Huxter et al., 2008; Montemurro et al., 2008; Pastalkova et al., 2008; Kayser et al., 2009). This conversion is thought to occur because such neurons receive phasic synaptic activity in addition to the primary excitatory drive. If field effects also participated in spike-phase encoding by providing feedback between the phasic LFP and individual neurons it would be advantageous since the amplitude of polarization resulting from a field effect is independent of membrane potential (Faber and Korn, 1989) and field effects could provide a common oscillatory reference frame. It is unclear however if fields with amplitudes sufficient to subserve this role indeed occur during sensory processing or behavior, and it seems unlikely to be the case for spike-phase encoding for hippocampal place cells (Harvey et al., 2009).

If field effects do indeed participate in computations in single neurons, an important consideration is how such effects are regulated. The onset (Fries et al., 2007; Buzsaki, 2002) and offset (Poulet and Petersen, 2008) of oscillations in the LFP accompany sensory processing and behavior and could also signify the regulation of the corresponding field effect. These events, as well as the strength, temporal and spatial characteristics of a field, are determined by network parameters such as synchronicity (Klausberger et al., 2003; Klausburger and Somogyi, 2008), and the balance of excitation and inhibition within a network (Atallah and Scanziani, 2009).

Field Effects and Transcranial Electrical Stimulation- Investigational Tool and Promising New Therapeutic Modality

Understanding field effects in the CNS may also have important clinical applications. Strong fields produced by surgically implanted electrodes positioned in the hippocampi, may be able to entrain seizures (Richardson et al., 2003; Sunderam et al., 2009), while weak DC and AC fields produced by the transcranial application of current have been shown to have a wide variety of effects that are potentially useful therapeutically (Wasserman, 2008).

In the case of transcranial DC stimulation (tDCs), it was well established, by Purpura and McMurtry (1965) for one, that applying anodal DC to the cortical surface increases neuronal activity and paroxysmal events, whereas cathodal stimulation reduces neuronal activity (Figure 2A). The effect appears to be primarily mediated by field interactions with voltage sensitive cation channels on the neuron (Chan et al., 1988; Lopez et al., 1991; Liebetanz et al., 2002). It has also been speculated that effects that outlast the stimulation (Reis et al., 2009) may be mediated by modulation of NMDA receptors (Liebetanz et al., 2002; Nitsche et al., 2003; Siebner et al., 2004), although this conclusion has been contested (Ardolino et al., 2005). Also, tDCs induced plasticity has been attributed to the involvement of catecholamines (Nitsche et al., 2004), acetylcholine (Kuo et al., 2007), and alterations of excitatory-inhibitory balance (Stagg et al., 2009).

Studying transcranial electrical stimulation may provide insights to the functional roles of field effects in neural circuits (Ozen et al., 2009), since fields similar in strength to those that occur endogenously influence memory encoding (Kirov et al., 2009), consolidation (Marshall et al., 2006), and perception (Kanai et al., 2008). For example, a slow AC field <1 Hz applied during non-REM sleep was shown to increase cortical slow oscillations and slow spindle activity and enhance retention in a declarative memory task in humans (Marshall et al., 2006). The mechanism that underlies this impressive result was investigated in an in vivo rat model (Ozen et al., 2009). Application of a similar transcranial 1 Hz signal could entrain spiking in neocortical neurons. Unexpectedly, the degree of entrainment was dependent on the intrinsic oscillatory state of the animal, as correlated with the stage of the sleep/wakefulness cycle. Entrainment was also observed in regions of cortex distant from the stimulating electrode, i.e., where the electric field amplitude was minimal. Therefore, network interactions act to amplify a field effect not only in vitro, but also in vivo, which may explain why transcranial application of weak fields can perhaps influence plasticity and induce dramatic and long lasting behavioral effects.

Conclusion

Over a decade's worth of progress in the study of the functional role of field effects in the nervous system supports the conclusion that such interactions should be considered when discerning the biophysical basis of network dynamics and computation. However, prudence is required in assigning functionality to biophysical mechanisms in neural systems, especially since field effects are difficult to experimentally define and antagonize. Experiments that will overcome these boundaries and offer more definitive evidence must simultaneously record intracellularly and extracellularly in vivo (Grenier et al., 2003; Harvey et al., 2009) to determine the actual transmembrane potential, simulate or partially negate field effects in this setting with electrical stimulation (Weiss et al., 2008), and implement computer simulations to confirm the experimental data (Mori et al., 2008; Anastassiou et al., 2010). The pace of research in this area is sure to accelerate, given the interest in clinical applications, and it is likely that in the decade to come functional field effect interactions will become increasingly recognized in diverse brain structures.

Conflict of Interest Statement

The research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.