Abstract
Recent demographics demonstrate an increase in the number of elderly spinal cord injury patients, motivating the desire for a better understanding of age effects on injury susceptibility. Knowing that age and disease affect neurological tissue, there is a need to better understand the sensitivity of spinal cord injury mechanics to variations in tissue behavior. To address this issue, a plane-strain, geometrically nonlinear, finite element model of a section of a generic human thoracic spinal cord was constructed to model the response to dorsal compression. The material models and stiffness responses for the grey and white matter and pia mater were varied across a range of reported values to observe the sensitivity of model outcomes to the assigned properties. Outcome measures were evaluated for percent change in magnitude and alterations in spatial distribution. In general, principal stresses (114–244% change) and pressure (75–119% change) were the outcomes most sensitive to material variation. Strain outcome measures were less sensitive (7–27% change) than stresses (74–244% change) to variations in material tangent modulus. The pia mater characteristics had limited (<4% change) effects on outcomes. Using linear elastic models to represent non-linear behavior had variable effects on outcome measures, and resulted in highly concentrated areas of elevated stresses and strains. Pressure measurements in both the grey and white matter were particularly sensitive to white matter properties, suggesting that degenerative changes in white matter may influence perfusion in a compressed spinal cord. Our results suggest that the mechanics of spinal cord compression are likely to be affected by changes in tissue resulting from aging and disease, indicating a need to study the biomechanical aspects of spinal cord injury in these specific populations.
Key words: age, finite element models, models of injury, traumatic spinal cord injury
Introduction
It is well established that the severity of damage resulting from spinal cord injury is strongly influenced by the mechanics of the impact (Anderson, 1985; Noyes, 1987; Kearney et al., 1988; Bresnahan et al., 1991; Behrmann et al., 1992; Basso et al., 1996; Gruner et al., 1996). The expanding aging population and recent reported increases in the numbers of elderly spinal cord injury patients (Jackson et al., 2004), however, motivate a need for improved understanding of the influence of age on injury susceptibility. Mechanical characterization of neural tissue has shown that tissue mechanical properties vary with age (Prange and Margulies, 2002) and disease affects tissue structures (Lovas et al., 2000; Bot et al., 2004). Knowing this, there is a need to better understand the sensitivity of spinal cord injury mechanics to variations in tissue behavior. However, acquiring and testing fresh human spinal cord tissue is quite difficult. Identifying which material properties have the greatest influence on injury mechanics a priori will allow for the direction of experimental resources toward characterizing the most critical materials.
The effect of variation in material moduli of the spinal cord constituents on the mechanics of injury has not been quantified and is thus poorly understood. The complexity of nervous tissue and the difficulty in maintaining tissue integrity for biomechanical testing have resulted in great variability in the observed material moduli and the assigned constitutive models. Reported mechanical properties have demonstrated substantial variations due to both the state of the tissue (Metz et al., 1970; Gefen and Margulies, 2004; Oakland et al., 2006; Garo et al., 2007) and the test parameters (Bilston and Thibault, 1996; Ichihara et al., 2001; Prange and Margulies, 2002; Ichihara et al., 2003; Fiford and Bilston, 2005). Additionally, while the spinal cord is often tested as a single structure (Bilston and Thibault, 1996; Fiford and Bilston, 2005; Oakland et al., 2006), the individual constituents of the cord have markedly different mechanical properties (Ichihara et al., 2001; Ichihara et al., 2003; Aimedieu and Grebe, 2004; Jin et al., 2006). Experimental observations conflict on whether the grey matter is more (Ichihara et al., 2001), less (Coats and Margulies, 2006), or equally (Ozawa et al., 2001) stiff than the white matter. Results from finite element analyses performed on a homogenous spinal cord suggest that tissue level mechanics are more sensitive to the choice of material constitutive model (i.e., orthotropic versus isotropic) than to the magnitude of the elastic modulus (Bilston, 1998). However, distributions of stresses within the spinal cord change when the grey and white matter and pia mater are modeled individually (Ichihara et al., 2001). Furthermore, representing the non-linear response of the spinal cord with a linear elastic model is common in finite element models (Scifert et al., 2000; Greaves et al., 2008), but the effect of this simplification on compression injury mechanics is unknown.
The overall goal of this study was to quantify the sensitivity of finite element-derived estimates of tissue level stresses and strains in the spinal cord to changes in the assumed material characteristics of the cord constituents. The specific objectives were to: (1) quantify the effect of variations in material modulus on peak values of stresses and strains in the grey and white matter and map the distribution of values across the spinal cord; and (2) quantify the changes in outcome measures resulting from using simpler linear elastic models to represent the non-linear behaviors of the grey and white matter. This study is unique, as it is the first to quantitatively assess the effects of variations in cord tissue material behavior on the internal tissue mechanics of spinal cord compression.
Methods
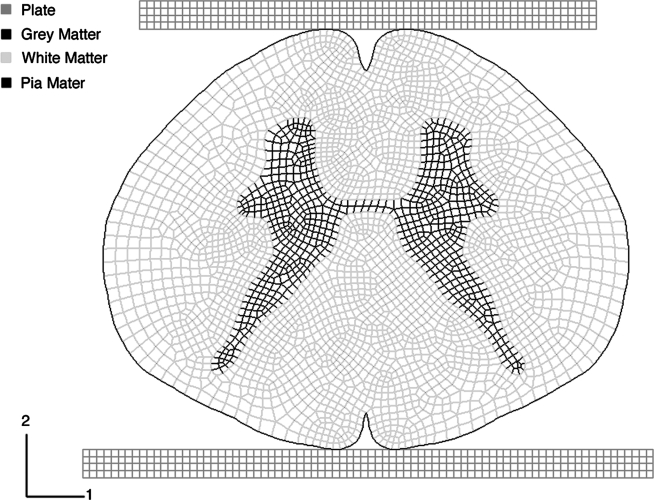
A plane-strain, geometrically nonlinear, finite element model of a section of a generic human thoracic spinal cord was constructed to model the response to dorsal compression (Fig. 1). A plane-strain analysis was selected to account for the substantial length-to-width ratio of a three-dimensional spinal cord. Additional analyses using plane stress and three-dimensional models confirmed that the plane-strain models reflected actual trends (see section on plane-strain models). Two flat plates (E = 17 GPa) bounded the spinal cord and a uniform compressive displacement was applied to the posterior side of the spinal cord to a depth of 1.5 mm or 30% compression. The compression was applied statically and computed implicitly. The contact between the spinal cord and loading plates was frictionless. The spinal cord was modeled (ABAQUS version 6.5; Abaqus Inc. Providence, RI) after analysis of a composite of grey matter, white matter, and pia mater, with geometry obtained from a published MRI scan of the human thoracic spinal cord (Schoenen and Faull, 2004). White and grey matter elements were modeled with an eight-node, plane-strain hybrid formulation to account for the nearly incompressible nature of spinal cord tissue (Table 1). Pia mater was modeled using three-node hybrid truss elements, which carried only tensile loading, similar to a membrane. The pia mater truss elements were tied to white matter nodes to enforce displacement compatibility. A mesh refinement analysis confirmed numerical convergence, and output reports and visual inspection of elements were used to confirm that excessive deformations did not influence the observed peak outcome values.
FIG. 1.
The finite element model of a generic human thoracic spinal cord. Grey and white matter materials were modeled using eight-node, plane-strain, hybrid elements. Pia mater was modeled using three-node truss elements.
Table 1.
The Different Material Models, Tangent Moduli, Element Types, and Number of Elements Used in Each Material Component of the Spinal Cord Finite Element Model
| Material | Model | Etangent (kPa) | No. of elements | Element |
|---|---|---|---|---|
| Gray matter | Hyperelastic, linear elastic | 65, 90, 115, 140, 165 | 666 | Eight-node plane-strain hybrid |
| White matter | Hyperelastic, linear elastic | 65, 90, 115, 140, 165 | 2424 | Eight-node plane-strain hybrid |
| Pia mater | Linear elastic | 600, 1200, 1800, 2400, 3000 | 142 | Three-node truss hybrid |
| Platens | Linear elastic | 17,000,000 | 350, 256 | Eight-node plane-strain |
The material models and stiffness responses for the grey and white matter and pia mater were varied across a range of reported values to compute the sensitivity of model outcomes to the assigned properties (Table 1). Because of a lack of data for fresh human spinal cord, the material characteristics for the grey and white matter were obtained by fitting mathematical material models to published experimental results for bovine spinal cord tissue (Ichihara et al., 2001). A third-order Ogden (Ogden, 1984) hyperelastic, incompressible, isotropic strain energy function (Eqn. 1) was used to model non-linear elastic responses of the grey and white matter, while the pia mater was modeled as linear elastic (Aimedieu and Grebe, 2004; Jin et al., 2006):
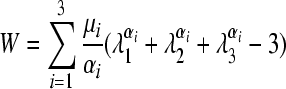 |
(1) |
in which λi are the principal stretches, λ1λ2λ3 = 1 for incompressibility and μi, αi (i = 1–3) represent six independent material parameters. For each material, only the tangent modulus was altered (Eqn. 2):
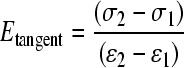 |
(2) |
in which Etangent is the tangent modulus and σi is the stress in the material at a given strain ɛi. The tangent modulus was calculated using ɛ1 = 0.3 and ɛ2 = 0.5, as the experimental data for both grey and white matter were nearly linear in this range (Ichihara et al., 2001). The material behavior at low strains (toe region) was kept the same for all the hyperelastic materials, consistent with the experimental findings (Ichihara et al., 2001). The six material parameters in the Ogden model were optimized to fit each prescribed tangent modulus (Table 2). In the linear elastic material models, the elastic moduli were the tangent moduli. Poisson's ratio (linear elastic) and incompressibility (hyperelastic) remained fixed in the material definition. To determine the importance of using the more complex material model for the white and grey matters, a second series of analyses was run using linear elastic models instead of hyperelastic models for those tissues. Displacement compatibility was enforced at all material interfaces. In total, 250 analyses were run.
Table 2.
Ogden Model Coefficients Corresponding to Each Tangent Modulus
| Etangent (kPa) | μ1 | α1 | μ2 | α2 | μ3 | α3 |
|---|---|---|---|---|---|---|
| 65 | −0.986 | −2.832 | 0.489 | −1.246 | 0.501 | −4.525 |
| 90 | −1.417 | −2.840 | 0.713 | −1.266 | 0.707 | −4.516 |
| 115 | −1.851 | −2.862 | 0.940 | −1.294 | 0.914 | −4.529 |
| 140 | −2.283 | −2.854 | 1.166 | −1.290 | 1.119 | −4.513 |
| 165 | −2.708 | −2.860 | 1.390 | −1.297 | 1.320 | −4.518 |
The stress and strain outcome measures were evaluated for magnitude and distribution across the spinal cord. Directional, principal, and shear strains, along with principal and shear stresses and pressure were recorded in both the grey and white matters. The overall force-displacement response of the cord to loading was also recorded. A single peak value (at the 95th percentile to eliminate any computational artifacts) was obtained for each of the outcome measures in each of the 125 hyperelastic models to examine the sensitivity of resulting stresses and strains to changes in material properties. A percent variability was obtained for each outcome measure by subtracting the minimum peak value of the 125 hyperelastic models from the maximum peak value and then dividing that range of outcome values by the mean peak value (Eqn. 3).
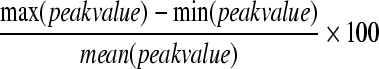 |
(3) |
Linear models were developed from stepwise regression analyses (JMP 7.0; SAS Institute Inc., Cary, NC) to determine the relative contribution of each material variable to the mechanical outcome measures. Variables included in the stepwise regression analysis were white matter modulus, grey matter modulus, interaction between white and grey matter moduli, and pia mater modulus. The contribution of each material parameter to the overall variability of a given outcome measure was determined by multiplying the R2 value for that material, as determined by the stepwise regression, by the percent variability for that outcome measure. For example, if the total variability of strain x is 40%, and the R2 value for white matter corresponding to strain x was 0.5, then the variability of strain x attributed to white matter variation would be 20%. The difference between the net R2 value and one following the stepwise regression was attributed to higher order interactions of material properties. Plots were generated to show the relative contribution of each material parameter to the overall variation in each outcome measure.
Locations of peak stresses were qualitatively analyzed by anatomic location within the spinal cord. Comparing the mechanical response of the constructed composite cord model to previously reported values of whole cord tangent moduli validated the model (Hung and Chang, 1981; Chang et al., 1988; Bilston and Thibault, 1996; Ozawa et al., 2001; Sparrey, 2004; Fiford and Bilston, 2005). An “effective” tangent modulus (Eff) of the whole cord complex for each model was approximated using the analytical solution for plane-strain compression of an elastic cylinder between two platens, which accounted for deformation of the cylinder contact surfaces (Eqn. 4) (Jawad and Ward, 1978):
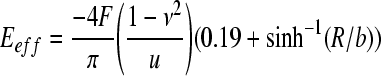 |
(4) |
in which F is the applied force, u is the axial deformation, ν = 0.5 is the Poisson ratio, R is the radius of the spinal cord (3.75 mm), and b is the contact width (4 mm) measured from the deformed finite element model.
Results
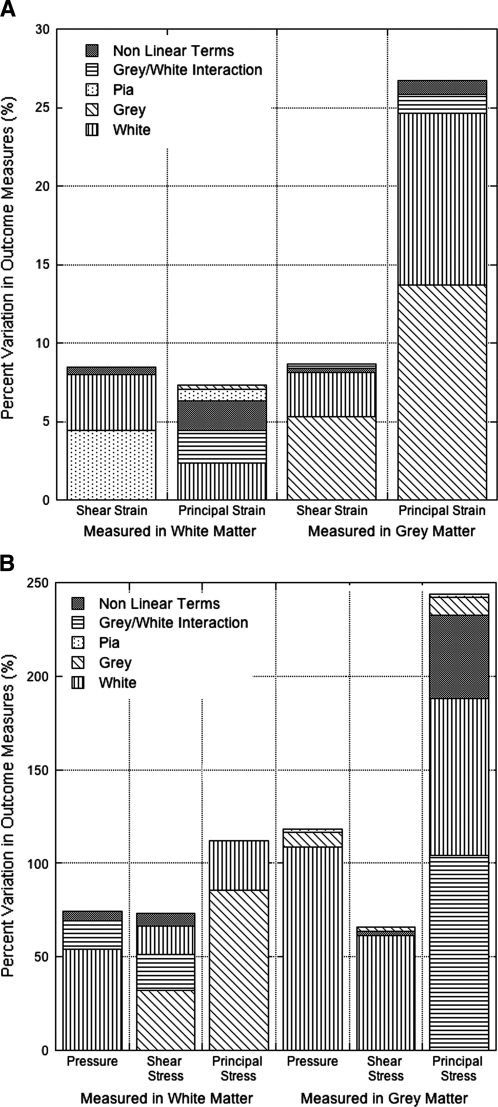
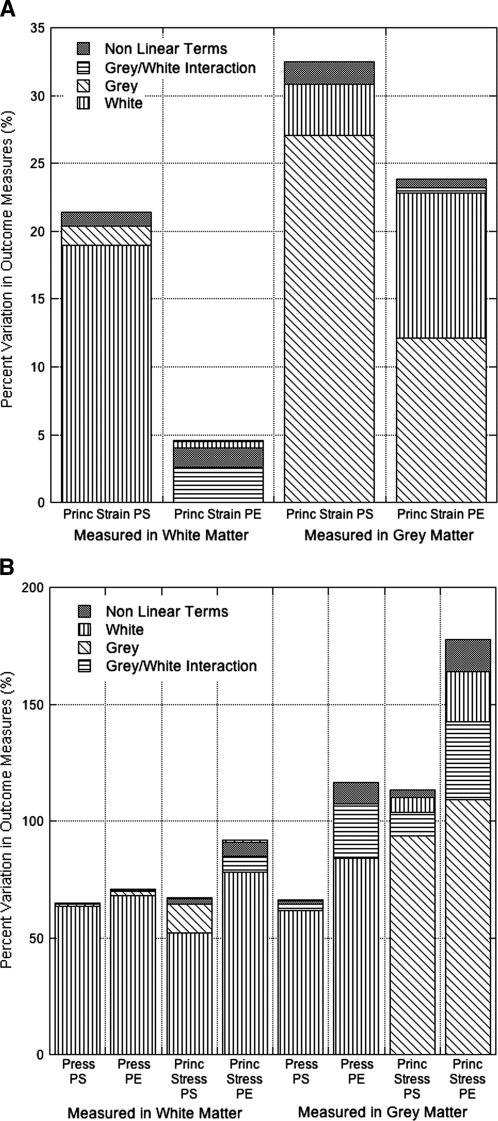
Principal stresses (114–244%) and pressure (75–119%) were the outcome measures most sensitive to material tangent modulus variations. In general, strain outcome measures were less sensitive (7–27%) than stresses (74–244%) to variations in material tangent modulus (Fig. 2). Whole cord mechanical response was most influenced by white matter properties (r2 = 0.91), while grey matter (r2 = 0.08) and pia mater (r2 = 0.002) properties had little effect. As expected, stresses and strains measured in the grey matter were most sensitive to changes in grey matter modulus, while white matter properties played a dominant role in outcome measures in the white matter. However, the pia mater modulus had very little effect on stress and pressure measurements, but was the main material (r2 = 0.52) affecting shear strain outcomes in the white matter. Furthermore, principal stresses (r2 = 0.43) and strains (r2 = 0.29) in the white matter were particularly sensitive to the interaction between grey and white matter material properties. Strains were much more robust to material property variations than stresses, and white matter properties significantly influenced pressure outcomes in both the grey and white matter.
FIG. 2.
The outcome measures observed in the grey and white matter for the hyperelastic material models. (A) The average variation in the strain outcome measures in the white matter and grey matter resulting from simultaneous variation of all the tangent stiffness properties in the hyperelastic models. (B) The average variation in stress and pressure outcomes, measured in the white and grey matter, resulting from simultaneous variation of all the tangent stiffness properties in the hyperelastic models. The percent variability in each outcome measure to changes in each individual material modulus is reflected by the plot colors. Grey/white interaction is the cross of the grey and white material properties, and indicates sensitivity to relative material properties. Nonlinear terms include all additional material interaction terms and nonlinear material property variables.
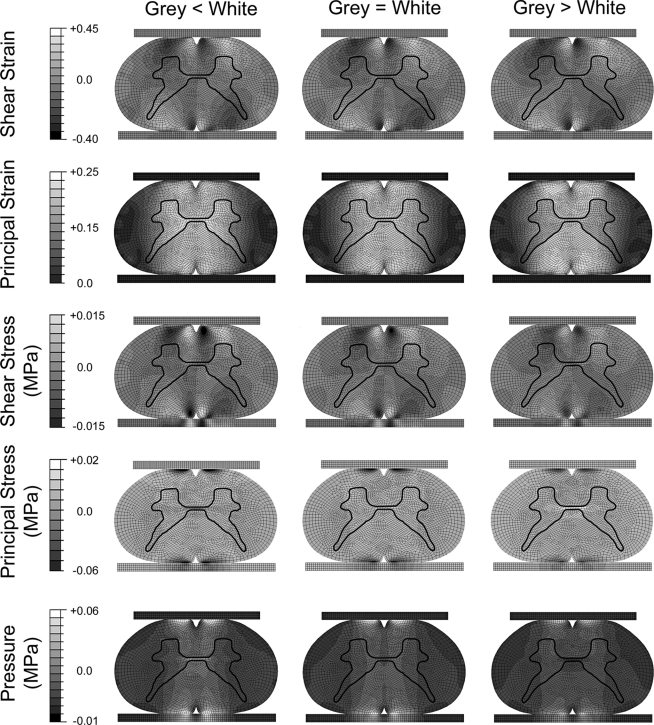
Material modulus parameters also influenced the spatial distribution of the stresses and strains across the spinal cord cross-section. Principal strains were concentrated in the dorsal and ventral white columns when the grey matter was assumed to be stiffer than the white matter (Fig. 3). Principal strains were concentrated in the central grey and white matter, but spread laterally to include parts of the dorsal and ventral grey horns when the grey matter was assumed to be less stiff than the white matter. Principal stresses were sensitive to relative properties between grey and white matter, with high tensile stresses developing in the central grey matter when the grey matter was stiffer than the white matter. Pressure in the central grey matter was elevated when the grey matter was less stiff, but was negative when the grey matter was stiffer. As expected, the distributions were similar for models when the magnitudes of difference between grey and white matter moduli were the same (i.e., grey matter moduli minus white matter moduli equaled 50 kPa). The distributions of shear strains and shear and compressive stresses were unaffected by changes in relative properties of the spinal cord tissue. All outcome measures showed peak values concentrated in the dorsal and ventral white matter columns when the grey and white matter stiffness values were equal.
FIG. 3.
Distribution of outcome measures resulting from different relative material properties. The left column shows results when grey matter (Etan = 65 kPa) was less stiff than the white matter (Etan = 165 kPa). The central column shows outcomes when grey (Etan = 115 kPa) and white matter (Etan = 115 KPa) properties were equal. The right column is outcomes when the grey matter (Etan = 165 kPa) is stiffer than the white matter (Etan = 65 kPa). The grey and white matter material boundary is outlined in each model. Shear outcomes show little sensitivity to variations in relative properties of the grey and white matter, while pressure and principal stress and strain patterns vary with changes in grey and white matter properties.
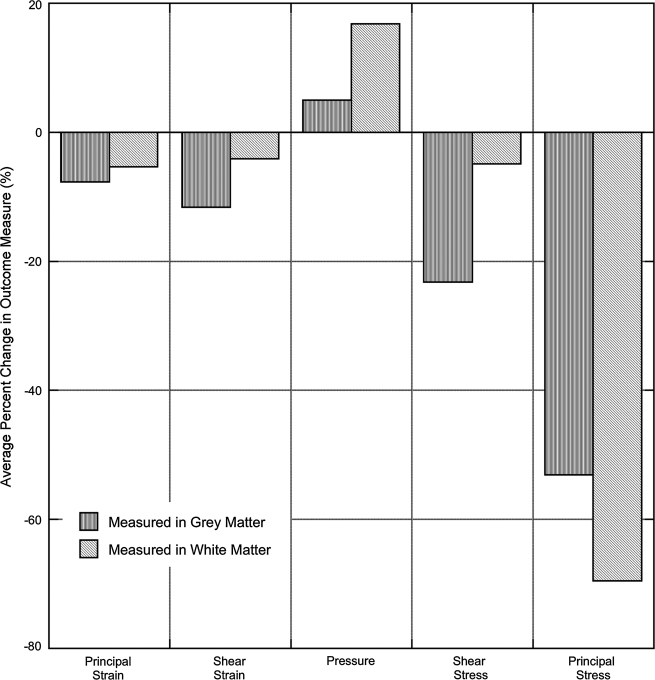
Generally, the linear elastic constitutive models predicted more concentrated areas of elevated stress and strain compared with the more diffuse distribution in the hyperelastic models. The use of a linear elastic constitutive model instead of the nonlinear Ogden model overestimated the strain and stress outcome measures (3–68%) but underestimated the pressure outcome (4–17%) (Fig. 4). Principal stress outcomes were most sensitive to choice of constitutive model, while strain measures were more robust. The differences due to choice of material model were greatest in the models having the least stiff grey and white matter (21%), and were minimized as the materials became stiffer (1.9%). The use of a linear elastic material model also affected the distribution of stresses and strains across the spinal cord cross-section.
FIG. 4.
Change in outcome measures resulting from using a linear elastic material model to represent a hyperelastic response. Negative values indicate that the linear elastic model overestimated the outcome measures, while positive values indicate an underestimation of the outcome. Each of the outcome measures was observed separately in the grey and white matter.
Plane-strain models
The use of a plane-strain assumption in developing the models in this study was guided by mechanical theory, which indicates that a plane strain assumption is suitable for models in which the third direction of strain is expected to be negligible (usually thick specimens). A plane-stress assumption, in contrast, is thought to be suitable when the third dimension of stress is negligible (typically for very thin specimens). In reality, both the plane-strain and plane-stress analyses fail to capture the complete behavior of a three-dimensional scenario, but are necessary to reduce computational costs. It has not been clearly established, however, how these theories apply to very soft and highly deformable materials such as the spinal cord. It was therefore necessary to evaluate how the plane-strain assumption influenced the outcomes observed in this study and how the outcomes compared with outcomes from plane-stress and three-dimensional models in order to be fully confident in the trends reported in this study.
Two sets of models were developed to compare outcomes with the plane-strain assumption. Twenty-five models were developed, identical to those models used in the study, with plane-stress elements assigned to the spinal cord and compression platens. The pia mater properties were held constant in these models, as they were shown to have a limited effect on the outcomes, while the grey and white matter properties were simultaneously altered through the range of hyperelastic parameters. Additionally, five three-dimensional models were generated by extruding the planar model geometry a length of 10 mm. Membrane elements were used in place of truss elements to represent the pia mater. Both the grey matter and pia mater properties were held constant, while only the white matter properties were altered. Each three-dimensional model required over 24 CPU hours as compared with less than 1 CPU hour for each plane-stress or plane-strain model.
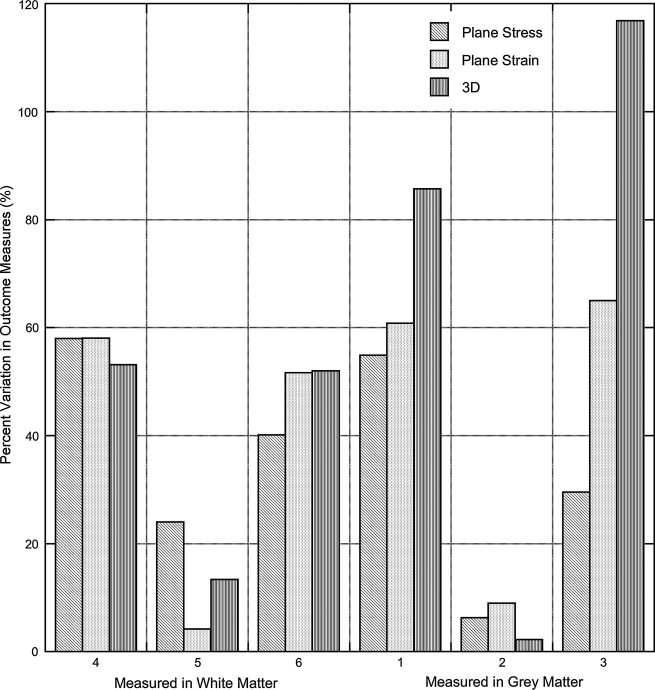
The observed trends in peak outcomes were the same for both the plane-stress and plane-strain models (Fig. 5). As in the plane-strain analysis, principal strains were the least sensitive to material moduli changes, while principal stresses were the most sensitive and white matter properties strongly influenced pressure outcomes in both the grey and the white matter. Pressure outcomes measured in the white matter showed little change (5%) while pressure variation in the grey matter decreased (51%) from the use of a plane-stress assumption when compared with the plane-strain models (Fig. 5B). As expected, the plane-strain analysis predicted slightly greater variability in both pressure and principal stress outcomes (71–178%) than the plane-stress analysis (65–113%), but the principal strain outcomes were less variable in the plane-strain models (5–24%) than in the plane-stress models (21–33%). The distributions of stresses and strains across the spinal cord section were unaffected by the use of a plane-stress or plane-strain assumption.
FIG. 5.
The outcome measures observed in the plane-stress and plane-strain analysis of the two-dimensional hyperelastic models. (A) The variation in outcome measures of principal strain observed in the grey and the white matter resulting from variations in grey and white matter material tangent moduli for each of the plane-stress (PS) and plane-strain (PE) assumptions. (B) The variation in outcome measures of principal stress and pressure observed in the grey and the white matter showed plane-strain (PE) analyses to predict greater variability than plane-stress (PS) analyses. The percent variability in each outcome measure to changes in each individual material modulus is reflected by the plot colors. Grey/white interaction is the cross of the grey and the white matter properties and indicates sensitivity to relative material properties. Nonlinear terms include all additional material interaction terms and nonlinear material property variables.
The variability in peak outcomes measured in the three-dimensional models demonstrated the same trends as those seen in the two-dimensional models (Fig. 6). The plane-strain models, however, better matched the variability in pressures and principal stresses in the three-dimensional model than the plane-stress assumption. The plane-stress and plane-strain models straddled the three-dimensional model principal strain outcomes. Both the plane-stress and plane-strain analyses accurately captured the three-dimensional model's stress, strain, and pressure distributions across the spinal cord.
FIG. 6.
Comparison of plane-stress, plane-strain, and three-dimension model predictions of outcome variability resulting from changes in white matter material moduli. Plane-strain analyses, in general, better reflect the variability of the three-dimensional (3D) model.
The comparison of plane-stress, plane-strain, and three-dimensional model outcomes demonstrates that both two-dimensional modeling techniques generate the same trends in material moduli sensitivity, and reflect the trends of a three-dimensional model without the excessive computational costs. It is critical to note, however, that all of the results and outcomes explored here report relative changes in outcomes due to material sensitivity. At this time there are no experimental measures of tissue level stresses and strains resulting from spinal cord compression with which to validate the magnitude of the outcome values predicted by these computational models. The results of this comparison between plane-stress, plane-strain, and three-dimensional modeling techniques demonstrates that the use of plane-strain models to explore spinal cord compression accurately reflects the sensitivity of spinal cord compression mechanics to variations in material moduli.
Discussion
Quantifying the variations in spinal cord compression mechanics with changes in tissue properties provides insight into the potential effects of age and disease on injury susceptibility. Furthermore, determining the sensitivity of a finite element model to its material constituents is necessary for understanding the accuracy required of each material property, and for designing models to minimize the sensitivity to material variations. The results of our study suggest that pressure measurements in the grey and white matter are particularly sensitive to white matter properties. Pressure measurements have been correlated with blood flow in experimental models of spinal cord compression (Carlson et al., 1997; Carlson et al., 2000). Our results suggest that studies modeling blood flow in the spinal cord require, as a minimum, accurate white matter properties. Conversely, strain measures in the white matter have been correlated with functional losses (Galbraith et al., 1993; Galle et al., 2007). For the type of compression loading between rigid platens that was simulated here, our results show that finite element models using strains as outcome measures are robust to variations in all material properties. Finally, the use of a linear elastic constitutive model resulted in concentrated areas of peak strains, which could lead to modeling problems in the forms of element distortion and convergence failure at large deformations. These results indicate that linear elastic constitutive models are not well suited for modeling spinal cord compression mechanics.
The finite element analysis presented here considered a range of material properties and characterized the sensitivity of a spinal cord compression model to a wide variety of material moduli and different constitutive models. The geometry of the model precisely replicated the human thoracic spinal cord with a refined mesh that accurately represented the morphology of the grey/white matter boundary and pia membrane. The use of the 95th percentile instead of peak values in our analysis was conservative but eliminated the influence of any potential computational artifacts resulting from the contact between the spinal cord and compression plate. The analysis was also completed using 100th-percentile values and confirmed the same trends as those reported here. The development of any computational model, however, requires that a number of assumptions be made regarding the geometry, materials, and interactions between components. The model was a planar representation of a three-dimensional structure, which eliminated the opportunity to observe axial strains, but was used because the lower computational costs enabled a comprehensive parameter study. The plane-strain assumption was shown to accurately reflect the outcomes of three-dimensional and plane-stress models (see section on plane-strain models, above). The use of static compression in place of a dynamic impact did not affect the overall findings of this study because we were interested in the peak stresses and strains resulting from the initial mechanical loading in these models, not the process of loading, or any possible residual compression. Using a viscoelastic representation of the spinal cord would have resulted in variation of the material stiffness with increased loading rates during the primary impact. The range of tangent moduli explored in this study (65–165 kPa) covered a broader spectrum of values than those observed in spinal cord tissue for loading rates varied over two orders of magnitude for grey (64–112 kPa) and white (31–65 kPa) matter (Ichihara et al., 2003). Finally, a paucity of experimental results for compression of the human spinal cord has made direct validation of this finite element model infeasible. The overall mechanical response of the composite spinal cord represented by the effective tangent modulus Eff (160–349 kPa), however, showed good agreement with published values of fresh spinal cord tangent moduli (3–298 kPa) from a variety of studies (Hung and Chang, 1981; Chang et al., 1988; Sparrey, 2004). The tangent moduli of the cord complex in this study was less stiff than that reported for human cervical spinal cord (1.23 MPa) (Bilston and Thibault, 1996). Postmortem storage and test methodology could have increased the specimen stiffness considerably over its in vivo condition (Gefen and Margulies, 2004).
Quantifying the sensitivity of finite element model outcomes to assumed material characteristics is important for understanding the context and general applicability of the model results. Finite element models are becoming more common in the study of spinal cord injury (Bilston, 1998; Scifert et al., 2000; Ichihara et al., 2001; Ichihara et al., 2003; Greaves et al., 2008); however, few of these models have considered the sensitivity of the model outcome to variations in the assumed material characteristics (Bilston, 1998; Ichihara et al., 2001). Bilston (Bilston, 1998) demonstrated variations in strains of up to 19%, with changes in material stiffness (±80%) and constitutive model in a finite element model of a homogeneous cord undergoing physiological flexion/extension motions. Our compression model showed similar variations in peak strain values for changes in material stiffness of ± 44% and variation in material model. In contrast to Bilston's findings, we found stresses to be more sensitive to material tangent modulus than the type of material constitutive model. This suggests that material tangent modulus is more important for models considering large deformation (injuries) than small deformation (physiologic motion) models. Ichihara et al. observed the qualitative changes in tissue deformation resulting from changes in the relative properties of the grey and the white matter, but did not explore a range of tangent moduli, constitutive models, or mechanical outcome measures (Ichihara et al., 2001). Our study is thus the first to comprehensively explore the effect of material characteristics of the cord constituents and tissue level mechanical outcomes in spinal cord compression. Finally, the minimal effect of variations in pial properties found in our study further substantiates the limited role of the pia in spinal cord compression mechanics observed in vitro (Ozawa et al., 2004). Therefore current published values of pia properties (Aimedieu and Grebe, 2004; Jin et al., 2006) are likely sufficient for use in many modeling efforts.
The effect of variations in spinal cord material properties on compression injury mechanics also has implications for understanding clinical spinal cord injuries. This study indicated that white matter properties had the greatest influence on pressure within the spinal cord. Since autoimmune diseases such as multiple sclerosis affect the structure of white matter tissue (Lovas et al., 2000; Bot et al., 2004), these results suggest that the mechanics of spinal cord compression in a patient with multiple sclerosis may result in different patterns of perfusion within the spinal cord. Additionally, increasing the moduli of all materials resulted in lower peak strains in the white matter. Pediatric neurological tissues have been shown to be more stiff than adult tissues (Prange and Margulies, 2002), and white matter strains have been correlated with functional damage (Galbraith et al., 1993; Galle et al., 2007). This suggests that spinal cords in children, because they have stiffer neurological tissues than adults, may be less susceptible to injury than those of adults.
Variations in the patterns of distribution of stresses and strains resulting from changes in material properties suggest that age and disease may affect the nature of functional deficits in addition to the magnitude of injury. The columnar organization of the spinal cord is such that specific functions (e.g., motor control, proprioception, and pain) are carried in particular locations of the spinal cord cross-section. Thus the pattern of injury determines the extent of functional deficits resulting from injury. Traumatic spinal cord injury often shows central cord damage. In this study, pressure, maximum principal stresses, and maximum principal strains showed a propensity for the highest values to occur in the central cord. This agrees well with a recent study showing maximum principal stress to correlate with injury in the white matter (Galle et al., 2007). The results of our study suggest that patterns of injury (and resulting deficits) will change with variations in material characteristics resulting from aging or disease. This expectation is corroborated by a recent study of injury patterns in acute spinal cord injury patients, showing that the presentation of clinical syndromes such as central cord, anterior cord, and posterior cord syndrome correlated with patient age (McKinley et al., 2007). Additionally, age was shown to affect the presentation and long-term recovery from spinal cord injury for equivalent injury modes (McKinley et al., 2003). However, the role of spinal cord degeneration in these outcomes was not isolated from other systemic effects of age. Our results suggest that changes in material properties are also likely to contribute to an overall increase in injury risk with increasing age.
In conclusion, our results demonstrated that tissue level stresses and pressures resulting from spinal cord compression were very sensitive to variations in material properties, and that distribution of elevated stresses and strains across the spinal cord were determined by both the grey and white matter moduli. Since material properties of neurological tissue are affected by aging and disease, our results suggest that the mechanics of spinal cord compression are likely to be affected by aging and disease. Further study is needed to understand the biomechanics of spinal cord injury in these specific populations.
Acknowledgments
This work was funded in part by Centers for Disease Control and Prevention grant UCSF-3915SC and a Chancellor's Professorship (T.M.K.) from the University of California–Berkeley.
Author Disclosure Statement
No competing financial interests exist.
References
- Aimedieu P. Grebe R. Tensile strength of cranial pia mater: preliminary results. J. Neurosurg. 2004;100:111–114. doi: 10.3171/jns.2004.100.1.0111. [DOI] [PubMed] [Google Scholar]
- Anderson T.E. Spinal cord contusion injury: experimental dissociation of hemorrhagic necrosis and subacute loss of axonal conduction. J. Neurosurg. 1985;62:115–119. doi: 10.3171/jns.1985.62.1.0115. [DOI] [PubMed] [Google Scholar]
- Basso D.M. Beattie M.S. Bresnahan J.C. Graded histological and locomotor outcomes after spinal cord contusion using the NYU weight-drop device versus transection. Exp. Neurol. 1996;139:244–256. doi: 10.1006/exnr.1996.0098. [DOI] [PubMed] [Google Scholar]
- Behrmann D.L. Bresnahan J.C. Beattie M.S. Shah B.R. Spinal cord injury produced by consistent mechanical displacement of the cord in rats: behavioral and histologic analysis. J. Neurotrauma. 1992;9:197–217. doi: 10.1089/neu.1992.9.197. [DOI] [PubMed] [Google Scholar]
- Bilston L.E. Finite element analysis of some cervical spinal cord injury modes; IRCOBI Conference; Goteborg. 1998. pp. 365–376. [Google Scholar]
- Bilston L.E. Thibault L.E. The mechanical properties of the human cervical spinal cord in vitro. Ann. Biomed. Eng. 1996;24:67–74. doi: 10.1007/BF02770996. [DOI] [PubMed] [Google Scholar]
- Bot J.C. Blezer E.L. Kamphorst W. Lycklama A.N.G.J. Ader H.J. Castelijns J.A. Ig K.N. Bergers E. Ravid R. Polman C. Barkhof F. The spinal cord in multiple sclerosis: relationship of high-spatial-resolution quantitative MR imaging findings to histopathologic results. Radiology. 2004;233:531–540. doi: 10.1148/radiol.2332031572. [DOI] [PubMed] [Google Scholar]
- Bresnahan J.C. Beattie M.S. Stokes B.T. Conway K.M. Three-dimensional computer-assisted analysis of graded contusion lesions in the spinal cord of the rat. J. Neurotrauma. 1991;8:91–101. doi: 10.1089/neu.1991.8.91. [DOI] [PubMed] [Google Scholar]
- Carlson G.D. Gorden C.D. Nakazowa S. Wada E. Warden K. LaManna J.C. Perfusion-limited recovery of evoked potential function after spinal cord injury. Spine. 2000;25:1218–1226. doi: 10.1097/00007632-200005150-00004. [DOI] [PubMed] [Google Scholar]
- Carlson G.D. Warden K.E. Barbeau J.M. Bahniuk E. Kutina-Nelson K.L. Biro C.L. Bohlman H.H. LaManna J.C. Viscoelastic relaxation and regional blood flow response to spinal cord compression and decompression. Spine. 1997;22:1285–1291. doi: 10.1097/00007632-199706150-00002. [DOI] [PubMed] [Google Scholar]
- Chang G.L. Hung T.K. Feng W.W. An in-vivo measurement and analysis of viscoelastic properties of the spinal cord of cats. J. Biomech. Eng. 1988;110:115–122. doi: 10.1115/1.3108415. [DOI] [PubMed] [Google Scholar]
- Coats B. Margulies S.S. Material properties of porcine parietal cortex. J. Biomech. 2006;39:2521–2525. doi: 10.1016/j.jbiomech.2005.07.020. [DOI] [PubMed] [Google Scholar]
- Fiford R.J. Bilston L.E. The mechanical properties of rat spinal cord in vitro. J. Biomech. 2005;38:1509–1515. doi: 10.1016/j.jbiomech.2004.07.009. [DOI] [PubMed] [Google Scholar]
- Galbraith J.A. Thibault L.E. Matteson D.R. Mechanical and electrical responses of the squid giant axon to simple elongation. J. Biomech. Eng. 1993;115:13–22. doi: 10.1115/1.2895464. [DOI] [PubMed] [Google Scholar]
- Galle B. Ouyang H. Shi R. Nauman E. Correlations between tissue-level stresses and strains and cellular damage within the guinea pig spinal cord white matter. J. Biomech. 2007;40:3029–3033. doi: 10.1016/j.jbiomech.2007.03.014. [DOI] [PubMed] [Google Scholar]
- Garo A. Hrapko M. van Dommelen J.A. Peters G.W. Towards a reliable characterisation of the mechanical behaviour of brain tissue: The effects of post-mortem time and sample preparation. Biorheology. 2007;44:51–58. [PubMed] [Google Scholar]
- Gefen A. Margulies S.S. Are in vivo and in situ brain tissues mechanically similar? J. Biomech. 2004;37:1339–1352. doi: 10.1016/j.jbiomech.2003.12.032. [DOI] [PubMed] [Google Scholar]
- Greaves C.Y. Gadala M.S. Oxland T.R. A three-dimensional finite element model of the cervical spine with spinal cord: an investigation of three injury mechanisms. Ann. Biomed. Eng. 2008;36:396–405. doi: 10.1007/s10439-008-9440-0. [DOI] [PubMed] [Google Scholar]
- Gruner J.A. Yee A.K. Blight A.R. Histological and functional evaluation of experimental spinal cord injury: evidence of a stepwise response to graded compression. Brain Res. 1996;729:90–101. [PubMed] [Google Scholar]
- Hung T.K. Chang G.L. Biomechanical and neurological response of the spinal cord of a puppy to uniaxial tension. J. Biomech. Eng. 1981;103:43–47. doi: 10.1115/1.3138244. [DOI] [PubMed] [Google Scholar]
- Ichihara K. Taguchi T. Sakuramoto I. Kawano S. Kawai S. Mechanism of the spinal cord injury and the cervical spondylotic myelopathy: new approach based on the mechanical features of the spinal cord white and gray matter. J. Neurosurg. 2003;99:278–285. doi: 10.3171/spi.2003.99.3.0278. [DOI] [PubMed] [Google Scholar]
- Ichihara K. Taguchi T. Shimada Y. Sakuramoto I. Kawano S. Kawai S. Gray matter of the bovine cervical spinal cord is mechanically more rigid and fragile than the white matter. J. Neurotrauma. 2001;18:361–367. doi: 10.1089/08977150151071053. [DOI] [PubMed] [Google Scholar]
- Jackson A.B. Dijkers M. Devivo M.J. Poczatek R.B. A demographic profile of new traumatic spinal cord injuries: change and stability over 30 years. Arch. Phys. Med. Rehabil. 2004;85:1740–1748. doi: 10.1016/j.apmr.2004.04.035. [DOI] [PubMed] [Google Scholar]
- Jawad S.A. Ward I.M. Transverse compression of oriented nylon and polyethylene extrudates. J. Mater. Sci. 1978;13:1381–1387. [Google Scholar]
- Jin X. Lee J.B. Leung L.Y. Zhang L. Yang K.H. King A.I. Biomechanical response of the bovine pia-arachnoid complex to tensile loading at varying strain-rates. Stapp Car Crash J. 2006;50:637–649. doi: 10.4271/2006-22-0025. [DOI] [PubMed] [Google Scholar]
- Kearney P.A. Ridella S.A. Viano D.C. Anderson T.E. Interaction of contact velocity and cord compression in determining the severity of spinal cord injury. J. Neurotrauma. 1988;5:187–208. doi: 10.1089/neu.1988.5.187. [DOI] [PubMed] [Google Scholar]
- Lovas G. Szilagyi N. Majtenyi K. Palkovits M. Komoly S. Axonal changes in chronic demyelinated cervical spinal cord plaques. Brain. 2000;123(Pt 2):308–317. doi: 10.1093/brain/123.2.308. [DOI] [PubMed] [Google Scholar]
- McKinley W. Cifu D. Seel R. Huang M. Kreutzer J. Drake D. Meade M. Age-related outcomes in persons with spinal cord injury: a summary paper. NeuroRehabilitation. 2003;18:83–90. [PubMed] [Google Scholar]
- McKinley W. Santos K. Meade M. Brooke K. Incidence and outcomes of spinal cord injury clinical syndromes. J. Spinal Cord Med. 2007;30:215–224. doi: 10.1080/10790268.2007.11753929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metz H. McElhaney J. Ommaya A.K. A comparison of the elasticity of live, dead, and fixed brain tissue. J. Biomech. 1970;3:453–458. doi: 10.1016/0021-9290(70)90017-5. [DOI] [PubMed] [Google Scholar]
- Noyes D.H. Correlation between parameters of spinal cord impact and resultant injury. Exp. Neurol. 1987;95:535–547. doi: 10.1016/0014-4886(87)90298-6. [DOI] [PubMed] [Google Scholar]
- Oakland R.J. Hall R.M. Wilcox R.K. Barton D.C. The biomechanical response of spinal cord tissue to uniaxial loading. Proc. Inst. Mech. Eng. [H] 2006;220:489–492. doi: 10.1243/09544119JEIM135. [DOI] [PubMed] [Google Scholar]
- Ogden R. Nonlinear Elastic Deformations. Dover Publications; Mineola, NY: 1984. [Google Scholar]
- Ozawa H. Matsumoto T. Ohashi T. Sato M. Kokubun S. Comparison of spinal cord gray matter and white matter softness: measurement by pipette aspiration method. J. Neurosurg. 2001;95:221–224. doi: 10.3171/spi.2001.95.2.0221. [DOI] [PubMed] [Google Scholar]
- Ozawa H. Matsumoto T. Ohashi T. Sato M. Kokubun S. Mechanical properties and function of the spinal pia mater. J. Neurosurg. Spine. 2004;1:122–127. doi: 10.3171/spi.2004.1.1.0122. [DOI] [PubMed] [Google Scholar]
- Prange M.T. Margulies S.S. Regional, directional, and age-dependent properties of the brain undergoing large deformation. J. Biomech. Eng. 2002;124:244–252. doi: 10.1115/1.1449907. [DOI] [PubMed] [Google Scholar]
- Schoenen J. Faull R.L.M. Spinal cord: cyto- and chemoarchitecture. In: Paxinos G., editor; Mai J., editor. The Human Nervous System. 2nd. Elsevier Academic Press; Boston: 2004. p. 1366. [Google Scholar]
- Scifert J. Totoribe K. Goel V. Traynelis C. Clark C. Spinal cord deformation in flexion and extension—A finite element study; Presented at the Proc. 22nd Annual EMBS International Conference; 2000. pp. 855–856. [Google Scholar]
- Sparrey C.J. Mechanical Engineering. University of British Columbia; Vancouver: 2004. The effect of impact velocity on cellular structures of the spinal cord. [Google Scholar]