Sensitivity of estimated muscle force in forward simulation of normal walking

Abstract

Generic muscle parameters are often used in muscle-driven simulations of human movement estimate individual muscle forces and function. The results may not be valid since muscle properties vary from subject to subject. This study investigated the effect of using generic parameters in a muscle-driven forward simulation on muscle force estimation. We generated a normal walking simulation in OpenSim and examined the sensitivity of individual muscle to perturbations in muscle parameters, including the number of muscles, maximum isometric force, optimal fiber length and tendon slack length. We found that when changing the number muscles included in the model, only magnitude of the estimated muscle forces was affected. Our results also suggest it is especially important to use accurate values of tendon slack length and optimal fiber length for ankle plantarflexors and knee extensors. Changes in force production one muscle were typically compensated for by changes in force production by muscles in the same functional muscle group, or the antagonistic muscle group. Conclusions regarding muscle function based on simulations with generic musculoskeletal parameters should be interpreted with caution.

Introduction

Muscles generate forces and exert joint torques during human walking. Individual muscle forces are not directly measurable so computer simulations based on musculoskeletal models are often used to estimate muscle forces and function during gait (Zajac et al., 2003; Erdemir et al., 2007). Muscle contraction dynamics are usually simulated with Hill-type muscle models, where estimated muscle force depends on several parameters, including maximum isometric force, optimal fiber length, tendon slack length, pennation angle, activation time and muscle path in the model (Zajac 1989). The values of muscle parameters determine the force-generating characteristics of each muscle, which vary with the size, gender, age and neuromuscular status of subjects (Lieber 1993; Narici et al., 2008; Thelen 2003). Therefore, an ideal musculoskeletal model should use subject-specific muscle parameters in order to accurately estimate muscle forces. However, because subject-specific muscle properties are difficult to measure and development of novel simulations is time-consuming, generic muscle parameters (Delp et al. 1990) were used in many simulation studies of normal walking (Anderson & Pandy, 2001, Neptune et al., 2001) and pathological gait (Higginson et al. 2006) where the muscle parameters of neuromuscular disorder subjects were quite different from the generic ones (Piazza 2006). As a result, it is necessary to evaluate the influence of using generic muscle parameters on musculoskeletal models.

There are generally two methods in the literature to evaluate the sensitivity of Hill-type muscle models to parameter perturbations. The first uses simple perturbation (Delp & Zajac 1992; Thelen 2003; Scovil & Ronsky 2006), in which each muscle parameter is perturbed and the change in output muscle force is calculated. The other one involves re-optimization (Heine et al., 2003; Redl et al. 2007), in which all output muscle forces are re-calculated after each muscle parameter is perturbed. We believe the second method is more appropriate for walking simulations because it calculates not only the force change of the perturbed muscle, but also the compensatory force changes of other muscles in the musculoskeletal model.

However, there have been a limited number of studies using re-optimization to determine muscle model sensitivity. Heine et al. (2003) examined the sensitivity of an EMG-driven Hill-type muscle model by comparing joint moments between generic and optimized muscle parameters, but this study was limited to elbow movement and muscles for which EMG signals were available. Recently, Redl et al. (2007) performed a sensitivity study for a simulation of human walking using static optimization but only four muscles were examined (gluteus medius, vasti, soleus and sartorius). Furthermore, few studies report the effect of perturbing one muscle on other muscles in the model, which represents a change in overall muscle coordination due to perturbation in one given muscle. Although Redl et al. (2007) used a summed cross-sensitivity ratio to quantify the summed effect of changing one muscle force on all other muscles, it was not clear how individual muscles responded. If one muscle force is sensitive to perturbation (i.e., its estimated muscle force would change), other muscles are likely to change their forces accordingly in order to maintain normal walking performance. Finally, there have been several muscle-driven simulations described in the literature with different number of muscles included (Neptune et al., 2001; Anderson & Pandy, 2001; Piazza 2006) and thus results are difficult to compare. Although the inclusion of many muscles is more realistic from a physiological perspective, this requires more model parameters to be specified and longer computational time to determine the optimal solution. It is unknown how individual muscle forces would change when a different number of muscles is included in the model.

In this study, we generated a generic simulation in OpenSim (Delp et al., 2007) to reproduce normal walking data. We perturbed the number of muscles and individual muscle parameters (maximum isometric force, optimal fiber length and tendon slack length). Individual muscle sensitivity was calculated relative to the nominal model-estimated muscle force throughout the gait cycle. The specific aims of this study were: (1) to evaluate how estimated muscle forces change due to the number of muscles included in a forward dynamics simulation; (2) to evaluate the sensitivity of individual muscles forces to perturbation in muscle parameters; and (3) to evaluate how other muscles respond to the perturbation of one muscle.

Methods

Experimental data

Three-dimensional kinematic and kinetic data were collected from 3 healthy young male subjects (height: 178.1 ± 7.2 cm; weight: 76.6 ± 11.7 kg; age: 20.7 ± 0.7 years) walking on a split-belt, motorized treadmill (Bertec Corp.) at self-selected speeds (1.296 ± 0.051 m/s). Subjects signed an informed consent approved by the human subjects review board. One static trial was recorded for each subject standing still for 30 seconds. Then each subject was asked to walk at self-selected speed on the treadmill for about 2 minutes. A 6-camera Motion Analysis system was used to record the three-dimensional locations of 27 markers in the static trial and 23 markers in the walking trial at 60Hz (medial knee and ankle markers were removed in the walking trial). Ground reaction forces were recorded from the treadmill at 600Hz. Experimental data were preprocessed in Evart 4.4.3 (Motion Analysis Corp.) and Matlab (MathWorks Inc.).

Musculoskeletal models

The musculoskeletal model was built in OpenSim (Delp et al. 2007) with 13 segments and 12 joints which enabled movements in the sagittal, frontal and coronal planes. It had 23 DOFs and was actuated by 34 muscle-tendon units, including soleus (SOL), medial gastrocnemius (GAS), tibialis anterior (TA), tibialis posterior (TP), vastus medius (VAS), rectus femoris (RF), biceps femoris short head (BFSH), biceps femoris long head (BFLH), iliacus (IL), adductor magnus (ADDM), gluteus maximus (GMAX), gluteus medius (three heads, GMED1, GMED2 and GMED3) and 6 spinal and abdominal muscles. Default muscle parameters (Table 1) were obtained from OpenSim (Delp et al. 2007). The model was built such that it could reproduce the experimental data while the number of muscles was minimum (i.e., at least one biarticular muscle and two uniarticular muscles per joint). The equations of motion for each musculoskeletal model were derived using Simbody (open-source order-n dynamics engine under development at Simtk.org). A more detailed description of the skeletal model can be found in previous publications (Delp et al., 2007; Xiao & Higginson 2008).

Table 1.

Default values of muscle parameters in the 34-muscle model (Delp et al. 2007).

	Maximum isometric force (N)	Optimal fiber length (m)	Tendon slack length (m)
GMED1	1119	0.0535	0.078
GMED2	873	0.0845	0.053
GMED3	1000	0.064	0.053
BFLH	2700	0.109	0.326
BFSH	804	0.173	0.0889
ADDM	2343	0.121	0.12
GMAX	1819	0.147	0.127
IL	1073	0.1	0.1
RF	1169	0.114	0.31
VAS	5000	0.107	0.116
GAS	2500	0.09	0.36
SOL	4000	0.08	0.22
TP	3600	0.031	0.31
TA	3000	0.098	0.223

Simulation development

OpenSim was used to generate forward dynamics simulations of one gait cycle for each subject (Delp et al. 2007). The model was first scaled to subject-specific geometry and mass based on the marker positions during the static trial. Inverse kinematics and residual reduction algorithms were applied in order to calculate the joint kinematics during a walking trial. Computed muscle control (Thelen and Anderson 2006) was then used to find the optimal muscle excitation patterns that minimize the weighted squared sum of muscle forces. Finally, each forward dynamics simulation was generated based on the optimal excitation patterns (Delp et al., 2007; Thelen & Anderson 2006) to validate the result of CMC such that the simulated kinematics and kinetics could match the desired trajectory (i.e. the experimental measurements). Simulation results for all subjects were normalized to one complete gait cycle (from right heel contact to the next heel contact) and averaged across subjects. Because healthy walking is symmetric, only the results from the right leg were reported.

Perturbation Analysis

Two types of perturbation were performed based on the simulation results. First, we perturbed the number of muscles included in the model by gradually increasing the number of muscles from 34 to 64. We started from the 34-muscle model and added extra muscles to the model in a random order while symmetry was preserved. New simulations were generated each time new muscles were added to the model. The resultant muscle forces following optimization were compared to the nominal case. Each subject had nine new simulations and resultant muscle forces were averaged across subjects.

Second, we bilaterally perturbed a subset of model parameters for leg muscles in the 34-muscle model (Table 1). Specifically, values of maximum isometric force, optimal fiber length and tendon slack length were perturbed by ±10% for each muscle (i.e., 3 parameters × 2 perturbation directions × 14 muscles = 84). Spinal and abdominal muscles were not perturbed in this study. A total of 84 new simulations per subject were generated to calculate individual muscle forces after perturbation. Resultant muscle forces were averaged across subjects for each perturbation condition.

The sensitivity of an individual muscle force to muscle parameter perturbation was quantified as

$${\mathrm{\epsilon }}_{i,j,k}=\frac{\frac{A_i-A_i^0}{A_i^0}}{\frac{P_{i,k}-P_{j,k}^0}{P_{j,k}^0}}$$ (1)

$$A_i={\displaystyle {\int }_0^T{F}_i\mathit{\text{dt}}}$$ (2)

where ε represents the sensitivity of muscle i (i=1 to 14) to the perturbation j (j = 1 to 6) of muscle k (k=1 to 14). $A_i^0\text{and}{A}_t$ are the integrated area of muscle force over the gait cycle before and after perturbation. $P_{j,k}^0\text{and}{P}_{j,k}$ are the values of parameter j before and after perturbation. $\frac{P_{j,k}-P_{j,k}^0}{P_{j,k}^0}$ represents the perturbation size and was 0.1 or −0.1 in our study. Sensitivity ε indicates the normalized change in one muscle force (muscle i) due to the normalized muscle parameter change (parameter j of muscle k). If |ε| is greater than 1 (i.e. overall muscle force change is greater than perturbation), we defined muscle i as sensitive to perturbation j of muscle k.

Calculated muscle sensitivity values were further analyzed in two ways. First, we examined each muscle’s sensitivity to its own parameter perturbations (Equation 1, set i = k for each j). We consider a muscle i sensitive to changes in parameter j if |ε_i,j,i| > 1. Next, we looked at the effect of one muscle’s perturbation on other muscles (Equation 1, i ≠ k for each muscle k). Muscle i was interpreted to be related to muscle k when |ε_i,j,k| > 1 (i ≠ k). All muscles that vary with muscle k represent those that enable a change in muscle coordination patterns due to perturbation of muscle k.

Results

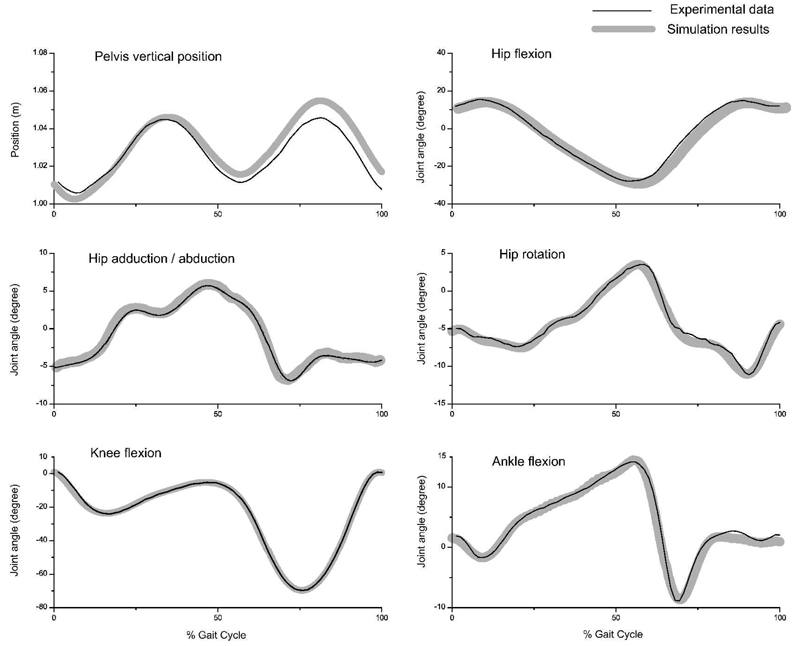
The OpenSim simulations of all models, including those with different sets of muscles, and before and after parameter perturbations, were able to reproduce the experimental walking data (Figure 1).

Figure 1.

Experimental and simulated kinematics. Experimental data were averaged from inverse kinematics of three young healthy subjects. Both inverse kinematics and forward simulation results were performed using OpenSim. 212×174mm (600 × 600 DPI)

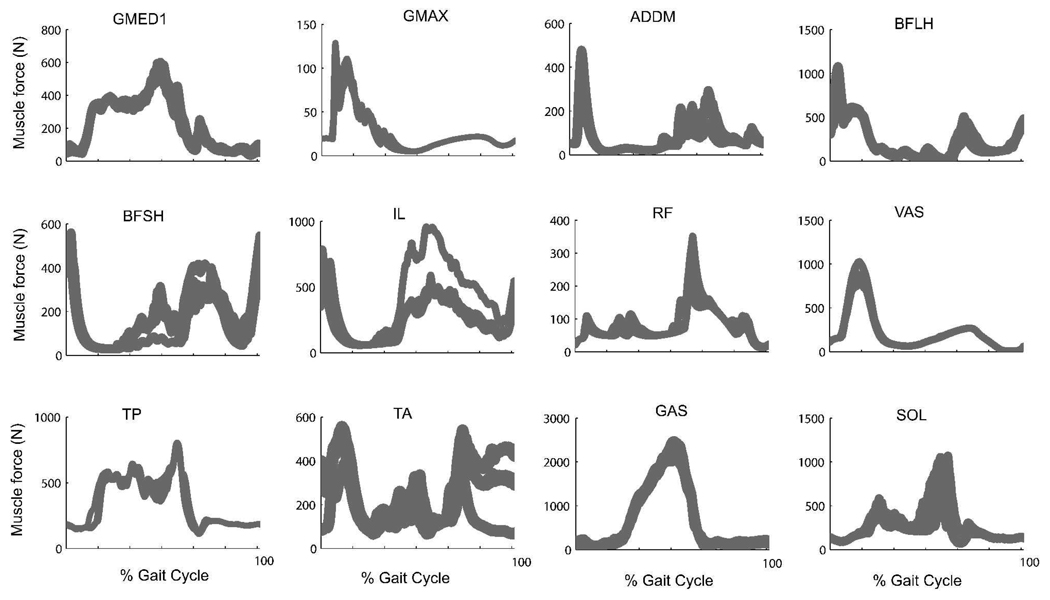
As we gradually increased the number of muscles in the model from 34 to 64 and compared individual muscle forces from each simulation (Figure 2), we found that most of the muscles could achieve the same muscle force patterns and only the magnitude but not the timing of calculated muscle forces changed.

Figure 2.

Comparison of muscle forces in models with different number of muscles included (ranging from 34 to 64 muscles). Results were averaged across three subjects with nine simulations each. All figures were normalized to one gait cycle starting from heel strike. Gray area indicates the possible range that muscle forces can achieve. 143×254mm (600 × 600 DPI)

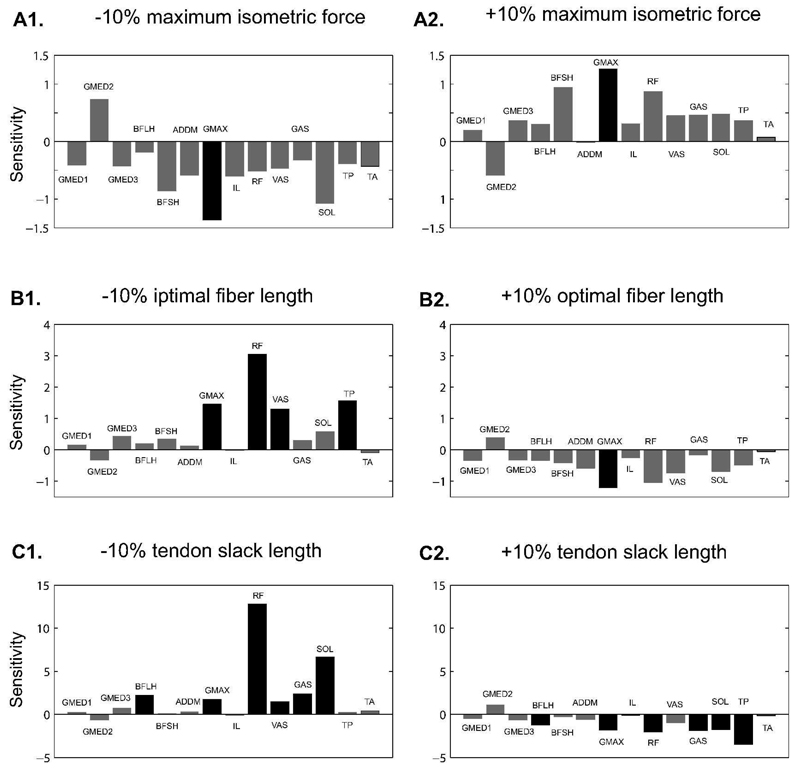
As we perturbed individual muscle model parameters (maximum isometric force, optimal fiber length, tendon slack length), generally muscles were not sensitive to perturbations in maximum muscle force except GMAX (Figure 3, A1 and A2). The model was more sensitive to tendon slack length perturbation than optimal fiber length (Figure 3, C1 and C2 compared with B1 and B2). Individual muscles responded differently to muscle parameter perturbation. Perturbation of maximum isometric forces only affected the output of GMAX (ε = −1.362 and 1.267 for −10% and +10% perturbations respectively). Perturbation of optimal fiber length altered the muscle force of: GMAX (ε = 1.455 and −1.198), RF (ε = 3.050 and −1.041), VAS (ε = 1.297, −10% only) and TP (ε = 1.541, −10% only). Seven muscles were sensitive to tendon slack length perturbation: BFLH (ε = 2.232 and −1.212), GMAX (ε = 1.758 and 1.793), RF (ε = 12.821 and −2.031), VAS (ε = 1.470, −10% only), GAS (ε = 2.38 and −.887), SOL (ε = 6.658 and −1.743) and TP (ε = −3.478, +10% only). The rest of the muscles (GMED1, GMED2, GMED3, ADD MAG, IL, BFSH and TA) were not sensitive to any of the perturbations.

Figure 3.

Individual muscle sensitivities to perturbations in muscle model parameters. (A1) −10% maximum isometric force perturbation; (A2) +10% maximum isometric force perturbation; (B1) −10% optimal fiber length perturbation; (B2) +10% optimal fiber length perturbation; (C1) −10% tendon slack length perturbation; (C2) +10% tendon slack length perturbation. Note that the scale on the y-axis is different for different perturbation methods. A muscle is considered to be sensitive to perturbation when the absolute value of sensitivity is greater than 1 (shown with darker bars). 215×209mm (600 × 600 DPI)

The perturbation in one muscle’s model parameters could alter the forces generated by other muscles. From our results, we found that perturbations in GMED, GMAX, ADD MAG, IL, BFSH, and TA had no large effect on other muscles. However, the muscle force of RF was increased when the tendon slack length of BFLH was decreased (Table 2, column BFLH). The perturbation in RF had implications for BFLH, BFSH and ADD MAG (Table 2, column RF). The perturbation in tendon slack length of VAS changed the muscle force of BFSH (Table 2, column VAS). Ankle plantarflexors generally had a large effect on other muscles in the model. Decreasing tendon slack length of SOL increased the output muscle force of TA but decreased that of TP (Table 2, column SOL). The perturbation in tendon slack length of TP changed the muscle forces of SOL and TA (Table 2, column TP). Finally, changes in tendon slack length of GAS affected the muscle forces of TA, SOL, VAS, BFSH and BFLH (Table 2, column GAS).

Table 2.

The sensitivity of overall muscle forces to perturbation of individual muscle parameters.

Sensitive muscles	Perturbed Muscles
	BFLH	RF	VAS	SOL	TP	GAS
BFLH	X	5.339	-	-	-	−1.417
BFSH	-	3.283	1.571	-	-	−2.032
RF	2.503	X	-	-	-	-
ADDM	-	−1.538	-	-	-	-
VAS	-	-	X	-	-	1.069
SOL	-	-	-	X	2.556	−0.1328
TP	-	-	-	−1.666	X	-
TA	-	-	-	6.258	1.939	5.47
GAS	-	-	-	-	-	X

Column: muscles of perturbation (−10% tendon slack length). Rows: muscles sensitive to the perturbation. If not sensitive, the value was shown with ‘-‘.

Discussion

Although muscle-driven forward dynamics simulation can be used to estimate individual muscle forces and functions, the confidence in the simulation results are limited by the accuracy of the parameters in the muscle model. The goal of this study was to investigate the effect of altering generic muscle parameters in the simulation of normal walking. We generated simulations in OpenSim and performed a perturbation study on key muscle parameters including maximum isometric force, optimal fiber length and tendon slack length.

We found that only the magnitudes of estimated muscle forces were sensitive to the number of muscles included in the model. The on-off timing was similar throughout the models. In other words, a model with 34 muscles could estimate similar muscle force patterns as 64 muscles as long as both models could reproduce the same experimental data. We conclude that some small muscles (in terms of force production ability) could be omitted in the model when their contributions are not of interest.

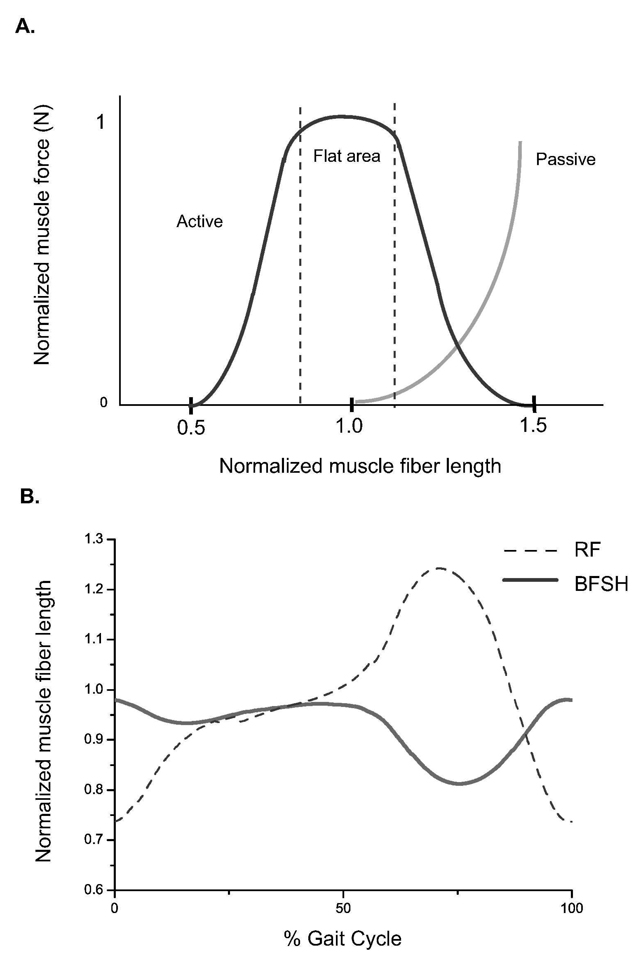
As we bilaterally perturbed three model parameters for each of the 14 muscles and examined individual muscle responses, we found that each muscle had different sensitivity values in response to perturbation (Figure 3). This is because each muscle has a different set of muscle parameter values and its own force-generating characteristics. In a Hill-type muscle model, muscle force depends on each muscle’s force-length characteristics (Zajac 1989, Figure 4A). If the muscle is operating on the curve where the slope is steep, a slight change in fiber length would result in large force change. In contrast, if the muscle is on the flat portion of the curve (near optimal fiber length), muscle force would not be sensitive to length perturbation. Since each muscle functions on a different portion of its force-length curve during walking, perturbation results should vary. For example (Figure 4B), the range of normalized RF muscle fiber length was 0.75 to 1.25 over a gait cycle of normal walking, while BFSH changed its muscle fiber length from 0.85 to 1.0. As a result, RF functions on the steep portion of the curve and BFSH is on the flat portion (Figure 4A). Therefore RF is more sensitive to optimal fiber length change than BFSH (Table 2, Row RF and BFSH). Generally our results (Figure 3) showed that ankle plantarflexors and knee extensors were sensitive to changes in tendon slack length and optimal fiber length, while knee flexors and hip muscles were not sensitive to any perturbation. It is worth mentioning that our results were based on healthy normal walking. If a different range of motion had been studied, individual muscles may function on a different part of force-length curve and its sensitivity might be different.

Figure 4.

(A) Muscle force-length curve in a Hill-type muscle model normalized to optimal fiber length. The curve becomes more flat when muscle fiber length is close to optimal fiber length (around 0.8 ~ 1.1 optimal fiber length). (B) Normalized muscle fiber length over a gait cycle for BFSH and RF. Normalized BFSH muscle fiber length (solid line) ranged from 0.85 to 1.0. RF (dashed line) operated on its normalized muscle fiber length curve from 0.75 to 1.25. 126×192mm (600 × 600 DPI)

We examined the effect of using generic muscle parameters on the estimation of overall muscle force patterns by perturbing each muscle’s parameters and calculating the sensitivities of all the other muscles in the model (Table 2). We found that the change of one muscle force was compensated by muscles in the same functional group and/or antagonistic muscle group. Muscles that were insensitive to perturbation would not change other muscles’ output. Because the simulation algorithm was trying to reach the same joint torques for each model, the change of one muscle force (and thus its muscle moment) would most likely be compensated by the muscle in the agonist or antagonist function group. If there was no significant change in muscle force, no muscle coordination change was needed. For example, RF (Table 2, column RF), the knee extensor and hip flexor, was related to knee flexor (BFSH) and hip extensors (BFLH and ADD MAG). Similarly, the change in muscle force of knee extensor VAS was compensated by knee flexor BFSH (Table 2, column VAS). Ankle plantarflexors, SOL and TP both induced muscle force changes in each other and dorsiflexor TA (Table 2, column SOL and TP). Biarticular muscle GAS (Table 2, column GAS) was related to both ankle muscles (TA and SOL) and knee muscles (VAS, BFLH and BFSH). The only exception was GMAX, which was sensitive to perturbation but did not induce any big change in the force generation of other muscles. One possible explanation for the limited impact of GMAX perturbations is that there are eight muscles that cross the hip joint in our model. The variation in muscle force of GMAX was compensated by many hip muscles such that the implication for each muscle force was small.

We limited our study to a fixed perturbation size (+10% and −10%) for only three muscle parameters. Scovil and Ronsky (2006) used a perturbation size of 50% while Redl et al. (2007) perturbed each muscle parameter by 2.5%, 5%, 7.5% and 10%. We found that 50% was too large for our model to reproduce the experimental data (we performed re-optimization after perturbation while Scovil & Ronsky (2006) did not). On the other hand, Redl et al. (2007) reported that perturbation size less than 10% showed the same trend as 10%. We believed 10% was large enough to provide useful information and small enough for the model to best reproduce the experimental data. Furthermore, we chose to perform perturbations on three muscle parameters only, namely maximum isometric force, optimal fiber length and tendon slack length, since other muscle parameters in a Hill-type muscle (e.g. muscle activation time and deactivation time) have been reported to be less sensitive (Delp & Zajac 1992; Out et al. 1996; Heine et al. 2003; Scovil & Ronsky 2006; Redl et al. 2007). There are some other factors that can influence the muscle forces from walking simulation, such as muscle moment arm and model dimensionality. However, the sensitivity of those factors is beyond the scope of this study.

We defined our sensitivity for each muscle based on the area change of each muscle force curve (Equation 1). Previous studies have defined sensitivity by calculating the average or integrated muscle force change at each time step (Lehman & Stark, 1982; Scovil & Ronsky 2006; Redl et al., 2007). Redl et al. (2007) addressed the limitation of using this type of instant ratio such that the sensitivity value could be unnecessarily large when the muscle force is very small (i.e. the muscle is inactive). In our study, we calculated sensitivity based on the change of area underneath each muscle force curve, which overcame this problem and also provided information on how muscle force changes over a gait cycle.

In this study, we performed a sensitivity study to examine the effect of using a generic muscle model for the estimation of muscle forces. Our results could be helpful for those interested in human movement modeling and simulation. We found that only magnitude of the estimated muscle forces was affected when changing the number of muscles included in the model, indicating it is not always necessary to use as many muscles in the model as possible. Our results also suggest that it is better to use accurate values of tendon slack length and optimal fiber length for ankle plantarflexors and knee extensors, but that changes in maximum isometric force within 10% of the generic model have little impact on estimated muscle forces. The sensitivity of an individual muscle force also had implications for muscles with complementary function; therefore muscle function analysis based on simulations with generic musculoskeletal parameters should be interpreted with caution. This study pointed out the important parameters that the model is most sensitive to. Although subject-specific muscle parameters are difficult to obtain via measurement (Piazza 2006) or optimization (Buchanan et al., 2005), the inclusion of these parameters will enhance the application of musculoskeletal simulations for the study of pathological movement patterns.