Kinetics of Regulated Actin Transitions Measured by Probes on Tropomyosin

Abstract

Changes in the muscle regulatory protein complex, troponin, are important for modulation of activity and may occur as a result of disease-causing mutations. Both increases and decreases in the rate of ATP hydrolysis by myosin may occur as dictated by changes in the distribution of actin-tropomyosin-troponin among its different states. It is important to measure the rates of transition among these states to study physiological adaptation and disease processes. We show here that acrylodan or pyrene probes on tropomyosin can be used to monitor the transition from active to intermediate and inactive states of actin-tropomyosin-troponin. Transitions measured in the absence of calcium had two phases, as previously reported for some other probes on troponin and actin. The first step was a rapid equilibrium that favored the formation of the intermediate state and had an apparent rate constant less than that of S1-ATP dissociation. The second fluorescence transition was slower, with an apparent constant that increased from ∼5 to 80/s over a range of 1–37°C. Only the initial rapid transition was seen in the presence of saturating calcium. The acrylodan probe had the advantage of yielding a larger signal than the pyrene probe. Furthermore, the acrylodan signal decreased in going from the active state to the intermediate state, and then increased upon going to the inactive state.

Introduction

Skeletal and cardiac muscles are controlled by the actin-binding proteins tropomyosin, troponin T, troponin I, and troponin C. This tropomyosin-troponin complex inhibits the ability of actin to stimulate myosin ATP hydrolysis and muscle contraction at low calcium concentrations. Calcium binding to troponin C produces a 90- to 100-fold increase in k_cat/K_M for the actin-activated ATPase activity of skeletal muscle regulatory proteins (1,2). A further eight- to ninefold increase in k_cat/K_M occurs when sufficient rigor-type myosin binds to actin to stabilize the active state (2). These features of ATPase activation can be explained by a model that has a minimum of two actin states with different capacities to stimulate ATP hydrolysis (3,4). Calcium provides partial stabilization of the active state, whereas rigor-type myosin binding fully stabilizes the active state.

Analyses of the multiphasic kinetics of S1 binding (5–9) and three-dimensional reconstructions of regulated actin filaments (10,11) indicate that regulated actin may exist in three states. We recently observed that the pattern of inhibition of ATPase activity of some disease-causing mutants of troponin I could be more readily explained by inclusion of the third state (12). To continue to explore disorders of the regulatory complex (12–14), as well as normal physiological changes (15) in regulated actin states, it is necessary to find probes that report the kinetics of transition among actin states.

Fluorescent probes on actin (5), tropomyosin (16–19), and troponin (7–9,20,21) report changes in state transitions. In this work, we focused on probes on tropomyosin because the position of tropomyosin on actin ultimately defines the activity of thin filaments. We worked under conditions that have the potential to define the rate constants for transitions in the regulatory complex. All transitions were studied as a function of temperature to emphasize important features and to make the results applicable to studies done under varied conditions. We utilized both pyrene and acrylodan probes on tropomyosin because they respond in different ways to changes in the state of regulated actin.

In the presence of calcium, a single transition was observed that was a rapid decrease in fluorescence of either pyrene or acrylodan probes on tropomyosin. In the absence of calcium, this rapid phase was followed by a slower transition that was a further decrease in pyrene excimer fluorescence or an increase in acrylodan fluorescence.

The results are consistent with a two-step transition from the active state of regulated actin to the inactive state. The first step, in the absence of calcium, was a rapid equilibrium that favored formation of the intermediate. The second step was a slower transition to the inactive state. Estimates of rate constants are given over the range of 1–37°C. Acrylodan has features that make it particularly useful for monitoring the kinetics of actin state changes.

Materials and Methods

Actin (22), myosin (23), and troponin and tropomyosin (24) were prepared from rabbit back skeletal muscle. Protein concentrations were determined using the following extinction coefficients (ɛ^0.1%) for 280 nm: actin, 1.15; myosin S1, 0.75; tropomyosin, 0.33; and troponin, 0.37. The molecular weights of the proteins were assumed to be as follows: actin, 42,000; myosin S1, 120,000; tropomyosin, 68,000; and troponin, 71,000.

Tropomyosin was reduced with dithiothreitol, dialyzed, and labeled with pyrene iodoacetamide (16,25) or acrylodan (17). Labeling was done using molar ratios of probe to protein of 2:1, 5:1, and 10:1. These conditions yielded labeling of 60–75% for pyrene and 70–100% for acrylodan. The extinction coefficients used were 2.2 × 10⁴ M⁻¹cm⁻¹ at 344 nm for pyrene, and 14,400 M⁻¹cm⁻¹ at 372 nm (26) for acrylodan.

Rates of actin state transitions were determined by rapid fluorescence measurements using a SF20 sequential mixing stopped flow spectrometer (Applied Photophysics, Leatherhead, United Kingdom). The temperature was controlled with a circulating water bath. The excitation wavelength was fixed with a monochrometer using a slit width of either 0.5 or 1 mm. Excitation light was selected with filters. Excitation for pyrene excimer fluorescence was at 340 nm and emission was monitored with an Oriel no. 51284 high-pass filter (Edmund Optics, Barrington, NJ) having a cut on midpoint at 517 nm. Alternatively, a 500 nm interference bandpass filter (No. NT46-157, Edmund Optics) was used to ensure that scattered light did not contribute to the signal. Acrylodan was excited with light at a wavelength of 391 nm and fluorescence was measured through a Schott GG 455 (Duryea, PA) high-pass filter with a 455 nm midpoint. In some cases, a 550 interference bandpass filter was used with an 80 nm width at half height (No. NT46-158, Edmund Optics). Light-scattering measurements were made by increasing the emission wavelength above the working range of the excitation filter (600 nm for the 455 nm high-pass filter). Each curve shown is the average of three or four measurements. The transitions were independent of the concentration of tropomyosin-troponin when ≥1 tropomyosin-troponin was added per five actin protomers. The transitions were for the same for the mixture of S1 isozymes as for the isolated A1-S1 isozyme.

The transition from the inactive state to the myosin-bound active state was measured by rapidly mixing actin-tropomyosin-troponin (regulated actin) with myosin S1. The reaction could be represented by the following equation:

$$\mathrm{I}+\mathrm{M}\rightleftarrows \text{IM}\underset{{\mathrm{k}}_{7\prime }}{\overset{{\mathrm{k}}_{8\prime }}{\rightleftarrows }}\text{XM}\underset{{\mathrm{k}}_{5\prime }}{\overset{{\mathrm{k}}_{6\prime }}{\rightleftarrows }}\text{AM}$$ (1)

where M is myosin S1, T is ATP, A is regulated actin in the active state, X is an intermediate state of regulated actin, and I is the inactive state.

The transition from the active state to the inactive state was measured by rapidly dissociating myosin from regulated actin with a high concentration of ATP. The reaction scheme could be represented by

$$\text{AM}+\mathrm{T}\underset{{\mathrm{k}}_2}{\overset{{\mathrm{k}}_1}{\rightleftarrows }}\text{AMT}\underset{\text{MT}\times {\mathrm{k}}_4}{\overset{{\mathrm{k}}_3}{\rightleftarrows }}\mathrm{A}\underset{{\mathrm{k}}_6}{\overset{{\mathrm{k}}_5}{\rightleftarrows }}\mathrm{X}\underset{{\mathrm{k}}_8}{\overset{{\mathrm{k}}_7}{\rightleftarrows }}\mathrm{I}.$$ (2)

ATP binding to S1-actin was made faster than the succeeding reactions by using high concentrations of ATP, so the rate constants k₁ + k₂ did not affect the analysis. All processes that led to the formation of X were much faster than the transition from X to I. As a result, the apparent rate constant from X to I was given by k₇ + k₈.

Fluorescence transients were simulated with ordinary differential equations. The following equations were used for the dissociation reaction of Eq. 2:

$$\begin{array}{l}\text{dAMT}/\text{dt}={\mathrm{k}}_4\times \mathrm{A}\left[\mathrm{t}\right]\times \text{MT}\left[\mathrm{t}\right]-{\mathrm{k}}_3\times \text{AMT}\left[\mathrm{t}\right],\\ \text{dMT}/\text{dt}={\mathrm{k}}_3\times \text{AMT}\left[\mathrm{t}\right]-{\mathrm{k}}_4\times \mathrm{A}\left[\mathrm{t}\right]\times \text{MT}\left[\mathrm{t}\right],\\ \text{dA}/\text{dt}={\mathrm{k}}_3\times \text{AMT}\left[\mathrm{t}\right]+\left({\mathrm{k}}_5/{\mathrm{K}}_{56}\right)\times \mathrm{X}\left[\mathrm{t}\right]-\left({\mathrm{k}}_5+{\mathrm{k}}_4\times \text{MT}\left[\mathrm{t}\right]\right)\times \mathrm{A}\left[\mathrm{t}\right],\\ \text{dX}/\text{dt}={\mathrm{k}}_5\times \mathrm{A}\left[\mathrm{t}\right]+\left({\mathrm{k}}_7/{\mathrm{K}}_{78}\right)\times \mathrm{I}\left[\mathrm{t}\right]-\left(\left({\mathrm{k}}_5/{\mathrm{k}}_{56}\right)+{\mathrm{k}}_7\right)\times \mathrm{X}\left[\mathrm{t}\right],\\ \text{dI}/\text{dt}={\mathrm{k}}_7\times \mathrm{X}\left[\mathrm{t}\right]-\left({\mathrm{k}}_7/{\mathrm{K}}_{78}\right)\times \mathrm{I}\left[\mathrm{t}\right],\\ \text{Fluor}\left[\mathrm{t}\right]=\text{Am}{\mathrm{p}}_{\mathrm{1}}\times \text{dX}/\text{dt}+\text{Am}{\mathrm{p}}_2\times \text{dI}/\text{dt}\end{array})$$ (3)

Because ATP binding at 2 mM was very fast, it was treated as an instantaneous event and was not included in the simulations. We observed that the transition from X to I was independent of the concentration of ATP, so that assumption was valid. K₅₆ is the ratio k₅/k₆ and defines [X]/[A] at equilibrium. K₇₈ is the ratio k₇/k₈ and defines [I]/[X] at equilibrium.

Fluorescence changes resulted from the formation of states X and I from state A. The function Fluor[t] is the sum of the fluorescence changes in going from states A to X, and X to I. That function was fitted to the fluorescent transients with the use of MLAB (Civilized Software, Bethesda, MD) and Mathematica (Wolfram Research, Champaign, IL). Rate constants k₃ and k₄ were defined by the light-scattering experiments. Rate constants k₅–k₈ were adjusted to fit the model to the data. Amp₁ and Amp₂ are the respective amplitudes of the signals for transitions of A to X, and X to A. In the case of pyrene excimer fluorescence, both Amp₁ and Amp₂ were negative. For acrylodan fluorescence, Amp₁ was negative and Amp₂ was positive.

Experimental results suggest that a rapid equilibrium was reached within a few milliseconds between states X and A. That transition was observable with both pyrene and acrylodan probes at low temperature. The primary signal observed at higher temperatures was the transition from the equilibrium mixture of A+X to state I. That signal resulted from the conversion of A to X, and X to I, both of which were limited by the rate k₇ + k₈.

The rate constants in Eqs. 1 and 2 are not equivalent. In Eq. 1 the transition among actin states occurs while actin is bound to myosin, but in Eq. 2 the actin is free of myosin. The transition described by Eq. 2 differs from normal muscle relaxation that is initiated by calcium sequestration. Previous investigators studied this process by monitoring force changes when skeletal (27) and cardiac (28) myofibrils were rapidly switched to a calcium-free solution.

Results

Regulated actin can be maintained in the active state by binding of nucleotide-free S1. Upon rapid addition of ATP, the S1 dissociates, allowing the regulated actin to return to its normal distribution (8). The inactive state is predominant in the absence of calcium. At saturating calcium, the intermediate state dominates, but the inactive and active states are thought to be significantly populated.

Fig. 1 shows the ATP concentration dependencies of S1 dissociation at 180 mM ionic strength for actin filaments containing either pyrene or acrylodan probes on tropomyosin. The rate of dissociation of S1 at 3°C and 2 mM ATP was >500/s in the presence of regulatory proteins and the absence of calcium. At temperatures higher than 9°C, the rate was too fast to measure (>600/s) except at subsaturating ATP concentrations. A concentration of 2 mM ATP was used in most studies.

Figure 1.

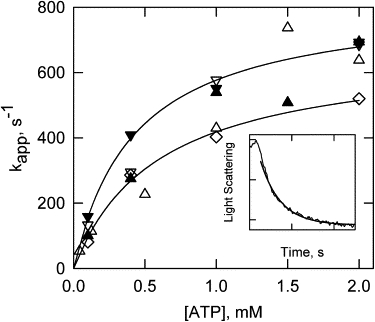
Rate of dissociation of S1 from actin-tropomyosin-troponin as a function of ATP concentration at three temperatures. Light scattering was used to measure dissociation of both acrylodan-labeled (open symbols) and pyrene-labeled tropomyosin (solid symbols). Reactions were run at 3°C (diamonds), 5.5°C (triangles up), and 9.9°C (triangles down). Solid lines are hyperbolic fits to acrylodan-tropomyosin at 3°C (bottom line) and to pyrene-labeled tropomyosin at 9.9°C (upper line). Inset: Plot of light-scattering intensity against time, showing dissociation of S1 at 3°C and 2 mM ATP. The heavy solid line is an exponential fit to the part of the curve past the mixing time (∼1 ms). Each tick on the abscissa is 4 ms. Conditions: 4 μM S1, 4 μM actin, 0.86 μM tropomyosin, and 0.86 μM troponin in 20 mM MOPS pH 7, 158 mM KCl, 2 mM EGTA, 4 mM MgCl₂, and 1 mM dithiothreitol.

The time courses of the tropomyosin changes were followed by changes in fluorescence of acrylodan or pyrene probes on tropomyosin. Fig. 2 A shows a series of acrylodan-tropomyosin fluorescence transients at different ATP concentrations. At low concentrations of ATP, a lag preceded a decrease in fluorescence, followed by a very slow partial recovery of fluorescence. The lag disappeared at higher ATP concentrations. Furthermore, the amplitude of the fast transition decreased with increasing ATP concentrations, as much of the reaction was completed within the mixing time of the stopped-flow device. Curve e of Fig. 2 A represents a control lacking a fluorescent probe on tropomyosin. The lack of any change shows that light scattering did not contribute to the fluorescence signals.

Figure 2.

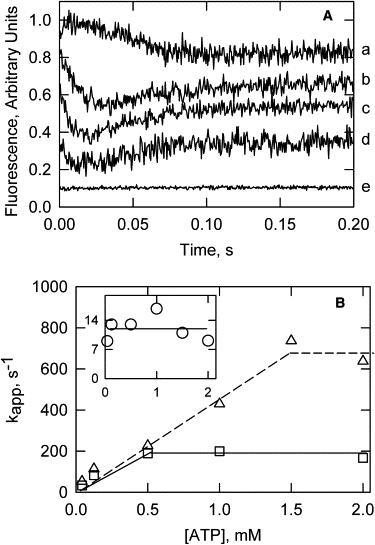
Effect of ATP concentration on the fluorescence changes of S1-actin-acrylodan-tropomyosin-troponin. Tropomyosin was labeled with acrylodan. (A) Fluorescence transients with final ATP concentrations of 0.062 (a), 0.25 (b), 0.5 (c), and 1.0 (d) mM ATP. Curve e is with 0.125 mM ATP final, but without a fluorescent probe on tropomyosin. (B) Apparent rate constants of S1 dissociation from Fig. 1 (triangles), the rapid fluorescence change (squares), and the slow fluorescence change (open circles in inset). Inset: k_app for the slow fluorescence transient versus [ATP]. Conditions were the same as in Fig. 1 with a temperature of 5.5°C.

The ATP dependencies of the apparent rate constants for S1 dissociation and the two fluorescence transients are compared in Fig. 2 B. The light-scattering transition, reproduced from Fig. 1, increased in rate with increasing ATP concentrations and leveled off at ∼700/s at 5.6°C. The rapid decrease in fluorescence reached a maximum rate of ∼200/s, although the slow phase had a maximum rate of ∼12/s. At temperatures exceeding 25°C, the rapid fluorescence decrease also became too fast to measure, and only the slow increase in fluorescence was observed. At these high temperatures, it was impossible to distinguish the rapid fluorescence change from light scattering.

When the apparent rate constant of S1-ATP detachment was greater than that of the first fluorescence transition, that fluorescence transition was independent of the ATP concentration. The apparent rate constant for the slow fluorescence increase was approximately constant over a wide range of ATP concentrations. At ATP concentrations > 1.0 mM, the two fluorescence transients appeared to be largely independent of the preceding steps.

It is likely that the rapid fluorescence decrease resulted from the transition of the active state to the intermediate state, and the slower increase resulted from the transition to the inactive state. If so, the slow fluorescence increase should be attenuated in the presence of calcium, where the final state is predominantly the intermediate state. Fig. 3 compares acrylodan fluorescence transients in the absence (Fig. 3 A) and presence (Fig. 3 B) of calcium under otherwise identical conditions. In the presence of calcium, the rapid fluorescence decrease was observed but the slow fluorescence increase did not occur. We occasionally observed a subsequent slow increase, but with an amplitude of only 15% of that seen in EGTA. This observation is consistent with the two rapid and slower changes resulting from formation of the intermediate and inactive states, respectively. The relative order of the fluorescence sensitivities for the acrylodan probe is active > inactive > intermediate.

Figure 3.

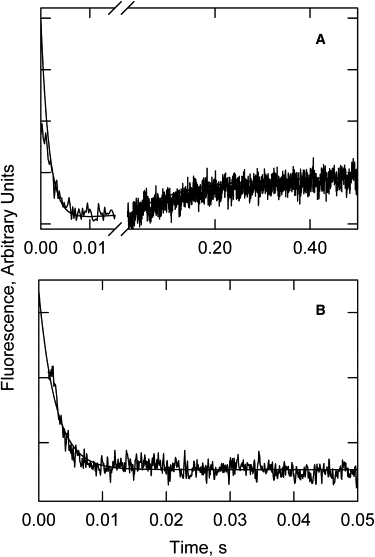
Time course of actin-acrylodan-tropomyosin-troponin fluorescence changes after dissociation of S1 with ATP. (A) Absence of calcium. The smooth curve is a simulation of Eq. 3 with k₅ + k₆ = 434/s; k₇ + k₈ = 7.5/s. (B) Presence of calcium; the fitted curve has k₅ + k₆ = 375/s. Conditions were the same as in Fig. 1 with a temperature of 9.9°C.

Pyrene probes on tropomyosin also report changes in the state of regulated actin. Fig. 4 A shows time courses of pyrene excimer fluorescence changes in the absence of calcium at different temperatures. Simple monoexponential fluorescence decays were observed between 15°C and 35°C. Complex transitions were seen below 15°C, with a rapid fluorescence decrease followed by a slower increase. The rapid decrease probably represents the transition from the active state to the intermediate state as it became slow enough to measure. However, the nature of the other transition was not established. Complexities in spectra have been reported as a result of S1 binding close to the site of the label (29). However, reducing the initial fraction of actin sites with bound S1 to 30% did not reduce the complexity of the transients (not shown) despite the decreased probability of having S1 adjacent to a probe. Further studies with pyrene were limited to ≥15°C, where the transitions were straightforward.

Figure 4.

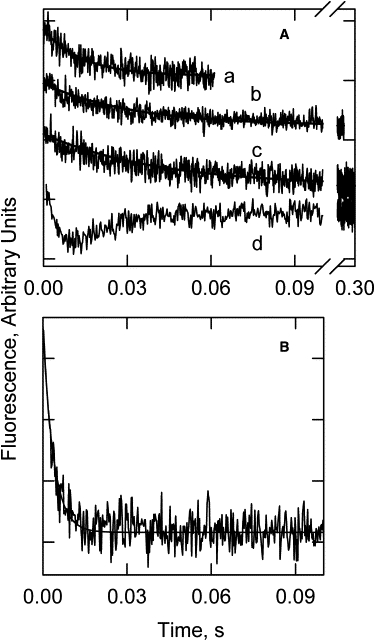
Time courses of pyrene tropomyosin fluorescence changes after rapid dissociation of S1 from S1-actin-pyrene-tropomyosin-troponin with ATP. (A) Absence of Ca²⁺. Pyrene tropomyosin transitions at 30°C, k_app = 70/s (a), 25°C, k_app= 28/s (b), 20°C, k_app = 21/s (c), and 1°C (d). (B) Saturating Ca²⁺ at 1°C, k_app = 268/s. The solid lines through the curves are simulations of Eq. 2. Conditions after mixing in the stopped flow: 4 μM F-actin, 3.6 μM S1, 0.86 μM pyrene-labeled tropomyosin, and 0.86 μM troponin in a buffer containing 20 mM MOPS, 142 mM KCl, 2 mM ATP, 2 mM EGTA, 6 mM MgCl₂, and 1 mM dithiothreitol. Other conditions are the same as in Fig. 1.

In the presence of saturating calcium and high ATP concentrations, pyrene excimer fluorescence decreased as a monoexponential function (Fig. 4 B). The apparent rate constant of the transition at 2 mM ATP was much larger than that of the decay observed in the absence of calcium. In the presence of calcium, pyrene excimer fluorescence reported the transition from the active state to the equilibrium mixture of active and intermediate states. In the absence of calcium, pyrene excimer fluorescence reported the transition from the equilibrium mixture of active and intermediate states to the inactive state.

Apparent rate constants for the single fluorescence transition of pyrene tropomyosin are shown as a function of ATP concentration in Fig. 5. At 20°C and 37°C, that transition was largely independent of the ATP concentration above 0.5 mM ATP. Additional complexities in the pyrene excimer transients were observed at low ATP concentration even at 20°C (curves e and f). No attempt was made to extract rate constants from curves generated at low ATP concentrations. Pyrene excimer transitions of tropomyosin could be interpreted most readily at temperatures of >10°C and at ATP concentrations of ≥1 mM.

Figure 5.

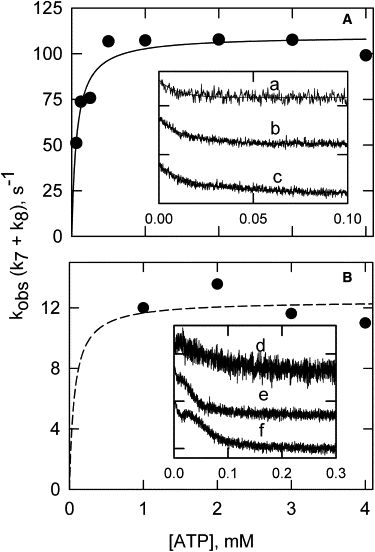
Observed rate constants for the tropomyosin pyrene excimer fluorescence change as a function of ATP concentration after mixing at 37°C (A) and 20°C (B). The insets show the changes in fluorescence as a function of time after rapid dissociation of S1 from S1-actin-tropomyosin-troponin with different concentrations of ATP (a and d = 1 mM, b and e = 125 μM, and c and f = 62.5 μM). Conditions after mixing in the stopped flow: 4 μM F-actin, 3.6 μM S1, 0.86 μM pyrene-labeled tropomyosin, and 0.86 μM troponin in a buffer containing ATP at concentrations shown, 2 mM EGTA, 6 mM MgCl₂, and sufficient KCl to reach an ionic strength of 180 mM. Note that the apparent rate constants for the slow transition could not be determined for the pyrene probe at low ATP concentrations and these values are not shown. The solid curve in A and the dashed curve in B are for an ATP concentration of 0.069 mM, giving 50% of the respective maximum rates.

In both the acrylodan-tropomyosin and pyrene-tropomyosin cases, the transitions from active to intermediate states were rapid equilibrium reactions that were often lost in the mixing time of the stopped-flow apparatus. To estimate the signal lost, we compared ATP chase studies with the slower binding of S1 to regulated actin filaments. Fig. 6 A shows that the increase in fluorescence of acrylodan tropomyosin-bound S1 stabilized the formation of the active state. Fig. 6 B shows the transition of the equilibrium mixture of active and intermediate states to the inactive state. The dashed line between Fig. 6, A and B, represents the rapid equilibrium formation of the distribution between the active and intermediate states. Fig. 6 B shows the transition from the equilibrium mixture of the active “a” and intermediate “x” states to the inactive “i” state.

Figure 6.

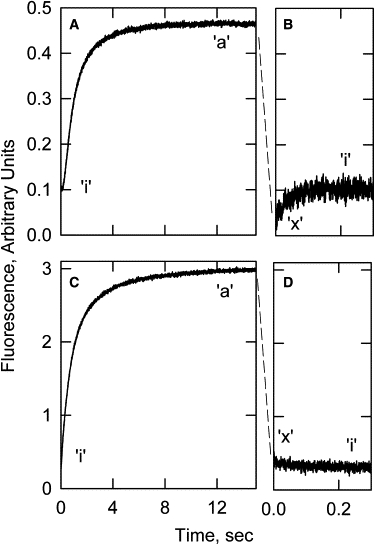
Fluorescence changes for formation of the active state from the inactive state compared with those observed in going from the active state to the inactive state. (A) Acrylodan-tropomyosin transition observed after mixing actin-troponin-tropomyosin with S1. (B) Acrylodan-tropomyosin transition observed after chasing S1 off S1-regulated actin with ATP. The decrease in fluorescence expected from A to B was too fast to measure. (C) Pyrene-tropomyosin transition observed after mixing actin-troponin-tropomyosin with S1. (D) Pyrene-tropomyosin transition observed after chasing S1 off S1-regulated actin with ATP. The major state present in each part of the curve is given as a for active, x for intermediate, and i for inactive. Conditions as in Fig. 1 but at 24.4°C.

The respective transitions with pyrene-labeled tropomyosin are shown in Fig. 6, C and D. The association reaction proceeded with a large increase in pyrene excimer fluorescence as shown in Fig. 6 C. The dashed line between Fig. 6, C and D, represents the rapid equilibrium formed between the active and intermediate states before the slower transition to the inactive state shown in Fig. 6 D. Thus, when the transition from the active state to the inactive state was triggered by the rapid addition of ATP, an initial rapid equilibrium was established between the active and intermediate states (k₅ + k₆) that was observable at low temperature. The major transition observed was from the mixture of active and intermediate states to the inactive state.

The transition from the intermediate state to the inactive state is generally thought to be spectrally silent for the pyrene probe. If that is the case, then the slow second phase in pyrene fluorescence occurred as a result of depletion of the residual active state remaining after the rapid equilibrium. If Fig. 6 C represents the total fluorescence change, then the difference between the amplitudes of Fig. 6, C and D, represents the amplitude of the transition from the active to the intermediate state. The fractions of intermediate and active state at equilibrium were 0.9 and 0.1, respectively, giving an equilibrium constant K₅₆ ≈ 9.

Values of k_app for the slow fluorescence transition (approximately k₇ + k₈) for pyrene and acrylodan probes are shown as a function of temperature in Fig. 7. The temperature dependencies of the rate constants were fitted separately for the pyrene and acrylodan probes. Transition rates were slower for acrylodan relative to pyrene over the entire temperature range, but the temperature dependencies of the curves were similar. Arrhenius plots for the data (Fig. 7, inset) are straight lines, indicating that there were no apparent changes in the rate-limiting step over the temperature range of 1–37°C.

Figure 7.

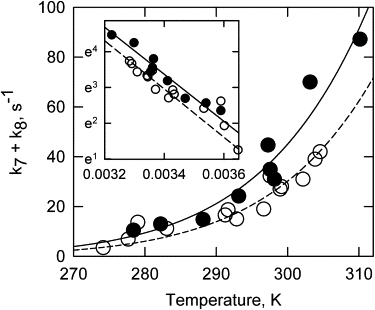
Temperature dependencies of rates of transition from the mixture of active and intermediate states to the inactive state (the second fluorescence transition). Apparent rate constants were measured by pyrene (solid circles) and acrylodan (open circles) probes on tropomyosin. The inset is an Arrhenius plot (ln apparent rate versus 1/T). The lines are best fits of the Arrhenius equation to the data.

When actin filaments were permitted to relax to the inactive state with an ATP chase in saturating calcium conditions, only the initial rapid phase was readily seen (Figs. 3 B and 4 B). The apparent rate constant for this transition was measured for the pyrene probe and is shown in Fig. 8. Over the temperature range of 1–20°C, the observed rate constant (solid squares) was similar to the initial rapid phase observed for acrylodan-labeled tropomyosin in EGTA (open circles). Measurements at higher temperatures were impractical because of the high values of the apparent rate constants.

Figure 8.

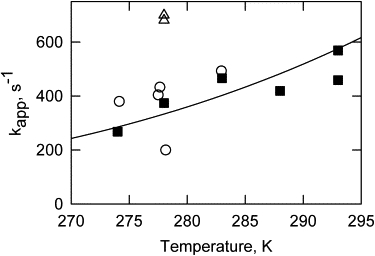
Temperature dependencies of apparent rate constants for the rapid transition of regulated actin from the active state to the equilibrium mixture of active and intermediate states. Measurements were made with acrylodan in EGTA (open circles), and pyrene in Ca²⁺ (solid squares). Open triangles show the rate of S1-ATP dissociation. The conditions are the same as in Fig. 1.

Discussion

The ability of actin to stimulate ATP hydrolysis by myosin is controlled by the position of tropomyosin on actin. A long-held hypothesis of regulation is that tropomyosin inhibits myosin binding to actin in the absence of calcium and therefore inhibits movement (30–32). The time course of events is consistent with this view (33), but it does not rule out other possibilities because of the difficulty of detecting weak-binding cross-ridges by x-ray diffraction.

Several observations suggest that tropomyosin is part of an allosteric apparatus. Myosin S1 binding to regulated actin is not blocked during steady-state ATP hydrolysis under a range of conditions (1,20,34). Cross-bridge attachment has been reported in relaxed permeabilized muscle fibers at physiological ionic strength (35). Although the position of tropomyosin on actin is affected by S1-ADP or rigor S1 binding, it is unaffected by S1 binding during ATP hydrolysis (36). Under some conditions, the inhibitory complex of troponin-tropomyosin increases the ability of actin to accelerate ATP hydrolysis of myosin by severalfold (37,38). Such activation above the rate in the absence of tropomyosin and troponin cannot be explained by the release of inhibition of binding. Rather, tropomyosin may be a S1-ADP sensor that responds by moving to a position of higher activity (4,20). Thus, calcium and S1-ADP both destabilize the inactive state of regulated actin. The total activity is the sum of that from myosin bound to each of the states. The two-state version of this parallel pathway model is consistent with steady-state ATPase activities (4) and equilibrium binding (1,21).

Trybus and Taylor (8) pointed out that a third state may be needed to explain calcium effects on the kinetics of S1 binding. McKillop and Geeves (5) made similar observations and proposed a hybrid three-state model. Analyses of regulated actin structure were also consistent with three states of regulated actin filaments (10,11,39). Additional kinetic approaches were also consistent with three states (7,9). Although we showed that it is possible for a two-state model to reproduce the kinetics of binding (40), we later found evidence of a functionally distinct intermediate state. Some mutations of cardiac troponin I produce greater than normal activity in EGTA and less than normal activity in calcium. This can be most readily explained if the structural intermediate has an intermediate ability to stimulate ATP hydrolysis (12). If the intermediate state has functional significance, and if changes in the amount of the intermediate may lead to dysfunction (12), then it becomes important to determine how these states are thermodynamically and kinetically related to each other.

Of the two probes examined here, the acrylodan probe gave a larger signal than was observed with pyrene excimer fluorescence. The acrylodan probe also showed two transitions in going from the active to the inactive state. Analysis of these states was facilitated by opposite changes in fluorescence amplitudes for the two transitions. Acrylodan measurements could also be extended to lower temperatures than pyrene measurements, enabling S1 dissociation to be distinguished from the transition between the active and intermediate states (Fig. 2 B). Pyrene excimer fluorescence has the advantage of producing little or no signal in going from the intermediate state to the inactive state (17). Because of this feature, we were able to estimate the equilibrium constant between the active and intermediate states, K₅₆, in EGTA to be ∼9.

We observed no evidence of cooperativity for transitions at high ATP concentrations; however, complex transients were observed at low ATP concentrations (Figs. 2 A and 5). Geeves and Lehrer (41) observed a lag with a pyrene probe on tropomyosin at lower ATP concentrations. However, Shitaka et al. (7) did not observe evidence of cooperative transitions of probes on TnT or TnI upon rapid reversal of S1 binding with ATP. It is possible that cooperative behavior is seen only when the rate of S1 dissociation rate is relatively low.

At high concentrations of ATP, we were able to obtain estimates of the apparent rate constants defining transitions between the active and intermediate states, and between the intermediate and inactive states. At low temperatures and using the acrylodan probe, we found that the rate constants for the rapid fluorescence transition (active to intermediate states) and the slow fluorescence transition (formation of the inactive state) were largely independent of ATP and S1-ATP dissociation (Fig. 2 B). Previous studies showed that S1-ATP dissociation was >2-fold faster than pyrene tropomyosin transitions over a wide range of ATP concentrations (7,8,41).

The value of the apparent rate constant from the active to the intermediate state in calcium-containing buffer between 277 and 283 K can be calculated by the following equation: k₅ + k₆ (T) ≈ 3.4 × 10⁵ × exp(−1.6 × 10⁴/(R × T)), where R = 8.314 J/K × mol. These results are consistent with rapid Forster energy transfer measurements between probes on actin and either TnI or TnT. At 20°C, 0.5 mM ATP, and 50 mM ionic strength, the observed rate constant was 400/s for a probe on TnT in both the presence and absence of calcium. For probes on TnI, apparent rate constants of 300/s in calcium and 400/s in EGTA were observed (9). We predict a value of 477/s at 293 K using different probes, a higher ionic strength, and a higher [ATP].

The rapid fluorescence transition was less well defined in the absence of calcium, and values were obtained most readily with the acrylodan probe. The apparent rate constants in EGTA for the acrylodan probe were generally faster than those measured at saturating calcium with the pyrene probe.

The transition to the inactive state occurred less rapidly than the preceding transitions. Values for the apparent rate constant from the transition from the intermediate to the inactive state (k₇ + k₈) were ∼1.6-fold faster when measured with a pyrene probe than with the acrylodan probe. These differences may have resulted from direct probe effects.

The temperature dependencies of the apparent rate constants for formation of the inactive state were similar for both probes. Arrhenius plots were linear and gave no evidence of a change in the rate-limiting step for the reaction. The rates at any temperature between 274 and 310 K may be calculated from k₇ + k₈ (T) = A × exp(−E_a/(R × T)). The frequency factor, A, was 5 × 10¹¹ M⁻¹ for pyrene and 2 × 10¹¹ M⁻¹ for acrylodan. The activation energies, E_a, for pyrene and acrylodan were 55,000 and 56,000 J, respectively. These values are within normal ranges for enzyme-catalyzed reactions (42).

This slow transition was not observed in earlier studies of energy transfer between actin and TnT (7), nor was it observed in fluorescence changes of pyrene tropomyosin at very low ATP concentrations (41). The slow transition was observed, however, in the kinetics of Forster energy transfer between probes on actin and TnI (9). At 20°C the slow phase had an apparent rate constant of 50/s. At the same temperature but at higher ionic strength and higher ATP, we observed apparent rate constants of 24/s for pyrene tropomyosin and 16/s for acrylodan tropomyosin.

The individual rate constants, k₅–k₈, cannot be determined from rapid kinetic studies alone because the fluorescence sensitivities of all species are unknown. Distributions have been estimated by a combination of kinetic and equilibrium studies (5), but such distributions are model-dependent (40,43). Image reconstruction of thin filaments at very low ionic strength produced estimates of state distributions (10) that were similar to those proposed by the Geeves group (5). In EGTA the blocked (inactive) and closed (intermediate) states account for ∼78% and 22% of total states, respectively. The distributions in calcium were estimated to be ∼20% blocked (inactive), 68% closed (intermediate), and 12% M (active), but the temperature and salt dependencies of these equilibrium constants are unknown. As a rough approximation, k₅ ≈ 6 × k₆ and k₇ ≈ 0.28 × k₈ in the presence of calcium; however, in EGTA, k₅ >> k₆ and k₇ ≈ 0.29 × k₈. It will be possible to obtain better estimates of these distributions as more troponin mutants that differ in their distributions are studied.

Placing these distributions into the parallel model of regulation requires that the intermediate state be more like the inactive state than the active state in terms of stimulating ATPase activity. Our estimate that the intermediate state in skeletal actin thin filaments has 4–15% of full activity satisfies that requirement (12). To be consistent with data suggesting that calcium exerts a strong control on ATPase cycling kinetics (1,34,44,45), it is also necessary to consider that the blocked state is not blocked toward binding S1 during steady-state ATP hydrolysis. Contrary to some opinions, the binding of myosin to regulated actin during steady-state ATP hydrolysis is not limited to low-ionic-strength conditions (1,20,34,35). Binding of rigor S1 and S1-ADP are inhibited in the absence of calcium. The implication is that the transition from S1-ATP to S1-ADP is blocked, and that therefore the transition between weak binding states and strong binding states is regulated.