Fast Reverse Propagation of Sound in the Living Cochlea

Abstract

The auditory sensory organ, the cochlea, not only detects but also generates sounds. Such sounds, otoacoustic emissions, are widely used for diagnosis of hearing disorders and to estimate cochlear nonlinearity. However, the fundamental question of how the otoacoustic emission exits the cochlea remains unanswered. In this study, emissions were provoked by two tones with a constant frequency ratio, and measured as vibrations at the basilar membrane and at the stapes, and as sound pressure in the ear canal. The propagation direction and delay of the emission were determined by measuring the phase difference between basilar membrane and stapes vibrations. These measurements show that cochlea-generated sound arrives at the stapes earlier than at the measured basilar membrane location. Data also show that basilar membrane vibration at the emission frequency is similar to that evoked by external tones. These results conflict with the backward-traveling-wave theory and suggest that at low and intermediate sound levels, the emission exits the cochlea predominantly through the cochlear fluids.

Introduction

In the mammalian ear, incoming sounds vibrate the eardrum and the middle ear bony chain (Fig. 1 A). The movement of the stapes changes the fluid pressure inside the cochlea, thus triggering basilar membrane (BM) vibrations that start at the base and move toward the apex of the cochlea (Fig. 1 B). As this forward traveling wave propagates, its amplitude increases and speed decreases, forming the maximum response at the best-frequency (BF) location. The sensory cells on the BM detect the vibration and convert the mechanical stimulus into electrical signals.

Figure 1.

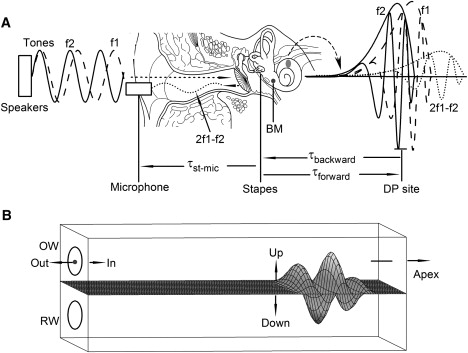
Diagram showing DP generation and propagation and measurement of the backward delay. (A) Two tones f1 and f2 enter the cochlea through the external and middle ear to result in traveling waves f1 and f2, which generate DPs at their overlapping location (DP site). DP was measured at the BM, at the stapes, and in the ear canal. (B) When a DP wave is generated at the apical side of the measured BM location, the propagation direction of the wave can be determined by the phase difference from the BM to stapes. The wave should propagate from a location with a phase lead, to a location with a phase lag. RW is the round window; OW, the oval window.

Figure 2.

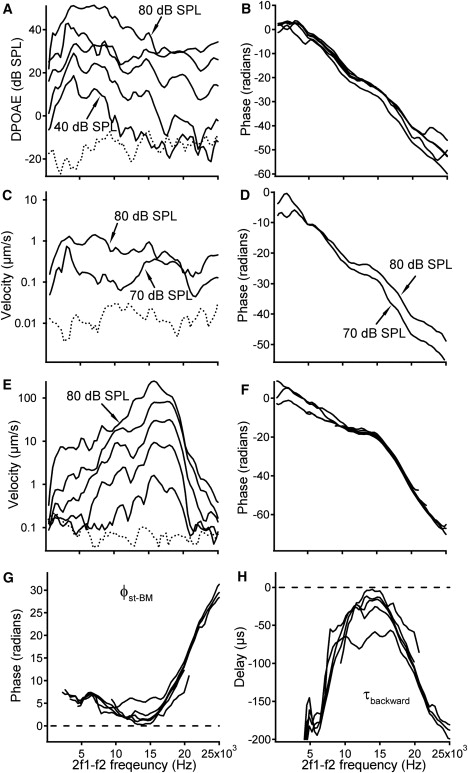
Backward propagation of the DP when f2/f1 = 1.25. (A and B) Magnitude of the DPOAE is frequency- and level-dependent, while the corresponding phase decreases with frequency. (C and D) Stapes DP magnitude and phase at 70 and 80 dB SPL. (E and F) Magnitude and phase of the BM DP. (G) Phase difference from the BM to stapes shows that stapes phase leads BM phase. (H) Negative delay from the BM to the stapes demonstrates that the DP arrives at the stapes earlier than at the measured BM location. Dotted lines in panels A, C, and E are measurement noise floors.

The cochlea also generates sounds, i.e., otoacoustic emissions (OAEs), which can be measured in the ear canal using a sensitive microphone. Since Kemp discovered the OAE (1), it has been increasingly used in clinics for diagnosing auditory disorders and in laboratories for estimating cochlear nonlinearity (2–6). To derive useful information from OAEs, it is critical to understand how they exit the cochlea. Based on mathematical modeling showing that a cochlear wave can propagate in both directions along the cochlear partition (7) and the fact that the OAE can be measured in the external ear canal, Kemp proposed that the OAE travels to the cochlear base as a backward traveling wave along the cochlear partition (8). Although external tone-induced cochlear traveling waves always travel in the apical direction regardless of the location of the source (9,10), the OAE backward wave was thought to be possible because it results from a sound source internal to the organ of Corti.

To demonstrate the expected backward traveling wave, Ren (11) used a scanning interferometer to measure BM vibrations at different longitudinal locations. It was found, however, that the phase of the BM vibration at the emission frequency decreases with the distance from the cochlear base, indicating a forward traveling wave. This result is consistent with other measurements of the OAE in the ear canal and/or at the BM as a function of frequency (12–16) and intracochlear pressures at different cochlear turns (17). The data is also consistent with a report that the cochlear partition vibration decreases as much as 155 dB/mm in the reverse direction (18). Similarly, Siegel et al. (19) found that the delay of the OAE is equal to or smaller than the forward delay of the cochlear traveling wave. The delay of the OAE, directly measured at the stapes (20), confirmed the finding of Siegel et al. To detect a possible small backward traveling wave, BM vibrations at the OAE frequency were measured at two longitudinal locations at sound levels as low as 40 dB SPL (0 dB SPL = 20 μPa) (21,22). It was found that the delay of the OAE at a basal location is smaller than that at a more apical location, indicating that the wave propagates in the apical direction. A similar finding was also reported by de Boer et al. (23). These experimental data led to a conceptual change in cochlear wave propagation and a modification of the cochlear model (24). Using a nonlinear hydrodynamic cochlear model, Vetesnik et al. (25) showed that the emissions are propagated almost instantaneously through the fluid.

However, the above experimental findings, especially the results from the scanning measurement, have been criticized because they are not consistent with predictions from classical cochlear models (23,26,27). There are experiments that are consistent with the backward-traveling-wave theory. The OAE delay was found to be ∼2 times that of the forward delay (28–32). Dong and Olson (33) recently measured the distortion product (DP) pressure near the BM and the OAE in the ear canal. The delay of the DP pressure near the BM was found to be smaller than that of the OAE. The discrepancy between reported experimental results was reviewed by Wilson (34). As there is no BM vibration data comparable to the reported DP pressure data available in the literature, the aim of this study was to determine the temporal relationship between the BM and stapes vibrations. DPs were measured as vibrations at the BM and at the stapes and as sound pressure in the ear canal using a sensitive laser interferometer and a microphone, where DP frequency was varied by changing f1 and f2 frequencies when the f2/f1 ratio was constant. Resulting data indicate that the stapes phase leads the BM and so does not support the backward-traveling-wave theory.

Materials and Methods

Animal preparation and general methods

Fifteen young, healthy Mongolian gerbils (40–80 g) were used in this study. Anesthesia was induced by intraperitoneal injection of ketamine (30 mg/kg) and intramuscular application of xylazine (5 mg/kg). The animal protocol was approved by the Institutional Animal Care and Use Committee of Oregon Health & Science University. Animal preparation and surgical approach were the same as in previous studies (11,22,35).

The sensitivity of the cochlea was monitored by measuring the compound action potential using a previously described method (35).

Signal generation and data acquisition

A LabVIEW-based (National Instruments, Austin, TX) program was used to control TDT hardware (System II; Tucker-Davis Technologies, Alachua, FL) for signal generation and data acquisition. Tone bursts at f1 and f2 with 1 ms rise-fall time were generated by a D/A converter. The length of the tones was 20 or 40 ms, determined by the frequencies of f1, f2, and DPs. Electrical signals were used to drive two earphones, and the f1 and f2 levels were controlled through two programmable attenuators. A sensitive microphone (10 B+ Etymotic Research, Elk Grove Village, IL) was used to measure the sound pressure in the ear canal. The microphone-earphone probe was connected to the external ear canal through a plastic coupler to form a closed sound field. The signals from the microphone amplifier and the interferometer decoder were digitized and averaged 10–40 times, depending on the signal level. The magnitude and phase of the average signal were obtained by use of the Fourier transform.

BM and stapes vibration measurements

Methods for measuring the BM vibration were described previously (11,22,35). Briefly, after the round window membrane was removed, a few gold-coated glass beads with ∼20-μm diameter were placed on the BM, and the object beam of a heterodyne laser interferometer (OFV 3000S; Polytec, Waldbronn, Germany) was focused on one of the beads through a long-working-distance objective. The voltage from the laser interferometer decoder was proportional to the velocity of the bead vibration along the optical axis.

For measuring the stapes vibration, a gold-coated glass bead was placed on the anterior surface of the anterior crus of the stapes. The animal head position was adjusted to allow the laser beam access to the beads in a direction as perpendicular to the stapes footplate as possible. The bead position and animal head position allow more laser incident light to be focused on the bead and more reflected light to reach the sensor head of the laser interferometer, which results in a high carrier signal level and low noise floor. To improve the signal/noise ratio further, a digital high-precision velocity decoder (VD-6; Polytec) was used in the current experiment. The noise floor for the stapes-vibration measurement was often as low as 0.01 μm/s (Fig. 2 C), corresponding to a ∼0.0001-nm displacement at 15 kHz.

Experimental design

Equal level f1 and f2 tones were presented to the ear canal to evoke the DPs in the cochlea. Responses were measured from the BM at the first cochlear turn, stapes, and ear canal at f1, f2, and DP frequencies. The DP frequency was varied by changing f1 and f2 when the f2/f1 was constant. Data were collected with different f2/f1 ratios. For the f2/f1 ratio of 1.25, the DP frequency was varied from 0.375 to 30 kHz with 0.375 kHz steps. A frequency resolution of 25 Hz was achieved by presenting 40-ms f1 and f2 tones. For the frequency ratio of 1.125, the DP frequency was changed from 0.35 to 35 kHz by 0.35 kHz steps. A 20-ms tone duration was used to achieve the frequency resolution of 50 Hz. The BM vibration and distortion product otoacoustic emission (DPOAE) were measured at f1 and f2 sound levels from 40 to 80 dB SPL in 10-dB steps, whereas the stapes vibration was measured at 70 and 80 dB SPL.

Data presentation and analysis

Magnitude and phase of the BM and stapes vibration velocities and the DPOAE sound pressure were presented as a function of frequency. The raw phase data was unwrapped and referred to time-zero of the electrical signal. The forward phase transfer function of the BM vibration was presented by the phase difference from the stapes to the measured BM place (ϕ_BM-st) as a function of f1 frequency (f_f1). ϕ_BM-st was calculated from the stapes (ϕ_st) and BM phase (ϕ_BM), i.e., ϕ_BM-st = ϕ_BM-ϕ_st, where the phase is in radians. The forward delay τ_forward was derived from ϕ_BM-st according to the equation

$${\tau }_{\text{forward}}=-{\varphi }_{\text{BM}-\text{st}}/\left(2\pi f_{\text{f}1}\right),$$

where τ_forward is in seconds and f_f1 is in Hz. The forward magnitude transfer function was presented by the ratio of the BM (M_BM) to stapes vibration (M_st) magnitude (R_BM/st) as a function of the f1 frequency. R_BM/st was obtained according to R_BM/st = M_BM/M_st, where M_BM and M_st are in μm/s.

Similarly, the backward phase transfer function was presented by phase difference from the measured BM phase to the stapes (ϕ_st-BM) as a function of 2f1-f2 frequency (f_2f1-f2). ϕ_st-BM was calculated from the BM (ϕ_BM) and stapes phase (ϕ_st), i.e., ϕ_st-BM = ϕ_st − ϕ_BM. The backward delay τ_backward was obtained according to equation τ_backward = −ϕ_st-BM/(2πf_2f1-f2), where τ_backward is in seconds and f_2f1-f2 is in Hz. As stapes vibration magnitude is ∼100 times smaller than that of BM vibration, the stapes DP was measured only at f1 and f2 levels of 70 and 80 dB SPL. Because of the linear middle ear reverse transmission, ϕ_st at lower stimulus levels was obtained by subtracting the middle ear-induced phase lag (ϕ_ME) from the DPOAE phase (ϕ_DPOAE), i.e., ϕ_st = ϕ_DPOAE − ϕ_ME, where ϕ_ME = ϕ_DPOAE-H − ϕ_st-H; ϕ_DPOAE-H and ϕ_st-H are the DPOAE and stapes DP phase at 80 dB SPL.

Results

Anesthesia and surgical procedures were well tolerated by all animals. Due to the vulnerability of high-frequency hearing and the time-consuming nature of data collection, only six among 15 animals showed <8 dB compound action potential threshold elevation at 18 kHz after data collection. Results in Figs. 2, 3, and 5 were from one animal and data in Fig. 4 were from five animals.

Figure 3.

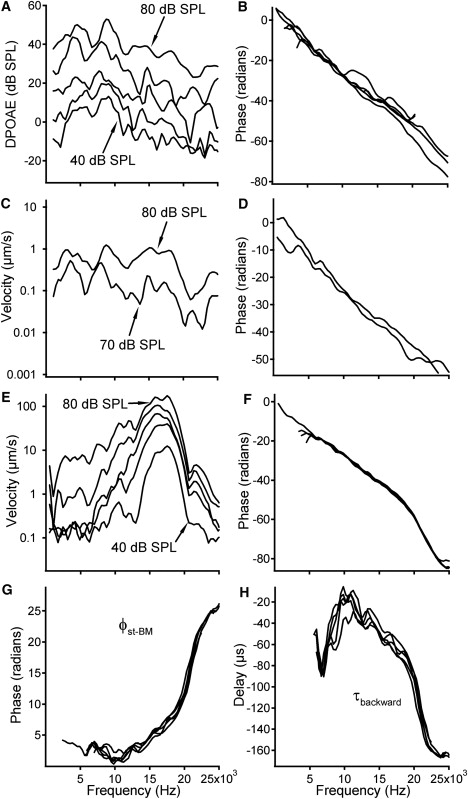
Backward propagation of the DP when f2/f1 = 1.125. The DPOAE (A and B), the stapes DP (C and D), and the BM DP responses (E and F) are similar to those in Fig. 2, A–F. (G) Positive phase difference confirms that the DP phase at the stapes leads BM DP phase. (H) Negative backward delay indicates that the stapes vibrates earlier than the BM.

Figure 5.

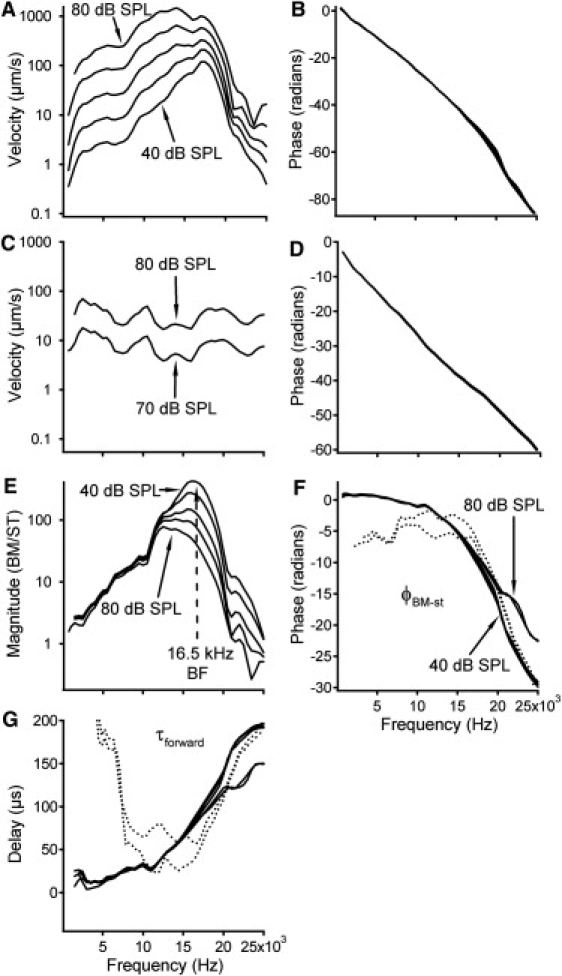
Forward propagation of BM vibration. (A and B) BM magnitude and phase responses. Panel A shows a sharp response peak at ∼16.5 kHz at 40 dB SPL, which broadens and shifts toward low frequencies as sound level increases. Phase progressively decreases with frequency (B). (C and D) Stapes magnitude and phase responses. (E) The forward magnitude transfer function shows a sharp peak response at low stimulus levels. The peak shifts toward low frequencies and the magnitude decreases with the sound level. (F) Phase slope decreases with frequency, indicating that the wave slows at high frequencies. This is confirmed by delays in panel G. Dotted lines in panels F and G are DP data collected at 70- and 80-dB SPL stimulus levels.

Figure 4.

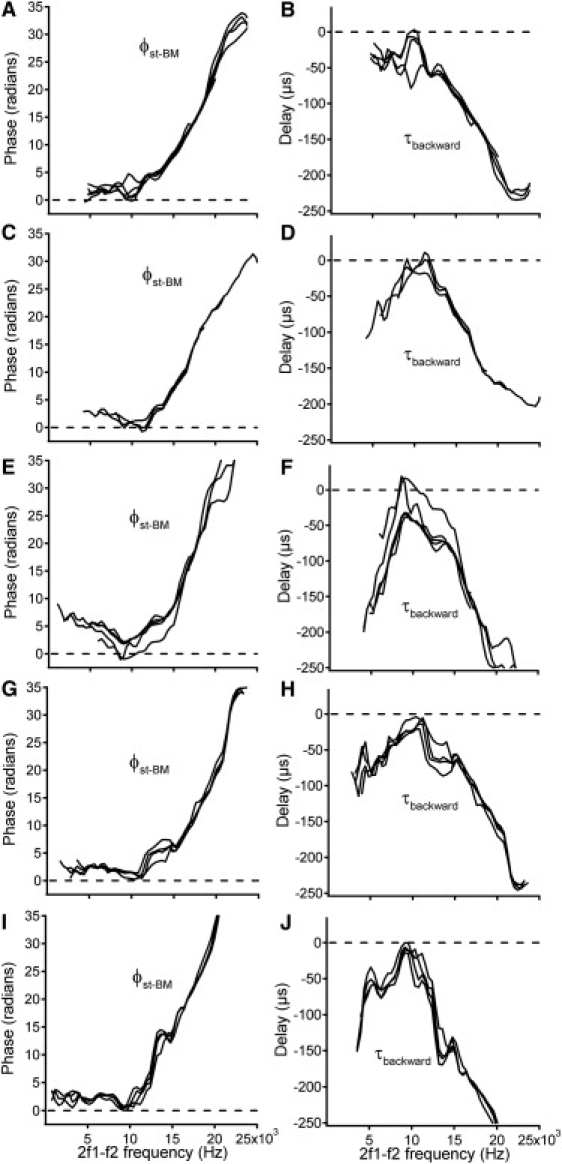
Phase difference and delay from the measured BM location to the stapes in five animals. Panels A, C, E, G, and I confirm data in Figs. 2G and 3G, and panels B, D, F, H, and J are consistent with Figs. 2H and 3H. These data show that the DP wave arrives at the stapes earlier than at the measured BM location. The f2/f1 ratios are 1.125 for A and B, 1.2 for C, D, G, H, I, and J, and 1.25 for E and F.

Backward propagation of the DP

A healthy cochlea generates a large number of DPs in response to a two-tone stimulus at frequencies f1 and f2. Among the different emissions, the DP at 2f1-f2 often has the highest magnitude. This study is therefore focused on this emission. Fig. 2 presents data acquired with an f2/f1 ratio of 1.25.

At a stimulus level of 40 dB SPL, the DPOAE magnitude increases with frequency, reaches a maximum near 5 kHz, and then gradually decreases to the noise floor, ∼−15 dB SPL at ∼15 kHz (Fig. 2 A). The magnitude increases as the stimulus level increases. The uneven separation between the curves in Fig. 2 A indicates that DPOAEs do not grow in proportion to the increase of the stimulus level. Furthermore, the nonparallel spaces between the curves indicate that growth also depends on the stimulus frequency. This frequency-dependent disproportional growth is pronounced at 70 and 80 dB SPL. The similarity between the DPOAE curves (Fig. 2 A) and DP magnitude responses at the stapes (Fig. 2 C) indicates that measurement artifacts do not cause these complex responses. The complex patterns of the DPOAE observed here are similar to those reported by others (33). DPOAE phase decreases with frequency in Fig. 2 B. The linear phase curves indicate a constant DPOAE group delay at different frequencies.

The magnitude and phase of the stapes vibration at the 2f1-f2 frequency were presented in Fig. 2, C and D. Although the magnitude changes with frequency, the overall shape of the magnitude curves is relatively flat. The phase of the stapes vibration at DP frequency in Fig. 2 D is similar to those of the DPOAE (Fig. 2 B), in which the phase lag increases with frequency. At a stimulus level of 80 dB SPL, the DP phase has a slope smaller than at 70 dB SPL, indicating a shorter delay.

BM vibration magnitude and phase at the DP frequency are presented in Fig. 2, E and F. The magnitude-frequency curves in Fig. 2 E are similar to those in response to a single tone (Fig. 5 E), which show a peak at ∼16.5 kHz. The peak broadens and saturates as the stimulus level increases. The phase (Fig. 2 F) decreases with frequency. Note that the phase decrease rate below ∼15 kHz is smaller than that above this frequency. In contrast to the stapes phase shown in Fig. 2 D, the BM phase showed no significant level-dependent change above 10 kHz, indicating that the stapes vibration is not caused directly by the BM vibration.

The backward phase transfer function from the observed BM location to the stapes is presented in Fig. 2 G. The most important finding from Fig. 2 G is that all phase values are near or above zero, i.e., the stapes phase is equal to or leads the BM phase. This result indicates either that the DP arrives at the stapes at the same time as at the BM or that the stapes vibrates earlier. The phase difference decreases with frequency and approaches zero at ∼14 kHz. Above this frequency, phase increases with frequency and reaches a maximum value of ∼30 radians, which is similar to the total accumulated phase lag in the forward propagation (Fig. 5 F).

The backward delay for the DP to propagate from the observed BM location to the stapes was calculated from the backward phase transfer function and is presented in Fig. 2 H. The delays in Fig. 2 H are negative both above and below the BF, indicating that the stapes vibrates earlier than the BM. As frequency increases, the delay value increases, reaches a maximum at ∼14 kHz and then decreases again. Even at the maximum, the delay value remains smaller than zero, indicating forward rather than backward propagation.

To illustrate the above finding graphically, the forward phase transfer function and the delay from the stapes to the measured BM location at 70- and 80-dB SPL stimulus levels were calculated from the same DP data as used in Fig. 2 and plotted in Fig. 5, F and G (dotted lines). As with the solid lines, the dotted lines show phase lags and positive delays, indicating that DPs propagate toward the apex.

To observe the effect of the f2/f1 ratio on backward propagation, the DP evoked with the f2/f1 ratio of 1.125 was also measured (Fig. 3). As in Fig. 2, the DPOAE (Fig. 3, A and B) and the DP vibration at the stapes (Fig. 3, C and D) shows broad-frequency responses and large phase lags. The magnitude response of the BM at the DP frequency (Fig. 3 E) also shows a peak near the BF. The response peaks in Fig. 3 E are sharper than those in Fig. 2 E, and the phase responses in Fig. 3 F show less level-dependent variation than those in Fig. 2 F. Despite these differences, the positive phase values in Fig. 3 G and negative delays in Fig. 3 H show that the DP arrived at the stapes earlier than at the observed BM location, at frequencies both above and below the BF.

To show repeatability of results, the backward phase transfer functions and delays from five other animals are presented in Fig. 4. These data are consistent with Figs. 2 and 3.

There are a number of data points near 10 kHz that show negative phase values in Fig. 4, A C, and E, and positive delays in Fig. 4, B, D, and F, which are consistent with the backward-traveling-wave theory. However, because these values are close to zero radians or zero μs and are not consistent across sound levels or animals, these data points are attributed to measurement variation.

Forward propagation of BM vibration

To compare the DP response to the conventional forward traveling wave, the BM response to the externally given f1 tone is presented in Fig. 5. The data were obtained by extracting the f1 component from the response to the two-tone stimulus. Fig. 5, A and B, presents the magnitude and phase of the BM vibration. At 40 dB SPL, the magnitude increases with frequency and reaches the maximum at ∼16.5 kHz, the BF. Above the BF, the magnitude decreases quickly. At frequencies near the BF, the magnitude increases less than the sound-level increase, revealed by the <10 dB separation between curves. In addition, the response peak broadens and shifts toward the low-frequency side with sound level increase. Phase data in Fig. 5 B show that the phase decreases with frequency. Because phase data result from the forward delay of the BM vibration and delays in the external ear, middle ear, and sound coupler (Fig. 1 A), the accumulated phase lag is >80 radians at 25 kHz.

Stapes responses to single tones at 70- and 80-dB SPL are presented in Fig. 5, C and D. Except for small oscillations, stapes vibration velocity shows a slight decrease with frequency (Fig. 5 C). The constant 10-dB separation between the two curves indicates a proportional growth with stimulus level. There is no obvious difference between the two phase curves (Fig. 5 D). These data indicate that the stapes response is linear.

The forward transfer function from the stapes to the measured BM location is presented in Fig. 5, E and F. The magnitude is presented by the ratio of the BM vibration velocity to that of the stapes vibration (Fig. 5 E). The magnitude increases with frequency and peaks at the BF of ∼16.5 kHz and then decreases above this frequency. At frequencies below ∼12 kHz, magnitude does not change with sound pressure, demonstrating a linear response over this frequency range. At frequencies near the BF, magnitude decreases as sound pressure increases, indicating nonlinear compressive growth. The sharp peak at the low sound level becomes broad and appears to shift toward the low-frequency side as the sound level increases. The phase transfer functions in Fig. 5 F (solid lines) show that the phase decreases progressively with frequency.

The forward delay from stapes to the observed BM location is shown by solid lines in Fig. 5 G. A positive delay indicates that waves propagate from base to apex, a negative value reflects a backward propagation, and the value of zero shows an infinite wave speed. Thus, positive delay values in Fig. 5 G demonstrate that BM vibration in response to the f1 tone is a forward wave. The figure also shows that the delay increases with frequency.

Discussion

In our previous experiments, we measured the longitudinal pattern of BM vibrations at different DP frequencies using a scanning laser interferometer (11) and quantified the DP group delays at the BM and at the stapes by varying f1 when f2 was constant (20). We also measured BM DPs at two longitudinal locations when the DP frequency was varied by changing f1 and f2 when the f2/f1 ratio was constant (22) or by changing f1 when f2 was fixed (21). These experiments showed no detectable DP backward traveling wave and demonstrated DP forward traveling waves. Two of our previous studies (11,20) showed that the stapes group delay is smaller than that of the BM, which was interpreted as evidence supporting the compression-wave theory. An assumption for this interpretation is that the initial DP phase at the DP generation place does not change with f1 when f2 is fixed. However, because the location and pattern of the BM response to a single tone is frequency-dependent, a change in f1 should result in changes in the overlapping pattern of the f1 and f2 traveling waves, and consequently a change in the initial DP phase. In addition, the relationship between the DP generation site and the recording location may also change with f1. These variables complicate the interpretations of group-delay data measured by varying f1. In the current experiment, the DP frequency was varied by changing f1 and f2 when the f2/f1 ratio was constant. A constant f2/f1 should result in a similar overlapping pattern of the f1 and f2 wave and keep the DP initial phase invariable. Despite the difference in the stimulus protocols, these results confirm our previous finding that the DP phase at the stapes leads that at the BM (11).

As the stimulus tones f1 and f2 propagate from the speakers to the stapes the speaker couplers, external ear, and middle ear introduce a delay. This delay is determined by the distance between the speakers and tympanic membrane and by the middle-ear forward delay. Similarly, the microphone-recorded emissions include the middle-ear backward delay and a delay introduced by the microphone coupler. The measured stapes DP (Fig. 2 D) and f1 (Fig. 5 D) phase-frequency curves do not exhibit a constant slope, although the middle-ear forward and backward group delays in gerbils should be constant at different frequencies (36,37). This noticeable phase deviation likely results from the standing waves in the external and middle ears and the sound system, which can cause significant errors for the delay measurement. To avoid these errors and simplify data interpretation, we quantified the backward phase transfer function by measuring phase difference from the BM to stapes. Similarly, the forward phase transfer function was measured using phase difference from the stapes to BM as a function of frequency. In a sensitive cochlea, however, the stapes vibration magnitude is >100 times smaller than the magnitude of the BM vibration at a peak-response frequency. To measure the stapes vibration reliably at relatively low sound levels, the sensitivity of the laser interferometer was improved by using a digital velocity decoder.

Great effort was made to measure the DP at low sound pressure levels. The minimal stimulus level of 40 dB SPL in this experiment is the lowest reported for BM DP or DP pressure measurements (11,13,16,17,22,33,38). Data in Figs. 2 E and 3 E show that at 40 dB SPL, the signal/noise ratio of BM DP is >20 dB at the peak-response frequencies. The low-level DP is important, because cochlear responses to low-level sound are more spatially specific than high-level responses (35). At high sound pressure levels, the region of maximal BM vibration shifts toward the base of the cochlea and a large section of the BM contributes to emission generation. This complicates the interpretation of DP measurements that were conducted at relatively high stimulus levels. Several studies have shown that emissions evoked by high-level stimuli arise through a different mechanism than the low-level ones (16,39–41). At high primary levels, the death of the animal as well as pharmacological manipulations that abolish the cochlear amplifier leads to quite small immediate changes in emission magnitude and phase, in contrast to the situation with primaries below 60 dB SPL.

It is a common consensus that DPs are generated within the region where the peaks of the two traveling waves overlap as a result of the cochlear nonlinearity (4,42–44). If f1 and f2 are both at a frequency lower than the BF of the site where BM vibrations are measured, the response peaks occur closer to the apex of the cochlea, as depicted schematically in Fig. 1 B. Therefore, if emissions resulting from such stimuli were to propagate out of the cochlea as a backward traveling wave, they would first appear at the measurement site at the BM and then at the stapes, producing a phase lead for the BM over the stapes. On the other hand, DPs also manifest as a pressure wave in the cochlear fluid near the DP generation place. This DP pressure propagates at the speed of sound in water and could reach the entire cochlea almost instantaneously (45). It causes the stapes to vibrate and results in a DPOAE in the ear canal. Like an external tone-induced cochlear fast wave, the DP compression wave would not cause the BM vibration instantaneously (45). Instead, it creates a DP pressure difference across the BM due to impedance difference between the oval and round window (10). This asymmetrical pressure initiates a forward traveling wave which can be detected by a sensitive laser interferometer. In this case, the stapes should vibrate earlier than the BM. The main finding of the current experiment is that the phase of the stapes vibration at the DP frequency leads the BM DP phase at frequencies not only above the BF, but also below this frequency (Fig. 2 G and Fig. 3 G). This indicates that the cochlea-generated DP arrives at the stapes earlier than at the observed BM location (Fig. 2 H and Fig. 3 H). This data supports the compression-wave theory and is inconsistent with the backward-traveling-wave mechanism.

However, the DP phase slope at low frequencies is not entirely consistent with that of a normal forward traveling wave. In contrast to an expected increase, the DP phase decreases with frequency and approaches zero at ∼10 kHz (Fig. 4, C, E, G, and I). This downward phase pattern is expressed as an upward trend in DP delay curves in Fig. 4, D, F, H, and J. The relationship between the DP generation place and the recording site may contribute to the unconventional phase-frequency pattern. When the generation region is far from the recording location, the recorded DP is a propagated DP component, and, when the two places are near each other, the recorded DP is dominated by a locally generated DP component. The propagated DP has a forward delay while the local DP shows no significant delay. As the DP frequency increases, the DP generation region moves toward the recording site and the recorded propagated component decreases while the local component increases, which results in a DP phase decrease with frequency. When the recording site is inside the generation region, the recorded DP is dominated by the local DP and the delay is close to zero. As f1 and f2 continuously increase, the DP generation area moves away from the recording site toward the base, and the recorded DP becomes more similar to a forward traveling wave showing a normal forward delay. Because the DP phase pattern below ∼10 kHz varies across animals, other mechanisms may have contributed to the low-frequency DP phase data. Despite the phase discrepancy at the low frequencies, the positive phase values in Fig. 4, C, E, G, and I, indicate that DPs arrive at the stapes earlier than at the BM.

The propagation of OAEs can also be studied by measuring the pressure in the cochlear fluids. Avan et al. (17) measured DP pressures in scala vestibuli and scala tympani far from the BM in the first and second turn of the guinea pig cochlea. Their data suggest that local filtering processes rather than propagation delays account for the overall emission delay. Dong and Olson (33) measured intracochlear DPs simultaneously with emissions in gerbils. They found in most cases that the phase of the emissions is similar to the ordinary forward-traveling-wave phase, but argue that the reverse traveling wave plays the more dominant role in DP reverse transmission. Although they found the DP pressure decreased when the tip of the pressure sensor was moved away from the BM (33) and this spatial variation indicates the existence of the DP traveling wave, because the DP pressure falls into the noise (∼50 dB) with distance from the BM, it cannot exclude a contribution by a compression wave to the emission (33). In addition, we suggest some of their data (33) are consistent with the compression-wave theory (in particular, the positive phase differences found in their Figs. 7–10, E and J). Further, because the pressure measurement at a single longitudinal location (33) provides limited information on the propagation direction of waves, we suggest that the spatial dropoff in DP pressure may also be interpreted as a result of a DP forward traveling wave, which has been shown by measuring BM vibration at DP frequencies (11,22).

Emissions cannot escape from the cochlea in the absence of fast pressure waves. Even if emissions generated near the cochlear apex were propagated to the base through a reverse traveling wave, these emissions would need to be transferred to the oval window to propagate through the middle ear and into the ear canal. As direct physical contact between the organ of the cochlear partition and the oval window is lacking, this transfer of energy can only occur through the fluid.

In summary, the DPOAE was evoked by f1 and f2 tones at sound pressure levels as low as 40 dB SPL. The DP at frequency 2f1-f2 was measured from the BM, stapes, and external ear canal. Data demonstrate that the stapes vibration at the emission frequency occurs earlier than the BM vibration. This result indicates a DP forward traveling wave, which conflicts with the backward-traveling-wave theory. However, current results are consistent with the compression-wave theory, in which the emission reaches the stapes dominantly through the cochlear fluids as compression wave, and consequently results in a secondary forward wave.