Micro- and Nanomechanical Analysis of Articular Cartilage by Indentation-Type Atomic Force Microscopy: Validation with a Gel-Microfiber Composite

Abstract

As documented previously, articular cartilage exhibits a scale-dependent dynamic stiffness when probed by indentation-type atomic force microscopy (IT-AFM). In this study, a micrometer-size spherical tip revealed an unimodal stiffness distribution (which we refer to as microstiffness), whereas probing articular cartilage with a nanometer-size pyramidal tip resulted in a bimodal nanostiffness distribution. We concluded that indentation of the cartilage's soft proteoglycan (PG) gel gave rise to the lower nanostiffness peak, whereas deformation of its collagen fibrils yielded the higher nanostiffness peak. To test our hypothesis, we produced a gel-microfiber composite consisting of a chondroitin sulfate-containing agarose gel and a fibrillar poly(ethylene glycol)-terephthalate/poly(butylene)-terephthalate block copolymer. In striking analogy to articular cartilage, the microstiffness distribution of the synthetic composite was unimodal, whereas its nanostiffness exhibited a bimodal distribution. Also, similar to the case with cartilage, addition of the negatively charged chondroitin sulfate rendered the gel-microfiber composite's water content responsive to salt. When the ionic strength of the surrounding buffer solution increased from 0.15 to 2 M NaCl, the cartilage's microstiffness increased by 21%, whereas that of the synthetic biomaterial went up by 31%. When the nanostiffness was measured after the ionic strength was raised by the same amount, the cartilage's lower peak increased by 28%, whereas that of the synthetic biomaterial went up by 34%. Of interest, the higher peak values remained unchanged for both materials. Taken together, these results demonstrate that the nanoscale lower peak is a measure of the soft PG gel, and the nanoscale higher peak measures collagen fibril stiffness. In contrast, the micrometer-scale measurements fail to resolve separate stiffness values for the PG and collagen fibril moieties. Therefore, we propose to use nanostiffness as a new biomarker to analyze structure-function relationships in normal, diseased, and engineered cartilage.

Introduction

Imaging methods for analyzing articular cartilage structure

Visual inspection and histology (1–3) and optical microscopy (4,5) allow for direct in vitro observation of fresh cartilage under near-physiological conditions but are limited to a spatial resolution of ∼200 nm. In contrast, electron microscopy (6–8) reveals ultrastructural details at molecular resolution but requires chemical fixation and dehydration of the cartilage, followed by metal staining or sputtering, so that the specimen is no longer in its native state. Other disadvantages of electron microscopy are the complexity and prolonged time requirements of the sample preparation procedures. Moreover, neither light nor electron microscopy can directly measure the cartilage's mechanical properties. In contrast, atomic force microscopy (AFM) allows for simultaneous imaging and stiffness measurements on a micrometer–nanometer scale in native samples, and thus can help elucidate the structure and mechanical properties of articular cartilage.

Overview of articular cartilage structure-mechanical property relationships

Aggrecan is the most abundant proteoglycan (PG) in articular cartilage and exhibits a bottle-brush structure. The function of aggrecan is strongly determined by the electrostatic repulsion of its glycosaminoglycan side chains, which carry highly negatively charged carboxyl and sulfate groups that repel each other (9). In physiological solution, the negative charges are balanced by an influx of positive ions (Na⁺ and Ca²⁺). This influx of ions results in an osmotic balance between the PGs and the surrounding synovial fluid, which in turn leads to the creation of a PG gel that causes cartilage to swell in physiological saline solutions. As a result of this swelling and the low water permeability of cartilage (10⁻¹⁵–10⁻¹⁶ m⁴/Ns), under applied loads the resulting osmosis-based cartilage structure is poroviscoelastic, which enables the tissue to store and dissipate energy upon mechanical deformation (10–13).

Collagen fibrils are the other principal matrix component in articular cartilage. As a result of extensive covalent cross-linking, they form a very strong three-dimensional (3D) collagen meshwork (14,15). Thus, articular cartilage is a composite biomaterial consisting of two interpenetrating 3D components (i.e., a PG gel and a cross-linked collagen meshwork) that can resist compressive, tensile, and shear forces. Each individual component of this tissue exhibits distinct physical and chemical properties. Hence, changes in the relative amounts of collagen, PGs, and water can affect the mechanical properties of cartilage, as frequently described in studies of cartilage pathology (11,12,16).

Overview of direct mechanical determination of articular cartilage stiffness

When tested at the micrometer–centimeter scale, articular cartilage behaves as a nonstructured and uniform material. This widely used first approximation allows measurement of the overall cartilage stiffness. Also, since cartilage is poroviscoelastic, any overall stiffness measurement produces an aggregate modulus, E^∗, which is the result of both elastic and viscous contributions to stiffness (see Fig. 4). Depending on the experimental loading conditions, the loading geometry employed by the articular cartilage exhibits a wide range of values of E^∗, from ∼1 MPa when loaded at a low frequency of <0.1 Hz (12,17) to ∼60 MPa at dynamic cyclic loads (40 Hz) (18). At low loading frequencies, the mobile water moves through the pores in the PG gel in response to the load, resulting in a lowering of the cartilage's stiffness. In contrast, at high loading frequencies, the cartilage's low permeability prevents the incompressible water from being displaced, resulting in the cartilage exhibiting a higher stiffness.

Figure 4.

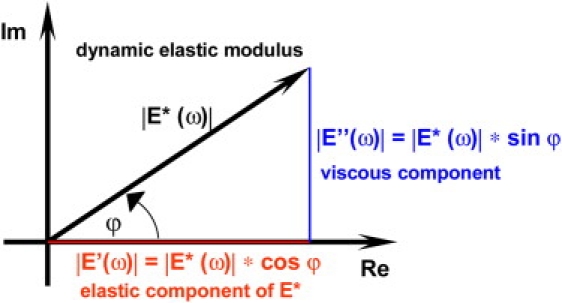
Illustration of stiffness parameter relationships for a viscoelastic material subjected to a cyclic dynamic force or deformation. At low frequencies, the magnitudes of force and deformation are out of phase, i.e., they do not reach maximum values simultaneously. This is expressed as the phase angle, ϕ, between their maximum values. As frequency is increased, ϕ decreases. In the limit ϕ = 0 and E^∗ = E′, i.e., the material behaves as an elastic solid. The out-of-phase behavior is due to the inability of the viscous portions of the material structure to store energy. Thus ϕ is a measure of energy loss and is also called the loss angle or loss tangent.

Articular cartilage millimeter-scale stiffness measurements

The most direct method for measuring cartilage stiffness is compression testing; however, this approach requires specimens with highly parallel top and bottom surfaces, which can only be achieved by cutting the cartilage off the bone and trimming the specimens. In compression tests, one must also decide which constraints best simulate the situation in vivo (e.g., lateral confinement) and whether the support plate and lateral confinement should be porous to allow movement of water out of the cartilage at low deformation rates. Since indentation testing avoids the need for cutting, numerous indentation testing devices have been employed to measure the quality or health/disease state of articular cartilage (19–21). These devices employ indenters, typically with a 1–2 mm tip diameter, to quantify the resistance to indentation (stiffness) in a manner similar to that used by the surgeon with a simple hand-held probe. Unfortunately, several investigators have reported that millimeter-scale indenter stiffness measurements are not sensitive to even substantial changes in cartilage structure associated with aging or early-stage osteoarthritis (20,22).

Choosing articular cartilage dynamic loading conditions

Stiffness tests of cartilage are often performed under displacement control. For example, a series of submillimeter-scale step compression or indentation displacements are applied (23). In such experiments, each displacement is maintained until the resultant force decays to an equilibrium value. An equilibrium modulus is then determined from the slope of the resultant set of force/displacement values. The force decay is a viscous stress relaxation in response to the imposed 3D structural change, where the relaxation results from slow movement of water through and out of the cartilage. These measurements can take hours to accomplish. The equilibrium modulus is thus related to the cartilage's permeability. In contrast, during gait, the articular cartilage needs to respond to a much faster cyclic loading through deformation. Even though the loads applied to cartilage are not technically controlled by the use of feedback steering to maintain a constant load function, the mechanical behavior of cartilage is best mimicked by load-controlled cyclic deformation. Under such conditions, the low permeability of cartilage significantly restricts the water's mobility through the tissue. Of most importance for diagnostic applications in a clinical environment, the measurements need to be fast. Therefore, we performed indentation testing at a rate of three indentations per second, corresponding to loading rates similar to gait (24,25).

In the context of exploring novel treatment modalities for osteoarthritis, we recently made the significant observation that all morphological and biomechanical changes that occur at the onset of this disease can solely be depicted on the nanometer scale (25). In particular, when we employed micrometer-size spherical tips for indentation-type (IT)-AFM, the microstiffness values of articular cartilage exhibited a Gaussian distribution with a peak at E^∗_micro = 1.3 ± 0.4 MPa (25), in good agreement with previously reported values of macroscopic compressive stiffness measurements obtained at similar loading frequencies (12). In contrast, when we mapped a cartilage surface by employing nanometer-size IT-AFM tips, the measured stiffness exhibited a bimodal distribution, with one peak exhibiting higher stiffness and one peak exhibiting lower stiffness. We assumed that the lower stiffness peak with values of E^∗_PG ∼20 kPa reflected the stiffness of the PG gel, whereas the higher stiffness peak with values of E^∗_Col ∼400 kPa reflected the stiffness of the collagen fibrils (24,25). In the study presented here, we modeled the composite nature of cartilage by creating a simple poly(ethylene glycol)-terephthalate (PEGT)/poly(butylene)-terephthalate (PBT)-fibril/agarose/chondroitin sulfate model with a cartilage-like structure, and compared the bimodality of its nanometer-scale stiffness with that of articular cartilage.

Materials and Methods

Cartilage sample preparation and IT-AFM measurements

Cartilage specimens were prepared as described previously (24). Briefly, porcine articular cartilage from freshly slaughtered pigs (within 1–2 h postmortem) was harvested from the femoral heads by cutting samples off the underlying bone with a sharp razor blade, yielding ∼5 mm × 5 mm pieces that were ∼2 mm thick. The specimens were stored in phosphate-buffered saline (PBS; 2.6 mM NaH₂PO₄, 3 mM Na₂HPO₄, 155 mM NaCl, 0.01% NaN₃ w/v, pH 7.2) supplemented with a protease inhibitor cocktail (Complete, Boehringer Mannheim, Mannheim, Germany). The samples were covered with the buffer solution and stored on ice. After the articular cartilage topography was imaged by contact-mode AFM at a scanning rate of ∼0.7 Hz, stiffness measurements were obtained by IT-AFM in the same buffer solution. Samples from three different pigs and from three different locations each were analyzed.

Osmotic loading of cartilage

The isotonic PBS solution contained 2.6 mM NaH₂PO₄, 3 mM Na₂HPO₄, 155 mM NaCl, 0.01% NaN₃ w/v, pH 7.2. The hypertonic PBS contained 2.6 mM NaH₂PO₄, 3 mM Na₂HPO₄, 2 M NaCl, 0.01% NaN₃ w/v, pH 7.2. Three cartilage samples each were tested separately.

Preparation of agarose and agarose/chondroitin sulfate gels

For exploratory calibration testing, agarose gels were prepared with 0.5%, 1.0%, 2.25%, and 3.5% (w/w) agarose (AGAR Noble; DIFCO Laboratories, Detroit, MI) in water. For the model material used here, 50 mg of agarose were stirred in 10 mL of PBS, heated up until the solution started to boil, and then cooled down to ∼50°C. Next, 200 mg chondroitin sulfate (chondroitin sulfate A from bovine trachea, C9819-5G; Sigma) was added and properly mixed, resulting in a concentration of 20 mg/mL of chondroitin sulfate in the gel. The melted agarose/chondroitin sulfate solution was used to prepare the specimens described below and to perform the swelling tests. Three gel samples were then tested in isotonic and hypertonic PBS.

PEGT/PBT-fibril/agarose/chondroitin sulfate gel model material

PolyActive (PEGT/PBT block copolymer; CellCoTech, Bilthoven, The Netherlands) fibrils were produced by means of the electro-spinning (ESP) technique (26,27). Briefly, the PEGT/PBT copolymer (1000 MW PEGT, 70% PEGT, 30% PBT) was dissolved in a mixture of 10 mL dichloromethane and 10 μL distilled water, and stirred at room temperature for 24 h. The ESP device consisted of a syringe pump (Harvard Apparatus, South Natick, MA), a high-voltage generator (0–30 kV; Brandenburg Ltd., South Croydon, Surrey, England) connected to a syringe (10 mL, 1.6 mm steel needle; Becton Dickinson, Franklin Lakes, NJ) containing the polymer solution, and a stainless-steel plate. An electrical field was applied between the needle (positive pole) and the stainless-steel plate (negative pole). A polymer jet from the spinneret (needle) was then collected as a nonwoven mesh of fibers onto glass microscopy slides (76 × 26 mm; Menzel, Braunschweig, Germany) placed on the stainless-steel plate. ESP resulted in the production of PEGT/PBT fibers of 2.9 ± 0.19 μm thickness, as measured based on scanning electron microscopy images.

A plastic ring (∼3 mm inner diameter, ∼0.2 mm thick, ∼1 mm high) was used to mix the PEGT/PBT-fibrils with the agarose/chondroitin sulfate gel for testing by AFM. This ring was placed onto a PEGT/PBT-fiber-coated glass slide. The fibril coating around the ring was removed with a scalpel. Then, a droplet of ∼50 μL of melted 1.0% (w/w) agarose gel was placed into the ring on top of the fibril mesh. For the swelling tests in this work, a droplet of the melted agarose/chondroitin sulfate was used instead. After solidification was achieved, the slide was kept in a cold room (4°C) for ∼15 min. The specimen was then removed from the glass slide by moving the ring laterally until it and the specimen were free of the slide. The specimen surrounded by the ring was then glued upside down onto a 10-mm-diameter Teflon disk with a 5-min curing epoxy (Devcon epoxy; ITW Brands, Wood Dale, IL). The upside-down orientation of the specimen ensured that the surface to be evaluated by AFM was populated with fibrils. To prevent drying, the specimen was covered with a droplet of PBS. Three samples were inspected per experimental condition.

AFM and indenter tips

AFM experiments were carried out with a MultiMode AFM and NanoScope IIIa controller (Veeco Metrology, Santa Barbara, CA). AFM tips of different diameters were selected and prepared as follows: For micrometer-scale measurements, hard borosilicate glass spheres (9000 series glass particle size standards 2–2000 μm; Thermo Fisher Scientific, Fremont, CA), diameter d = 10 μm, were glued onto tipless rectangular cantilevers (type NSC12; NT-MDT, Moscow, Russia) with nominal spring constants k in the following ranges: 6.5 N/m ≤ k ≤ 27.5 N/m for probing cartilage, and 0.2 N/m ≤ k ≤ 0.7 N/m for probing the model material (Fig. 1 A). For nanometer-scale experiments, pyramidal tips with a nominal tip radius ≤ 20 nm on V-shaped cantilevers with a nominal spring constant of 0.06 N/m (type NPS; Veeco) were employed (Fig. 1 B). The spring constant was measured for each cantilever by means of the thermal noise method (28). The actual diameter of each micrometer-size tip was determined with the use of scanning electron microscopy images.

Figure 1.

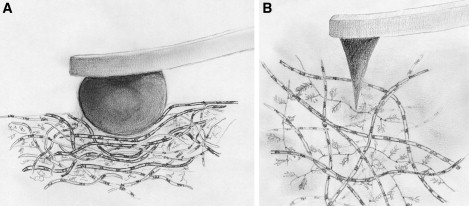
Cartoon showing the interaction of a micrometer-size spherical tip (A) and a nanometer-size pyramidal (B) AFM cantilever tip with cartilage.

Stiffness measurements obtained by IT-AFM

Measurements of micro- and nanostiffness (dynamic aggregate modulus, E^∗) were obtained by IT-AFM as described previously (24). Briefly, maps of load-displacement curves were recorded in a regular grid over the sample surface by employing the force-volume mode. An individual set of data consisted of 4096 load-displacement curves obtained at a rate of three full loading cycles per second in a 64 × 64 curve grid covering sample areas of ∼15 μm × 15 μm. Each force curve consisted of 512 data points. For microscale measurements, a maximum deflection of 150 nm was chosen, which corresponded to a maximum applied load of ∼2.0 μN for the cartilage measurements (with k = 13.5 N/m) and a maximum applied load of ∼105 nN for the model material (with k = 0.7 N/m; d = 7.7 μm). For nanoscale measurements, a maximum deflection value of 30 nm was set, resulting in a maximum applied load of ∼1.8 nN (with k = 0.06 N/m) to probe both authentic articular cartilage and the model material.

Stiffness data acquisition and calculations

Stiffness values for cartilage and the model material were obtained from IT-AFM unloading curves. The use of data from unloading (rather than loading) curves ensures that the displacement data do not contain any irreversible (e.g., plastic) deformation or other extraneous displacement effects. The fundamental IT-AFM stiffness values obtained were force-displacement slopes. A slope was defined as the mean ratio of cantilever deflection (an expression of force) to piezoelectric displacement in the initial unloading part of the load-displacement curve, as described in our previous work (24). We set the maximum value for nanostiffness to one (corresponding to a slope of one) and displayed all other values at the nanoscale relative to one. The value for microstiffness obtained on articular cartilage (0.15 M NaCl) was set to 0.5. The bin width was set by dividing the maximum value = 1 × 50 (bars), yielding a dimensionless bin width of 0.02. Slope values alone are sufficient to determine and compare micro- and nanostiffness distributions of IT-AFM measurements. The slopes from a given square grid of IT-AFM measurements were then used to create a slope histogram. The subsequent calculation of microstiffness aggregate modulus (E^∗) values from the slope data was performed as previously described (24) (see also Appendix I). To calculate the nanostiffness aggregate modulus (E^∗ values), the functional relationship y(x) = (21/(1 − x)) − 21 was derived from a calibration curve using agarose gels (24) (see also Appendix I).

Results

Articular cartilage exhibits a scale-dependent mechanical behavior: micro- versus nanostiffness

As documented in Fig. 2 A, when articular cartilage is imaged with a ∼10-μm-diameter spherical tip (see Fig. 1 A), the sample surface appears relatively uniform and flat. However, to demonstrate that recording the image and the force map of the same specimen area is meaningful, we show a location that exhibits some coarse surface irregularities. Although such a micrometer-size AFM tip cannot resolve the cartilage's fine structural elements, such as individual collagen fibrils, the force map displayed in Fig. 2 B, which is derived from 64 × 64 (i.e., 4096) IT-AFM curves, clearly correlates with the surface irregularities observed in the AFM height image shown in Fig. 2 A. Fig. 2 C reveals that the unloading slope histogram for the 4096 force curves in Fig. 2 B exhibits a narrow Gaussian distribution centered about a slope of 0.53. Fig. 2 D displays an averaged curve, giving a calculated microstiffness of E_micro = 1.3 ± 0.4 MPa.

Figure 2.

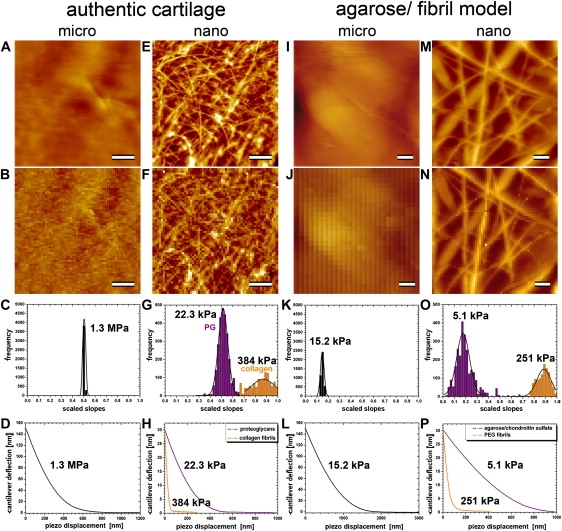
Images and IT-AFM measurements of stiffness of articular cartilage and a PEGT/PBT-fibril/agarose/chondroitin sulfate gel composite at the micro- and nanometer scales. Images and force maps on cartilage are scaled to a height of 400 nm, whereas images and force maps on the model material are scaled to a height of 2000 nm. All scale bars correspond to 2 μm. (A–D, first column) Micrometer-scale information for cartilage. (A and B) The corresponding nanometer scale data. (C) Distribution of raw stiffness values (scaled slopes) obtained from the IT-AFM force/displacement curves. (D) Distribution of force curves and the value of E^∗. (E–H, second column) Analogous information obtained at the nanometer scale. The third and fourth columns show analogous images and data for the model material.

Fig. 2 E shows the AFM height image of the same articular cartilage surface, but now recorded by a sharp, nanometer-size tip (see Fig. 1 B). At this resolution, individual collagen fibrils appear as bright filamentous structures that are separated by nonstructured darker areas. The corresponding force map in Fig. 2 F, which represents a 12 μm × 12 μm specimen area, also shows the locations of the individual collagen fibrils on the articular cartilage surface. Therefore, any two adjacent points in this 64 × 64 pixel force map are spaced 187.5 nm apart. As documented in Fig. 2 G, calculation of the slope for each pixel in this force map yielded a histogram with a bimodal distribution, with the two Gaussian fits being centered about slopes of 0.51 and 0.87, respectively. Accordingly, Fig. 2 H reveals the two averaged force-displacement curves computed from the 2% of curves centered about the peaks of the two Gaussian fits (corresponding to an average of a few hundred curves, depending on the width of the Gaussian fit). From these, nanostiffnesses of 22.3 ± 1.5 kPa and 384 ± 50 kPa, respectively, were calculated and found to be ∼100× and ∼6× less than the corresponding microstiffness of 1.3 MPa that was determined with a micrometer-size tip (see Fig. 2, C and D).

Comparison of authentic articular cartilage with a model gel-microfiber composite

Next, we wanted to test our hypothesis that the bimodal distribution shown in Fig. 2 G is caused by an interaction of the sharp, nanometer-size tip with the two different structural components comprising the cartilage (i.e., the collagen fibrils and the PG moiety). For this purpose, we prepared a PEGT/PBT-fibril/agarose/chondroitin sulfate gel composite material to mimic articular cartilage's relatively stiff collagen meshwork and the softer PG gel moiety. Probing the resulting model material by IT-AFM at the micro- and nanometer scale clearly confirmed that its composite structure consisted of stiff fibrils and a soft matrix similar to that of cartilage.

Accordingly, Fig. 2 I displays an AFM image of the model material recorded by a micrometer-size spherical tip (see Fig. 1 A). Next, from the same specimen area and using the same spherical tip, 64 × 64 force-displacement curves were recorded. The resulting force map is shown in Fig. 2 J, and Fig. 2 K reveals the distribution of microstiffness slope values for the 4096 points from the force map in Fig. 2 J. Fig. 2 L displays the averaged force-displacement curve computed from the 2% of curves centered about the peak of the Gaussian fit (see Fig. 2 K), from which a microstiffness of 15.2 ± 0.5 kPa was calculated. Compared to cartilage (see Fig. 2 C), the Gaussian distribution is slightly wider and centered about a much lower slope value (0.15 vs. 0.54 for cartilage). The corresponding E^∗ value calculated from the slope data (15.2 ± 0.5 kPa) shows that the microstiffness of the model material amounted to only 0.66% of the stiffness of cartilage (i.e., 1.3 MPa; see Fig. 2 D).

In contrast to Fig. 2 I, which was recorded by a micrometer-size spherical tip, Fig. 2 M displays an AFM height image of the model material registered by a sharp, nanometer-size pyramidal tip (see Fig. 1 B). At this scale, the PEGT/PBT fibrils can clearly be resolved in both the AFM height image (Fig. 2 M) and the corresponding force map recorded by IT-AFM of the same specimen area (Fig. 2 N). Analogously to the case with cartilage (see Fig. 2 G), the slope histogram shown in Fig. 2 O exhibits a bimodal distribution, with the two Gaussian fits being centered about slopes of 0.18 and 0.89, respectively. Accordingly, Fig. 2 P reveals the two averaged force-displacement curves computed from the 2% of curves centered about the peaks of the two Gaussian fits. From these, the nanostiffnesses of 5.1 ± 1.2 kPa and 251 ± 40 kPa, respectively, were calculated and found to be ∼3× smaller and ∼6× larger, respectively, than the corresponding microstiffness of 15.2 ± 0.5 kPa that was determined with a micrometer-size tip (see Fig. 2, K and L). Hence, in contrast to its microstiffness, the model material's nanostiffness is within the same order of magnitude as that of articular cartilage for both its hard (i.e., the PEGT/PBT-fibrils) and soft (i.e., the agarose/chondroitin sulfate gel) phases.

Effects of ionic-strength changes on the micro- and nanostiffness of authentic articular cartilage and a model gel-microfiber composite—a comparison

To ascertain the effect of osmotically induced changes in water content and the resultant water pressure within cartilage and the model material, we probed the micro- and nanostiffness of both articular cartilage and the model material in isotonic PBS buffer and hypertonic PBS. We performed measurements by exchanging the buffer in the fluid cell of the AFM without moving the positions of the tip and sample. We expected that, as a result of osmotic effects, an increase in salt concentration would decrease water content and increase the nanostiffness of the gel phase. Also, we wanted to determine how much a decrease in water content in the gel phase would affect the overall microstiffness. As shown in Fig. 3 A, the change to hypertonic PBS increased the slope of the cartilage microstiffness by 21% but did not affect its unimodal frequency distribution. Fig. 3 B shows the corresponding effects of the change from isotonic to hypertonic PBS on cartilage nanostiffness. The bimodal distribution of nanostiffness was maintained. However, the slope of the lower peak increased by 28%, whereas the increase in slope of the higher peak was insignificant.

Figure 3.

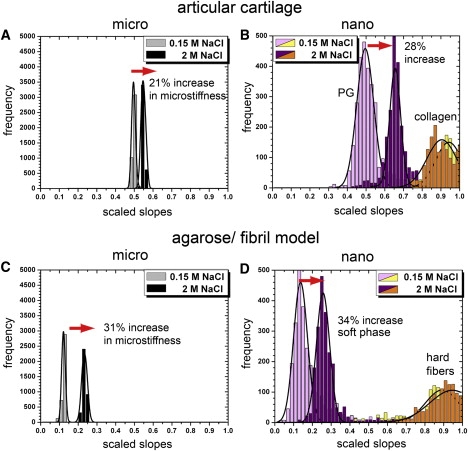
Stiffness distributions of cartilage and the model material at the micro- and nanometer scales and at two different ionic strengths of the PBS bathing solution. Stiffness is expressed as the scaled slopes of the IT-AFM unloading curves (see text).

Fig. 3, C and D, reveal the analogous results for the model material. As in cartilage, the microstiffness (Fig. 3 C) of the model material was also unimodal under both ionic strengths, but hypertonicity increased the stiffness slope by 31%. Again, as in cartilage, the nanostiffness (Fig. 3 D) was bimodal. Hypertonicity increased the stiffness (slope) of the lower peak by 34%, whereas the increase in slope of the higher peak was again negligible. In contrast, an agarose model material lacking the chondroitin sulfate moiety did not change the stiffness at either scale when exposed to hypertonic PBS (data not shown).

Discussion

Micro- versus nanometer-scale dynamic stiffness measurements

Fig. 1 shows what the indenter “sees” during imaging and what it “feels” in indentation testing when the articular cartilage surface is probed at the (A) micrometer or (B) nanometer scale. In particular, the micrometer-size tips assess the overall tissue resistance to deformation, where multiple structural elements of the tissue are deformed in concert. In contrast, a nanometer-sized tip can assess the stiffness of cartilage at the level of the fibrils alone and the gel alone. Stiffness changes potentially reveal structural changes, especially in the gel phase. This information is relevant because of the important role played by PGs (in particular the charged glycosaminoglycan chains) in normal cartilage function and the structural changes that occur in aging and osteoarthritis (12,16,25,29,30).

Source of unimodal microstiffness distributions in articular cartilage

For both cartilage and the model material, indentation stiffness at the micrometer scale, as shown in Fig. 2, A–D, and I–L, reveals a uniform appearance in both images and force maps, and a homogeneous (unimodal) distribution of stiffness values. This homogeneity can be explained by the large size of the IT-AFM tip relative to the molecular-scale structures within the cartilage, i.e., the size of a 10-μm-diameter tip is three orders of magnitude larger than the nanometer-scale PG structures and two orders of magnitude larger than the collagen fibril meshwork of typically d = 50–150 nm in articular cartilage.

Source of bimodal nanostiffness distributions in articular cartilage

We hypothesized that the interaction between the nanoindenter and the PG gel in articular cartilage would produce a lower stiffness peak, and the interaction with the resilient collagen fibrils would produce a higher stiffness peak, as shown in Fig. 2 G. The results obtained at the nanometer-scale with the model material also showed a bimodal distribution of stiffness, as was observed in cartilage. In addition, exposing the model material to hypertonic saline instead of isotonic saline, as shown in Fig. 3, shifted the lower stiffness peaks upward while the upper stiffness peak remained unchanged. Since in both cartilage and the model material only the porous gel structure with a high density of negatively charged surface is influenced by changes in ionic strength, these results strongly support our hypothesis that the lower peak represents the stiffness of the PG gel, whereas the upper peak is a measure of the stiffness of the collagen fibrils.

Relative stiffness of cartilage and the model material

The structural and physicochemical differences between cartilage and our model system explain the differences in stiffness at both the micro- and nanometer scales.

• 1)The collagen fibrils of cartilage form a 3D collagen meshwork with extensive cross-linking by covalent bonds, which provides superior resistance to deformation but also greatly inhibits the movement of the soft PG moiety during loading. Because of its low permeability, the cartilage initially tends to deform rather than decrease in volume, and consequently places the collagen meshwork under tension, resulting in a high initial overall stiffness.
• 2)In contrast, in the model material, the PEGT/PBT fibrils are neither cross-linked nor spatially stabilized by any strong interactions, and therefore do not offer the same resistance to gel-induced deformation.

Accuracy of calculated values of E^∗ for collagen and PEGT/PBT fibrils

A spring constant of k = 0.06 N/m is optimal for probing the gel phase, but it does not allow one to quantitatively measure the stiffness of the collagen fibrils with the same accuracy. To compute values of nanostiffness from the slopes, we employed the calibration curve established by Stolz et al. (24): y(x) = (21/(1 − x)) − 21. However, this calibration curve exhibits an asymptotic behavior that results in large errors for slopes close to one. Since it is difficult to reliably measure the nanostiffness of hard fibrils using a k = 0.06 N/m cantilever, we present the results with large standard deviations (see Appendix II).

Effects of ionic strength on cartilage stiffness

Our measured increase of microstiffness by osmotic loading is in general agreement with previous observations (10,11,13,16,31–35). However, we measured a change of microstiffness of only ∼21% in hypertonic PBS compared to published values of ∼50% in hypertonic PBS and a 1 M NaCl bathing solution (13,31,35). This apparent discrepancy may be explained by major differences between the experimental setups: Eisenberg and Grodzinsky (13) performed confined compression tests by employing a porous indenter (diameter d = 6.4 mm) that was capable of taking up and retaining significant amounts of water, whereas we performed indentation tests using a much smaller (d = 10 μm) spherical indenter. Furthermore, those authors applied much larger forces to the cartilage, which resulted in substantial indentation depths. Also, they trimmed off the surface and thus probed deeper zones, whereas we tested the intact surface by applying indentation depths on the order of only ∼1 μm. Therefore, we tested the superficial zone, where PGs are less dense than in the deeper zones (35,36). Moreover, protocols for compression testing of cartilage typically employ much lower loading rates or use a series of short discrete compressive strains to measure the equilibrium stiffness. We measured the dynamic aggregate modulus E^∗ at a rate of three indentations per second. Cartilage stiffness is strongly affected by the deformation rate, and therefore the higher stiffness measured in this study may be at least partly the result of the higher rates employed.

Relation of IT-AFM cartilage nanostiffness values to reported values for isolated cartilage structures

In previous studies, single collagen fibrils exhibited stiffness in tension and indentation of a few gigapascals (37,38). However, it is difficult to directly compare those results with the IT-AFM-measured nanostiffness of collagen in native cartilage. The IT-AFM values reported here are much lower (e.g., 384 kPa). They are in effect a measure of the dynamic bending stiffness of a collagen fibril that is part of a cross-linked meshwork and embedded in the PG moiety. In contrast, the mechanical behavior of isolated aggrecan gels at physiologically relevant concentrations of 20–80 mg/mL (31,34) exhibited stiffness of only ∼1 kPa (39,40). However, measurements of the isolated components do not take into account their behavior within the tissue. In particular, PGs in articular cartilage are cross-linked. Therefore, our higher values of E_Pg = 22.3 ± 1.5 kPa for the cartilage gel phase measured in situ reflect the intact cross-links in PG. These results are even more plausible when we consider the contribution made by the dynamically cross-linked meshwork of collagen fibrils to the PG nanostiffness.

Value of nanometer-scale dynamic stiffness measurements

Nanomechanical structures govern the functional behavior and success or failure of engineered cartilage. Our composite model provides a material that can be tuned by adjusting the total PEGT/PBT content, fibril length, fibril diameter distribution, and fibril orientation, and by creating an interfibrillar meshwork by introducing covalent cross-links. In addition, the density and other parameters of the agarose/chondroitin sulfate moiety can be modified by varying the charged groups or the concentration of agarose, or including a low concentration of polyacrylamide. Such a tunable artificial tissue could be valuable for interpreting and even predicting structure-mechanical property relationships on different length scales, and the resultant data could be used to further improve engineered cartilage.

Conclusions

A primary challenge in evidence-based medicine is the need for early detection of various diseases, such as osteoarthritis (25), artherosclerosis (41), and cancer (42), ideally at the presymptomatic stage. AFM-based indentation testing has yielded some encouraging results in terms of detecting systematic changes in the nanostiffness of articular cartilage during the progression of osteoarthritis (43). Monitoring scale-dependent changes in tissue plasticity during disease progression or in response to different treatment modalities may lead to the development of novel diagnostic tools (44) and therapeutic interventions. Nevertheless, there still remain a number of technical difficulties involving data collection and analysis that must be overcome before AFM-based indentation testing can be moved from the bench to the patient (42). In this study, we have attempted to explain the observed scale-dependent stiffness of articular cartilage when measured by IT-AFM, and to rationalize this finding in terms of cartilage biology and pathology (25). It is hoped that the insights gained will be more generally applicable to scale-dependent analyses, and enhance our understanding of tissue mechanics.

Appendix I: Deformation Rate-Dependent Mechanical Response of Articular Cartilage

The functional stiffness of articular cartilage is |E^∗|, the dynamic elastic modulus, as explained in Fig. 4. |E^∗| is a function of the rate of deformation and can be determined from cyclic load/displacement data. The rate employed should reflect the transient loading-unloading time of normal ambulation (i.e., walking or running). In humans, this is in the range of a few hundred milliseconds (45). Therefore, we performed indentation measurements at a rate of three complete loading/unloading cycles per second, corresponding to a tip unloading time of ∼150 ms. Even after hundreds of loading/unloading cycles, we did not observe any progressive change in the load/displacement behavior, persistent residual indentations (which would be indicative of yield and plastic flow), or effects indicative of material fatigue.

Appendix II: Calculation of Stiffness Values from Indentation Curves

Indentation tests were originally developed in the field of materials science (46) and more recently have been applied to study soft biological tissues at different scales of architectural organization (24,25). Mechanical properties, such as the dynamic elastic modulus, E^∗ (or stiffness, to use the more general term), can be obtained from unloading load-displacement curves as shown in Fig. 5 A. E^∗ (= E) was calculated from the following equation:

$$E=\frac{\sqrt{\pi }}{2}\left(1-{\nu }^2\right)\frac{S}{\sqrt{A}}$$

ν = Poisson's ratio, and S [N/m] = contact stiffness (the slope of the initial part of the unloading regime of the load-indentation curve);

$$S=\frac{dP}{dh}$$

P [N] = applied force onto the indenter, h [m] = indentation; A [m²] = is the projected area of the spherical indenter at depth of indentation;

$$A=\pi ·{\rho }^2$$

ρ = radius of the indenter as measured perpendicular to the tip axis at the depth of contact;

$$\rho =\sqrt{h_c\left(2r-h_c\right)}$$

r = radius of the indenter, and h_c = depth of contact. To simplify the analysis, h_c = h was assumed, where h is the total depth of indentation.

Figure 5.

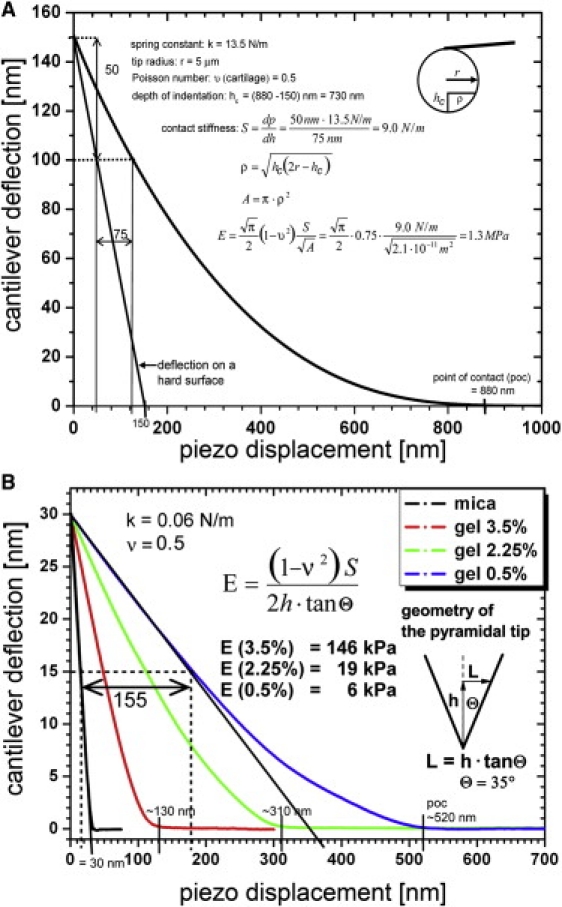
Graphs illustrating data and calculation of the dynamic elastic modulus (E^∗) at the (A) microscale (microstiffness) and (B) nanoscale (nanostiffness) from IT-AFM data. A shows a force-displacement curve measured with a spherical indenter on articular cartilage. In addition, the curve of constant compliance (1 (nm/nm)) has been drawn in, and exhibits the force related to deflection of the AFM cantilever when in contact with a hard surface that allows no indentation to take place. B shows data and calculations of the dynamic elastic nanoscale modulus (nanostiffness) exemplified on three agarose gels exhibiting strengths of 0.5%, 2.25%, and 3.5%. The graph displays the corresponding averaged force-displacement curves.

For the pyramidal tips as shown in Fig. 5 B, E is calculated as follows:

$$E=\frac{\left(1-{\nu }^2\right)S}{2h·\tan \theta }$$

where θ is the half-opening angle of the tip (Fig. 5, inset).

The indentation equations are based on Hertz's law, which is only true for linear elastic materials. The rationale for using them in this application is that the measured displacements are small and the displacement rate is high. Further, a Poisson's ratio of 0.5 was assumed, i.e., it was assumed that volume was conserved during deformation. Reported values of Poisson's ratio for cartilage range from 0.0 to 0.4, and also likely depend on deformation rates (see Table 3 in Mankin et al. (47)). Consequently, the values of E^∗ reported here are approximate and to some extent peculiar to the experimental methods and calculation assumptions employed.

Appendix III: Accuracy of Measuring Stiffness

If the cantilever is much stiffer than the stiffness of the material being indented, it will not deflect much and is thus an insensitive means of measuring force. If it exhibits a too-low spring constant, then too little indentation will occur at a given force. In particular, in IT-AFM on cartilage with a nanometer-size indenter tip, the probe will interact with both the gel phase and the much stiffer collagen fibrils. Therefore, both a well-matched, low-stiffness cantilever (for testing the gel phase) and a higher-stiffness cantilever (for testing the collagen fibrils) are required to prevent errors due to mismatch of the spring constant in stiffness measurements. Unfortunately, the stiffness of the cantilever cannot be adjusted during the measurement and has to be selected in advance. In our work, the selected spring constant value, k = 0.06 N/m, was suitable for accurately testing the gel phase; however, it reduced the accuracy of measurements of the collagen fibrils, as expressed as large standard deviations in the calculated stiffness values. Similarly, the spring constant value, k = 0.06 N/m, was suitable for accurately testing soft gels (∼0.5% agarose), as shown in Appendix II (Fig. 5, B), but it gradually overestimated the calculated values of nanostiffness for higher gel strengths. The IT-AFM measurement is most sensitive when the cantilever spring constant, k, and the contact stiffness, S = dP/dh ∼2rE/(1 − ν²), are of similar magnitude.

A calibration curve (sometimes also called blind calibration) was established in a previous study (24) to improve the quantitative capabilities of this method. The main advantage of this approach is that actual knowledge of the tip shape is not required.