Interplay between Intrinsic Noise and the Stochasticity of the Cell Cycle in Bacterial Colonies

Abstract

Herein we report on the effects that different stochastic contributions induce in bacterial colonies in terms of protein concentration and production. In particular, we consider for what we believe to be the first time cell-to-cell diversity due to the unavoidable randomness of the cell-cycle duration and its interplay with other noise sources. To that end, we model a recent experimental setup that implements a protein dilution protocol by means of division events to characterize the gene regulatory function at the single cell level. This approach allows us to investigate the effect of different stochastic terms upon the total randomness experimentally reported for the gene regulatory function. In addition, we show that the interplay between intrinsic fluctuations and the stochasticity of the cell-cycle duration leads to different constructive roles. On the one hand, we show that there is an optimal value of protein concentration (alternatively an optimal value of the cell cycle phase) such that the noise in protein concentration attains a minimum. On the other hand, we reveal that there is an optimal value of the stochasticity of the cell cycle duration such that the coherence of the protein production with respect to the colony average production is maximized. The latter can be considered as a novel example of the recently reported phenomenon of diversity induced resonance.

Introduction

Living cells are subjected to fluctuations with different intensities, scales, and origins. Randomness in genetic expression, cell-to-cell variability of the internal biochemical machinery, diversity in proliferation times, and disorder/noise in the medium compose, altogether, the uncertain environment in which cells are born, further mature, and die. Whether cells simply offer resistance to, or contrarily benefit from, noise is an open question with a major biophysical interest. Ultimately, variability (randomness) is crucial to life: life promotes variability and variability secures life (1).

Mostly during this last decade, the role of cellular-based fluctuations, singularly those concerning the effect of randomness in gene expression, has been reviewed in detail (2–7). In particular, many efforts have been devoted to discern between the so-called intrinsic and extrinsic components of noise and to assess their distinctive effects and origins (5,8,9). This has been made possible, in the main, through the use of dual reporter techniques implemented both in prokaryotes (9) and eukaryotes (6). Parallel to the interest in a better understanding of the origin and characteristics of cell-based noise, more and more attention has been drawn toward the elucidation of the eventual biological functionality that this randomness might have. Whether the important observable is the noise frequency, rather than its strength, was an important issue raised by Austin et al. (10), with the ultimate goal to map the structure of gene networks to noise spectrum. The somehow inverse question, to see whether both internal and external noise effects could be effectively suppressed in appropriately designed genetic architectures (negative-feedback loops), was formulated by Dublanche et al. (11). Still at the level of gene circuitry, the possibility to construct noise-based switches and amplifiers for gene expression had been previously addressed by Hasty et al. (12). The issue of noise in differentiation dynamics, and in particular the role it might play in selecting cells for competence, has been very recently raised by Süel et al., and Maamar et al. (13,14). In addition, the method by which promoter-mediated transcriptional noise drives phenotypic variability has been characterized by Blake et al. (15). Finally, with a different twist, the possibility of using extracellular noise to induce stochastic synchronization and promote coherence in multicellular environments was claimed by Zhou et al. (16) and more recently by Ullner et al. (17).

In this context, the stochastic dynamics of the gene regulatory network controlling the cell cycle has been studied from different perspectives, including its robustness and noise tolerance (18–21), the elucidation of cell-cycle dependent pathways affecting the fluctuations in gene expression (22), and the contribution of intrinsic and extrinsic components to the variability of the cell cycle (23). Yet, somehow surprisingly, less attention has been paid to the role played by the variability induced by the inherent stochasticity of the duration of the cell cycle in cell processes, particularly in protein expression. The episodes of cellular life are started/terminated by rather unpredictable events of cell division. In this respect, fluctuations in the duration of the cell cycle should be viewed, on the timescale of an evolving population, as long-memory fluctuations, similar to other random effects related to life-lasting constitutive components of the cell, and very different from the short-memory of the biochemical noisy processes.

In this article, we address the role assumed by the interplay between these two stochastic contributions in regard to protein production in bacterial colonies. We show that cells may profit from the disparity of scales of the different components of the total noise. To that end, we model a well-characterized simple experimental setup: the dilution protocol. This approach supposed a major breakthrough in the research of the functionality of genetic networks (24). In short, it is a protein regulation/expression experiment where cells are filled with repressor molecules that inhibit the expression of a protein. Repressor molecules dilute after cell division, and both protein and repressor levels are registered by fluorescence microscopy as a function of time. This simultaneous characterization allows us to quantify, at the single-cell level, the relation between the repressor concentration and the protein production rate: i.e., the gene regulatory function (GRF).

Within this framework, our goals are twofold. First, by taking such a reference experimental system as a calibrating tool, we implement a faithful modeling of the dilution method that includes the gene regulation/expression processes. As a result, we confirm the Hill-like functionality of the GRF and analyze, by means of in silico experiments, the effect of distinct stochastic contributions. Second, we unveil what we believe to be novel constructive effects arising from the interplay between gene-based noise and variability in cell proliferation. As shown below, such interplay counterintuitively contributes to set an optimum phase of the cell cycle for which noise in protein concentration is minimal. It might also drive the coordination of multicellular systems by coherently regulating protein production.

The article is organized as follows. The Methods: Modeling Approach section introduces our modeling and it is separated in two subsections that respectively address the gene regulation scheme and the description of the cell cycle duration and its fluctuations. The Results section is divided into three main subsections—the first one reporting numerical experiments to reproduce the gene regulatory function and the analysis of its stochastic contributions, and the last two featuring original aspects of the constructive interplay between intrinsic and cell cycle based noises. Finally, in the Discussion we summarize our main conclusions and propose different experiments to test our predictions.

Methods: Modeling Approach

By tracking the behavior of individual cells of a colony subjected to protein regulatory processes and molecular dilution due to division events, we aim at modeling the experimental procedure that permits us to obtain the GRF at the single cell level (24). In regard to the timescales, two distinctive modeling modules can be distinguished.

First, protein expression is regulated within each cell by binding and unbinding events of repressor molecules to gene operator sites. Second, at a larger timescale, cells undergo division as a consequence of the cell cycle progression. These events dilute the concentration of repressor molecules by halving them between the cell and its progeny. In addition, the cell-cycle phase modifies the gene regulatory properties by changing, due to cell maturation, the protein production rate.

Gene regulation and protein production

Fig. 1 summarizes the reactions that account for gene regulation and protein production in our model following the experimental gene construct of Rosenfeld et al. (24). Despite the right operator of bacteriophage λ promoter has three binding sites, only two of them are accessible to cI repressor molecules. Thus, we effectively describe the operator of the gene that encodes for protein P (CFP fluorescent protein) to have two binding sites. The latter can be either empty (Ø), or occupied (^∗), by repressor molecules (R, i.e., cI protein), in dimer form (R₂). That is, there are four possible occupancy states of the operator. We represent these by O_ij, with i and j indicating the binding sites. We note that the cooperativity exponent of the gene regulatory function (∼2 in experiments) does not depend on the functional form of the repressor (i.e., either monomeric or multimeric) but on the number of binding sites of the operator accessible to it.

Figure 1.

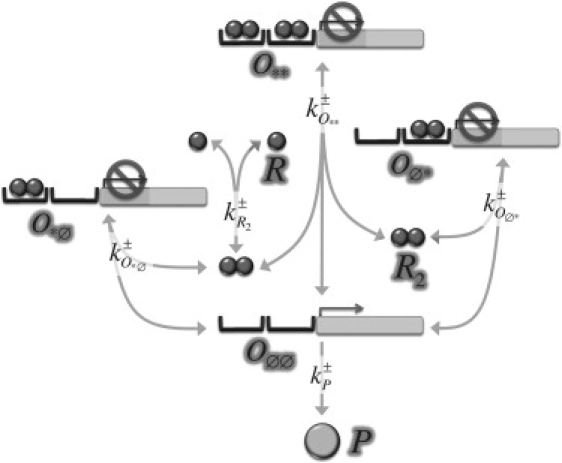
Schematic representation of the reactions driving protein expression. The operator controlling gene expression has four possible occupancy states (O_øø, O_ø∗, O_∗ø, and O_∗∗). Transitions between those states depend on binding events of repressor molecules (R²) after monomer (R) dimerization. Arrows representing possible reactions have been labeled by their kinetic rates (see the expressions in Eq. 2). All reactions are assumed to be reversible except for that of protein P production. The latter may occur only if no repressor dimer binds to the operator.

Although basal expression rates can be always expected, experiments reveal that protein expression under the control of such promoter is tightly regulated by repressor molecules; consequently, we consider protein production only if the operator is at state O_∅∅, i.e., a nonleaky system. We further assume an effective description for protein production such that transcription and translation processes are summarized by a single step with an effective reaction rate, k_P⁺, which depends on time (see below). Thus, protein expression is described by means of the irreversible reaction,

$$O_{\varnothing \varnothing }\stackrel{k_P^{+}}{\to }{O}_{\varnothing \varnothing }+P\text{.}$$ (1)

On the other hand, the reactions that describe the reversible repressor dimerization dynamics and the binding-unbinding events read

$$\begin{array}{l}R+R\underset{k_{{\overline{R}}_2}^{-}}{\overset{k_{R_2}^{+}}{\rightleftharpoons }}{R}_2,R_2+O_{\varnothing \varnothing }\underset{k_{O_{\ast \varnothing }}^{-}}{\overset{k_{O_{\ast \varnothing }}^{+}}{\rightleftharpoons }}{O}_{\ast \varnothing },\\ R_2+O_{\varnothing \varnothing }\underset{k_{O_{\varnothing \ast }}^{-}}{\overset{k_{O_{\varnothing \ast }}^{+}}{\rightleftharpoons }}{O}_{\varnothing \ast },2R_2+O_{\varnothing \varnothing }\underset{k_{O_{\ast \ast }}^{-}}{\overset{k_{O_{\ast \ast }}^{+}}{\rightleftharpoons }}{O}_{\ast \ast }.\end{array}$$ (2)

For the sake of simplicity, and following previous modeling approaches of the λ right operator (25–27), we disregard transitions of the operator state from one to two (and correspondingly two to one) occupied binding sites (see Fig. 1). Moreover, the experimental results reveal that protein degradation (both that of the repressor R and the protein P) is negligible within the temporal scale of our interest (several cell cycles, i.e., hours) and consequently is ignored hereafter in our scheme. Therefore, despite there being seven species in our model, the number of kinetic equations can be reduced up to five by invoking the conservation laws of

$$\begin{array}{l}R+2R_2+2O_{\varnothing \ast }+2O_{\ast \varnothing }+4O_{\ast \ast }={\Lambda }_{R}V,\\ O_{\varnothing \varnothing }+O_{\ast \ast }+O_{\ast \varnothing }+O_{\varnothing \ast }={\Lambda }_{O}V,\end{array}$$ (3)

where V ≃ 1.5 μm³ stands for the cell volume (by taking into account that the cell volume is V ≃ 1.5 μm³, thus lnM ≃ 0.9 molecules/cell) in Escherichia coli and Λ_R and Λ_O denote the total concentration of repressor molecules and operator sites (genetic material), respectively. The expressions in Eq. 3 indicates that, during a cell cycle, the amount of repressor molecules and the number of operator binding sites (gene copies) do not vary. Note that these enforce the constraint that replication of the genetic material within a cell cycle does not contribute to an increase of the operator binding sites. Yet, we include this effect in an effective manner by means of the aforementioned temporal dependence of the protein production rate k_P⁺ as we detail below.

The unavoidable intrinsic fluctuations associated to the reduced and discrete number of the operator states, proteins, and repressing molecules can be implemented in our model by deriving the corresponding Master equation from Eqs. 1 and 2. This probabilistic equation can be exactly solved (numerically) using a modified Gillespie algorithm that takes into account the fact that the reaction rates, i.e., k_P⁺, depend on time (28). Alternatively, if stochastic effects are still expected to be relevant but the number of molecules/states is not too small (N being the number of molecules/states: N ≳ 10), an approximated, yet accurate, description is possible using Langevin equations obtained from the Master equation by means of expansion methods. In particular, the so-called Kramer-Moyal expansion (29) leads to the stochastic differential equations (interpreted in Ito sense)

$$\begin{array}{c}{\dot{c}}_P=k_P^{+}{c}_{O_{\varnothing \varnothing }}+{\xi }_P\sqrt{\frac{k_P^{+}{c}_{O_{\varnothing \varnothing }}}{V}},\\ {\dot{c}}_R=-2k_{R_2}^{+}{c}_R^2+2k_{R_2}^{-}{c}_{R_2}+2{\xi }_R\sqrt{\frac{k_{R_2}^{+}{c}_R^2+k_{R_2}^{-}{c}_{R_2}}{V}},\\ {\dot{c}}_{O_{{\varnothing }_{\ast }}}=-k_{O_{\varnothing \ast }}^{-}{c}_{O_{\varnothing \ast }}+k_{O_{\varnothing \ast }}^{+}{c}_{O_{\varnothing \varnothing }}{c}_{R_2}+{\xi }_{O_{\varnothing \ast }}\sqrt{\frac{k_{O_{\varnothing \ast }}^{-}{c}_{O_{\varnothing \ast }}+k_{O_{\varnothing \ast }}^{+}{c}_{O_{\varnothing \varnothing }}{c}_{R_2}}{V}},\\ {\dot{c}}_{O_{{\ast }_{\varnothing }}}=-k_{O_{\ast \varnothing }}^{-}{c}_{O_{\ast \varnothing }}+k_{O_{\ast \varnothing }}^{+}{c}_{O_{\varnothing \varnothing }}{c}_{R_2}+{\xi }_{O_{\ast \varnothing }}\sqrt{\frac{k_{O_{\ast \varnothing }}^{-}{c}_{O_{\ast \varnothing }}+k_{O_{\ast \varnothing }}^{+}{c}_{O_{\varnothing \varnothing }}{c}_{R_2}}{V}},\\ {\dot{c}}_{O_{\ast \ast }}=-k_{O_{\ast \ast }}^{-}{c}_{O_{\ast \ast }}+k_{O_{\ast \ast }}^{+}{c}_{O_{\varnothing \varnothing }}{c}_{R_2}^2+{\xi }_{O_{\ast \ast }}\sqrt{\frac{k_{O_{\ast \ast }}^{-}{c}_{O_{\ast \ast }}+k_{O_{\ast \ast }}^{+}{c}_{O_{\varnothing \varnothing }}{c}_{R_2}^2}{V}},\end{array}$$ (4)

where c_X stands for the concentration of species X and ξ_X denotes uncorrelated white noise terms with zero mean:

$$\langle {\xi }_S\left(t\right)\rangle =0,$$

$$\langle {\xi }_X\left(t\right){\xi }_{X^{\prime }}\left(t^{\prime }\right)\rangle ={\delta }_{{\mathit{X,\; X}}^{\prime }}\delta \left(t-t^{\prime }\right)\text{.}$$

We make use of these alternative descriptions (Master and Langevin equations) throughout the text.

Cell division and cell cycle

In the reference experimental system, extrinsic noise is claimed to encompass fluctuations in cellular metabolites, ribosomes, and polymerases. Although intrinsic fluctuations has been proved to have short correlation times (white noise), extrinsic fluctuations, often the dominant source of biochemical noise, exhibit long correlation times of the order of the cell cycle (24). As a matter of fact, other sources of long-time correlated extrinsic fluctuations can be envisioned. As time evolves, cell lineages develop asynchronously in a colony, thus reproducing the stochastic nature of the cell cycle (see Fig. 2 A). In turn, the dilution of proteins of the regulatory process under consideration is affected at the timescale of the cell cycle by such stochasticity (23). This perturbation can be further transmitted over generations through the halving processes. Herein, we focus on the effect induced by the randomness of the cell-cycle duration and the division processes. We implement those events as follows. We define an internal clock for each cell and a corresponding variable t ∈ [0, τ], which denotes the time lasted up to completion of a cell cycle. At division time, τ, the clock is reset, repressor molecules unbind from the operators, the gene copies duplicate and are distributed between the original cell and its daughter, repressor molecules and proteins are binomially distributed, and the duration of their cell cycles are newly and independently assigned. We point out that volume change (cell growth) is disregarded in our modeling. Yet, we consider that the duplication of the cellular material during the cell cycle effectively modifies the protein production rate as experimentally reported (24). We implement such temporal dependence of the production rate as

$$k_P^{+}=k_P^{+}\left(t\right)=k_0{2}^{\frac{t}{\tau }}.$$

Figure 2.

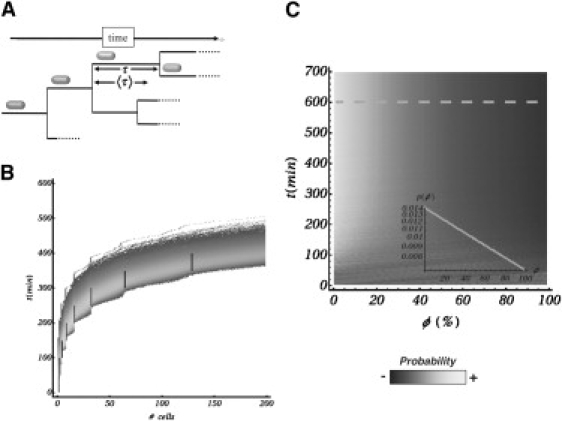
Stochasticity in the cell cycle. (A) Due to cell divisions, the repressor concentration decreases over time, leading to an increase in protein production. The duration of the cell cycle is a stochastic variable that promotes cell-to-cell variability in protein production over time. (B) Comparison between a deterministic and a stochastic dynamics in terms of the colony size (number) over time. In the deterministic dynamics (segments), all cells divide at the same time, leading to a steplike behavior. Conversely, the stochastic dynamics introduce a scattering in the number of constituents that increases over time. Yet, the average follows the deterministic behavior. (C) Density plot indicating the probability of finding a cell in a particular phase of the cell cycle as a function of time (ϕ = 0/100 stands for the beginning/end of the cell cycle). This quantity reaches a stationary state after some cell cycles (∼〈τ/σ_τ) only if the dynamics of the cell cycle is stochastic. (Inset) Probability (in log scale) once a stationary state is reached (dashed line). The exponential decay is characteristic in age-balanced bacterial cultures (see text).

That is, cell maturation exponentially modifies the protein production rate, k_P⁺, by doubling it from k₀ at cell birth up to 2k₀ at division time. As for the stochastic duration of the cell cycle, we propose a simple rule,

$$\tau =\gamma t_{\det }+\left(1-\gamma \right)t_{\text{sto}},$$

where t_det and t_sto denote, respectively, the deterministic and stochastic components of the duration of the cell cycle, and γ ∈ [0, 1] is a parameter that weights their relative importance, i.e., γ = 1/0 stands for a fully deterministic/stochastic duration of the cell cycle. Note that we retain the fact that before division, cells must mature and grow and consequently the cell cycle must have a minimum duration γt_det. The stochastic part, t_sto, is supposed to be exponentially distributed and its probability density reads (29)

$$\rho \left(t_{\text{sto}}\right)=\frac{1}{t_{\det }}{e}^{-\frac{t_{\text{sto}}}{t_{\det }}}\text{.}$$

The exponential decay can be justified by means of probabilistic arguments because it accounts for the time between random events that occur continuously and independently at a constant average rate (i.e., the Poisson processes that fairly describe many enzymatic reactions). In fact, as shown below (Fig. 2 C), the exponential distribution is able to reproduce the exponential decay of the cell-age distribution in bacterial colonies as experimentally reported. Such two phase approach for describing the cell cycle duration has been similarly hypothesized by other researchers and has been experimentally tested in bacteria (e.g., Staphylococcus albus) (25,26).

According to these definitions, the parameters that are usually characterized experimentally in relation to the duration of the cell cycle, i.e., the average duration and standard deviation, read

$$\langle \mathit{\tau }\rangle =t_{\det },$$

$${\sigma }_{\tau }=\left(1-\gamma \right)t_{\det }\text{.}$$

Moreover, in terms of 〈τ〉 and σ_τ, the probability density for the duration of the cell cycle becomes fully specified,

$$\rho \left(\tau \right)=\frac{\theta \left(\tau -\langle \tau \rangle +{\sigma }_{\tau }\right)}{e{\sigma }_{\tau }}{e}^{-\frac{\tau -\langle \tau \rangle }{{\sigma }_{\tau }}}\text{.}$$ (5)

In the previous equation, τ ∈ (0, ∞) and θ(·) stands for the Heaviside step function. Following the experiment of Rosenfeld et al. (24), we take τ = (50 ± 10) min for the calibration of the parameters of our model: t_det = 50 min and γ = 0.8. Fig. 2 B shows the comparison between deterministic (synchronous) and the proposed stochastic (asynchronous) dynamics for the temporal evolution of a bacterial colony in terms of the number of components. The agreement between the proposed cell-cycle model and experiments can be assessed by examining some statistical properties of the colony growth. A particularly relevant quantity is the probability p(ϕ) of finding at a particular time a cell at phase ϕ of the cell cycle (ϕ = 0: beginning of the cell cycle; ϕ = 100: end of the cell cycle), which is the so-called cell-age distribution. Evolving from a single cell by duplication, Fig. 2 C shows p(ϕ) by means of a density plot. We note that a stationary state (age-balanced population) is reached after ∼〈τ〉/σ_τ cell cycles. In a deterministic synchronous dynamics, a stationary state is obviously never obtained. Once at the steady state (dashed line), p(ϕ) exhibits an exponential decay (inset plot),

$$p\left(\varphi \right)=\mathcal{N}{2}^{1-\frac{\varphi }{100}},$$

where N is a normalization constant, indicating that in an age-balanced colony the fraction of bacteria at the beginning of the cell cycle doubles that at the end of the cycle, as observed in experiments (25,26,30). This sort of counterintuitive effect is because for every cell that divides (end of the cell cycle), two new cells start their cell cycle. Importantly, we stress that the reported constructive role of the stochasticity of the duration of the cell cycle does not depend on the specific functional form of ρ(τ) as long as it reproduces asynchronous stochastic divisions in a realistic way (25,26,31).

Results

Parameters calibration: protein dilution experiments

Following the experimental prescriptions, we calibrate the parameters of our model by considering a single chromosomal integrated gene copy. According to the experimental results, the colony-averaged GRF that specifies the protein production rate as a function of the concentration of repressor satisfies a Hill-like functional relation,

$$GRF\left({\Lambda }_R\right)=\frac{K}{1+{\left(\frac{{\Lambda }_R}{\beta }\right)}^n},$$

with measured values K = (244 ± 17)nM/ min, β = (55 ± 10)nM, and n = 2.4 ± 0.3, for the unrepressed protein production rate, the repressor concentration at half-maximal expression, and the cooperativity exponent, respectively.

To obtain the corresponding in silico GRF in our in silico experiments, we first calibrate our model and estimate its constants using experimental data (see Supporting Material). A Gillespie-like simulation starts with a single cell filled with ∼7.5 × 10³ repressor molecules (∼8.3 μM). Such concentration avoids protein production as prescribed by the experimental setup. We then track in time the concentration of this species together with the protein production at the single cell level. As time evolves, the concentration of repressor within a cell diminishes due to division, thus increasing the probability of the operator to be in the unbound state, O_øø, and then triggering protein production. Fig. 3 A shows, for a number of cell lineages, the typical outcome of an in silico experiment. The GRF was obtained by computing as a function of the repressor concentration the averaged protein production (in time and over cells within the same generation, i.e., cells that have undergone the same number of divisions). Fig. 3 B depicts the GRF obtained in our modeling and its fit to a Hill function. We obtain, in agreement with experimental results, the values

$$\widehat{K}=\left(245.56\pm 0.05\right)\text{nM}/\min ,$$

$$\widehat{\beta }=\left(54.1\pm 0.06\right)\text{nM},$$

$$\widehat{n}=2.416\pm 0.005\text{.}$$

Figure 3.

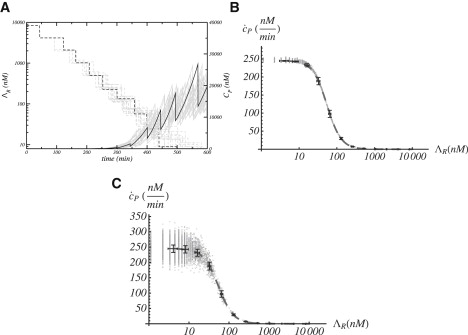
Protein production and gene regulatory function in the in silico dilution experiments. (A) Protein and repressor concentration as a function of time. Different lines indicate a number (16) of representative cell lineages. The trajectory for a particular cell lineage has been highlighted. (B) Gene regulatory function obtained by means of the protein dilution process: individual cells (shaded crosses), colony average (points with error bars), and fit to Hill function (long-dashed line). (C) Same as panel B when variability in the production rate is considered (see text).

As mentioned above, the cooperativity exponent obtained in experiments requires the gene operator to interact with two repressing molecules independently of its multimeric form. That is, if one operator site is suppressed, then $\widehat{n}$ decreases and $\widehat{\beta }$ increases (data not shown), in agreement with experiments that introduce a point mutation in the λ right operator (VN mutation) (24).

Importantly, we point out that the error bar of the GRF is in fact very small when compared to experiments. This indicates that the experimental deviation, with respect to the average value, cannot be attributed to short memory stochasticity (intrinsic noise) or to the long memory fluctuations (diversity/variability) that are introduced by the binomial partition of proteins and repressors and/or the stochasticity of the cell cycle duration. To clarify the origin of the large fluctuations in the GRF, we perform an in silico experiment that effectively introduces cell-to-cell variability in the protein production rate, which is done by trying to mimic the role played by other extrinsic fluctuations in the reference experiment. Such an in silico experiment is implemented as follows. By assuming that extrinsic randomness is caused by a large number of independent factors that directly modify the gene production rate during the cell cycle (metabolites, ribosomes, and polymerases among others), we invoke the central limit theorem (29). We then introduce a quenched stochastic perturbation to the protein production rate, k₀, that is Gaussian distributed, with standard deviation as experimentally reported for the unrepressed production rate: ±17 nM/min. At division time, that value for the cell and progeny is updated. This effectively leads to long memory effects. Results are shown in Fig. 3 C. Lacking this sort of extrinsic noise, because the Gaussian fluctuations of k₀ average out, the average behavior (with respect to the previous case) does not change. Yet, the noise of the GRF increases notably for low repressor (if protein production leaking is considered, then the noise in the GRF spreads to large repressor concentration too (data not shown)),

$$\widehat{K}=\left(245.7\pm 0.5\right)\text{nM}/\min ,$$

$$\widehat{\beta }=\left(54.0\pm 0.6\right)\text{nM},$$

$$\widehat{n}=2.40\pm 0.05\text{.}$$

Alternatively, large fluctuations in the GRF could also emerge in plasmids systems due to binomial partition of genetic material. This feature in fact may mask the stochasticity due to extrinsic fluctuations. Note that if each plasmid contributes with a bare production rate k₀, then the protein production rate of a given cell reads mk₀ (m being the number of plasmid copies received after binomial partition at division time). The latter causes some cells to be more or less productive than other cells, even if they contain the same amount of repressors. This effectively introduces diversity in the protein production rate with a long-memory of the order of the cell cycle that is further transmitted over generations. To test this hypothesis, we perform additional in silico experiments where we implement several copies (plasmids) of the gene encoding for protein P (25 copies), and let them distribute binomially after cell division (results are summarized in the Supporting Material). As mentioned above, despite the protein production rate (in which the in silico experiment does not include extrinsic noise), the GRF shows a large noise in this case too.

Constructive interplay between intrinsic fluctuations and the stochasticity of the cell cycle

We now focus on different aspects featuring what we claim to be constructive roles arising from the interplay between different stochastic contributions. As a beginning scenario, to stress the cooperative effects between randomness with disparate timescales, we consider the role played by intrinsic fluctuations and the variability introduced by the stochasticity of the cell cycle duration in terms of protein concentration. For the sake of simplicity, and trying to disregard other effects and to develop analytical calculations, we restrict our analysis to the unrepressed situation, Λ_R = 0, when protein production is maximal (we also disregard extrinsic fluctuations in the protein production rate k₀, i.e., Gaussian dispersion). Still, the net outcome (the existence of a phase in the cell cycle where protein concentration noise reaches a minimum) also applies to the dilution protocol.

Protein production increases over the cell cycle in an exponential fashion. Thus, we expect that the intrinsic component of the noise (herein the term “noise” is understood as the ratio between the dispersion and the average) of protein concentration will decrease over time. On the other hand, the extrinsic component of the noise, due to the stochasticity of the cell cycle duration, is expected to grow, inasmuch as cell-to-cell asynchrony in protein production increases over time. As a result, the total noise (intrinsic+extrinsic) should show a minimum during the cell cycle, i.e., there should be an optimal phase of the cell cycle that minimizes the noise in protein concentration. We have tested this argument both analytically and numerically as follows. Let us introduce first some formal definitions: for a fluctuating quantity, z, the total (relative) noise can be defined as the dimensionless ratio between the dispersion, σ_z, and the average, $\widehat{z}$,

$${\eta }_z=\frac{{\sigma }_z}{\widehat{z}},$$

where $\widehat{z}$ is the average with respect to intrinsic and extrinsic fluctuations and to

$${\sigma }_z^2=\widehat{z^2}-{\widehat{z}}^2.$$

Following Swain et al. (7), total averages can be separated in terms of the intrinsic and extrinsic components as

$$\widehat{f\left(z\right)}=\overline{\langle f\left(z\right)\rangle },$$

where hereafter in this section 〈·〉 stands for the averages taken with respect to the intrinsic noise and $\overline{.}$ for those relative to the extrinsic fluctuations. Moreover, the total noise can be in turn separated into intrinsic and extrinsic components by splitting the dispersion term:

$$\begin{array}{c}{\sigma }_z^2=\overline{\langle z^2\rangle }-{\overline{\langle z\rangle }}^2=\overline{\langle z^2\rangle }-\overline{{\langle z\rangle }^2}+\overline{{\langle z\rangle }^2}-{\overline{\langle z\rangle }}^2=\\ =\left(\overline{\langle z^2\rangle }-\overline{{\langle z\rangle }^2}\right)+\left(\overline{{\langle z\rangle }^2}-{\overline{\langle z\rangle }}^2\right)={\sigma }_z^2{,}_{\text{Intrinsic}}+{\sigma }_z^2{,}_{\text{Extrinsic}}.\end{array}$$

Consequently, we need to calculate three different averages of the protein concentration. By taking into account the same realization of the cell cycle duration and averaging Eq. 4 over realizations of the intrinsic noise, we obtain

$$\langle {\dot{c}}_P\rangle =k_P^{+}\left(t\right){\Lambda }_O.$$

That is,

$$\langle c_P\rangle =\frac{k_0{\Lambda }_O\tau }{\ln \left(2\right)}\left(2^{t/\tau }-1\right).$$ (6)

As for the evolution equation of the second moment, we note that variable changes, when dealing with Ito Langevin equations, must be carefully done because the regular rules of calculus do not apply. The latter is because some second-order differential terms do not vanish. In particular, one must take into account the so-called Ito lemma: dW_P²(t) = dt, where W_P(t) stands for the Wiener process that characterizes, by differentiation, the white noise term that appear in the Langevin equations (dW_P(t) = ξ_Pdt). By using the Ito lemma, a straightforward calculation leads to

$$\left(\dot{c_P^2}\right)=k_P^{+}\left(t\right){\Lambda }_O\left(2c_P+\frac{1}{V}\right)+\frac{{\xi }_P}{V^{1/2}}2c_P\sqrt{k_P^{+}\left(t\right){\Lambda }_O}.$$

Note that the second term of the right-hand side of this equation would not appear using the regular rules of calculus. Therefore, by averaging over the intrinsic noise we get

$$\begin{array}{l}\langle \dot{c_P^2}\rangle =k_p^{+}\left(t\right){\Lambda }_O\left(2\langle c_P\rangle +\frac{1}{V}\right)\\ =k_0{\Lambda }_O{2}^{t/\tau }\left(\frac{2k_0{\Lambda }_O\tau }{\text{In}\left(2\right)}\left(2^{t/\tau }-1\right)+\frac{1}{V}\right).\end{array}$$

That is,

$$\langle c_P^2\rangle =\frac{k_0{\Lambda }_O\left(2^{t/\tau }-1\right)\tau }{V{\left(\ln \left(2\right)\right)}^2}\left[k_0{\Lambda }_O\tau V\left(2^{t/\tau }-1\right)+\ln \left(2\right)\right].$$ (7)

If we now average Eqs. 6 and 7 over ρ(τ) from Eq. 5, we obtain $\overline{\langle c_P^m\rangle }$ with m = 1, 2. Squaring that result for the case m = 1 leads to ${\overline{\langle c_P\rangle }}^2$. Similarly, by squaring Eq. 6 and then averaging over ρ(τ), one can easily compute $\overline{{\langle c_P\rangle }^2}$. To calculate these statistical terms numerically we implement in silico two different copies, P₁ and P₂, of our gene of interest in each DNA copy of every cell as in the experimental setup (24) (see Supporting Material for details).

Fig. 4, A–C, shows the behavior of the intrinsic and extrinsic noise as a function of time and also the value of ${\eta }_{c_P}$ as a function of $\widehat{c_P}$ (also as a function of time). As expected, ${\eta }_{c_P}$ displays a nonmonotonous behavior indicating the existence of an optimal phase of the cell cycle (alternatively an optimal concentration of protein) for which noise is minimal. Fig. 4 A and B show the intrinsic and extrinsic components of the noise as a function of $\widehat{c_P}$. Note the monotonous behavior (decreasing and increasing, respectively) in both separate cases. Consequently, we demonstrate that minimization of the total noise results from a cooperative interplay. Note in all cases the excellent agreement between the analytical and numerical calculations (both Langevin and Gillespie-like schemes).

Figure 4.

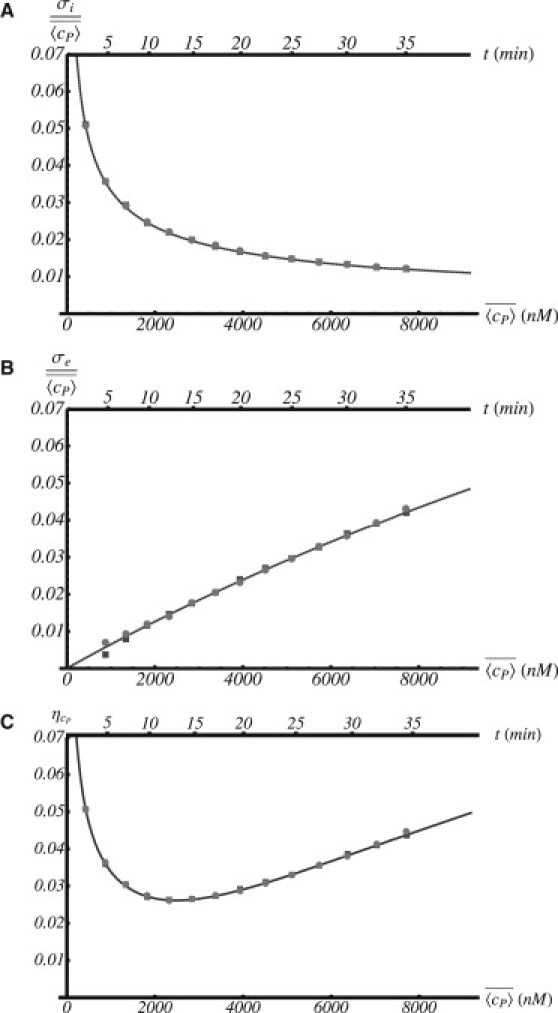
Noise in protein concentration as a function of the protein concentration/time (bottom/top axes): (A) intrinsic noise, (B) extrinsic noise, and (C) total noise. In all cases, the solid curve and the circles and square symbols (mostly indistinguishable) stand for analytical calculations and Gillespie and Langevin simulations, respectively. Intrinsic/extrinsic noise decreases/increases as time (concentration) develops. As a result of the trade-off between intrinsic and extrinsic noise, there is an optimal value of the concentration/time for which noise becomes minimum.

Colony protein production coherence: resonant aspects

In a number of biological processes, as for example the response signal to stress, protein production rate is the observable of interest that either drives further, or becomes modified due to, signaling. We shift our attention to this quantity and study the constructive role that develops due to the interplay between different stochastic components in relation to the collective behavior of the colony. As in the previous case for the sake of simplicity, and trying to disregard other effects, we restrict our analysis to the unrepressed situation and disregard extrinsic fluctuations in the protein production rate. We also note that the numerical results in this section were obtained using the Langevin description. For a given cell lineage, i, at a given (laboratory) time, t, the protein production relative to the average rate of the whole colony reads

$$\Delta \dot{P_i}\left(t\right)={{\dot{c}}_P\left(t\right)|}_i-\langle {\dot{c}}_P\left(t\right)\rangle .$$

Note that averages 〈·〉 here refer, overall, to both intrinsic and proliferation-induced variability fluctuations. Thus, this quantity measures the fluctuations of the protein production rate in a cell of the colony. Protein production increases at a nonlinear rate during the cell cycle due to cell maturation as effectively accounted by k_P⁺(t). As a function of the stochasticity of the cell cycle duration, two extreme, albeit unlikely, situations could be envisioned. If the cell colony would grow deterministically (i.e., by means of synchronous divisions), γ = 1, then ${{\dot{c}}_P\left(t\right)|}_i$ would show a time-periodic pattern subjected to intrinsic fluctuations, while $\langle {\dot{c}}_P\left(t\right)\rangle$ would exhibit the same pattern but noise free, as intrinsic fluctuations average out (for a large enough population). As a consequence, $\Delta \dot{P_i}\left(t\right)$ would just reproduce the i^th cell intrinsic noise. On the other hand, if the cell colony would grow totally at random (i.e., by means of purely asynchronous divisions), γ = 0, then ${{\dot{c}}_P\left(t\right)|}_i$ would show a noisy-non-periodic pattern, while $\langle {\dot{c}}_P\left(t\right)\rangle$ would rapidly reach a constant value as the culture balances its age. Thus, $\Delta \dot{P_i}\left(t\right)$ would feature in this case the noisy nonperiodic protein production of i^th cell. Importantly, in both cases the memory of $\Delta \dot{P_i}\left(t\right)$ would be quickly lost. Simply stated, $\Delta \dot{P_i}\left(t\right)$ will behave in both cases as unpredictable in the course of time. In one case, this is due to the effect of intrinsic fluctuations and in the other as a direct consequence of extrinsic noise (here the randomness in the cell cycle duration). The important issue is whether or not some sort of predictability could be recovered under realistic conditions of cell proliferation. In fact, we could expect that, for intermediate values of the stochasticity of the cell cycle, a balanced situation might hold and the protein production of the cell with respect to the colony (progeny) could perform in a more coherent way.

To analyze this effect, we perform in silico experiments by growing a colony from a single cell and we compute the autocorrelation function of the quantity $\Delta \dot{P_i}\left(t\right)$ by tracking every lineage. To evaluate its coherence, we average $\Delta \dot{P_i}\left(t\right)$ autocorrelation over all the lineages that evolve from this primordial cell and take the corresponding Fourier transform.

Next, we evaluate at the dominant frequency of the power spectrum (highest peak), the ratio between the height of the peak (a measure of the strength of the periodic behavior) and its width (an indicator of the variability of the periodicity).

Finally, we repeat up to ∼50 times such protocol for different values of γ. Our in silico experiments show that there is indeed an optimal value of γ for which protein production with respect to the colony is generated in a more regular fashion displaying an oscillatory behavior (see Fig. 5). That value turns out to be γ ≃ 0.9 when 8 h are analyzed (∼10 cell cycles). Strikingly enough this value is significantly close to the biologically relevant case for the dilution protocol experiment γ ≃ 0.8. We point out that the γ-position of the maximum depends slightly on the number of cell cycles considered, yet there is always a maximum close to γ = 1, unveiling a robust and constructive effect of the interplay between intrinsic fluctuations and the stochasticity of the duration of the cell cycle.

Figure 5.

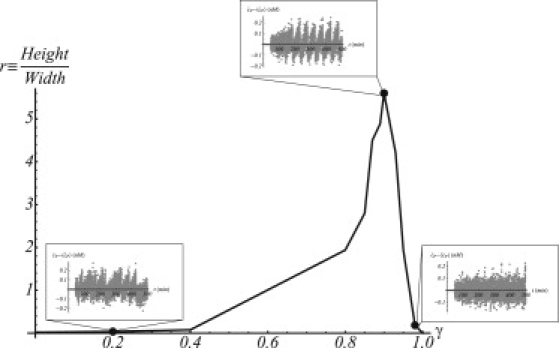
Coherence in protein production fluctuations of the colony as a function of the stochasticity of the cell cycle. There is an optimal value of the stochasticity for which coherence is maximal (γ ≃ 0.9). (Insets) Fluctuations of protein production for different values of γ and for a representative cell lineage.

Discussion

Stochasticity in cell processes is a promising research topic that covers a wide spectrum of viewpoints from the characterization of the noise sources to their role in terms of the biological functionality. Within this framework herein, we have addressed for the first time the constructive effects that arise due to the interplay between the stochasticity of the cell cycle duration and the intrinsic noise of biochemical processes. To that end, and following the experimental prescriptions of Rosenfeld et al. (24), we have proposed a quantitative model that reproduces the dilution protocol in bacterial colonies including the random effects of intrinsic and extrinsic noise, variability due to binomial partition of molecules, and diversity from a stochastic proliferation (duration of the cell cycle). This simple, yet realistic, scheme has allowed us to evaluate the contributions of those distinct stochastic components to the overall noise experimentally reported in the GRF. Our results let us to conclude that noise in the GRF mostly arises from extrinsic fluctuations that directly modify the protein production rate in the timescale of the cell cycle and introduce cell-to-cell diversity. Contrarily, randomness derived from the binomial partition of protein and repressors, biochemical intrinsic noise due to low numbers of molecules, and variability in the cell-cycle duration, do not contribute significantly to the large noise experimentally reported according to our simulations. Moreover, we show that when dealing with plasmids, binomial distribution of genetic material introduces diversity effects that may mask the effect of extrinsic noise in the GRF.

In addition, we explore and unveil different features directly rooted to the role of diversity in proliferation. We discover the existence of an optimal phase in the cell cycle for which randomness in protein concentration becomes minimal. In this regard, a lot of effort has been done to understand how noise is transmitted through gene cascades for obtaining a robust pattern of gene expression (e.g., the telephone game) (32–36). Network architecture and connectivity have been proven to play a crucial role in this regard. Moreover, it has been experimentally shown that noise in protein levels becomes minimum in essential genes and that functionality and fitness are reduced otherwise. Thus, noise minimization processes help to secure a robust cellular behavior that has been related with a trait acted on by natural selection. Although all studies, in this sense, have focused on the steady-state properties of this mechanism, our study shows how noise minimization can be dynamically attained during the course of the cell cycle by means of a trade-off of different noise sources. Whether this particular mechanism implies a specific functionality is unknown at this point. One hypothesis is that cell maturation might require the existence of some phase during the life cycle when, generically, biochemical constituents, although prone to uncertainties, should be secured with minimum variability. In any case, the phenomenon by itself contributes to the understanding of the mechanisms leading to biological robustness.

The last result of our study refers to the coherence in protein production rather than protein concentration. The global dynamical trend of protein production is determined by the periodicity of the cell cycle and the increase of protein production. On top of that, protein production fluctuations have stochastic contributions from intrinsic noise (fast timescales) and extrinsic noise (slow timescales). As a result, the characteristic timescale of the fluctuations develops from a balance of these contributions that can only resonate for intermediate values of the stochasticity of the cell cycle duration (note that γ implies a characteristic timescale). In a formal sense, the disclosed example of coherence enhancement leading to sustained oscillations constitutes a novel, to our knowledge, realization of a generic phenomenon termed noise-induced coherence resonance in the field of nonlinear noisy systems (37). More precisely, in our case this coherence enhancement arises directly from the diversity in the cell-cycle realization, and thus could be qualified as a novel example of a recently reported phenomenon: diversity-induced resonance (38). Such counterintuitive noise-sustained predictability is a rather striking outcome of our modeling for this particular toylike cell culture. Whether it has real significance and, furthermore, biological functionality in more realistic in vivo scenarios, is a most challenging open question at this point. In any case, one could speculate whether cells could harness such temporal regularity and use it as a simple quorum-sensing signal to undertake decisions at the colony-size level as individual cells proliferate. Although not justifying cell-to-cell diversity in division, cells would instead benefit from the unavoidable presence of such variability to sustainably program their collective behavior. Indeed, it has been suggested that systems showing diversity-induced coherence might profit from it to optimize the response to an external stimulus (38).

Our study falls into the field of biophysical theory and modeling. Yet, by focusing on an experimental system that has been profusely characterized, we calibrate all parameters with experimental data and show that our modeling is able to quantitatively reproduce the experimental results of the dilution protocol. We then believe that the predicted constructive roles due to the interplay of different noise sources can be experimentally tested. The latter relies on the possibility of controlling the cell cycle duration and its stochasticity. In this regard, different methods for growing cultures with synchronized cell divisions, thus minimizing the standard deviation of the cell cycle duration, have been proposed (39,40). These depend on treatments of the cultures either before growth (e.g., temperature or light intensity shifts, thymine or nitrogen starvation, Percoll density gradients) or periodically during growth (e.g., illumination changes, glucose starvation). A more elaborate approach, which would allow a tighter control of the cell-cycle duration, rests on driving the cell division apparatus at a more fundamental level. In bacteria, such machinery comprises >15 different proteins (41). The tubulin homolog FtsZ is key in this process, as it recruits all other components of the divisome (41,42). In fact, mutant strains where FtsW (a protein that stabilizes the FtsZ ring) has been suppressed grow without dividing, and this property has been used to check the effect of intrinsic fluctuations in gene regulatory processes (see (13)). Placing FtsZ and/or FtsW under the control of an inducible promoter can then be used to drive the formation of the septation ring and consequently control the duration of the cell cycle in a more-or-less precise way (43).

Summarizing, by quantitatively modeling the dilution protocol experiments that helped to characterize the gene regulatory function at the single cell level, our study is able to explore the interplay between the variability of the cell cycle duration and other noise sources in bacterial colonies. Our results show that the trade-off of different noise sources with disparate statistical properties leads to constructive roles. We expect that the predicted phenomenology drives further experimental research in the field to reveal whether it plays a biological function.

Supporting Material

One figure, two tables, and five equations are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00325-5.