Abstract
Of the many ongoing controversies regarding the workings of the sarcoplasmic reticulum (SR) in cardiac myocytes, two unresolved and interconnected topics are 1), mechanisms of calcium (Ca2+) wave propagation, and 2), speed of Ca2+ diffusion within the SR. Ca2+ waves are initiated when a spontaneous local SR Ca2+ release event triggers additional release from neighboring clusters of SR release channels (ryanodine receptors (RyRs)). A lack of consensus regarding the effective Ca2+ diffusion constant in the SR (DCa,SR) severely complicates our understanding of whether dynamic local changes in SR [Ca2+] can influence wave propagation. To address this problem, we have implemented a computational model of cytosolic and SR [Ca2+] during Ca2+ waves. Simulations have investigated how dynamic local changes in SR [Ca2+] are influenced by 1), DCa,SR; 2), the distance between RyR clusters; 3), partial inhibition or stimulation of SR Ca2+ pumps; 4), SR Ca2+ pump dependence on cytosolic [Ca2+]; and 5), the rate of transfer between network and junctional SR. Of these factors, DCa,SR is the primary determinant of how release from one RyR cluster alters SR [Ca2+] in nearby regions. Specifically, our results show that local increases in SR [Ca2+] ahead of the wave can potentially facilitate Ca2+ wave propagation, but only if SR diffusion is relatively slow. These simulations help to delineate what changes in [Ca2+] are possible during SR Ca2+release, and they broaden our understanding of the regulatory role played by dynamic changes in [Ca2+]SR.
Introduction
In cardiac myocytes, the sarcoplasmic reticulum (SR) functions as the main Ca2+ storage organelle, and the concentration of Ca2+ within the SR ([Ca2+]SR) is determined by the balance between release through ryanodine receptors (RyRs) and uptake via pumps in the SR membrane (sarcoendoplasmic reticulum Ca2+ ATPase (SERCA)). With each heartbeat, local increases in intracellular [Ca2+] ([Ca2+]i) trigger release of SR Ca2+ in the form of thousands of individual units known as Ca2+ sparks, and the resulting cellular Ca2+ transient leads to myocyte contraction (1,2). Under pathological conditions such as Ca2+ overload, however, a spontaneous Ca2+ spark from a cluster of RyRs can trigger release from neighboring RyR clusters, and these sparks in turn trigger additional clusters, resulting in a regenerative Ca2+ wave (3). The global increase in [Ca2+]i during a wave causes Ca2+ extrusion via the Na+-Ca2+ exchanger, and the resulting inward current depolarizes the cell membrane (4). Since these inappropriate depolarizations can trigger dangerous arrhythmias, understanding the mechanisms of Ca2+ wave propagation is essential for the treatment of pathologies such as heart failure.
Diffusion of Ca2+ within the cytoplasm and triggering of neighboring RyR clusters via Ca2+-induced Ca2+ release clearly plays an important role in the propagation of cardiac Ca2+ waves (3). However, increases in cytosolic [Ca2+] due to release are accompanied by dynamic local changes in [Ca2+]SR (5–7). It is not clear how these changes might facilitate or hinder wave propagation. Recently, Keller et al. proposed that during Ca2+ waves, increases in [Ca2+]SR at unactivated sites may increase the sensitivity of RyR clusters and promote propagation (8). This hypothesis was based on the observation, in Ca2+-overloaded guinea pig myocytes, that partial inhibition of SERCA caused a decrease in wave velocity, although there was no change in wave amplitude or resting [Ca2+]. Since SERCA inhibition would be expected to increase cytosolic [Ca2+], thereby accelerating Ca2+ waves (9), these authors reasoned that dynamic changes in [Ca2+]SR influence wave propagation (8).
This hypothesis has been difficult to test directly, however, due to technical limitations. Small regions of junctional SR (JSR) associated with release sites have volumes (0.008 fL (6)) much smaller than the spatial resolution of confocal microscopes (imaging volume ∼0.06 fL), so fluorescence from neighboring SR contributes to the measured signal. In addition, because the dye most commonly used to measure [Ca2+]SR, fluo-5N, has an affinity (400 μM (6)) two to three times less than diastolic [Ca2+]SR, this indicator is operating near saturation during the Ca2+ overload conditions associated with waves. Given these considerations, it is clear that local and transient increases in [Ca2+]SR would be very difficult to detect. Complicating matters further is the fact that the speed of Ca2+ diffusion within the SR is not known precisely. Two recent experimental estimates of the SR Ca2+ diffusion constant differed by nearly an order of magnitude (10,11).
Here, we address these controversies through computational modeling. We simulate spatiotemporal changes in cytosolic and SR [Ca2+] during Ca2+ waves and examine systematically how these dynamic changes are influenced by model parameters controlling SR Ca2+ diffusion and SERCA activity. Our results show that sensitization of RyR clusters by local increases in [Ca2+]SR can indeed occur during Ca2+ waves, but only if Ca2+ movement within the SR is slow.
Methods
Model geometry
The model employed in this study (Fig. 1) simulates Ca2+ movements in two cellular compartments: release from SR to cytoplasm, uptake from cytoplasm to SR, and buffering and diffusion in each. The partial differential equations governing changes in free [Ca2+], described below, are therefore of reaction-diffusion form. The model contains a single RyR cluster/μm3. Each cluster is assumed to contain 56 channels and wrap around a transverse (T) tubule. RyR clusters are separated by distances of 2 μm in the longitudinal direction, and 0.5 μm and 1 μm in the two transverse directions. As our interest is in studying longitudinal propagation of Ca2+ waves, the model consists of an array of 20 sarcomeres placed end-to-end longitudinally. The overall dimensions are therefore 40 × 0.5 × 1 μm. The cytoplasm and network SR (NSR) are homogeneously distributed, with volumes (Table 1) calculated using standard cell volume percentages in rat ventricular myocytes (2). We assume that the T-tubule, which has a diameter of 200 μm and runs in the z direction, perpendicular to the plane of the figure, acts as a diffusion barrier.
Figure 1.
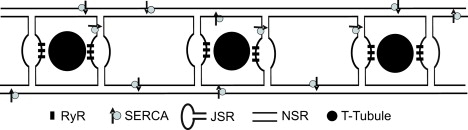
Ca2+ wave model schematic. Each release site is placed beside a transverse tubule and is located at a distance d from its neighbors. The default distance d between RyR clusters in the longitudinal direction, left to right in the figure, is 2 μm; results shown in Figs. 4, 6, and 7 also consider the case where d = 1 μm. A single cluster containing 56 RyRs is assumed to wrap completely around each T-tubule. For clarity of illustration, this is drawn as two clusters on either side of the T-tubule. NSR connects the regions of JSR associated with each release site. SERCA pumps are homogeneously distributed throughout the NSR.
Table 1.
Geometric parameters
| Parameter | Definition | Value |
|---|---|---|
| VSS | Sub-space volume | 1.0 × 10−12μL |
| VJSR | Junctional SR volume | 3.2 × 10−12μL |
| VNSR | Network SR volume | 3.2 × 10−10μL |
| VCYT | Cytoplasmic volume | 4.6 × 10−9μL |
In the two transverse directions, we apply reflective or no-flux boundary conditions. This is equivalent to assuming that in these two directions, RyR clusters spaced every 0.5 and 1 μm behave identically. Changes in [Ca2+] during longitudinal propagation of Ca2+ waves can therefore be calculated by considering the thin geometry described. Because the application of longitudinal no-flux boundary conditions at the 1st and 20th sarcomeres induces small boundary effects, only changes in [Ca2+] in the middle sarcomeres are displayed in the article (see Figs. 2–7).
Figure 2.
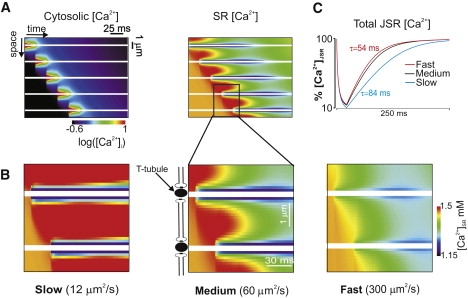
(A) Space-time image of cytosolic [Ca2+] (on a logarithmic scale) during a Ca2+ wave (left), with the corresponding image of SR [Ca2+] (right). Transverse tubules are indicated by horizontal white lines. (B) Spatiotemporal changes in [Ca2+]SR within two sarcomeres are displayed for three values of DCa,SR: 12 μm2/s (slow; left), 60 μm2/s (medium; middle), and 300 μm2/s (fast; right) Slow SR diffusion causes the most dramatic increases in [Ca2+]SR above the baseline value (1500 μM) in unactivated regions. (C) Recovery of total JSR [Ca2+] after release at an individual site depends on DCa,SR. Time constants range from 54 ms (fast) to 84 ms (slow).
Figure 3.
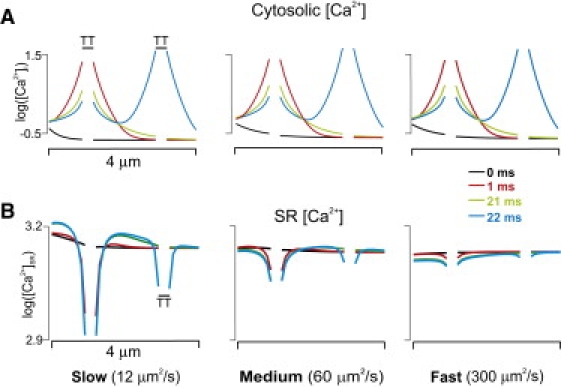
Logarithmic plots of [Ca2+]i versus location (A) at different times during a Ca2+ wave for DCa,SR = 12 μm2/s (left), 60 μm2/s (middle), and 300 μm2/s (right), with the corresponding logarithmic plots of [Ca2+]SR (B). The speed of SR Ca2+ diffusion can greatly influence [Ca2+]SR but has little effect on [Ca2+]i.
Figure 4.
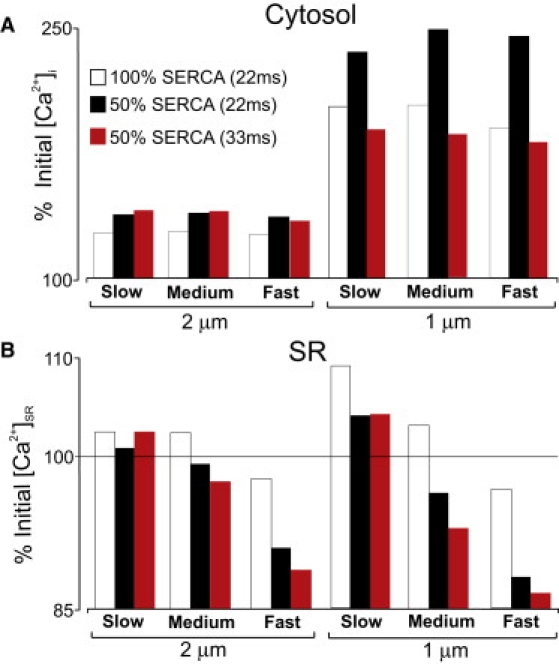
Effects of SERCA inhibition on [Ca2+]i (A) and [Ca2+]SR (B) at the target site. Bars show percentage changes in [Ca2+] with normal and partially blocked SERCA for different values of DCa,SR and different spacing between release sites.
Figure 5.
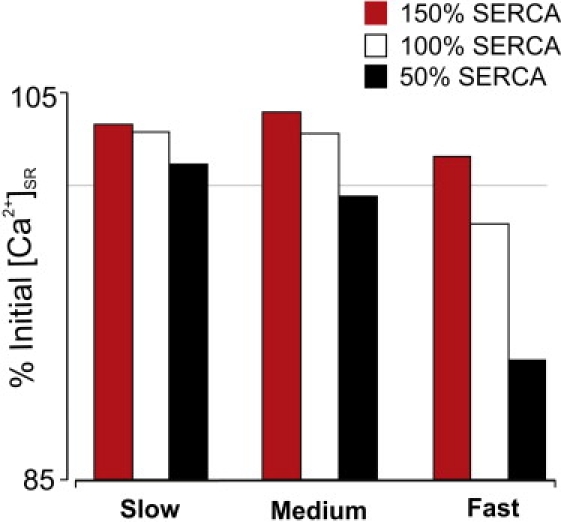
Effects of SERCA stimulation on [Ca2+]i and [Ca2+]SR at the target site. Increasing SERCA activity leads to a decrease in [Ca2+]i, and an increase in [Ca2+]SR for all values of DCa,SR.
Figure 6.
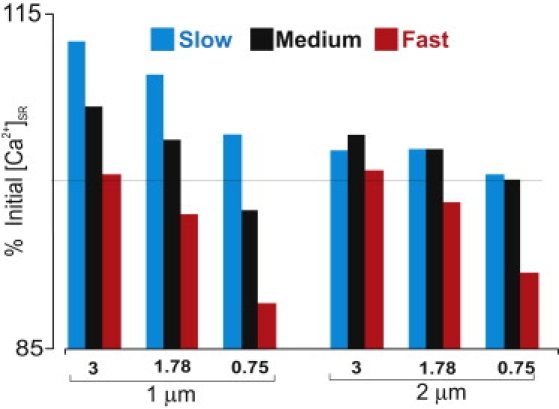
Effects of SERCA pump [Ca2+]i dependence with cluster spacing of 1 μm (left) and 2 μm (right). In either case, the exponent in the equation describing SERCA activity (η) was set to either 3, the control value of 1.78, or 0.75. An increased exponent leads to greater increases in [Ca2+]SR, and slow diffusion favors accumulation of [Ca2+]SR, in all cases.
Figure 7.
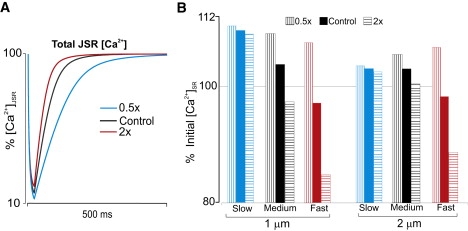
(A) Time course of JSR refilling for different values of NSR-to-JSR transfer rate v. (B) Percentage changes in target site [Ca2+]SR for different values of v and DCa,SR.
Model equations
The following sequence of events dictates the differential equations that define the model. Ca2+ is released from clusters of RyRs into a small volume, or subspace, between the SR and T-tubule membranes. From the subspace, Ca2+ is transferred to the cytoplasmic region, where it diffuses, binds to buffers, and is taken into the NSR by SERCA pumps. At the same time, release causes [Ca2+] to decrease in the JSR, and this depletion leads to Ca2+ transfer from NSR to JSR. Important features of each process are mentioned briefly before the full equations are presented.
Ca2+ release flux, Jrelease, from each RyR cluster is calculated as
| (1) |
where is the permeability of a single RyR channel, is the number of open channels in the cluster, and Vss is the volume of the subspace. As described in more detail below, we assume for simplicity that at any time, either all RyRs are open or all RyRs are closed, in which case Jrelease = 0.
In each subspace, Ca2+ can be buffered by calmodulin, sarcolemmal membrane, and SR membrane. Parameters for these buffers, assumed to be immobile in the small subspace, are given in Table 2. Binding to each buffer is described by standard buffering equations, i.e., for a generic buffer B,
| (2) |
where [B] is the concentration of free buffer, [B]Total is the total concentration of buffer (constant at each grid volume), and kon and koff are the on and off rates, respectively. The rate of change of free buffer is therefore –JB for each buffer. Fluxes corresponding to the individual buffers are added to compute, at each grid volume, the overall flux of Ca2+ onto or off of buffers.
| (3) |
Table 2.
Buffering parameters
| Parameter | Definition | Value | |
|---|---|---|---|
| [CaM]Total | Total calmodulin concentration | 24 μM | |
| Calmodulin Ca2+ on rate constant | 100 μM−1 s−1 | ||
| Calmodulin Ca2+ off rate constant | 38 s−1 | ||
| [TRPN]Total | Total troponin concentration | 70 μM | |
| Troponin Ca2+ on rate constant | 39 μM−1 s−1 | ||
| Troponin Ca2+ off rate constant | 20 s−1 | ||
| [SL]Total | Total SL membrane buffer concentration | 900 μM | |
| SL membrane buffer Ca2+ on rate constant | 115 μM−1 s−1 | ||
| SL membrane buffer Ca2+ off rate constant | 1000 s−1 | ||
| [SR]Total | Total SR membrane buffer concentration | 47 μM | |
| SR membrane buffer Ca2+ on rate constant | 115 μM−1 s−1 | ||
| SR membrane buffer Ca2+ off rate constant | 100 s−1 | ||
| [CSQ]Total | Total calsequestrin concentration | 10.0 × 103μM | |
| KCSQ | Calsequestrin Ca2+ dissociation constant | 0.63 × 103μM | |
| [JUN]Total | Total junctate concentration | 10.0 × 103μM | |
| KJUN | Junctate Ca2+ dissociation constant | 0.217 × 103μM |
The efflux (Jefflux) of Ca2+ from subspace to cytoplasm is calculated as
| (4) |
where τSS_CYT is the time constant of Ca2+ transfer between subspace and cytoplasm.
Changes in [Ca2+]SS are dictated by the balance of the above-mentioned fluxes, i.e.,
| (5) |
As in the subspace, Ca2+ in the cytoplasm can bind to buffers: a mobile buffer, calmodulin, and a stationary buffer, troponin. The equations governing binding of Ca2+ to these buffers are identical to those listed above for subspace buffers (Eq. 2). The quantities and affinities of these buffers (Table 2) are similar to those used in previous studies (12,13), and, as described below, the resulting effective diffusion constant is consistent with previous modeling studies and experimental measurements. This provides confidence that the results are not unique to our parameter choices. The rate of change of the free mobile buffer calmodulin depends on diffusion of buffer in addition to JB, i.e.,
| (6) |
where DB is the diffusion coefficient of calmodulin.
Ca2+ in the cytoplasm is also taken up into the NSR by SERCA pumps. The pump flux (Juptake) is described by the formulation of Shannon and co-workers (14):
| (7) |
where νSERCA is the maximum rate of uptake, Kmf and Kmr are forward and reverse dissociation constants, and η is the Hill exponent. In most simulations we assume that SERCA pumps are homogeneously distributed throughout the network SR, implying spatially constant νSERCA. In other simulations (see Fig. S3 of the Supporting Material), we consider heterogeneous SERCA distributions with activity maxima either at the T-tubules or at the M-lines between the T-tubules.
Ca2+ leak from the SR through RyRs is calculated as
| (8) |
where νleak defines the rate of leak. Table 3 contains values for SERCA and leak parameters.
Table 3.
Sarcoplasmic reticulum Ca2+ flux parameters
| Parameter | Definition | Value |
|---|---|---|
| νSERCA | Maximal SERCA pump rate | 865 μM/s |
| Kmf | Forward half-saturation constant for Ca2+-ATPase | 0.24 μM |
| Kmr | Reverse half-saturation constant for Ca2+-ATPase | 1.7 × 103μM |
| η | Cooperativity constant for Ca2+-ATPase | 1.78 |
| vleak | Jleak rate constant | 5.1 × 10−4 s−1 |
| PRyR | Permeability of RyR channels | 0.22 × 10−8μL/s |
Hence, the rate of change for [Ca2+]CYT is given by
| (9) |
When Ca2+ release occurs, the depleting JSR is replenished via diffusion of Ca2+ from NSR to JSR (Jrefill), calculated in the model as
| (10) |
where τNSR_JSR is the time constant of transfer between NSR and JSR. In this case, [Ca2+]NSR refers to the concentration in the grid cell adjacent to the JSR. In the manuscript, we refer to the rate of transfer, v, which is the reciprocal of τNSR_JSR. The balance equation for [Ca2+]JSR is
| (11) |
where VSS and VJSR are the subspace and JSR compartment volumes, respectively. The rapid buffering approximation (15) defines the buffering factor, βJSR, and the volume ratio rescales the flux to account for the difference in compartment volumes. We have included calsequestrin and junctate (16) as the calcium binding proteins in the JSR (see Table 2 for buffer parameters). is defined as
| (12) |
where and are the total concentrations, and and are the dissociation constants, of calsequestrin and junctate, respectively.
Finally, the rate of change for is calculated as
| (13) |
where DCa_SR is the diffusion constant for Ca2+ in the NSR. Diffusion constants and parameters controlling intercompartment transfer are provided in Table 4. Jrefill is calculated from Eq. 10 in NSR elements that are adjacent to JSR and is zero elsewhere.
Table 4.
Diffusion coefficients
| Parameter | Definition | Value | |
|---|---|---|---|
| Diffusion coefficient of Ca2+ within cytoplasm | 300 μm2 s−1 | ||
| Diffusion coefficient of Ca2+ within NSR | 12–300 μm2 s−1 | ||
| Diffusion coefficient of calmodulin and Ca2+-calmodulin | 70 μm2 s−1 | ||
| Spatial step sizes | 0.1 μm | ||
| Transfer rate of Ca2+ from subspace to cytoplasm | 4 × 10−5 s | ||
| Transfer rate of Ca2+ from NSR to JSR | 0.012 s |
Simulation protocol
Free and bound [Ca2+] in all compartments are initially assumed to be at steady state. Free cytoplasmic [Ca2+] and SR [Ca2+] are set at 0.215 and 1500 μM, respectively, to simulate a state of Ca2+ overload associated with frequent spontaneous Ca2+ waves. Because we use the bidirectional SERCA pump formulation of Shannon et al. (14) and assume a very low rate of passive leak, changes in νSERCA have a negligible effect on the steady-state levels of cytosolic and SR [Ca2+]. Ca2+ waves are simulated using a simplified protocol that eliminates the complexities caused by stochastic gating of RyRs. All RyR channels in a cluster are opened for a fixed duration of 22 ms, and RyR clusters are opened sequentially, at intervals determined by the assumed cluster spacing and wave velocity. For instance, under control conditions, we assume that waves propagate at 91 μm/s (8), which implies that sites spaced 2 μm apart open at 22-ms intervals. Our simplified protocol provides for precise control of the wave velocity, which allows us to determine how the velocity itself affects the resulting changes in cytsosolic and SR [Ca2+]. For instance, we perform two sets of simulations with partially inhibited SERCA, one in which wave velocity remains 91 μm/s (22-ms intervals), and a second set for which wave velocity is reduced to 69 μm/s (8), implying an interval of 33 ms between cluster openings.
To verify that our parameters for compartment volumes, buffers, and intercompartment fluxes are reasonable, we simulated a triggered Ca2+ transient by opening 90% of RyR clusters over a period of 120 ms. The decay and recovery of SR [Ca2+] obtained in this simulation (Fig. S1) was very similar to experimental measurements of Ca2+ scraps (6), thereby providing confidence in our parameter choices.
Comparison of effective DCa,CYT with previous models
We assume that the cytosolic diffusion constant of free Ca2+, DCa,CYT, is 300 μm2/s. After taking into account the capacities and mobilities of Ca2+ buffers, this translates to an effective DCa,CYT of ∼38 μm2/s. This is consistent with the classic measurements of Allbritton et al. (17), as well as with other computational studies of Ca2+ movements in heart cells (see Table 5). We calculated effective diffusion coefficients using the equation (18)
| (14) |
where refers to the mobile buffers listed in Table 2, N is the number of mobile buffers, and M is the number of total buffers, mobile and stationary.
Table 5.
Comparison of effective diffusion coefficients
Results
The model consists of an array of 20 RyR clusters arranged linearly, with constant spacing between them (Fig. 1). Under the assumption of uniform wave propagation in the longitudinal direction, this is equivalent to simulating many identical clusters in the transverse plane. [Ca2+] in the cytosol and SR depends on release through RyR clusters, diffusion, buffering, and uptake via SERCA pumps. To avoid variability due to stochastic gating of RyRs, we simulate Ca2+ waves by opening the channels for fixed durations and at fixed intervals, with intervals determined by the cluster spacing and wave velocity (see Methods). We further assume that 1), each RyR cluster opens for 22 ms; and 2), initial concentrations of [Ca2+]SR and [Ca2+]i are 1500 and 0.215 μM, respectively (to simulate Ca2+ overload). With this simple protocol, we investigate how model parameters affect [Ca2+]SR at the unactivated target site immediately ahead of the Ca2+ wave.
Fig. 2 A, which shows cytosolic [Ca2+] in an ∼10-μm region during a simulated Ca2+ wave, illustrates that the wave results from sequential openings of RyR clusters along the linear array. Cytosolic [Ca2+] is shown on a logarithmic scale, because the relative changes are much more extreme than those in [Ca2+]SR. Along with [Ca2+]i, the model also simulates the accompanying spatiotemporal changes in [Ca2+]SR (Fig. 2 A; right). Fig. 2 B shows [Ca2+]SR as a function of space and time within two sarcomeres for three values of DCa,SR: 12 μm2/s (slow; left), 60 μm2/s (medium; middle), and 300 μm2/s (fast; right). The first two values are similar to the recent experimental estimates (10,11), whereas the last represents an extreme case. For comparison, the free and effective Ca2+ diffusion coefficients in the cytosol are 300 μm2/s and 38.8 μm2/s, respectively. In the color scheme used to display the images, the resting level of [Ca2+]SR is orange, red represents an increase above the diastolic level, and colder colors indicate local depletion of [Ca2+]SR. T-tubules are indicated in white because [Ca2+]SR and [Ca2+]i are undefined at these locations along this particular line. Ca2+ in the cytosol and SR can, however, diffuse around the T-tubules (see Fig. 1).
The results show that extremely rapid diffusion (DCa,SR = 300 μm2/s) leads to a shallow Ca2+ gradient and lower [Ca2+]SR ahead of the wave. For intermediate or slow diffusion, however, [Ca2+]SR at the target site can increase above the initial value, as predicted by Thul et al. (19), with a DCa,SR of 5 μm2/s. Since [Ca2+]SR depletes at the activated site, this clearly does not result from diffusion within the SR. Instead, released Ca2+ travels toward the target site in the cytosol and then is pumped into the SR by SERCA, as previously proposed by Jafri and Keizer (9). Slow SR diffusion allows this local increase in [Ca2+]SR to persist. To estimate how SR diffusion influences measurable quantities such as restitution of Ca2+ spark amplitude, we performed simulations in which release occurred from a single RyR cluster. The recovery after release of total [Ca2+] (free plus bound to calsequestrin) in the JSR (Fig. 2 C) shows that slow diffusion is consistent with measurements of Ca2+ spark amplitude restitution (5,7), whereas medium and fast diffusion lead to somewhat faster recovery.
Fig. 3 displays semilogarithmic plots of cytosolic and SR [Ca2+] versus location at different times, with the breaks in each plot indicating T-tubules. These confirm the impression from the images in Fig. 2: DCa,SR has little effect on cytosolic [Ca2+] during the wave but can influence local, time-dependent changes in [Ca2+]SR. Fast diffusion attenuates gradients in SR [Ca2+], whereas slow diffusion enhances these gradients. Moreover, when diffusion is slow, Ca2+ in front of the wave can transiently increase above diastolic levels, potentially allowing for sensitization of RyRs before they are activated by cytosolic [Ca2+].
We next investigated the effects of partial (50%) inhibition of SERCA. Since experiments have demonstrated that this reduces Ca2+ wave velocity (8), we increased the interval between consecutive activations from 22 to 33 ms. Fig. 4 compares the percentage changes in [Ca2+]i (Fig. 4 A) and [Ca2+]SR (Fig. 4 B) at the target site for three cases: 1), complete SERCA activity just before activation of the target site at 22 ms; 2), partial SERCA inhibition, but assuming 22-ms intervals between activations; and 3), partial SERCA inhibition just before activation of the target site at 33 ms. The same three values of DCa,SR were considered, and the results confirm that SR Ca2+ diffusion has little effect on cytosolic [Ca2+]. Regardless of DCa,SR, however, inhibition of SERCA leads to an increase in cytosolic [Ca2+] and a decrease in [Ca2+]SR. If dynamic local changes in [Ca2+]SR played no role in Ca2+ wave propagation, these changes in cytosolic Ca2+ would be expected to accelerate rather than retard Ca2+ waves. The most striking observation in Fig. 4 concerns how the interval between release site activations influences [Ca2+]SR. Extending the interval from 22 to 33 ms leads to a decline in target site [Ca2+]SR for medium or fast diffusion, but an increase when diffusion is slow. The results therefore suggest that if slowed propagation due to SERCA inhibition results from a longer time required for an increase in [Ca2+]SR at the target site, then slow diffusion in the SR is the most plausible scenario.
We considered the possibility that three simplifications in our model could have influenced the results. One is the fact that we treat the cell as a closed system and ignore the effects of Na+-Ca2+ exchange (NCX), which will extrude Ca2+ from the myocyte during waves (4). Simulations that include either low levels of NCX, as in rat myocytes (20), or high levels of NCX, as in rabbit or guinea pig myocytes (20), show that including NCX has little effect on target site [Ca2+]SR (Fig. S2). Two other simplifications we considered were a uniform distribution of SERCA pumps in the SR membrane, and the use of the rapid buffering approximation in the JSR. Relaxing these simplifications had virtually no effect on the model predictions (Fig. S3 and Fig. S4).
Although RyR clusters are primarily located at Z-lines, implying a longitudinal spacing of ∼2 μm, the effective distance between spark sites may be considerably shorter due to nonjunctional RyR clusters (21,22) or irregularities in cellular structure (23,24). We therefore performed additional simulations in which the spacing between release sites was 1 μm rather than 2 μm. Fig. 4 (right) shows that in this case, dynamic changes in [Ca2+]SR are more dramatic, although the overall trends are the same. This further confirms that RyR sensitization by increased [Ca2+]SR requires relatively slow SR diffusion.
We also performed simulations in which SERCA activity was increased rather than decreased (Fig. 5). For all values of DCa,SR, this condition leads to decreased cytosolic [Ca2+] and increased SR [Ca2+] at the target site. The overall trend is the same, that sensitization of unactivated RyR clusters by increased [Ca2+]SR is more likely with slow than with fast SR diffusion. In a similar way, this general trend holds regardless of the exponent (η) in the equation describing SERCA uptake (Eq. 7). For η = 3, 1.78, or 0.75, fast SR diffusion leads to either a decrease or a smaller increase in [Ca2+]SR at the target site (Fig. 6), whether RyR clusters are spaced 1 μm (left) or 2 μm (right) apart. Based on biochemical data, an exponent of ∼2 is generally considered most realistic (25).
Further simulations altered the rate of Ca2+ transfer between network SR and junctional SR, referred to here as v. This parameter influences both the speed of JSR refilling (Fig. 7 A) and [Ca2+]SR at the target site (Fig. 7 B). Consistent with the effects of altering DCa,SR (Figs. 2 and 3), slower NSR-to-JSR transfer (decreased v) causes an increase in [Ca2+]SR at the target site for either 1-μm or 2-μm spacing. Of particular interest, though, is how target site [Ca2+]SR is influenced by the interplay between DCa,SR and v. When SR Ca2+ diffusion is slow, changes in v have little effect on target site [Ca2+]. However, when DCa,SR is higher, changes in v can cause more pronounced effects. This result implies that if NSR to JSR refilling is highly heterogeneous, as recent evidence suggests (26), then slow SR diffusion would allow for greater robustness in the changes in [Ca2+]SR experienced at remote sites.
Discussion
In this study, we used mathematical modeling to address two current interrelated controversies in cardiac cellular physiology: 1), can sensitization wave fronts in the SR contribute to the propagation of Ca2+ waves?; and 2), what is the speed of Ca2+ diffusion within the SR? These issues were investigated by simulating Ca2+ release from regularly spaced RyR clusters, as would occur during Ca2+ waves, and monitoring the resulting changes in cytosolic and SR [Ca2+]. Our results indicate that, consistent with the hypothesis proposed by Keller et al. (8), local increases in [Ca2+]SR can occur ahead of a propagating wave, thereby potentially sensitizing unactivated RyRs. These local increases in [Ca2+]SR do not result from diffusion within the SR; instead, Ca2+ released from an activated RyR cluster diffuses in the cytosol toward an unactivated target site, then is taken into the SR by SERCA pumps. Slow rather than fast SR Ca2+ diffusion therefore promotes the accumulation of [Ca2+]SR at unactivated sites. Partial inhibition of SERCA attenuates these local increases in [Ca2+]SR, possibly accounting for the slower Ca2+ wave propagation observed under these conditions (8), although alternative explanations are possible (see below).
Work performed in recent years has provided compelling evidence for the hypothesis that dynamic local changes in SR [Ca2+] play a major role in the regulation of SR Ca2+ release. Sobie et al. proposed that local depletion of [Ca2+]SR was responsible for the termination of Ca2+ sparks (27), and experiments performed at roughly the same time (28–30) produced data that supported this hypothesis. More recent studies have further documented the importance of local SR depletion in the regulation of both Ca2+ sparks (26,31) and Ca2+ waves (32,33). This study extends this general idea by exploring the possibility that local increases in [Ca2+]SR, in addition to local decreases, may influence SR Ca2+ release dynamics.
Two important features of our model are that 1), SR Ca2+ release occurs at discrete sites; and 2), each Ca2+ spark is treated as a discrete, all-or-none event. This general mechanism has been termed fire-diffuse-fire in mathematical models of waves (34). In a continuum model that did not take the discrete-site nature of Ca2+ release into account, we would expect different predictions about local changes in [Ca2+]SR. Ca2+ released into the cytosol through a single RyR in a continuum model will diffuse to a neighboring channel very quickly, since the channels are infinitely close. This second channel will immediately begin to open, because continuum models treat RyR open probability as a fraction between zero and one. SERCA at the second site will take Ca2+ into the SR at the same time that the partially open RyR is releasing Ca2+, and the change in local [Ca2+]SR will depend on whether release or uptake is greater. Because the maximum flux of Ca2+ through RyRs is orders of magnitude greater than the maximum rate of SERCA activity in cardiac myocytes, it is likely that realistic models will predict Ca2+ depletion rather than Ca2+ accumulation at the second RyR. This highlights the importance of considering the fire-diffuse-fire nature of Ca2+ waves in mathematical treatments of this phenomenon.
It has been difficult to unambiguously determine the effects of SERCA activity on Ca2+ wave velocity in experiments, and apparently contradictory results are present in the literature. For instance, O'Neill et al. observed that SERCA inhibition slowed Ca2+ waves (35), whereas Lukyanenko et al. reported an increase in Ca2+ wave velocity (36). The difficulty of interpretation arises from the fact that SERCA inhibition (stimulation) is likely to cause a decrease (increase) in the level of [Ca2+]SR just before wave initiation. Since wave velocity depends on the quantity of Ca2+ released during each Ca2+ spark (37), and this in turn depends on the prewave SR load, it is difficult in most experiments to delineate the separate contributions to Ca2+ wave velocity of SERCA activity and prewave [Ca2+]SR. Keller et al. (8) modulated SERCA activity rapidly using brief flashes of ultraviolet light combined with a photosensitive SERCA inhibitor. It therefore seems likely that these authors were able to measure decreased Ca2+ wave velocity before substantial changes in prewave [Ca2+]SR. However, decreased wave velocity due to lower [Ca2+]SR, rather than to SERCA inhibition per se, must still be considered as an alternative explanation for these results.
An important limitation of our simulation approach should be mentioned. Because we impose on our model the time and location-dependent SR Ca2+ release flux responsible for the Ca2+ wave, we cannot make predictions about how the time course of Ca2+ release itself may be altered by different interventions. RyR gating may be modified by pharmacological agents, phosphorylation, or mutations, and this model cannot capture how these may influence the dynamics of Ca2+ waves. The benefit of our strategy, on the other hand, is that the conclusions do not depend on specific assumptions regarding the factors that influence RyR gating. Our results do, of course, depend on SERCA activity as well as physical parameters such as diffusion constants, Ca2+ buffers, and the distance between RyR clusters. Because our simulation protocol is relatively simple, we could explore the influence of the important parameters rather systematically. Although the extent of the change in [Ca2+]SR in front of the Ca2+ wave depended on the parameter values in a particular simulation, a general trend was observed in which slow SR Ca2+ movements favored RyR sensitization at the target site, whereas fast Ca2+ movements led to depletion ahead of the wave. In future work, we plan to integrate this spatial model of multiple RyR clusters with a stochastic simulation of RyR gating to more thoroughly explore the factors that influence Ca2+ wave velocity, local changes in [Ca2+]SR, and the transition between stable Ca2+ sparks and unstable Ca2+ waves.
In conclusion, the simulations presented in this study investigated the dynamic local changes in [Ca2+]SR that occur in cardiac myocytes during Ca2+ waves. We can safely conclude that for the experimentally measured DCa,SR (10,11), it is possible that [Ca2+]SR increases near unactivated RyR clusters. Moreover, slow SR Ca2+ diffusion seems easiest to reconcile with the experimental observations of Keller et al. (8). Although the model predicts relatively small (<8%) increases in target site [Ca2+]SR, these occur at the same time that [Ca2+] is elevated on the cytosolic side. The combined effect on RyR open probability of these two changes in [Ca2+] is likely to be considerably greater than the effect of either in isolation. Future studies that combine experimental measurements with mathematical analyses will provide additional insight into the mechanisms underlying Ca2+ waves, and hopefully suggest strategies for preventing these potentially arrhythmogenic events.
Supporting Material
Four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00316-4.
Supporting Material
Acknowledgments
This article was supported by National Institutes of Health grants HL076230 and GM071558 (E.A.S.) and based in part upon work supported by the National Science Foundation under grant 0443843 (M.S.J. and E.A.S.).
References
- 1.Guatimosim S., Dilly K., Lederer W.J. Local Ca2+ signaling and EC coupling in heart: Ca2+ sparks and the regulation of the [Ca2+]i transient. J. Mol. Cell. Cardiol. 2002;34:941–950. doi: 10.1006/jmcc.2002.2032. [DOI] [PubMed] [Google Scholar]
- 2.Bers D.M. Kluwer Academic Publishers; Dordrecht, The Netherlands: 2001. Excitation-Contraction Coupling and Cardiac Contractile Force. [Google Scholar]
- 3.Cheng H., Lederer M.R., Cannell M.B. Calcium sparks and [Ca2+]i waves in cardiac myocytes. Am. J. Physiol. 1996;270:C148–C159. doi: 10.1152/ajpcell.1996.270.1.C148. [DOI] [PubMed] [Google Scholar]
- 4.Pogwizd S.M., Schlotthauer K., Bers D.M. Arrhythmogenesis and contractile dysfunction in heart failure: Roles of sodium-calcium exchange, inward rectifier potassium current, and residual β-adrenergic responsiveness. Circ. Res. 2001;88:1159–1167. doi: 10.1161/hh1101.091193. [DOI] [PubMed] [Google Scholar]
- 5.Brochet D.X., Yang D., Cheng H. Ca2+ blinks: rapid nanoscopic store calcium signaling. Proc. Natl. Acad. Sci. USA. 2005;102:3099–3104. doi: 10.1073/pnas.0500059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shannon T.R., Guo T., Bers D.M. Ca2+ scraps: local depletions of free [Ca2+] in cardiac sarcoplasmic reticulum during contractions leave substantial Ca2+ reserve. Circ. Res. 2003;93:40–45. doi: 10.1161/01.RES.0000079967.11815.19. [DOI] [PubMed] [Google Scholar]
- 7.Sobie E.A., Song L.S., Lederer W.J. Local recovery of Ca2+ release in rat ventricular myocytes. J. Physiol. 2005;565:441–447. doi: 10.1113/jphysiol.2005.086496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Keller M., Kao J.P.Y., Niggli E. Calcium waves driven by “sensitization” wave-fronts. Cardiovasc. Res. 2007;74:39–45. doi: 10.1016/j.cardiores.2007.02.006. [DOI] [PubMed] [Google Scholar]
- 9.Jafri M.S., Keizer J. On the roles of Ca2+ diffusion, Ca2+ buffers, and the endoplasmic reticulum in IP3-induced Ca2+ waves. Biophys. J. 1995;69:2139–2153. doi: 10.1016/S0006-3495(95)80088-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Swietach P., Spitzer K.W., Vaughan-Jones R.D. Ca2+-mobility in the sarcoplasmic reticulum of ventricular myocytes is low. Biophys. J. 2008;95:1412–1427. doi: 10.1529/biophysj.108.130385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wu X., Bers D.M. Sarcoplasmic reticulum and nuclear envelope are one highly interconnected Ca2+ store throughout cardiac myocyte. Circ. Res. 2006;99:283–291. doi: 10.1161/01.RES.0000233386.02708.72. [DOI] [PubMed] [Google Scholar]
- 12.Faber G.M., Silva J., Rudy Y. Kinetic properties of the cardiac L-type Ca2+ channel and its role in myocyte electrophysiology: a theoretical investigation. Biophys. J. 2007;92:1522–1543. doi: 10.1529/biophysj.106.088807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shannon T.R., Wang F., Bers D.M. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys. J. 2004;87:3351–3371. doi: 10.1529/biophysj.104.047449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Shannon T.R., Ginsburg K.S., Bers D.M. Reverse mode of the sarcoplasmic reticulum calcium pump and load-dependent cytosolic calcium decline in voltage-clamped cardiac ventricular myocytes. Biophys. J. 2000;78:322–333. doi: 10.1016/S0006-3495(00)76595-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wagner J., Keizer J. Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 1994;67:447–456. doi: 10.1016/S0006-3495(94)80500-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Treves S., Feriotto G., Zorzato F. Molecular cloning, expression, functional characterization, chromosomal localization, and gene structure of junctate, a novel integral calcium binding protein of sarco(endo)plasmic reticulum membrane. J. Biol. Chem. 2000;275:39555–39568. doi: 10.1074/jbc.M005473200. [DOI] [PubMed] [Google Scholar]
- 17.Allbritton N.L., Meyer T., Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- 18.Irving M., Maylie J., Chandler W.K. Intracellular diffusion in the presence of mobile buffers. Application to proton movement in muscle. Biophys. J. 1990;57:717–721. doi: 10.1016/S0006-3495(90)82592-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Thul R., Smith G.D., Coombes S. A bidomain threshold model of propagating calcium waves. J. Math. Biol. 2008;56:435–463. doi: 10.1007/s00285-007-0123-5. [DOI] [PubMed] [Google Scholar]
- 20.Bassani J.W., Bassani R.A., Bers D.M. Relaxation in rabbit and rat cardiac cells: species-dependent differences in cellular mechanisms. J. Physiol. 1994;476:279–293. doi: 10.1113/jphysiol.1994.sp020130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sobie E.A., Guatimosim S., Lederer W.J. The Ca2+ leak paradox and rogue ryanodine receptors: SR Ca2+ efflux theory and practice. Prog. Biophys. Mol. Biol. 2006;90:172–185. doi: 10.1016/j.pbiomolbio.2005.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lukyanenko V., Ziman A., Lederer W.J. Functional groups of ryanodine receptors in rat ventricular cells. J. Physiol. 2007;583:251–269. doi: 10.1113/jphysiol.2007.136549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hayashi T., Martone M.E., Hoshijima M. Three-dimensional electron microscopy reveals new details of membrane systems for Ca2+ signaling in the heart. J. Cell Sci. 2009;122:1005–1013. doi: 10.1242/jcs.028175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Soeller C., Crossman D., Cannell M.B. Analysis of ryanodine receptor clusters in rat and human cardiac myocytes. Proc. Natl. Acad. Sci. USA. 2007;104:14958–14963. doi: 10.1073/pnas.0703016104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lytton J., Westlin M., MacLennan D.H. Functional comparisons between isoforms of the sarcoplasmic or endoplasmic reticulum family of calcium pumps. J. Biol. Chem. 1992;267:14483–14489. [PubMed] [Google Scholar]
- 26.Zima A.V., Picht E., Blatter L.A. Termination of cardiac Ca2+ sparks: role of intra-SR [Ca2+], release flux, and intra-SR Ca2+ diffusion. Circ. Res. 2008;103:e105–e115. doi: 10.1161/CIRCRESAHA.107.183236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sobie E.A., Dilly K.W., Jafri M.S. Termination of cardiac Ca2+ sparks: an investigative mathematical model of calcium-induced calcium release. Biophys. J. 2002;83:59–78. doi: 10.1016/s0006-3495(02)75149-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Szentesi P., Pignier C., Niggli E. Sarcoplasmic reticulum Ca2+ refilling controls recovery from Ca2+-induced Ca2+ release refractoriness in heart muscle. Circ. Res. 2004;95:807–813. doi: 10.1161/01.RES.0000146029.80463.7d. [DOI] [PubMed] [Google Scholar]
- 29.Terentyev D., Viatchenko-Karpinski S., Györke S. Luminal Ca2+ controls termination and refractory behavior of Ca2+-induced Ca2+ release in cardiac myocytes. Circ. Res. 2002;91:414–420. doi: 10.1161/01.res.0000032490.04207.bd. [DOI] [PubMed] [Google Scholar]
- 30.Terentyev D., Viatchenko-Karpinski S., Györke S. Calsequestrin determines the functional size and stability of cardiac intracellular calcium stores: mechanism for hereditary arrhythmia. Proc. Natl. Acad. Sci. USA. 2003;100:11759–11764. doi: 10.1073/pnas.1932318100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Domeier T.L., Blatter L.A., Zima A.V. Alteration of sarcoplasmic reticulum Ca2+ release termination by ryanodine receptor sensitization and in heart failure. J. Physiol. 2009;587:5197–5209. doi: 10.1113/jphysiol.2009.177576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.MacQuaide N., Dempster J., Smith G.L. Assessment of sarcoplasmic reticulum Ca2+ depletion during spontaneous Ca2+ waves in isolated permeabilized rabbit ventricular cardiomyocytes. Biophys. J. 2009;96:2744–2754. doi: 10.1016/j.bpj.2008.12.3944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stevens S.C., Terentyev D., Györke S. Intra-sarcoplasmic reticulum Ca2+ oscillations are driven by dynamic regulation of ryanodine receptor function by luminal Ca2+ in cardiomyocytes. J. Physiol. 2009;587:4863–4872. doi: 10.1113/jphysiol.2009.175547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dawson S.P., Keizer J., Pearson J.E. Fire-diffuse-fire model of dynamics of intracellular calcium waves. Proc. Natl. Acad. Sci. USA. 1999;96:6060–6063. doi: 10.1073/pnas.96.11.6060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.O'Neill S.C., Miller L., Eisner D.A. Interplay between SERCA and sarcolemmal Ca2+ efflux pathways controls spontaneous release of Ca2+ from the sarcoplasmic reticulum in rat ventricular myocytes. J. Physiol. 2004;559:121–128. doi: 10.1113/jphysiol.2003.058917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lukyanenko V., Subramanian S., Gyorke S. The role of luminal Ca2+ in the generation of Ca2+ waves in rat ventricular myocytes. J. Physiol. 1999;518:173–186. doi: 10.1111/j.1469-7793.1999.0173r.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Keizer J., Smith G.D., Pearson J.E. Saltatory propagation of Ca2+ waves by Ca2+ sparks. Biophys. J. 1998;75:595–600. doi: 10.1016/S0006-3495(98)77550-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Soeller C., Cannell M.B. Estimation of the sarcoplasmic reticulum Ca2+ release flux underlying Ca2+ sparks. Biophys. J. 2002;82:2396–2414. doi: 10.1016/S0006-3495(02)75584-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Izu L.T., Wier W.G., Balke C.W. Theoretical analysis of the Ca2+ spark amplitude distribution. Biophys. J. 1998;75:1144–1162. doi: 10.1016/s0006-3495(98)74034-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pratusevich V.R., Balke C.W. Factors shaping the confocal image of the calcium spark in cardiac muscle cells. Biophys. J. 1996;71:2942–2957. doi: 10.1016/S0006-3495(96)79525-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


