Abstract
Infection rate is an estimate of the prevalence of arbovirus infection in a mosquito population. It is assumed that when infection rate increases, the risk of arbovirus transmission to humans and animals also increases. We examined some of the factors that can invalidate this assumption. First, we used a model to illustrate how the proportion of mosquitoes capable of virus transmission, or infectious, is not a constant fraction of the number of infected mosquitoes. Thus, infection rate is not always a straightforward indicator of risk. Second, we used a model that simulated the process of mosquito sampling, pooling, and virus testing and found that mosquito infection rates commonly underestimate the prevalence of arbovirus infection in a mosquito population. Infection rate should always be used in conjunction with other surveillance indicators (mosquito population size, age structure, weather) and historical baseline data when assessing the risk of arbovirus transmission.
Introduction
There are approximately 100 arboviruses that can infect humans and cause considerable morbidity and mortality and another 40 that can infect livestock with important economic impacts.1 The prevalence of viral infection in field-collected mosquitoes is a common surveillance indicator2 that is used to assess the risk of transmission of viruses such as West Nile virus (WNV) or western equine encephalomyelitis virus (WEEV) to humans and domestic animals. Other surveillance indicators of risk include sentinel animal seroconversions and animal or human infection data.2
When uninfected mosquitoes acquire virus from a vertebrate host, they go through a latent phase known as the extrinsic incubation period (EIP), which is the time that it takes the virus to disseminate into mosquito organs including the salivary glands from which transmission to subsequent vertebrate hosts occurs.3 The duration of the EIP varies among mosquito species, individual mosquitoes, and virus species, and is modulated by external factors such as temperature. In this study, we refer to those mosquitoes that have the ability to transmit virus as infectious. Uninfected, latent, and infectious mosquitoes can all potentially be found in a sample of mosquitoes collected for arboviral surveillance. Ideally, we would use that sample to estimate the proportion of mosquitoes in the population that are infectious because this measure would be more directly related to risk of arbovirus transmission. This method would involve individual mosquito testing for virus dissemination to the salivary glands or actual transmission (e.g., salivation into a capillary tube). However, there is no practical way to do this with large numbers of field-collected mosquitoes. Thus, the proportion of infected mosquitoes, or infection rate,4 is estimated as a substitute (Figure 1).
Figure 1.
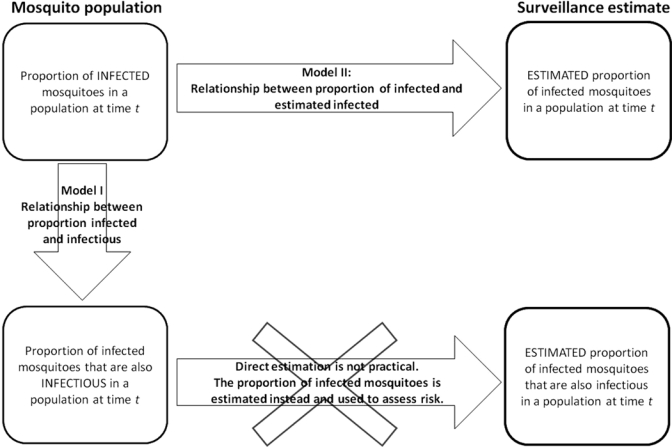
Estimation of the proportion of infected mosquitoes and its use to assess risk because direct estimation of the proportion of infected mosquitoes that are infectious is not practical. For this estimation to be useful in the assessment of risk, it is important to understand the relationships between infected and infectious mosquitoes, and between the population infection rate and its estimate. Both relationships are studied here in Models I and II.
It is assumed that when the mosquito infection rate increases, the risk of arbovirus transmission also increases.4 This assumption relies on the proportion of infected mosquitoes being a good approximation of the proportion of infectious mosquitoes. It also requires reliable estimates of the proportion of infected mosquitoes in the population. However, there are many factors that could invalidate this assumption. Environmental variation could introduce unpredictability into how many latent mosquitoes survive to become infectious, and the reliability of estimated infection rates can be compromised by biases (discussed below) introduced during mosquito collecting and virus testing.
Temperature is one of the best studied factors affecting the EIP and the rate of virus dissemination in a mosquito, thus directly influencing the proportion of latent mosquitoes that become infectious. Laboratory studies have shown that approximately 40% of Culex pipiens mosquitoes infected with WNV will develop a disseminated infection after 15 days of incubation at 20°C, but this fraction increases to almost 90% at 30°C.5 In the case of Cx. pipiens quinquefasciatus and WNV, 33% of infected mosquitoes will develop disseminated infections after 13 days of incubation at 25°C, and 81% will have disseminated infections after 13 days at 30°C.6 Dissemination is necessary for viral transmission, and some studies report that 90% of Cx. pipiens mosquitoes with disseminated WNV infections transmit the virus by bite.7,8
Another example of temperature modulating transmission is WEEV vectored by Cx. tarsalis. In a laboratory experiment, 30% of mosquitoes were capable of transmitting virus to chickens after 6 days of incubation at 32°C, but the proportion decreased to 20% after 12 days. At 25°C, only 4% of mosquitoes were capable of transmission after 6 days, but the fraction increased to 35% after 12 days.9 A different experiment found that approximately 70% of the infected Cx. tarsalis transmitted virus orally to capillary tubes seven days post-infection at 30°C, but after 12 days this fraction had decreased to approximately 12%. At 20°C approximately 25% of mosquitoes were transmitting virus after 7 days, but the percentage increased to approximately 60% after 12 days.10 Possible explanations for a reduction in transmission over time at 30–32°C include the ability of some Cx. tarsalis females to modulate viral dissemination from the mesenteron to the salivary glands or a decrease in the secretory function of the salivary glands caused by cell pathologic changes.9,10 Dissemination responses to changes in temperature are non-linear for WEEV in Cx. tarsalis. Clearly, temperature is a critical factor that modifies the response of mosquitoes to the virus, and this induced variation reduces our capacity to predict the relationship between the proportion of infected and infectious mosquitoes.
In the field, mosquitoes endure daily changes in temperature and variations of the microclimatic conditions in their resting sites during non-active periods.11 This temperature variability will cause a population of mosquitoes to contain infected individuals in different stages in the development of a disseminated infection. Consequently, mosquito samples taken on consecutive days could yield similar estimated infection rates, but the infectiousness rate could be different from one day to the next.
Ideally, to estimate the proportion of infected mosquitoes in a population, we would take a large sample of mosquitoes using an unbiased trapping method such that all individuals are equally likely to be collected. The mosquitoes would be tested individually for the presence of the virus with an assay that can detect the specific virus every time and at any concentration. Those ideal conditions are usually not met and surveillance methods introduce biases that affect the reliability of the estimated infection rates.
Trapping methods often introduce biases because they target a particular physiologic stage of the adult mosquito population (host-seeking females, gravid females, resting adults) or they attract some mosquito species more than others.2 Sampling techniques will also affect the sample size obtained, both in absolute numbers of mosquitoes and in the proportion of the population. Because not all mosquitoes are equally likely to be captured, sampling introduces a bias that affects the relationship between the actual population infection prevalence and the estimated infection rate. It is important to remember that in some cases a collecting bias towards a particular mosquito stage in the population, such as gravid females, is desirable to increase the chances of detecting virus presence in the mosquito population.
Other biases are introduced by the virus detection process. Individual testing of mosquitoes in most cases is not feasible for logistic and financial reasons. Thus, a cost-effective alternative to individual testing is to aggregate mosquitoes in groups or pools and test those for virus.4,12 There are many assays that can be used to detect virus in mosquito pools including plaque assays in Vero cell culture, TaqMan assays (reverse transcription–polymerase chain reaction [RT-PCR]), VecTest, enzyme-linked immunosorbent assays, or immunoassays. These assays differ in their power to discriminate among viruses and in their ability to detect the virus particles or plaque-forming units (PFU) at different concentrations.13,14
The quantity of virus in a mosquito pool affects the outcome of the different assays because each assay has a threshold concentration below which virus usually cannot be detected. The quantity of virus in mosquitoes is affected by time and temperature. The mean body titer of Cx. tarsalis females infected with WNV held at temperatures between 22°C and 30°C was significantly higher than the titer in those females held at temperatures between 14°C and 18°C.15 In another study with Cx. tarsalis and WEEV, body titers after incubation at 15°C ranged between 102.8 and 108.7 PFU/body (mean = 106.0 PFU/body) for mosquitoes that did not transmit virus into a capillary tube (latent), and between 105 and 108.1 PFU/body (mean = 106.9 PFU/body) for those mosquitoes that did transmit the virus (infectious). At 30°C, the titers ranged between 102.7 and 107.5 PFU/body (mean = 105.6 PFU/body) for latent mosquitoes, and between 104.1 and 107.7 PFU/body (mean = 106.4 PFU/body) for infectious mosquitoes.10 Statistical tests comparing those means were not reported by these authors. Virus titer distributions for other mosquito-virus systems in the field or in the laboratory are largely unknown. Failure to detect virus can occur when the infected mosquitoes (or mosquito) present in a pool have low virus titers, and the assay used needs a high concentration of virus particles to produce a positive result.
After mosquito pool assaying, the information on the number of mosquitoes collected in the sample, the number of pools that tested positive for virus, and the number of mosquitoes in each individual pool are used to calculate the estimated infection rate. There are various ways to conduct this calculation but the two most commonly reported are the minimum infection rate (MIR) and the maximum likelihood estimator (MLE) of the proportion of infected mosquitoes. The MIR is the ratio of the number of positive pools to the total number of mosquitoes in the sample. It is by definition the minimum infection proportion and it assumes that only one infected individual is present in a positive pool.16 The MLE is the value of the proportion of infected mosquitoes P, that maximizes the likelihood of n pools of size m to be virus positive, where P is the parameter for a binomial distribution.4,17,18 The MIR is considered appropriate to use when infections in the mosquito population are at low levels, but during periods of high transmission it will largely underestimate mosquito infections. Thus, the use of the MLE coupled with variable size pooling is recommended.17,19 A field study comparing the MIR and MLE estimated infection rates (pool size = 5) with the infection rates calculated from individual mosquitoes did not find major differences among the values generated.20 However, this pool size is rather small for arbovirus surveillance and the lack of a difference might not have much relevance for field studies. The MLE has the advantage that there are algorithms available that consider variations in pool size.17
Infection rates (e.g., MIR) are frequently reported as a measure of virus activity among mosquitoes. However, studies assessing the associations between mosquito infection rates and human or domestic animal disease incidence are limited. A recent study used a 25-year weekly data set from Massachusetts to show that human cases of infection with eastern equine encephalitis virus were positively associated with the number of infected Culiseta melanura per trap night and with weekly estimates of mosquito infection with eastern equine encephalitis virus.21 The study also observed that the MIR reached values ≥ 1.0 at approximately week 31 in years when human cases were reported, contrary to years without human cases.21 Important thresholds of mosquito infection above which human illness can be expected have been determined for other viruses. For example, in Arizona, an MIR ≥ 4 for WNV from weekly Culex mosquito pools is considered a high level of viral activity and human cases are expected to occur.22 In California, an MIR ≥ 5 for WNV, also from weekly Culex mosquito pools, is an indicator of increased risk of transmission and could lead to emergency planning or to the declaration of an epidemic if other risk factors have also increased concurrently.23 Although associations exist and mosquito infection rates are used in surveillance, infection rates have limitations. The lack of detection of infection in mosquitoes is not necessarily an indication of absence of viral activity.24 Also, some virus detection methods could detect unviable virus RNA in mosquitoes (using PCR methods), which would bias estimates of infection, and it is not possible to easily separate infected and infectious mosquitoes.25 We explored some of the sources of error and limitations of infection rates.
As mentioned earlier, it is often assumed that as the estimated infection rate increases, the risk of transmission of arboviruses to humans and animals also increases. Basic questions arise from this assumption: does the proportion of infectious mosquitoes increase with the proportion of infected mosquitoes, and can we obtain reliable estimates of infection that reflect changes in the proportion of infected mosquitoes in the population? In this study, we used a model to examine how incubation temperature, mosquito survival, mosquito species, and virus species, influence the relationship between the proportion of infected and infectious mosquitoes (Model I, Figure 1). Additionally, we used numerical simulations to examine how the process of mosquito sampling, pooling, and virus testing affect the relationship between the proportion of infected mosquitoes in the population and estimated proportions calculated from field samples (Model II, Figure 1). Specifically, the simulations considered the sample size, the pool size, and virus concentration needed in the pool to show a positive test result.
The results of our study are a reminder of why changes in infection rates are not always associated with changes in risk of transmission and that this can be due to biologic and methodologic factors. They also indicate that our estimated infection rates usually underestimate the population prevalence of infection, that they might not be direct indicators of increases in transmission risk, and that they should always be used in conjunction with other indicators and variables when making an evaluation of virus transmission risk. A more integrated approach toward mosquito surveillance using infection rate in conjunction with other indicators of risk is necessary to assess changes in the risk of arbovirus transmission and to determine the actual need for public health alerts.
Methods and Results
Model I: Relationship between mosquito infection and infectiousness.
This model follows a cohort of mosquitoes that became infected with a virus during the first blood meal, and calculates the proportion of those infected mosquitoes that become infectious at different times t as a result of virus dissemination. Data on arbovirus dissemination in mosquitoes from two different and well documented mosquito-virus systems were obtained from the literature and were used as parameters in this model: Cx. tarsalis-WEEV and Cx. pipiens quinquefasciatus-WNV. Two constant incubation temperatures of 20°C and 30°C were considered.
Following previous similar models,26,27 the proportion of surviving mosquitoes in a cohort that are infectious at time t (INSt), was calculated as INSt = pt × INFt × Dt–t1, where p is the daily survival rate of the mosquitoes, pt is the proportion of mosquitoes surviving after t days, INFt is the proportion of mosquitoes at time t that carry the virus, and Dt–t1 is the percentage of infected mosquitoes that show dissemination after t −inus; t1 days of incubation under a particular temperature. Here, t1 is the time (in days) of the first and only infectious blood meal. Dissemination was used here as an approximation for infectiousness for the Cx. pipiens quinquefasciatus-WNV system.5,6 Data on WEEV transmission by Cx. tarsalis in the laboratory were available.9,10
A single value for the proportion of infected mosquitoes (INFt) was considered for the present model. The term INFt included latent and infectious mosquitoes as dissemination progressed over time. It was assumed that 1% of the surviving mosquitoes in the cohort became infected with the virus during the first blood meal at time t1. This assumption is a combination of the proportion of blood meals taken on infectious hosts and the probability of infection after an infectious meal. Infection rates in cohorts of mosquitoes in the laboratory do not tend to decrease with time at fixed temperatures.5,10 Thus, the proportion of infected mosquitoes was kept constant at 1% of the surviving mosquitoes at subsequent times.
The model followed the proportion of infected and infectious mosquitoes in a cohort during four gonotrophic cycles. A gonotrophic cycle was considered as the time required for a mosquito to take a blood meal, go through oogenesis, and lay eggs. We assumed that the mosquitoes can take a blood meal immediately after oviposition. We calculated INSt at the end of each of five gonotrophic cycles because they marked the times of a potential blood meal, thus, the times of potential transmission of the virus from the mosquito to a vertebrate host. The times t at which INSt was calculated were t1 = time of the first blood meal and the only blood meal when mosquitoes became infected, t2–5 = times of the second, third, fourth, and fifth blood meals. The time of mosquito emergence was t0.
Estimates of the minimum duration of the gonotrophic cycle for Cx. tarsalis and Cx. pipiens quinquefasciatus are shown in Table 1. It has been observed for other mosquito species that increases in temperature reduce the duration of the gonotrophic cycle. In a laboratory study conducted on Anopheles albimanus, the duration of the gonotrophic cycle was significantly reduced from 88.4 hours (range = 81.8–94.9 hours) at 24°C, to 69.1 hours (range = 64.6–73.6 hours) at 30°C.28 This finding indicates that an increase of 6°C would reduce the gonotrophic cycle of this mosquito by an average of 19.3 hours. The field calculations of longer-lived Cx. pipiens quinquefasciatus during the winter in Calcutta (Table 1) and the information for An. albimanus support our assumption that the gonotrophic cycle length should decrease approximately one day from 20°C to 30°C. In this study, we consider a gonotrophic cycle of five days at 20°C and four days at 30°C for both species. Time from emergence to the first blood meal is approximately two days for Cx. tarsalis and Cx. pipiens quinquefasciatus.26,30 A previous modeling study with Cx. tarsalis used a value of 2.5 days from emergence to the first blood meal to represent variations in their calculations (2–3 days).26 We use continuous values of t and consider that at 30°C blood meals were taken at 2.5 (first), 6.5, 10.5, 14.5, and 18.5 days of age. Adjusting for a longer lifespan at lower temperatures, we consider that at 20°C the first blood meal was taken at 3.5 days of age and the subsequent meals were taken at 8.5, 13.5, 18.5, and 23.5 days of age.
Table 1.
Duration of the gonotrophic cycle and daily survival rates obtained from the literature for Culex tarsalis and Cx. pipiens quinquefasciatus
| Species | Minimum duration of gonotrophic cycle, days | Daily survival rate (p) | Location of collection | Reference |
|---|---|---|---|---|
| Cx. tarsalis | 4 | 0.87 | Bakersfield, Kern County, CA: May and August. Average temperatures for Bakersfield are 22°C (May), 29°C (August).29 | 26 |
| 5 | 0.84 | Sheridan, Placer County, CA: July. Average temperature for Yuba City (30 km northwest of Sheridan) is 25°C (July).29 | 30 | |
| Cx. pipiens quinquefasciatus | 6 | 0.91 | Calcutta, India: winter months. Winter temperatures in Calcutta range between 12°C and 27°C.32 | 31 |
| 4 | 0.81 | Calcutta, India: summer months. Summer temperatures in Calcutta range between 24°C and 38°C.32 | 31 | |
| 2–3 | 0.87–0.88 | Monterrey, Mexico: June. Mean annual temperature in Monterrey is 28°C.33 | 33 |
Two daily survival rates were used in the model. A survival rate of p = 0.85 was used for the 30°C temperature for both mosquito species and p = 0.90 was used for the 20°C temperature. The possible effects of age and infection status on mosquito survival were not considered. Estimates of survival rates for Cx. tarsalis and Cx. pipiens quinquefasciatus are shown in Table 1. In Calcutta, India, higher survival rates were observed for Cx. pipiens quinquefasciatus during the winter months than in the summer months.31 Higher survival rates at cooler temperatures have also been observed for Cx. tarsalis in the laboratory.34 These observations support the selection of p = 0.90 for the 20°C temperature.
Rates of dissemination previously reported in the literature for WNV in Cx. pipiens complex mosquitoes and for WEEV in Cx. tarsalis studied under constant temperature conditions are shown in Figure 2. Those dissemination rates were the bases for estimating Dt–t1 at different times in the model. Given that for all mosquitoes the infectious blood meal was the first one, t1 was equal to 3.5 days at 20°C, and 2.5 days at 30°C. The Dt–t1 values for the all time steps are shown in Figure 2.
Figure 2.
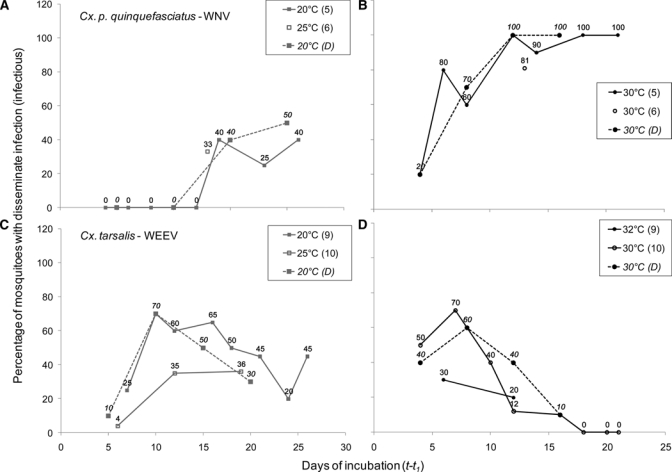
Dissemination of virus in mosquitoes at different temperatures. Each panel shows two dissemination curves with values taken from the literature (references cited in parenthesis in legends), and a third curve of values that were estimated and used as parameters (D) for Model I. (A and B) West Nile virus dissemination in Culex pipiens5 and Cx. pipiens quinquefasciatus.6 (C and D) Western equine encephalomyelitis virus dissemination in Culex tarsalis.9,10 For the Cx. tarsalis–western equine encephalomyelitis virus system, percentages correspond to oral transmission and not dissemination, and the values were approximated from figures in the original publications.
The model was implemented using Microsoft Excel (Redmond, WA).35 The mosquito-virus systems selected to illustrate different patterns of dissemination over time are only two among many types in these systems, and simplifications such as constant survival rates, fixed temperatures, and equating dissemination to infectiousness are acknowledged. However, this model illustrates the variation of patterns that can arise in the relationship between infection and infectiousness and therefore has broader implications.
Results for Model I.
The results of this model illustrate differences in viral dissemination in a cohort of mosquitoes at two temperatures (Figure 3). At 20°C, WEEV in Cx. tarsalis starts disseminating faster than WNV in Cx. pipiens quinquefasciatus. In the cohort, the highest proportion of surviving Cx. tarsalis mosquitoes that became infectious occurred 10 days after the infectious blood meal (t = 13.5 days). After this time, the proportion of infectious mosquitoes decreased because of mosquito mortality and a decrease in WEEV dissemination. The highest proportion of surviving Cx. pipiens quinquefasciatus that became infectious at 20°C occurred 20 days after initial exposure with the virus (t = 23.5 days). Under these conditions, the peak of infectiousness of Cx. tarsalis with WEEV would be reached by the third blood meal. For WNV in Cx. pipiens quinquefasciatus, it would be reached by the fifth blood meal, a point not likely to be reached by mosquitoes in nature.
Figure 3.
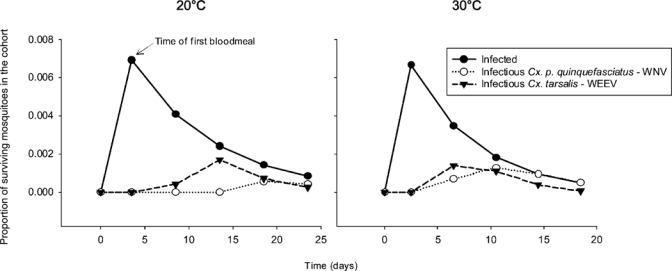
Results of Model I showing relationship between infection and infectiousness, modified by incubation time and temperature on two mosquito-virus systems. The number of mosquitoes in the cohort decreases over time (daily survival rate p = 0.90 at 20°C and p = 0.85 at 30°C), and 1% of the surviving mosquitoes acquire virus during the first blood meal. The proportion of infectious mosquitoes in the cohort changes as dissemination occurs. Simulated dissemination for western equine encephalomyelitis virus in Culex tarsalis shows a different pattern than simulated dissemination for West Nile virus in Cx. pipiens quinquefasciatus at both temperatures.
At 30°C, dissemination progressed faster for both viruses, and Cx. tarsalis infectiousness with WEEV peaked by the second blood meal (t = 6.5 days). Infectiousness for Cx. pipiens quinquefasciatus with WNV increased steadily until all surviving mosquitoes became capable of virus transmission by the fourth blood meal.
Considering both temperature regimens, the peak of the proportion of surviving mosquitoes that were infected occurred during the first blood meal, but the peaks in the proportion of surviving mosquitoes that were infectious occurred days after. Therefore, the peaks of infection and infectiousness do not coincide. Thus, variability in dissemination over time causes the proportion of infectious mosquitoes to not be a constant fraction of the number of infected mosquitoes, even under these simplified conditions.
Model II: Relationship between population infection prevalence and estimated infection rate.
The process of estimating infection rates using samples taken from a mosquito population was modeled using numerical simulations. The simulations consisted of sampling a hypothetical population of mosquitoes with a known infection rate, randomly grouping the sampled individuals into pools, and simulating viral assays with different abilities to detect virus (Figure 4). Variations were introduced on sample size (200, 2000), pool size (20, 50) and in the ability of the assay to detect the virus (low, high). All the simulations were conducted using R software 2.7.0.36
Figure 4.
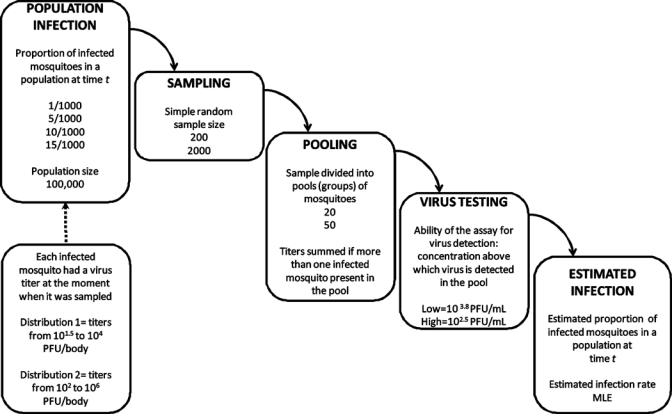
Design for the simulations of Model II to study the relationship between proportion of infected mosquitoes in a population and the infection rate.
Hypothetical mosquito populations consisted of 100,000 individuals. Each population had two attributes: proportion of infected mosquitoes and a distribution of virus titers among infected mosquitoes. Four proportions of infected mosquitoes in the population were considered: 1/1,000, 5/1,000, 10/1,000, or 15/1,000. Two virus titer distributions were used. Distribution 1 had titers between 101.5 and 104 PFU/body, and Distribution 2 had titers between 102 and 106 PFU/body. These patterns approximate those observed in Cx. pipiens 4–30 days post-infection with WNV at 18–20°C (Distribution 1) and at 26–30°C (Distribution 2).5 Titers were assigned randomly to each infected mosquito in the population using a uniform distribution. By randomly assigning titers, we were assuming that mosquitoes at any point in the virus extrinsic incubation period could be collected at any particular time. The two distributions overlap, but this has also been observed in Cx. tarsalis infected with WEEV and WNV.10,15 Our goal was to determine how these titer distributions interact with the virus detection ability of the assays to influence the resulting value of the estimated infection rate.
Because simple random sample sizes of 200 and 2,000 were drawn with replacement, each repeated sample was taken from the original population. A total of 1,000 samples of each size were taken from each hypothetical population. It was assumed that only females were sampled and that they were all equally likely to be collected regardless of their age, gonotrophic status or feeding status (empty, bloodfed). These sample sizes were selected to represent small and large values that could be common during surveillance. The probability of the sample containing infected mosquitoes increases asymptotically for small and large samples as the proportion of infected mosquitoes in the population increases.
Each sample was divided into groups or pools, as is usually done in surveillance studies to screen large numbers of mosquitoes, and each pool was tested for the presence of virus. Two pool sizes were considered, 20 and 50 mosquitoes. Each sample of 200 mosquitoes was divided into 4 pools of 50 or 10 pools of 20. Each sample of 2,000 mosquitoes was divided into 40 pools of 50 or 100 pools of 20. The mosquitoes were randomly assigned to each pool.
Each simulated pool was individually evaluated for the presence of virus. Plaque-forming units of virus were assumed to be individual discrete units, and if more than one infected mosquito was present in the pool their titers were summed. The total PFUs in the pool was then divided by 2.5 to generate a PFU/mL concentration for each pool to simulate typical homogenization and extraction methods (using 2.5 mL of diluent as for the VecTest).13
Two viral assays with different virus detection ability were simulated. The first one was an assay that could only detect virus at concentrations ≥ 103.8 PFU/mL. This was called the low detection ability assay. The second one was an assay that detected virus at concentrations ≥ 102.5 PFU/mL. This was called the high detection ability assay. The concentration threshold for the low detection ability assay is based on reports that WNV in a pool can be detected up to a minimum concentration of 103.8 PFU/mL with the VecTest13 or 103.7 PFU/mL with RT-PCR.37 The threshold for the high detection ability assay was selected based on reports that the VecTest and RT-PCR can detect virus in pools of 50 Cx. tarsalis containing only one infected female, which had been inoculated with 100 PFU of virus and held at 28°C for 3 days.14 Culex tarsalis females that were infected with WNV by feeding on infected birds developed virus titers close to 102.5 PFU/mL 2–3 days post infection.15 This finding suggests that WNV could be detected at lower levels than other studies have reported, and we used 102.5 PFU/mL as a conservative threshold. The low detection ability assay will often require two infected mosquitoes in a pool using Distribution 2 (only one if titer is ≥ 104.2 PFU/mL) to detect virus and will always require ≥ 3 mosquitoes in a pool using Distribution 1.
Once the results for all the pools from a given sample were obtained, the estimated infection rate was calculated for that sample by using the MLE.4 The MLE was calculated by using PoolInfRate 3.0 (Division of Vector-Borne Infectious Diseases, Centers for Disease Control and Prevention, Atlanta, GA, www.cdc.gov/ncidod/dvbid/westnile/software.htm). The MLE expresses the number of infected mosquitoes per 1,000 in the population. When all pools are positive, PoolInfRate will not calculate the MLE. Theoretically, in that case, the estimate of the proportion of infected mosquitoes in the population would be 1 (100% infected).
For each of the eight populations studied (four infection prevalence values × two titer distributions), eight estimated infection rate (MLE) frequency distributions were obtained with each of the sampling and testing procedures (two sample sizes × two pool sizes × two virus testing schemes). Each frequency distribution has a particular number of possible MLE outcomes determined by sample size. For example, a sample of 200 mosquitoes can be divided into 4 pools of 50 and a sample of 2,000 mosquitoes can be divided into 40 pools of 50. When one has 4 pools, and 0, 1, 2, or 3 of the pools are virus positive, the only possible MLE outcomes (as calculated with PoolInfRate 3.0) in those cases are 0, 4.93, 11.35, and 20.20 infected mosquitoes/1,000, respectively.
To explore which sample sizes, pool sizes, or virus detection assays were more likely to produce estimated infection rates close to the true population infection rate, their MLE frequency distributions were compared by using descriptive statistics (within population comparisons). Median, minimum and maximum values, and percentage of samples that produced estimates under the population infection rate (percentage of underestimation), were calculated for each frequency distribution. Even MLE values of 0.01 infected mosquitoes/1,000 below the population infection rate were considered underestimates.
To determine if MLE distributions were different between populations, pairwise comparisons of distributions were conducted by using a Kolmogorov-Smirnov test (between population comparisons). The pairwise comparisons tested differences between MLE frequency distributions for populations with 1/1,000 infected mosquitoes versus MLE frequency distributions for population with 5/1,000 infected mosquitoes. It follows that the other comparisons were between 1/1,000 versus 10/1,000, 1/1,000 versus 15/1,000, 5/1,000 versus 10/1,000, 5/1,000 versus 15/1,000, and 10/1,000 versus 15/1,000. A Bonferroni correction for multiple comparisons was applied and the overall probability to test the null hypothesis of equal distributions was 0.05/6 = 0.0083. Comparisons were made between distributions that were generated with the same sample size, pool size, and virus detection method. This comparison was necessary because those factors determine the number of outcomes in the distribution, and for the Kolmogorov-Smirnov test one needs the same number of outcomes in both groups being compared.
Results for Model II.
Frequency distributions with a total of 1,000 MLE values were obtained after simulated sampling, pooling, and testing of mosquitoes from hypothetical populations. A total of eight frequency distributions were obtained for each population (Figure 5).
Figure 5.
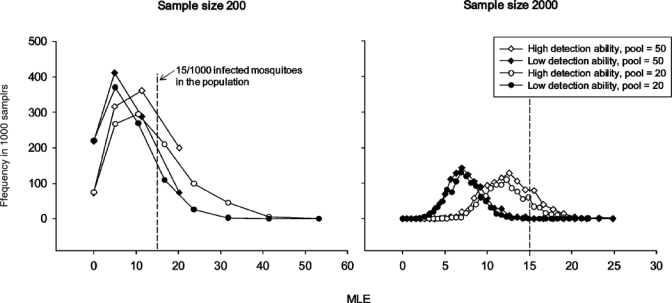
Results of Model II showing eight frequency distributions of 1,000 maximum likelihood estimator values each, which were obtained for a hypothetical mosquito population that had a proportion of 15 infected mosquitoes/1,000 and virus titer Distribution 2. Most outcomes fell below the population infection rate (dashed vertical line) that they attempt to estimate. Descriptive statistics for these distributions can be found in Table 4.
The descriptive statistics for the within population comparisons of the frequency distributions are shown in Tables 2 and 3. When hypothetical populations followed viral titer Distribution 1 (101.5–104 PFU/mosquito body), the median MLE values fell well below the population infection rate that they were attempting to estimate (Figure 6A and B) and underestimation was always > 80% (Table 2). When simulated tests with low virus detection ability were used with samples from a population with titer Distribution 1, virus detection failed in a large number of positive samples and most MLE had values of zero (Table 2). For example, we knew that 17.4% of the 1,000 samples of size 200 taken for the population with infection rate 1/1,000 and Distribution 1 contained at least one infected mosquito. However, none of those samples produced positive pools after the simulation with the low detection ability assay and the MLE values were all 0.
Table 2.
Median maximum likelihood estimator values, minimum and maximum values, and percentage of maximum likelihood estimator values under the population infection rate (percentage underestimations) for 32 frequency distributions calculated for hypothetical mosquito populations with viral titer Distribution 1
| Population infection rate | Sample size | Pool size | Low virus detection ability | High virus detection ability | ||||
|---|---|---|---|---|---|---|---|---|
| MLE | Minimum–maximum | % Underestimation | MLE | Minimum–maximum | % Underestimation | |||
| 1/1,000 | 200 | 20 | 0 | 0 | 100 | 0 | 0–10.51 | 99.8 |
| 50 | 0 | 0 | 100 | 0 | 0–11.35 | 99.9 | ||
| 2,000 | 20 | 0 | 0 | 100 | 0.50 | 0–2.03 | 82.6 | |
| 50 | 0 | 0 | 100 | 0.50 | 0–2.08 | 82.3 | ||
| 5/1,000 | 200 | 20 | 0 | 0 | 100 | 0 | 0–16.68 | 91.9 |
| 50 | 0 | 0 | 100 | 0 | 0–20.20 | 92.8 | ||
| 2,000 | 20 | 0 | 0–0.50 | 100 | 2.03 | 0–6.90 | 98.5 | |
| 50 | 0 | 0–0.50 | 100 | 2.08 | 0–7.71 | 97.8 | ||
| 10/1,000 | 200 | 20 | 0 | 0–4.99 | 100 | 4.99 | 0–23.67 | 81.5 |
| 50 | 0 | 0–4.93 | 100 | 4.93 | 0–20.20 | 83.2 | ||
| 2,000 | 20 | 0 | 0–0.50 | 100 | 4.14 | 0–10.43 | 99.8 | |
| 50 | 0 | 0–0.50 | 100 | 4.39 | 0–10 | 99.9 | ||
| 15/1,000 | 200 | 20 | 0 | 0 | 100 | 4.99 | 0–31.77 | 97.3 |
| 50 | 0 | 0–4.93 | 100 | 4.93 | 0–20.20* | 98.0 | ||
| 2,000 | 20 | 0 | 0–0.50 | 100 | 4.14 | 0.5–9.23 | 100 | |
| 50 | 0 | 0–0.50 | 100 | 4.39 | 0.5–10.83 | 100 | ||
Two of the samples produced all positive pools and were excluded because maximum likelihood estimator (MLE) values cannot be calculated with all positive pools.
Table 3.
Median maximum likelihood estimator values, minimum and maximum values, and percentage of maximum likelihood estimator values under the population infection rate (percentage underestimations) for 32 frequency distributions calculated for hypothetical mosquito populations with viral titer Distribution 2
| Population infection rate | Sample size | Pool size | Low virus detection ability | High virus detection ability | ||||
|---|---|---|---|---|---|---|---|---|
| Median MLE | Minimum–Maximum | % Underestimation | Median MLE | Minimum–maximum | % Underestimation | |||
| 1/1,000 | 200 | 20 | 0 | 0–4.99 | 92.3 | 0 | 0–10.51 | 85.3 |
| 50 | 0 | 0–4.93 | 92.3 | 0 | 0–11.35 | 85.3 | ||
| 2,000 | 20 | 0.50 | 0–2.03 | 80.0 | 0.50 | 0–3.60 | 52.5 | |
| 50 | 0.50 | 0–2.08 | 80.1 | 0.50 | 0–3.79 | 53.2 | ||
| 5/1,000 | 200 | 20 | 0 | 0–23.67 | 92.6 | 4.99 | 0–31.77 | 80.7 |
| 50 | 0 | 0–20.20* | 93.3 | 4.93 | 0–20.20* | 85.5 | ||
| 2,000 | 20 | 2.03 | 0–6.34 | 98.8 | 4.14 | 1–11.04 | 75.3 | |
| 50 | 2.08 | 0–7 | 97.3 | 3.79 | 1.01–10.83 | 70.9 | ||
| 10/1,000 | 200 | 20 | 4.99 | 0–23.67 | 80.8 | 4.99 | 0–31.77 | 58.8 |
| 50 | 4.93 | 0–20.20 | 82.6 | 4.93 | 0–20.20* | 62.3 | ||
| 2,000 | 20 | 4.14 | 0.50–9.23 | 100 | 7.47 | 2.03–16.20 | 86.1 | |
| 50 | 4.39 | 0.50–9.21 | 100 | 7.71 | 2.08–14.51 | 78.4 | ||
| 15/1,000 | 200 | 20 | 4.99 | 0–41.38 | 86.1 | 10.51 | 0–53.20 | 63.7 |
| 50 | 4.93 | 0–20.20* | 91.9 | 11.35 | 0–20.20* | 75.2 | ||
| 2,000 | 20 | 6.90 | 2.03–14.20 | 100 | 10.50 | 4.68–21.94 | 88.9 | |
| 50 | 7 | 1.54–14.51 | 100 | 11.69 | 4.39–24.86 | 83.2 | ||
Some samples (< 5%) produced all positive pools and were excluded because maximum likelihood estimator (MLE) values cannot be calculated with all positive pools.
Figure 6.
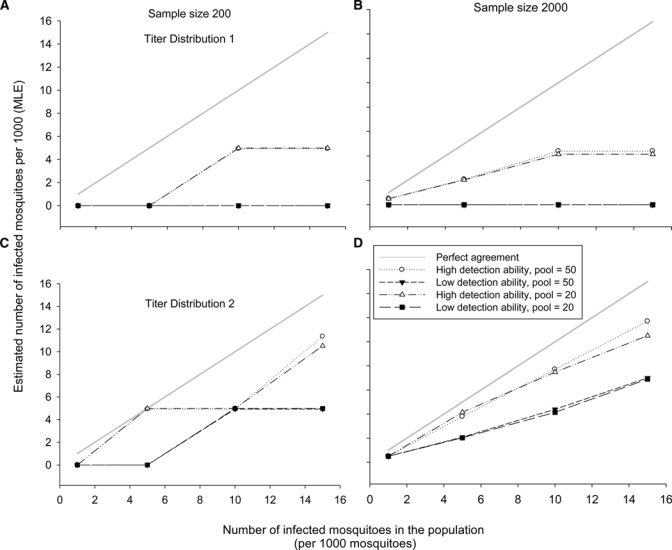
Results of Model II showing the median outcomes of the estimated infection rate (maximum likelihood estimator [MLE]) frequency distributions (see Tables 2 and 3) obtained after simulated sampling and testing of mosquitoes coming from hypothetical populations with increasing infection prevalence (1, 5, 10, and 15 infected mosquitoes/1,000). Plots A and B correspond to median MLE outcomes for populations with viral titer Distribution 1. Because the estimation usually did not differ between different pool sizes, the lines are sometimes superimposed. Plots C and D correspond to median MLE outcomes for populations with viral titer Distribution 2. A gray solid line indicating perfect agreement between population prevalence and estimated infection rate is included for comparison purposes.
When hypothetical populations had a viral titer Distribution 2 (102–106 PFU/mosquito body), median estimated infection rates (MLE) were relatively closer to the population infection rate, especially when a test with high viral detection ability was simulated (Table 3 and Figure 6C and D). However, underestimation remained the rule. The frequency distributions with median MLE closer to the true value were obtained when population infection rates were 5/1,000 and the high viral detection ability test was simulated. Sample sizes of 2,000 tended to produce frequency distributions with median MLEs that increased with the population values, especially when combined with high viral detection ability tests (Figure 6D).
These results suggest that viral titer interacts with the ability of the test to detect virus, affecting the distribution of MLE outcomes: lower titers are largely undetected by assays with low ability to detect virus. Also, simulated large sample sizes and assays with high detection ability produced median MLE values that best approximated the population infection rate in the hypothetical populations (Figure 6D). The two pool sizes produced almost identical MLE frequency distributions. Thus, the effect of pool size in these simulations was minimal.
Kolmorogov-Smirnov pairwise comparisons tested if the MLE frequency distributions were significantly different as the population infection rates increased (between population comparisons). Significant differences in the MLE frequency distributions were detected only between populations with infection prevalence of 1/1,000 and 10/1,000 and between 1/1,000 and 15/1,000, but only when the frequency distributions came from samples sizes of 2,000 and when the populations had titer Distribution 2 (Table 4). Thus, estimated infection rates only reflected changes in the actual population infection when the difference in prevalence was ≥ 10 times larger and when titers in mosquitoes were high and large samples were taken.
Table 4.
Results of the Kolmogorov-Smirnov test comparing maximum likelihood estimator frequency distributions*
| Sample size and viral titer | Ability to detect virus | Pool size | 1/1,000 vs. 10/1,000 | 1/1,000 vs. 15/1,000 | ||
|---|---|---|---|---|---|---|
| D | P | D | P | |||
| 2000, Distribution 2 | Low | 20 | 0.46 | 0.00081 | 0.51 | 0.00012 |
| 50 | 0.33 | 0.07 (NS) | 0.47 | 0.003 | ||
| High | 20 | 0.32 | 0.04 (NS) | 0.46 | 0.00081 | |
| 50 | 0.40 | 0.02 (NS) | 0.43 | 0.007 | ||
Results support significant differences among maximum likelihood estimator frequency distributions obtained for populations with infection rates of 1/1,000, and populations with infection rates of 10/1,000 or 15/1,000. The Bonferroni correction was applied (alpha = 0.05/6). NS = no significant difference.
Discussion
The results of this study suggest that estimated infection rates are more likely to reflect changes in infection prevalence in the mosquito population only when the sampling and virus testing are conducted in the best available conditions (i.e., large samples paired with assays that can detect virus at low concentrations). However, even under those conditions, infection estimates from samples are highly likely to underestimate the infection rate in the mosquito population. More importantly, these estimated infection rates are not straightforward indicators of changes in the risk of arbovirus transmission. This finding is caused by the variation among mosquitoes to complete the EIP and disseminate virus as a consequence of temperature, the time elapsed after initial infection, and the particular mosquito and virus species. For example, consider the cohort in Model I. If mosquitoes in the cohort were sampled shortly after the initial blood meal and tested under the best available conditions, the estimate of infection prevalence would be approximately 1%, the hypothetical population value. However, the risk of transmission at this point is null because there has not been any virus dissemination. Conversely, if the surviving mosquitoes were sampled around the time of the second or third blood meals, the proportion of infectious mosquitoes would be greater, but there would not be an associated significant increase in the estimated infection rate (still at 1%). Thus, when similar estimated infection rates are obtained from mosquito samples taken at different times or places, these estimates may not carry the same information about risk of virus transmission. In a larger context, if similar values of estimates of infection are obtained for the same mosquito–virus system at different periods, these estimates may not be equivalent because of variation introduced by differences in mosquito survival and environmental temperature over time. Similar infection rates estimated for two mosquito–virus systems would also be not comparable because of variations in the rate of virus dissemination associated with the biology of the system.
Model I considers only a single cohort of mosquitoes, but a population would be composed of numerous cohorts of mosquitoes at different ages. Depending on the species and environmental conditions, recruitment to the population can occur infrequently, in large emergences or steadily over time. Our model would be more appropriate to situations with infrequent, large emergences and illustrates the problem of interpretation of infection rates in the field. We anticipate that continual recruitment to a population, and the resulting variation in timing of blood meals, would increase the discrepancy between the infected and infectious populations. Further research is needed on populations with a dynamic age structure and its effect on infection dynamics.
To have a more direct measure of infectiousness, field-collected mosquitoes could be tested individually in the laboratory for virus dissemination to the salivary glands. Also, traps baited with susceptible hosts could be placed in the field to capture biting mosquitoes, test them for virus, and later test the host for infection. In that way, one would have an estimate of mosquito infection paired with a measure of transmission.38,39 However, these methods are seldom feasible, practical, or affordable for long-term surveillance programs.
Thus, estimated infection rates are necessary, and there is a large body of research dealing with ways to increase the reliability of our estimates of infection.4,12,16–19,40–42 One common recommendation is to take large samples of mosquitoes41,42 because infection is a rare event and a large sample increases the probability of collecting an infected mosquito, improving the accuracy of the estimated infection rate. In the laboratory, grouping mosquitoes in small pools is recommended to minimize the random error of the estimated infection rate because small pools approach individual mosquito testing.4,40,42 However, smaller pools would make the testing less cost-effective,12 and may be beyond the reasonable limits of public health infrastructures in many areas. The limits of pool size would not only be determined by budget and facilities but also by the maximum pool size recommended for a particular assay on the basis of its chemistry.4,42 Results from our numerical simulations point to the ability of an assay to detect virus, together with the sample size, as important factors affecting the reliability of the estimates of infection. When viral titers in the population were low (Distribution 1) or the population infection rate was low (1/1,000), the viral assay with low virus detection ability (meaning it needed relatively high concentrations of virus to produce a positive result) frequently underestimated (or failed to detect) the population infection prevalence. Therefore, using assays with the highest known detection ability is recommended. Because ideal conditions to estimate infection rates (large samples, small pools, and assays with high ability to detect virus) are difficult to achieve, it is of utmost importance to understand how biases accumulate throughout the estimation process and to be aware of them when making assessments or decisions about transmission risk based on infection rates.
One of the most important goals when monitoring infection rates is to detect changes that could be related to increased risk of arbovirus transmission to animals and humans. To determine if changes are unusual, it is necessary to calculate a baseline infection rate.43 Increases in infection rates could occur prior to or during outbreaks due to virus amplification events when biological and environmental factors are ideal for large numbers of mosquitoes to transmit virus to a large population of susceptible amplification hosts.44 Infection rates could also change after viremic hosts are introduced into an area.45 The reliability of the methods that we use to estimate infection rates, and the range of the baseline information that we have, will determine our capacity to identify unusual changes in virus activity.
However, in addition to baseline estimated infection rate data, information on other mosquito population parameters and environmental variables is necessary to determine if unusual arboviral transmission is occurring. Monitoring changes in the abundance of parous females, changes in the relative abundance of the total mosquito population, temperature, and rainfall patterns, among others, are necessary indicators that should be used in conjunction with estimated infection rates in assessing risk.2 These factors should also be investigated for extended periods to determine baseline patterns during transmission season and then compare these values to periods of epizootic and epidemic transmission.
The use of multiple criteria for risk assessment is the current procedure in some areas, such as California and Florida. These surveillance programs have a set criteria used to determine the level of risk of mosquito-borne arbovirus transmission, and have defined appropriate responses according to the assessed level of risk.23,46 Data on factors such as weather conditions, vector abundance, mosquito infection rates, sentinel chicken seroconversion, dead bird detection, and human cases are compared to historical data to determine the level of risk (e.g., normal season versus emergency) and the actions that need to be taken (public announcements, mosquito control, etc.).23,46
We acknowledge that the risk of transmission is not only a function of the proportion of infectious mosquitoes in a population, but also a function of their abundance and biting preferences. Recently, new measures of risk assessment have been proposed and could be more useful when comparing the risk in different areas or seasons, or the risk arising from different mosquito species. These are 1) the density of infected mosquitoes, resulting from the product of mosquito abundance and the estimated infection prevalence;19,47 2) the probability that a mosquito species will infect a mammal,48 which is calculated as the product of abundance, proportion of blood meals taken from mammals, the estimated infection rate, and the fraction of infected mosquitoes that will subsequently transmit virus by bite; and 3) the vector index, which considers multiple species and is calculated as the summation of the product of the average number of mosquitoes of each species per trap times the proportion of infected mosquitoes of each species.49 Although these indicators of risk need more parameters and consequently need to meet more assumptions, they might be better than infection rates alone given that they consider more complexities of the systems under surveillance. The calculation of the parameters for these risk estimates for different species and for different geographic areas is necessary. If used for surveillance, indicators of risk should not be aggregated over broad areas or long periods to account for the spatio-temporal heterogeneity in virus transmission.19
In addition to the factors examined here, there are many other factors that may influence the relationships between infection rates and risk of transmission. For example, the risk of transmission of a particular virus can change when multiple mosquito vector species are considered together. Virus strains could also vary in their dissemination rates under different temperatures,50 which would add another level of complexity to the relationship. In this study, we did not examine other environmental factors such as larval rearing conditions that can affect the susceptibility of mosquitoes to become infected and/or infectious.51 In our second model, we simulated two viral titer distributions, but empirical data on the distribution of titers in field-collected mosquitoes is limited. One study documented coarse variations in titers among different virus and mosquito species over space and time, and suggested that monitoring high titers of virus in mosquitoes in the field could help to identify species with higher vector competence and to observe the effects of temperature in the progression of the virus amplification cycle.52 In our study, we assumed that viral titers can be summed when more than one infected mosquito is present in a pool, but it is necessary to investigate how having multiple positive mosquitoes in a pool determines virus concentration. We did not consider other factors that could introduce biases and error in estimation, such as trapping biases and the false-positive detection of virus.
In Florida, field experiments using sentinel chickens to estimate the rate of virus transmission by Cx. nigripalpus showed that transmission is low in relation to estimated infection rates,38,39 and many factors that we studied here were considered to explain this occurrence. These field studies support the idea that incorporation of information on the mosquito population (age structure, abundance and estimated infection rate), virus (strain, species-specific dissemination rates), and the environment (temperature) are necessary to make assessments of the risk of virus transmission.
The results from our simplified models remind us that estimates of mosquito infection prevalence may not be directly related to the risk of transmission of arboviruses to animals and humans. The general assumption that increases in infection rates indicates increases in the risk of arbovirus transmission might not be reliable as supported by field data. It is important to remember that 1) there are biases that sampling and virus testing methods introduce in our estimates, which will cause them to generally underestimate the population infection rate; 2) similar estimated infection rates across locations, time, and for different mosquito and virus species might not indicate similar risk of arbovirus transmission because of variations in dissemination rates; 3) arbovirus baseline data are necessary to define unusual changes in transmission activity; and 4) use of other surveillance indicators in conjunction with estimated infection rates is necessary to fully assess the risk of arboviral transmission.
Acknowledgments
We thank K. Pesko for collaborating during the initial work in this study; Drs. M. Reiskind, J. F. Day, and L. P. Lounibos for reviewing the manuscript and providing many useful suggestions; and Carol Thomas for assisting in manuscript preparation.
Footnotes
Financial support: This study was supported by the National Institutes of Health (grant AI42164).
Authors' addresses: Dulce M. Bustamante, Escuela de Biologia, Universidad de San Carlos, Ciudad Universitaria, Guatemala City, Guatemala, E-mail: dulce_mariab@hotmail.com. Cynthia C. Lord, Florida Medical Entomology Laboratory, Department of Entomology and Nematology, University of Florida, Vero Beach, FL, E-mail: clord@ufl.edu.
References
- 1.Eldridge BF, Scott TW, Day JF, Tabachnick WJ. In: Medical Entomology. Eldridge BF, Edman JD, editors. Dordrecht, The Netherlands: Kluwer Academic Publishers; 2004. pp. 415–460. (Arbovirus diseases). [Google Scholar]
- 2.Moore CG, McLean RG, Mitchell CJ, Nasci RS, Tsai TF, Calisher CH, Marfin AA, Moore PS, Gubler DJ. Guidelines for Arbovirus Surveillance Programs in the United States. Fort Collins, CO: Centers for Disease Control and Prevention; 1993. [Google Scholar]
- 3.Kyle JL, Harris E. Global spread and persistence of dengue. Annu Rev Microbiol. 2008;62:71–92. doi: 10.1146/annurev.micro.62.081307.163005. [DOI] [PubMed] [Google Scholar]
- 4.Chiang CL, Reeves WC. Statistical estimation of virus infection rates in mosquito vector populations. Am J Hyg. 1962;75:377–391. doi: 10.1093/oxfordjournals.aje.a120259. [DOI] [PubMed] [Google Scholar]
- 5.Dohm DJ, O'Guinn ML, Turell MJ. Effect of environmental temperature on the ability of Culex pipiens (Diptera: Culicidae) to transmit West Nile virus. J Med Entomol. 2002;39:221–225. doi: 10.1603/0022-2585-39.1.221. [DOI] [PubMed] [Google Scholar]
- 6.Richards SL, Mores CN, Lord CC, Tabachnick WJ. Impact of extrinsic incubation temperature and virus exposure on vector competence of Culex pipiens quinquefasciatus Say (Diptera: Culicidae) for West Nile virus. Vector Borne Zoonotic Dis. 2007;4:629–636. doi: 10.1089/vbz.2007.0101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Turell MJ, O'Guinn M, Oliver J. Potential for New York mosquitoes to transmit West Nile virus. Am J Trop Med Hyg. 2000;62:413–414. doi: 10.4269/ajtmh.2000.62.413. [DOI] [PubMed] [Google Scholar]
- 8.Turell MJ, O'Guinn M, Dohm DJ, Jones JW. Vector competence of North American mosquitoes (Diptera: Culicidae) for West Nile virus. J Med Entomol. 2001;38:130–134. doi: 10.1603/0022-2585-38.2.130. [DOI] [PubMed] [Google Scholar]
- 9.Kramer D, Hardy JL, Presser SB. Effect of temperature of extrinsic incubation on the vector competence of Culex tarsalis for western equine encephalomyelitis virus. Am J Trop Med Hyg. 1983;32:1130–1139. doi: 10.4269/ajtmh.1983.32.1130. [DOI] [PubMed] [Google Scholar]
- 10.Reisen WK, Meyer RP, Presser SB, Hardy JL. Effect of temperature on the transmission of western equine encephalomyelitis and St. Louis encephalitis viruses by Culex tarsalis (Diptera: Culicidae) J Med Entomol. 1993;30:151–160. doi: 10.1093/jmedent/30.1.151. [DOI] [PubMed] [Google Scholar]
- 11.Meyer RP, Hardy JL, Reisen WK. Diel changes in adult mosquito microhabitat temperatures and their relationship to the extrinsic incubation of arboviruses in mosquitoes in Kern County, California. J Med Entomol. 1990;27:607–614. doi: 10.1093/jmedent/27.4.607. [DOI] [PubMed] [Google Scholar]
- 12.Cowling DW, Gardner IA, Johnson WO. Comparison of methods for estimation of individual-level prevalence based on pooled samples. Prev Vet Med. 1999;39:211–225. doi: 10.1016/s0167-5877(98)00131-7. [DOI] [PubMed] [Google Scholar]
- 13.Ryan J, Dave K, Emmerich E, Fernandez B, Turell M, Johnson J, Gottfried K, Burkhalter K, Kerst A, Hunt A, Wirtz R, Nasci R. Wicking assays for the rapid detection of West Nile and St. Louis encephalitis viral antigens in mosquitoes (Diptera: Culicidae) J Med Entomol. 2003;40:95–99. doi: 10.1603/0022-2585-40.1.95. [DOI] [PubMed] [Google Scholar]
- 14.Chiles RE, Green EN, Fang Y, Goddard L, Roth A, Reisen WK, Scott TW. Blinded laboratory comparison of the in situ enzyme immunoassay, the VecTest wicking assay, and a reverse transcription-polymerase chain reaction assay to detect mosquitoes infected with West Nile and St. Louis encephalitis viruses. J Med Entomol. 2004;41:539–544. doi: 10.1603/0022-2585-41.4.539. [DOI] [PubMed] [Google Scholar]
- 15.Reisen WK, Fang Y, Martinez VM. Effects of temperature on the transmission of West Nile virus by Culex tarsalis (Diptera: Culicidae) J Med Entomol. 2006;43:309–317. doi: 10.1603/0022-2585(2006)043[0309:EOTOTT]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 16.Gu W, Lampman R, Novak RJ. Problems in estimating mosquito infection rates using MIR. J Med Entomol. 2003;40:595–596. doi: 10.1603/0022-2585-40.5.595. [DOI] [PubMed] [Google Scholar]
- 17.Gu W, Lampman R, Novak RJ. Assessment of arbovirus vector infection rates using variable size pooling. Med Vet Entomol. 2004;18:200–204. doi: 10.1111/j.0269-283X.2004.00482.x. [DOI] [PubMed] [Google Scholar]
- 18.Walter SD, Hildreth SW, Beaty BJ. Estimation of infection in populations of organisms using pools of variable size. Am J Epidemiol. 1980;112:124–128. doi: 10.1093/oxfordjournals.aje.a112961. [DOI] [PubMed] [Google Scholar]
- 19.Gu W, Unnasch TR, Katholi CR, Lampman R, Novak RJ. Fundamental issues in mosquito surveillance for arboviral transmission. Trans R Soc Trop Med Hyg. 2008;102:817–822. doi: 10.1016/j.trstmh.2008.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Condotta SA, Hunter FF, Bidochka MJ. West Nile virus infection rates in pooled and individual mosquito samples. Vector Borne Zoonotic Dis. 2004;4:198–203. doi: 10.1089/vbz.2004.4.198. [DOI] [PubMed] [Google Scholar]
- 21.Hachiya M, Osborne M, Stinson C, Werner BG. Human eastern equine encephalitis in Massachusetts: predictive indicators from mosquitoes collected at 10 long term trap sites, 1979–2004. Am J Trop Med Hyg. 2007;76:285–292. [PubMed] [Google Scholar]
- 22.Frank B. Minimum infection rates. A tool for using mosquito trap catches to predict human disease incidence. 2004. http://www.azdhs.gov/phs/edc/edrp/es/pdf/billfrankminimuminfectionrates.pdf Available at. Accessed August 2009.
- 23.California Department of Public Health California mosquito-borne virus surveillance and response plan. 2009. http://www.cdph.ca.gov/HealthInfo/discond/Documents/2009Mosq-SurvRespPlan.pdf Available at. Accessed August 2009.
- 24.Georgia Department of Community Health Mosquito surveillance in Georgia. 2009. http://oasis.state.ga.us/Arboviral/index_mosquito.asp Available at. Accessed August 2009.
- 25.Day JF, Burgess J, Focks DA, Shroyer D. In: Florida Mosquito Control Response to the Challenge of West Nile Virus. Technical Bulletin of the Florida Mosquito Control Association No. 4. Rutledge CR, Day JF, Lord CC, O'Meara GF, Rey JR, Tabachnick WJ, editors. Fort Meyers, FL: Florida Mosquito Control Association; 2003. pp. 2–8. (Surveillance issues). [Google Scholar]
- 26.Reisen WK, Milby MM, Reeves WC, Meyer RP, Bock ME. Population ecology of Culex tarsalis (Diptera: Culicidae) in a foothill environment of Kern County, California: temporal changes in female relative abundance, reproductive status, and survivorship. Ann Entomol Soc Am. 1983;76:800–808. [Google Scholar]
- 27.Gordon-Smith CE. Factors influencing the transmission of western equine encephalomyelitis virus between its vertebrate maintenance hosts and from them to humans. Am J Trop Med Hyg. 1987;37((Suppl.)):33S–39S. doi: 10.4269/ajtmh.1987.37.33s. [DOI] [PubMed] [Google Scholar]
- 28.Rua GL, Quinonez ML, Velez ID, Zuluaga JS, Rojas W, Poveda G, Ruiz D. Laboratory estimation of the effects of increasing temperatures on the duration of gonotrophic cycle of Anopheles albimanus (Diptera: Culicidae) Mem Inst Oswaldo Cruz. 2005;100:515–520. doi: 10.1590/s0074-02762005000500011. [DOI] [PubMed] [Google Scholar]
- 29.Country Studies California weather. 2008. http://countrystudies.us/united-states/weather/California/ Available at. Accessed August 2008.
- 30.McHugh CP. Survivorship and gonotrophic cycle length of Culex tarsalis (Diptera: Culicidae) near Sheridan, Placer County, California. J Med Entomol. 1999;27:1027–1030. doi: 10.1093/jmedent/27.6.1027. [DOI] [PubMed] [Google Scholar]
- 31.Chandra G, Seal B, Hati AK. Age composition of the filarial vector Culex quinquefaciatus (Diptera: Culicidae) in Calcutta, India. Bull Entomol Res. 1996;86:223–226. [Google Scholar]
- 32.Kolkata, cultural capital of India Kolkata weather. 2008. www.kolkata.org.uk/weather-climate.html Available at. Accessed August 2008.
- 33.Elizondo-Quiroga A, Flores-Suarez A, Elizondo-Quiroga D, Ponce-Garcia G, Blitvich BJ, Contreras-Cordero JF, Gonzalez-Rojas JI, Mercado-Hernandez R, Beaty BJ, Fernandez-Sales I. Gonotrophic cycle and survivorship of Culex quinquefasciatus (Diptera: Culicidae) using sticky ovitraps in Monterrey, northeastern Mexico. J Am Mosq Control Assoc. 2006;22:10–14. doi: 10.2987/8756-971X(2006)22[10:GCASOC]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 34.Reisen WK. Effect of temperature on Culex tarsalis (Diptera: Culicidae) from the Coachella and San Joaquin valleys of California. J Med Entomol. 1995;32:636–645. doi: 10.1093/jmedent/32.5.636. [DOI] [PubMed] [Google Scholar]
- 35.Microsoft Corporation . Microsoft Office Excel. Redmond, WA: Microsoft Corporation; 2007. [Google Scholar]
- 36.R Development Core Team . R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2008. [Google Scholar]
- 37.Hadfield TL, Turell M, Dempsey MP, David J, Park EJ. Detection of West Nile virus in mosquitoes by RT-PCR. Mol Cell Probes. 2001;15:147–150. doi: 10.1006/mcpr.2001.0353. [DOI] [PubMed] [Google Scholar]
- 38.Rutledge CR, Day JF, Lord CC, Stark LM, Tabachnick WJ. West Nile virus infection rates in Culex nigripalpus (Diptera: Culicidae) do not reflect transmission rates in Florida. J Med Entomol. 2003;40:253–258. doi: 10.1603/0022-2585-40.3.253. [DOI] [PubMed] [Google Scholar]
- 39.Vitek CJ, Richards SL, Mores CN, Day JF, Lord CC. Arbovirus transmission by Culex nigripalpus in Florida, 2005. J Med Entomol. 2008;45:483–493. doi: 10.1603/0022-2585(2008)45[483:atbcni]2.0.co;2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Abel U, Schosser R, Süss J. Estimating the prevalence of infectious agents using pooled samples: biometrical considerations. Zentralbl Bakteriol. 1999;289:550–563. doi: 10.1016/s0934-8840(99)80009-7. [DOI] [PubMed] [Google Scholar]
- 41.Gu W, Novak RJ. Detection probability of arbovirus infection in mosquito populations. Am J Trop Med Hyg. 2004;71:636–638. [PubMed] [Google Scholar]
- 42.Katholi CR, Unnasch TR. Important experimental parameters for determining infection rates in arthropod vectors using pool screening approaches. Am J Trop Med Hyg. 2006;74:779–785. [PubMed] [Google Scholar]
- 43.Shroyer DA. The 1990 Florida epidemic of St. Louis encephalitis: virus infection rates in Culex nigripalpus. J Fla Mosq Control Assoc. 1991;62:69–71. [Google Scholar]
- 44.Day JF. Predicting St. Louis encephalitis virus epidemics: lessons from recent, and not so recent, outbreaks. Ann Rev Entomol. 2001;46:111–138. doi: 10.1146/annurev.ento.46.1.111. [DOI] [PubMed] [Google Scholar]
- 45.Broom AK, Lindsay MDA, Johansen CA, Wright AE, Mckenzie JS. Two possible mechanisms for survival and initiation of Murray Valley encephalitis virus activity in the Kimberley region of Western Australia. Am J Trop Med Hyg. 1995;53:95–99. [PubMed] [Google Scholar]
- 46.Florida Department of Health . Surveillance and Control of Selected Mosquito-Borne Diseases in Florida. 2009 Guidebook. Tallahassee, FL: Division of Environmental Health; 2009. [Google Scholar]
- 47.Ezenwa VO, Godsey MS, King RJ, Guptill SC. Avian density and West Nile virus: testing associations between biodiversity and infectious disease risk. Proc Biol Soc. 2006;273:109–117. doi: 10.1098/rspb.2005.3284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kilpatrick AM, Kramer LD, Campbell SR, Alleyne O, Dobson AP, Daszak P. West Nile virus risk assessment and the bridge vector paradigm. Emerg Infect Dis. 2005;11:425–429. doi: 10.3201/eid1103.040364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gujral IB, Zielinski-Gutierrez EC, LeBailly A, Nasci R. Behavioral risk for West Nile virus disease, northern Colorado, 2003. Emerg Infect Dis. 2007;13:419–425. doi: 10.3201/eid1303.060941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kilpatrick AM, Meola MA, Moudy RM, Kramer LD. Temperature, viral genetics, and the transmission of West Nile virus by Culex pipiens mosquitoes. PLoS Pathog. 2008;4:e1000092. doi: 10.1371/journal.ppat.1000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Alto BW, Lounibos LP, Higgs S, Juliano SA. Larval competition differentially affects arbovirus infection in Aedes mosquitoes. Ecology. 2005;86:3279–3288. doi: 10.1890/05-0209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Nasci RS, Mitchell CJ. Arbovirus titer variation in field-collected mosquitoes. J Am Mosq Control Assoc. 1996;12:167–171. [PubMed] [Google Scholar]


