Time Scale and Adjusted Survival Curves for Marginal Structural Cox Models

Abstract

Typical applications of marginal structural time-to-event (e.g., Cox) models have used time on study as the time scale. Here, the authors illustrate use of time on treatment as an alternative time scale. In addition, a method is provided for estimating Kaplan-Meier–type survival curves for marginal structural models. For illustration, the authors estimate the total effect of highly active antiretroviral therapy on time to acquired immunodeficiency syndrome (AIDS) or death in 1,498 US men and women infected with human immunodeficiency virus and followed for 6,556 person-years between 1995 and 2002; 323 incident cases of clinical AIDS and 59 deaths occurred. Of the remaining 1,116 participants, 77% were still under observation at the end of follow-up. By using time on study, the hazard ratio for AIDS or death comparing always with never using highly active antiretroviral therapy from the marginal structural model was 0.52 (95% confidence interval: 0.35, 0.76). By using time on treatment, the analogous hazard ratio was 0.44 (95% confidence interval: 0.32, 0.60). In time-to-event analyses, the choice of time scale may have a meaningful impact on estimates of association and precision. In the present example, use of time on treatment yielded a hazard ratio further from the null and more precise than use of time on study as the time scale.

In time-to-event data analysis, the epidemiologist must articulate the event of interest as well as the time origin and time scale. The “time origin” is the point at which each individual starts being at risk for the event of interest, and the “time scale” is the metric on which the risk sets are constructed and times to event are measured (1). For example, in a study where the event of interest is sexually acquired human immunodeficiency virus (HIV), the origin might be the age of sexual debut, with the associated time scale being duration of sexual activity.

Choice of origin and time scale (hereafter, collectively time scale) will not affect estimates of the rate ratio from Poisson regression models (unless those estimates are stratified by time); in such models, person-time is considered exchangeable, and the sum of person-years and number of events are invariant to the choice of time scale. However, the choice of time scale may affect estimates of the hazard ratio from Cox proportional hazards models (2, 3). Although the sum of person-years and number of events both again remain invariant, the composition of the risk sets, and therefore who serves as a comparator to whom, may differ with choice of time scale.

In randomized clinical trials where treatment is assigned at the beginning of the trial, a natural time origin is randomization date, and the associated time scale is time since randomization. Disregarding any run-in period, the time since randomization coincides with the time on study. Similarly, in this setting, the time on study typically coincides with time on treatment (for at least 1 study arm). In contrast, in observational cohort studies, the time on study does not typically coincide with the time on treatment, though some have called for such new-user designs (4).

To date, implementations of marginal structural (5) Cox proportional hazards (6) models in observational cohort studies have typically used time on study as the time scale (7–17); these studies have not considered the role of time scale on estimates of effect (18, 19). Here, we compare the use of time on study and time on treatment as competing time scales in marginal structural Cox proportional hazards models. We also extend time-fixed inverse probability of treatment weighted adjusted survival curves (20, 21) to allow for 1) time-varying inverse probability of treatment and censoring (IPTC) weights and 2) time on treatment as the time scale.

MATERIALS AND METHODS

Study population

This analysis used information from the Multicenter AIDS Cohort Study (MACS) (22) that, beginning in 1984, enrolled 6,972 homosexual and bisexual men in Baltimore, Maryland; Chicago, Illinois; Pittsburgh, Pennsylvania; and Los Angeles, California, as well as from the Women's Interagency HIV Study (WIHS) (23) that, beginning in 1994, enrolled 3,772 women in New York, New York; Chicago, Illinois; Los Angeles and San Francisco, California; and Washington, DC. Every 6 months, participants in both studies completed an extensive interviewer-administered questionnaire regarding antiretroviral therapy use and provided a blood sample for the determination of CD4 cell count and HIV viral load. Exposures and covariates were updated at these 6-month study visits, while outcomes were under continuous monitoring. Positive enzyme-linked immunosorbent assays with confirmatory Western blots were used to determine HIV seropositivity. Institutional review boards approved all protocols and informed consent forms, which were completed by study participants in both cohorts.

This report focuses on reanalysis (9) of 1,498 participants who were HIV positive, were free of clinical acquired immunodeficiency syndrome (AIDS), and had not initiated highly active antiretroviral therapy (HAART) at a study visit by September 1995, just prior to the availability of HAART in the United States; follow-up began between September 1995 and March 2000. Participants were followed through April 2002 for primary diagnosis of clinical AIDS or death. Clinical AIDS was defined by 1993 Centers for Disease Control and Prevention criteria and required diagnosis of a clinical AIDS-defining illness; that is, a CD4 count of <200 cells/mm³ or a CD4 percent of <14 by itself was not considered clinical AIDS (24). Deaths were ascertained by using death certificate abstractions upon notification and National Death Index searches, as described previously (9). Participants who missed 2 consecutive study visits were classified as dropouts and censored at the date of the last visit. Participants alive and free of clinical AIDS in April 2002 were administratively censored.

The primary exposure was initiation of treatment with HAART. The definition of HAART was based on recommendations from the Department of Health and Human Services and Kaiser Panel guidelines (25) and has been described previously (9). Once participants reported HAART initiation, they were assumed to have remained on HAART for the duration of follow-up, which correctly classified 94% of the observed person-time (9).

Statistical methods

We estimated the parameters of a marginal structural Cox proportional hazards model of the form

(1)

where $X_{it}$ is a time-varying indicator of HAART initiation prior to week t for individual i = 1 to N and week t = 1 to T_i from study entry; T_i is the time (in weeks) from study entry to AIDS or death for participant i; 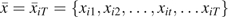is one of T + 1 possible treatment histories under the intent-to-treat assumption, “once initiated, always treated,” namely, never treated $\{0,0,\text{…},0\}$ to always treated 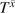$\{1,1,\text{…},1\}$; is the potential time from study entry to AIDS or death under treatment history 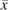, and 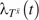is the potential hazard of AIDS or death at time t from study entry under treatment history 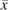, ${\text{λ}}_0\left(t\right)$ is an unspecified hazard of AIDS or death at time t from study entry in the reference (i.e., untreated) group, ${\text{α}}_1$ is the log hazard ratio comparing always treated with never treated, and ${\text{α}}_p^{\prime }$ is the transpose of the column vector of log hazard ratios for the p components of baseline covariate vector L_i0. This marginal structural model can be estimated by using IPTC weights W_it (defined in Appendix 1) under the assumptions of consistency (26, 27), positivity (28, 29), no unmeasured confounding or selection bias, and correct model specification as

(2)

where the superscript W_it indicates that the hazard of AIDS at time t from study entry for observed treatment history 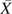, that is, λ_T 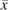(t), is weighted by W_it, ${\text{β}}_1$ is the log hazard ratio, and 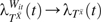, and therefore ${\text{β}}_1\to {\text{α}}_1$, if the above stated assumptions are met, as previously described (5, 8).

To accommodate time-varying IPTC weights, we approximate the marginal structural Cox model by a pooled logistic regression model (30) of the form

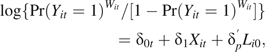(3)

where Y_it is an indicator of AIDS or death in week t for participant i; ${\text{δ}}_1$ is a discrete-time approximation to the continuous-time hazard ratio; and ${\text{δ}}_1\cong {\text{β}}_1$ if the risk of AIDS or death in any week is less than 10% (31). This condition is met in our example. Note that if one were to use the cumulative log-log link function in equation 3, rather than the logistic link function, the resulting ${\text{δ}}_1$ would be equivalent to the continuous-time hazard ratio, but the difference due to choice of link function is trivial in our case. Fitting equation 3 with ${\text{δ}}_{0t}$ parameterized by a series of indicators for weeks allows the reference group hazard to be largely unrestricted (only assumed constant within weeks); we fit equation 3 by parameterzing ${\text{δ}}_{0t}$ with a series of indicator variables for 6-month increments in follow-up. Note that, if one used the cumulative log-log link and parameterized ${\text{δ}}_{0t}$ by using an intercept and either the single variable t or log(t), the resulting model is a discrete-time version of the Gompertz or Weibull survival model for t, respectively (32).

Under the assumptions of no unmeasured confounding or selection bias, the IPTC-weighted study population provides an unbiased representation of the association between exposure and outcome in that population (5). Therefore, 2-dimensional graphical depictions (e.g., histograms, survival curves, and so on) contrasting the weighted treatment groups provide an unbiased illustration of the causal contrast (20).

Define Q_i as time of first exposure (i.e., Q_i = t if $x_{it-1}=0$ and $x_{it}=1$; otherwise Q_i = T_i). Formally, 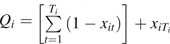. Q_i is therefore the time of HAART initiation for those who are observed to initiate HAART and is the time to AIDS, death, or censoring for those that do not initiate HAART. The person-time contributions using time on study as the time scale are then [0, Q_i] among the untreated and [Q_i, T_i] among the treated.

The IPTC-weighted Kaplan-Meier survival curves for the treated (x = 1) and untreated (x = 0) are then defined as

(4)

where $d_{tx}={\displaystyle {\sum }_{i=1}^N{W}_{it}\times Y_{it}\times 1(X_{it}=x)}$ is the weighted number of events for group x at week t, $1(·)$ is the indicator function for the argument •; similarly, $r_{tx}={\displaystyle {\sum }_{i=1}^N{W}_{it}\times 1(a<t\le b)\times 1(X_{it}=x)}$ is the weighted risk set at week t (20, 21), where {a, b} are defined as {0, Q_i} if x = 0 and {Q_i, T_i} if x = 1. This is simply an IPTC-weighted version of the extended (to allow for late entries) Kaplan-Meier estimator (3) and can be calculated simply as the extended Kaplan-Meier in the weighted study population. The risk sets defined above allow a single individual to contribute to both untreated and treated risk sets at disjoint times from study entry.

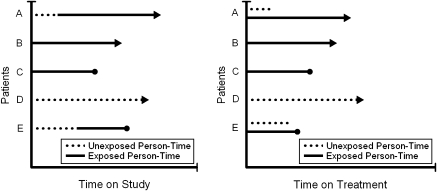
Now, we redefine the parameter we wish to estimate by considering time on treatment (i.e., time since initiation of HAART) V as an alternative to time on study T. Note that V does not represent baseline covariates. The person-time contributions are then [0, Q_i] among the untreated and [Q_i − Q_i, T_i − Q_i] among the treated. If participant i does not initiate HAART during follow-up (i.e., $X_{i{T}_i}=0$), then Q_i = T_i by definition, and participant i contributes only untreated person-time; otherwise, rewriting the treated time as [0, T_i − Q_i] shows that individual i may contribute to both untreated and treated risk sets at the same time, in terms of V. For example, participant i may contribute in the risk set for the untreated at time 6 months from study entry and in the risk set for treated at time 6 months from HAART initiation. Under this alternative time scale, each measured unit of person-time appears only once in the analysis, although 2 units of person-time for the same individual may appear in the same risk set. Furthermore, because each person can contribute only a single event to the analysis, variance correction for repeated events is unnecessary. A schematic diagram comparing the 2 time scales is shown in Figure 1. As shown in Figure 1, this change in time scale is achieved in practice by “resetting the clock” for participants when they initiate HAART; here, contributions to untreated person-time are invariant by time scale.

Figure 1.

Schematic diagram comparing time-on-study time scale and time-on-treatment time scale.

Formally, a time v under time scale V relates to a time t under time scale T as a function of t, x_it, and Q_i as $v=\left[\right(1-x_{it}\left)\right(t\left)\right]+\left[\right(x_{it}\left)\right(t-Q_i+1\left)\right]$. A marginal structural Cox model analogous to equation 1 but using this alternative time scale V in place of T is

(5)

where ${\text{ϕ}}_1\ne {\text{α}}_1$, except in settings where the choice of time scale is irrelevant (refer to Discussion). Again, as in equation 2, we estimate ϕ under the assumptions of no unmeasured confounding or selection bias using IPTC weights, and we approximate ϕ by using a weighted pooled logistic model analogous to equation 3. We compared the precision of estimated hazard ratios using confidence interval ratios (i.e., the ratio of the upper to the lower confidence limit).

IPTC-weighted Kaplan-Meier curves for this alternate time scale are created analogously to equation 4 but, among the treated, {a, b} are defined as {0, T_i − Q_i}. SAS, version 9.1, software (SAS Institute, Inc., Cary, North Carolina) was used to implement the above-described methods, and code to implement the IPTC-weighted Kaplan-Meier curves is provided in Appendix 2. We plot the complement of the IPTC-weighted Kaplan-Meier survival curves as an estimate of the cumulative incidence.

In addition to the time scales discussed here, we controlled for calendar time and age in adjusted as well as weight and structural models using restricted cubic splines (with knots at the 5th, 35th, 65th, and 95th percentiles). Control for additional confounders and functional forms of weight models are described in Appendix 1.

RESULTS

Table 1 shows characteristics at study entry by gender/cohort for the 1,498 participants. The median age at study entry was 42 years among men and 36 years among women; 79% of men and 16% of women were Caucasian. About 14% of men and 19% of women entered this study with CD4 cell counts less than 200 cells/mm³, while 61% and 57%, respectively, had CD4 counts greater than 350 cells/mm³. More women than men (35% vs. 14%) entered this study with plasma RNA levels less than or equal to 400 copies/mL. During follow-up, 323 incident cases of clinical AIDS and 59 deaths occurred, a rate of approximately 6 per 100 person-years for the combined endpoint. The remaining 1,116 participants were censored; 77% of those 1,116 were still under observation at study completion in April 2002.

Table 1.

Characteristics of 1,498 HIV-positive US Men and Women at Study Entry, 1995–2000

	Men (n = 506)		Women (n = 992)
	No.	%	No.	%
Agea	42 (37, 46)		36 (31, 42)
Caucasian race	398	78.7	163	16.4
Antiretroviral therapy
None	330	65.2	568	57.3
Monotherapy	61	12.1	260	26.2
Combination therapy	115	22.7	164	16.5
HAART	0	0	0	0
CD4 count, cells/mm3
<50	9	1.8	38	3.8
50–199	61	12.1	150	15.1
200–350	129	25.5	244	24.6
>350	307	60.7	560	56.5
CD4 count, cells/mm3,a	410 (275, 568)		389 (247, 553)
HIV RNA, copies/mL
≤400	73	14.4	349	35.2
401–10,000	124	24.5	148	14.9
>10,000	309	61.1	495	49.9
Log10 HIV RNA, copies/mLab	4.4 (3.9, 4.9)		4.6 (4.1, 5.5)
≥1 HIV-related symptomc	105	20.8	291	29.3

Abbreviations: HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus.

^aMedian (quartiles).

^bAmong persons with detectable levels (i.e., >400 copies/mL).

^cPersistent fever, diarrhea, night sweats, and weight loss.

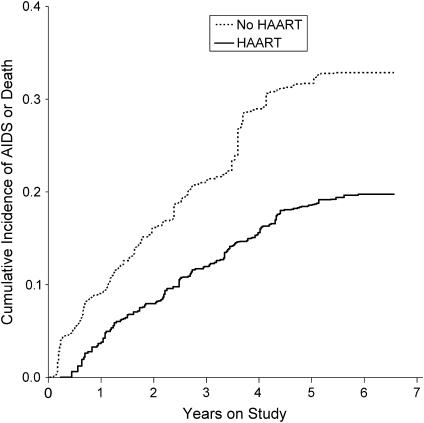
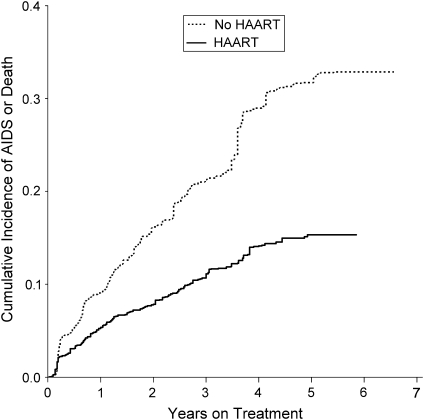
Figure 2 shows the cumulative incidence by treatment group with the x-axis being time on study, while Figure 3 shows the cumulative incidence by treatment group with the x-axis being time on treatment. As noted in Materials and Methods, the untreated curve is identical in Figures 2 and 3, and both curves are adjusted for confounding and censoring by using IPTC weights.

Figure 2.

Inverse probability of treatment and censoring weighted cumulative incidence by treatment with highly active antiretroviral therapy (HAART) on time to acquired immunodeficiency syndrome (AIDS) or death for 1,498 human immunodeficiency virus-positive US men and women, 1995–2002. Time scale is time on study.

Figure 3.

Inverse probability of treatment and censoring weighted Kaplan-Meier curves for the effect of highly active antiretroviral therapy (HAART) on time to acquired immunodeficiency syndrome (AIDS) or death for 1,498 human immunodeficiency virus-positive US men and women, 1995–2002. Time scale is time on treatment (i.e., time since HAART initiation).

Results from unadjusted, adjusted, and weighted (i.e., marginal structural) models are provided in Table 2 for both time scales. Using time on study, we observed no apparent benefit of treatment for unadjusted and adjusted models and a strong beneficial effect for the weighted model. Specifically, the hazard ratio from the marginal structural model was 0.52 (95% confidence interval (CI): 0.35, 0.76). These results replicated previously reported results (9). Previously published results were as follows: unadjusted hazard ratio = 0.98 (95% CI: 0.76, 1.26); adjusted hazard ratio = 0.81 (95% CI: 0.61, 1.07); and weighted hazard ratio = 0.54 (95% CI: 0.38, 0.78). The slight differences are due to differences in the coarseness of time categorization.

Table 2.

Estimated Effect of Highly Active Antiretroviral Therapy on Time to Acquired Immunodeficiency Syndrome or Death for 1,498 HIV-positive US Men and Women, 1995–2002

	Hazard Ratio	95% Confidence Interval
Unadjusted
Time on study	0.97	0.76, 1.24
Time on treatment	0.70	0.57, 0.86
Adjusteda
Time on study	0.81	0.61, 1.06
Time on treatment	0.67	0.53, 0.85
Weighteda
Time on study	0.52	0.35, 0.76
Time on treatment	0.44	0.32, 0.60

Abbreviations: HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus.

^aAccounting for age, race, sex, baseline and current CD4 count, baseline and current HIV RNA, follow-up time, calendar time, prophylaxis for Pneumocystis carinii, and non-HAART antiretroviral therapy.

Using time on treatment, we observed essentially equivalent results in unadjusted and adjusted models and a notably stronger hazard ratio in the marginal structural model. However, in contrast to using time on study, with time on treatment as the time scale there is a benefit of treatment apparent in the unadjusted and adjusted models. Specifically, we observed an unadjusted hazard ratio of 0.70 (95% CI: 0.57, 0.86) and an adjusted hazard ratio of 0.67 (95% CI: 0.53, 0.85). The hazard ratio from the marginal structural model was 0.44 (95% CI: 0.32, 0.60). All 3 results using the time-on-treatment time scale were more precise (i.e., had smaller confidence interval ratios) than the analogous results using time on study as the time scale.

The hazard ratios from the marginal structural models were calculated by using stabilized weights (refer to Appendix 1), which means that they are conditional, rather than purely marginal estimates of hazard ratio; these results are therefore not strictly interpretable as what we would expect to obtain from a randomized controlled trial. In contrast, Figures 2 and 3 represent unconditional estimates of the hazard ratio, and they were drawn by using unstabilized weights; the marginal hazard ratios corresponding directly to these figures are hazard ratio = 0.59 (95% CI: 0.38, 0.92) for time on study and hazard ratio = 0.45 (95% CI: 0.33, 0.62) for time on treatment. As expected, these unstabilized (purely marginal) estimates have wider confidence intervals than the analogous estimates calculated by using stabilized IPTC weights.

Last, we investigated the effect of change of time scale on constancy of the hazard ratios before and after the median event time in each time scale (87 weeks under time on study and 58 weeks under time on treatment). The effect of HAART on the hazard or death of AIDS increased with time under both time scales, but the coefficient from the product term and associated P value were both stronger under the time-on-treatment time scale (Table 3).

Table 3.

Estimated Time-dependent Effect of Highly Active Antiretroviral Therapy on Time to Acquired Immunodeficiency Syndrome or Death for 1,498 HIV-positive US Men and Women, 1995–2002^ab

	Hazard Ratio	95% Confidence Interval	Categorical Interaction at Median Event Time				Pinteraction
			Hazard Ratio (≤Median)	95% Confidence Interval	Hazard Ratio (>Median)	95% Confidence Interval
Time on study	0.52	0.35, 0.76	0.68	0.40, 1.16	0.46	0.30, 0.73	0.268
Time on treatment	0.44	0.32, 0.60	0.61	0.42, 0.90	0.32	0.21, 0.48	0.017

Abbreviations: HAART, highly active antiretroviral therapy; HIV, human immunodeficiency virus.

^aModels account for age, race, sex, baseline and current CD4 count, baseline and current HIV RNA, follow-up time, calendar time, prophylaxis for Pneumocystis carinii, and non-HAART antiretroviral therapy.

^bResults are from weighted analysis only. The table gives separate estimates of hazard ratio up to and after the median event time (87 weeks under time on study and 58 weeks under time on treatment).

DISCUSSION

The choice of time scale may affect both visual and numerical descriptions of effects in settings in which a time-varying treatment is subject to time-varying confounding affected by prior treatment. In the example presented, using time on treatment as the time scale yielded a 1.18-fold stronger estimate of the hazard ratio (0.44 compared with 0.52) and a 1.16-fold tighter confidence interval than using time on study as the time scale. Time-on-treatment results are closer to what we would expect from a randomized trial of HAART versus non-HAART. For example, Hammer et al. (33) reported a hazard ratio of 0.50 (95% CI: 0.33, 0.76) for the effect of HAART compared with dual therapy for the outcome of AIDS or death. We would expect to see a stronger effect because we are comparing HAART with a combination of dual, mono, and nontherapy (34) and because of the noncompliance reported by Hammer et al. (33). Thus, in the present example, time on treatment appears to be a more appropriate time scale for addressing the central research question.

To date, marginal structural models have typically used time on study as the time scale. However, there are advantages of using time on treatment as the time scale. Given the stated assumptions, a marginal structural model estimates the same parameter one would recover from a fully compliant randomized trial free from dropout. However, using time on study as the time scale, the marginal structural model recovers the average hazard ratio across a series of randomized trials, with randomization at each sequential timepoint. In contrast, using time on treatment as the time scale, the average hazard ratio more closely mimics what one would obtain in a standard randomized trial with the average taken over time since treatment initiation, albeit with the above-stated caveat that the inclusion of baseline covariates in the final structural model renders the estimate conditional rather than fully marginal. Moreover, departures from the proportional hazards assumption may be more scientifically compelling, or apparent, using time on treatment rather than time on study as the time scale, as illustrated above.

However, there are many cases when time on study is biologically meaningful, such as when study time begins with an acute event of interest, such as a diagnosis of HIV or an acute myocardial infarction. There are also settings in which results will be (nearly) invariant to choice of time scale. Outside the context of marginal structural models, prior work suggests that, in time-to-event analyses, one chooses the origin and time scale that are most strongly associated with the event (2) or that one adequately (i.e., flexibly) models such important time scales when using an alternate time scale (19). In the setting in which the time to event follows an exponential distribution (i.e., a constant hazard), the choice of time scale will matter little. When the origin of the chosen time scale is a strong risk factor for the event of interest, but unrelated to treatment, differences in the obtained hazard ratio may be largely due to the noncollapsibility of the hazard ratio (35, 36) rather than due to confounding by time.

The present work is subject to limitations. First, defining time on treatment is complicated if participants move on and off treatment during follow-up. This complication is similar to the choice of time scale with repeated events within the same participant (37). Here, we made an “intent-to-treat” assumption, namely, that participants remained on treatment after initiation regardless of time scale. This intent-to-treat assumption renders the complication of participants moving on and off treatment moot, at the cost of misclassifying 6% of person-time. Second, typical implementations of marginal structural models stabilize the IPTC weights using a subset of measured baseline covariates. Stabilization improves the variance of the final estimates of association, as was demonstrated here. However, if baseline factors are used to stabilize the weights, these baseline factors must then be included in the final structural model to ensure control of confounding; this inclusion means that the final model estimates are both conditional on these baseline covariates (rather than fully marginal) and imposes the additional assumption that the inclusion of such covariates is properly specified in the structural model. Because IPTC-weighted Kaplan-Meier survival curves are calculated from the simple weighted study population, one must stratify the weighted study population curves to take advantage of stabilization by baseline factors. To obtain unstratified Kaplan-Meier curves that control for confounding due to baseline and time-varying factors, the epidemiologist may exclude baseline covariates from stabilization of the IPTC weights. We took this latter approach to constructing the Kaplan-Meier curves. Last, there are subtly different specifications for the effect of calendar time in the structural models under the 2 time scales; care must be taken when (as in this case) calendar time is a strong confounder. When fitting a marginal structural model using pooled logistic regression (where the time scale is an explicit component of the model), if one models all time scales simultaneously, then one can build survival curves based on any time metric present in the model (38). However, inclusion of multiple time scales when unnecessary may adversely affect precision.

This report makes 2 contributions. First, we illustrate differences in causal effects that may be observed when using competing time scales in the context of marginal structural models. Second, we provide a method for displaying IPTC-weighted Kaplan-Meier survival curves adjusted for both time-fixed and time-varying confounding and emigrative selection bias. Both contributions have the potential to increase understanding of marginal structural models—the first because time on treatment may be a more appropriate time scale in many scientific applications, and the second because prior applications of marginal structural models have rarely included confounding and censoring-adjusted survival curves, which help to visually depict associations.

Glossary

Abbreviations

AIDS

acquired immunodeficiency syndrome

CI

confidence interval

HAART

highly active antiretroviral therapy

HIV

human immunodeficiency virus

IPTC

inverse probability of treatment and censoring

APPENDIX 1

Inverse Probability of Treatment and Censoring Weights

We account for measured confounding and emigrative selection bias in the marginal structural model using stabilized inverse probability of treatment and censoring (IPTC) weights (5). In general, IPTC weights are defined as $W_{it}=W_{it}^X\times W_{it}^C$, where

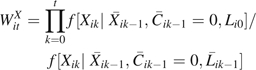and

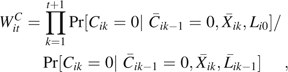where $f[·|·]$ is the conditional density function evaluated at the observed covariate values for a given participant, which was assumed to be logistic (9), and 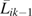is the vector of time-varying covariate histories measured up to week k – 1 including baseline covariates L_i0, and C_ik is 1 if participant i is censored because of dropout by week k and 0 otherwise. In our case, the intent-to-treat assumption leads to a simplification of the treatment history, and the treatment weights are as follows: if $X_{it-1}$ = 1, then $W_{it}^X=W_{it-1}^X$; else

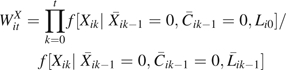The covariates included in the weights were as follows: age and calendar time (both modeled as restricted cubic splines with knots at the 5th, 35th, 65th, and 95th percentiles), race, sex, CD4 count (baseline and updated), viral RNA (baseline and updated), use of non-HAART antiretroviral therapy, use of cotrimoxazole prophylaxis, and presence of HIV symptoms (reported persistent fever, diarrhea, night sweats, or weight loss). All time-varying variables were lagged 1 visit. For more detail on covariate selection, refer to reference 9, and for further details on the estimation of IPTC weights in general, refer to reference 28. The distribution of the weights was as follows: mean, 1.03; median, 0.91; first percentile, 0.21; 99th percentile, 4.41; minimum, 0.12; and maximum, 28.5. The mean (minimum/maximum) weights for treated and untreated person-time were 1.03 (0.15/28.5) and 1.03 (0.12/10.3), respectively. These data exhibit adequate positivity, and when weights were truncated at first and 99th percentiles, the hazard ratio changed by 0.01 under both time scales.

Note that IPTC-weighted Kaplan-Meier curves were estimated by using alternate weights in which L_i0 was removed from the numerator (but not the denominator) of both $W_{it}^X$ and $W_{it}^C$. As a result, and in contrast to prior analyses (9, 39, 40), models that use these alternate weights need not include L_i0 in the final structural model. This allows the weights to control for time-fixed and time-varying confounding, and therefore the Kaplan-Meier curves drawn from such weighted data account for both time-fixed and time-varying confounding. A cost of using such weights is a loss in efficiency because the weights are less stable than those defined above.

APPENDIX 2

SAS Code for Adjusted Survival Curves