The Divergence of Chimpanzee Species and Subspecies as Revealed in Multipopulation Isolation-with-Migration Analyses

Abstract

The divergence of bonobos and three subspecies of the common chimpanzee was examined under a multipopulation isolation-with-migration (IM) model with data from 73 loci drawn from the literature. A benefit of having a full multipopulation model, relative to conducting multiple pairwise analyses between sampled populations, is that a full model can reveal historical gene flow involving ancestral populations. An example of this was found in which gene flow is indicated between the western common chimpanzee subspecies and the ancestor of the central and the eastern common chimpanzee subspecies. The results of a full analysis on all four populations are strongly consistent with analyses on pairs of populations and generally similar to results from previous studies. The basal split between bonobos and common chimpanzees was estimated at 0.93 Ma (0.68–1.54 Ma, 95% highest posterior density interval), with the split among the ancestor of three common chimpanzee populations at 0.46 Ma (0.35–0.65), and the most recent split between central and eastern common chimpanzee populations at 0.093 Ma (0.041–0.157). Population size estimates mostly fell in the range from 5,000 to 10,000 individuals. The exceptions are the size of the ancestor of the common chimpanzee and the bonobo, at 17,000 (8,000–28,000) individuals, and the central common chimpanzee and its immediate ancestor with the eastern common chimpanzee, which have effective size estimates at 27,000 (16,000–44,000) and 32,000 (19,000–54,000) individuals, respectively.

Introduction

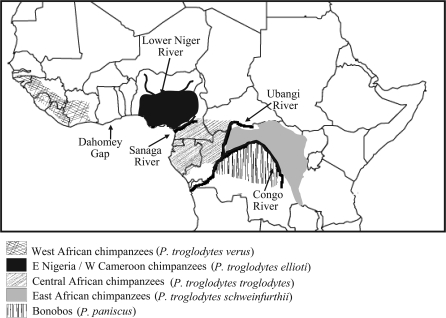
Today, wild chimpanzees still live in several forested regions in the lowest latitudes of sub-Saharan Africa (fig. 1). Because they are our own species’ closest living relatives and because divergence among chimpanzee species and subspecies appears to be early in the speciation process, the divergence among chimpanzee taxa has frequently been a focus of phylogenetic and population genetic research (Miyamoto et al. 1987; Morin et al. 1992; Kaessmann, Wiebe, and Paabo 1999; Deinard and Kidd 2000; Stone et al. 2002; Yu et al. 2003; Won and Hey 2005; Fischer et al. 2006; Becquet and Przeworski 2007; Becquet et al. 2007; Caswell et al. 2008).

FIG. 1.

Geographic distribution of chimpanzee species and subspecies (Schwartz 1934; Hill 1969; Gonder et al. 2006).

The largest taxonomic distinction among chimpanzees lies between the gracile chimpanzee, or bonobo (Pan paniscus), and the robust or common chimpanzee, Pan troglodytes, and is based on both morphological and genetic data (Coolidge 1933; Ferris et al. 1981; Shea and Coolidge 1988; Gagneux et al. 1999; Kaessmann, Heissig, et al. 1999; Deinard and Kidd 2000). Within P. troglodytes, three subspecies have been recognized for some time (Groves 2001): the western common chimpanzee, P. troglodytes verus in West Africa; the central common chimpanzee, P. troglodytes troglodytes in Central Africa; and the eastern common chimpanzee, P. troglodytes schweinfurthii in East Africa. Although these subspecies are geographically separated, data supporting their distinction as subspecies are limited. Gene tree estimates are far from being monophyletic for subspecies (Yu et al. 2003), even for X chromosomal loci (Kaessmann, Wiebe, and Paabo 1999) and mitochondrial genes (Morin et al. 1994; Gagneux et al. 1999; Gonder 2000). At the morphometric level, there is also some overlap among subspecies, particularly between the central and eastern populations (Shea and Coolidge 1988; Lockwood et al. 2004; Pilbrow 2006).

In genetic studies of diverging populations, very often, a key question is the role that gene flow plays in the divergence process (Millicent and Thoday 1961; Maynard Smith 1966; Endler 1977; Felsenstein 1981; Rice and Hostert 1993; Barton 2001). Because moderate levels of gene flow can prevent divergence, at least in a model of selective neutrality, a finding that divergence has occurred despite gene flow can be a signal that natural selection is driving the divergence process. By contrasting the patterns of variation within and among species, for the various genes, it can be possible to develop a demographic model of the divergence process including, possibly, the movement of genes between populations. Isolation-with-migration (IM) models, which include parameters for population sizes, gene exchange, and time of population splitting, have become a common framework for statistical analyses of divergence (Nielsen and Wakeley 2001; Hey and Machado 2003; Hey and Nielsen 2004; Hey 2006; Noor and Feder 2006; Becquet and Przeworski 2007; Hey and Nielsen 2007; Beaumont 2008; Nosil 2008; Nosil et al. 2009). However, until recently, analyses have been limited to pairs of populations. A two-population IM analysis necessarily assumes that no gene exchange has occurred between the two populations under investigation and other populations, and it assumes that the ancestral population had a constant size indefinitely into the past. An IM model with multiple populations and a population phylogeny can allow for complex histories that violate the assumptions of a two-population model.

This study applies a recently developed method for the analysis of divergence of multiple closely related populations to the bonobo and the three subspecies of the common chimpanzee (Hey, 2010). The method requires a phylogenetic tree with population splitting events ordered in time. Recent studies of chimpanzee divergence using genomic-scale data or large numbers of loci indicate that the phylogeny represented as a Newick string, for these four populations, is: (((eastern, central), western), bonobo) (Becquet et al. 2007; Caswell et al. 2008). This is also the phylogeny that was supported by mitochondrial (Morin et al. 1994) and Y-chromosomal loci (Stone et al. 2002).

Recently, a fourth population or subspecies of common chimpanzee, which lives in eastern Nigeria and western Cameroon north of the Sanaga River, has been recognized on the basis of mitochondrial and dental evidence (Gonder et al. 1997; Kormos et al. 2003; Gonder et al. 2006; Pilbrow 2006). This population had been called P. troglodytes vellerosus (Gonder 2000; Gonder et al. 2006); however, a recent reexamination of the collection records for the type specimen of P. troglodytes vellerosus indicates that it came from Gabon and not from the north of the Sanaga (Oates 2006). Oates et al. (2009) suggest the name P. troglodytes ellioti for the population in eastern Nigeria and western Cameroon. So far, the only published genetic data for this population come from the mitochondria (Gonder et al. 1997; Gonder et al. 2006), and it has not been included in this study.

Methods

Data

In addition to the demographic assumptions of an IM model, several assumptions are made of the data to which the model is applied:

• Individuals are sampled at random from the populations.

• Patterns of genetic variation follow a neutral model in which mutations are neutral or deleterious (Kimura 1983). Under this model, the overall substitution rate will be the neutral mutation rate and, if recombination rates are high between loci, polymorphism levels within populations will be proportional to the neutral mutation rate (Charlesworth et al. 1993).

• Individual loci have not experienced intralocus recombination in the history of the species under investigation.

• Separate loci are freely recombining with respect to each other.

Data from several studies that had reported DNA sequence data for the study of chimpanzee divergence were used for the present study. The large majority of loci are for noncoding regions of the genome, and none of the loci showed evidence of natural selection, as reported in the original papers. Yu et al. (2003) sequenced 50 noncoding autosomal loci from 9 bonobos and 17 common chimpanzees (6 western, 5 central, and 2 eastern). Fischer et al. (2006) sequenced an additional 19 noncoding autosomal regions from 18 bonobos and 20 individuals from each of the 3 subspecies of the common chimpanzee. Fischer et al. also extended the sequenced region for seven of the loci studied by Yu et al. (2003), and for these loci, we used the data of Fischer et al. (2006).

Because the data for these 69 loci were obtained by sequencing DNA amplified from diploid individuals, they often include multiple heterozygous positions. To estimate two separate sequences in these cases, the PHASE program (Stephens et al. 2001) was run, assuming no recombination, on each population, in each case estimating two haplotypes for each individual at each locus. After estimating haplotypes, loci were examined for evidence of recombination. For those loci that showed evidence of recombination since the common ancestor of the chimpanzee sequences, as revealed by the four-gamete test (Hudson and Kaplan 1985), the largest portion of the data that did not reveal evidence of recombination was used (Hey and Nielsen 2004).

Five other loci for which multiple individuals of most of the chimpanzee taxa were available were also included: portions of the apolipoprotein B (APOB) and HOXB6 loci (Deinard and Kidd 2000); a portion of the X-linked locus Xq13.3 (Kaessmann, Wiebe, and Paabo 1999); a portion of the nonrecombining portion of the Y chromosome (Stone et al. 2002); and the ND2 gene from the mitochondria (Stone et al. 2002). These individual X-linked, Y-linked, and mitochondrial loci were assigned inheritance scalars of 0.75, 0.25, and 0.25, respectively (Hey and Nielsen 2004).

One of the loci of Yu et al. (2003) revealed no variation and so was excluded. In total, there were 73 loci with an average total sequence length per individual of 45,276 bp. The average number of variable sites per locus is 7.72, excepting the ND2 gene, which had 96 variable positions. In analyses with just two closely related populations, some loci had zero variation, in which case they were excluded from that analysis. Because each locus receives its own mutation rate scalar (Hey and Nielsen 2004), the effect on the analysis of excluding a locus with zero variation depends primarily on the prior distribution of mutation rate scalars. In other words, if the prior were such that, had the locus been included, the results indicate the locus is expected to show more variation than was observed, then excluding the locus would bias the results. Because most loci in this study had low amounts of variation and because the prior distribution is uniform on a log scale over eight orders of magnitude (Hey and Nielsen 2004), excluding loci with zero variation should have negligible affect.

Working with Population Migration Rates

Migration rate parameters in IM analyses are scaled by the mutation rate, that is, m = M/u, where M is the migration rate per generation per gene copy. However, it is often easier to think of migration in units of the effective number of migrant gene copies per generation (i.e., the population migration rate) rather than the actual mutation rate per gene copy or per mutation event. For example, one way to estimate the rate at which population 1 has received migrants from population 2 is to calculate the quantity $2N_1{M}_{2\to 1}=(4N_{1}u\times M_{2\to 1}/u)/2$ using the estimated values of the parameters $4N_{1}u$ and $M_{2\to 1}/u$. A better way to assess 2NM, which permits likelihood-ratio tests and estimates of confidence intervals (CIs), is to estimate the marginal posterior density for 2NM by an appropriate integration over the joint posterior density for the population size and migration parameters (Hey, 2010).

Exponential Prior Distributions for Migration Parameters

Nielsen and Wakeley (2001) originally developed their method using uniform (i.e., constant) parameter priors for each of the population size, migration, and splitting time parameters, leaving the investigator to select an upper bound for each parameter (and setting the lower bound at zero). Uniform priors are simple and they lead to posterior densities that are directly proportional to the likelihood over the range of the prior distribution, thus opening the door to likelihood-based analyses such as likelihood-ratio tests of nested models (Nielsen and Wakeley 2001; Hey and Nielsen 2007). In the paper describing IM analyses for multiple populations, exponential distributed priors for migration were introduced (Hey, 2010). Exponential distributions proceed from zero to positive infinity and have their highest density at zero. One reason for considering an exponential prior is that, because divergence is not expected unless gene flow is low, IM analyses on populations that already exhibit some divergence begin with prior evidence of limited gene flow. A second reason is that many analyses with limited data and high upper bounds on migration and splitting time tend to return estimates suggestive of an island model with gene flow and splitting time estimates at the upper limit of the prior distribution. An exponential prior with a mean value for the mutation-scaled migration rate, , set to 0.5 was used as a prior distribution in a four-population model, and the results were compared with those for uniform priors on m.

Parameter Conversions

Converting estimates of the splitting time parameter t = Tu, to a time estimate in years, requires the geometric mean of the substitution rate for all or some of the loci used in the study (Hey and Nielsen 2004; Won and Hey 2005). All sequences were aligned and compared with their human counterparts and the substitution rate estimated assuming 6 My since the time of splitting of the ancestral species (Chen and Li 2001; Glazko and Nei 2003; Wildman et al. 2003). It is possible the actual divergence was more recent (Hobolth et al. 2007) or closer to 7–8 My (Brunet et al. 2002; Vignaud et al. 2002; Lebatard et al. 2008), in which case the time estimates obtained here can be rescaled accordingly. For estimating the effective population sizes from the population size parameter estimates, a generation time is also required. In a previous paper, 15 years per generation was assumed for the chimpanzees (Won and Hey 2005); however, this is probably an underestimate, and so, here a value of 20 years is used, consistent with estimates from the wild (Gage 1998). This is also the value used in most recent population genetic studies involving chimpanzees (Wooding et al. 2005; Fischer et al. 2006; Caswell et al. 2008).

Computations

To assess how results change as more populations are added to the model, the program for multipopulation IM analyses was run first on pairs of populations, then on three populations, and finally on all four sampled chimpanzee populations. Based on a previous study (Won and Hey 2005), upper bounds on population size parameters were set to 4.0 and for the oldest population splitting time, to 1.0. For the migration parameters, the upper bound can have a large affect on the analyses in cases where the true history has included migration and where there is not a very large amount of data (Hey, 2010). Analyses were begun with an upper bound of the migration parameter, m′, of 1.0 that should allow estimation of fairly high population migration rates (i.e., the product of 2NM for the maximal values of the population size and migration parameters is 2.0, i.e., 4.0 × 1.0/2). Higher values for m′ were also considered for three-population and four-population models.

Ensuring adequate mixing of the Markov chain is sometimes difficult, particularly for large data sets and particularly for histories that include gene exchange. For the analyses reported here, adequate mixing was ensured by using large numbers (between 40 and 120) of heated Metropolis-coupled Markov chains (Geyer 1991; Hey and Nielsen 2004) for each run and by allowing runs to proceed for sufficient durations to the point where individual runs appeared to have achieved stationarity and where multiple independent runs gave very similar results. Within runs, stationarity was assessed by 1) using autocorrelations of splitting time terms over the course of the run; 2) comparing parameter estimates generated using genealogies sampled in the first and second halves of the run; and 3) visually inspecting trend plots for splitting time terms. Each analysis was based on genealogies sampled from multiple (two to four) independent runs. Table 1 shows the burn-in duration, heating parameters used, and runtimes for each of the analyses.

Table 1.

Runtime Information.

Model	Figure No.	4Nu Priora	t Priora	m Priora	βmaxb	No. of Chainsc	Burn-in (Steps)d	Total Processor Runtime (days)e
Two populations: eastern and central	2	4.0	1.0	1.0	0.75	40	106	9
Two populations: eastern and western	2	4.0	1.0	1.0	0.75	40	106	9
Two populations: central and western	2	4.0	1.0	1.0	0.75	40	106	13
Two populations: bonobo and eastern	2	4.0	1.0	1.0	0.75	40	106	9
Two populations: bonobo and central	2	4.0	1.0	1.0	0.75	40	106	9
Two populations: bonobo and western	2	4.0	1.0	1.0	0.75	40	106	9
Three common chimpanzee populations	3	4.0	1.0	1.0	0.75	65	106	9
Three common chimpanzee populations	3	4.0	1.0	2.0	0.45	100	106	20
Four populations	4	4.0	1.0	1.0	0.75	70	106	21
Four populations	6	4.0	1.0	2.0	0.6	100	1.5 × 106	30
Four populations	6	4.0	0.7	5.0	0.6	120	1.5 × 106	56
Four populations	6	4.0	1.0	0.5f	0.75	70	1.5 × 106	12

^aThe upper bound on the prior distribution for the MCMC simulation.

^bThe heating exponent for the most heated chain in the Markov chain simulation.

^cThe number of Metropolis-coupled chains in the Markov chain simulation.

^dThe number of steps in the Markov chain simulation after initialization before samples begin to be taken.

^eThe summed time over all processors used for the analysis.

^fThe mean value of the exponential prior for migration.

Simulations

Simulated data sets were used to assess the overall quality of fit between the actual chimpanzee data and the IM model that was estimated using those data. For the analysis of all four chimpanzee populations, 200 data sets were simulated using the estimated parameter values, each identical in number of loci, sample sizes, and mutation models to the original data set. To compare real and simulated data, counts were made of each of the four types of polymorphic site for each pair of species: shared polymorphisms, fixed differences, polymorphisms restricted to one population, and polymorphisms restricted to the second population (Wakeley and Hey 1997). Counts of these four types of polymorphisms, taken together, are known to be sensitive to divergence history, including gene flow (Wakeley and Hey 1997; Wang et al. 1997; Becquet and Przeworski 2007). For the four-population data set, there are six species pairs, for a total of 24 statistics. To measure the overall distance of a data set from the mean pattern, the mean of each summary statistic was calculated for the 200 simulated data sets. A chi-square statistic was used to indicate the overall distance of a data set from the mean:

The distance of the actual data from the mean of the simulated data sets was then compared with the distribution of distances found for the simulated data sets.

These simulated data sets provide a simplified kind of posterior predictive check of the fit between data and model. Under a full posterior predictive check, the parameter values that are used for each simulated data set are a random draw from the estimated joint posterior density. However, a four-population IM model with 73 loci has a total of 101 parameters (i.e., 7 population size parameters, 18 migration rate parameters, 3 splitting times, and 73 mutation rate scalars), and only the density for the population size and migration parameters can be estimated jointly (Hey and Nielsen 2007). We cannot know for sure what the effect will be of basing simulations on parameter estimates from the marginal posterior densities; however, because of the lack of variance in parameter values used, the variance among simulated data sets will probably be lower than would be observed under a full posterior predictive check.

Results

Two-Population Analyses

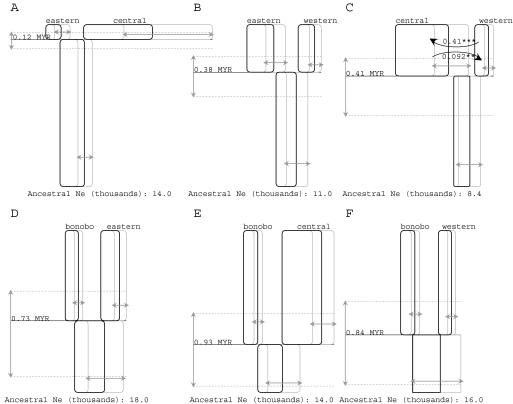
The chimpanzee analysis was begun by first examining all six pairs of species in a two-population IM model. In order to summarize results in a visually accessible way, a computer program was written to scan the output files of the IM analyses and to generate a diagram of the estimates and CIs of the model parameters. Figure 2 shows the results in graphical form for all six pairs of populations, with the pairs of common chimpanzee subspecies in the top row (A–C) and comparisons involving the bonobo on the bottom row (D–F). These figures show parameter estimates and CIs (95% highest posterior density estimates) for population sizes and splitting times. For population migration rates (i.e., 2NM), an arrow is depicted if a rate of zero is rejected at the level of P < 0.05 or less. These are likelihood-ratio tests proposed by Nielsen and Wakeley (2001) and that were shown to be useful, albeit fairly conservative, for 2NM (Hey, 2010). Summarizing some of the main points that emerge:

• The divergence time estimates are fairly consistent with each other and with the reported phylogenetic tree for these four populations (((eastern, central), western), bonobo) (Becquet et al. 2007; Caswell et al. 2008).

• The divergence times between the central and western, and between these and the bonobo, are quite similar to estimates previously obtained under the IM model with a data set of 48 of the loci used here. Won and Hey (2005) estimated splitting times between the bonobo and the western and central common chimpanzees at 859,000 and 899,000 years, respectively, and between the western and central common chimpanzees at 422,000 years.

• Migration is indicated between the central and western populations in both directions, with a higher estimated rate and a higher log-likelihood-ratio (LLR) statistic for gene flow (forward in time) from the western into the central. In a previous IM analysis, only the latter migration was detected (Won and Hey 2005). It is also important to recognize that estimated values of 2NM are nonzero in a number of the analyses; however, in these other cases, the estimated probability that the migration rate was zero was also fairly high, and the LLR statistic had a low value (full results are given in Supplementary Material online).

• The larger estimated size for the central population in the analysis with the eastern, relative to the size estimate in the analysis with the western population, is in the direction expected in a two-population analysis where one population has received genes from a third population. Under this interpretation, the central population appears larger when analyzed with the eastern because it has received genes from the western population and because in the analysis with the eastern population, there are no parameters to account for this gene flow.

• Population size estimates are smaller for the central and western populations and the bonobo than were found in similar analyses with fewer loci (Won and Hey 2005). However, this is explained by the fact that the earlier study used a generation time of 15 years, whereas this study uses 20 years. In other respects, the estimated population sizes in the two studies are similar.

• Population sizes vary but are mostly consistent across the different comparisons. The width of the boxes in figure 2 are all scaled in the same way, and so by comparing these widths for a population in each of the three contrasts in which it appears, we gain an impression of the effect of imposing a two-population model on the estimation process. Consistently, the central population is estimated to have the largest population size.

FIG. 2.

Histories for all six population pairs are represented as boxes (for sampled and ancestral populations), horizontal lines (for splitting times) and curved arrows (for migration). Time is represented on the vertical axis in each figure, with the sampled species and subspecies names given at the top of each figure at the most recent time point. (A–C) Comparisons among common chimpanzee subspecies, with a common scaling of the vertical axis for splitting time comparisons. (D–F) Comparisons between the bonobo and common chimpanzee populations with a common scaling of the vertical axis for splitting time comparisons. For all figures, the 95% highest posterior density intervals are shown with arrows in gray for population sizes (i.e., box widths) and splitting times (dotted lines). Migration arrows represent the population migration rate (i.e., 2NM) from the source population to the receiving population (i.e., forward in time). Only those population migration rates that were found to be statistically significant using a likelihood-ratio test are shown in which case the estimated value of 2NM is given as well as the significance level. Asterisks identify curves that are statistically significant by the test of Nielsen and Wakeley (2001): *P < 0.05; **P < 0.01, and ***P < 0.001.

Common Chimpanzee Three-Population Analyses

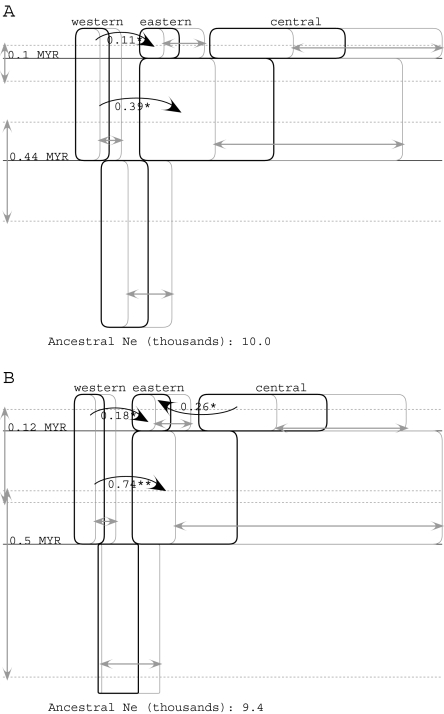
Figure 3 shows the results for a three-population model of the common chimpanzee populations considered under different priors for migration. The upper panel shows the results for an upper bound on migration of m′ = 1.0, whereas the lower panel shows the results for a migration rate upper bound of m′ = 2.0:

• The population size and splitting time estimates are similar in both parts of figure 3 and similar to those in figure 2.

• The central population and the ancestor of the eastern and central populations are estimated to have been roughly three times larger than other populations.

• Given the similar sizes for the central population and its immediate ancestor, it appears as if the population we currently recognize as the central population has persisted as a large population since before the origin of the eastern population and that this large population may have given rise to the eastern population by a founder event.

• The CIs on population sizes, and especially splitting times, are larger when the upper bound on migration is higher (fig. 3B).

• Both panels A and B indicate nonzero migration from the western population into the ancestor of the eastern and central populations and from the western population into the eastern population, something that was not observed in the two-population analysis. In addition, statistically significant migration is estimated from the central to the eastern population when the migration rate upper bound is higher (panel B).

FIG. 3.

IM analyses for the three subspecies of common chimpanzee. Results are shown for an upper bound on the migration parameter, m, of 1.0 (A) and an upper bound of 2.0 (fig. 3B). See figure 2 for further explanation of the meaning of symbols.

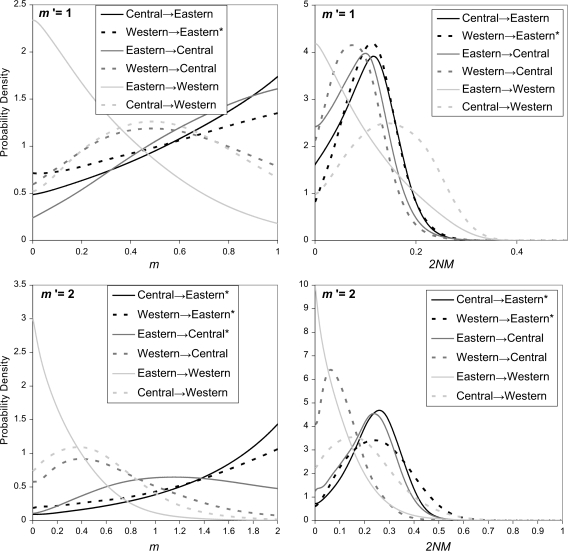
The evidence of migration from the western to the eastern population seems unlikely given the present day geography (fig. 1). However, most of the pairs of sampled populations showed some evidence of migration, and migration rate estimates for these three-population models are clearly sensitive to the upper bound of the migration rate. Figure 4 shows the posterior densities for all six m and 2NM terms for period 1, for two different upper bounds on the migration rate. Five of the six curves, for both m and 2NM regardless of the prior on m, have nonzero peaks, and two of the curves for m have peaks at the upper bound of m. Note that whereas the curves for 2NM fall well within the plotted range, this is partly a result of the well-defined posterior densities for the population size parameters. None of the migration parameters have estimated posterior probabilities for m that approach zero as m approaches 1, and the posteriors for two of the migration rates suggest an every increasing relationship with the upper bound on m (i.e., western→eastern and central→eastern). These are also the two migration parameters for which a rate of zero is rejected for 2NM when the upper bound on m is 2.0 (fig. 3).

FIG. 4.

Estimated marginal posterior densities for m and 2NM for period 1 in three-population models for the common chimpanzee. Curves for m are shown on the left and for 2NM on the right. Curves generated under a uniform prior with an upper bound of m′ = 1 are shown on the top and curves generated with m′ = 2 are shown on the bottom.

Four-Population Analyses

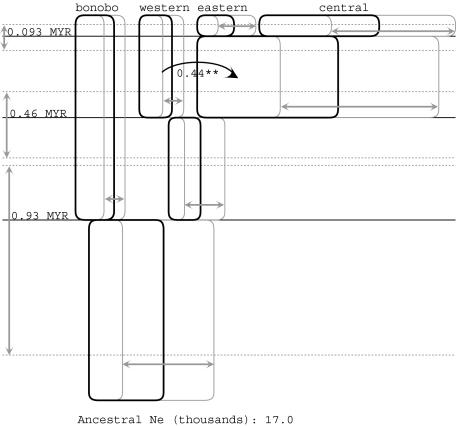
The results of a four-population IM analysis with m′ = 1 are summarized in figure 5. The overall picture for splitting times and population sizes is quite consistent with the histories described in figures 2 and 3. For migration, the only significant value of 2NM in the four-population model (of 18 population migration rates) is for migration from the western into the ancestor of the central and eastern populations, as observed for the three-population analyses.

FIG. 5.

Four populations in IM analyses with an upper bound on the migration parameter, m′ = 1. See figure 2 for further explanation of the meaning of symbols.

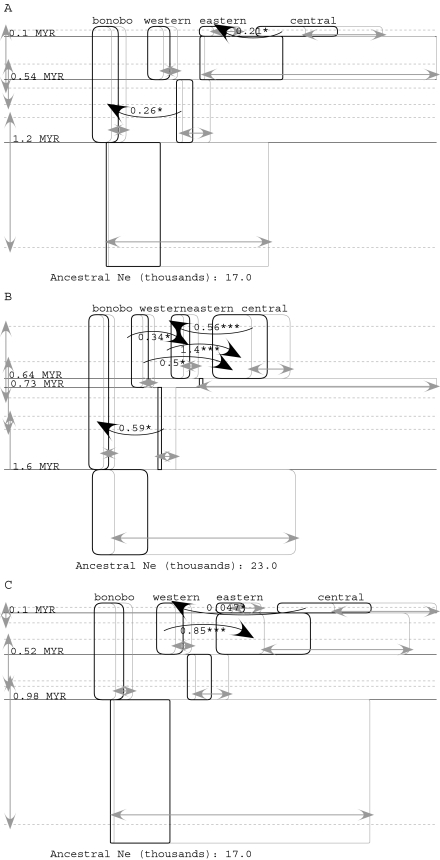
Figure 6 shows the results for four populations with three different types of prior distributions on the migration rates (6A, m′ = 2; 6B, m′ = 5; and 6C, an exponential prior with ). Unlike the case with the three-population model, in which increasing the upper bound on migration had a moderate effect on the estimated history, for four populations, increasing the migration rate upper bound changes things quite a lot. In figure 6A relative to figure 5, the splitting time estimates have increased, the CIs for splitting times and population sizes have increased, and the single significant population migration rate has been replaced by two others. In figure 6B with a much higher upper bound on migration, the estimated model has little resemblance to those generated with smaller upper bounds. The Markov chain Monte Carlo (MCMC) mixing was very poor under this model, and in order to obtain estimates, the upper bound on splitting times was reduced from 1.0 to 0.7 and the estimate of the oldest splitting time falls at this upper bound (which is why there is no upper CI for this splitting time in fig. 6B). Figure 6A and particularly 6B offer a tale of caution with regard to the dependency that migration prior distributions can have on the results. In cases where data are limiting and do not dominate the posteriors for migration—which will often be the case with models of multiple populations—the choice of migration priors can have a large effect.

FIG. 6.

Results for four-population models under different prior distributions for m. (A) Uniform prior with m′ = 2. (B) Uniform prior with m′ = 5. (C) Exponential prior with 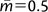. See figure 2 for further explanation of the meaning of symbols.

When an exponential prior distribution for migration is used, the estimated model is similar to that for m′ = 1; however, the CIs are wider, and one additional population migration rate is found to be statistically significant. This is migration from the central to the western population, which had also been found to be significant in a two-population model with m′ = 1 (fig. 2C).

The Quality of Fit between Data and Model

Based on the four-population analysis summarized in figure 5, 200 data sets were simulated using the estimated values of the demographic and mutation scalar parameters. Each simulated data set included 73 loci and was the same size and used the same mutation models as the actual data. Twenty-four summary statistics were measured for the data and for each of the simulated data sets (table 2). To assess the degree to which the simulated data resemble the real data, a chi-square statistic of departure from the mean of the simulations was calculated for each data set. The value of this statistic was 44.9, which placed it at position 81 in the distribution of 200 simulated values. In other words, 40% of the simulations had a lower chi-square statistic (better fit) than that for the real data, whereas 59% had a higher value (worse fit).

Table 2.

Counts of Wakeley and Hey (1997) Statistics and Results of Simulations of a Four-Population Model^a.

Population 1	Population 2	S1b	S2c	SSd	SFe
Bonobo	Eastern	121	118	98	1
		103.7 (13.3)	124.9 (16.9)	100.4 (14.3)	2.1 (2.1)
Bonobo	Central	102	199	88	3
		86.3 (12.7)	196.8 (18.8)	82.9 (13.5)	1.6 (1.9)
Bonobo	Western	125	118	113	1
		106.3 (13.3)	98.4 (13.6)	118.8 (16.2)	0.7 (1.2)
Eastern	Central	39	161	1	40
		47.4 (11.5)	145.3 (17.9)	2.6 (3.8)	50.3 (10.8)
Eastern	Western	112	110	19	9
		113.5 (16.6)	82.4 (11.5)	23.4 (9.2)	14.9 (6.3)
Central	Western	181	81	19	22
		182.5 (18.5)	63.8 (9.9)	11.6 (7.3)	18.0 (6.9)

^aPolymorphism counts summed across all loci are shown in the first row, with mean values (standard deviations) from simulations shown in the second row.

^bNumber of base positions that were polymorphic in population 1 but not population 2.

^cNumber of base positions that were polymorphic in population 2 but not population 1.

^dNumber of base positions that were polymorphic in both populations.

^eNumber of base positions that showed a fixed difference between the two populations.

Discussion

The different subspecies of the common chimpanzee share much of their genetic variation (Deinard and Kidd 1999; Kaessmann, Wiebe, and Paabo 1999; Deinard and Kidd 2000; Yu et al. 2003; Fischer et al. 2006) so that until recently, the branching history of the common chimpanzee subspecies has not been well resolved. With much larger data sets, including a data set of over 300 microsatellite loci (Becquet et al. 2007) and some shotgun resequencing of genomes (Caswell et al. 2008), it is now clear that the most closely related of the studied populations are the central and eastern populations of the common chimpanzee. This splitting event was followed, back in time, by the separation of the ancestor of these two populations and the western common chimpanzee population. Finally, the oldest split is, as expected, between the bonobo and the common chimpanzee. This history, with multiple splitting events that are well separated by hundreds of thousands of years, is well reflected in all the analyses shown here, including the multiple pairwise analyses and the multipopulation analyses.

For population sizes and splitting times, the major picture that emerges from the two-, three-, and four-population analyses is a consistent one. Indeed, it is not difficult to imagine estimating the phylogeny for all four populations simply on the basis of the pairwise analyses shown in figure 2. The general portrait that emerges is that the chimpanzee radiation dates to roughly 900,000 years ago (this changes to 1.05 Ma if a human/chimpanzee speciation time of 7 Ma is used for mutation rate calibration) and that effective population sizes have mostly been between 5,000 and 10,000 individuals. The exceptions to this range of population sizes are larger estimates for the central population (≈27,000), the ancestor it shares with the eastern population (≈32,000), and the ancestor of all four populations (≈17,000).

Gene Flow

In many contexts where gene flow and divergence are studied together, the populations being investigated are sympatric or parapatric. In the case of chimpanzees, the borders between populations are primarily large rivers and it is possible, given that chimpanzees are poor swimmers (Angus 1971) and notwithstanding their adjacent geographies, that chimpanzee populations have diverged as essentially allopatric populations. However, the multipopulation analyses suggest that there has been gene flow from the western population into the ancestor of the eastern and central populations. This gene flow parameter is statistically significant in the three- and four-population models (figs. 3 and 5), and it seems likely that the signal of gene flow identified in the western to the central population in a two-population analysis (fig. 2C) reflects this same history. When the upper bound on the migration prior is set to 1.0, the estimate of 2NM for genes moving from the western population into the ancestor of the eastern and central populations (as time moves forward) is consistently about 0.4. Using Wright’s formula relating F_st to 2NM in a diploid population, this value corresponds to an F_st of 0.556 (Wright 1951). This parameter also appears as significant when an exponential prior is used with an estimated value of 0.85 (fig. 6C). However, the finding of statistical significance for this particular gene flow parameter is also clearly sensitive to the model and to the migration prior that is being used. The level of significance varies among analyses (e.g., P < 0.05 in fig. 3A and P < 0.01 in fig. 5), and for higher upper bounds in a four-population model (fig. 6A and B), this term is not statistically significant, although it is close to significance when the upper bound on migration is 2.0 as in figure 6A (results not shown).

Other migration rate terms show even more variability among models, such as in the case of gene flow from western to central in a two-population model (fig. 2C), which does not appear in other models, or gene flow from western to eastern and central to eastern that appears in a three-population model (fig. 3) but not a four-population model (fig. 5). Some of this can be attributed to statistical significance being a threshold observation. Thus, for example, gene flow from western to eastern, which is significant at the P < 0.05 level in three-population models (fig. 3), is nearly significant in a four-population model (results not shown). However, models that differ in the number of sampled populations also differ greatly in the number of parameters, and there is probably considerable potential for correlations among parameters to change depending on the number of populations, and these could be contributing to the variability in findings of statistically significant migration rates.

In general, the migration results are less clear than for population sizes and splitting times, not only in terms of wider CIs for parameter estimates but also in terms of sensitivity to prior distributions. Given the population size estimates, the choice of an upper bound on migration of 1.0 (as used in analyses for figs. 2, 3A and 5) is sufficient to obtain estimates of moderate migration rates. For example, estimates of 4Nu range from about 0.2 to 1.5 (see Supplementary Material online), in light of which an upper bound on migration of 1.0 corresponds roughly to an upper bound on 2NM in the range of 0.1–0.75. Such values would represent substantial gene flow but not “high” gene flow (e.g., 2NM ≥ 1 would be considered fairly high because it is at this level where divergence is considerably limited in the absence of selection, Wright 1931). However, to be able to make clearer statements on the history of gene flow during chimpanzee divergence and to adequately investigate multipopulation IM models that include histories with higher rates of gene flow (i.e., higher upper bounds) will require substantially more data than were used here.

One potential way to handle the difficulties that arise in selecting a migration prior is to use an exponential prior on migration. An exponential prior should make tests of migration even more conservative and will shift estimated migration rates to lower values unless data really dominate the prior distribution, but they do offer a way to consider high migration rates even when there are not a lot of data. In the case explored, with a mean value of migration on the prior distribution of 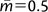, a strong signal of gene flow was found from the western to the ancestor of the eastern and central populations. Interestingly, significant gene flow was also observed (fig. 6C) from the central to the western population, something that was also indicated in the pairwise analyses (fig. 2C).

Comparisons with Other Studies

Table 3 compares the estimates reported here with those of the previous studies of Won and Hey (2005), Becquet and Przeworski (2007), and Caswell et al. (2008). All numbers in table 3 are scaled assuming a human/chimpanzee divergence time of 6 Ma and a generation time of 20 years. The numbers in table 3 for the present study are the same as those used for figure 6 and are similar to those reported by Won and Hey (2005) based on pairwise studies using a subset of 48 of the loci used for the present study.

Table 3.

Splitting Time, Effective Population Size Estimates and CIs in Different Studies.

Parameter	Caswell et al. (2008)a	Won and Hey (2005)b	Becquet and Przeworski (2007)c	This Studyd
Eastern/central ancestor split time (Ma)	—	—	0.22 (0.14–1.40)	0.093 (0.041–0.157)
Common chimpanzee ancestor split time (Ma)	0.44 (0.37–0.51)	0.42 (0.26–0.63)	0.38 (0.27–0.94)	0.46 (0.35–0.65)
Common bonobo split time (Ma)	1.11 (0.98–1.24)	0.87e (0.59–1.33)	0.77e (0.58–1.00)	0.93 (0.68–1.54)
Eastern Ne	—	—	16,600e (5,100–71,800)	8,200 (4,600–13,100)
Central Ne	118,000 (91,000–159,000)	18,900e (12,800–30,000)	23,100e (8,500–59,700)	26,900 (16,100–43,900)
Western Ne	9,100 (8,100–10,000)	6,000e (4,000–8,400)	10,100e (7,700–21,100)	7,400 (5,400–10,000)
Bonobo Ne	—	—	10,400e (7,800–15,200)	8,500 (6,400–11,000)
Eastern and central ancestor Ne	—	—	46,000 (33,500–75,100)	31,600 (18,600–54,000)
Common chimpanzee ancestor Ne	16,000 (12,400–19,600)	4,600 (180–9,900)	13,000e (2,200–22,400)	7,100 (3,500–12,500)
Common chimpanzee and bonobo ancestor Ne	20,900 (16,400–25,500)	11,900e (23–22,200)	32,900 (22,200–48,700)	16,800 (7,500–28,000)

^aSplit times adjusted for 6-My (rather than a 7 My) human/chimpanzee divergence. Intervals are 90% credible intervals estimated from bootstrap analyses.

^bIntervals are 90% highest posterior density values estimated from marginal posterior densities.

^cSplit times adjusted for 6-My (rather than a 7 My) human/chimpanzee divergence. Intervals are 95% CIs.

^dFour-population model (fig. 5). CIs are 95% highest posterior density intervals estimated from marginal posterior densities.

^eThe original study provided estimates from two or three pairwise analyses. Estimates are means from the original study. CIs represent the lowest and highest individual values reported from the pairwise analyses.

Becquet and Przeworski (2007) developed a method for studying an IM model for two populations that share a single symmetric migration parameter and that use summary statistics of data from multiple loci. Appropriate data are those that fit an infinite-sites mutation model (Kimura 1969), and the summary statistics are those of Wakeley and Hey (1997) (the same that are used here to check the quality of the fit of the four-population model using simulated data). The method of Becquet and Przeworski assigns mutation scalars for the MCMC simulation directly from relative levels of outgroup divergence rather than allowing them to vary as parameters as is the case in the method used here (Hey and Nielsen 2004). However, their method has the advantage of being applicable to loci that have had histories of intralocus recombination, unlike the present method or those in the other studies included in table 3. The estimates of Becquet and Przeworski are qualitatively similar to those found here, although their estimated population sizes tend to be larger and their estimated time for the most recent population split is over twice what is reported here (table 3). They also found evidence of gene flow (significantly nonzero on the basis of reported CIs) between all three pairs of common chimpanzees. Much of the data that Becquet and Przeworski (2007) used for their chimpanzee study were the same as those used for the present study (Yu et al. 2003; Fischer et al. 2006), and so, it seems likely that the differences in the estimates are a function of the differences in the methods of analysis.

Caswell et al. (2008) collected genomic shotgun sequences from a bonobo and an eastern chimpanzee and considered these together with previously reported genomic data on western and central chimpanzees. They generated alignments for many short regions of the genome, each with data from four or five species and then estimated population sizes and splitting times using a series of moment estimators on branch length estimates. Their study includes a large amount of data; however, their method for estimating demographic history does not include migration parameters; and their approach is very different than the likelihood-based method used here or the approximation to likelihood that was used by Becquet and Przeworski (2007). Results of Caswell et al. resemble those found here and those of the other studies in table 3, particularly when CIs are considered. However, they report a splitting time for the bonobo and common chimpanzee, which is about 20% higher than that found here (1.1 Ma, after adjusting for the fact that Caswell et al. used a mutation rate based on a 7-My divergence between humans and chimpanzees), and their population size estimates are consistently larger than those reported here. In particular, estimated size of Caswell et al. of the central population is over four times the estimate reported here, and the CIs of the two studies for this population do not overlap (table 3). This contrast is noteworthy given our estimate that the immediate ancestor of this population had experienced gene flow from the eastern population. If a sampled or ancestral population had been receiving genes in a way that was not accounted for by the model, then we expect that the estimated sizes of that populations would be elevated by the additional unaccounted for variation that was introduced by that gene flow (Beerli 2004; Slatkin 2005; Won et al. 2005). In a separate analysis, Caswell et al. did find evidence of gene flow from central to western (as observed in the two-population analyses in fig. 2C) using simulations and patterns of differential single nucleotide polymorphism sharing among populations.

Some portion of the difference in effective population size estimates, between the current study and the studies of Caswell et al. and Becquet and Przeworski, may be due to a tendency of the current method to underestimate effective population sizes. Particularly for ancestral population sizes, and for smaller data sets, the current method exhibits a bias toward underestimates of population sizes in simulation studies (Hey, 2010).

Considering Intragenic Recombination

The assumption of zero intragenic recombination, within the genealogy of the sampled loci, is required by the methodology and yet is probably false for many data sets. Here, we have applied the usual practice of pruning the data for a locus to conform to a bifurcating genealogy by deleting all but one incongruent haplotype block (Hey and Nielsen 2004). This practice is widespread when preparing data for IM analyses, and yet it necessarily leads to a biased sample of loci. Recently, Strasburg and Rieseberg (2009) assessed the performance of the IMa program (Hey and Nielsen 2007) in the face of failed assumptions, including that of intragenic recombination. They simulated data with intragenic recombination and then applied the four-gamete criterion to identify haplotype blocks for inclusion in the IM analysis. As expected, data simulated with recombination, but then pruned to apparently nonrecombining blocks, lead to estimates of population sizes for the sampled populations, and especially the ancestral population, which are biased downwards. Splitting times and migration rate estimates were not much affected by this type of data pruning (Strasburg and Rieseberg 2009). The bias found by Strasburg and Rieseberg for ancestral population sizes may explain why the estimates obtained here are consistently lower than those obtained by Becquet and Przeworski (table 3) using a method that does not assume zero intragenic recombination.

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).