Kinetics of Nanoparticle Targeting by Dissipative Particle Dynamics Simulations

Abstract

Dissipative Particle Dynamics simulations are applied to study nanoparticle targeting to a cell surface containing a high concentration of receptors. We found that the normalized number of bound ligands follows an exponential growth function 1 - exp(-t/τ), with the lifetime τ increasing as a function of the binding strength. With increasing binding energy, the shape of the adsorbed nanoparticle becomes ellipsoidal due to a large number of stably bound ligands, most of which are positioned on the nanoparticle periphery. For a low degree of functionalization of homogeneously distributed ligands, the kinetics of nanoparticle attachment slows down due to interference by non-functional chains, the overall number of bound ligands at equilibrium decreases, although the stability of ligand attachment increases. Janus-like nanoparticles with functionalized chains positioned on one side of the nanoparticle exhibit more rapid binding to the cell surface with a large equilibrium number of stably bound ligands.

1. Introduction

Targeted polymeric nanoparticles can act as unique vessels in various biomedical applications such as drug/gene delivery, imaging, photodynamic therapy, etc.^1–8 Polymer-tethered nanoparticles protect their payload (hydrophobic drugs, DNA or imaging agents) during transport and increase their bioavailability, while remaining innocuous inside the blood stream.^2–8 The nanoparticles can be delivered to the diseased site either by passive or active targeting. In passive targeting, the accumulation of the nanoparticles is achieved by the enhanced permeability and retention effect (EPR),^3,4,6,8 because of leaky vasculature and the low lymphatic drainage, which prolongs the residence time of nanoparticles in the tumor. At the same time, active targeting mediated by specific interactions between ligands (or antibodies), which are attached to a nanoparticle via flexible polymer tethers and receptors overexpressed at the pathological site is preferred, as it can enhance internalization and retention of nanoparticles at the targeted site, reduce the potential side effects of drug administration and increase the efficiency of treatment.^3,4,6,8 Despite the rapidly growing number of publications devoted to targeted nanoparticle drug delivery and imaging, the understanding of the details of nanoparticle-receptor surface interactions remains very limited. In this paper, we discuss the dynamics of ligand-tethered nanoparticle attachment to a receptor surface utilizing dissipative particle dynamics (DPD) simulations.

While the local dynamics of polymeric nanoparticle targeting to cell surface receptors is evidently important for practical applications, it is rather difficult to assess experimentally. Some of the experimental techniques include surface plasmon resonance measurements,⁹ fluorescence techniques combined with flow,^10,11 magnetophoresis and Electron Spin Resonance measurements for magnetic nanoparticle uptake by cells (which includes both binding and internalization).¹² The obtained experimental data illustrate the complex process of nanoparticle attachment to cell surface, often involving nanoparticle diffusion and flow effects^10,11,13 or the kinetics of both binding and internalization together.¹² To gain further microscopic details of this process, mathematical and computer modeling can be rather useful. For instance, the complex process of nanoparticle binding can be separated in special limits to diffusion- or transport-controlled (rapid binding to surfaces) and reaction-controlled (slow binding) cases.^10,13 Decuzzi and Ferrari¹⁴ constructed a steady-state equilibrium mathematical model of nanoparticles for vascular targeting, which consists of three steps: tethering, rolling adhesion, and firm adhesion. In this model, binding affinity is defined based on the total hydrodynamic force, the shear stress at the wall, and the bond reactive compliance. Several kinetic models separate the binding and internalization parts of the nanoparticle targeting process.^12,14,15 Ghaghada et al.¹⁵ built a population balance model with parameterized multiple kinetic rates to analyze their experimental data on folate-targeted drug carrier binding. Through a simple geometrical model of the ligands, ability to reach the receptors, they predict that optimization can be achieved by varying the tether length and the number of ligands.

In addition to aiding the analysis of experimental data,^11,13 computer modeling can also be a source of independent insights on the kinetics of nanoparticle targeting.¹⁶ Dynamic computer simulations can provide the details of the adsorption kinetics and explore dynamics of targeted nanoparticle. It can also be an effective tool to address the effect of different parameters on nanoparticle targeting kinetics. In this article, we apply Dissipative Particle Dynamics (DPD) simulations^17,18 to investigate the details of the dynamics of ligand-mediated nanoparticle attachment to a cell surface. DPD simulations allow simulations on mesoscopic space and time scales, significantly exceeding the limits of molecular dynamic simulations while accurately addressing hydrodynamic interactions.^18,19 DPD has been successfully applied to reproduce and predict phase behavior and properties of diblock copolymers^18,20,21 and surfactant aggregates ^22–24 as well as static and dynamic properties of polymer solutions and melts in the bulk and on surfaces.^25,26 In our simulations, we will consider a planar surface with a high density of homogeneously distributed receptors, such as found for integrins on metastatic cancer cells.²⁷ The nanoparticles’ ability to selectively attach to the cell membrane and be internalized depends on ligand-receptor binding strength, nanoparticle size and shape,^28,29 ligand density,⁹ and receptor distribution. The computer simulations discussed in this paper focus on the effect of ligand-receptor binding energy and degree of functionalization by ligands on the dynamics of nanoparticles attachment in the absence of flow. We hope that the obtained results will lead to a better understanding on how to achieve an optimized nanoparticle design that enhances the targeted binding on receptor surfaces and will guide further experimental research on kinetics of nanoparticle targeting.

This paper is arranged in the following way. In the simulation details section, we describe our simulation approach to nanoparticle adsorption. Then, we will examine the kinetics of ligand-mediated nanoparticle attachment to the receptor surface: the time needed by the nanoparticle to achieve stable attachment and the time-dependence of the number of bound ligands for different ligand-receptor binding energies. Next, we look into the equilibrium properties of adsorbed nanoparticle, including shape, distance from the surface, and distribution of bound ligands on the surface. We will also discuss dynamic properties of attached nanoparticle such as nanoparticle surface drift velocity and stability of attached ligands for different binding strengths. Furthermore, we will discuss the effect of the degree of functionalization of the nanoparticle by ligands and their distribution on the kinetics of nanoparticle attachment. We will consider homogeneous distribution of ligands and a Janus-type nanoparticle with functionalized ligands arranged on only one side of the nanoparticle. Lastly, we will summarize our findings in the Conclusions.

2. Simulation Details

To study the dynamics of nanoparticle adsorption we applied DPD simulations. DPD is a Langevin dynamics technique, which uses a short-range, soft repulsive potential to control the interaction between the particles and which has been successfully applied to study polymer systems.^17,18,20,21 We applied a coarse-grained approach, neglecting the atomistic details and modeling multiple atoms as a single bead, in order to extend the timescale to a level necessary to address the dynamics of nanoparticle adsorption. Each diblock copolymer chain, which becomes a part of a nanoparticle upon self-assembly, contained 12 DPD particles (A₄B₈) with 4 hydrophobic (A) and 8 hydrophilic (B) beads linearly connected. The end-monomer of the hydrophilic block was designated as a targeting group for functionalized chains and otherwise was considered to be a regular monomer for non-functional chains. It has been shown using DPD simulations that a chain containing N = 5–100 united atoms follows scaling relationships for the radius of gyration, relaxation time and diffusion coefficients in dilute solution, with a Flory exponent of 0.5 or 0.6 for theta- and good solvents respectively.^25,26 DPD simulations of diblock copolymer melts with a comparable size to those considered here, closely followed the classical phase diagram for diblock copolymer melts.¹⁸ Therefore, we expect that our chosen chain size will correspond to experimentally relevant cases. In addition to the polymer chains which contributed to nanoparticle formation as discussed below, the rest of the simulation box was filled with 40,872 solvent molecules. Each solvent molecule was represented by a single bead.

The interaction forces between different beads in the DPD formulation include a conservative force, f^C, a bead-spring force of the bonded monomers, f^S, a dissipative force, f^D, and a random force, f^R:

$$\begin{array}{l}{\mathbf{f}}_{\text{ij}}={{\mathbf{f}}_{\text{ij}}}^{\text{C}}+{{\mathbf{f}}_{\text{ij}}}^{\text{S}}+{{\mathbf{f}}_{\text{ij}}}^{\text{D}}+{{\mathbf{f}}_{\text{ij}}}^{\text{R}}\\ =[-a_{\text{ij}}(r_{\text{c}}-r_{\text{ij}})-K(r_{\text{s}}-r_{\text{ij}})-\gamma {\text{w}}^{\text{D}}({\mathbf{r}}_{\text{ij}}/{\text{r}}_{\text{ij}}·{\mathbf{v}}_{\text{ij}})+\sigma {\text{w}}^{\text{R}}({\zeta }_{\text{ij}}{(\mathrm{\Delta }t)}^{-1/2})]{\mathbf{r}}_{\text{ij}}/r_{\text{ij}}\text{for}{r}_{\text{ij}}<r_{\text{c}}\end{array}$$ (1)

where a_ij is the repulsion factor, r_ij and v_ij are the distance and velocity vectors of the particle i with respect to particle j, r_c and r_s are cutoff distances for conservative and bead-spring forces, K is the spring constant, γ is the friction coefficient, σ= (2γk_bT)^½ is the noise amplitude, w^Dand w^R are the weight functions (w^D= (w^R)² = (r_c - r_ij)² ), ζ_ij is the Gaussian random number, and Δt is the time step. The diblock copolymer chains are modeled as bead-spring chains with an applied harmonic potential and the spring constant was set equal to 50–100 (in reduced DPD units).^24–26 We use the cutoff radius, r_c, as the unit of length, k_bT as the unit of energy, and the mass of the DPD particle as the unit of mass. The DPD simulations were carried out for k_bT = 1, the friction coefficient¹⁷ γ=3.0, and the number density for polymer and solvent particles,²³ ρ = 3.0. The process of nanoparticle adsorption was monitored as a function of DPD timesteps, with a relatively small timestep Δt=0.02 (compared to 0.06).^17,30 For the chosen timestep the temperature fluctuated with standard deviation of 0.4%. Newton’s equation of motion was integrated using the Verlet algorithm. Using a similar set of parameters, the classical result for polymer end-to-end distance R_o ~ N^0.59 and the relaxation time τ~ R_o³ can be reproduced for dilute polymer solutions which indicates that DPD can describe correctly the thermodynamics and dynamics of polymer solutions.²⁶

For the repulsion factor in a conservative force for default interactions, we used a_ii = 25 k_bT/r_c (to match the compressibility of liquid water at room temperature). Since k_bT/r_c=1, we will drop this term for subsequent reference to the repulsion factors. Specifically, the repulsion factors between like beads of ligands, hydrophobic, hydrophilic blocks and solvent beads were a_LL = a_AA = a_BB = a_SS = 25. Additionally, interactions between different types of beads of the hydrophilic block, ligands and solvent were also set a_LB = a_LS = a_BS = 25. The repulsion factors between hydrophobic beads and either beads of hydrophilic block, ligands or solvent were a_AB = a_AL = a_AS = 45. These higher values of repulsion factors were chosen to ensure automatic self-assembly of a diblock copolymer nanoparticle in our DPD simulations. In the course of our simulations, we modeled 50 A₄B₈ chains, which readily form a single nanoparticle upon self-assembly, which we take to be a good representation of an equilibrium aggregation number for a spherical nanoparticle formed from A₄B₈ chains. The radius of the gyration for the nanoparticle is 3.70, and the ratio of the core size (average radial position of the outermost hydrophobic bead from the center of the nanoparticle core, 2.18) to the nanoparticle size (average radial position of the ligands, 5.17) is ≈ 0.42. Experimentally, the polymer nanoparticle core is often considered to be “kinetically frozen”. To model such a nanoparticle in our simulations (and ensure that relative positioning of all chains around the nanoparticle core remain the same) we “crosslinked” the outer hydrophobic beads adjoining to the core block. We note that our nanoparticle core can be deformed (corresponding to a rubbery polymer) but the hydrophilic blocks are tethered constantly to the nanoparticle core, similar to the experimental reality. For instance, biodegradeable core-crosslinked nanoparticles³¹ have been manufactured to prevent premature disintegration inside the body, and to achieve prolonged circulation increasing the bioavailability at the tumor site.

The supercell used in our simulations was 24×24×24 with periodic boundary conditions in the x and y directions, while parallel cell walls were placed at z=0 and z=24 (for a snapshot see supporting information). Each wall consisted of 2 × ρ (=6) layers of “frozen” particles, stacked in a staggered manner. The density of the wall particles was kept the same as the flowing particles, as suggested in the literature.³² The wall particles do not move at all during the simulation and the cell wall surface acts as the location of the receptors with each bead capable of interacting with ligands. In these simulations we considered the limit of high density of clustered receptors, so that any receptor on the wall could readily interact with the ligands on the nanoparticle surface. Very high concentrations of integrins on human cancer cell lines has been reported experimentally, with integrin counts higher than 100,000/cell.³³ Receptors are often distributed inhomogeneously with a rather high concentration (e.g. comparable to the receptor size for activated α_vβ₃ receptors) in a specific area of the cell. We varied the repulsion factor between the ligand and the wall a_LW, while repulsion factors between the wall and all other beads including solvent, a_SW, were constant and equal to 25. The binding strength between the ligands and the wall is defined by the difference between ligand/wall repulsion factor and solvent/wall, Δa =| a_LW– a_SW | In our simulations, Δa varies between 5 (weak binding, repulsion factor for ligand/wall is very close to solvent/wall) and 25 (strong binding, repulsion factor for the ligand/wall is close to zero). The experimentally reported binding energies between the ligands and receptors vary between 5 and 35 kT,³⁴ similar to the range considered here. Low repulsion factors for ligand-wall interactions may cause unphysical overlapping of DPD beads, so we have adapted the following procedure to prevent wall penetration: any bead that collides with the surface is bounced back indiscriminately, using a “no-slip” boundary condition, where both the normal and tangential components of the particle momentum are inverted.³⁵ The wall particles are frozen (T=0) to prevent their diffusive movement. The combination of frozen wall particles and bounce-back reflections has been used successfully before.^32,35,36 Simulations were conducted using the modified LAMMPS, a parallel-processing-enabled molecular dynamics code that is developed by Sandia National Laboratory.

3. Results and Discussion

Initial Nanoparticle Attachment

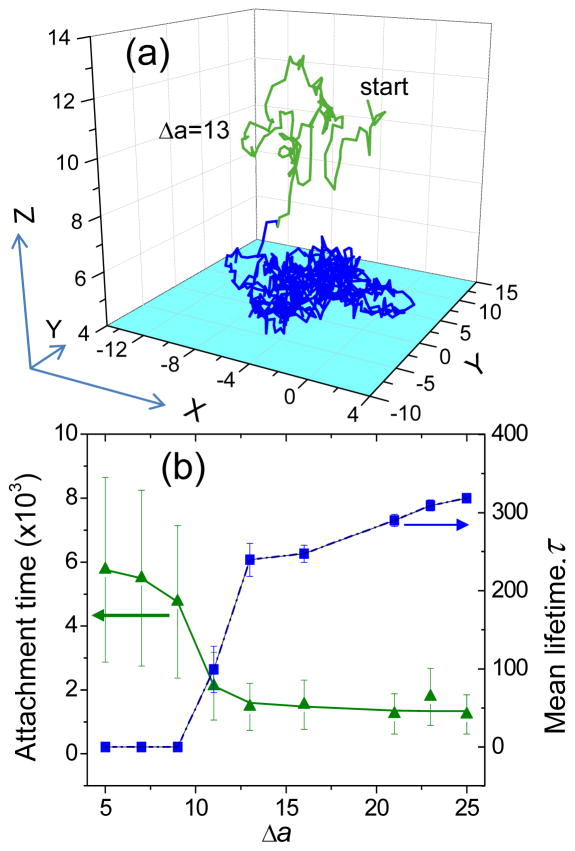
The nanoparticle is initially inserted at the center of the simulation box (x=0, y=0, z=12) between the two flat walls, and then it moves randomly according to the DPD forces within the supercell and interacts with the walls in their vicinity. We show in Fig. 1a, a typical trajectory (observed over 10⁶ simulation steps) of a 100% functionalized nanoparticle with an intermediate binding strength Δ_a= 13, that travels in the bulk over some distance (green path) and then attaches to the surface (blue path). We note that nanoparticle has equal chances to adsorb to either wall, which both contribute to the overall statistics of adsorption kinetics. When the nanoparticle attains z ≈ 6, it starts sensing the attractive interactions with the surface, then 1 or 2 end-functionalized chains extend over the gap between the nanoparticle and the surface, and establish the first contact. This is the initial viscoelastic elongation of nanoparticle tethers that transiently bonds to the cell substrate.¹⁴ If the binding strength is sufficiently large, these initially attached ligands will help pull the nanoparticle towards the surface to minimize tether stretching, otherwise the nanoparticle will detach from the surface. As nanoparticle adsorption proceeds, the surface attraction continues to draw the nanoparticle down to z ≈ 4.5, and more chains become attached to the surface, until the number of attached ligands reaches the equilibrium value. We define a stable contact with a surface as an attachment, which progresses with time to the equilibrium level of binding for a given binding strength.

Figure 1.

(a) A typical trajectory of a nanoparticle with Δa=13, in the bulk (green) and while attached (blue), (b) Time required for initial stable contact and mean lifetime (τ) for establishing the equilibrium number of bound ligands (see eq.2).

The time needed for the nanoparticle to establish a stable contact with receptor surface depends on the distance it must travel before encountering the surface and the ligand-receptor binding strength. Figure 1b highlights the difference in the time to establish a stable contact with the surface for the nanoparticles with different binding strengths. These results are obtained based on 10 different simulation runs for each of the considered binding strengths. In all cases, the initial position of the nanoparticle was the same. For a weak binding strength (Δa ≤ 9), the nanoparticle requires more time (t>4000) to reach the surface and initialize a stable attachment. The probability of detachment is very high in this case and nanoparticle spends only 10–25% of the time being bound to the receptor surface. In the strong binding region, (Δa > 9) the nanoparticle requires a relatively shorter time (t ≈ 1200–1800) to establish a stable attachment, as the probability of detachment decreases. Above a certain binding strength (Δa≈12), nearly any initial contact between a ligand and a surface results in a stable attachment, so that the time to establish a stable contact with receptor surface becomes independent on the binding strength. In this case, nanoparticles stay bound to the surface more than 95% of the time.

Kinetics of Micelle Adsorption

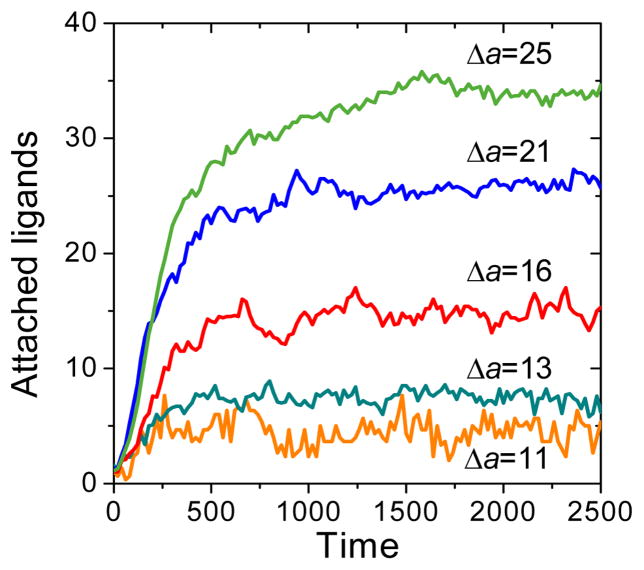
After the first stable nanoparticle attachment, the number of bound ligands on the surface increases rapidly, as shown in Fig. 2 for Δa = 11–25. The fluctuation in the number of attached ligands is more pronounced at low binding strength, because the absolute number is relatively small, and the likelihood of nanoparticle detachment is very high. As attached ligands accumulate locally at the surface (>20 bound ligands), their tethers fill the space between the nanoparticle core and cell surface thereby hindering any further ligand attachment process such that longer times are required to reach the equilibrium number of bound ligands. Nevertheless, the overall pattern of nanoparticle adsorption is very similar for both low and high binding strengths. Indeed, normalization of adsorption curves in Figure 2 by the equilibrium number of attached ligands for each Δa yields very similar curves, which can be successfully fitted by the exponential growth function y=1-exp(−t/τ) (see supporting information). The fact that single-exponential function can be used to fit the normalized adsorption curve indicate that ligand attachment seems to follow simple first-order kinetics, i.e. ligand attachment occurs nearly independently of each other:

$$\begin{array}{c}\frac{dm}{dt}=k_a(m_o-m)-k_{d}m\\ \frac{m(t)}{m_{eq}}=1-e^{-t/\tau }\end{array}$$ (2)

where k_a and f_d are the effective rate constants for adsorption and desorption, m_o and m_eq are the maximum possible number of bound ligands (which can reach the surface) and equilibrium number of bound ligands (for a given binding energy) respectively and τ =1/(k_a+k_d) is the mean lifetime needed for the equilibrium number of bound ligands to be achieved. The ligands adsorption curve shown in Figure 2 is consistent with the nanoparticles adsorption model observed in in vitro experiments.^11,12 We can rationalize the similarity by noting that ligands attach independently of each other (no cooperativity).

Figure 2.

Time-dependence of the number of attached ligands, measured from the time of the first stable contact (averaged over 10 simulation runs).

The mean lifetime τ as determined from eq 2 upon fitting our simulation data (Figure 2) is shown in Figure 1b in comparison with the time needed for the nanoparticle to establish a stable contact with the receptor surface. As is seen from Figure 1b, in general, the time to achieve the equilibrium binding is considerably shorter than the time to establish the stable contact with the surface. The latter depends also on the initial position of the nanoparticle relative to the surface, i.e. for a larger box size it would be even larger (assuming nanoparticle starts from the same position in the center of the box). We note that τ was determined only for Δa = 11–25. For lower binding strengths, attachment is very unstable with the equilibrium number of bound ligands being very low (as discussed below). With an increase in the adsorption strength, the mean lifetime τ firstly increases and then saturates.

Equilibrium Properties of Attached Nanoparticles

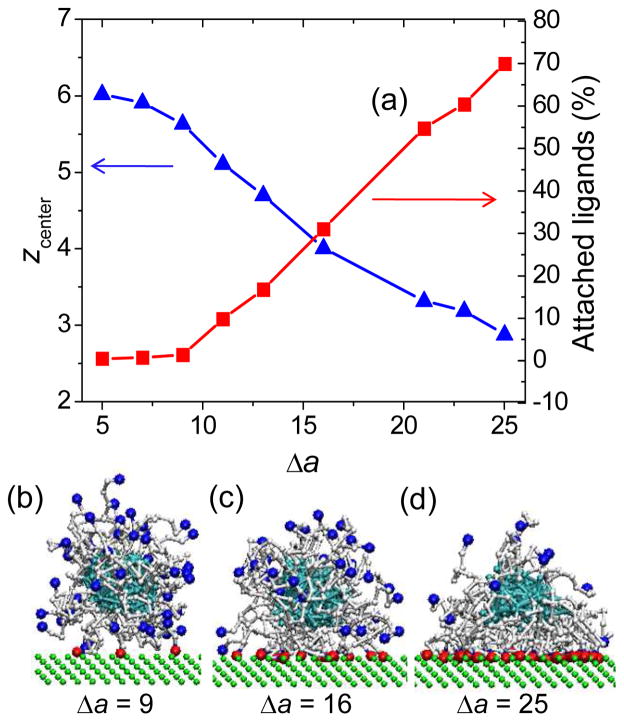
At long adsorption times, an attached nanoparticle will reach an equilibrium state with regards to the number of attached ligands, nanoparticle shape and distribution of attached ligands on the cell surface. The equilibrium number of attached ligands was determined either based on the plateau level achieved at long adsorption time as shown in Figure 2 for intermediate to high adsorption strengths or based on the average number of bound ligands over the comparable simulation time for low adsorption strengths (Δa = 5–9). In the latter case, a weak nanoparticle attachment (1–5 bound ligands) exists only for a short period of time with longer stretches of time during which the nanoparticle is freely moving in solution. The equilibrium fraction of attached ligands is presented in Figure 3a as a function of adsorption strength, Δa. The absolute number of attached ligands is listed in Table 1. At high binding strength (Δa = 25), the nanoparticle becomes very strongly attached to the surface with nearly 70% of ligands being attached to the surface. In the intermediate range of binding strengths, the fraction of attached ligands increases nearly linearly. This trend is in part due to the high density of receptors of the surface – each new ligand reaching the surface can easily find a corresponding receptor to bind.

Figure 3.

Upper: (a) Z-position of the nanoparticle center of mass above the surface, z_center. and the equilibrium number of attached ligands, as functions of binding strength. Error bars are comparable with the symbol size. Lower: snapshots of the attached nanoparticle for (b) Δa=9 (c) Δa=16, and (d) Δa=25.

Table 1.

Nanoparticle adsorption profile: average number of attached ligands, probability of attachment, mean lifetime (τ) calculated using equation 2, nanoparticle aspect ratio (R_gx/R_gz), and drift velocity of attached nanoparticles (v_d).

Δa	Attached ligands	Probability of attachment	τ (fitting)	Aspect ratio (Rgx/Rgz)	Drift velocity, vd (× 10−2)
5	0.15± 0.3	0.11 ± 0.05	-	1.000 ± 0.002	2.7 ± 0.1
7	0.3 ± 0.4	0.20 ± 0.1	-	1.002 ± 0.002	2.7 ± 0.1
9	0.6 ± 0.6	0.26 ± 0.4	-	1.005 ± 0.005	2.6 ± 0.1
11	4.8 ± 1.3	0.98 ± 0.05	99 ± 30	1.002 ± 0.002	2.52 ± 0.04
13	8.4 ± 0.9	1.00 ± 0.02	239 ± 21	1.015 ± 0.006	2.40 ± 0.03
16	15.1 ± 0.9	1.00 ± 0.01	247 ± 11	1.05 ± 0.01	2.28 ± 0.02
21	28.0 ± 1.0	1.00 ± 0.01	290 ± 8	1.10 ± 0.02	2.05 ± 0.02
23	30.2 ± 0.9	1.00 ± 0.01	309 ± 7	1.14 ± 0.04	2.00 ± 0.02
25	34.5 ± 0.8	1.00 ± 0.01	318 ± 5	1.21 ± 0.06	1.92 ± 0.01

One of the equilibrium characteristics of adsorbed nanoparticles is the average z-position of nanoparticle center of mass relative to the cell surface, z_center. As is seen from Figure 3a, at a low binding strength (Δa = 5–9), z_center ≈ 6, which is somewhat larger than the average distance from nanoparticle center to a ligand in a bulk, r_ligand≈ 5.2. At these low binding strengths, the interaction of nanoparticle with the surface occurs via the transient binding of 1–5 ligands brought to the surface by extended tethers, as a snapshot shows on Figure 3b (for Δa =9). As discussed above, such an attachment is very unstable and exists only for a short period of time, so that the equilibrium average number of bound ligands is less than 1. Obviously in this case, the overall shape of the nanoparticle remains spherical as in the bulk with the radius of gyration of the nanoparticle in x-, y- and z-directions being equal, i.e. R_g,_x= R_g,_y= R_g,_z ≈ 2.13 – 2.14. For the intermediate adsorption strengths (Δa = 9–16), the equilibrium z-position of an adsorbed nanoparticle (z_center ≈ 4–5) is about the average distance from nanoparticle center to a ligand in the bulk solution. In this case, the nanoparticle attachment is more stable as the equilibrium number of bound ligands increases to 10–15 (Figure 3a). Figure 3c shows the snapshot of attached nanoparticle for Δa = 16. As is seen, the overall shape is still approximately spherical with a slight decrease in z-direction R_g,_z < R_g,_x= R_g,_y (see Table 1). At large binding strengths (Δa>16), the equilibrium z-position of adsorbed nanoparticle (z_center ≈3) becomes smaller than the average distance from the nanoparticle center to a ligand in a bulk, as a large number of bound ligands (25–35) brings the nanoparticle center closer to the surface. The nanoparticle shape becomes more oblate and even cone-like at Δa = 25, as shown in Figure 3d with R_g,_x= R_g,_y= 2.25, while R_g,_z= 1.87, and the aspect ratio R_g,_x/R_g,_z is 1.21. We note that in this case, not only the overall nanoparticle shape, but also the nanoparticle core becomes deformed. Such deformation of the nanoparticle is likely to be responsible for the increase in adsorption time at later stages of adsorption as seen in Figure 2 for Δa = 25 and Figure 1b (for mean lifetime τ).

The polymeric tethers used to stabilize/protect nanoparticles in the drug delivery applications are normally very flexible with the spring constants of about 0.1 to 100 mN/m.³⁴ Thus deformation of nanoparticle corona can be expected in most experimental cases, including liposomes and to some extent dendrimers. Besides of the overall nanoparticle shape change, for core-crosslinked nanoparticles deformation³¹ of nanoparticle core is possible as well.

We note that in this study we do not consider cell membrane deformation. The deformation might be driven by the binding process or by an independent cause, such as natural membrane movement. The most likely deformation driven by the binding process is the endocytosis process which will engulf the nanoparticle into the cell. In such a case, the deformation leads to concave membrane surface that may result in a higher number of attached ligands, if the membrane deformation occurs on the timescales comparable with the time of nanoparticle attachment. The nanoparticle shape might not get distorted in this case, because bound ligands can be readily accommodated by the changing shape of the membrane. On the other hand, if membrane deformation leads to a convex surface, the number of attached ligands will be lower and nanoparticle shape distortion even stronger than predicted above.

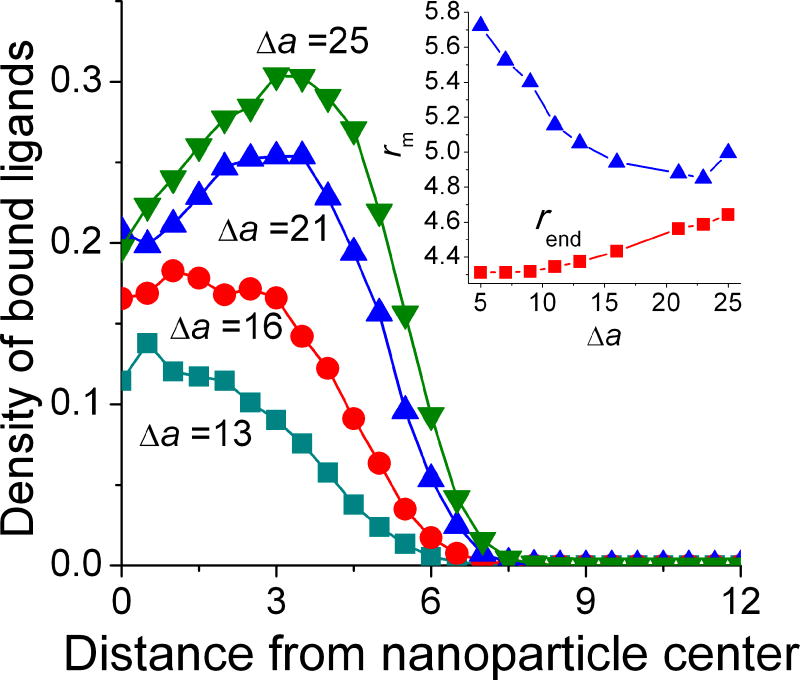
Another equilibrium property of attached nanoparticles is the distribution of bound ligands on the cell surface, shown in Figure 4. The bound ligand distribution is obtained by normalizing the number of bound ligands in the bins separated by concentric circles (with the center determined by the projection of the nanoparticle center of mass on the cell surface), by the area of the bins. For the low-to-intermediate adsorption strengths, the maximum density of bound ligands corresponds to the surface area directly under the nanoparticle. As discussed above, in this range of adsorption strengths, the nanoparticle shape remains nearly spherical and the ligands bound to the surface are those located between nanoparticle core and cell surface (Figure 3c). The end-to-end distance of the diblock copolymers carrying ligands bound to the surface (~5–6) is similar to the average z-position of nanoparticle center of mass relative to the cell surface, z_center and is noticeably larger than the average end-to-end distance for the diblock copolymers, r_end≈ 4.3–4.5 (Figure 4, inset). With an increase of binding strength, the number of attached chains increases, which expands the overall binding area on cell surface. Even though the end-to-end distance of the diblock copolymers carrying bound ligands is somewhat smaller than that at low adsorption strengths, the chains remain slightly more stretched compared to the unbound chains. In order to achieve a large fraction of bound ligands, the area directly underneath the nanoparticle becomes somewhat depleted of bound ligands, with the maximum binding density occurring on the periphery of the nanoparticle projection to the cell surface. The surface accessibility under the nanoparticle center is very limited due to the high tether density in this area, while on the periphery the surface accessibility is limited only by the ligand-receptor binding strength which should be sufficiently high to overcome entropic barrier for tether stretching. Polyethylene glycol typically used in biomedical applications is rather flexible,³⁴ thus this prediction is expected to hold for a range of experimental systems (as long as cell membrane deformation occurs on a timescale exceeding the nanoparticle adsorption time).

Figure 4.

The density of bound ligands as a function of the radial distance in xy plane from the projection of nanoparticle center, for Δa = 13–25; the inset shows the average end-to-end distance of each diblock copolymer chain that constitutes the nanoparticle (overall and attached only ) as a function of binding strength. Error bars are comparable with the symbol size.

Based on the bound ligand distribution, as shown in Figure 4, the furthest binding locations on the surface are about 8. This value can be compared with theoretical estimation by Ghaghada et al.,¹⁵ which is based on consideration of geometrical factors such as the fully-extended tether length, L, position of nanoparticle above the surface, z_center and the core size R_xm:

$$l_{max}=R_{xm}+\sqrt{L^2-z_{\mathrm{center}}^2}$$ (3)

Using L=8 in eq 3 for A₄B₈ chains modeled in our simulations and taking into account an oblate spheroid shape of nanoparticle observed at high adsorption strengths (thus using the x- or y- component of absorbed nanoparticle core radius R_xm or R_ym in eq 3) we arrived at 8.7–9.8 for Δa= 13–25, which slightly exceeds our simulation results. We note that in our simulations all fully-extended tethers, no matter where they originate on the nanoparticle core, can reach the surface. As a result, the actual location of ligand attachment is not determined by the accessibility of the surface, but rather depends on other factors, like local tether monomer density (which would depend on density of tether grafting on the nanoparticle core or aggregation number) or ligand-receptor binding strength.

Adsorbed Nanoparticle Mobility and Ligand-Receptor Binding Stability

One way to characterize mobility of a nanoparticle is by calculating its drift velocity. Drift velocity is defined as: $v_d\equiv 1/N{\sum }_{i=0}^N\mathrm{\Delta }{d}_i/\mathrm{\Delta }{t}_i$, where N is the number of pertinent timesteps, Δd_i is the traveling distance of the nanoparticle center of mass between timesteps i and i + 1, and Δt_i is the time difference. The bulk drift velocity is about v_d≈ 0.028 (in dimensionless units), which is naturally independent of the binding strength. When a nanoparticle attaches to the surface via ligand-receptor interactions, in our simulations it can still move on the surface as we consider surface with a high density of receptors, where bound ligands can move from one receptor to another without paying an enthalpic or entropic (for a given tether conformation) penalty. As expected, the adsorbed nanoparticle movement is slower than in the bulk as it encompasses all bound chains. Drift velocities of adsorbed nanoparticle are given in Table 1 for different binding strengths. At lower binding strengths, the drift velocity of an adsorbed nanoparticle is rather similar to that in the bulk (e.g. v_d=0.027 at Δa=5), as nanoparticle is only loosely adsorbed on the surface. With an increase in binding strength, the drift velocity of adsorbed nanoparticle decreases nearly linearly to v_d=0.019 at Δa=25 when nearly 70% of ligands are bound and the nanoparticle motion is considerably restricted.

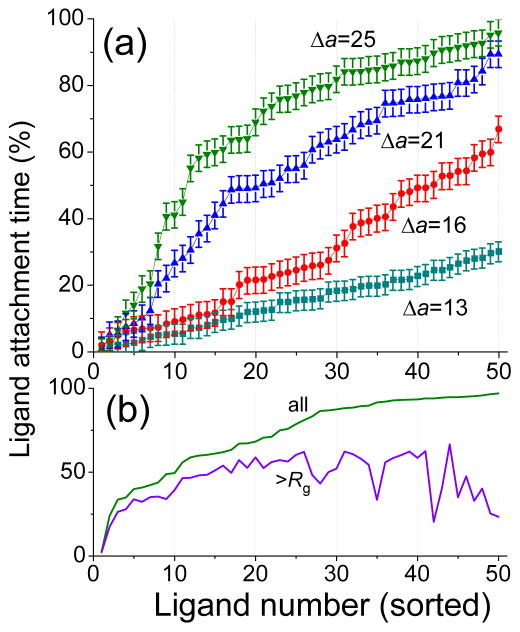
The microscopic origin of the mobility of an adsorbed nanoparticle is related to the stability of ligand-receptor binding. It can be characterized by the accrued percentage of time the ligand stays bound to a receptor (not necessarily the same one), which can be obtained by monitoring each individual ligand continuously over a certain period of time. Figure 5a exhibits the attachment time percent tally for each ligand sorted from the lowest to the highest at different binding strengths (Δa = 13, 16, 21 and 25). At a relatively weak binding strength (Δa =13), the fraction of attached ligands is low and the attachment time percent tally varies nearly linearly between 1–30%, implying that any ligand has a chance to bind to a receptor on the surface at least once. This illustrates the statistical and chelate binding effect³⁷ possessed by a nanoparticle acting as a large multivalent-ligand: when a ligand detaches from a receptor, there is another receptor nearby and another ligand that is ready to bind to this receptor, thus creating the interchangeability of the ligands and relatively high mobility of adsorbed nanoparticle. At a higher binding strength, Δa = 16, a larger number of ligands is bound and the disparity in the ligand attachment time percent tally increases. There is a larger local ligand concentration, which can activate subsite binding: two neighboring ligands (located between nanoparticle core and cell surface) can interchangeably bind receptors in their local vicinity, so that the percentage of time these ligands stay bound exceeds that for ligands on the periphery of the nanoparticle. This stabilizes attachment and decreases mobility of adsorbed nanoparticle. As the binding becomes stronger, the ligand attachment time percent tally becomes a step-like function with two populations of ligands: those being attached most of the time and ligands which primarily remain free. To quantify this observation we separate in Figure 5b for Δa =25, the ligand attachment time percent tally into contributions by ligands with the binding locations that lie within R_g (i.e. inside the circle corresponding to the maximum of bound ligand density in Figure 3) and the ones which are bound on the periphery of this area. As is seen, the latter contribute primarily to the lower part of the tally, i.e. bound less than 50% of the time, whereas the former exhibit more stable attachment to receptors. High binding strength ensures stable nanoparticle attachment with a relatively low drift velocity as a high concentration of ligands at the cell surface favors the statistical rebinding of ligands-receptors pairs.

Figure 5.

(a) Fraction of time ligand is bound to a receptor for each ligand (sorted from the lowest to the highest) for Δa = 13–25, (b) and specifically for Δa = 25, with the parsed data based on the binding location (>R_g). Error bars for plot b are similar to plot a.

Effect of Degree of Functionalization by Ligands

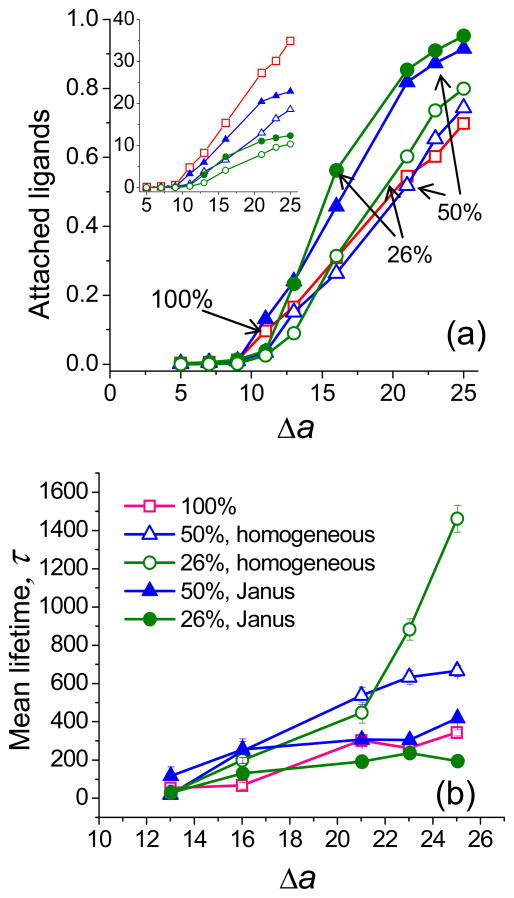
One of the important design parameters for nanoparticles is the degree of functionalization by ligands (which can be relatively easily controlled experimentally). All preceding results are obtained for 100% functionalized nanoparticle, i.e. all chains contained one targeting group at the end. In this section we will discuss the influence of degree of functionalization and distribution of ligands (discussed below) on the kinetics and thermodynamics of nanoparticle targeting. Figure 6a shows the equilibrium number (inset) and fraction of bound ligands for nanoparticles with 26%, 50%, and 100% of the chains carrying targeting groups. Firstly, we will discuss the case of spatially homogeneous distribution of ligands. As is seen with an increase in the number of functional groups, the absolute number of bound ligands increases proportionally: 10.4, 18.8, and 34.5 bound ligands at Δa =25 for 26%, 50%, and 100% of functionalization, respectively (Figure 6a, inset). To some extent, the effect of a reduction of the degree of functionalization is somewhat similar to a reduction of the ligand-receptor binding strength: there is a smaller number of bound targeting groups, the time nanoparticle spends attached to the surface is lower, the shape of attached nanoparticle is more spherical, its center of mass is located at a larger distance from the surface, the area of ligand attachment to cell surface is smaller and the drift velocity of attached nanoparticle on a surface is larger. At the same time, the fraction of bound ligands is higher for the lower degree of functionalization: 0.8, 0.74 and 0.69 at Δa =25 for 26%, 50%, and 100% of functionalization, respectively (Figure 6a). A smaller number of ligands implies less competition for reaching the cell surface and binding to receptors, such that the efficiency of ligand use increases with a decrease in degree of functionalization. The only exception from this rule concerns low adsorption strengths when having a large density of ligands improves nanoparticle chances to get attached to cell surface (see supporting information). There is an interesting kinetic implication of this effect: the mean lifetime τ considerably increases with the decrease of ligand functionalization (Figure 6b). For example, even though a smaller absolute number of ligands is attached at equilibrium at Δa =25 for a nanoparticle with 26% of functionalization by ligands, it takes considerably longer time for the ligands to reach a surface while penetrating through non-functional polymer chains. At the same time, when ligands bind to the surface they are more likely to stay attached – the stability of ligand attachment noticeably increases with a decrease of degree of functionalization (see supporting information). The ligand attachment time percent tally becomes a step-like function at lower binding strengths for nanoparticles with low degree of functionalization. This is likely due to a combination of statistical binding³⁷ (when a ligand detaches from a receptor there is another receptor nearby to bind) and a volume exclusion effect (the probability that a considerable change in tether conformation will pull the ligand away from the surface is low, due to the presence of neighboring non-functionalized chains, which enhances the probability of ligand rebinding to a receptor).

Figure 6.

(a) Fraction of attached ligands and (b) mean lifetime τ as a function of binding strength Δa for nanoparticles with different degrees of functionalization (100% -squares, 50% triangles, 26% circles) and ligand distribution (solid symbols - Janus-like nanoparticle, open symbols – nanoparticle with homogeneous ligand distribution). The inset shows the number of attached ligands as a function of Δa. Error bars are comparable with the symbol size.

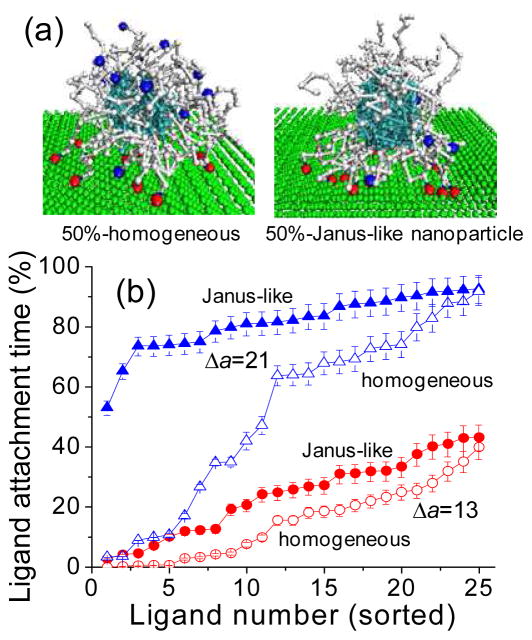
As is seen from Figure 6a, even at the highest binding strength considered, the fraction of bound ligands is lower than 0.8 (for 26% of functionalization) even though there is a large concentration of receptors and all ligands can physically reach the surface. The reason for this is the considerable entropic penalty for tether stretching to reach the surface. Thus, it would be interesting to consider the situation in which all functionalized chains were positioned on one side (or surface area) of the nanoparticle, while all non-functional chains on another side (Figure 7a). Such Janus-type nanoparticle can be in principle synthesized in a similar way as discussed in Ref 38. A Janus-type nanoparticle with a large number of ligands on one side is expected to have a very strong affinity to the receptor surface. Indeed our simulation results show that nearly all ligands are bound, 12.3 (of 13) and 22.9 (of 25), which corresponds a fractional binding of 0.95 and 0.92 at high adsorption strength (Δa =25) for a Janus-type nanoparticle with 26% and 50% of functionalization, respectively (Figure 6a). The fraction of bound ligands is noticeably higher for Janus-type nanoparticle compared to a nanoparticle with the same number of homogeneously distributed ligands. This trend persists for nearly all range of binding strengths considered. It is interesting to note that for Janus-type nanoparticle the increase in the fraction of adsorbed ligands with an increase in Δa follows sigmoidal profile (Figure 6a) with a saturation level at high adsorption strengths determined by the number of available ligands.^39,40 In contrast, for nanoparticles with homogeneously distributed ligands, the saturation level is not reached for the highest adsorption strength considered (Δa =25). The center of mass of Janus-type nanoparticle is slightly closer to the cell surface than for the homogeneously distributed ligand case and its shape is only slightly elongated in the direction perpendicular to the surface as non-functional chains are spread-out away from the surface (Figure 7a).

Figure 7.

(a) Snapshots of the homogeneous and Janus-like nanoparticles at Δa = 21, where the blue beads represent the functionalized ligands, and the red beads are attached ligands, (b) Fraction of time ligand is bound to a receptor for each ligand of 50%-functionalized nanoparticle (solid symbols – Janus, open – homogeneous) sorted from the lowest to the highest attachment for Δa = 13, 21.

There are also interesting kinetic features of targeting for Janus-type nanoparticles. Compared to the homogeneously distributed ligand case, Janus-type nanoparticles spend a larger fraction of time being bound and correspondingly have somewhat lower drift velocity on the surface, especially for a lower percent of functionalization. More importantly, Janus-type nanoparticles achieve the equilibrium number of bound ligands noticeably quicker than nanoparticles with the same number of homogeneously distributed ligands: the mean equilibration lifetime τ is nearly twice shorter for Janus-type nanoparticles with 50% of functionalization and it is 5–8 times shorter for Janus-type nanoparticles with 26% of functionalization (Figure 6b). As discussed above, nanoparticles with a low fraction of homogeneously distributed ligands have to undergo a slow process of ligand penetration through the high density tether area near the surface contributed by non-functional chains. Janus-type nanoparticles have the kinetic advantage of binding as functionalized chains are surrounded by the similar chains, so that non-functional chains do not interfere with the binding process. Additionally, having a large local concentration of ligands allows active chelate and subsite binding of neighboring ligands³⁷ which can interchangeably bind receptors in their local vicinity. As a result, the bound ligands of Janus-like nanoparticles exhibit higher stability compared to nanoparticles with the same number of homogeneously distributed ligands (Figure 7b). For instance for Δa = 21, the ligand attachment time percent tally for 50% functionalized Janus-type nanoparticles ranges from 50% to 90% compared to step-like 0% to 90% the ligand attachment time percent range for nanoparticles with homogeneously distributed 50% functionalized chains. For a Janus-like nanoparticle, ligands can easily substitute one another on the surface and their tethers are on average less stretched compared to the nanoparticles with homogeneously distributed ligands.

Therefore, a Janus-type nanoparticle exhibits a faster binding process leading to a larger fraction of bound ligands at equilibrium, which are more stably bound to a cell surface compared to a nanoparticle with the same number of homogeneously distributed ligands. This quick and strong attachment of Janus-type nanoparticle can produce better binding selectivity, which can be a desirable property of the nanoparticle in targeted delivery, with the optimal number of ligands being dependent on the binding strength.⁴⁰ Thus, while manufacturing a nanoparticle with homogeneous ligand distribution could be easier than creating a Janus-type nanoparticle, the latter might be a very attractive alternative to produce a nano-carrier with superior targeting performance.

4. Conclusions

In this article, we use DPD simulations to study the dynamics of nanoparticle targeting on a cell surface densely covered with receptors. In the initial approach of the nanoparticle to the surface, a few extended tethers end-functionalized by ligands form transient bonds with the receptors. If the ligand-receptor binding strength is sufficiently large, these initial bonds will eventually pull the nanoparticle close to surface and stabilize the attachment by formation of additional ligand-receptor bonds. We found that to achieve a stable attachment (leading with time to an equilibrium number of bound ligands), a nanoparticle with a low ligand-receptor binding strength takes the longest time and the number of bound ligands is very low (1–4). Such a nanoparticle stays adsorbed on the surface only a short period of time (10–20%). A larger binding strength results in a shorter time needed to establish stable attachment of a nanoparticle and a large number of bound ligands at equilibrium. We found that the time evolution of the number of bound ligands (since the moment of a stable nanoparticle attachment) follows a simple exponential growth function: m(t)/m_eq =1−exp(−t/τ), independently of ligand-receptor binding strength although the mean lifetime τ increases with an increase in binding strength. This may be due in part to a lower detachment rate for higher binding energies and the hindered motion of ligand-bearing tethers during the later stages of attachment. At high binding strengths, the nanoparticle shape becomes distorted in order to accommodate a higher number of attached ligands. This deformation of nanoparticle shape may also contribute to the increased mean lifetime τ. Deformation of the nanoparticle corona can be expected in most of experimental cases, as tethers are normally rather flexible (such as PEO³⁴). Cell membrane deformation (which was not considered in this paper) can also play a role in nanoparticle binding, especially if it occurs on the comparable timescale. Thus a concave membrane shape would enhance binding and possibly prevent nanoparticle shape distortion. We have also examined the mobility of adsorbed nanoparticle and the stability of ligand-receptor bonds and found that at low binding strength the loosely attached nanoparticle can easily drift along the surface as the number of bound ligands is low and almost any ligand has a chance to be bound to the surface from time to time. At high binding strength the large number of bound ligands considerably decreases the surface mobility of attached nanoparticle. The pattern of bound ligands with respect to the position of the nanoparticle also depends on the binding energy. For higher binding energy the bound ligands are situated not only directly underneath of the core of adsorbed nanoparticle (as is the case for low binding strengths), but are preferably located on the periphery of the nanoparticle. The stability of ligand-receptor binding of the latter is on average lower than the former as the tethers are more extended and hence pay larger entropic penalty.

We have also investigated the effect of the degree of functionalization and ligand distribution on the thermodynamics and kinetics of nanoparticle targeting. We found that in all cases, the normalized (by the equilibrium value) number of bound ligands still follows single exponential growth function. For homogeneously distributed ligands a lower percentage of nanoparticle functionalization results not only in a lower number of bound ligands and weaker overall attachment, but also leads to a considerably slower kinetics of attachment. Interference of non-functional chains is believed to be the main reason for this effect at longer adsorption times. At the same time, a low degree of functionalization also implies a more efficient use of ligands, as a larger fraction of ligands is bound and bound ligands are more stable. Here non-functional groups surrounding bound ligands support binding by keeping bound ligand in place. This observation may have important implications for polymer nanoparticle internalization – slow binding may be preferable for receptor clustering and increased stability of attachment may be beneficial for internalization by receptor signaling pathways. We also considered Janus-like nanoparticles with functionalized ligands placed at one side (or surface area) of a nanoparticle. We found that for all binding strengths considered, such a ligand arrangement speeds up the binding process and results in stronger, more stable attachment employing nearly all ligands. Such Janus-like nanoparticles can be rather useful for binding already existing receptor clusters and could also enhance selectivity of targeting when employing weak ligand-receptor interactions.