Abstract
Postural control requires the coordination of force production at the limb endpoints to apply an appropriate force to the body. Subjected to horizontal plane perturbations, quadruped limbs stereotypically produce force constrained along a line that passes near the center of mass. This phenomenon, referred to as the force constraint strategy, may reflect mechanical constraints on the limb or body, a specific neural control strategy or an interaction among neural controls and mechanical constraints. We used a neuromuscular model of the cat hindlimb to test the hypothesis that the anatomical constraints restrict the mechanical action of individual muscles during stance and constrain the response to perturbations to a line independent of perturbation direction. In a linearized neuromuscular model of the cat hindlimb, muscle lengthening directions were highly conserved across 10,000 different muscle activation patterns, each of which produced an identical, stance-like endpoint force. These lengthening directions were closely aligned with the sagittal plane and reveal an anatomical structure for directionally constrained force responses. Each of the 10,000 activation patterns was predicted to produce stable stance based on Lyapunov stability analysis. In forward simulations of the nonlinear, seven degree of freedom model under the action of 200 random muscle activation patterns, displacement of the endpoint from its equilibrium position produced restoring forces, which were also biased toward the sagittal plane. The single exception was an activation pattern based on minimum muscle stress optimization, which produced destabilizing force responses in some perturbation directions. The sagittal force constraint increased during simulations as the system shifted from an inertial response during the acceleration phase to a viscoelastic response as peak velocity was obtained. These results qualitatively match similar experimental observations and suggest that the force constraint phenomenon may result from the anatomical arrangement of the limb.
Keywords: musculoskeletal model, postural control, simulation
INTRODUCTION
The maintenance of standing posture involves neural mechanisms spanning cortex to spinal cord, mechanical properties of muscles, and anatomical arrangement of muscles and joints to balance forces and moments about the center of mass (CoM). It has been claimed that intrinsic muscle mechanics may or may not provide postural stability (Loram and Lakie, 2002; Morasso and Schieppati, 1999; Winter et al., 1998), that spinal reflexes may or may not provide stability (Masani et al., 2003; van Soest and Rozendaal, 2008) and that active attention may or may not be required (Shumway-Cook and Woollacott, 2000). While there are many different neural and biomechanical mechanisms that can contribute to the control of posture and balance in humans and animals, it is difficult to attribute measured behavioral characteristics to any particular subsystem in such integrated and redundant physiological systems. Here, our goal was to examine the extent to which features of postural responses to perturbation can be attributed to the biomechanical characteristics of the musculoskeletal system independent of any particular neural strategy used to activate muscles.
The fundamental postural task is to maintain the CoM within the base of support (BoS). The strictest sense of this results in stability, in which the CoM is held at a fixed point within the BoS and returns to that point following perturbation. Simple objects, such as tables and chairs, achieve this stability through passive mechanics. Their response to perturbation is strictly defined by physics and rigorously reproducible. Animals only approximate such strict stability, generally maintaining the CoM within a small neighborhood marked by constant motion known as postural sway. The response to perturbation is much more variable in organisms but still consists of stereotypical phases with qualitative similarity between trials and between animals.
Cats subjected to postural perturbations during quiet standing generate a characteristic temporal sequence of reaction forces in response to a translation, or sliding motion, of the support surface in the horizontal plane (Macpherson, 1988a; Ting and Macpherson, 2004). The immediate response to horizontal plane perturbations is similar in both cats and tables and consists of a change in force, in each limb, aligned with the direction of the perturbation. This response occurs before measurable changes in muscle electromyograms (EMG). In the cat, changes in muscle EMG begin at 20–30 ms, coincident with the stretch reflex latency, and a second, more powerful change in EMG begins around 50 ms, in response to more integrated sensory input from the perturbation (Ting and Macpherson, 2004). Force changes resulting from this change in muscle activity, in the ‘active’ phase between 100–150 ms, are constrained to the direction of initial postural force, regardless of the direction of perturbation (Macpherson, 1988a). This phenomenon is called the force constraint phenomenon. During the active phase, the summed forces across all of the four limbs oppose the perturbation, although no individual limb force may lie along the direction of the perturbation.
The force constraint phenomenon may arise from multiple sources, including global neural strategies that integrate sensory information and motor commands across the body, intrinsic constraints of musculoskeletal mechanics both within a limb and across multiple limbs, or a local neural strategy where careful selection of a stance muscle activation pattern tunes the system to produce directionally biased forces. Constraining force production may represent a simplifying neural strategy that limits functional neuromuscular redundancy (Macpherson and Fung, 1999; McKay and Ting, 2008). Damage to the central or peripheral nervous systems results in substantial deficits in balance control and force constraint (Deliagina et al., 2007; Macpherson et al., 2007; Macpherson and Fung, 1999). While damage to neural systems may disrupt postural stability by altering the neural response to perturbation, postural disruption may also result from defects in both initial stance and postural tone selected by the nervous system. The contribution of these mechanisms is difficult to evaluate experimentally, because changes to any one aspect propagate throughout the system.
The relationship between the neural activation of muscles and directionally constrained force outputs following postural perturbations is not clear. Active muscular responses to postural perturbations vary continuously with perturbation direction, where the resulting forces are directionally constrained resulting in similar endpoint force direction, despite different patterns of muscle activity (Macpherson, 1988b). Across individuals, muscle activity patterns vary greatly during both quiet stance and in postural responses whereas the force patterns are surprisingly stereotypical (Macpherson, 1988b; Torres-Oviedo et al., 2006). This suggests that the force outputs are substantially influenced by the musculoskeletal properties of force generation in the limb independent of variation in muscle activity due to neural activity.
Our prior studies suggest that both hindlimb musculoskeletal anatomy and careful control of muscle activation may be important in the generation of directionally biased forces. Using a static musculoskeletal model of the cat hindlimb, we showed that the feasible force set (FFS) in the cat hindlimb is directionally biased not toward the CoM but in the anterior–posterior direction (McKay et al., 2007). However, constraining muscle activation to a limited set of experimentally derived muscle synergies does bias the FFS toward the CoM (McKay and Ting, 2008). This suggested that the nervous system can counteract an anatomical bias in force direction and superimpose its own directional constraint during postural responses to perturbation. Muscle coordination is important in quasi-static conditions, because the direction of the endpoint force attributed to a single muscle depends strongly on torques at all joints in the kinematic chain (van Antwerp et al., 2007). Similarly, the Lyapunov stability of the limb is strongly dependent on the preferential activation of intrinsically stable muscle-moment arm units (Bunderson et al., 2008). These results indicate that the mechanical outputs and properties of the hindlimb depend on the particular pattern of muscle activation, and suggests that careful selection of that activation pattern is required to achieve postural stability and manifest the force constraint phenomenon.
However, the dynamic effects of perturbations on the cat hindlimb model are yet unknown as our prior studies have focused on static and quasi-static analysis techniques. During an external perturbation, dynamic interactions within the limb play a significant role in determining the resultant joint torques and limb configuration. Muscle moment arms change, and muscle force generation changes with joint angle and velocity. The response to a perturbation is affected by hindlimb musculoskeletalal anatomy as well as the activation-dependent stiffness and viscosity of muscles. The pattern of muscles used during quiet standing varies significantly across individuals (Torres-Oviedo et al., 2006; Torres-Oviedo and Ting, 2007) and may affect the evolution of a perturbation. Variations in background muscle tension may also influence afferent signals that govern short-latency stretch reflex responses (Burke et al., 1978). Such reflexes enhance muscle stiffness by altering the activation of the muscle following stretch (Nichols and Houk, 1976). All of these mechanisms have the potential to significantly filter the effects of a perturbation on the limb but are not addressed by static analysis.
In this paper we use a mathematical model to test the hypothesis that horizontal forces produced in response to endpoint displacement are an emergent feature of the musculoskeletal anatomy, length feedback and the postural tone of the muscles. This hypothesis was first tested by examining a linearized model of the cat hindlimb to determine whether the production of stance-like forces constrains the mechanical action of individual muscles. We predicted that the generation of a stance-like endpoint force, which constrains joint torques, may reduce the variability in the direction of single muscle actions, which are dependent on joint torques produced by other muscles (van Antwerp et al., 2007). Second, we determined whether muscle length feedback is sufficient to provide stability by examining the Lyapunov stability of the linearized model. We predicted that the addition of physiological reflex gains would reduce the requirement of carefully selected stance activation pattern for stability. Finally, we tested whether the model exhibited the force constraint by examining forward simulations of the fully dynamic hindlimb model during horizontal plane perturbations and, if so, whether force constraint is dependent on a specific stance-like muscle activation pattern.
MATERIALS AND METHODS
Neuromechanical model
The seven degree of freedom (d.f.) cat right hindlimb model has been described elsewhere (Bunderson et al., 2008; Burkholder and Nichols, 2004; McKay et al., 2007). Briefly, the model consists of a pelvis fixed to ground, a three d.f. hip, two d.f. knee, two d.f. ankle, with a three d.f. pin constraint at the metatarsal–phalangeal joint (MTP). The equations of motion for the system were expressed in the generalized coordinate system, θ=[θHF,θHA,θHR,θKE,θKA,θAE,θAA]T, and limb motion was described by the vector equation:
| (1) |
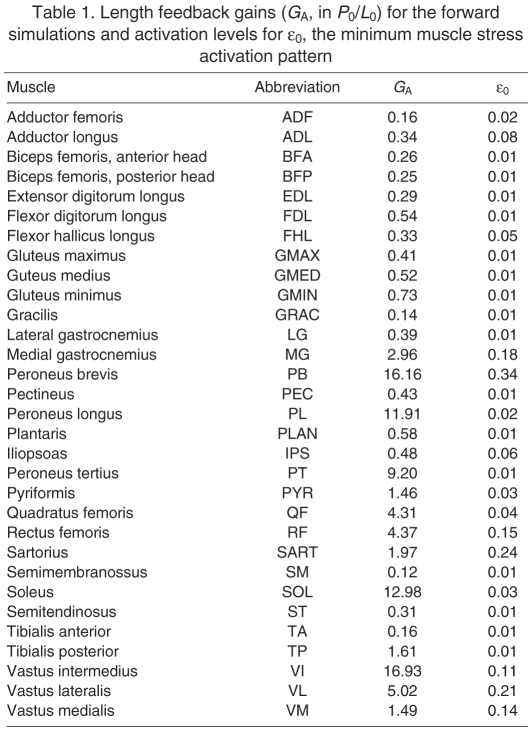
where M is the inertia matrix, is the centrifugal and Coriolis torques, is the gravitational torque, R is the moment arm matrix, J is the Jacobian mapping joint velocities to the translational velocity of the MTP, is the vector of muscle forces, is the resultant force at the MTP joint, is a vector of muscle fiber lengths, is a vector of muscle activation values. For clarity, the state dependence of the variables is omitted in future references. The 31 muscles that span the limb were modeled using a Zajac-style Hill muscle model, with elastic tendon and architectural parameters taken from the literature (Roy et al., 1997; Sacks and Roy, 1982) and tendon slack lengths set so that each muscle would be at 95% optimal fiber length (L0) when maximally activated in the reference posture. The fiber length feedback model is a direct linear feedback of fiber length using gains (GA, Table 1) derived from ramp-and-hold experiments in decerebrate cats (Burkholder and Nichols, 2004; Nichols, 1989; Wilmink and Nichols, 2003).
Table 1.
Length feedback gains (GA, in P0/L0) for the forward simulations and activation levels for ε0, the minimum muscle stress activation pattern
Selection of activation patterns
There are many more muscles than degrees of freedom at the endpoint, and a 24-dimensional space of muscle forces will produce an identical endpoint force. Muscle activation pattern also influences stiffness of each joint and the kinematic response to perturbation. To evaluate the effect of diverse muscle activation patterns on the response to mechanical perturbation, the model performance was evaluated using many different stance-like activation patterns. Consistent features of the model response observed across all muscle activation patterns were considered to be properties of musculoskeletal anatomy and independent of a tuned neural activation strategy.
Muscle activation patterns were chosen to produce a stance-like force at the MTP () derived from experiments (7.93 N vertical, 0.91 N rostral, −0.54 N lateral). Activation patterns were chosen by projecting 10,000 random muscle force vectors (), into the solution space by quadratic programming with the cost function:
| (2) |
and constraints:
| (3) |
| (4) |
This optimization finds the muscle force vector () closest to the random muscle force vector () that satisfies static equilibrium (Eqn 3) and produces the desired endpoint force. To allow changes in activation without saturation, muscle force vectors were further constrained to be between (99% of maximum force) and (1%). Previous work showed that 10,000 patterns allow the mean and covariance of 74% of muscles to converge (Bunderson et al., 2008). Due to computational intensity of forward simulation, a subset of 200 activation patterns was selected for forward simulation. These sets of activation patterns are intended to be representative of the 24-dimensional solution space of Eqn 3 but do not likely span the extremes of that space.
In addition to the random activation patterns, one special activation pattern (ε0, Table 1) that satisfied the desired background force as well as a minimum muscle stress solution was selected. The minimum muscle stress solution (Crowninshield and Brand, 1981; Harris and Wolpert, 1998) minimizes the sum of squares muscle stress across all muscles and has been used by multiple researchers to drive simulations from experimental results (Prilutsky and Zatsiorsky, 2002; Thelen and Anderson, 2006). This activation pattern is the result of an optimization and will represent an extreme of the muscle activation solution space.
Muscle lengthening direction
Displacement of the endpoint moves each joint and lengthens or shortens each muscle. In the mechanically redundant limb, the kinematics of this response depend on the muscle activation pattern. Under a given activation pattern, there is one direction of endpoint motion that maximally increases muscle length due to the combination of joint angle changes induced. This direction coincides with the change in ground reaction force due to a change in muscle activation, and therefore describes the relationship between endpoint behavior and muscle behavior, in the same way that moment arm describes the relationship between joint and muscle behavior. Joint flexion, and therefore the direction of maximal muscle lengthening, depends on the joint stiffnesses and muscle activation pattern when the endpoint is moved. Muscle lengthening affects the intrinsic response of the muscles and the proprioceptive sensory information encoded by that muscle and available to the nervous system. If lengthening directions are conserved across activation patterns, it suggests that the transformation between endpoint displacement and muscle or neural response will be resistant to variability in the stance activation pattern. In this case, the mechanical response to perturbation and the proprioceptive input to the nervous system would be independent of a carefully selected stance activation pattern.
To determine the extent to which the activation pattern influenced the instantaneous kinematics of perturbation, the direction of maximum lengthening for each muscle of the linearized system was determined. Because the system is kinematically redundant, there is not a one-to-one relationship between endpoint displacement and joint displacement, and the Cartesian muscle lengthening direction (), must be determined from the kinetics of the system and the relative flexibility of each joint. The joint stiffness matrix (KJ=d/dθ, where is the vector of joint torques) was approximated by linearizing the equation of motion:
| (5) |
where
| (6) |
The endpoint stiffness (KE=d/d, where is the endpoint displacement) is then (J K −1J JT)−1, and muscle lengthening direction (d/d)=R(dθ/d)(d/d)(d/d) is:
| (7) |
where is the vector of muscle lengths.
This relationship depends on muscle force and activation pattern, and different activation patterns may allow very different kinematic responses by the limb. The lengthening direction () was determined for each of the 10,000 activation patterns described above.
Linear stability analysis
We also investigated whether a special muscle activation pattern is required to stabilize the limb. We previously showed that a carefully selected stance activation pattern can result in limb stability, and an activation pattern specifically selected to provide stability may pose an additional constraint on the acceptable stance activation patterns. However, the requirement for a specially stable stance activation pattern is based on muscles operating at 95% L0, where the force–length relationship has a very low stiffness (0.3 P0/L0, where P0 is the maximum isometric force of the muscle. The addition of muscle fiber length feedback to simulate muscle spindle Ia homonymous feedback could stabilize the limb independent of the chosen muscle activation pattern (Bunderson et al., 2008) and release a constraint on neural flexibility. The experimentally derived length feedback gains ranged from 0.16 to 16.16 P0/L0, with a mean of 3.1 P0/L0 (Burkholder and Nichols, 2000), and this added stiffness may stabilize the system enough to obviate the need for a special stance activation pattern.
The Lyapunov stability of the linearized model was determined for all 10,000 stance-like activation patterns with and without length feedback. Eqn 1 was rewritten as a first-order differential equation and linearized by Taylor series expansion to the form:
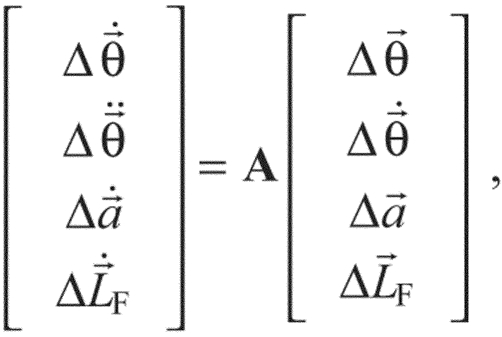 |
(8) |
where A is the state matrix defined by:
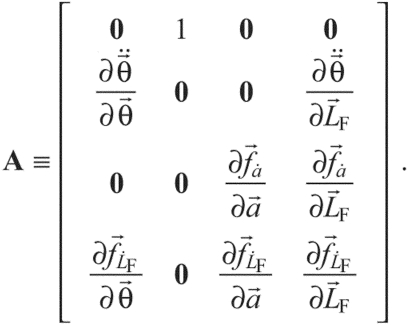 |
(9) |
This yields a different A for every activation pattern. A system is Lyapunov stable, or asymptotically stable, if the real part of all eigenvalues (λ) of A are negative; thus, if the largest eigenvalue is less than zero, the system will be stable. The eigenvalues of A provide the time constants (τ=1/λ) of the response, and the eigenvalue closest to zero will have the slowest response.
Response to perturbation
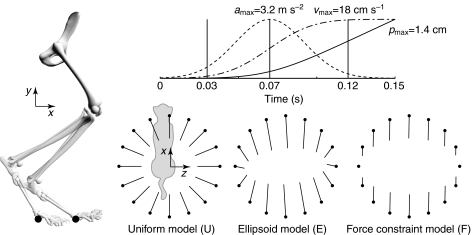
To explicitly determine whether the system displays the force constraint phenomenon, forward dynamic simulations were performed. The endpoint of the hindlimb was perturbed from an initial stance-like posture with an acceleration pulse as in the experimental postural perturbation conditions (Macpherson, 1988a). The magnitude and direction of endpoint force response was examined at three time points during horizontal plane ramp perturbations, using the constraint:
| (10) |
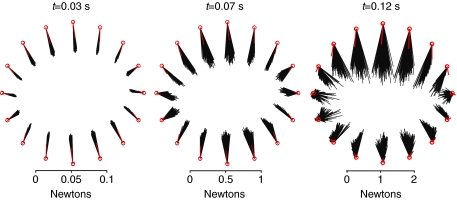
where was a Gaussian profile acceleration pulse centered at 0.07 s, producing a maximum endpoint velocity of 18 cm s−1 (Fig. 1). Perturbations were applied in 16 directions (), and the analysis was repeated for 200 stance-like activation patterns. The endpoint force response was evaluated at t=0.03 s, when acceleration reached 20% of maximum, at t=0.07 s, corresponding to the peak of acceleration, and at t=0.12 s, when acceleration fell below 8% of maximum.
Fig. 1.
Forward simulations with ramp endpoint displacements were performed in 16 directions spaced evenly in the horizontal plane. The endpoint ramp perturbations had a peak acceleration (amax) of 3.2 m s−2, peak velocity (vmax) of 18 cm s−1 and displacement (pmax) of 1.4 cm at 150 ms. Endpoint force responses are evaluated at t=0.03, 0.07 and 0.12 s. Three idealized models represent potential endpoint force responses to the perturbations. In the uniform model (U) the change in endpoint force is opposite the imposed endpoint displacement and the magnitude of the response is equal in all directions. In the ellipsoid model (E) there is an axis of maximum response and orthogonal to it an axis of minimum response. The direction of the response is equal to the perturbation direction when the limb is perturbed along these axes. In the force constraint model (F) the response direction is constant for all perturbation directions and the magnitude varies as the dot product between perturbation direction and response direction.
At each time point, the force response was compared with three idealized models (Fig. 1). The uniform model (U) predicts force responses to be opposite to the imposed endpoint displacement and equal to each other in magnitude, as are seen in the ‘passive’ response of experimental observations (Macpherson, 1988a). The force response was given by Δ=k, where k is a scalar constant. Conceptually, this is equivalent to fixing the endpoint to its initial position by a simple, linear spring. The force response of the ellipsoid model (E) is an extension of the ‘stiffness ellipse’ used in human reaching (Mussa-Ivaldi et al., 1985), derived from segmental inertia and muscle properties. The E response was given by Δ=(JT(xK+M)−1JT)−1, where stiffness (K) and inertia (M) are matrices determined from the linearized equations of motion and is a unit vector in the direction of endpoint displacement. Note that this approximation omits velocity-dependent effects, primarily the force–velocity relationship. Conceptually, this is equivalent to replacing each of the muscles in the limb with a simple spring, and differs from the U model by the addition of inertia and the geometric transformation between the endpoint and joint displacements. The force constraint model (F) predicts forces constrained along a fixed axis and scaled by the projection of the displacement direction onto the force direction, corresponding to the ‘active’ response of experimental observations (Macpherson, 1988a). The F response was given by Δ=(k·), where is a unit vector in the direction of force constraint, chosen to give maximum agreement with the simulated data. Conceptually, this is equivalent to fixing the endpoint by a spring to a rail. The spring can slide freely along the rail but resists displacements perpendicular to the rail. Similarity between the simulated force responses and the idealized models was determined by the sum of squared deviations between the simulation results and each model.
Force responses were qualitatively compared with experimental data from eight cats (Jacobs and Macpherson, 1996; Macpherson et al., 2007; Torres-Oviedo et al., 2006). Time periods corresponding to ‘passive’ mechanical responses (0–50 ms after perturbation onset), ‘stretch reflex’ responses (60–110 ms) and ‘active’ responses (120–160 ms) were compared with simulation time t=0.03 s, t=0.07 s and t=0.12 s, respectively. Experimental times are reported in milliseconds and simulation times in seconds. No special effort was made to normalize posture, size or initial activation of the model to match experimental conditions, and quantitative comparison between the simulation and experimental results is not considered to be meaningful.
RESULTS
Muscle activation sets limb kinematics
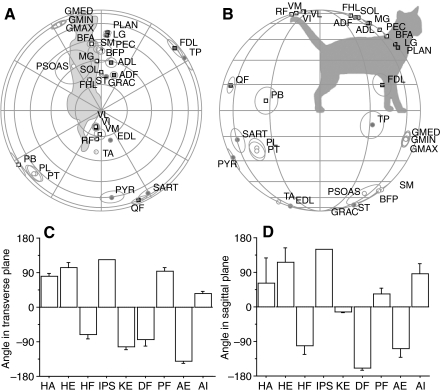
The lengthening direction for each muscle (Fig. 2) was highly consistent across activation patterns. The response of any one muscle under any one activation pattern was symmetrical, with cosine tuning about its lengthening direction; the amount of lengthening of that muscle depended on the degree of alignment between the three-dimensional displacement vector and the lengthening direction, and was proportional to the dot product of those vectors. Thus, perturbations in the plane perpendicular to the lengthening direction produced no change in muscle length. The consistency of lengthening directions indicated that muscle activation constrained the instantaneous kinematics of perturbation. While we have previously seen that the direction of endpoint force production may vary by 180 deg, depending on torques at remote joints (van Antwerp et al., 2007), the standard deviation (s.d.) of the lengthening direction across 10,000 activation patterns for each muscle was on average only 3.5 deg. This suggests that production of a specific endpoint force, which defines the individual joint torques, also constrains the joint stiffnesses and mechanical action of the muscles, regardless of the particular muscles used to achieve that endpoint force.
Fig. 2.
The direction of the endpoint motion producing maximum response for each muscle was calculated from the linearized state equations for the model. The mean response directions across all 10,000 activation patterns is shown in the transverse (A) and sagittal (B) planes. Abbreviations in A and B are in Table 1. The hemisphere of the response direction is indicated by the symbol (circle, downward; square, upward; solid, rightward; outline, leftward). The angular standard deviation of each muscle for the 10,000 patterns is represented by circles around each muscle. Mean pulling direction for individual muscle groups in the transverse plane (C) and in the sagittal plane (D) are concentrated at ±90 deg. HA, hip adductors; HE, hip extensors; HF, hip flexors; IPS, iliopsoas; KE, knee extensors; DF, ankle dorsiflexors; PF, ankle plantarflexors; AE, ankle everters; AI, ankle inverters.
Generation of the dictated stance-like force completely determines the torque at all seven joints but allows differences in joint stiffness and concomitant variation in the kinematic response to perturbation. This variation (Eqn 6) results from muscle stiffness (R d/dθ) and from the change in moment arm with joint angle ( dR/dθ), both dependent on the specific activation pattern. For example, the LG and the SM can generate similar knee flexion torques but the shorter LG fascicles will result in about 50% greater stiffness.
The consistency in muscle lengthening direction was maintained even when random activation patterns produced unconstrained endpoint force directions. Muscle lengthening directions of the unconstrained muscle activation sets ( in Eqn 2) had a mean s.d. of 3.9 deg vs 3.5 deg for the activation sets that produce the stance-like force. Thus, the functional activation of muscles, rather than the specific selection of joint torques, imposes this directional constraint. The realistic redundancy of muscles in the hindlimb model, which has 31 muscles and seven joints, each of which is crossed by at least eight muscles, may minimize the functional consequences of variations in muscle activation patterns.
Most of the maximal lengthening directions were close to the parasagittal plane and substantially elevated from the horizontal plane, with only 20% of muscles within 30 deg of horizontal. The only muscles with lengthening directions more than 35 deg from the sagittal plane were the ankle everters [PB (peroneus brevis), PL (peroneus longus), PT (peroneus tertius)] and ankle inverters [FDL (flexor digitorum longus), TP (tibialis posterior)], supporting the view that these muscles primarily provide lateral support for the ankle and the limb. This means that only five muscles have length changes due to lateral displacements, only five small muscles will have substantial force changes in response to lateral displacements and only five muscles will contribute directly restoring forces.
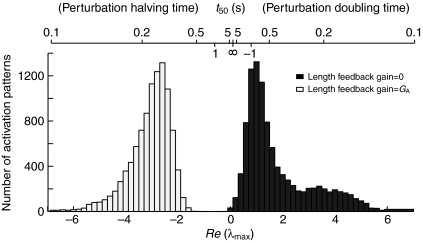
Length feedback sets stability
For all 10,000 activation patterns, the limb was unstable without muscle fiber length feedback and stable when physiological length feedback gains were included (Fig. 3). The Lyapunov stability analysis showed that length feedback was adequate to provide stable posture, independent of a carefully selected stance activation pattern. Adding a uniform length feedback gain of only 0.5 P0/L0 to the intrinsic stiffness of 0.3 P0/L0 was sufficient to stabilize 98% of activation patterns (data not shown). This suggests that only a small amount of length feedback or muscle stiffness, much less than the maximum slope of the force–length relationship (4.3 P0/L0), is sufficient to provide Lyapunov stability. Although it is possible to find activation patterns that provide intrinsic stability, the stiffness of the intact system suggests that this may not be an important criterion in selecting a stance activation pattern.
Fig. 3.
The Lyapunov stability of the model depends on length feedback. The distribution of the largest real component of the eigenvalues (λmax) of the linearized equations of motion is shown across 10,000 activation patterns. The value of λmax is greater than zero for all 10,000 activation patterns in the model without length feedback (black square) and less than zero for all 10,000 activation patterns in the model with length feedback (white square). Also shown is the perturbation halving/doubling time (t50).
Limb anatomy constrains force responses
Force responses were constrained to a narrow window of direction for each perturbation direction, in forward simulations using 200 randomly chosen activation patterns (Figs 4 and 5). At t=0.03, the raw response plot of Fig. 4 looks homogeneous, and the endpoint force response appears to be directed opposite to the direction of perturbation. Fig. 5 reveals that these center-directed populations do have systematic variation with perturbation direction and do not exactly oppose the perturbation. The force amplitude is greater for anterior/posterior (AP)-directed perturbations than for medial/lateral (ML). The response direction is slightly biased towards the AP direction, but there is a smooth and uniform transition in responses between the cardinal directions. At t=0.12, the AP response bias is most distinct. Responses to ML perturbations are small in amplitude, with significant AP components, while responses to AP perturbations are large in amplitude. The system response transitions between AP-directed responses over just three perturbation directions at t=0.12 s, where the transition appears over five to six directions at t=0.03.
Fig. 4.
Horizontal plane projections of the endpoint force response to perturbations in several directions. Simulations based on 200 random activation patterns (black lines) and ε0 (red lines) in each direction, with length feedback. Initially (t=0.03 s), the horizontal component of the endpoint response is largely independent of activation pattern. Responses to sagittal plane perturbations produce slightly larger amplitude responses but are nearly opposite the direction of perturbation. At the peak of acceleration (t=0.07 s), the response remains consistent across activation patterns and the directional bias remains subtle. As the constant velocity phase begins (t=0.12 s), the response direction is distinctly biased in amplitude and direction towards the sagittal plane. At this time point, lateral perturbations produce responses much smaller in amplitude and much more variable in direction. The response of the minimum muscle stress activation pattern (ε0) is shown in red.
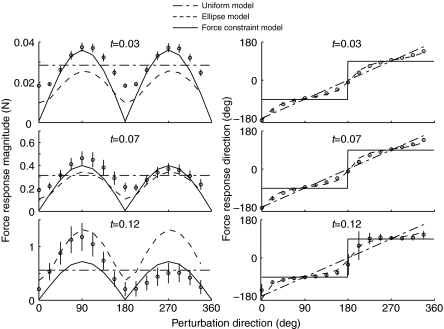
Fig. 5.
Magnitude and direction of simulated force responses as a function of perturbation direction. Symbols represent means ± s.d. In the case of direction, error bars are frequently smaller than the plot symbol. Standard deviations across all perturbation directions are 0.6 deg at 0.03 s, 1.6 deg at 0.07 s and 6 deg at 0.12 s. Solid lines represent force constraint model, aligned to −91 deg; dashed line represents ellipsoid model and dash–dotted line represents uniform model.
Endpoint force variability increased during the perturbation as muscle forces became a larger contribution and the action of different muscles produced different torques, different joint accelerations and different limb postures, further altering force generation by individual muscles. At simulation time 0.03 s, 95% of endpoint force responses were within 7.5 deg of the mean but by 0.12 s, the 95% confidence interval (CI) had spread to 69 deg. On average, length feedback contributed to changes in muscle force production of 0.02% (root mean square, r.m.s.) at 0.03 s, 1.1% at 0.07 s and 15% at 0.12 s. At each time and each perturbation direction, the responses form a uniform population well described by a single normal distribution. There do not appear to be multiple, qualitatively different, response patterns, and we see no indication of a unique subspace of muscle activations to consider better suited for posture than the rest.
Minimizing muscle stress appears to minimize joint stiffness and compromise limb stability. The minimum muscle stress solution was expected to represent an extreme of the stance–force solution space, and its responses to perturbation are also at the extremes of the population of responses. These responses were small in magnitude and not constrained to a single axis (Fig. 4) at any time point. By 0.12 s, the responses to lateral perturbations were directed away from the starting position, indicating substantially greater instability than any of the randomly selected activation sets.
Simple models match different aspects of the forward simulations
The E model matched well at all time points, while the U model was closer in the early phase and the F model was closer in the late phase (Fig. 5). The r.m.s. error in force magnitude was 31% at 0.03 s, 36% at 0.07 s and 95% at 0.12 s for the U model, and the r.m.s. error in direction was 15 deg, 16 deg and 41 deg for the same time points. E model errors were 37%, 32% and 118% in magnitude and 5 deg, 10 deg and 28 deg in direction, and F errors were 27%, 31% and 54% in magnitude and 41 deg, 41 deg and 29 deg in direction. At each time point, the E model had the smallest direction error, and the F model had the smallest magnitude error. The simplest models, U and F, represent the force direction of the early and late response, respectively. Force direction at 0.03 s is approximately opposite to the displacement (r.m.s. error 15 deg), and at 0.12 s is approximately direction constrained (r.m.s. error 29 deg).
The simulation response directions most closely matched the E model, which is a linearized approximation of inertia and muscle tendon unit stiffness only. The E model captured the direction of the early responses, which are relatively unbiased while the system is dominated by inertia. The E model also captured the bimodal, AP distribution of force direction at t=0.12 s. This suggests that the force constraint requires only segmental inertia, muscle stiffness and appropriate muscle moment arms. Both the E and F models captured the strong AP bias in the amplitude of force responses but neither displayed the asymmetry in force magnitude that the simulations developed at later time points.
Our primary interest was the direction of force responses, and the E model captured this aspect of the simulation results far more accurately than either the U or the F model. The error in E model increased as variability among the different activation patterns increased but the model faithfully represents the mean response. The F model does qualitatively capture the directional bias that develops at later time and higher muscle forces. Both cats (Macpherson, 1988a) and humans (Henry et al., 2001) demonstrate the force constraint phenomenon represented by the F model. The U and F models are extremely simple but make a satisfactory first approximation to the early, homogeneous response (U model) and the later, directional response (F model). This transition is captured by the more complex E model.
Comparison with experimental data
The variability in endpoint force direction produced by the simulations in response to endpoint perturbations across different muscle activation patterns was similar to the variability observed in experiments and provides some guidance in evaluating similarity between the simulations and experiments. In the simulations, the s.d. of endpoint force direction ranged between 1.2 deg and 62 deg (Fig. 5), and the 95% CIs ranged from 3 deg to 122 deg. In the experimental results, angular s.d. ranged from 6 deg to 122 deg (Fig. 6), and the CIs ranged from 14 deg to 245 deg. In the experimental data, ML perturbations are extremely variable between animals but perturbation directions that look qualitatively consistent across cats and across trials have s.d.<14 deg and CI<27 deg. In the qualitatively consistent perturbation directions, variation between trials is greater than variation between animals. In the simulation results, ML responses are also most variable across activation sets, and perturbation directions that look qualitatively consistent have s.d.<7 deg and CI<13 deg. Based on these variabilities, we considered 10 deg deviations between model and experiment to be small.
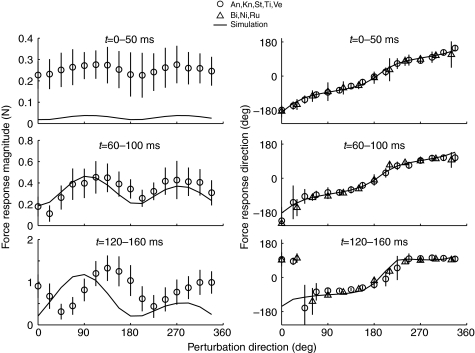
Fig. 6.
Postural responses summarized from eight animals: Bi, Ni and Ru (Jacobs and Macpherson, 1996) and An, Kn, St, Ti and Ve (Macpherson et al., 2007; Torres-Oviedo et al., 2006) with corresponding simulation response for comparison. Animals from Jacobs and Macpherson are not shown in the magnitude plots because variation of perturbation amplitude with direction distorts the magnitude response. Experiment time (t) 0–50 ms precedes active muscle responses, and force responses, like the simulation responses at t=0.03, deviate only slightly from the perturbation direction. By experiment time window 60–100 ms, force response deviates noticeably from the direction of perturbation. By experiment time 120–160 ms (simulation time 0.12 s), force responses are strongly constrained along the −83 deg to 97 deg axis. There is a narrow range of perturbation angles perpendicular to the bias axis where the response is more variable in direction and amplitude. Experimental force magnitudes are close to simulation force magnitudes only in the middle window. During experiment time 120–160 ms, force magnitudes are similar in amplitude but offset by 45 deg in phase. Both model and experiment respond more vigorously to forward (0–180 deg) perturbations than to backward (180–360 deg) perturbations during this active phase. Means ± s.d.
The simulated force responses qualitatively match several features of in vivo perturbation responses (Fig. 6). On the whole, simulation force magnitudes did not match the amplitude or distribution of the experimental force magnitudes but the force directions were very similar. Simulated forces at t=0.03 s were much smaller in magnitude but very similar in direction to ‘passive’ forces measured experimentally 0–50 ms after perturbation. At t=0.07 s, the variations in simulated force magnitude and direction were very similar to forces measured during the ‘stretch’ response 60–100 ms after perturbation. The force magnitudes of both simulation and experiments show a symmetrical bias, with maxima 180 deg apart. In the first time bin, both show force maxima at 90 deg and 270 deg but the peak experimental force direction progressively increases to 135 deg and 315 deg in the third time bin, while the peak simulation amplitudes remain at 90 deg and 270 deg. In the simulations, direction of peak response magnitude is aligned with the force constraint axis but the experimental peak force magnitude occurs 35 deg offset from the force constraint axis. Force directions were very similar in simulations and experiments, exhibiting a bimodal distribution near ±90 deg across all perturbation directions. Notably, for perturbations of 0–33.5 deg, experimental force directions were opposite to the simulated force directions but were nonetheless oriented in one of the predicted modes at ±90 deg.
Both the simulation and experimental force responses are more closely aligned to the sagittal plane than to the axis of stance-like force. The difference in force constraint direction, in the late time window, between the simulation results (−91 deg) and the experimental observations (−83 deg) is small but the difference between the force constraint direction and the stance-like force for either simulations (−91 deg vs −59 deg) or experiments (−83 deg vs −67 deg) is not. Our framing of the force constraint hypothesis predicted that endpoint force responses would be aligned with the direction of stance-like force, as has been seen in intact animal models (Macpherson, 1988a; Ting and Macpherson, 2004). The simulated postural responses consistently diverged from the stance-like force by 20–30 deg but diverged from the sagittal plane by only 0–8 deg. The experimental data also consistently diverged from the stance force by 10–25 deg but diverged from the sagittal plane by 0–20 deg as well. Both the simulations and the experiments are consistent with hindlimb forces constrained near the sagittal plane of the limb, although the experimental results are slightly tilted towards the stance force axis.
DISCUSSION
Force constraint emerges from musculoskeletal mechanics
The experimental response to perturbations follows a repeatable pattern of epochs that seem to integrate increasingly complex mechanical information (Macpherson, 1988a; Ting and Macpherson, 2004). The current study demonstrates that some of this complexity results from the biomechanical response to the limb itself, without need for changes in the neural activation of muscles. The initial epoch, of about 20 ms in cats, occurs without changes in muscle EMG, and endpoint force response is mostly opposite to the perturbation. A short latency, 30 ms, period of EMG activity follows, in which EMG is similar for horizontal plane translations and surface rotations that impose similar foot angle displacements but contradictory CoM displacements (Macpherson, 1988b; Ting and Macpherson, 2004). Allowing for electromechanical delay, EMG activity during this period contributes to force changes in the 50–100 ms time window. There follows a moderate latency period, beginning around 50 ms, of EMG activity, which is opposite for toe-equivalent translations and rotations but similar for similar CoM perturbations (Ting and Macpherson, 2004). This EMG activity contributes to force responses during the ‘active’ phase, 100–150 ms after the perturbation initiation. This is the approximate point at which the present simulations terminate. Finally, at long latency, a more variable period with much larger EMG amplitude changes is presumed to include volitional activity. The initial, or ‘passive’, period includes no neural component and demonstrates no force constraint. The short latency period appears to incorporate mechanical information from the homonymous limb, and the force constraint phenomenon is not experimentally resolved. The medium latency period appears to incorporate information including the CoM, and does demonstrate force constraint but the force constraint during this phase is predicted by the present single-limb simulations.
The concentration of pulling directions along the sagittal plane allows the massive AP-aligned muscles to dominate the mechanical response, and the endpoint force response takes on an AP orientation, regardless of the perturbation direction. As the toe is displaced during a perturbation, the change in limb configuration is dictated by segmental inertia and joint viscoelasticity. The anatomical arrangement of muscles causes large length changes in most muscles in response to AP perturbations and makes those same muscles insensitive to ML perturbations. As a consequence, very little of the limb directly opposes ML perturbations. A nearly lateral perturbation, for example, will stretch FDL and TP, shorten PB, PL and PT but have little effect on other muscles, such as SART (sartorius) or GMAX (gluteus maximus). Any change in force in SART or GMAX will cause primarily AP endpoint force, again as a consequence of the limb anatomy and muscle moment arms.
The mechanical constraints of the limb can be seen in experimentally evoked EMG patterns. In experimental animals, horizontal plane perturbations elicit increased EMG activity in muscles over a broad range of perturbation directions, following a more-or-less cosine tuning function (Honeycutt et al., 2009; Macpherson, 1988b; Torres-Oviedo et al., 2006). Cosine tuning appears to have a basis in musculoskeletal anatomy and muscle lengthening directions and may be the ideal structure for sensory neurons (Todorov, 2002). The cosine tuning of muscle lengthening should be reflected in cosine tuning of proprioceptive feedback from muscle spindles. These spinal pathways have latency appropriate for the early phase of the postural response, and length or velocity feedback from cosine tuned muscles seems sufficient to induce the cosine tuned EMG activity observed in both intact and decerebrate cats (Honeycutt et al., 2009; Macpherson, 1988b). Many muscles have lengthening directions near the vertical axis of the limb (Fig. 2), and the EMG of many muscles during horizontal plane perturbations is closely correlated with vertical force (Jacobs and Macpherson, 1996). However, they found that two muscles, GLUT and SART, which have nearly horizontal lengthening directions, were also correlated with vertical force.
Similarities in the simulated and experimental variability of force directions in response to perturbations further suggest that constrained force directions arise from musculoskeletal mechanics, and that neural mechanisms can only alter force directions within a limited range. As each simulation with a given muscle activation pattern and initial condition always produces the same endpoint force, our results demonstrate the importance of examining the possible sources and structure of variability inherent in biological systems. In both simulations and experiments, the greatest variability in endpoint force direction coincides with minima in endpoint force magnitude. In the experiments the greatest variability in direction and minimum magnitude occurs at perturbation directions of 45 deg and 225 deg. In the simulations the greatest variability in direction and minimum magnitude occurs at 0 deg and between 180 deg and 202.5 deg. These perturbation directions are far from the sagittal plane and induce the smallest change in length for most muscles but are where the response will be most sensitive to changes in the muscle lengthening direction. Near the maximal lengthening direction of a muscle, the amount of lengthening is relatively insensitive to activation pattern; orthogonal to the maximum lengthening direction, where the absolute amount of lengthening is small, the response is most sensitive to changes in direction or activation pattern. Therefore, the amount of length change and consequent force change, for most muscles, will be most sensitive to the exact stance-like activation pattern for ML perturbations. By contrast, near the maximum lengthening direction of a muscle, small differences arising from variation in the stance activation pattern have a relatively small effect on the amount of muscle stretch due to a perturbation in that direction. The result is that the limb anatomy acts as a mechanical filter, such that perturbations in the ML directions coincide with the smallest mechanical signal and the smallest signal-to-noise ratio, and the resultant force output is most variable.
Musculoskeletal contributions toward stability
The linearized model, stabilized by length feedback, had time constants around 300 ms, which is similar to the long latency, voluntary epoch, and suggests that the instantaneous limb and muscle mechanics may provide transient, incomplete stability while longer latency processes compute a more global response. The eigenvalues of the linearized model correspond to time constants (1/λmax) between 0.2 s and 0.5 s, and the musculoskeletal mechanics may provide limited stability in the context of a complex mechanical environment, as a stop-gap role during the recruitment of higher neural responses. Length feedback or stretch reflex contributions to postural responses are small (Horak and Macpherson, 1996), and can sometimes be in opposition to the stabilizing postural force (Carpenter et al., 1999; Ting and Macpherson, 2004). Despite the omission of relatively long delays associated with stretch reflexes (~20 ms), length feedback contributions to the simulation results were negligible for the first two timepoints, as result of small displacements. Length feedback did improve the response of ε0, which lacked the intrinsic stiffness associated with co-contraction and became unstable more rapidly in the absence of length feedback (data not shown). Muscle spindles also encode stretch velocity and perhaps acceleration, and addition of higher-order feedback may increase the stabilizing influence of spindle feedback beyond length feedback.
Redundancy
Neuromuscular redundancy is often presented looking down from the perspective of the nervous system, as a problem of selecting the appropriate muscles to perform a desired task, or looking in from the perspective of the scientist, as a problem of determining which muscles contributed to an observed endpoint force (Ting and Macpherson, 2005; Tresch et al., 1999). Neuromuscular redundancy arises from muscles operating in antagonistic and synergistic groups, so a desired torque can be produced by a continuum of synergist and antagonist co-activation. If we look at redundancy from the perspective of a perturbation, the many-to-few mapping of muscles onto the endpoint becomes a few-to-many distribution of information. In this context, redundancy appears as clustering of muscle lengthening directions near the vertical poles of the sagittal plane. Looking up from the endpoint, redundancy defines the distribution of a perturbation onto the muscles, and encodes perturbation information in a unique pattern of length changes across the musculature. Because the lengthening directions are biased to the sagittal plane, the resultant change in muscle force, whether due to intrinsic mechanics, length feedback or more complex neural processing, is mechanically constrained to the sagittal plane. Therefore, the structure of the musculoskeletal mechanics imposes strong correlations in sensory signals across the limb that also affect the dimension of the motor response.
The emergent mechanical behavior of the limb may simplify acquisition of new tasks. Because the system is indifferent to the specific activation pattern at the level of endpoint force and at the level of endpoint stiffness, careful selection of an optimum activation pattern is not necessary. The neural control of a task may change substantially with training (Enoka, 1997), and the consistency of perturbation mechanics suggests that feedback control in response to an externally imposed perturbation can be performed independent of the feedforward program of a skilled or ballistic task.
Neural contributions to force constraint
There are several mechanisms by which the nervous system could drive the expression of the force constraint phenomenon. The nervous system could sense the postural perturbation, then select and activate muscles to counter the perturbation. In this paradigm, it may be advantageous to select muscles using pre-defined synergies with consistent and robust mechanical actions. The nervous system does, unquestionably, recruit muscles in a directionally deterministic fashion in response to perturbations (Honeycutt et al., 2009; Jacobs and Macpherson, 1996; Macpherson, 1988b; Macpherson et al., 2007), and that recruitment must contribute to the force response of the limb and the ability of the animal to maintain posture. The simulations and even the E model, which lacks any such control structure, demonstrate the force constraint phenomenon and suggest that directionally constrained force production is a mechanical phenomenon laid over any control response rather than an active strategy of the nervous system. In this case, the neural response must work within the directionally constrained force outputs of the four limbs to produce the full range of force directions necessary to counteract perturbations from all directions.
The second sense in which the nervous system could drive the force constraint phenomenon is by voluntary creation of conditions that coerce the mechanical force constraint to produce the appropriate forces, including selection of the specific muscles used to generate the stance-like force, fine tuning of the stance-like force or selection of a special stance posture (Ting et al., 2009). The sense in which the initial activation would be considered to represent a specific neural strategy would be if some, but not all, of the stance-like activation sets would also have demonstrated the force constraint. However, the directional bias in force response is observed for any muscle activation pattern, which indicates that no special stance activation pattern is required to obtain strong direction bias in the endpoint response. Further, we consider the imposition of a stance-like force to be a mechanical constraint rather than the result of any specific neural strategy. Mechanically, each hindlimb must produce approximately 25% of the cat weight, and typically produces a horizontal plane force of less than 1.0 N (~2.5% weight), directed posterior and lateral or away from the CoM. We interpret the horizontal plane shear forces as manifestation of the torque required to suspend the CoM between the limbs, and therefore consider the ‘down, out and back’ force to be a mechanical requirement. This mechanical requirement limits the available muscle activation space but the modeled activation sets included 65±30% of activation range, depending on the muscle and could be reduced to no fewer than 14 principal components (Bunderson et al., 2008).
The nervous system does choose the initial posture, and the initial posture strongly influences the experimental manifestation of the force constraint phenomenon (Macpherson, 1994). The force constraint phenomenon disappears in animals constrained to stand with very narrow stances, and becomes exaggerated at long inter-paw distances. This does not appear to be a consequence of mechanical constraints in the hindlimb at difference stance lengths, as the feasible force set maintains its shape at different inter-paw distances (McKay and Ting, 2008), but may reflect mechanical constraints emerging from interaction among the limbs or changes in the neural strategy of standing. Our simulations have not investigated other stance lengths, and it is not clear whether nonlinear simulation would reveal constraints not apparent in the linear analysis of McKay and Ting (McKay and Ting, 2008).
Regardless of the contributions of the nervous system, the dynamic characteristics of the musculoskeletal system play a large role in determining motor output. Great care must therefore be taken in attributing particular motor output features to explicit neural control mechanisms. The nervous system can shape motor outputs to modify the dynamic properties of the musculoskeletal system and generate energetically efficient motor behaviors (Collins et al., 2005; Verdaasdonk et al., 2009) but may not directly specify a detailed kinematic path. As stated by Raibert and Hodgkins, ‘Rather than issuing commands, the nervous system can only make suggestions which are reconciled with the physics of the system and task [at hand]’ (Raibert and Hodgkins, 1993). In general, motor behaviors emerge from complex neuromechanical interactions, and an integrative analysis is essential to correctly attribute features of those behaviors to neural or biomechanical factors.
Overall, our results demonstrate that hindlimb musculoskeletal mechanics greatly influence the sagittal-plane force directions produced in response to postural perturbations, and therefore greatly influence the degree to which any neural strategy or variation in muscle activation pattern can dictate the resulting force direction in response to perturbations. Our results suggest that the neural strategy has a limited window within which endpoint forces can be manipulated. In simulations, the force constraint directions are similar to experimental force directions and explained by both nonlinear simulations and the E model, composed of purely linear springs imposed on the limb anatomy. There are deviations between the simulated and experimental results, including differences in force magnitude and asymmetry in the experimental response direction. The degree to which these reflect interaction among the four limbs and body of the experiments, neural constraints or an active neural strategy (Ting and McKay, 2007; McKay and Ting, 2008) remains to be seen.
ACKNOWLEDGEMENTS
This work was supported by NIH grants HD032571 and HD46922. The NIH had no role in the design, performance or interpretation of the study. Deposited in PMC for release after 12 months.
REFERENCES
- Bunderson N. E., Burkholder T. J., Ting L. H. (2008). Reduction of neuromuscular redundancy for postural force generation using an intrinsic stability criterion. J. Biomech. 41, 1537-1544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke D., Hagbarth K. E., Lofstedt L. (1978). Muscle spindle activity in man during shortening and lengthening contractions. J. Physiol. 277, 131-142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkholder T. J., Nichols T. R. (2000). The mechanical action of proprioceptive length feedback in a model of cat hindlimb. Motor Control 4, 201-220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkholder T. J., Nichols T. R. (2004). Three-dimensional model of the feline hindlimb. J. Morphol. 261, 118-129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter M. G., Frank J. S., Silcher C. P. (1999). Surface height effects on postural control: a hypothesis for a stiffness strategy for stance. J. Vestibular Res. 9, 277-286 [PubMed] [Google Scholar]
- Collins S., Ruina A., Tedrake R., Wisse M. (2005). Efficient bipedal robots based on passive-dynamic walkers. Science 307, 1082-1085 [DOI] [PubMed] [Google Scholar]
- Crowninshield R. D., Brand R. A. (1981). A physiologically based criterion of muscle force prediction in locomotion. J. Biomech. 14, 793-801 [DOI] [PubMed] [Google Scholar]
- Deliagina T. G., Zelenin P. V., Beloozerova I. N., Orlovsky G. N. (2007). Nervous mechanisms controlling body posture. Physiol. Behav. 92, 148-154 [DOI] [PubMed] [Google Scholar]
- Enoka R. M. (1997). Neural adaptations with chronic physical activity. J. Biomech. 30, 447-455 [DOI] [PubMed] [Google Scholar]
- Harris C. M., Wolpert D. M. (1998). Signal-dependent noise determines motor planning. Nature 394, 780-784 [DOI] [PubMed] [Google Scholar]
- Henry S. M., Fung J., Horak F. B. (2001). Effect of stance width on multidirectional postural responses. J. Neurophysiol. 85, 559-570 [DOI] [PubMed] [Google Scholar]
- Honeycutt C. F., Gottschall J. S., Nichols T. R. (2009). Electromyographic responses from the hindlimb muscles of the decerebrate cat to horizontal support surface perturbations. J. Neurophysiol. 101, 2751-2761 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horak F. B., Macpherson J. M. (1996). Postural orientation and equilibrium. In Handbook of Physiology, Exercise: Regulation and Integration of Multiple Systems, vol. 12 (ed. Rowell L. B.), pp. 255-292 New York: Oxford; [Google Scholar]
- Jacobs R., Macpherson J. M. (1996). Two functional muscle groupings during postural equilibrium tasks in standing cats. J. Neurophysiol. 76, 2402-2411 [DOI] [PubMed] [Google Scholar]
- Loram I. D., Lakie M. (2002). Direct measurement of human ankle stiffness during quiet standing: the intrinsic mechanical stiffness is insufficient for stability. J. Physiol. 545, 1041-1053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macpherson J. M. (1988a). Strategies that simplify the control of quadrupedal stance. I. Forces at the ground. J. Neurophysiol. 60, 204-217 [DOI] [PubMed] [Google Scholar]
- Macpherson J. M. (1988b). Strategies that simplify the control of quadrupedal stance. II. Electromyographic activity. J. Neurophysiol. 60, 218-231 [DOI] [PubMed] [Google Scholar]
- Macpherson J. M. (1994). Changes in a postural strategy with inter-paw distance. J. Neurophysiol. 71, 931-940 [DOI] [PubMed] [Google Scholar]
- Macpherson J. M., Fung J. (1999). Weight support and balance during perturbed stance in the chronic spinal cat. J. Neurophysiol. 82, 3066-3081 [DOI] [PubMed] [Google Scholar]
- Macpherson J. M., Everaert D. G., Stapley P. J., Ting L. H. (2007). Bilateral vestibular loss in cats leads to active destabilization of balance during pitch and roll rotations of the support surface. J. Neurophysiol. 97, 4357-4367 [DOI] [PubMed] [Google Scholar]
- Masani K., Popovic M. R., Nakazawa K., Kouzaki M., Nozaki D. (2003). Importance of body sway velocity information in controlling ankle extensor activities during quiet stance. J. Neurophysiol. 90, 3774-3782 [DOI] [PubMed] [Google Scholar]
- McKay J. L., Ting L. H. (2008). Functional muscle synergies constrain force production during postural tasks. J. Biomech. 41, 299-306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKay J. L., Burkholder T. J., Ting L. H. (2007). Biomechanical capabilities influence postural control strategies in the cat hindlimb. J. Biomech. 40, 2254-2260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morasso P. G., Schieppati M. (1999). Can muscle stiffness alone stabilize upright standing? J. Neurophysiol. 82, 1622-1626 [DOI] [PubMed] [Google Scholar]
- Mussa-Ivaldi F. A., Hogan N., Bizzi E. (1985). Neural, mechanical, and geometric factors subserving arm posture in humans. J. Neurosci. 5, 2732-2743 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols T. R. (1989). The organization of heterogenic reflexes among muscles crossing the ankle joint in the decerebrate cat. J. Physiol. 410, 463-477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols T. R., Houk J. C. (1976). Improvement in linearity and regulation of stiffness that results from actions of stretch reflex. J. Neurophysiol. 39, 119-142 [DOI] [PubMed] [Google Scholar]
- Prilutsky B. I., Zatsiorsky V. M. (2002). Optimization-based models of muscle coordination. Exercise Sport Sci. Rev. 30, 32-38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raibert M. H., Hodgkins J. (1993). Legged robots. In Biological Neural Networks in Invertebrate Neuroethology and Robotics (ed. Beer R., Ritzmann R., McKenna T.). Boston: Academic Press; [Google Scholar]
- Roy R. R., Kim J. A., Monti R. J., Zhong H., Edgerton V. R. (1997). Architectural and histochemical properties of cat hip ‘cuff’ muscles. Acta Anatomica 159, 136-146 [DOI] [PubMed] [Google Scholar]
- Sacks R. D., Roy R. R. (1982). Architecture of the hind limb muscles of cats: functional significance. J. Morphol. 173, 185-195 [DOI] [PubMed] [Google Scholar]
- Shumway-Cook A., Woollacott M. (2000). Attentional demands and postural control: the effect of sensory context. J. Gerontol. 55, M10-M16 [DOI] [PubMed] [Google Scholar]
- Thelen D. G., Anderson F. C. (2006). Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. J. Biomech. 39, 1107-1115 [DOI] [PubMed] [Google Scholar]
- Ting L. H., Macpherson J. M. (2004). Ratio of shear to load ground-reaction force may underlie the directional tuning of the automatic postural response to rotation and translation. J. Neurophysiol. 92, 808-823 [DOI] [PubMed] [Google Scholar]
- Ting L. H., Macpherson J. M. (2005). A limited set of muscle synergies for force control during a postural task. J. Neurophysiol. 93, 609-613 [DOI] [PubMed] [Google Scholar]
- Ting L. H., McKay J. L. (2007). Neuromechanics of muscle synergies for posture and movement. Curr. Opin. Neurobiol. 17, 622-628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ting L. H., van Antwerp K. W., Scrivens J. E., McKay J. L., Welch T. D., Bingham J. T., DeWeerth S. P. (2009). Neuromechanical tuning of nonlinear postural control dynamics. Chaos 19, 026111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E. (2002). Cosine tuning minimizes motor errors. Neural Computation 14, 1233-1260 [DOI] [PubMed] [Google Scholar]
- Torres-Oviedo G., Ting L. H. (2007). Muscle synergies characterizing human postural responses. J. Neurophysiol. 98, 2144-2156 [DOI] [PubMed] [Google Scholar]
- Torres-Oviedo G., Macpherson J. M., Ting L. H. (2006). Muscle synergy organization is robust across a variety of postural perturbations. J. Neurophysiol. 96, 1530-1546 [DOI] [PubMed] [Google Scholar]
- Tresch M. C., Saltiel P., Bizzi E. (1999). The construction of movement by the spinal cord. Nat. Neurosci. 2, 162-167 [DOI] [PubMed] [Google Scholar]
- van Antwerp K. W., Burkholder T. J., Ting L. H. (2007). Inter-joint coupling effects on muscle contributions to endpoint force and acceleration in a musculoskeletal model of the cat hindlimb. J. Biomech. 40, 3570-3579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Soest A. J., Rozendaal L. A. (2008). The inverted pendulum model of bipedal standing cannot be stabilized through direct feedback of force and contractile element length and velocity at realistic series elastic element stiffness. Biol. Cybern. 99, 29-41 [DOI] [PubMed] [Google Scholar]
- Verdaasdonk B. W., Koopman H. F., van der Helm F. C. (2009). Energy efficient walking with central pattern generators: from passive dynamic walking to biologically inspired control. Biol. Cybern. 101, 49-61 [DOI] [PubMed] [Google Scholar]
- Wilmink R. J., Nichols T. R. (2003). Distribution of heterogenic reflexes among the quadriceps and triceps surae muscles of the cat hind limb. J. Neurophysiol. 90, 2310-2324 [DOI] [PubMed] [Google Scholar]
- Winter D. A., Patla A. E., Prince F., Ishac M., Gielo-Perczak K. (1998). Stiffness control of balance in quiet standing. J. Neurophysiol. 80, 1211-1221 [DOI] [PubMed] [Google Scholar]