The mechanical and metabolic basis of myocardial blood flow heterogeneity

Abstract

Precise measurements of regional myocardial blood flow heterogeneity had to be developed before one could seek causation for the heterogeneity. Deposition techniques (particles or molecular microspheres) are the most precise, but imaging techniques have begun to provide high enough resolution to allow in vivo studies. Assigning causation has been difficult. There is no apparent association with the regional concentrations of energy-related enzymes or substrates, but these are measures of status, not of metabolism. There is statistical correlation between flow and regional substrate uptake and utilization. Attribution of regional flow variation to vascular anatomy or to vasomotor control appears not to be causative on a long-term basis. The closest relationships appear to be with mechanical function, but one cannot say for sure whether this is related to ATP hydrolysis at the crossbridge or associated metabolic reactions such as calcium uptake by the sarcoplasmic reticulum.

Introduction

Blood flows in the heart have been recognized for a long time as being spatially heterogeneous (26, 37, 79, 86, 111). The heterogeneity, demonstrated conclusively to have a coefficient of variation of about 25%, not due to methodological error, in normal awake animals (52), seemed curiously high. After all, the heart is a mono-functional organ in which the cells form a syncytium such that all cells are excited and contract with each beat of the heart. Yet one observes approximately eight-fold to ten-fold ranges of flows. The distribution of flows is not quite Gaussian, but is higher-peaked, has standard deviations of 25 – 30%, and has extended tails toward both low and high flows. (The distributions are slightly leptokurtic, and mostly not skewed.) Methodological error is only 5 to 7% (13, 78). Because the variation is so much larger than methodological error it demands explanation in terms of the physiology. Following a brief overview of the methods and their error, we discuss causation by looking at associations with substrate, then with anatomy, with vasomotor control, and finally with the mechanics of cardiac contraction.

Methods of regional flow measurement

Microsphere methods

For more than three decades the standard microsphere method has been to measure the deposition of particles or molecules injected into the inflow, with the assumption that the particle deposition density is distributed in proportion to the regional flow. Measures have been made of particle concentration in the tissue, and interpreted as indicating flow relative to the mean flow in the whole heart. As will be described in the section Measures of heterogeneity, the estimation of spatial heterogeneity is dependent on the spatial resolution used to calculate the variance. Since the relationship is a fractal, such that log(variance) versus log(tissue unit size) is a straight line, reports of variance have been inconsistent. It would be best to report variance at a consistent unit size relative to the heart size, e.g., at the level of 0.4% of heart mass (divided into 250 pieces) or of 1% (divided into 100 equal size pieces).

The use of macroaggregated albumin particles, with particle sizes mainly above ten microns, was introduced by Ueda et al. (92) and Taplin et al. (89). Quantitation using macroaggregated albumin was possible (79, 80), but was not regarded as a particularly robust method because of the diversity of particle sizes, and albumin macroaggregates were soon replaced by fifteen-micron diameter microspheres (26, 111). This method also demonstrated substantial heterogeneity of regional myocardial blood flows, and suggested, further, that in normal hearts the flows to the subendocardial region were higher than flows to the subepicardial region. (In contrast, under ischemia or stressed conditions, the subendocardial flows are relatively low.)

The information from deposition of particles corresponded with that from tracer washout studies (7, 109), such that methods using diffusible materials and methods using trapped particles gave essentially similar measures of local flow, as was summarized by Bassingthwaighte et al. (8). Thompson et al. (90) had anticipated this in their use of tracer water. The observations of Falsetti et al. (37) were similar. The microsphere techniques were improving (26, 52, 71) using methods which are well summarized in a review by Heymann et al. (48)].

The studies of the baboon heart by King et al. (52) clearly revealed the extent of the heterogeneity; they used higher spatial resolution than had been used previously, measuring flows in about 250 pieces of the heart, each about 0.4% of the cardiac mass. King et al. (52) established the general perspective that at this spatial resolution the standard deviation of the flows is 20 – 30% of the mean. Later analysis of these same studies (53) showed that the regional flows were stable over long periods of time, from a few hours up to a day, in four to six repeated observations. This observation challenged the notion that large temporal fluctuations in regional flows occurred normally, thus provoking a search for an explanation for the stable spatial variation. As Deussen and Bassingthwaighte (36) commented, a region with a flow of 25% of the mean flow does not receive enough oxygen to allow it to survive if it consumes oxygen at the average rate for the heart. This observation gave a firm background on which to examine the effects of regional ischemia or other pathophysiological interventions (105).

The use of varicolored microspheres avoided using radioactivity (55), and it has been found even more convenient to use varicolored fluorescent microspheres (41). The use of fluorescent microspheres had an unexpected advantage, compared with the use of radiotracer microspheres, in that fluorescent microspheres did not leach out over a few month period, and so fluorescent microspheres should now be recognized as the marker of choice for determining flow distributions when long periods of time precede sacrifice (78, 99).

Molecules as deposition markers for flow distribution

If a tracer is highly extracted and retained for a long time in the tissue then it can serve as a deposition marker for flow. Molecules should be better than microspheres since there can be no bias due to the hydrodynamics at branch points (107). Tracer water, D₂O, was used by Thompson et al. (90). The markers with large volumes of distribution and therefore long retention were potassium and thallium, and more recently sestamibi (91) and rotenone (96) have been considered. Potassium was first used by Love and Burch (64). None of these markers except water is highly extracted during a single pass through the heart, but the fraction which was extracted was retained for a long enough time that the heart could be removed and diced into small pieces for the measurement of local concentrations and the estimation of flow. A highly extracted tracer, desmethylimipramine (62), proved superior technically since it had 96 – 99% extraction. This extraction was so high that it could be used to evaluate the fifteen-micron diameter microsphere technique for the first time. Bassingthwaighte et al. (13), comparing the molecular microsphere IDMI (iododesmethylimipramine) with standard tracer microspheres, showed that the molecular microsphere had an error of about 2%, whereas the fifteen-micron spheres had errors of 5 – 7%, just as had been predicted by Buckberg et al. (26) and Nose et al. (71), and seen by King et al. (52). The molecular microsphere, however, could provide much higher resolution since many molecules are deposited in small regions, and so the agent was useful in estimating flows at very high spatial resolution using autoradiography (88).

Imaging for regional blood flows

Regional blood flow imaging has been accomplished using positron emission tomography (PET; 61, 85), magnetic resonance imaging (MRI; 56, 104), and even ultrasound (101). All of these methods depend on the mean transit time of tracer through the regional tissue volume, so the methods are dependent on the flow and the regional volume of distribution for the tracer. For the ultrasound bubble images, the dependence is on transit within the vascular space. Therefore it is important to remember that what one measures with the technique is transit time, which is the volume of distribution divided by the flow. If there were substantial heterogeneity in the volume of blood per milliliter tissue within the myocardium, the ultrasound method would give variation in transit time that was unrelated to flow: higher local blood volume would give a longer transit time for the same flow than a region with a smaller volume. The use of ¹⁵O-water by PET is one of the safest methods in this regard because ¹⁵O-water would be distributed in all tissue water space, not just the vascular space that accounts for approximately 12 to 15% of total water content. The water content of a normal heart is relatively precisely known being 0.78 ± 0.01 ml/g (110), although it can go up as high as 83 – 84% in edematous tissue. The exchanges of ¹⁵O-water and ³HHO are completely flow-limited in the heart, there being no effective barrier between the blood and the myocyte water space (10, 19, 109). The great advantage of methods where information is obtained by external detection (PET, MRI, and ultrasound) is that they are noninvasive and can be repeated. In contrast, the microsphere techniques are destructive, requiring removal of the heart and cutting it into pieces. The clinically favored technique is still thallium imaging using ²⁰¹Tl and SPECT (single photon emission-computed tomography). Since thallium is readily visualized (although with low resolution) and is well-retained, it gives fairly good estimates of flow even if, because of its incomplete extraction, it underestimates flow in high-flow regions (17). Because of its long half-life (74 hours) thallium recirculates for long enough to redistribute over the first several hours and therefore its retention at late times in low-flow regions gives evidence for tissue viability.

Accounting for heterogeneity is important when analyzing outflow dilution data for the estimation of capillary and cell permeability surface-area products, PS, and tissue metabolic rates, since the relationships to flow, F, are nonlinear. The microsphere data describing the flow distributions are used in the analysis of multiple-indicator dilution using models with multiple flow paths in parallel (54). When microsphere data are not available then the effective dispersion method of Haselton et al. (47) or the transit time method of Rose and Goresky (83) can be used and are improvements over using a single path model. We feel, however, that both underestimate the real dispersion. Cousineau et al. (29, 30) argue for the correctness of the transit time method, but their argument is not wholly convincing because the tissue pieces used for the microsphere estimates were too large (2% of heart weight) to reveal the true, broader level of heterogeneity that becomes evident with more refined spatial sectioning.

Measures of heterogeneity

Heterogeneity can be described by the variance, the standard deviation, or by a relative measure such as the relative dispersion, RD. The RD is the standard deviation divided by the mean, and is therefore identical to the coefficient of variation.

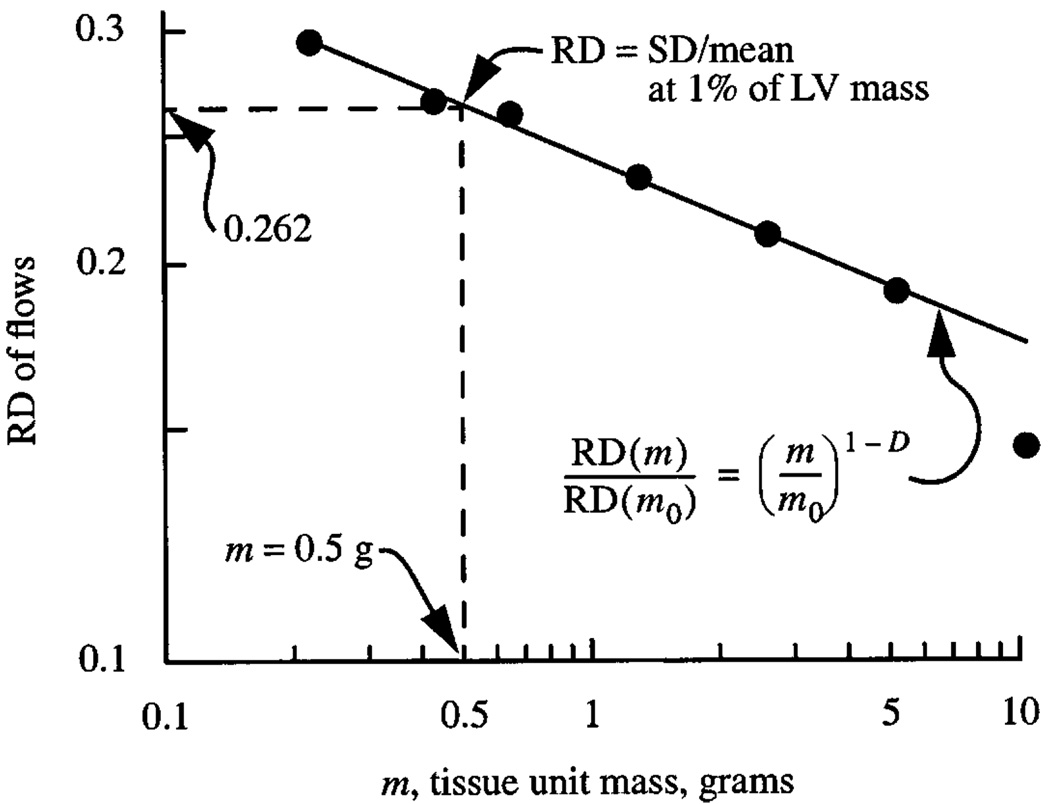
The measurement of variance in any property of any spatial domain in which the choice of unit size is arbitrary has a fundamental problem: the more refined the spatial resolution used, the greater is the apparent variance, as in Fig. 1. This is true for population densities within a continent and for tissue concentrations within an organ. For regional flows in the heart these variations are not random, for there is correlation in flows among near-neighbor regions. The correlation can be found either by the method of fractal dispersional analysis described by Bassingthwaighte et al. (12) and by Bassingthwaighte and van Beek (11), or by looking at the spatial autocorrelation structure (14). The nearest-neighbor correlation coefficient, r₁, is related to the fractal dimension D, r₁ = 2^3–2D −1. The spatial autocorrelation function between neighbors separated by n − 1 pieces of a given size, r₁, r₂, … r_n, falls off as a power law function of the distance between one region and another. This power law scaling, seen in the autocorrelation function and in the relationship between the log apparent heterogeneity and log spatial resolution, indicated that the flow distribution behaves as a statistical fractal measure, that is, it shows self-similarity. The self-similarity, the percentage diminution in correlation coefficient with stepping a specific distance in any direction, is the same for the same step in distance, independent of actual location. Alternatively, the percent diminution in apparent heterogeneity as larger and larger pieces of tissue in which to examine the local flow are taken, is the same for any specific percent enlargement, independent of the actual unit size. By either approach, the fractal dimension, D, is about 1.20 to 1.25 and the near-neighbor correlation coefficient, r₁, is about 0.61. An equivalent measure is the Hurst coefficient, H, where H = 2 − D. A high H, 0.5 < H < 1, indicates smoothness and high near-neighbor correlation. A low H, 0 < H < 0.5, indicates roughness and negative near-neighbor correlation. With H = 0.5 there is a random relationship with zero correlation.

Fig. 1.

Normalization of heterogeneity estimate. The RD, relative dispersion of regional flows, is the standard deviation of the regional flows in regions of size m in grams divided by the mean flow for all the regions together, in this case the whole left ventricle, LV. The LV mass was 50 g. The dashed vertical line at 0.5 g, 1% of LV mass, intercepts the observed fractal relationship at RD = 0.262. The regression equation is RD(m) = 0.232 (m/m₀)^−0.18 using m₀ = 1 g. The fractal dimension D = 1.18. (Data are from 11 sheep. See (12)).

The description of the diminution in correlation with distance, or the number of intervening units or tissue volume elements, is given by the expression for correlation between the n^th units (14, 67):

$$r_{\mathrm{n}}=\frac{1}{2}\{{|\mathrm{n}+1|}^{2\mathrm{H}}-2{|n|}^{2\mathrm{H}}+{|n-1|}^{2\mathrm{H}}\},$$ (1)

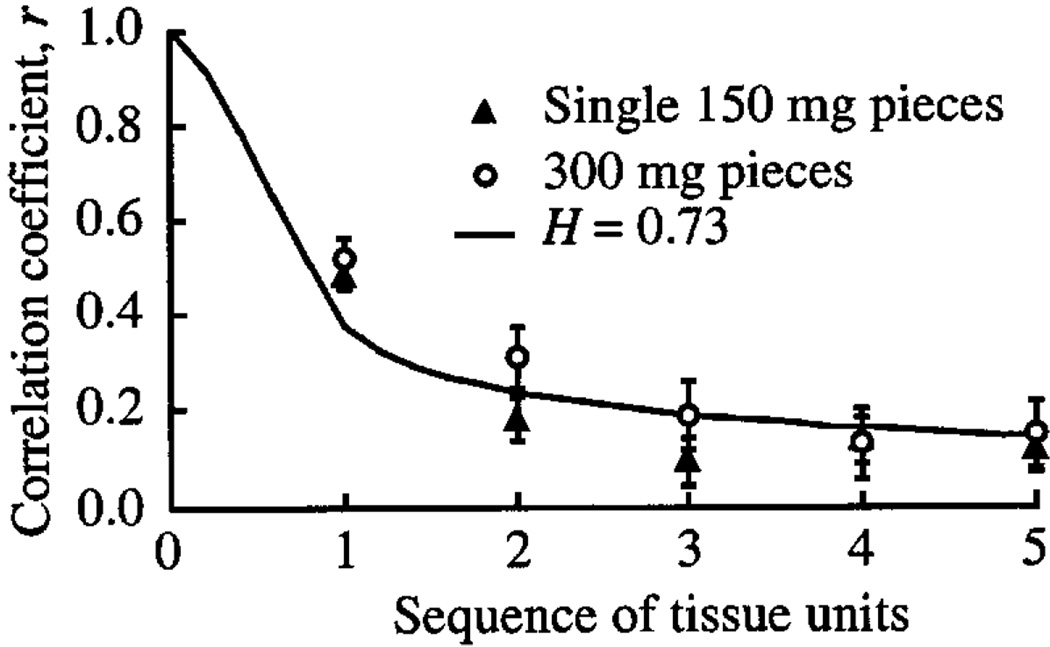
, where n is the number of units of any chosen uniform size between the points of observation. The absolute value signs allow noninteger values of n, or negative values, or values less than one. This expression fits cardiac data at two different volume element sizes (Fig. 2). The figure shows a self-similarity test, namely that the same relationship for the correlation falloff holds for two different piece sizes, thus fulfilling the standard fractal phrasing “self-similarity independent of scale”. The autocorrelation function for n > 2 is a power law function, r_n/r_{n − 1} = [n/(n − 1)]^{2H − 2}. The line shown in Fig. 2, when plotted on log-log axis, becomes straight for n > 2. That these regional flows are fractal is not an explanation, but is an important statistical description of the heterogeneity and the correlation, and provides a basis for relating structure to function.

Fig. 2.

Correlation between flows in successive tissue units in a series. Sequence number 1 means adjacent units. The correlation, given by the line described by Eq. 1, falls off similarly for 150-mg units (▲) and 300-mg units (○), even though the latter are actually twice the distance between centers. A value of H = 0.73 or D = 1.27 describes the falloff.

A recommendation on how the observed heterogeneity should be reported can be derived by taking a utilitarian view about the spatial resolution: from a point of view of refined measures of regional flows, resolution better than 500 tissue pieces is seldom exceeded (e.g., (13)); this is 0.2% of total mass. When a heart is cut into 500 pieces the RD can always be calculated for larger pieces by combining nearest-neighbor regions and redoing the calculation. A relationship such as is shown in Fig. 1 can always be found by combining neighboring pieces; the RD must decrease monotonically with increasing tissue unit size simply because the variation within each unit is removed by considering each tissue piece as if it were internally uniform. A standardized reporting of heterogeneity could be that at any particular unit size, e.g., 1 gram. However, that is not a useful measure by which to compare mouse and human hearts. A better standardization is to report RD at a particular fractional mass, e.g., at 1% of the LV mass as in Fig. 1.

An alternative is to report both the RD and the fractal dimension as in the expression:

$$\frac{\text{RD}(m)}{\text{RD}(m_0)}={\left(\frac{m}{m_0}\right)}^{1-\mathrm{D}},$$ (2)

where m is the tissue unit size, grams, m₀ is an arbitrary reference size, e.g., 1 gram, and D is the fractal dimension, giving RD(m) = 0.232 m^−0.178; the value 0.232 is the RD(m = 1 g). Choosing m₀ as 1% of LV mass would give generality in the reporting since RD(m₀) would give the reference value directly. For the data from the 50g heart in Fig. 1 with 1% of mass being 0.5g, the RD(m = 0.5) = 0.262.

Causes of the heterogeneity of regional flows

The cause of the regional variation of flow has not been easy to find, and we cannot claim that it has been found yet. Global phenomena paved the way for thinking about it. Starling’s Law of the heart, hardly a law in the traditional sense, summarized the observations that increased filling of the ventricular cavity and stretching myocardial fibers before a contraction resulted in increased strength of contraction and increased cardiac output. Starling showed that such stretching also increased the metabolic rate. Increased heart rate and increased work load were both associated with increased metabolism. It was also recognized that when coronary artery flow was reduced, metabolism diminished. How well do these global observations fit with local cause and effect relationships?

Energy substrate abundance

Of the major substrates, glucose, fatty acid, and oxygen, only oxygen appears to be in limited supply in normal hearts, the trans-coronary extraction being 50 to 75%. Glucose extraction is only 2% or 3% (57) and fatty acid extraction is about 30%. Franzen et al. (38) measured the regional concentrations of creatine kinase, lactate dehydrogenase, ATP, and glycogen, that is, two enzymes, one for cellular energetics, and one for glucose and lactate metabolism, and two energy sources, one being ATP, the main substrate for energy supply, and the other, glycogen, the storage vehicle for glucose. They compared regional flows measured by microsphere deposition to the local concentrations of these substances in 27 to 54 samples per heart. While they found the relative dispersions, RD (the coefficients of variation, the standard deviation divided by the mean), for each of these to be of the order of 20%, roughly the same as for flow (with the exception of ATP, whose RD equals 8%), there were only weak associations between the local concentrations and the local flows. Actually, this is what one should expect in a normal heart: normal regulatory responses are to keep each concentration at a steady level despite changes in its rate of turnover. Other measurements of substrate or enzyme concentrations have similarly failed to show significant correlation with flows.

Substrate uptake rates

After polishing the cut surfaces of quick-frozen pieces of myocardium, Weiss et al. (102) measured spectrophotometrically the hemoglobin saturation with oxygen in small arteries and veins, and demonstrated that more oxygen was used in high-flow regions than in low-flow regions. Caldwell et al. (27) observed that the local capacity for the uptake of fatty acid was proportional to the regional flows in the hearts of dogs running on the treadmill. This suggested that the transport capacity for fatty acid uptake was matched to the flow, but not necessarily matched to fatty acid metabolism since it was tracer uptake that was being measured. Sonntag et al. (87) observed increased deoxyglucose uptake in high-flow regions. Likewise, van Beek et al. (95) observed that the turnover of acetate was high in high-flow regions compared to low-flow regions; since this was the only substrate provided, they concluded that local flow must be nearly proportional to local O₂ consumption. Recently, Decking et al. (31) using ¹³C-pyruvate found a similar relationship. Li et al. (61) found linear associations between oxygen consumption and flow, measuring ¹⁵O-oxygen consumption by positron emission tomography (PET); their model accounted for the nonlinearity in oxygen binding by hemoglobin and myoglobin, extending the modeling analysis developed for rabbit hearts by Deussen and Bassingthwaighte (36). Thus, one may reasonably conclude there is growing evidence that substrate utilization and oxygen utilization are both proportional regional flows. Because there is no barrier limitation to water or oxygen exchange between blood and tissue in the heart (36), the effective capillary permeability-surface area product, PS_c, for all forms of water is close to infinite, so high values (PS_c > 100 ml g⁻¹ min⁻¹) are appropriate in the model analysis for estimating oxygen consumption from ¹⁵O-oxygen or ¹⁸O-oxygen.

Intratissue diffusional path length heterogeneity is evident for oxygen and water. Capillaries are not exactly arrayed in nice hexagonal lattices with matched entrances and exits. There is a combination of variation in intercapillary distances and variation in positions of arterial to capillary entrances and venous exits, which means that neighboring capillaries have different tracer concentrations, allowing net flux from one to another. This is a kind of mining process involving both convection and diffusion. This heterogeneity of diffusional lengths is represented in the model by using a diffusion coefficient divided by a heterogeneity in path lengths, which is in effect a spatial dispersion coefficient (19), and is in all of our models for blood-tissue exchange (e.g., (15)). Omission of this term forced Rose and Goresky (84) to use artifactually low parameter values for PS_c in order to fit their model to the data, ignoring the fact that water is flow-limited and has a PS_c too high to be measured (108).

Influences of cardiac and coronary anatomy

An increase in flow itself appears to increase oxygen utilization, the Gregg effect. Likewise, coronary flow reduction leads to a shortening of systole and a lengthening of diastole, giving a little more time for subendocardial perfusion (69). The mechanism is not known but may be as straightforward as a reduction in vascular and interstitial pressures leading to a decrease in tissue stiffness.

The influences of cardiac structure and of the distribution of coronary arteries on regional flows remain an enigma. Comparing one heart to another, there has been no consistent regional localization of low-flow or high-flow regions (13, 52, 74), though each heart is consistent to itself under varied flows in the absence of administered vasodilators. This apparently random relationship between the anatomy and the flow distributions seems odd since the arrangements of the fibers and sheets of the myocardial tissue itself (60, 65), and the branching of the coronary vascular system, are much the same from animal to animal of a given species. If there were consistent locations of relatively low or relatively high flows, one would have expected these to be revealed with the high resolution observations of King et al. (52) on baboons, of Austin et al. (5, 6) on dogs and of Bassingthwaighte et al. (13) on sheep. The flow heterogeneity in the lungs (40) and in the kidney (44) has the same basic characteristic: near-neighbor regions have similar flows.

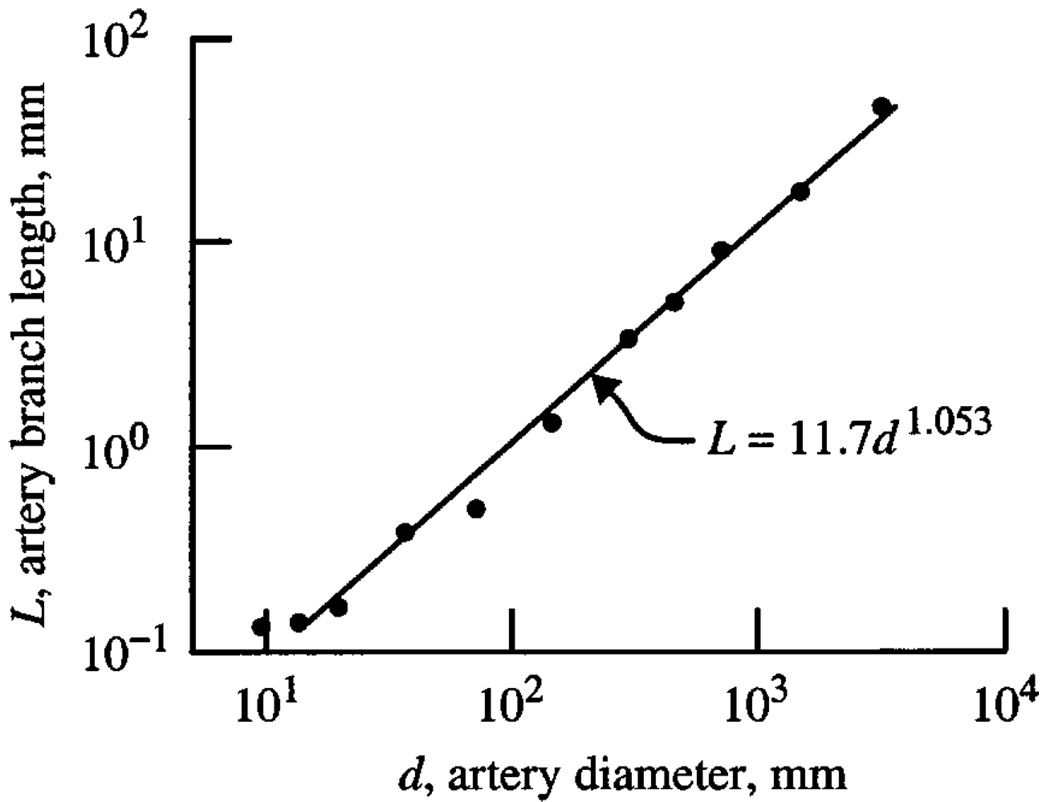
The branching arterial network is a fractal, which is to say that the ratios of diameters of daughter to parent vessels are approximately constant, independent of the diameter. The lengths of segments between branch points in daughter branches are likewise proportional to the length of the parent segment. An example is shown in Fig. 3, the data from Kassab et al. (49, 50), which shows a power law relationship between element length versus diameter, i.e., diameter is proportional to length. The data points are averages at each order, using a diameter-defined Strahler ordering scheme. Van Bavel and Spaan (93) found similar relationships using a slightly different scheme and demonstrated also the variability in the relationship.

Fig. 3.

Analysis of casts of the coronary left anterior descending arterial tree of a pig heart: length, L, of average element (i.e., segments in series) of a given generation versus the average diameter, d, of the lumen. The logarithmic slope is 1.053. (The data points are average values from (50), Table 1, left anterior descending coronary artery.)

Kassab has found, as others did previously, that the network is almost fully dichotomously branching with 1% or fewer trifurcations. This allows simplified algorithmic descriptions of the tree, such as provided by Pelosi et al. (72), Zamir and Chee (112), and Beard and Bassingthwaighte (19, 20). Van Beek et al. (94) showed that a dichotomously branched fractal system would reproduce the dispersion of regional flows observed in normal hearts.

A corollary observation is that the power-law (self-similar, fractal) relationships are seen for tracer washout from the organ. Water is flow-limited in its exchange between tissue and blood, meaning that there is neither barrier-limitation nor other diffusional limitation to the exchange. Following a bolus injection of ¹⁵O-water into the inflow, the outflow concentration diminishes as 1/t³, a power law relationship (16). This too could be explained in terms of the dichotomously branching network of vessels. More interestingly, Beard and Bassingthwaighte (20) found that an artificially constructed vascular network, built using the statistics of the connectivity matrix measured by Kassab et al. (50) in the pig heart coronary arterial system gave a remarkably complete description of the distribution of the flows in the heart by reproducing the following: 1) the degree of heterogeneity observed in normal hearts; 2) the spatial self-similarity in flows; 3) fractal spatial correlation all with the same fractal dimension found in animal studies; and 4) the washout of intravascular tracer gave slopes of t⁻³, i.e., decayed in proportion to the reciprocal of time cubed. Thus even if it is not completely clear why the system is fractal, it is clear that fractal descriptions are the appropriate statistics to use and that model systems derived from real data reproduce the results very nicely.

The comprehensive studies by Ghassan Kassab deserve special mention, for he and his colleagues have not only presented massive amounts of detailed data on the coronary circulation, but have used the data to give new levels of understanding of physiological function. The study by Zhou et al. (113) carefully extends the work of Murray (70) and demonstrates that the exponent relating parent and daughter diameters, lengths, and so on, which Murray estimated to be 3.0 for optimal energy conditions at a single bifurcation, should be in fact higher, 3.45 to 3.65 to fit the anatomic data. The analyses cover the whole coronary tree down to the terminal arterioles and thereby summarize the diameter/length data most succinctly via the power law scaling relationships. Using a normalized diameter, d_N (which is the diameter at the N^th generation divided by the diameter of the source artery) and a normalized length l_N (which is the total length of all of the arterial segments down to the N^th generation starting with the same source artery), the relationship is

$$d_{\mathrm{N}}=l_{\mathrm{N}}^{\frac{4-3\epsilon }{4(3-\epsilon )}}$$ (3)

where ε is an equivalent resistance factor for the network. When ε = 0 this reduces to Murray’s cubic relationship. For coronary trees, ε is calculated from the log-log slope of fluidic resistance divided by l_N versus V_N, the volume of all segments up to the N^th generation. The power-law relationship has a theoretical slope of ε − 2, giving values of ε from −0.65 to −0.45 and values of the exponent of L_N of 1/2.63 to 1/2.44 for the network instead of Murray’s 1/3 for a single bifurcation.

Vasomotor influences

It was originally suspected that the regional variation in flow, measured by microspheres, was due simply to the fact that there were fluctuating flows everywhere and that the microspheres caught a snapshot of an individual state. Arguing against this was the fact that most users of the microsphere technique made prolonged injections, of the order of thirty seconds to one minute, so that any “snapshot” effect would be averaged over at least the duration of the injection: this is another way of saying that any regional fluctuations in flow would have to be very slow with respect to the injection duration for vasomotion to be the explanation. However, the clinching argument was really provided by King and Bassingthwaighte (53) who showed that the same regions remained stable in their relative flows during rest and moderate exercise over periods of hours and up to one day. Deussen et al. (35) confirmed these observations and extended them by showing that adrenergic stimulation caused proportional increases in flow regionally, so that the same patterns of flow were observed in the stimulated state as in the resting state.

This stability is interesting in view of the fact that cerebral stimulation of the coronary vessels can be quite focal, and specific regions of the myocardial vasculature can be constricted by stimulation of cerebral nuclei (e.g., (73), but see (4) for comprehensive reviews). Clinically, it is recognized that on uncommon occasions there is a regional myocardial infarction apparently induced by a cerebral stroke (22, 68). Walter Randall and colleagues, in examining neural influences on myocardial function, observe that stellate ganglia stimulation could cause regional coronary vasoconstriction (81). It would certainly be reasonable to expect that regions heavily endowed with sympathetic nerve endings might be more responsive to sympathetic influences than those that are not. Likewise, if there are spatial variations in local β-adrenergic release, then one might expect the kind of positive associations that have been seen between cAMP or norepinephrine and coronary vasodilator responses (82, 103).

The distensibility of the arteries depends on the active vasomotor tone and relaxes to the passive pressure-volume relationships when there is complete vasodilation (106). Kassab and Malloi (51) show that coronary compliances are small in large coronaries and proportionately higher in smaller vessels, consistent with the data of Cornelissen et al. (28).

The question of whether or not there is capillary recruitment with vasodilation and increases of flow in the myocardial microcirculation is not firmly answered. We suspect that there is almost no recruitment. The idea that surface area increases with higher flows has been inferred from model-based estimates of capillary permeability-surface area products, PS_c, over a range of flows in both anesthetized animals and in isolated blood-perfused hearts. Most often the PS_c was estimated from the Crone-Renkin-Bohr expression, PS_c = −F log_e(1 − E), where E is fractional extraction; this formula does not account for “back-diffusion”, tracer reflux from the interstitial fluid back into the capillary, and therefore underestimates PS_c especially at low flows. Harris et al. (46) used single capillary models for the analysis of outflow dilution curves obtained at different flows on the assumption that the myocardial flows are uniform throughout the heart, and found that the estimates of PS_c increased with increasing flows (46). Guller et al. (45) made similar observations but pointed out that the effects of heterogeneity on the estimates of PS_c had not been properly ascertained. Goresky et al. (43) expressed the same concern and in 1976 Rose and Goresky (83) tried to use an assumed constant PS_c in all regions to account for the heterogeneity by using a multicapillary model. They attempted to estimate the heterogeneity itself from the extraction of sucrose during transcapillary passage. In their modeling it was assumed that PS_c was uniform throughout the heart, and that the shortest transit times represented outflow from the highest flow regions. This was a good idea. The combined use of multiple indicator dilution (MID) curves with microsphere deposition (e.g., (57)) allows modeling analysis of MID without making assumptions about the flow, and model fits to data at different flows suggest very little increase in PS_c at high flow.

Cousineau et al. (30) revisited the issues in studies on anesthetized closed-chest dogs while making changes in flow with dipyridamole, with cardiac pacing, and with carotid occlusion to increase cardiac after-load. As in the earlier studies, they showed estimates of PS_c which increased with increasing flow, and this appeared to be pretty much independent of how flow was increased, though there was a tendency for the increases with dipyridamole (an adenosine transport blocker) to plateau at lower levels of PS_c. In this study, flow was estimated from the indicator dilution curves themselves, represented by the transit-time based estimates of flow per unit interstitial space, again using sucrose as the interstitial space marker and albumin as the vascular marker. They did not use microspheres to estimate the flow, having satisfied themselves that the analytical approach gave reasonable estimates compared with the microspheres in a previous study (29). The results appear to reveal that their methodological approach is erroneous, because the estimates of capillary transit-time heterogeneity approach zero at higher flows of 0.2 to 0.25 ml s⁻¹ ml⁻¹ interstitial space. This flow is still low, only about 1.1 ml g⁻¹ min⁻¹, we calculate from their interstitial space measurement of 0.09 ml/g (29). Zero heterogeneity is impossible: no one reports uniform flows even at the highest perfusion levels.

Cousineau et al.’s estimate of interstitial space of 0.09 to 0.1 ml/g appears much too low. Gonzalez and Bassingthwaighte (42) obtained ISF volumes of 0.21 ± 0.03 ml/g (SD, N = 432) in intact rabbits by the equilibration with blood of ¹⁴C-sucrose and ⁵⁸CoEDTA, trustworthy indicators of ECF space. The estimates obtained in isolated blood-perfused dog hearts by Guller et al. (45) were closer to 0.3 ml/g for the extravascular sodium space, but this must exceed ISF space by about 0.05 ml/g because of Na entry into myocytes, given that intracellular sodium is about 10 to 12 mM and cell water space is 0.55 ml/g. The likely source of error in the interpretations of Cousineau et al. is that, to exclude recirculated indicator from their analysis, they extrapolate the downslopes of the indicator dilution curves monoexponentially (not as a power law, which we now know is a better descriptor) and therefore systematically underestimate the transit time, and therefore the interstitial volume. Because power-law tails decay slowly compared to exponentials this might give as much as a 50% error in mean transit time for sucrose, for which PS_c is low and the tail is long. The real problem in estimating the degree of recruitment with increases in flow is that in vivo measurement of indicator dilution curves is always compromised by recirculation, rendering the form of a tail obscure and its length inevitably underestimated by a single exponential. If one is to extrapolate the downslope of a curve it would be by far preferable to use the power-law relationship (which is equivalent in effect to the multiexponential form with many exponentials) and so improve estimates of transit time (16, 18, 20).

A complicating issue is that it would be rational to believe that the capillary surface area is higher in regions of high metabolism and high oxygen demand. While there are higher capillary densities in endocardium than in epicardium (63), there are no known measurements of capillary densities in high-flow versus low-flow regions. This is something that should be done and can be done technically with the combination of microspheres and Microfil (Canton Biomedical, Inc.) measurements of capillary density as used by Bassingthwaighte et al. (9). If instead of there being a uniform PS_c for sucrose throughout all regions there were higher PS_c’s (higher capillarity without a change in the permeability) in the high-flow regions compared to low-flow regions, this would very likely explain the interpretation of recruitment from increases in the apparent PS_c with increases in flow. The reason for this statement is that then when flow is low the apparent PS_c’s are underestimated greatly when using the Crone-Renkin expression, PS_c = −F log_e (1 − E).

Thus, in view of the limitations to the mathematical analysis that have implied recruitment, we do not think there is any real proof of it. One way to examine the question might be to inject an externally detectable tracer such as iodinated albumin into the inflow at a moderately high flow and then to reduce the flow before very much of the tracer has washed out of the heart, and thereby to be able to detect whether or not there is some tracer that does not wash out at all, even after a long time. If derecruitment led to trapping of tracer as derecruited vessels ceased flow while containing tracer albumin, it would not wash out. The alternative hypothesis would be that the washout is diminished in proportion to flow and that there is no de-recruitment in actuality but merely regional reductions in flow compared to the overall flow.

Mechanical factors in cardiac contraction

Mechanical factors fall into two classes: mechanical effects on coronary regional resistance, and myocardial workload, metabolic rate, and its relationship to local vasoregulatory factors. In the first category are some obvious factors, e.g., in the subendocardial region during systole the intratissue pressures rise to levels preventing coronary inflow. Subendocardial flow is mainly diastolic. Another influence is aortic perfusion pressure: the Gregg effect is the increase in cardiac force of contraction when aortic pressure is raised. This may be due in part to the lengthening of the coronary vessels (and the tissue surrounding them) when pressure is raised, a “garden hose” effect increasing the sarcomere lengths prior to excitation. Rapid pacing of the heart increases the diastolic fraction of the cardiac cycle, compromising preferentially the subendocardial flows. Likewise, Merkus et al. (69) observe that a reduction in coronary perfusion pressure beyond an obstruction effectively reduces the diastolic time fraction (and subendocardial flow), while reducing aortic pressure in the absence of coronary stenosis increases the diastolic time fraction.

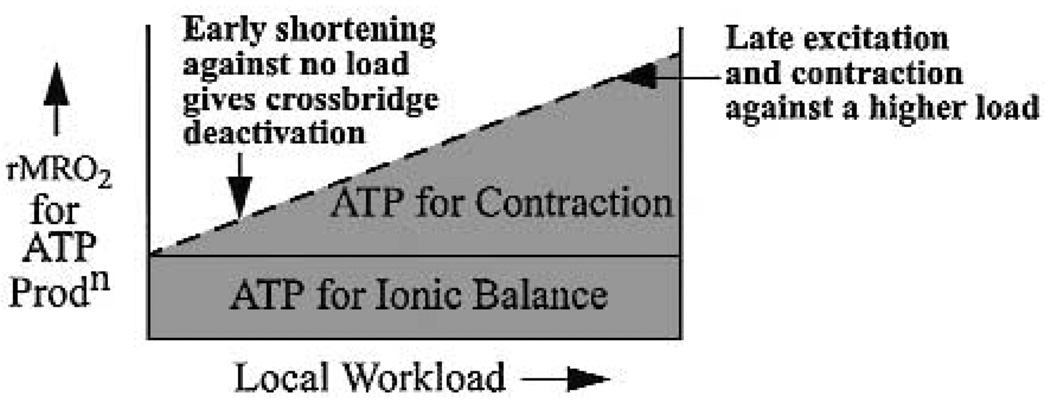
Probably the clearest cause of the local flow heterogeneity is the heterogeneity of local work and local ATP hydrolysis for contraction. This is consistent with the observations at the global level where more work requires more oxygen consumption. One reason that some regions may require less ATP than others is that they contract earlier, when the initial load is small, so they do not have to develop as much tension as later contracting fibers. The idea is shown in Fig. 4 for an abnormal situation in which electrical pacing at a ventricular site results in marked disparities of the time of activation in different regions.

Fig. 4.

Diagram of oxygen consumption with respect to local needs for ATP. ATP required for ionic balance is probably almost independent of work load, except perhaps for Ca⁺⁺ cycling, and myosin ATPase flux is related to local work.

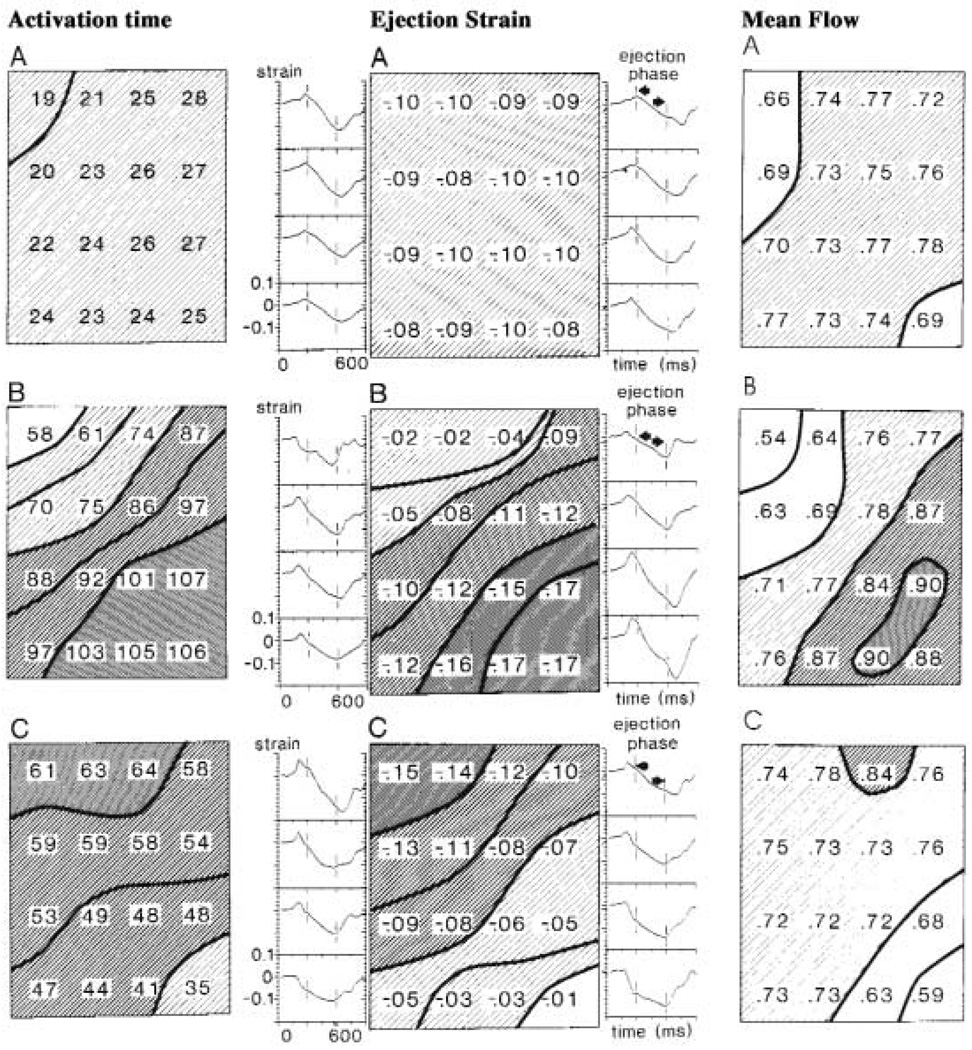
Shown in Fig. 5, a composite figure made from the publications of the Maastricht group of Reneman, Arts, Alessie, van der Vusse and Prinzen (75), are data on hearts paced from three different sites. On changing the site of activation from normal sinus rhythm (upper panels, A) to either right ventricular outflow tract (RVOT; middle panels, B), or LV apex (LVA; lower panels, C), the regional myocardial blood flow (rMBF) diminished at sites that were activated early after the pulse, compared to when normal sinus stimulation was used. Contrarily, flows became higher at sites activated later by the spreading excitation. Note that the earliest activated sites (indicated by the activation times in the left panels) tend to shorten quickly during the isovolumetric phase of systole before ejection begins. A clear example of this is the strain pattern with LV apical stimulation shown in the right lower corner of the lowest center panel: fractional shortening was great, almost 10%, before ejection began and rMBF was reduced to 0.59 ml g⁻¹ min⁻¹ (indicated by the value in the right lower corner of the right lower panel). This region had less ejection-phase strain (the value −0.01 mapped numerically in the right lower corner of the bottom panel of the middle column of panels) and had less blood flow (right panels). Late activated sites often exhibit stretching in the pre-ejection phase (lengthening their sarcomeres and putting them at a different initial position on the Starling curve) and show greater shortening during the ejection phase; their flows increase compared with the control state.

Fig. 5.

Electrical activation, regional shortening patterns and blood flows in a 5 by 4 cm patch of dog LV free wall divided into 16 regions. Upper panels (A): Normal sinus activation. Middle panels (B): RV outflow tract stimulation. Lower panels (C): LV apical stimulation. Left column of panels: Electrical activation times, ms. Middle column: Strains (fractional length changes) during systolic ejection phase are shown numerically, negative sign indicating shortening; to the sides are continuous recordings of the regional segment lengths between epicardial markers. Pre-ejection negative strain → shortening deactivation. Right column: rMBF values in underlying myocardium by the microsphere technique. (Composite figure made from various figures of (75), with permission.)

These results have been confirmed in later studies by the Maastricht group (32, 33, 76). They found the relationship between activation time and ejection phase strain is consistent and independent of the site of activation: early activation leads to only small shortening strain during ejection, and late activation leads to large ejection phase shortening. They also showed that there was a striking inverse relationship between isovolumetric phase strain and ejection phase strain: those regions shortening early against a relaxed ventricle contributed less to the external work of the heart. Late-activated regions hypertrophy with chronic pacing and early-activated region atrophy (77, 98).

These data appear to explain the observations by McGowan et al. (66) that scintiscans of patients with left bundle branch block (LBBB) showed septal perfusion deficiency despite having normally patent coronary arteries. Early-activated regions (the septum in LBBB) require less blood flow. More recent studies summarized in an editorial by Altehoefer (3) have made the observation that F-deoxyglucose uptake in the septum is reduced out of proportion to flow in LBBB, leading to a summary description as “reversed mismatch” in FDG uptake and flow. We surmise that this phenomenon is due primarily to early septal contraction against no load. The resultant “shortening deactivation” reduces ATP requirements in the septum (58) relative to those in the free wall of the LV which contracts later and against more load. But there is still the question of why FDG uptake might be reduced even more than flow. As Altehoefer states “further studies should aim to investigate larger patient populations”.

The data make sense in terms of theories of cardiac muscle contraction. The early-activated site, compared to late-activated sites, has fast and almost isotonic initial shortening during the isovolumetric phase of systole because it contracts against relaxed myocardium, but during the ejection phase has smaller and more nearly isometric strain. The early isotonic shortening induces “shortening deactivation”, or what Brutsaert and colleagues (23–25) thought of as “load-dependent relaxation”. This has been explored by David Allen (1, 2) and pulled together in a quantitative comprehensive theoretical study by Landesberg and Sideman (58, 59). Rapid shortening against low resistance causes reduction in the amount of calcium bound to myosin ATPase in the “strong” form, and reduces ATP hydrolysis. This is termed “shortening deactivation”. The small ejection phase strains in these same regions would give a second reason for reduced ATP usage. This is likely to be the underlying metabolic mechanism for the redistribution of the local flows. These phenomena are relevant to the mechanisms underlying the observations of “mismatches” of flow and metabolism.

We do not yet know whether or not there are shifts away from glycolysis and TCA cycle utilization of glucose when muscle work is reduced, but this does occur with total cardiac unloading of hearts transplanted into the abdomen of a cloned rat (34). ¹¹C-acetate could be used as a metabolic control, since its entry into the TCA cycle is unimpeded by preliminary reactions such as glycolysis for glucose or acyl-CoA formation and transport across the mitochondrial membrane for fatty acid as summarized in the review by van der Vusse et al. (97).

The mechanism for a reduction in glycolysis with reduced load is not known. Regulation of fatty acid utilization at malonyl CoA can play a role, i.e., if lowering ATP utilization were reflected in a diminished inhibition of fatty acid utilization (39). Local unloading leads to fetal gene expression (TGFβ and cfos), as observed by Taegtmeyer’s group (34). This could be causally related to the inhibition of glycolysis. Either mechanism can explain the low glucose uptake that has been so provocative and confusing and led to Altehoefer’s commentary (3). A third possibility is that NO is playing a regulatory role. Certainly a reduction in local endothelial shear stress secondary to a reduction of flow leads to a reduction in NO release by endothelial cells. Since decreased NO release shifts metabolism away from glucose and toward fatty acid metabolism, as shown by Hintze’s group (21), this would fit the observations in LBBB.

Direct proof that rapid shortening with deactivation of the crossbridges reduces the ATP usage locally in comparison with late-activated, more highly stressed regions can at this point only be inferred from the data. No experiments have been done in which local oxygen utilization has been measured while changing from normal activation to an abnormal pacing site. Presumably this must be done in acute experiments, or at least within a few days, for van Oosterhout et al. (100) have shown that cardiac remodeling occurs and that the flow per unit mass of tissue returns toward normal levels of flow per gram of tissue after six months of pacing. The cardiac remodeling is characterized by atrophy of the region at the pacing site and hypertrophy in the late-activated parts of the LV wall. In the hypertrophying regions, which are at first performing more work per gram and have increased flows, the flow per gram diminishes as myofilament mass is added.

Discussion and conclusions

That the heterogeneity of flow gives a relative dispersion of 20 to 30% is amply documented. That the distribution of flows is stable is also now well documented. That there is an association between local flows and local substrate utilization, but not local enzyme concentrations or low concentrations of energy stores, also appears to be clear. That the responses to increases in cardiac demand are met by proportional increases in flow in all regions, without any significant changes in relative dispersion, is also borne out by repeated experimental results. What is still unproven, but nevertheless compelling, is that local flows and oxygen consumption are driven by local needs for ATP. The likeliest basis for this need is to supply ATP for hydrolysis at the crossbridge, via myosin ATPase, and the theories of crossbridge energetics provide a sensible basis for this explanation.