Abstract
The competing reaction pathways and the corresponding free energy barriers for cocaine hydrolysis catalyzed by an anti-cocaine catalytic antibody, mAb 15A10, were studied by using a novel computational strategy based on the binding free energy calculations on the antibody binding with cocaine and transition states. The calculated binding free energies were used to evaluate the free energy barrier shift from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis for each reaction pathway. The free energy barriers for the antibody-catalyzed cocaine hydrolysis were predicted to be the corresponding free energy barriers for the cocaine hydrolysis in water plus the calculated free energy barrier shifts. The calculated free energy barrier shift of −6.33 kcal/mol from the dominant reaction pathway of the cocaine benzoyl ester hydrolysis in water to the dominant reaction pathway of the antibody-catalyzed cocaine hydrolysis is in good agreement with the experimentally-derived free energy barrier shift of −5.93 kcal/mol. The calculated mutation-caused shifts of the free energy barrier are also reasonably close to the available experimental activity data. The good agreement suggests that the protocol for calculating the free energy barrier shift from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis may be used in future rational design of possible high-activity mutants of the antibody as anti-cocaine therapeutics. The general strategy of the free energy barrier shift calculation may also be valuable in studying a variety of chemical reactions catalyzed by other antibodies or proteins through non-covalent bonding interactions with the substrates.
Introduction
As is well known, cocaine abuse and addiction are a major medical and public health problem in our society. The disastrous medical consequences of reinforcing and toxic effects of cocaine have made the development of an anti-cocaine medication a high priority. It is commonly believed that dopamine transporter (DAT), a protein that brings synaptic dopamine back to presynaptic neuron (dopamine reuptake), is responsible for the rewarding effects of cocaine. Cocaine mediates its reinforcing and toxic effects by blocking the reuptake of neurotransmitter dopamine. By binding to DAT, cocaine increases concentration of synaptic dopamine and produces such feelings as reward and pleasure.1–4 Based on the pharmacology, pharmacodynamic approach was used to design small molecules such as DAT inhibitors and dopamine receptor antagonists to decrease cocaine toxicity.1,2,4 However, the classical pharmacodynamic approach has failed to yield a clinically useful small-molecule inhibitor/antagonist due to the difficulties inherent in blocking a blocker.1,4 An alternative to the pharmacodynamic approach is the pharmacokinetic approach, which means to find an enzyme or antibody to prevent cocaine from crossing the brain-blood barrier. The pharmacokinetic approach is recognized as the most promising strategy for the development of anti-cocaine medication and, therefore, has received more and more attention.1,2,4,5 One way of this approach is to design a catalytic antibody that catalyzes cocaine metabolism through hydrolysis. The catalytic antibodies are considered as a class of artificial enzymes.
Various anti-cocaine catalytic antibodies have been developed.6–8 Of all anti-cocaine catalytic antibodies reported in literature so far, monoclonal antibody (mAb) 15A106 has the highest catalytic activity with KM = 220 µM and kcat = 2.3 min−1. This catalytic antibody was elicited from a stable structural analog of the transition state for cocaine hydrolysis in aqueous solution at physiologic pH (7.4), i.e. the hydroxide ion-catalyzed hydrolysis of cocaine. Antibody 15A10 catalyzes the hydrolysis of cocaine benzoyl ester to produce two biologically inactive metabolites, i.e. ecgonine methylester and benzoyl acid, and gives a rate acceleration of kcat/k0 = 23,000 (kcat is the catalytic rate constant for the antibody-catalyzed hydrolysis of cocaine at the benzoyl ester; k0 is the first-order rate constant for the spontaneous hydrolysis of the cocaine benzoyl ester, i.e. the hydrolysis of cocaine benzoyl ester in water). Previous studies showed that mAb 15A10 blocked the reinforcing effect of cocaine self-administration in rat models9,10 and reduced cocaine-induced seizures and deaths in a dose-dependent manner.9 However, the catalytic efficiency of mAb 15A10 is still so low that an extremely high dose of the antibody (15–50 mg/kg) would be needed to produce the desirable protective effects.11 It is highly desirable to design a high-activity mutant of the catalytic antibody with a significantly improved catalytic efficiency (kcat/KM) or catalytic rate constant (kcat). As demonstrated in other protein engineering efforts,12–18 an appropriate computational enzyme mutant design, followed by site-directed mutagenesis and catalytic activity tests, could eventually lead to discovery of an enzyme mutant with a sufficiently higher catalytic efficiency against cocaine.
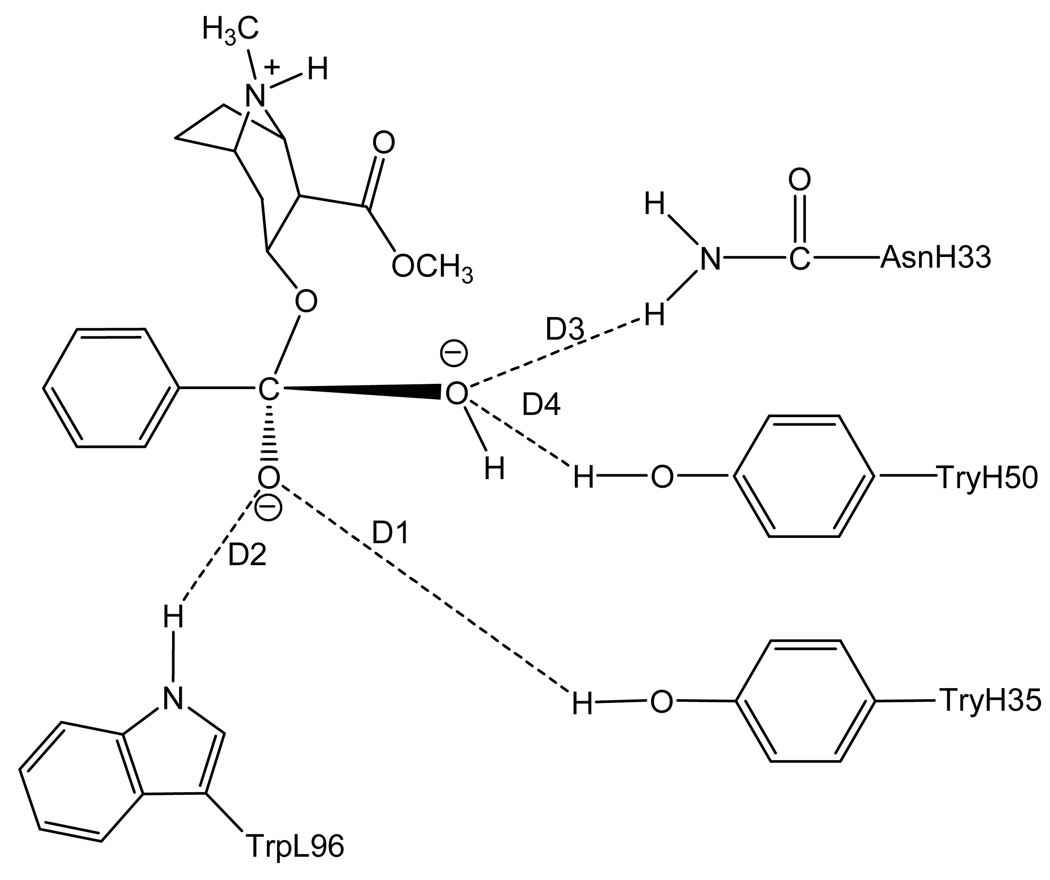
To rationally design a high-activity mutant of the catalytic antibody, one first needs to understand the detailed mechanism concerning how the antibody catalyzes hydrolysis of cocaine and develop a reliable computational strategy and protocol to evaluate the free energy barrier for the antibody-catalyzed hydrolysis of cocaine. Concerning the catalytic mechanism of the antibody-catalyzed hydrolysis of cocaine, the reported X-ray crystal structure of mAb 15A106 did not show a nucleophile which attacks the carbonyl carbon of cocaine to initialize the cocaine hydrolysis, although the X-ray crystal structure did suggest that three amino acid residues, i.e. TrpL96, AsnH33, and TyrH35, likely form an oxyanion hole in a shallow binding pocket. Based on the X-ray crystal structure, the mechanism for the antibody-catalyzed hydrolysis of cocaine should be completely different from those known for the ester hydrolysis catalyzed by an esterase. The catalytic antibody only can bind with cocaine during the cocaine hydrolysis process, without changing the fundamental reaction pathways for the cocaine hydrolysis in aqueous solution. As the dominant reaction pathway for cocaine hydrolysis in aqueous solution is associated with the hydroxide ion-catalyzed cocaine hydrolysis, the most likely mechanism of the antibody-catalyzed cocaine hydrolysis is that the catalytic antibody helps to stabilize the transition state for the rate-determining step of the hydroxide ion-catalyzed cocaine hydrolysis. See Figures 1 to 4 for the schematic representations of cocaine and the transition state structures binding with mAb 15A10.
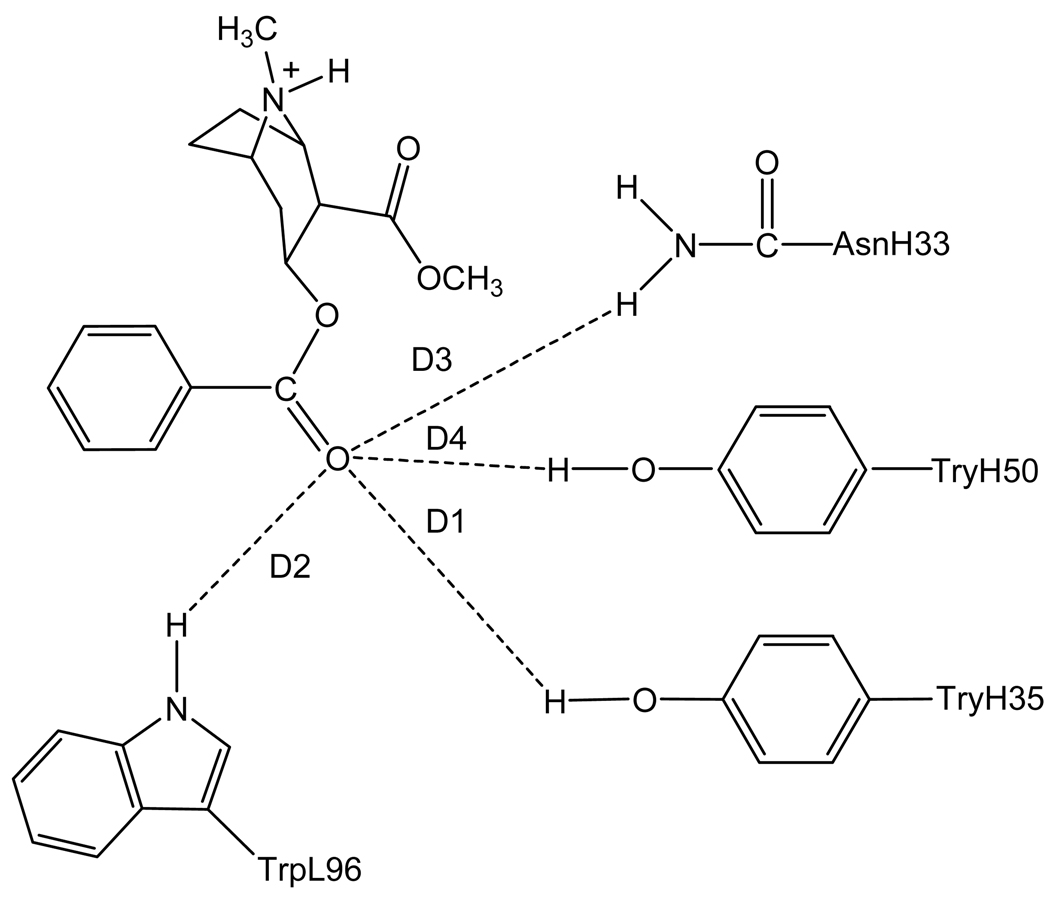
Figure 1.
Schematic representation of cocaine binding with the antibody. The dashed lines refer to the key distances between cocaine and the antibody.
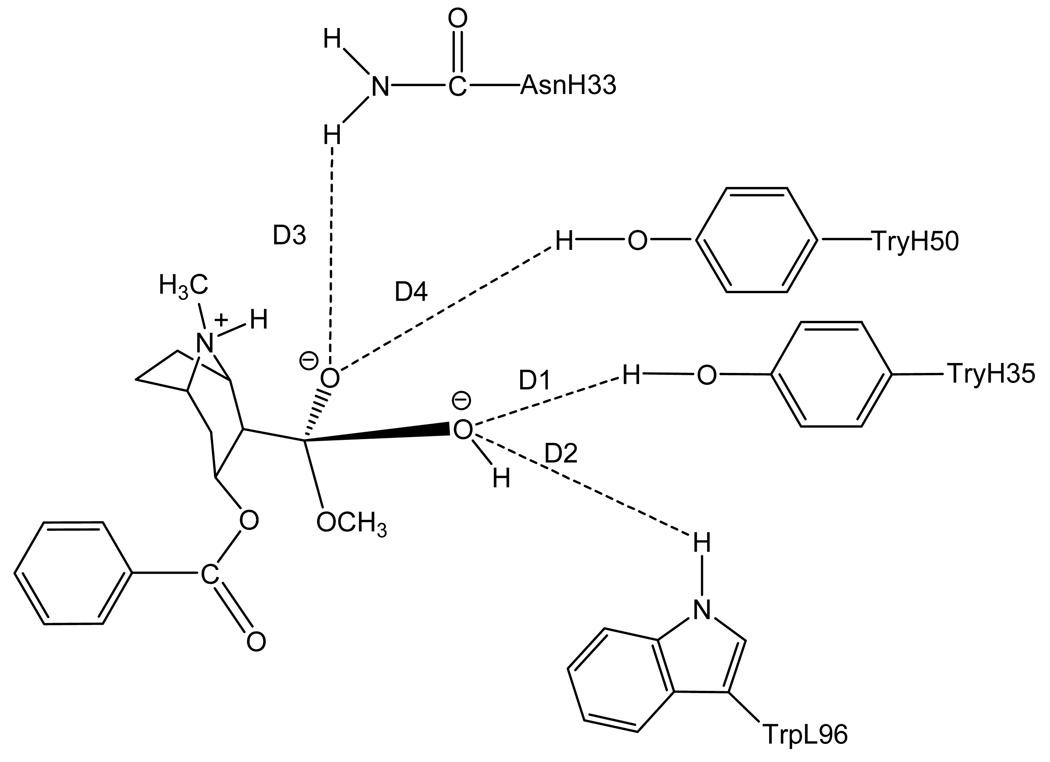
Figure 4.
Schematic representation of TS1met binding with the antibody. The dashed lines refer to the key distances between TS1met and the antibody.
Further, our recently reported first-principles reaction coordinate calculations19,20 on the cocaine hydrolysis demonstrated three competing reaction pathways for the hydroxide ion-catalyzed cocaine hydrolysis in water: two pathways correspond to the hydrolysis of cocaine at the benzoyl ester, whereas the other pathway corresponds to the hydrolysis of cocaine at the methyl ester. The pathway corresponding to the cocaine methyl ester hydrolysis has the lowest free energy barrier in water, which is consistent with the experimental kinetics.21 Obviously, mAb 15A10 should not be expected to equally stabilize the transition states for all of the competing reaction pathways. It is likely that this catalytic antibody more favorably stabilize the transition state for one of the competing reaction pathways associated with the hydrolysis of cocaine at the benzoyl ester.
In order to identify the most favorable reaction pathway for the antibody-catalyzed cocaine hydrolysis and to better understand the catalysis of the catalytic antibody, in the present study, we have developed a novel computational strategy to calculate the free energy barriers for the competing reaction pathways of the antibody-catalyzed cocaine hydrolysis. According to the computational strategy, we first carried out molecular docking, molecular dynamics (MD) simulations, and binding free energy calculations to study how the antibody binds with cocaine and the transition-state structures determined by the first-principles reaction coordinate calculations on the competing reaction pathways. The calculated binding free energies, along with the free energy barriers determined by the first-principles reaction coordinate calculations on the hydroxide ion-catalyzed cocaine hydrolysis in water, lead to the computational predictions of the free energy barriers of the antibody-catalyzed cocaine hydrolysis for all of three competing reaction pathways, thus enabling us to determine the dominant reaction pathway for the antibody-catalyzed cocaine hydrolysis. The calculated energetic results are in good agreement with available experimental kinetic data, suggesting that the computational strategy and protocol are reliable for studying the reaction pathways and free energy barriers for the antibody-catalyzed cocaine hydrolysis and other antibody-catalyzed reactions.
Computational Methods
General computational strategy
As well known, direct reaction coordinate calculations on a reaction system involving a protein or antibody (which is considered to be an artificial protein) and the predictions of the corresponding free energy barriers would be very time-consuming. To simplify the calculations of the free energy barriers for the antibody-catalyzed hydrolysis of cocaine, we consider the following reaction systems:
| (1) |
| (2) |
| (3) |
Reaction (1) is the hydroxide ion-catalyzed hydrolysis of cocaine in aqueous solution without the antibody. In reaction (1), cocaine(aq) and HO−(aq) represent the solvated cocaine molecule and solvated hydroxide ion, respectively. TS1(aq) refers to the transition state for the first step, which is the rate-determining step, of the hydroxide ion-catalyzed cocaine hydrolysis in aqueous solution without the antibody. The free energy barrier (or the activation free energy), ΔGav(aq), for reaction (1) is calculated as the Gibbs free energy change from cocaine(aq) + HO−(aq) to TS1(aq):
| (4) |
Three competing reaction pathways were uncovered in our recently reported first-principles reaction coordinate calculations19,20 on the hydroxide ion-catalyzed hydrolysis of cocaine in water. The rate-determining transition states for these three competing reaction pathways are denoted by TS1ben-Re, TS1ben-Si, and TS1met (see Figures 1 to 4). TS1met is the transition state for the hydroxide ion-catalyzed hydrolysis of cocaine at the methyl ester. For the hydroxide ion-catalyzed hydrolysis of cocaine at the benzoyl ester, the nucleophilic hydroxide ion can approach from two faces, denoted by Si and Re, of the carbonyl to form two stereoisomer tetrahedral intermediates (R and S) through two different transition-state structures, denoted by TS1ben-Re and TS1ben-Si, respectively. The free energy barrier was calculated for each reaction pathway at the high level of first-principles electronic structure calculations that accurately account for the solvation effects by using our recently developed fully polarizable continuum model (FPCM).22–26
Reactions (2) and (3) represent the antibody-catalyzed hydrolysis of cocaine. In reactions (2) and (3) taking place in aqueous solution, cocaine-antibody (aq) represents the complex between the antibody and the cocaine molecule, whereas TS1-antibody(aq) refers to the complex between the antibody and the rate-determining transition state of cocaine hydrolysis. Hence, reaction (2) refers to the binding of cocaine to the antibody, whereas reaction (3) represents the chemical reaction process starting from the cocaine-antibody binding complex, i.e. cocaine-antibody(aq). The free energy barrier for the antibody-catalyzed hydrolysis of cocaine can be evaluated as the Gibbs free energy change from the cocaine-antibody(aq) + HO−(aq) to TS1-antibody(aq):
| (5) |
Further, let us consider the binding between the antibody and the rate-determining transition state TS1, i.e.
| (6) |
The Gibbs free energy changes of reactions (2) and (6) give
| (7) |
| (8) |
where ΔGbind(cocaine,aq) is the binding free energy for cocaine binding with the antibody and ΔGbind(TS1,aq) is the binding free energy for the rate-determining transition state (TS1) binding with the antibody.
An appropriate use of Eqs.(4), (5), (7), and (8) gives
| (9) |
| (10) |
Reactions (9) and (10) indicate that the free energy barrier shift, ΔΔGav, from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis is equal to the binding free energy change from the cocaine-antibody binding to the TS1-antibody binding. Because we have already known the free energy barriers, i.e. the ΔGav(aq) values, for the cocaine hydrolysis in water based on our previous first-principles reaction coordinate calculations, the task of the free energy barrier calculations on the antibody-catalyzed hydrolysis processes can be simplified as the calculations of the binding free energies, i.e. ΔGbind(cocaine,aq) and ΔGbind(TS1,aq), for the antibody binding with cocaine and the transition states.
Further, even without knowing ΔGav(aq), the calculated ΔΔGav value can be used to estimate the ratio (kcat/k0) of the catalytic rate constant kcat for the antibody-catalyzed cocaine hydrolysis to the rate constant k0 of the corresponding cocaine hydrolysis in water by using the conventional transition state theory (CTST):27
| (11) |
where kB is the Boltzmann constant, T is the absolute temperature, and h is Planck’s constant. In addition, the calculated ΔGbind(cocaine,aq) value can be used to evaluate the dissociation constant (Kd) for the cocaine-antibody binding:
| (12) |
The calculated Kd can be compared to the reported Michaelis-Menten constant (KM), as KM ≈ Kd under the rapid-equilibrium assumption.28,29
For each reaction pathway, the binding free energies ΔGbind(cocaine,aq) and ΔGbind(TS1,aq) were calculated by performing molecular docking of our previously optimized structures of cocaine and TS1 to mAb 15A10, followed by molecular dynamics (MD) simulations and binding free energy calculations on the docked cocaine-antibody and TS1-antibody complexes in a water bath. Below, we describe the computational details.
Molecular docking and molecular dynamics simulation
Molecular docking and molecular dynamics (MD) simulation were carried out to determine the best possible binding mode for mAb 15A10 binding with each “ligand”, i.e. cocaine, TS1ben-Re, TS1ben-Si, or TS1met. The initial structure of mAb 15A10 used in our molecular docking and MD simulations came from the X-ray crystal structure (1NJ9) deposited in the Protein Data Bank.30 Since the crystal structure is a dimer, two of the four chains, i.e. the high (H) and low (L) chains, were used to build the antibody structure (monomer). The initial structures of cocaine and the transition states (i.e. TS1ben-Re, TS1ben-Si, and TS1met) used were the geometries optimized at the B3LYP/6-31+G* level as reported in our previous first-principles reaction coordinate calculations.19 The optimized geometry of cocaine is associated with a local minimum on the potential energy surface, whereas the optimized geometries of the transition states are associated with first-order saddle points on the potential energy surface. The geometries optimized at the B3LYP/6-31+G* level were used, in the present study, to perform ab initio electronic structure calculations at the HF/6-31G* level using Gaussian03 program31 and to determine the electrostatic potentials at points selected according to the Merz-Singh-Kollman scheme.32,33 Based on the calculated electrostatic potential, the restrained electrostatic potential (RESP) protocol34,35 implemented in the Antechamber module of the Amber8 program was used to calculate the RESP charges used in the molecular docking and MD simulations with cocaine, TS1ben-Re, TS1ben-Si, and TS1met.
Molecular docking with each “ligand”, i.e. cocaine, TS1ben-Re, TS1ben-Si, or TS1met, was performed by using AutoDock program version 3.0.37 For the ligands, all flexible torsion angles were allowed to rotate during the docking, while all of the bond lengths and angles were fixed. During the docking process, the Lamarkian genetic algorithm (LGA)37 was applied to the conformational search for the antibody-ligand binding structure. Among a series of docking parameters, the grid size used in the docking was 60 × 60 × 60 and the used grid space was the default value of 0.375 Ǻ.38 For molecular docking with each ligand, the best binding structure with the most intermolecular hydrogen bonds (see Figures 1 to 4) was selected as the initial structure of the antibody-ligand complex for MD simulation.
A critical issue15–18,39 should be addressed before describing how we performed any MD simulation on a transition state structure. In principle, MD simulation using a classical force field (molecular mechanics) can only simulate a stable structure corresponding to a local minimum on the potential energy surface, whereas a transition state during a reaction process is always associated with a first-order saddle point on the potential energy surface. Hence, MD simulation using a classical force field cannot directly simulate a transition state without any restraint on the geometry of the transition state. Nevertheless, in theory, if we can technically remove the freedom of imaginary vibration in the transition state structure, then the number of vibrational freedoms (normal vibration modes) for a nonlinear molecule will decrease from 3N – 6 to 3N – 5. The transition state structure is associated with a local minimum on the potential energy surface within a subspace of the reduced vibrational freedoms (i.e. subspace of the 3N – 5 freedoms), although it is associated with a first-order saddle point on the potential energy surface with all of the 3N – 6 vibrational freedoms. Theoretically, the vibrational freedom associated with the imaginary vibrational frequency in the transition state structure can be removed by appropriately freezing the reaction coordinate. The reaction coordinate corresponding to the imaginary vibration of the transition state is generally characterized by a combination of some key geometric parameters. Thus, we just need to maintain the bond lengths of the forming and breaking covalent bonds during the MD simulation on a transition state.15 The forming and breaking covalent bonds in the transition state will be called “transition” bonds below, for convenience. Specifically for transition state structures TS1ben-Re, TS1ben-Si, and TS1met depicted in Figures 1 to 4, the reaction coordinate is mainly related to the partial covalent bond (C–O) between the hydroxide oxygen and a carbonyl carbon of the cocaine. This C–O bond is considered to be a transition bond in this study. During the MD simulations on the systems involving TS1ben-Re, TS1ben-Si, or TS1met, we just needed to fix the length of this transition bond along with other bond lengths involving the carbonyl carbon of the cocaine and bond angles centered on the carbonyl carbon of the cocaine, starting from the fully optimized transition state geometries at the B3LYP/6-31+G* level without antibody. All of the other geometric parameters were allowed to move during the MD simulations.
It should be pointed out that the only purpose of performing the above-mentioned MD simulation on a transition state is to estimate the interaction energy between the reaction center and the protein environment in the transition state. An implied approximation used in the MD simulations on a transition state is that the length of the transition bond and the related geometric parameters in the transition state do not significantly/dramatically change from the cocaine hydrolysis without antibody to the cocaine hydrolysis with the antibody. This approximation should be reasonable because there is no covalent bonding between the antibody and the transition state structure of cocaine hydrolysis. Even if the length of the transition bond and the related geometric parameters within the reaction center do change significantly, the interaction energy between the reaction center and the protein environment is not expected to change significantly, in light of our previous QM, MD, and QM/MM calculations/simulations on butyrylcholinesterase-catalyzed hydrolysis of cocaine.12,16,18
To carry out the MD simulations, the topologic and coordinate files of the antibody-ligand complexes were built with LEap module of the Amber8 package. The cocaine-antibody complex has a net charge of −3, whereas each TS1-antibody complex has a net charge of −4. Each complex was neutralized by adding three or four sodium counterions and was solvated in a rectangular box of TIP3P water molecules40 with a solute-wall distance of 10 Å. The energy minimization and MD simulation were performed by using the Sander module of the Amber8 package in the way similar to what we did for other protein-ligand systems.12–15,17,18,41–45 First, the solvent molecules were minimized for 5000 cycles and equilibrated for 10 ps to make sure that they were in an equilibrated condition. Second, the solvent, ligand, and side chains of the antibody were allowed to move during a 1000-cycle energy minimization to adjust the positions of the ligand atoms in the binding pocket. Then the whole system was energy-minimized for 1000 cycles. This system was gradually heated from T = 10 K to T = 100 K for 20 ps before the MD simulation at 100 K for 1.2 ns in order to further relax the antibody-ligand binding and obtain the best possible binding structure. To obtain the best possible binding mode, the available intermolecular hydrogen bonds formed after the energy minimization were restrained during the heating and the first 200 ps of the MD simulation at 100 K, and then the whole complex was relaxed for 1 ns to obtain a stable MD trajectory. The time step used in the MD simulation was 2 fs. Periodic boundary condition was used in the NPT ensemble with Berendsen temperature coupling and P = 1 atm with isotropic molecular-based scaling. The SHAKE algorithm46,47 was used to fix all covalent bonds containing hydrogen atoms. The non-bonded pair list was updated every 25 steps. The particle mesh Ewald (PME) method was used to treat long-range electrostatic interactions.48 10 Å was used as the none-bonded cutoff. During the MD simulation, the coordinates of the simulated complex were saved every 1 ps.
Binding free energy calculation
The binding free energies between mAb 15A10 and the ligands were calculated with a molecular mechanics-Poisson-Boltzmann surface area (MM-PBSA) method.49 In the MM-PBSA method, the free energy of the ligand binding with the antibody, ΔGbind, is calculated from the difference between the free energy of the receptor-ligand complex (Gcpx) and the sum of the free energies of the unbound receptor (Grec) and ligand (Glig) as following
| (13) |
The binding free energy ΔGbind includes three items: MM gas-phase binding energy (ΔEMM), solvation free energy (ΔGsolv), and entropy contribution (−TΔS). The sum of ΔEMM and ΔGsolv is denoted by ΔEbind. The MM gas-phase binding energy ΔEMM was calculated with the Sander modules of Amber8 program. The solvation free energy is the sum of the electrostatic solvation free energy (ΔGPB) and the nonpolar solvation energy (ΔGnp). In detail, ΔGPB was calculated with the finite-difference solution to the Poisson–Boltzmann (PB) equation implemented in the Delphi program50,51 by using the same RESP charges as used in the aforementioned molecular docking and MD simulations. The dielectric constants used for the solute and the solvent water were 1 and 80, respectively. The MSMS program52 was used to calculate solvent accessible surface area (SASA) in Eq. (18) to obtain the nonpolar solvation energy, with parameters γ = 0.00542 kcal/Ǻ2 and β = 0.92 kcal/mol.
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
The entropy contribution to the binding free energy (−TΔS) was obtained by using a local program developed in our own lab. In this method, the entropy contribution is attributed to two contributions: solvation free entropy (ΔSsolv) and conformational free entropy (ΔSconf),
| (19) |
The solvation entropy is gained by the tendency of water molecules to minimize their contacts with hydrophobic groups in protein.53 It has been demonstrated that the solvation entropy is temperature-dependent, and can be calculated with heat capacity.54,55
| (20) |
where ΔCp,ap and ΔCp,pol are the apolar and polar heat capacity. are the temperatures in which the apolar and polar hydration entropy are zero, and their values reported in literature are 385.15 K56 and 335.15 K57, respectively. The value of temperature T used in Eq. (20) was 298.15 K. For the calculation of apolar and polar heat capacities, the apolar and polar heat capacity changes for the protein-ligand binding can be expressed as a linear combination of apolar and polar solvent-accessible surface area differences ΔSASAap and ΔSASApol.
| (21) |
| (22) |
where ac(T) and bc(T) are temperature-dependent coefficients. In low temperature (T < 353 K) situation, the heat capacities can be seen as temperature-independent, and the values of ac(T) and bc(T) reported in literature are 0.45 and −0.26, respectively.55
The conformational entropy (ΔSconf) is related to the change of the number of rotatable bonds during the binding process. For a four-atom unit X-A-B-Y, if the middle bond A-B is a non-backbone single bond with at least one carbon atom among A and B and none of atoms X and Y is hydrogen, it is regarded as a rotatable bond. In the binding site of the protein in the protein-ligand complex, if any one of the four atoms involved in a rotatable bond in the protein/ligand is within a distance of 5 Ǻ from any of the ligand/protein atoms, this bond will be regarded as non-rotatable. The contribution to the binding free energy from the conformational entropy change is proportional to the number (ΔNrot) of the lost rotatable bonds during the binding:53
| (23) |
in which w is the scaling factor to be calibrated. Hence, our MM-PBSA calculations include an adjustable parameter, i.e. w, in the calculation of the free energy contribution from the conformational entropy,
| (24) |
although all of the other parameters used in our MM-PBSA calculations are the standard parameters reported in literature or the default parameters of the Amber8 program. This adjustable parameter, w, was calibrated to be 0.6871 kcal/mol (when four effective digits were kept) by fitting the calculated ΔGbind value for the cocaine-antibody binding to the corresponding experimental ΔGbind value of −4.97 kcal/mol determined by the KM value of 220 µM. Thus, w = 0.6871 kcal/mol was used for our MM-PBSA calculations on all of the complexes in this study.
The final binding free energy ΔGbind for each antibody-ligand binding complex was taken as the average of the ΔGbind values calculated for 100 snapshots of the MD-simulated complex. The 100 snapshots were taken from the last 500 ps of the MD trajectory, with one snapshot for every 5 ps.
The MD simulations were performed on an HP supercomputer (Superdome with 256 shared-memory processors) or on an HP XC Linux cluster at the Center for Computational Sciences, University of Kentucky. The other computations were carried out on SGI Fuel workstations in our own laboratory.
Results and Discussion
Binding structures
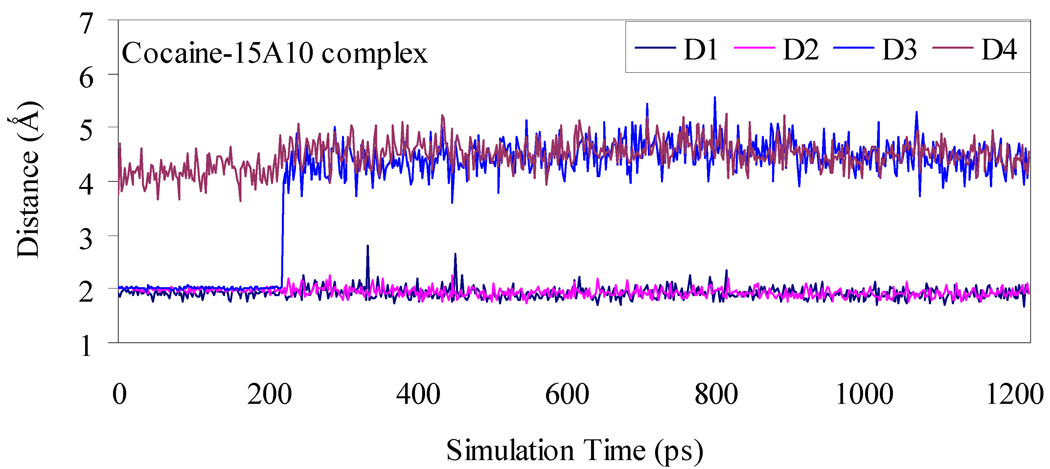
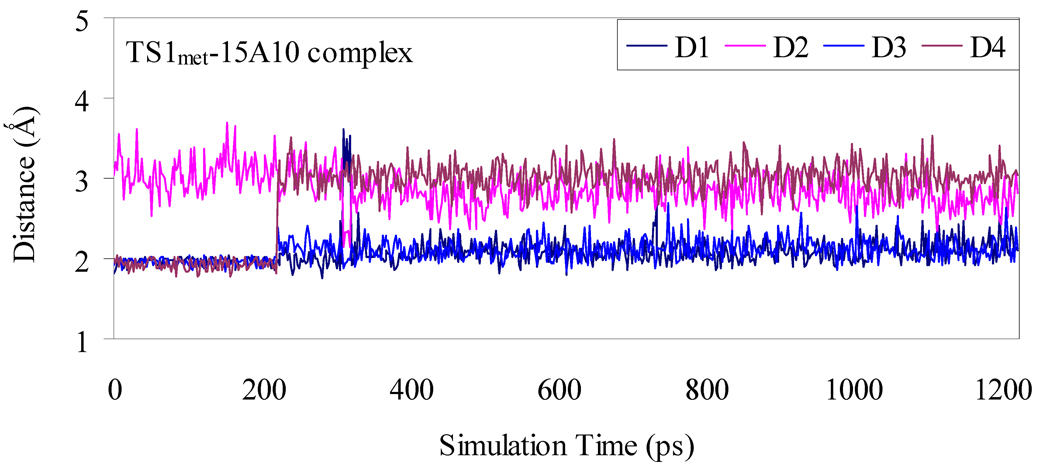
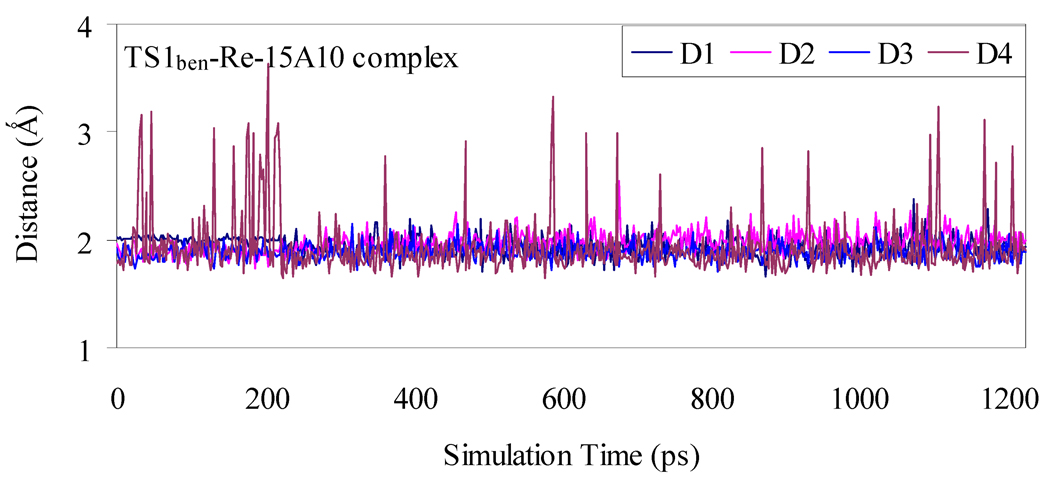
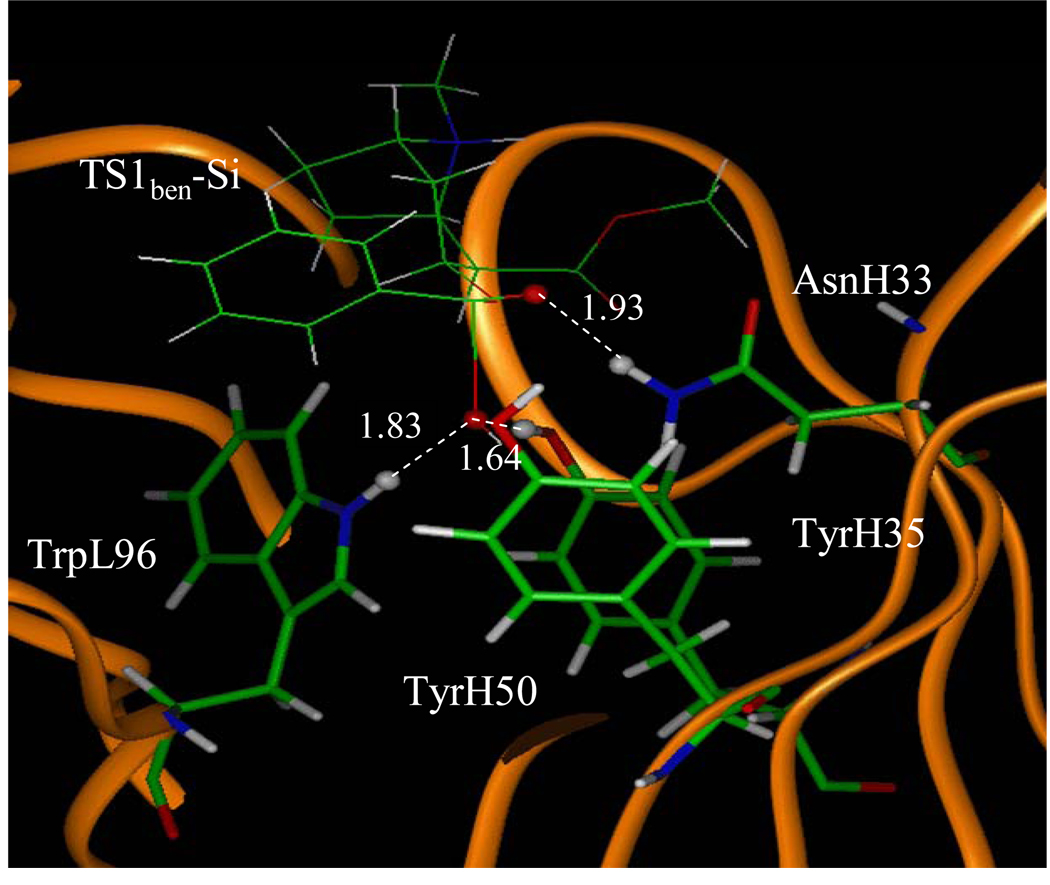
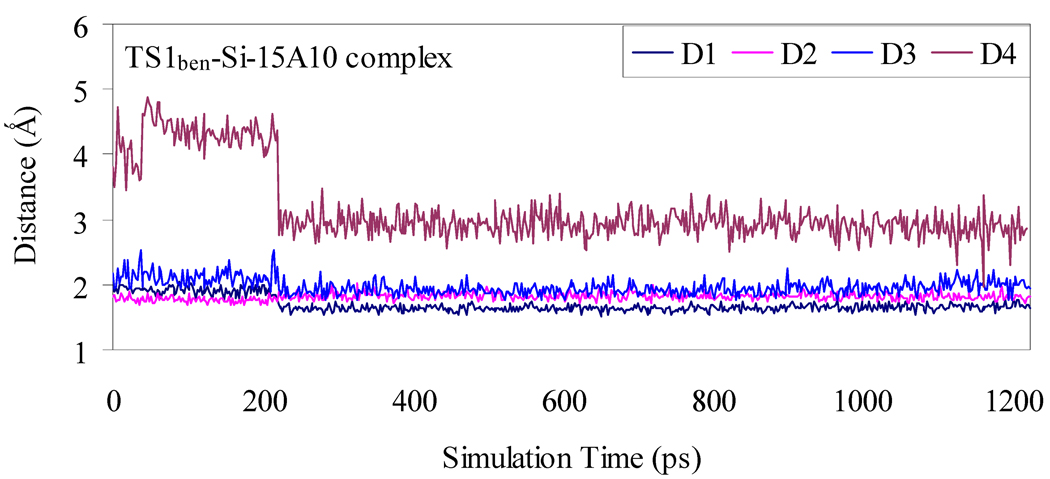
Depicted in Figures 1 to 4 are the schematic representations of the MD-simulated structures of mAb 15A10 binding with the four different ligands, including cocaine, TS1ben-Re, TS1ben-Si, and TS1met. As shown in the figures, the antibody binds with cocaine, TS1ben-Re, TS1ben-Si, and TS1met mainly through some of four potential hydrogen bonds with the side chains of residues TyrH35, TrpL96, AsnH33, and TyrH50 (D1 to D4, see Figures 1 to 4). The representative snapshots of the MD-simulated complexes are shown in Figures 5 to 8, giving the average H••••O distances involved in the hydrogen bonds between the antibody and ligand. Depicted in Figures 9 to 12 are the time-dependence of the H••••O distances (D1 to D4) involving TyrH35, TrpL96, AsnH33, and TyrH50.
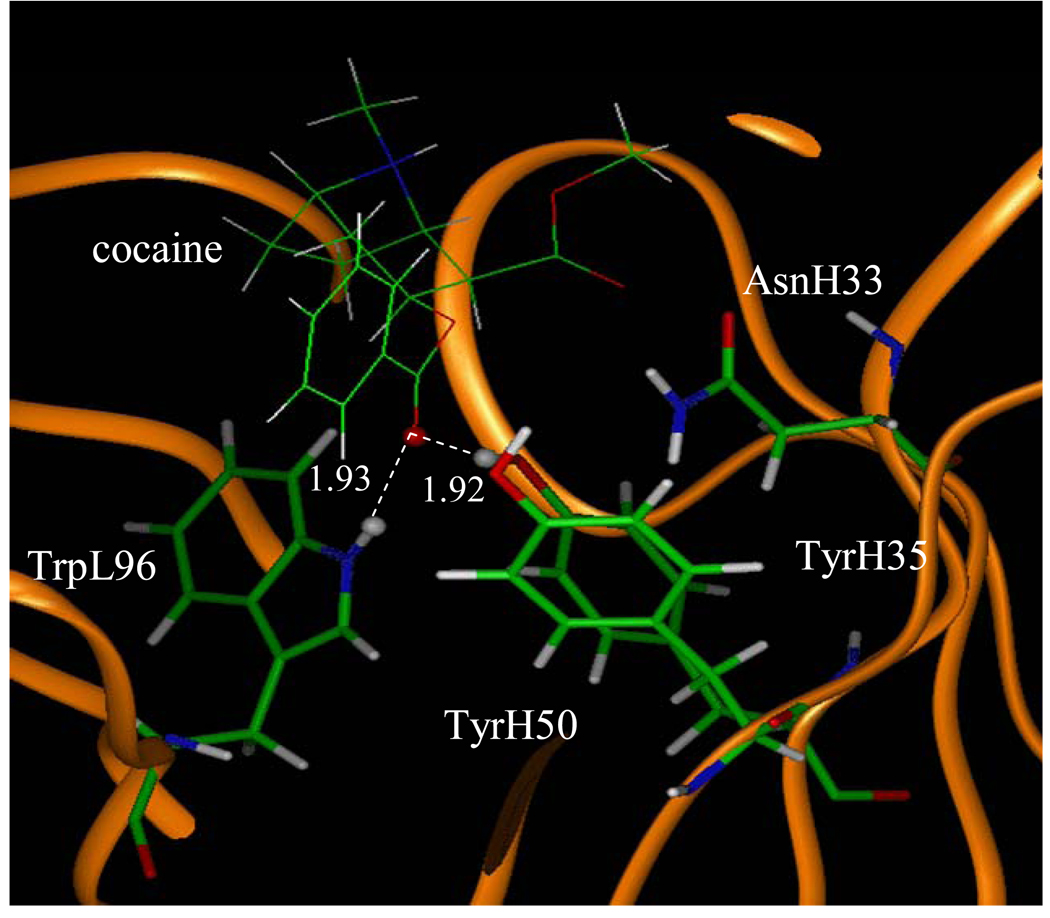
Figure 5.
The MD simulated structure of cocaine binding with the antibody. The key distances indicated in the figure are the simulated average distance (Å).
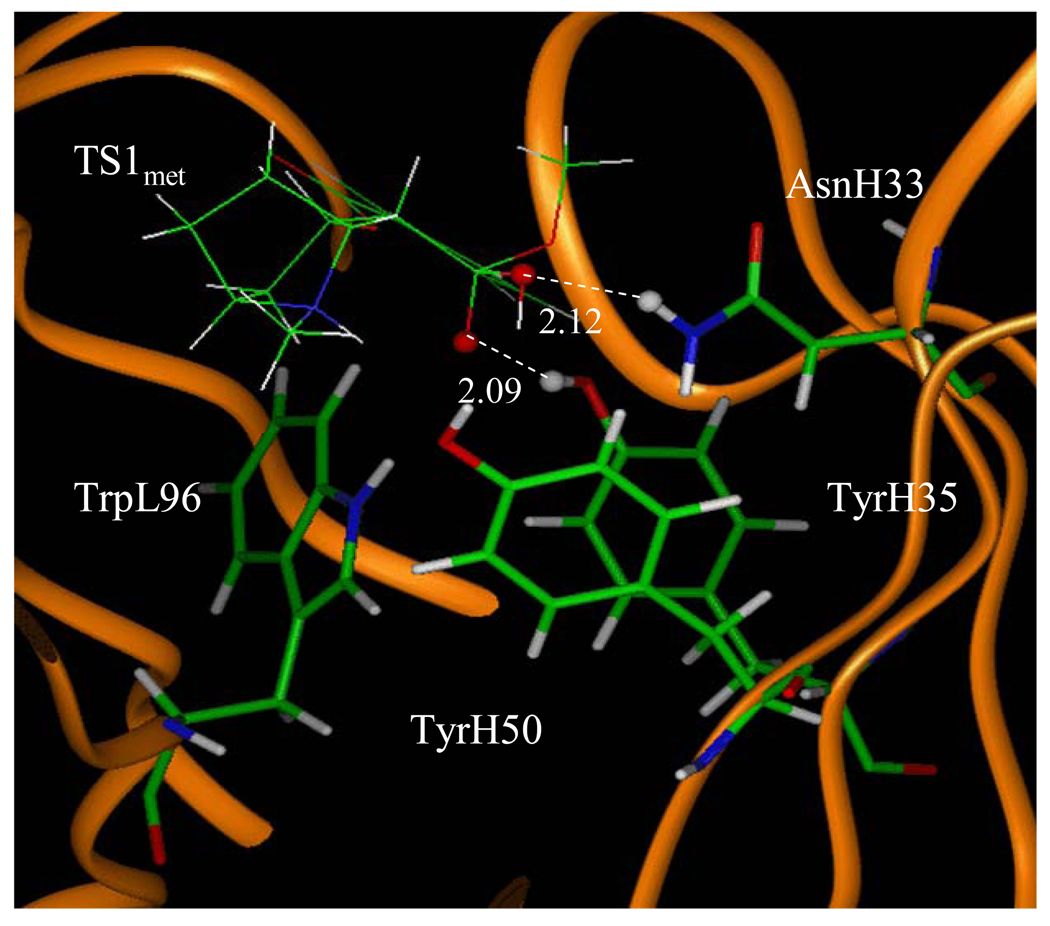
Figure 8.
The MD simulated structure of TS1met binding with the antibody. The key distances indicated in the figure are the simulated average distance (Å).
Figure 9.
Plots of the key internuclear distances versus the simulation time for cocaine binding with the antibody. See Figure 1 for the definitions of distances D1, D2, D3, and D4.
Figure 12.
Plots of the key internuclear distances versus the simulation time for TS1met binding with the antibody. See Figure 4 for the definitions of distances D1, D2, D3, and D4.
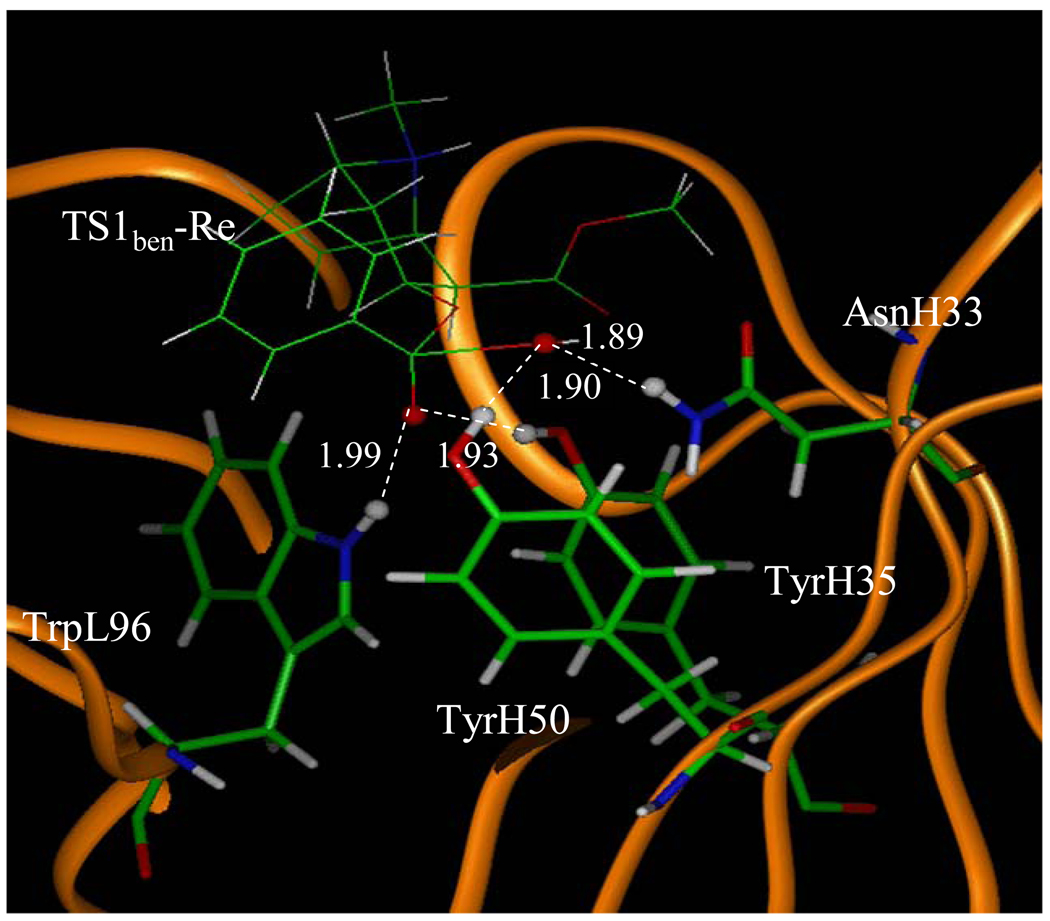
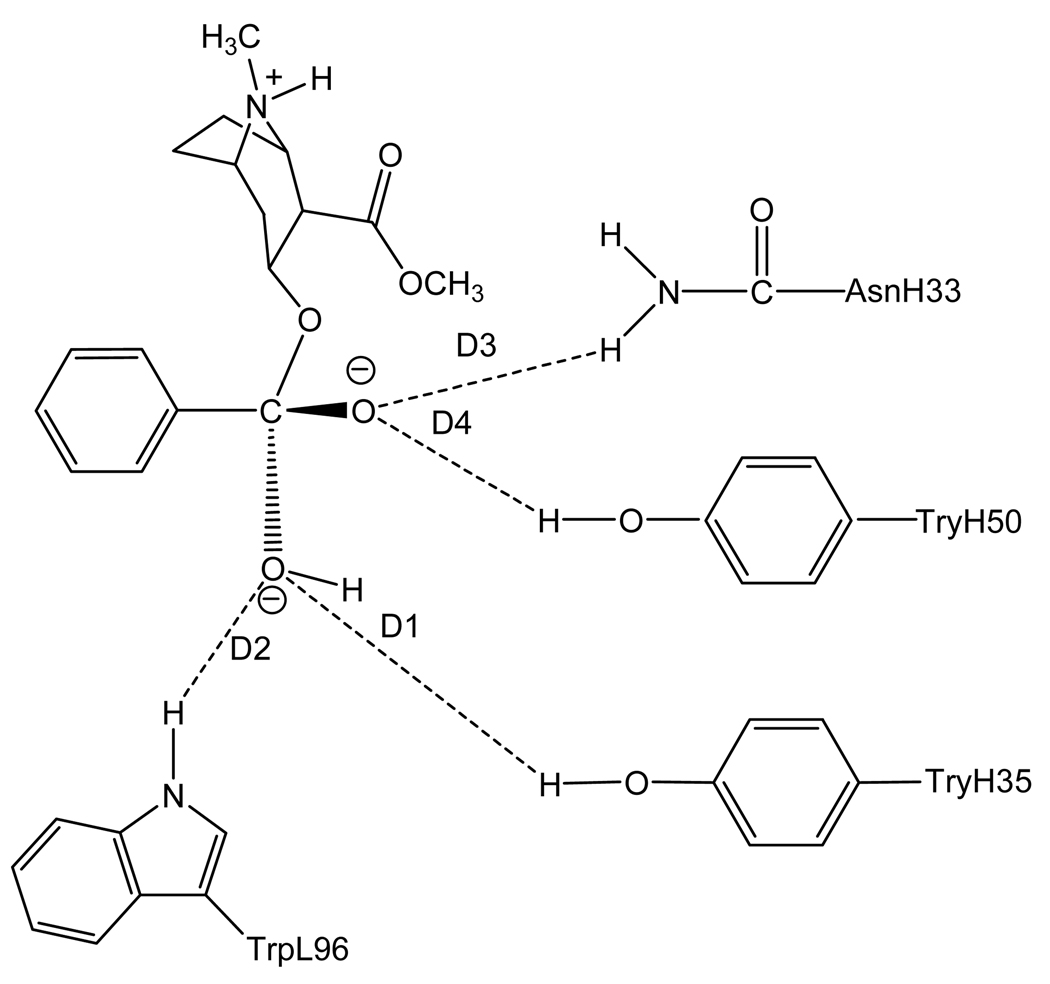
A survey of these figures reveals two hydrogen bonds for the antibody binding with cocaine, four hydrogen bonds with TS1ben-Re, three hydrogen bonds with TS1ben-Si, and two hydrogen bonds with TS1met. For the antibody binding with cocaine, as seen in Figures 1, 5, and 9, although there were three hydrogen bonds between the antibody and the carbonyl oxygen of cocaine benzoyl ester in the initial structure (obtained from molecular docking) used for the MD simulation, only two of the three hydrogen bonds (i.e. with the side chains of TyrH35 and TrpL96) were kept during the MD simulation. The average H••••O distances, denoted by D1 and D2 in the figures, for these two hydrogen bonds are 1.92 and 1.93 Ǻ, respectively. For the antibody binding with TS1ben-Re, as seen in Figures 6 and 10, all of the four hydrogen bonds (associated with D1 to D4 in Figure 2) in the initial structure were kept during the MD simulation, with the simulated average distances of 1.93, 1.99, 1.89, and 1.90 Ǻ for D1, D2, D3, and D4, respectively. Compared to the two hydrogen bonds of the antibody binding with cocaine, the overall strength of the four hydrogen bonds in the antibody binding with TS1ben-Re should be much stronger. For the antibody binding with TS1ben-Si, as seen in Figures 7 and 11, three hydrogen bonds associated with D1 to D3 (see Figure 3) existed in both the initial structure and the MD-simulated structure. The MD-simulated average D1, D2, and D3 values are 1.64, 1.83, and 193 Ǻ, respectively. Compared to the antibody binding with TS1ben-Re, the antibody binding with TS1ben-Si did not involve a hydrogen bond between TS1ben-Si and TyrH50. The overall strength of the three hydrogen bonds in the antibody binding with TS1ben-Si should also be stronger than that with cocaine. Thus, the transition states TS1ben-Re and TS1ben-Si are expected to be stabilized by the antibody relative to the cocaine binding with the same antibody.
Figure 6.
The MD simulated structure of TS1ben-Re binding with the antibody. The key distances indicated in the figure are the simulated average distance (Å).
Figure 10.
Plots of the key internuclear distances versus the simulation time for TS1ben-Re binding with the antibody. See Figure 2 for the definitions of distances D1, D2, D3, and D4.
Figure 2.
Schematic representation of TS1ben-Re binding with the antibody. The dashed lines refer to the key distances between TS1ben-Re and the antibody.
Figure 7.
The MD simulated structure of TS1ben-Si binding with the antibody. The key distances indicated in the figure are the simulated average distance (Å).
Figure 11.
Plots of the key internuclear distances versus the simulation time for TS1ben-Si binding with the antibody. See Figure 3 for the definitions of distances D1, D2, D3, and D4.
Figure 3.
Schematic representation of TS1ben-Si binding with the antibody. The dashed lines refer to the key distances between TS1ben-Si and the antibody.
However, for the antibody binding with TS1met, the MD simulation only revealed two weak hydrogen bonds (corresponding to D1 and D3 in Figure 4) with the side chains of TyrH35 and AsnH33. The overall strength of the two hydrogen bonds in the antibody binding with TS1met should be weaker than that of the two hydrogen bonds in the cocaine-antibody binding, due to the longer H••••O distances (2.09 and 2.12 Å in the TS1met-antibody binding versus 1.92 and 1.93 Å in the cocaine-antibody binding). Thus, the transition state TS1met is not expected to be stabilized by the antibody relative to the cocaine binding with the antibody.
A remarkable feature of the simulated structures is that, in addition to the previously recognized residues TyrH35, TrpL96, and AsnH33 that could form the oxyanion hole, TyrH50 is also important for stabilizing the transition state TS1ben-Re as TyrH50 forms a strong hydrogen bond with transition state TS1ben-Re.
Binding free energies
Summarized in Table 1 are the binding free energies calculated with the MM-PBSA approach for the antibody binding with cocaine, TS1ben-Re, TS1ben-Si, and TS1met. As seen in the table, the calculated entropy contributions for the four complexes are close to each other, with values ranging from 13.03 to 13.83 kcal/mol. This is reasonable, because the entropic contribution is mainly determined by the sizes and shapes of the antibody and ligand involved in the binding. The calculated van der Waals contributions to the binding free energies for all of the complexes, except for TS1met, are also very close to each other, ranging from −27.56 to −28.24 kcal/mol. This is because the binding modes in the three complexes (with cocaine, TS1ben-Re, and TS1ben-Si) are similar. For the complex with TS1met, the van der Waals contribution (−35.79 kcal/mol) is significantly different due to the remarkably different binding mode. In TS1met, it is the methyl ester group (rather than the benzoyl ester group) with the hydroxide ion that interacts with the binding site of the antibody. The calculated electrostatic contributions to the binding free energies for the four complexes are quite different, with −93.09, −44.57, −65.91, and −11.45 kcal/mol for cocaine, TS1ben-Re, TS1ben-Si, and TS1met, respectively. Correspondingly, the solvation shifts calculated for the four complexes are also very different, ranging from 32.71 to 103.19 kcal/mol. Overall, the binding free energies calculated for the antibody binding with cocaine, TS1ben-Re, TS1ben-Si, and TS1met are −4.97, −11.30, −9.61, and −0.79 kcal/mol, respectively. The calculated binding free energy of −4.97 kcal/mol for the antibody binding with cocaine is consistent with the binding free energy of −4.97 kcal/mol estimated from the experimental KM value of 220 µM.
Table 1.
Energetic results (kcal/mol) obtained from the MM-PBSA calculations at T = 298.15 K and P = 1 atm) for the antibody binding with cocaine, TS1ben-Re, TS1ben-Si and TS1met.
| ligand in the complex |
Calc. | Expt.a | ||||||
|---|---|---|---|---|---|---|---|---|
| ΔEele | ΔEvdw | ΔEMM | ΔGsolv | ΔEbind | −TΔS | ΔGbind | ΔGbind | |
| cocaine | −93.09 | −28.10 | −121.20 | 103.19 | −18.00 | 13.03 | −4.97 | −4.97 |
| TS1ben-Re | −44.57 | −27.56 | −72.13 | 47.00 | −25.13 | 13.83 | −11.30 | |
| TS1ben-Si | −65.91 | −28.24 | −94.16 | 71.17 | −22.99 | 13.38 | −9.61 | |
| TS1met | −11.45 | −35.79 | −47.24 | 32.71 | −14.53 | 13.74 | −0.79 | |
Estimated from the experimental KM value of 220 µM reported in ref. 6.
Free energy barriers and rate acceleration
Based on the calculated binding free energies, the free energy barrier shift, ΔΔGav, from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis was evaluated for each reaction pathway. As seen in Table 2, the free energy barrier shifts calculated for the reaction pathways associated with TS1ben-Re, TS1ben-Si, and TS1met are −6.33, −4.64, and 4.18 kcal/mol, respectively. So, mAb 15A10 significantly stabilizes the transition states for the hydrolysis of cocaine benzoyl ester, whereas it significantly destabilizes the transition state for the hydrolysis of cocaine methyl ester, relative to the cocaine-antibody binding. Based on our previous first-principles electronic structure calculations accounting for the solvent effects,19 the free energy barriers for the reaction pathways associated with TS1ben-Re, TS1ben-Si, and TS1met of the cocaine hydrolysis in water in the physiologic pH (7.4) should be 25.9, 28.6, and 20.1 kcal/mol, respectively. Based on the previously calculated free energy barriers and the barrier shifts calculated in the present study, the free energy barriers for the reaction pathways associated with TS1ben-Re, TS1ben-Si, and TS1met of the antibody-catalyzed cocaine hydrolysis are predicted to be 19.6, 24.0, and 24.3 kcal/mol, respectively. These energetic results show that the dominant reaction pathway for the antibody-catalyzed cocaine hydrolysis is associated with transition state TS1ben-Re, although the dominant reaction pathway for the cocaine hydrolysis in water is associated with transition state TS1met.
Table 2.
Free energy barriers (ΔGav in kcal/mol) calculated for three competing reaction pathways of the cocaine hydrolysis.
| Reaction pathway | ΔGav(aq) (SRS)a |
ΔGav(aq) (pH 7.4)b |
ΔΔGavc | ΔGav(antibody) (pH 7.4)d |
|---|---|---|---|---|
| cocaine + HO− → TS1ben-Re | 16.9 | 25.9 | −6.33 (−5.93) | 19.6 |
| cocaine + HO− → TS1ben-Si | 19.6 | 28.6 | −4.64 | 24.0 |
| cocaine + HO− → TS1met | 11.1 | 20.1 | 4.18 | 24.3 |
Free energy barriers determined by the first-principles electronic structure calculations (ref. 19) for the cocaine hydrolysis in water using the standard reference state (SRS), i.e. 1 M, for all molecular species, including [HO−] = 1 M, at T = 298.15 K.
Free energy barriers determined for the cocaine hydrolysis in water at the physiologic pH (7.4) at T = 298.15 K. The free energy barrier shift from the standard reference state of [HO−] = 1 M to pH 7.4 is 9.0 kcal/mol when T = 298.15 K.
The free energy barrier shift from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis (determined by using the data in Table 1). The value −5.93 kcal/mol in parenthesis was the free energy barrier shift derived from the experimental rate acceleration (kcat/k0 = 23,000) using Eq.(11).
Free energy barriers calculated for the antibody-catalyzed cocaine hydrolysis at the physiologic pH (7.4) at T = 298.15 K.
Further, when you only consider cocaine hydrolysis at the benzoyl ester, the reaction pathway with the lowest free energy barrier is always associated with transition state TS1ben-Re for both the cocaine hydrolysis in water and the antibody-catalyzed cocaine hydrolysis. Hence, for the hydrolysis of cocaine benzoyl ester, the calculated free energy barrier shift of −6.33 kcal/mol can directly be compared with the experimental rate acceleration (kcat/k0 = 23,000).6 According to Eq.(11), when the rate acceleration (kcat/k0) is 23,000, the corresponding free energy barrier shift should be −5.93 kcal/mol at T = 298.15 K. The experimentally-derived free energy barrier shift of −5.93 kcal/mol is close to the calculated free energy barrier shift of −6.33 kcal/mol. In light of the good agreement between the calculated energetic results and available experimental data, it should be interesting to employ the same computational protocol to calculate the free energy barriers for the cocaine hydrolysis catalyzed by various mutants of the anti-cocaine catalytic antibody for future rational design of possible high-activity mutants of the catalytic antibody against cocaine.
For further validation, the same computational protocol (with the above-calibrated w value of 0.6871 kcal/mol) was also used to examine the cocaine hydrolysis catalyzed by two antibody mutants (i.e. AsnH33Ala and TyrH35Phe) for which the relative experimental activity data are available. Here, mutation AsnH33Ala means that Asn33 residue of the high chain is changed to Ala residue, whereas mutation TyrH35Phe refers to that Tyr35 residue of the high chain is changed to Phe residue. The MD trajectories and the simulated binding structures are provided as supporting information. The calculated energetic results are summarized in Tables 3 to 5, in comparison with available experimental data. As seen in Table 5, the calculated shift of the free energy barrier from the wild-type antibody to the TyrH35Phe mutant is 0.55 kcal/mol, which is close to the experimental free energy barrier shift, 0.85 kcal/mol, derived from the reported activity change from 100% to 24%.6 The calculated shift of the free energy barrier from the wild-type antibody to the AsnH33Ala mutant is 3.50 kcal/mol, which is also consistent with the experimental observation6 that the catalytic activity of the AsnH33Ala mutant was 0% (i.e. < 0.5%) of the wild-type against cocaine. The activity change from 100% to < 0.5% is associated with a free energy barrier change of > 3.14 kcal/mol. Hence, the calculated mutation-caused shifts of the free energy barrier are also reasonably close to the available experimental activity data.
Table 3.
Energetic results (kcal/mol) obtained from the MM-PBSA calculations at T = 298.15 K and P = 1 atm for the cocaine binding with the antibody mutants.
| antibody | ΔEele | ΔEvdw | ΔEMM | ΔGsolv | ΔEbind | −TΔS | ΔGbind |
|---|---|---|---|---|---|---|---|
| AsnH33Ala | −85.77 | −26.13 | −111.90 | 94.83 | −17.07 | 13.27 | −3.80 |
| TyrH35Phe | −80.7 | −29.01 | −109.72 | 93.23 | −16.49 | 11.98 | −4.51 |
Table 5.
Mutation-caused shifts of free energy barrier (ΔGav in kcal/mol) calculated for cocaine hydrolysis catalyzed by the antibody mutants in comparison with available experimental data.
| antibody | Calc. | Expt. | ||
|---|---|---|---|---|
| ΔΔGava | Relative ΔGavb | Relative activityc | Relative ΔGavb | |
| Wild-type | −6.33 | 0 | 100% | 0 |
| AsnH33Ala | −2.83 | 3.50 | 0% (i.e. < 0.5%) | > 3.14 |
| TyrH35Phe | −5.08 | 0.55 | 24% | 0.85 |
The free energy barrier shift from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis corresponding to the wild-type antibody and its mutants.
Mutation-caused shift of the free energy barrier, i.e. ΔΔGav – ΔΔGav (wild-type). The experimental shifts are derived from the experimental relative activity data (i.e. < 0.5% and 24%).
Experimental activity of the mutant relative to the wild-type antibody (data from ref. 6).
Conclusion
The free energy barriers for the competing reaction pathways of the cocaine hydrolysis catalyzed by an anti-cocaine catalytic antibody, mAb 15A10, were predicted, in the present study, by using a novel computational strategy based on the binding free energy calculations on the antibody binding with cocaine and the transition states. On the basis of the calculated binding free energies, we were able to evaluate the free energy barrier shift from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis for each reaction pathway. The free energy barriers for the antibody-catalyzed cocaine hydrolysis were predicted to be the corresponding free energy barriers for the cocaine hydrolysis in water plus the calculated free energy barrier shifts. Based on the predicted free energy barriers, the dominant reaction pathway for the antibody-catalyzed cocaine hydrolysis was determined. The calculated free energy barrier shift of −6.33 kcal/mol from the dominant reaction pathway of the cocaine benzoyl ester hydrolysis in water to the dominant reaction pathway of the antibody-catalyzed hydrolysis of cocaine benzoyl ester is in good agreement with the experimentally-derived free energy barrier shift of −5.93 kcal/mol (corresponding to the experimental rate acceleration kcat/k0 = 23,000), while the calculated binding free energy of −4.97 kcal/mol for the cocaine-antibody binding is consistent with the experimentally-derived binding free energy of −4.97 kcal/mol (estimated from the experimental KM value of 220 µM). The calculated mutation-caused shifts of the free energy barrier are also reasonably close to the available experimental activity data.
In light of the good agreement between the calculated energetic results and available experimental kinetic data, the computational protocol for calculating the free energy barrier shift from the cocaine hydrolysis in water to the antibody-catalyzed cocaine hydrolysis may be useful in future rational design of possible high-activity mutants of the catalytic antibody as anti-cocaine therapeutics. The general computational strategy for calculating the free energy barrier shift may also be valuable for studying a variety of chemical reactions catalyzed by other antibodies or proteins through non-covalent bonding interactions with the substrates.
Supplementary Material
Table 4.
Energetic results (kcal/mol) obtained from the MM-PBSA calculations at T = 298.15 K and P = 1 atm for the TS1ben-Re binding with the antibody mutants.
| antibody | ΔEele | ΔEvdw | ΔEMM | ΔGsolv | ΔEbind | −TΔS | ΔGbind |
|---|---|---|---|---|---|---|---|
| AsnH33Ala | −32.94 | −26.86 | −59.80 | 40.98 | −18.82 | 12.20 | −6.62 |
| TyrH35Phe | −33.08 | −28.89 | −61.96 | 43.95 | −18.01 | 8.42 | −9.59 |
Acknowledgments
The research was supported by NIH/NIDA (grant R01 DA013930 to C.-G. Zhan). The authors also acknowledge the Center for Computational Sciences (CCS) at University of Kentucky for supercomputing time on HP Superdome (with 4 nodes and 256 processors) and on IBM X-series Cluster (with 34 nodes and 1,360 processors).
Footnotes
Supporting Information Available. Eight figures for the MD trajectories and the simulated structures for the mutants of the catalytic antibody binding with cocaine and the transition state; complete citations of references 9, 31, 36, and 49. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Gorelick DA, Gardner EL, Xi ZX. Drugs. 2004;64:1547. doi: 10.2165/00003495-200464140-00004. [DOI] [PubMed] [Google Scholar]
- 2. http://ibogaine.mindvox.com/index.html?Media/Lancet01.html~mainFrame.
- 3.Johanson CE, Fischman MW. Pharmacol. Rev. 1989;41:3. [PubMed] [Google Scholar]
- 4.Carroll FI, Howell LL, Kuhar MJ. J. Med. Chem. 1999;42:2721. doi: 10.1021/jm9706729. [DOI] [PubMed] [Google Scholar]
- 5.Gorelick DA. Drug Alcohol Depend. 1997;48:159. doi: 10.1016/s0376-8716(97)00119-1. [DOI] [PubMed] [Google Scholar]
- 6.Larsen NA, de Prada P, Deng SX, Mittal A, Braskett M, Zhu X, Wilson IA, Landry DW. Biochemistry. 2004;43:8067. doi: 10.1021/bi049495l. [DOI] [PubMed] [Google Scholar]
- 7.Pozharski E, Moulin A, Hewagama A, Shanafelt AB, Petsko GA, Ringe D. J. Mol. Biol. 2005;349:570. doi: 10.1016/j.jmb.2005.03.080. [DOI] [PubMed] [Google Scholar]
- 8.Zhu X, Dickerson TJ, Rogers CJ, Kaufmann GF, Mee JM, McKenzie KM, Janda KD, Wilson IA. Structure. 2006;14:205. doi: 10.1016/j.str.2005.10.014. [DOI] [PubMed] [Google Scholar]
- 9.Mets B, et al. Proc. Natl. Acad. Sci. U.S.A. 1998;95:10176. doi: 10.1073/pnas.95.17.10176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Baird TJ, Deng SX, Landry DW, Winger G, Woods JH. J. Pharmacol. Exp. Ther. 2000;295:1127. [PubMed] [Google Scholar]
- 11.Cooper ZD, Narasimhan D, Sunahara RK, Mierzejewski P, Jutkiewicz EM, Larsen NA, Wilson IA, Landry DW, Woods JH. Mol. Pharmacol. 2006;70:1885. doi: 10.1124/mol.106.025999. [DOI] [PubMed] [Google Scholar]
- 12.Zhan C-G, Zheng F, Landry DW. J. Am. Chem. Soc. 2003;125:2462. doi: 10.1021/ja020850+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gao DQ, Zhan C-G. J. Phys. Chem. B. 2005;109:23070. doi: 10.1021/jp053736x. [DOI] [PubMed] [Google Scholar]
- 14.Hamza A, Cho H, Tai HH, Zhan C-G. J. Phys. Chem. B. 2005;109:4776. doi: 10.1021/jp0447136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pan YM, Gao DQ, Yang WC, Cho H, Yang GF, Tai HH, Zhan C-G. Proc. Natl. Acad. Sci. U.S.A. 2005;102:16656. doi: 10.1073/pnas.0507332102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhan CG, Gao DQ. Biophys. J. 2005;89:3863. doi: 10.1529/biophysj.105.070276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gao D, Cho H, Yang W, Pan Y, Yang G, Tai HH, Zhan CG. Angew. Chem. Int. Ed. 2006;45:653. doi: 10.1002/anie.200503025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gao DQ, Zhan C-G. Proteins. 2006;62:99. doi: 10.1002/prot.20713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zhan C-G, Deng SX, Skiba JG, Hayes BA, Tschampel SM, Shields GC, Landry DW. J. Comput. Chem. 2005;26:980. doi: 10.1002/jcc.20241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhan CG, Landry DW. J. Phys.Chem. A. 2001;105:1296. [Google Scholar]
- 21.Li P, Zhao K, Deng SX, Landry DW. Helve. Chim. Acta. 1999;82:85. [Google Scholar]
- 22.Zhan CG, Bentley J, Chipman DM. J. Chem. Phys. 1998;108:177. [Google Scholar]
- 23.Zhan CG, Chipman DM. J. Chem. Phys. 1998;109:10543. [Google Scholar]
- 24.Zhan CG, Chipman DM. J. Chem. Phys. 1999;110:1611. [Google Scholar]
- 25.Zhan CG, Landry DW, Ornstein RL. J. Phys. Chem. A. 2000;104:7672. [Google Scholar]
- 26.Chen X, Zhan CG. J. Phys. Chem. A. 2004;108:6407. [Google Scholar]
- 27.Alvarez-Idaboy JR, Galano A, Bravo-Perez G, Ruiz ME. J. Am. Chem. Soc. 2001;123:8387. doi: 10.1021/ja010693z. [DOI] [PubMed] [Google Scholar]
- 28.Anderson WB, Board PG, Anders MW. Chem. Res. Toxicol. 2004;17:650. doi: 10.1021/tx034099+. [DOI] [PubMed] [Google Scholar]
- 29.Houston JB, Galetin A. Arch. Biochem. Biophys. 2005;433:351. doi: 10.1016/j.abb.2004.09.010. [DOI] [PubMed] [Google Scholar]
- 30.Bernstein FC, Koetzle TF, Williams GJ, Meyer EF, Jr, Brice MD, Rodgers JR, Kennard O, Shimanouchi T, Tasumi M. J. Mol. Biol. 1977;112:535. doi: 10.1016/s0022-2836(77)80200-3. [DOI] [PubMed] [Google Scholar]
- 31.Frisch MJT, et al. Gaussian 03. Pittsburgh, PA: Gaussian, Inc; 2003. revision A. l. [Google Scholar]
- 32.Singh UC, Kollman PA. J. Comput. Chem. 1984;5:129. [Google Scholar]
- 33.Besler BH, Merz KM, Kollman PA. J. Comput. Chem. 1990;11:431. [Google Scholar]
- 34.Bayly CI, Cieplak P, Cornell WD, Kollman PA. J. Phys. Chem. 1993;97:10269. [Google Scholar]
- 35.Cornell WD, Cieplak P, Bayly CI, Kollman PA. J. Am. Chem. Soc. 1993;115:9620. [Google Scholar]
- 36.Case DAD, et al. AMBER 8. San Francisco: University of California; 2004. [Google Scholar]
- 37.Morris GM, Goodsell DS, Halliday RS, Huey R, Hart WE, Belew RK, Olson AJ. J. Comput. Chem. 1998;19:1639. [Google Scholar]
- 38.Morris GM, Goodsell DS, Huey R, Hart WE, Halliday S, Belew R, Olson AJ. AutoDock Version 3.0.5. La Jolla, CA: 2001. [Google Scholar]
- 39.Eksterowicz JE, Houk KN. Chem. Rev. 1993;93:2439. [Google Scholar]
- 40.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J. Chem. Phys. 1983;79:926. [Google Scholar]
- 41.Hamza A, Cho H, Tai HH, Zhan C-G. Bioorg. Med. Chem. 2005;13:4544. doi: 10.1016/j.bmc.2005.04.053. [DOI] [PubMed] [Google Scholar]
- 42.Hamza A, Zhan C-G. J. Phys. Chem. B. 2006;110:2910. doi: 10.1021/jp0550762. [DOI] [PubMed] [Google Scholar]
- 43.Koca J, Zhan C-G, Rittenhouse RC, Ornstein RL. J. Am. Chem. Soc. 2001;123:817. doi: 10.1021/ja000439r. [DOI] [PubMed] [Google Scholar]
- 44.Koca J, Zhan C-G, Rittenhouse RC, Ornstein RL. J. Comput. Chem. 2003;24:368. doi: 10.1002/jcc.10217. [DOI] [PubMed] [Google Scholar]
- 45.Zhan C-G, de Souza ON, Rittenhouse R, Ornstein RL. J. Am. Chem. Soc. 1999;121:7279. [Google Scholar]
- 46.Berendsen HJC, Postma JPM, Vangunsteren WF, Dinola A, Haak JR. J. Chem. Phys. 1984;81:3684. [Google Scholar]
- 47.Ryckaert JP, Ciccotti G, Berendsen HJC. J. Comput. Phys. 1977;23:327. [Google Scholar]
- 48.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J. Chem. Phys. 1995;103:8577. [Google Scholar]
- 49.Kollman PA, et al. Acc. Chem. Res. 2000;33:889. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- 50.Gilson MK, Sharp KA, Honig BH. J. Comput. Chem. 1988;9:327. [Google Scholar]
- 51.Jayaram B, Sharp KA, Honig B. Biopolymers. 1989;28:975. doi: 10.1002/bip.360280506. [DOI] [PubMed] [Google Scholar]
- 52.Sanner MF, Olson AJ, Spehner JC. Biopolymers. 1996;38:305. doi: 10.1002/(SICI)1097-0282(199603)38:3%3C305::AID-BIP4%3E3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 53.Raha K, Merz KM., Jr J. Med. Chem. 2005;48:4558. doi: 10.1021/jm048973n. [DOI] [PubMed] [Google Scholar]
- 54.Bardi JS, Luque I, Freire E. Biochemistry. 1997;36:6588. doi: 10.1021/bi9701742. [DOI] [PubMed] [Google Scholar]
- 55.Gomez J, Freire E. J. Mol. Biol. 1995:252–337. doi: 10.1006/jmbi.1995.0501. [DOI] [PubMed] [Google Scholar]
- 56.Baldwin RL. Proc. Natl. Acad. Sci. U.S.A. 1986;83:8069. doi: 10.1073/pnas.83.21.8069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.D'Aquino JA, Gomez J, Hilser VJ, Lee KH, Amzel LM, Freire E. Proteins. 1996;25:143. doi: 10.1002/(SICI)1097-0134(199606)25:2<143::AID-PROT1>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.