Abstract
Inflammatory Bowel Disease (IBD) is an immunoinflammatory illness of the gut initiated by an immune response to bacteria in the microflora. The resulting immunopathogenesis leads to lesions in epithelial lining of the colon through which bacteria may infiltrate the tissue causing recurring bouts of diarrhea, rectal bleeding, and mal-nutrition. In healthy individuals such immunopathogenesis is avoided by the presence of regulatory cells that inhibit the inflammatory pathway. Highly relevant to the search for treatment strategies is the identification of components of the inflammatory pathway that allow regulatory mechanisms to be overridden and immunopathogenesis to proceed. In vitro techniques have identified cellular interactions involved in inflammation-regulation crosstalk. However, tracing immunological mechanisms discovered at the cellular level confidently back to an in vivo context of multiple, simultaneous interactions has met limited success.
To explore the impact of specific interactions, we have constructed a system of 29 ordinary differential equations representing different phenotypes of T-cells, macrophages, dendritic cells, and epithelial cells as they move and interact with bacteria in the lumen, lamina propria, and lymphoid tissue of the colon.
Simulations revealed the positive inflammatory feedback loop formed by inflammatory M1 macrophage activation of T-cells as a driving force underlying the immunopathology of IBD. Furthermore, strategies that remove M1 from the site of infection, by either i) increasing its potential to switch to a regulatory M2 phenotype or ii) increasing the rate of reversion (for M1 and M2 alike) to a resting state, cease immunopathogenesis even as bacteria are eliminated by other inflammatory cells.
Based on these results, we identify macrophages and their mechanisms of plasticity as key targets for mucosal inflammation intervention strategies. In addition, we propose that the primary mechanism behind the association of PPARγ mutation with IBD is its ability to mediate the M1 to M2 switch.
1. Introduction
Inflammatory Bowel Disease (IBD) is a chronic illness of the gut characterized by a recurring inflammatory response to bacteria in the lumen microflora resulting in lesions of the epithelial lining and lamina propria (Swidsinski et al., 2002). The lamina propria is the tissue site where immune cells initially recognize bacterial antigen prior to migrating to the distal lymphoid tissue to mount the inflammatory response. IBD results in two clinical manifestations, Crohns disease and ulcerative colitis, in which the patient experiences relapses of diarrhea, rectal bleeding, and malnutrition as bacteria from the lumen leak into the lamina propria through the lesions in the epithelial barrier (Cho, 2008). Over 1 million people are afficted by IBD in North America and 4 million worldwide resulting in a severe decrease in quality of life as well as significant health care-related costs (Stenson, 1995). Total expenses exceed $15 billion annually in the U.S. not including indirect expenses of treating complications such as recurrent pancreatitis, abscesses, intestinal obstruction, anemia, thromboses, perianal lesions, arthritis, uveitis, iritis, or cutaneous lesions (Braverman, 2003; Barba et al., 2002).
In a healthy individual, immune cells of the gut mucosa remain largely inactive towards the 1014 bacteria that compose the microflora. This tolerance to most bacterial strains is attributed to the prominent presence of regulatory immune cells that may be triggered by the commensal microflora and whose functions are antagonistic to inflammatory pathways triggered by small, transient populations of pathogenic bacteria.
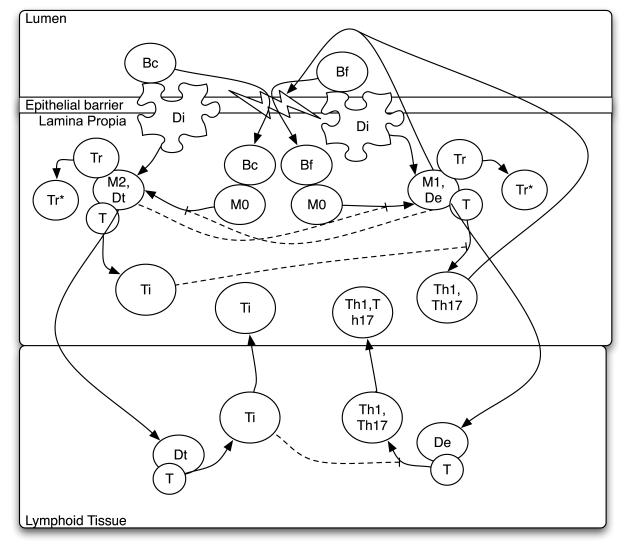
For an illustration of immune response pathways in the gut mucosa, please look to Figure 1. The inflammatory pathway portrayed is currently believed to occur as follows: Inflammation is initiated when resting antigen presenting cells, dendritic cells and macrophages, endocytose bacterial antigen at the initial site of infection, the lumen. In the lamina propria (LP), these cells then differentiate to inflammatory or effector phenotypes, termed M1 macrophages (M1) and effector dendritic cells (De) secreting inflammatory mediators including factors that aid infiltration of additional resting macrophage and dendritic cell precursors (monocytes) as well as T-cells into the LP. De and M1 present antigen to resting T-cells while secreting cytokines IL-12, IFN-γ,TNF-α, and IL-23 inducing their differentiation to pro-inflammatory T-helper cells (Th), specifically Th1 or Th17 phenotypes, that also secrete inflammatory mediators (Iwasaki, 2007; Gordon & Taylor, 2005). Antigen presenting cells may also migrate away from the infection site to the lymphoid tissue where they contact and stimulate a larger concentration of T-cells that will, in turn, relocate to the infection site in the lamina propria. There, Th1 and Th17 act synergistically with M1 and De to recruit more monocytes and promote their differentiation to the pro-inflammatory M1 and De phenotypes closing a positive feedback loop.
Figure 1.
Biological model of crosstalk between inflammatory and regulatory pathways in the gut. Solid lines represent either a reaction that induces cell differentiation from one type to another or the promotion by a cell type of a particular reaction. Dotted lines represent an inhibitory effect of a cell type on an interaction. The inflammatory pathway (right) is triggered by pathogenic (foreign) bacteria, Bf, and the regulatory pathway (left) is triggered by residential (commensal) bacteria, Bc. Each is described in the text along with other abbreviations.
Immunopathogenesis results from secretion of toxic peroxide anions, proteases, and oxygen/ nitrogen radicals by M1 and Th1-activated cells that kill the invading bacteria, but also cause indiscriminate tissue damage. In sterile organ systems, the inflammatory process generally ceases once the antigen population is eliminated and immune cells are no longer stimulated directly. However, in the gut, inflammation induced by bacterial microflora presents a scenario where the antigen population cannot be eliminated allowing the collateral cost of immunopathogensis to mount and become more harmful to the host than the invading bacteria itself. Compounding the problem, inflammation-induced damage to the epithelial barrier between the lumen and lamina propria allows increased permeability and infiltration of bacteria into the lamina propria, thereby allowing heightened macrophage and dendritic cell stimulation completing another positive feedback loop that magnifies the inflammatory responses during IBD (Figure 1).
In healthy individuals, to avoid this occurrence, the gut mucosa contains various regulatory factors such as M2 macrophages (M2), tolerogenic dendritic cells (Dt), and T-regulatory cells that are analogous to, and act antagonistically with, their inflammatory counter parts M1, De, and Th1/ Th17. In the regulatory pathway, binding of ligands recognized as self, including commensal bacteria, to specific surface receptors of resting macrophages and dendritic cells induce their differentiation to M2 and Dt as opposed to M1 and De. One such receptor is the peroxisome proliferator-activated receptor, PPARγ, expressed in T-cells, dendritic cells, macrophages, and epithelial cells (Spiegelman, 1998; Mansen et al., 1996). This process is aided by the presence of anti-inflammatory cytokines IL-10 and TGF-β that inhibit pro-inflammatory cytokine secretion and down-regulation of co-stimulatory molecule expression (Asseman et al., 1999). The net result is that, upon antigen presentation by M2 and Dt, resting T-cells differentiate to a T-regulatory phenotypes. These are called induced T-regulatory cells (Ti) because their resting precursors have the ability to become Th1 upon stimulation by IFN-γ+IL-12 secreting M1 and De. In contrast, natural T-regulatory cells (Tr) are T-cells that are pre-destined to be regulatory cells independent of the cytokine environment. Both Ti and Tr secrete IL-10 and TGF-β promoting further M2 and Dt creation. In addition, Tr has been shown to bind effector dendritic cells with high affinity and inhibit their stimulation of resting T-cells to inflammatory phenotypes (Onishi et al., 2008).
In the current biological model of gut homeostasis commensal bacteria-mediated stimulation is largely responsible for upholding the basal population of regulatory factors that inhibit the inflammatory responses of their neighboring cells (Figure 1). This normally allows the presence of a small population of inflammatory immune cells in response to the occasional invasion of pathogenic bacteria while the system remains inactive towards nonpathogenic strains in the microflora that maintain gut function. In abnormal cases, such as IBD, this low-level inflammatory response is able to mount, from an initially small population, to a much larger population able to override the suppressive activity of its regulatory anatagonists. An area of key interest to IBD intervention is identification of the specific interactions of the inflammatory pathway that allow this cascade effect to take hold and subsequent immunopathogenesis to proceed.
Many of the mentioned interactions involved in inflammatory-regulatory crosstalk have been identified in vitro. It is yet to be identified which of these in vitro observed mechanisms lie behind the immunopathogenic cell dynamics observed in vivo during inflammation. For example, IBD recovery is associated with increased levels of T-regulatory cells in animal models (Powrie et al., 1993; Hontecillas & Bassaganya-Riera, 2007). Is this due to Trspecific activity, such as the direct disruption of De-mediated T-cell stimulation, or its role as one of many IL-10 secreting cells, which could have numerous downstream effects?
There is still no cure for IBD and the only available treatments include those that universally weaken mucosal immunity leaving the patient vulnerable to opportunistic pathogens (Bassaganya-Riera et al., 2004). Identifying the specific regulatory functions that mediate the chronic inflammatory response would provide new strategies for more sophisticated treatment options.
Towards this goal we have developed a system of 29 ordinary differential equations describing the movement, interaction, and activation of inflammatory regulatory macrophages, T-cells, and dendritic cells in the presence of bacteria and cytokines in the lumen, lamina propria, and lymphoid tissue regions of gut mucosa. In silico, we induced chronic inflammation by allowing resting macrophages and dendritic cells to differentiate to inflammatory phenotypes upon contact with bacteria of the microflora. We then traced dynamics of inflammation markers back to specific interactions identifying those that override regulatory factors and sustain an immunopathogenic inflammatory response.
2. Methods
2.1. Mathematical model
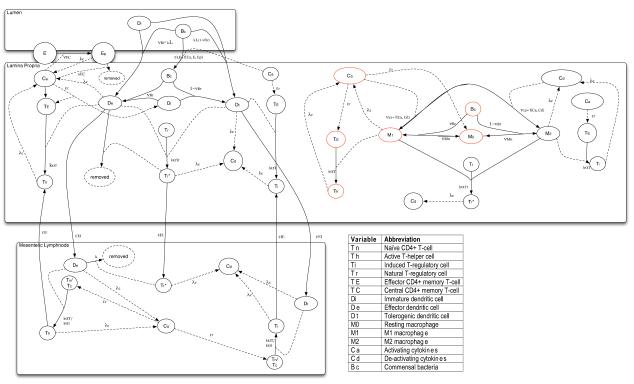
Our model describes population dynamics of immune cells and epithelial cells as they interact, flow, and differentiate over time in response to dynamic populations of cytokines and bacteria (Figure 2). The populations are further compartmentalized by three locations between which the cells may migrate: i) the lumen, where bacteria reside, which is denoted by the superscript ‘L’ ii) the lamina propria, more generally termed the effector site of the immune response, denoted by the superscript ‘E’ and iii) the mesenteric lymph node, the inductive site of the immune response, denoted by the superscript ‘I’. In the following equations capital roman letters denote variables, lowercase and greek letters denote parameters, and subscripts the cell phenotype. An organized list of model parameters and their corresponding symbols is given in Appendix A. A list of the variables is given in Appendix B.
Figure 2.
Scheme of mathematical model of interacting populations represented explicitly in the model in the three location compartments: i) the lumen (top) ii) the lamina propria (middle), and iii) mesenteric lymph node (bottom). Solid arrows indicate cell transition from one population pool to another and are labelled with the rate or probability of this transition. Dashed arrows point from populations to the transition which they positively influence. The symbols for these parameters are described in Appendix A, table A.1. Red circles highlight the specific positive feedback loop that drives exponential growth of the activating cytokine population and epithelial cell depletion in the IBD model where Bc is able to stimulate Di and M0 to inflammatory phenotypes, De and M1.
Cytokines
Some parameter values are dependent on cytokine levels. The model includes an activating cytokine group, Ca, in the inductive site (Equation 1) and effector site (Equation 2) that represents factors secreted by inflammatory phenotypes including IFN-γ, TNF-α , pro-inflammatory cytokines, proteases and free radicals such as nitric oxide. The second group is deactivating cytokines, Cd, representing IL-10 and TGF-β (Equations 3 and 4). As a simplifying assumption, the different cytokines are secreted at the same constant rate, λc, from active cells of different phenotypes and degrade at a constant rate, μc. This decision was reinforced by a lack of significant sensitivity of immune cell population levels to these particular parameters.
| (1) |
| (2) |
| (3) |
| (4) |
Bacteria
Equations 5 and 6 represent bacteria in the lumen and lamina propria compartments, respectively, where λb, ϕb, and μb are birth rate, crowding co-efficient, and death rate. In the healthy model, this population is largely composed of commensal bacteria. Bacteria may migrate from the lumen to the lamina propria at a rate, ∊LE, where . Note that this function evaluates to 0 in the absence of activating cytokines (), increasing as concentration rises and the epithelial cell concentration (E + Ep) falls. This represents epithelial cell modification by pro-inflammatory cytokines, which increases permeability and lesion formation (Yang et al., 2003). The parameter q controls the cytokine level at which migration occurs and y∊ is the rate at which the bacterial migration increases with respect to and E + Ep levels. Bacteria are eliminated by inflammatory epithelial cells (Ep) and M1 macrophages (), which secrete microbicides, as well as uptake by resting antigen presenting cells (, , and ). This is represented by the terms in equation 5 and in equation 6 where kL and k are contact rates between individual cells in the lumen and lamina propria, respectively.
| (5) |
| (6) |
Epithelial Cells
Equation 7 describes the dynamics of cells of the epithelial lining as they replicate and die at constant rates, λE and μE respectively. The parameter ϕE is a crowding co-efficient that allows population growth to cease at the healthy basal concentration of 104/mL (Artis, 2008), representing an intact barrier composed of normal epithelial cells (E) as well as cytokine-secreting pro-inflammatory epithelial cells (Ep). The term represents transition of an epithelial cell to a pro-inflammatory epithelial cell, Ep, described in equation 8. This represents the ability of cytokines encompassed in the activating group to induce secretion of pro-inflammatory mediators by epithelial cells(Artis, 2008). The term in equation 8 represents death induced by cytopathic factors, also present in the activating cytokine group. The assumption here is that the same pathways that lead to factors that stimulate epithelial cells to secrete cytokines, such as IFN-γ, are coupled with those that produce free radicals and proteases.
| (7) |
| (8) |
Dendritic Cells
Immature dendritic cells are present in the lamina propria (, Equation 9), of which a subset are localized to the epithelial barrier allowing dendrites to extend through epithelial cells into lumen to contact bacteria (Iwasaki, 2007). This subset is represented as dendritic cells in the lumen compartment (, Equation 11). The immature dendritic cell population is fed by monocytes from the blood at rates λd (Equation 10) and λdl (Equation 12) such that each that transfers to one of the activated dendritic cell compartments is replaced with a net increase of the population in the presence of inflammatory cytokines (Janeway et al., 2001). This increase occurs with the term , which represents general recruitment of leukocytes by inflammatory mediators encompassed in the activating cytokine group and is applied to all resting cell populations in the model (Janeway et al., 2001). The recruitment rate, ∊r, is likely different for each resting cell population, but we make the assumption of one parameter value for all populations.
The population is assume to be determined by the limited space near the epithelial barrier that can be occupied, which would not increase with the amount of inflammatory cytokines, Ca. This population, therefore, remains constant even under inflammatory conditions.
Upon contact with bacteria, a cell of the or population becomes either an effector dendritic cell (, Equation 13), with the probability νBc, or tolerogenic dendritic cell (, Equation 14) where νBc is the fraction of commensal bacteria that induces an inflammatory phenotype. In a healthy person, this should be negligible and is set to a value of 0. After a period in the lamina propria, corresponding to the migration rate ∊EI, the presenting dendritic cells migrate to the lymph node joining the and populations. Here they can stimulate resting T-cells until they die at a rate of μd.
The terms in equation 13 and in equation 15 represent contact with active natural T-regulatory cells in the effector and inductive sites respectively. Upon contact with active natural T-regulatory cells, effector dendritic cells are rendered anergic, unable to secrete activating cytokine or stimulate resting T-cells (Onishi et al., 2008). We represent this by effectively removing them from the system upon contact with active T-regulatory cells ( and ). kT is the contact rate between antigen presenting cells and T-regulatory cells. This is set to be greater than the contact rates between all other cells, k, due to evidence that natural T-regulatory have a higher affinity for dendritic cells than do conventional T-cells (Onishi et al., 2008).
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
Macrophages
Undifferentiated, resting M0 macrophages (, Equation 17) are only represented in the lamina propria and not the mesenteric lymph node. This is under the assumption that, due to compartmentalization of a typical lymph node, the impact of macrophage-derived cytokines on T-cell differentiation is negligible compared to that of the dendritic cell-derived cytokines. Observations that macrophages participate primarily in plasma B-cell differentiation support this assumption (Junt et al., 2007; Mohr et al., 2009). The population is fed by monocytes from the blood at the rate λm (Equation 18). Similar to the function for immature dendritic cell replenishment (λd, Equation 9), λm is a function that allows replacement of each transferred to one of the activated macrophage pools from an implied, unlimited monocyte pool with a net increase of . Upon contact with bacteria that manages to invade from the lumen, a M0 becomes a M1 macrophage (, Equation 19) or M2 macrophage (, Equation 20) and secretes activating or de-activating cytokine for the period of activation. This is represented by the terms in equation 19 and in equation 21. As mentioned, νBc is the fraction of commensal bacteria that induces an inflammatory phenotype and is set to 0.
Macrophages may switch phenotypes as the cytokine ratio changes in the lamina propria so that M1 switches to M2 with a probability proportional to the Cd/Ca ratio and M2 switches to M1 with a probability proportional to the Ca/Cd ratio. This is represented by the terms and in equations 19 and 20 respectively . The term represents reversion of activated macrophages back to the resting state at a rate of νM0, a process believed to play a role in quelling inflammation once pathogen is eliminated. Though reversion is determined by environmental factors that change dynamically as the immune response progresses (Gordon & Taylor, 2005), we treat this parameter as a constant for the sake of simplification. In the absence of an experimental measurement we initially set νM0 to a value of 0. Neither calibration (discussed below in section 2.3) nor validation (section 2.4) of the model indicated a need to include this mechanism in order to observe characteristic cessation of inflammation. This may be interpreted as a model assumption that the frequency of reversion to an inactive state is negligible.
Macrophage lifespan is also dynamic and may be tissue dependent. We also assume this parameter to be a constant for the sake of simplicity, corresponding to the rate μm.
| (17) |
| (18) |
| (19) |
| (20) |
T-cells in the inductive site
The model includes two resting T-cell populations in the mesenteric lymph node, naive T-cells (Tn, Equation 21) and central memory T-cells (Tc, Equation 22). Naive and central memory T-cells may flow in and out of the lymph node at constant rates λt and μt, but not to the effector site of the lamina propria (Sallusto et al., 2004; Janeway et al., 2001). They may also be recruited by inflammatory factors in the lymph node, represented by the term .
Resting T-cells contact antigen presenting dendritic cells and may be stimulated with a probability, αt or αT, meant to encompass the probability that the antigen presented is recognized by the specific T-cell. This is represented by the terms and , where k is the same cell contact rate as in the effector site. The probability of stimulation of a memory T-cell, αT, is greater than that for a naive T-cell, αt, as memory T-cells have less stringent antigen specificity (Janeway et al., 2001). Upon stimulation, the resting T-cell enters either the active T-helper cell pool (Th, Equation 23) or induced T-regulatory pool (Ti, Equation 24) depending on the dendritic cell phenotype (Iwasaki, 2007). Th secretes activating cytokine and Ti secretes deactivating cytokine. Upon creation in the inductive site, these cells proliferate at a rate of pt. After a 48 hour maturation period, corresponding to the rate ∊IE, the T-cell will migrate to the effector site(Janeway et al., 2001). Note that this rate is applied to each active T-cell population as a whole, which does not allow migration to be specific to recently matured T-cells. Rather, the terms and , taken from equations 23 and 24, apply an exponential distribution of residence times with an average of 48 hours over all active T-cells. This simplification strategy was chosen over the use of a delay term, which would be more biologically accurate, but at the cost of a significantly more complicated set of equations.
The term in equation 22 represents the fraction of active T-cells that become central memory T-cells once de-activated in the effector site. The parameter μT is the rate of de-activation and νT is the fraction that revert to resting state. Roughly 60% of these de-activated T-cells will be central memory T-cells and the rest will go on to be effector memory T-cells (TE), represented in equation 25 and discussed below(Sallusto et al., 2004; Marzo et al., 2005).
| (21) |
| (22) |
| (23) |
| (24) |
T-cells in the effector site
Equation 25 represents the resting effector memory T-cell population in the lamina propria (TE). This is a subset of memory T-cells that only circulate in peripheral tissues distinct from central memory T-cells that circulate among lymphoid tissue. Memory T-cells enter and exit the LP via the blood at rates ∊BE and ∊EB respectively. The rate at which memory T-cells infiltrate the tissue from the blood is assumed to be independent of the current tissue concentration, TE. Once in the tissue, TE is in contact with both presenting macrophages and dendritic cells and may be stimulated with a probability of αT under the assumption that the antigen specificity is generally the same as for central memory T-cells. The term represents the fraction of de-activated T-cells that become effector memory T-cells.
Equations 26 and 27 represent inflammatory T-helper cells () and induced T-regulatory cells () in the lamina propria. A stimulated TE enters one of these two pools depending on the phenotype of antigen presenting cell represented by the terms in equation 26 and in equation 27. Upon stimulation of effector memory T-cells, the resulting active T-cells ( and )proliferate at a lower rate, pT, than those born from naive and central memory T-cells, pt (Geginat et al., 2003). The term and represent infiltration of T-cells activated in the inductive site into the effector site.
| (25) |
| (26) |
| (27) |
Natural T-regulatory cells
Equation 28 describes resting natural T-regulatory cells as they enter and exit the effector site via the blood. As with effector memory T-cells, resting natural T-regulatory cells are assumed to infiltrate the tissue with a rate that is independent of the concentration of cells already in the tissue site. At the infection site, Tr are stimulated by antigen presenting cells of both inflammatory and regulatory phenotypes. This interaction is represented by the term , where we assume a stimulation rate that is the same as other memory T-cells, αT. A stimulated cell then becomes an active natural T-regulatory cell (, Equation 29). cells migrate from the effector site to the inductive site via draining lymph, entering the population (Equation 30). Here they carry out their primary regulatory function by inhibiting effector dendritic cell stimulation of T-cells, represented in equations 13 and 15 (Shevach, 2002; Onishi et al., 2008). While activated, the cell proliferates at a rate of pTr. Calibration of pTr such that the CD4+ T-cell concentration in the lymph node stays within measured ranges in vivo (Haase, 1999) lead to a lower value than for the proliferation rate of conventional T-cells, pt. This decreased proliferation rate is supported by the fact that Tr expresses decreased levels of IL2R compared to helper T-cells (Walker et al., 2003). We assume the rate of deactivation for natural T-regulatory cells is the same for induced T-regulatory cells, μT, as is the fraction that revert back to the resting state as opposed to undergoing apoptosis, νT.
| (28) |
| (29) |
| (30) |
2.2. Simulations
The system of differential equations was solved using the LSODA algorithm in COPASI (Hoops et al., 2006). The system was solved over 3000 time units, where one time unit, t, is approximately 6 hours. During calibration, transition rates were estimated based on this time scale. However, due to uncertainty in the rates, it is best to view the system as a model of qualitative dynamics. We, therefore, do not seek to make any temporal predictions based on model time.
2.3. Sensitivity analysis
Sensitivities of each variable to each parameter of the model was determined in COPASI. For this task COPASI uses metabolic control analysis (MCA), a method developed to carry out sensitivity analysis of metabolic systems. In short, MCA studies the relative control exerted by each step on the system’s variables by applying a perturbation to the step being studied and then measuring the effect on the variable of interest after the system has settled to a new steady state. For a more in depth description please refer to Reder et al.(Reder, 1988).
2.4. Parameter assignment and model calibration
Parameter values for a healthy individual were gathered from literature, where possible, using mouse, pig, and human data (Appendix A). Unknown parameters were approximated with expert knowledge or estimated from a range. In some cases optimization was carried out in COPASI using the particle swarm algorithm.
The model was calibrated to fit specific criteria for gut homeostasis in the absence of foreign bacteria at steady-state (Figure 3A). The criteria included: i) T-cell numbers reflect those measured in lymphoid tissue of healthy individuals. Specifically, concentrations of naive T-cells and memory T-cells are approximately 1.2·108/mL in the lymph node(Haase, 1999) and dendritic cells are 106/mL (Catron et al., 2004). ii) No commensal bacteria is seen in the lamina propria, but the lumen population upholds a regulatory immune cell population. iii) The lumen bacteria stays within a concentration of 1011 – 1012/mL (Artis, 2008). iv) The epithelial cell layer remains unchanged from an initial concentration of 104/mL (Artis, 2008). v) Active and resting natural T-regulatory cells compose approximately 10% of the total CD4+ T-cell population (Asano et al., 1996). vi) The level of deactivating cytokine-secreting cells in the lamina propria are significantly higher than activating cytokine-secreting cell levels (Uhlig et al., 2006). The system was deemed to have converged when the relative change in concentration in a single time step was less than 10−5.
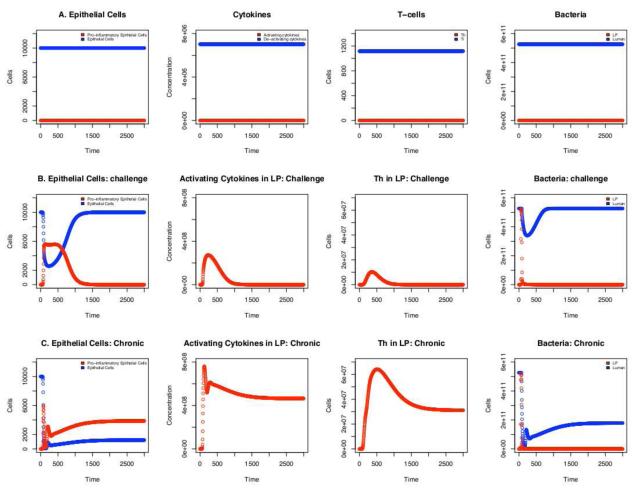
Figure 3.
Timecourse of fluctuations in select populations. A) Homeostasis: In the absence of an inflammatory response to bacteria in the lumen, the epithelial cell barrier remains intact and epithelial cells do not secrete inflammatory factors. Deactivating cytokines and induced T-regulatory cells are maintained at a basal level while activating cytokines and inflammatory T-helper cells are absent. Bacteria is compartmentalized to the lumen with no detectable invasion of the lamina propria (LP). B) Dysentery: The extended model that includes pathogenic bacteria that triggers an inflammatory response in macrophages and dendritic cells, epithelial cell erosion is seen as inflammatory markers rise in conjunction with translocation of bacteria into the LP. C) Chronic Inflammation: When a small fraction (0.0001) of bacteria in the lumen triggers an inflammatory response in macrophages and dendritic cells, the total epithelial cell population remains reduced in conjunction with elevated inflammatory markers and continued migration of bacteria into the lamina propria where it is readily eliminated by immune cells. This is typically seen in cases of inflammatory bowel disease.
A more detailed explanation of parameter assignment and range estimation is given in Appendix A.
2.5. Validation
To validate the model, we sought to replicate cell dynamics observed in pigs experimentally infected with pathogenic bacteria strains (Hontecillas et al., 2005; Jonasson et al., 2006). To do this we added a pathogenic bacterial population (Bf), recognized by antigen presenting cells as foreign, to the model. In this extended model, the Bf population induces inflammatory phenotypes in resting dendritic cells and macrophages upon contact and act competitively with commensal bacteria. Specifically, the extension involves slight modifications to equations for resting macrophages (, Equation 17) and activated macrophages ( and , Equations 19 and 21) by replacing the terms in equation 17, in equation 19, and in equation 20 with , , and respectivley. represents the concentration of foreign bacteria in the effector site. The terms assume that all contact events with foregin bacteria lead to an inflammatory M1 phenotype and those with commensal bacteria lead to a tolerogenic M2 phenotype. With these same assumptions applied to dendritic cells the terms in equations 9 and 10, in equations 11 and 12, in equation 13, and in equation 14 are replaced with the terms , , and respectivley. Equations 31 and 32 describe interdependent dynamics of the competing bacterial populations. All parameters are considered identical between the two populations, where γ is a competition coefficient. The full equations of these populations directly affected by the introduction of foreign bacteria are given in Supplementary Materials.
| (31) |
| (32) |
The model was validated by adding the presence of foreign bacteria with these modification and initiating simulations with a Bf concentration of 108/mL in the lumen. Under these conditions, the model produced the same qualitative population dynamics as those in the animal studies carried out by Hontecillas et al. (Hontecillas et al., 2005) and Jonas-son et al. (Jonasson et al., 2006) (Figure 3B). Specifically; i) The most significant cell population increase is among inflammatory phenotypes. ii) Inflammation coincided with a depletion of the epithelial cell layer by 2%. iii) Inflammation and epithelial cell depletion coincided with an increased rate of bacterial migration across the epithelial barrier and accumulation in the lamina propria. iv) Inflammation coincided with an increased rate of M2 macrophages switching to M1 v) Recovery was observed coinciding with reversion of all macrophages back to M2, return of the epithelial cell concentration to the basal level, reduction of inflammatory cell types to near homeostatic levels (concentration of < 1 in the case of cells and < 10 in the case of activating cytokines), and elimination of bacteria from the lamina propria.
2.6. IBD model
To induce IBD in the model of healthy mucosa, we changed the parameter νBc, the rate of M0 or transition to De or M1 upon contact with bacteria of the microflora, from 0 to increasingly positive values. IBD was defined as a new steady-state in which there is an increased level of inflammatory markers including activating cytokines (Ca), T-helper cells (Th), M1 macrophages (M1), and effector dendritic cells(De) in conjunction with decreased epithelial cell concentration (E+Ep), representing chronic lesion presence. A positive value for νBc could represent a number of plausible causes of IBD such as: i) Impairment of the regulatory pathway in antigen-presenting cells where the default is the inflammatory pathway; ii) Dysfunction of specific pattern recognition receptors leading to recognition of residential bacteria as foreign; iii) Change in composition of the residential bacterial population, i.e. microflora imbalance. The latter is associated with IBD in the literature (Ott et al., 2004; Swidsinski et al., 2002).
3. Results
3.1. Impairment of antigen presenting cell tolerance pathways causes IBD
Commensal bacteria should not induce inflammatory phenotypes in dendritic cells or macrophages, De or M1, in a healthy individual (Strober et al., 2002). For this reason, in the healthy model we set the rate of this occurrence, νBc, to 0 causing all immature dendritic cells and resting macrophages to enter the tolerogenic dendritic cell and M2 macrophage pools upon stimulation by bacteria of the microflora, assumed to be commensal. To represent a dysfunctional regulatory pathway or a microfloral imbalance, we set νBc to values greater than 0 and observed cell dynamics. When νBc = 0.0001 a new steady-state is reached in which populations of inflammatory cells and activating cytokine remain above homeostatic levels and epithelial cell concentration remains roughly 50% reduced even after elimination of bacteria from the lamina propria compartment. These are characteristics of chronic inflammation as observed in IBD. With this model of IBD, we next sought to determine the mechanism by which the inflammatory cytokine population was held above homeostatic levels, thereby increasing epithelial erosion.
3.2. Significance of macrophage plasticity in chronic inflammation triggered by the gut microflora
Macrophage phenotypes are highly plastic. When IL-10 is present, inflammatory M1 macrophages may differentiate to regulatory M2 macrophages. Similarly, in the presence of IFN-γ and TNF-α, a M2 may convert to a M1 (Gordon & Taylor, 2005). To capture this behavior in our model we set the rate at which activating cytokine-secreting M1 switches to deactivating cytokine-secreting M2, ν12, and the rate of M2 to M1, ν21, as functions of cytokine levels shown here in equations 33 and 34:
| (33) |
| (34) |
Cd is the concentration of deactivating cytokines and Ca the concentration of activating cytokines in the location compartment. The parameter ∊ controls the threshold ratios of cytokine concentrations at which the macrophage population switches from one phenotype to the other. Specifically, the lower the value of ∊, the higher the Cd/Ca ratio must be to induce the M1 to M2 switch. The parameter yν determines the change in the rate at which the phenotype transition occurs with respect to the changing environmental cytokine ratio by determining the gradient at which the function moves between 0 and 1. Both ∊ and yν have values of 1 in the healthy and IBD models. In the IBD model (Figure 4A), sensitivity analysis revealed that all immune cells were more sensitive to these parameters than to any other in the model, with the concentration of M1 being negatively correlated to both, as would be expected. This indicates that the observed cell dynamic, i.e. heightened inflammation, is largely dependent on the switch between M1 and M2. Indeed, mutations that inhibit the activity of the receptor PPARγ, which is involved in induction of M2-associated genes and suppression of M1-associated genes, are significantly linked with clinical IBD (Odegaard et al., 2007; Dubuquoy et al., 2003).
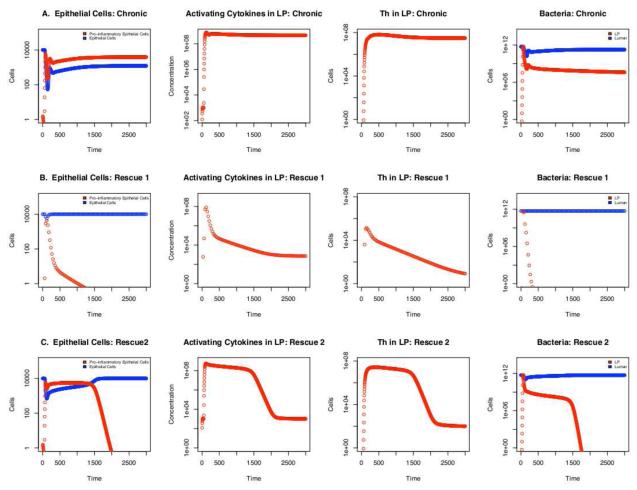
Figure 4.
Timecourse of fluctuations in select populations. The y-axis is in log scale to better compare population levels under chronic inflammation and rescue scenarios. A) Chronic inflammatory conditions of νBc = 0.0001, ∊ = 1, and νM0 = 0. B) When the following parameter values are applied; νBc = 0.0001, ∊ = 2, and νM0 = 0 requiring a lower de-activating cytokine concentration to induce transition from M1 to M2 in activated macrophages. This may also represent a higher activating cytokine threshold for inducing the opposite transition of M2 to M1. C) The following parameter values are applied; νBc = 0.0001, ∊ = 1, and νM0 = 0.015 representing a system in which activated macrophages may become deactivated. As the value νM0 increases this recovery period is shortened (not shown).
When ∊ was increased from 1 to 2, the system showed rapid epithelial cell recovery coupled with severe reduction in inflammatory markers, Ca and Th, in the LP (Figure 4B). This change represents a decreased sensitivity of the M2 population to pro-inflammatory cytokines in terms of induction of M1-associated genes and suppression of genes conferring its regulatory capacities. A very similar pattern was seen when yν was increased to 2 (data not shown), which could represent a quicker switch back to M2 as inflammatory IFN-γ and TNF-α levels decrease with antigen elimination. We choose to focus on the effects of the parameter ∊, however, as it is directly translatable to the biological system in terms of cytokine presence and receptor availability, factors readily manipulated in a laboratory setting. Under these rescue conditions, activating cytokine and Th levels remain above homeostatic levels in conjunction with De (not shown) keeping the bacterial population at 0 in the lamina propria compartment. Yet, in the absence of M1, the inflammatory response shown in Figure 4B is not coupled with immunopathogenesis, i.e. the total epithelial cell concentration is maintained at the homeostatic level eventhough effector cell concentrations are higher than homeostatic levels and bacteria is successfully eliminated from the LP. The model, therefore, indicates that removal of M1 from the system should allow epithelial cell recovery even in the face of an effective inflammatory response to residential bacteria.
Following this hypothesis, we also attempted to rescue the system from IBD by allowing activated macrophages to return to a resting state. Activated macrophages are known to revert to their undifferentiated precursor, M0, in the absence of specific chemokines, cytokines and survival factors (e.g., IL-12, IL-6, TNF-α , Monocyte Chemotactic Protein-1, and Macrophage Colony-Stimulating Factor) secreted during the immune response to bacteria (Yona & Gordon, 2007). In our initial, healthy model this reversion rate, νM0, is set to 0 as an experimental measurement was not available and the function was not necessary for recovery from severe dysentery in the validation step (section 2.4). In the IBD model, setting this reversion rate to > 0.015 allows eventual recovery over a period of time inversely proportional to the parameter value (Figure 4C).
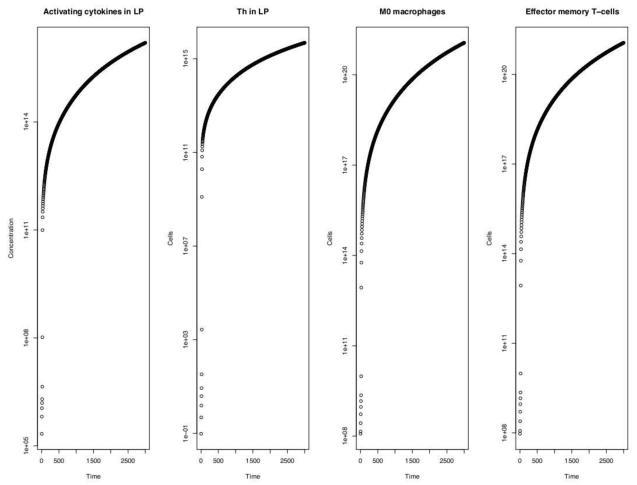
3.3. M1 is a key component of the inflammatory loop including Th and immune cell precursors in the lamina propria
In the case of relatively large values of νBc (> 0.01), the cell populations that showed growth over time proportional to the activating cytokine population were the helper T-cells (Th) specifically in the lamina propria location, M1 macrophages (M1), resting macrophages (M0), and effector memory T-cells (TE), also in the lamina propria (Figure 5). This indicates that the mechanism of M1 driven hyper-inflammation and immunopathogenesis lies in the particular positive feedback loop for activating cytokine production that involves its secretion by helper T-cells in the lamina propria (highlighted in Figure 2). Specifically, as Ca levels in the lamina propria rise via secretion by Th and M1, there is an increased recruitment of effector memory T-cells (TE) and M0. The additional M0 cells generate M1 via microfloral bacteria stimulation which leads to greater Th creation from the increasing TE pool. Both newly created Th and M1 cells secrete more activating cytokines, thereby closing the loop.
Figure5.
Timecourse of cell populations in the system that grow in proportion to the activating cytokine levels (far left) when νBc ≥ 0.01. This indicates their critical roles in the positive feedback pathway described in section 3.3 of the main text.
We tested the effect of disrupting this loop under two scenarios. In the first we reduced the rate, ∊r, at which TE and M0 cells are recruited by activating cytokines by a factor of 10. This represents integrin inhibition, a proposed treatment of inflammation disorders (Rutgeerts et al., 2009). Simulations showed that reduced recruitment actually exacerbated immunopathogenesis with a 29% reduction in the already-depleted epithelial layer and a 17% increase in activating cytokine levels in the LP. Though a lower ∊r intuitively leads to fewer inflammatory cell precursors at the site of the infection initially and, therefore, reduced Ca levels, it also leads to a delay in an effective immune response allowing the small amount of bacteria that is in the LP to proliferate to a larger number ultimately eliciting inflammatory responses from a greater number of cells as they eventually enter the tissue at a slower rate.
In the second scenario, we removed the ability of antigen presenting cells to stimulate memory T-cells by setting the rate of stimulation upon contact, αT, to 0. This removed ability of macrophages and dendritic cells of either phenotype to stimulate memory T-cells (Equations 22 and 25). Removal of this mechanism did little to ameliorate chronic inflammation. Though Ca levels were reduced by 33%, the epithelial layer remained depleted by 40% from homeostatic levels. However, when we removed M1 and De-mediated stimulation, specifically (i.e. leaving Dt and M2-mediated stimulation intact), we see complete return to a healthy state in which Ca levels are reduced by > 99.9%, bacteria is completely removed from the LP, and the epithelial cell concentration is completely restored. The reason for this is that removal of memory T-cell simulation by both phenotypes resulted not only in reduced Th and activating cytokine levels, but also reduced Ti and deactivating cytokine levels. This reduction in the deactivating cytokine concentration in proportion to that in the activating cytokine concentration returns a Ca/Cd ratio that still upholds a pathogenic value for the M2 to M1 switch rate, ν21. Removal specifically of M1 and De-mediated stimulation, however, only leads to a reduction in Th and, subsequently, Ca levels lowering the Ca/Cd ratio and reducing the rate of the M2 to M1 transition. Hence, inhibition of memory T-cell stimulation may be an effective intervention of hyperinflammation and immunopathogenesis, but only if it is specifically targeted to M1 and De-mediated stimulation while leaving M2 and Dt capable of associating with and stimulating memory T-cells.
3.4. Tr mechanisms were ineffective in rescuing the system from IBD
To assess the overall impact of natural T-regulatory cells we eliminated them altogether from the healthy system and found that recovery from colitis was still seen, though it was delayed. This indicates that the mechanisms of Tr activity included in the model, e.g. secretion of IL-10 and TGF-β and removal of effector dendritic cells, would not be sufficient to account for its ability to inhibit acute inflammation, in the case of dysentery, or allow recovery from chronic colitis, as seen in animal studies (Riley et al., 2009).
4. Conclusions
Our objective is to understand the critical interactions between the two competing pathways, inflammation and tolerance, that uphold gut homeostasis in healthy individuals. We focus on those mechanisms of inflammatory and regulatory pathway crosstalk that mediate IBD-like chronic inflammation. Though the underlying cell interactions have been characterized in vitro, their net effects in the context of complex immunological networks of dynamic populations is still unknown. In this study we took a systems approach to investigate consequences of these interactions in a simulated in vivo context of the gut mucosa comprised of the lumen, lamina propria, and mesenteric lymph node.
We simulated IBD caused by an inflammatory response to microfloral bacteria. Analysis identified M1 as a main culprit of unregulated inflammation and key target for IBD therapy, specifically by intervention at points of macrophage plasticity. This conclusion is supported by previous predictions that the M2 to M1 switch has a significant influence on tuberculosis pathogenesis in the lungs (Day et al., 2009). The result advises further research into rescue strategies that remove M1 from the site of infection by either i) increasing its potential to switch to M2 or ii) increasing the rate of reversion (for M1 and M2 alike) to a resting state.
PPARγ is a cell receptor expressed on T-cells, macrophages, dendritic cells, and epithelial cells that has been implicated in IBD prevention (Spiegelman, 1998; Mansen et al., 1996). Specifically, clinical observations yielded a significant association between deleterious PPARγ mutations and Crohn’s disease and the receptor was down-regulated in colons of patients with ulcerative colitis (Sugawara et al., 2005; Dubuquoy et al., 2003) . In addition, various studies have shown that PPARγ ligands are able to ameliorate acute inflammation, particularly in the colon (Katayama et al., 2003; Bassaganya-Riera et al., 2004). Though activation of this receptor represents a promising new therapy, the key mechanism of its anti-inflammatory effect is unknown. PPARγ is a receptor of endogenous lipids [i.e., prostaglandins or hydroxy-containing PUFA] that are produced during various homoestatic processes and has been shown to participate in a number of anti-inflammatory mechanisms including induction of anergy in inflammatory T-cells, enhanced regulatory T cell responses, suppression of inflammatory responses by macrophages, differentiation of macrophages towards an M2 phenotype, and suppression of T-cell effector responses (Odegaard et al., 2007; Lytle et al., 2005; Hontecillas & Bassaganya-Riera, 2007; Wohlfert et al., 2007; Odegaard et al., 2007; Odegaard et al., 2008; Mokdad et al., 2001; Desvergne & Wahli, 1999; Nesto et al., 2003). This work suggests that the specific mechanism underlying the PPARγ association with IBD prevention is PPARγ-mediated differentiation of M1 macrophages into M2 macrophages in the presence of anti-inflammatory cytokines IL-4, IL-13, IL-10, and TGF-β. Studies are underway to examine whether rescue from experimentally induced IBD can be achieved by treatment of mice with PPARγ ligands and subsequent differentiation of macrophages into an M2 phenotype.
Simulation results also indicate that increasing the rate at which activated macrophages revert back to a resting state can quell a chronic inflammatory response. Indeed, it is plausible that macrophage de-activation is a key function by which IL-10 is able to suppress IBD experimentally (Lang et al., 2002; Strober et al., 2002). The model, therefore, predicts that depriving the system of chemokines and cytokines that allow macrophages (both M1 and M2 alike) to stay activated should allow recovery from inflammation. This prediction may be tested by experiments in which mice experiencing chronic colitis are rescued by administration of chemokine inhibitors through various techniques (i.e. competitive inhibition with receptor antibodies, knockout mice, siRNA experiments), removing their ability to prolong the activation state.
In our model, active Tr effector activity included secretion of de-activating cytokines, meant to represent characteristic secretion of IL-10, and increased affinity for antigen-presenting cells coupled with an ability to deactivate effector dendritic cells upon contact (Onishi et al., 2008). Although activated CD25+ natural T-regulatory cells are associated with rescue from colitis, presence of Tr did not have an impact on altering the course of immunopathogenesis or recovery in our system. It did, however, affect the length of the recovery period. This surprising outcome could be explained by the fact that induced T-regulatory cells are the main effectors behind these in vivo observations. Alternatively, the most effective mechanism by which Tr prevents, or ameliorates, colitis may not have been correctly defined in this version of the model. These include other contact-dependent actions such as inhibition of IL-12 secretion and induction of cytolysis in inflammatory cells (Shevach, 2002). Future versions of the model will also include alternative routes of activated natural T-regulatory cell traffic, specifically stimulation of resting T-cells in the inductive site followed by migration to the effector site.
Previous models have demonstrated immune regulation of inflammation as a factor in clinical effects of specific bacteria such as H. pylori and tuberculosis (Wigginton & Kirschner, 2001; Blaser & Kirschner, 1999; Day et al., 2009). In this study we present an abstract model of the gut mucosal immune system that incorporates regulatory mechanisms of both adaptive and innate immunity, multi-location migration of cells, and cross talk between antigen presenting cells and T-cells. The goal was to specify the immune cells that are upholding a pathogenic immune response to a non-pathogenic bacterial population. Some drawbacks to the mathematical approach taken here is that articulating the system in to ordinary differential equations (ODEs) can only capture the dynamics of each cell population as a whole assuming deterministic, average behavior by each individual cell. However, biological systems are known to act stochastically due to attributes, such as cytokine secretion and association time with stimulating factors, that vary widely across individual cells belonging to the same population. Additionally, the randomness introduced by cell movement leads to non-uniform distribution across single tissue sites. Because of ODE-induced assumptions of determinism and homogeneity, that are surely violated by the system in reality, dynamics predicted by an ODE model may not accurately reflect those seen in nature. In cases where such randomness, introduced by individual behavior, is believed to significantly affect the outcome of the system another approach, such as individual or agent based models (ABM), may be more appropriate (Bauer A., 2009).
While modeling approaches cannot replace traditional experimentation, they provide a conceptual framework for organizing existing data and focusing experiments through formulation of novel hypotheses. Thus, computer models of the immune system become necessary tools for tracing data gathered and mechanisms elucidated at the molecular and cellular levels back into an in vivo setting. The high-level model presented here is general enough to apply to other relevant mucosal sites including lungs, genital tract, and nasal passages with minor modifications and is useful for identifying the critical motifs of complex mucosal immunity that warrant more detailed investigation.
Future work will include a higher resolution exploration of the mechanisms identified here including specific cytokine populations and strain-specific responses to commensal and pathogenic bacteria by immune cells in the gut. In addition, further estimation and calibration carried out in COPASI with this model will be used to develop an ABM counterpart, the ENteric Immunity SImulator (ENISI). Similar experiments carried out with ENISI will illuminate the effect of allowing individual randomness on the behavior of the system as a whole.
Supplementary Material
5. Acknowledgments
We thank our external collaborators and members of the Network Dynamics and Simulation Science Laboratory( NDSSL ) for their suggestions and comments. This work has been supported by NIH-NIGMS MIDAS project 5 U01 GM070694-05 and NIH MIDAS project 2U01GM070694-7.
6. Appendix A: Parameters
Table A.1 lists the values for parameters. When possible, constant values were assigned according to experimental data cited in the References column. For transition rates such as death, de-activation, and migration rates, measurements from the literature were in the form of an average lifespan or dwell time for an individual cell type in a particular location. In order to avoid introducing the complication of delay-differential equations, we used the common strategy of modeling cell death and movement as affecting a fixed proportion of cells in each time interval, resulting in an exponential distribution of lifetimes with the experimentally observed mean, x, or a half-life of x ln 2.
In the case where measurement for a parameter was not found in the literature, the value was estimated from a range arbitrarily chosen or reasoned such that population dynamics fit the criteria for homeostasis listed in section 2.4 of the main text.
The unknown parameters ∊BE and ∊EB, representing the rate at which resting T-cells enter and exit the lamina propria, were formally optimized from the arbitrary range of 10−12 – 100. This was done by taking the ordinary least squares (OLS) estimate that minimized the net change in memory T-cell concentration before and after an inflammatory response. The OLS estimate was found with the particle swarm algorithm (Clerc & Kennedy, 2002) in COPASI.
‘Estimation’ in the Reference column indicates parameters estimated from a range where formal OLS analysis was not deemed necessary. For example, λc, the secretion rate assigned to both activating and de-activating cytokines, was not possible to gather from the literature as each group represents numerous cytokines that are secreted at different rates in reality. In fact, even secretion of a single type of cytokine is highly variable among individual cells of the same population. Acknowledging this fact, we sought to merely make the amount of activating (Ca) and de-activating cytokine (Cd) populations proportional to the concentrations of the cells that produce them. We initially assigned λc an arbitrary value of 0.25 per 6 hours corresponding to 1 per day. The cytokine degradation rate, μc, was then assigned the value of 0.075 for an average lingering period of 3 days in the extracellular environment. These values yielded the desired dynamics and sensitivity analysis showed them to not be highly influential on the system. Hence, their values were not modified. The same challenge was met in determining the value for ∊r, the rate of resting immune cell recruitment by Ca. This is also an artifical parameter given that, in reality, each cell type is recruited by different cytokines grouped in the Ca population at different rates. ∊r was initially assigned a value of 1 and then increased by a factor of 10 until we observed complete elimination of bacteria from the LP.
The parameters y∊ and q of the bacterial migration function, ∊LE, were initially set to 1. y∊ was then increased by 1 and q decreased by a factor of 10 until bacterial migration to the LP was detected in conjunction with inflammatory conditions, and E + Ep = 5.1 · 103/mL, yet not upon recovery, Ca < 10/mL and E + E = 104/mL.
As explained in the main text, the rate of activated macrophage reversion to a resting state, νM0, is set to 0. This is because a value could not be found in the literature as the actual rate is based on numerous chemical factors not included in the model. A value of 0 resulted in experimentally predicted inflammation cessation in the validation step. For this reason we did not feel justified in applying an arbitrarily positive value to this parameter.
The bacterial competition coefficient, γ, was assigned a range of 10−15 – 10−10 allowing the term to evaluate to 0.001 – 100 in equation 6 under the initial conditions of concentration being 1012/mL. The value 2 · 10−12 was then chosen as the maximum value that resulted in noticeable depletion of the foreign bacterial population, starting at a concentration of 108/mL, in the presence of commensal bacteria (described in Equations 31 and 32), but without complete decimation in absence of immune cells.
In other cases we were able to take a more analytical approach to determining parameter ranges based on the dynamics desired. For example, the chosen range for the rate at which epithelial cells transition to pro-inflammatory epithelial cells, νEC, was based on the fact that for recovery to be seen following the inflammation-driven elimination of pathogenic bacteria, the normal epithelial cell population could not be lowered to 0, inducing the constraint in equations 7 and 8. We predicted that levels should reach a peak population on the order of 108, the level of T-helper cells measured in tissue (Haase, 1999; Hontecillas et al., 2005). Given that E = 104/mL and , approximately, at their peak concentrations, 10−8 was chosen as the maximum value for νEC. For this reason it was assigned the range 10−8 – 10−10. The value 5 · 10−9 resulted in the characteristic recovery of epithelial cells after a transient decline coinciding with inflammation as seen in Figure 3B. The constraint for the rate of epithelial cell death by activating cytokines, μCE in equation 7, is that it must be less than νCE. For this reason it was assigned the value of 5 · 10−10.
‘Approximated’ indicates that values were not estimated from a range nor based on values found in the literature directly, but were reasoned based on knowledge of the system.
For example, the cell contact rates k and kL were initially assigned the value 10−12 under the assumption that each cell has an approximate volume of 1μm3. The parameter k was then estimated from this base value by increasing its value to 10−11, which yielded complete bacterial elimination from the lamina propria when coupled with the parameter ∊r=100. As mentioned in the main text, the rate of contact between natural T-regulatory cells and antigen presenting cells, kT, was then assigned to be greater than k following the observation that T-regulatory cells have higher affinity for dendritic cells than conventional T-cells (Onishi et al., 2008).
The birth rate of non-specific bacteria, λb, is based on the assumption that bacteria would double in the lumen every 6-12 hours in anaerobic conditions such as exist in the colon. The death rate μb was then calculated to uphold a population of approximately 1012/mL based on the accepted concentration of bacteria in the colonic lumen (Artis, 2008).
The death rate of macrophages can be tissue specific and depend on the chemical environment. We assumed this lifespan to be 1 month corresponding to the parameter μm.
The parameter νT, the fraction of T-cells that become memory T-cells, was estimated to be approximately 1/500 based on the observation that one T-cell proliferates to approximately 500 clones (Geginat et al., 2003) and atleast one of those clones will be a memory T-cell.
The fraction of inflammation-inducing bacteria of the microflora, νBc, was assumed to be 0 under the assumption that a healthy individual has only a negligible quantity of pathogenic bacteria in the colon at any given time.
The parameters λm, λd, λdl, ∊LE, ν12, and ν21 are not constant but rather are determined by their corresponding equations.
The unit t refers to time units, which was approximated to 6 hours for parameter assignment. The units D, M, T, and C refer to active dendritic cells, macrophages, T-cells, and cytokines irrespective of their inflammatory/regulatory status. B refers to bacteria.
Table 1. A.1.
Parameter values
| Symbol | Description | Value | Reference |
|---|---|---|---|
| Birth/death | |||
| λt | inflow rate of naive T-cells | 3 · 107 cells · t−1 | (Janeway et al., 2001) |
| λc | rate of cytokine production | 0:25cells−1 · t−1 | estimated |
| λm | rate of M0 creation | ||
| λd | rate of creation | ||
| λdl | renewal rate of | ||
| λE | birth rate of epithelial cells | 2 · E−1 | (Kelly et al., 2004) |
| λb | birth rate of bacteria | 2 · B−1 | approximated |
| μt | removal rate of Tn | 0.25 ·t−1 | (Janeway et al., 2001) |
| μT | rate of active T-cell deactivation | 0.05 · t−1 | (Janeway et al., 2001) |
| μc | rate of cytokine degradation | 0.075 · t−1 | estimated |
| μm | death rate of macrophages | 0.0075 · t−1 | approximated |
| μdi | death rate of immature dendritic cells | 0.0006 · t−1 | (Kamath et al., 2002) |
| μd | dendritic cell death rate | 0.12 · t−1 | (Lanzavecchia & Sal- lusto, 2001) |
| μE | epithelial cell death rate | 0.5 · t−1 | (Kelly et al., 2004) |
| μce | death rate, E by inflammatory factors | 5 · 10−10C−1 · t−1 | estimated |
| μb | death rate, bacteria | 1 · t−1 | (Artis, 2008) |
| pt | T-cell proliferation rate from Tn, TC | 0.122 · t−1 | (Swerdlin et al., 2008) |
| pT | T-cell proliferation rate from TE | 0.03 · t−1 | (Sallusto et al., 2004) |
| pTr | proliferation rate, Tr | 0.05 · t−1 | (Janeway et al., 2001) |
| ϕE | crowding co-efficient, epithelial cells | 0.00015 | (Artis, 2008) |
| ϕb | crowding co-efficient, bacterial cells | 1.9−12 | (Artis, 2008) |
| γ | competition coefficient, bacteria | 2−12 | estimated |
| Migration | |||
| ∊r | recruitment rate | 100cells · C−1 · t−1 | estimated |
| ∊IE | cell migration rate, inductive site to effector site |
0.125 · t−1 | (Janeway et al., 2001) |
| ∊EI | cell migration rate, effector site to in- ductive site |
0.25 · t−1 | (von Andrian & Mempel, 2003) |
| ∊LE | bacteria migration rate, lumen to ef- fector site |
||
| y∊ | parameter of ∊LE | 4 | estimated |
| q | parameter of ∊LE | 0.0001 | estimated |
| ∊BE | inflow rate, blood to effector site | 0.025 · t−1 | optimized |
| ∊EB | outflow rate, effector site to blood | 10−10 · t−1 | optimized |
| Contact/interactions | |||
| αt | rate of naive T-cell stimulation by dendritic cells |
10−6 · D−1 | (Janeway et al., 2001) |
| αT | rate of memory T-cell stimulation | 10−4 (D+M)−1 | (Janeway et al., 2001) |
| νT | fraction of active T-cells that become memory T-cells |
0.002 · T−1 1 |
approximated |
| νBc | fraction of Br that induce inflamma- tory response |
0 · B−1 | approximated |
| νM0 | rate of M1 or M2 reversion to Mo | 0 · M−1t−1 | estimated |
| ν12 | rate that M1 switches to M2 | ||
| ν21 | rate that M2 switches to M1 | ||
| νEC | rate that E switch Ep | ||
| k | rate of contact between individuals | 10−11 cells · 1−12 | estimated |
| kL | rate of contact between individuals specifically in the lumen |
10−12 cells · 1−12 | approximated |
| kT | rate of contact between Tr and anti- gen presenting cells |
10−10 cells · 1−10 | approximated |
Table 2. A.2.
Population levels in homeostasis
| Symbol | Description | Initial concentration |
|---|---|---|
| Inductive site | ||
| Tn | Naive CD4+ T-cells | 1.2 · 108(Haase, 1999) |
| TC | CD4+ Central Memory T-cells | 1.2 · 108 |
| Active CD4+ T helper cells | 0 | |
| Induced T regulatory cells | 177 | |
| Active natural T regulatory cells | 63 | |
| Activating cytokines | 0 | |
| Deactivating cytokines | 1.6218 · 107 | |
| Effector dendritic cells | 0 | |
| Tolerogenic dendritic cells | 4.39 · 106(Catron et al., 2004) | |
| Anergic dendritic cells | 0 | |
| Effector site | ||
| TE | CD4+ Effector T-cells | 9.3 · 107 |
| Active CD4+ T helper cells | 0 | |
| Induced T regulatory cells | 1117.25 | |
| Active natural T regulatory cells | 3 | |
| Resting natural T regulatory cells | 2.99 · 107 | |
| Activating cytokines | 0 | |
| Deactivating cytokines | 7.02 · 106 | |
| Undifferentiated macrophages | 1.2 · 108 | |
| Activating macrophages | 0 | |
| Deactivating macrophages | 0 | |
| Immature dendritic cells | 1.2 · 108(Hogue et al., 2008) | |
| Effector dendritic cells | 0 | |
| Tolerogenic dendritic cells | 2.105 · 106 | |
| E | Epithelial cells | 104(Kelly et al., 2004) |
| Ep | Pro-inflammatory epithelial cell | 0 |
| Commensal bacteria | 0 | |
| Foreign bacteria (Non-commensal) | 0 | |
| Lumen | ||
| Commensal bacteria | 5.26 · 1011(Artis, 2008) | |
| Foreign bacteria (Non-commensal) | 5.26 · 1011(Artis, 2008) | |
| Immature dendritic cells that extend to the lumen | 1 · 106 | |
7. Appendix B: Variable concentrations in homeostasis
Table A.2 lists the concentrations of variables in steady state, representing homeostasis prior to addition of pathogenic bacteria, as in the validation step, or any changes in the νBc parameter. Included are references to experimental measurements in agreement with the steady-state values. The steady-state was obtained by setting initial values of all active, inflammatory cells and activating cytokines to 0 and regulatory cell types in the lamina propria to 0.1. Resting cells were assigned initial values reflecting those found in the literature. Specifically, the effector memory T-cell concentration was intially 5.7 · 107, resting natural T-regulatory cell concentration was 9.3 · 106, and that of residential bacteria was set to 1010. The immature dendritic cell population was assigned an initial concentration of 1.2 · 108, a value taken from a previously published model of dendritic cell activation and migration (Hogue et al., 2008). We then assumed approximately the same concentration for resting macrophages. Assumptions and approximations used in calculating target concentrations from patient data were that the average body contains 700g of lymphoid tissue, an approximation first used by Haase et al. (Haase, 1999), that 1g of tissue=1mL and 1mL of tissue=1cm3. All concentrations are in units of mL−1
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Artis D. Epithelial-cell recognition of commensal bacteria and maintenance of immune homeostasis in the gut. Nat Rev Immunol. 2008;8(6):411–20. doi: 10.1038/nri2316. [DOI] [PubMed] [Google Scholar]
- Asano M, Toda M, Sakaguchi N, Sakaguchi S. Autoimmune disease as a consequence of developmental abnormality of a t cell subpopulation. Journal of Experimental Medicine. 1996;184(2):387–396. doi: 10.1084/jem.184.2.387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asseman C, Mauze S, Leach MW, Coffman RL, Powrie F. An essential role for interleukin 10 in the function of regulatory t cells that inhibit intestinal inflammation. J Exp Med. 1999;190(7):995–1004. doi: 10.1084/jem.190.7.995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barba G, Rebouissoux L, Le Bail B, Lamireau T. [recurrent pancreatitis revealing crohn’s disease] Arch Pediatr. 2002;9(10):1053–5. doi: 10.1016/s0929-693x(02)00054-4. [DOI] [PubMed] [Google Scholar]
- Bassaganya-Riera J, Reynolds K, Martino-Catt S, Cui Y, Hennighausen L, Gonzalez F, Rohrer J, Benninghoff AU, Hontecillas R. Activation of ppar gamma and delta by conjugated linoleic acid mediates protection from experimental inflammatory bowel disease. Gastroenterology. 2004;127(3):777–91. doi: 10.1053/j.gastro.2004.06.049. [DOI] [PubMed] [Google Scholar]
- Bauer A, Beauchemin C, P. A. Agent-based modeling in host-pathogen systems: the successes and challenges. Information Sciences. 2009;179:1379–1389. doi: 10.1016/j.ins.2008.11.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaser MJ, Kirschner D. Dynamics of helicobacter pylori colonization in relation to the host response. Proc Natl Acad Sci U S A. 1999;96(15):8359–64. doi: 10.1073/pnas.96.15.8359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braverman IM. Skin signs of gastrointestinal disease. Gastroenterology. 2003;124(6):1595–614. doi: 10.1016/s0016-5085(03)00327-5. [DOI] [PubMed] [Google Scholar]
- Catron DM, Itano AA, Pape KA, Mueller DL, Jenkins MK. Visualizing the first 50 hr of the primary immune response to a soluble antigen. Immunity. 2004;21(3):341–347. doi: 10.1016/j.immuni.2004.08.007. [DOI] [PubMed] [Google Scholar]
- Cho JH. The genetics and immunopathogenesis of inflammatory bowel disease. Nat Rev Immunol. 2008;8(6):458–66. doi: 10.1038/nri2340. [DOI] [PubMed] [Google Scholar]
- Clerc M, Kennedy J. The particle swarm - explosion, stability, and convergence in a multidimensional complex space. Ieee Transactions on Evolutionary Computation. 2002;6(1):58–73. [Google Scholar]
- Day J, Friedman A, Schlesinger LS. Modeling the immune rheostat of macrophages in the lung in response to infection. Proc Natl Acad Sci U S A. 2009;106(27):11246–51. doi: 10.1073/pnas.0904846106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desvergne B, Wahli W. Peroxisome proliferator-activated receptors: nuclear control of metabolism. Endocr Rev. 1999;20(5):649–88. doi: 10.1210/edrv.20.5.0380. [DOI] [PubMed] [Google Scholar]
- Dubuquoy L, Jansson EA, Deeb S, Rakotobe S, Karoui M, Colombel JF, Auwerx J, Pettersson S, Desreumaux P. Impaired expression of peroxisome proliferator-activated receptor gamma in ulcerative colitis. Gastroenterology. 2003;124(5):1265–76. doi: 10.1016/s0016-5085(03)00271-3. [DOI] [PubMed] [Google Scholar]
- Geginat J, Lanzavecchia A, Sallusto F. Proliferation and differentiation potential of human cd8+ memory t-cell subsets in response to antigen or homeostatic cytokines. Blood. 2003;101(11):4260–6. doi: 10.1182/blood-2002-11-3577. [DOI] [PubMed] [Google Scholar]
- Gordon S, Taylor PR. Monocyte and macrophage heterogeneity. Nat Rev Immunol. 2005;5(12):953–64. doi: 10.1038/nri1733. [DOI] [PubMed] [Google Scholar]
- Haase AT. Population biology of hiv-1 infection: viral and cd4(+) t cell demographics and dynamics in lymphatic tissues. Annual Review of Immunology. 1999;17:625–656. doi: 10.1146/annurev.immunol.17.1.625. [DOI] [PubMed] [Google Scholar]
- Hogue IB, Bajaria SH, Fallert BA, Qin S, Reinhart TA, Kirschner DE. The dual role of dendritic cells in the immune response to human immunodeficiency virus type 1 infection. J Gen Virol. 2008;89(Pt 9):2228–39. doi: 10.1099/vir.0.83600-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hontecillas R, Bassaganya-Riera J. Peroxisome proliferator-activated receptor gamma is required for regulatory cd4+ t cell-mediated protection against colitis. J Immunol. 2007;178(5):2940–9. doi: 10.4049/jimmunol.178.5.2940. [DOI] [PubMed] [Google Scholar]
- Hontecillas R, Bassaganya-Riera J, Wilson J, Hutto DL, Wannemuehler MJ. Cd4+ t-cell responses and distribution at the colonic mucosa during brachyspira hyodysenteriae-induced colitis in pigs. Immunology. 2005;115(1):127–35. doi: 10.1111/j.1365-2567.2005.02124.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoops S, Sahle S, Gauges R, Lee C, Pahle J, Simus N, Singhal M, Xu L, Mendes P, Kummer U. Copasi–a complex pathway simulator. Bioinformatics. 2006;22(24):3067–74. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
- Iwasaki A. Mucosal dendritic cells. Annual Review of Immunology. 2007;25:381–418. doi: 10.1146/annurev.immunol.25.022106.141634. [DOI] [PubMed] [Google Scholar]
- Janeway C, Travers P, Walport M, Shlomchik M. Immunobiology: The immune system in health and disease. 5 edition Garland Publishing; 2001. [Google Scholar]
- Jonasson R, Andersson M, Rasback T, Johannisson A, Jensen-Waern M. Immunological alterations during the clinical and recovery phases of experimental swine dysentery. J Med Microbiol. 2006;55(Pt 7):845–55. doi: 10.1099/jmm.0.46538-0. [DOI] [PubMed] [Google Scholar]
- Junt T, Moseman EA, Iannacone M, Massberg S, Lang PA, Boes M, Fink K, Henrickson SE, Shayakhmetov DM, Di Paolo NC, van Rooijen N, Mempel TR, Whelan SP, von Andrian UH. Subcapsular sinus macrophages in lymph nodes clear lymph-borne viruses and present them to antiviral b cells. Nature. 2007;450(7166):110–4. doi: 10.1038/nature06287. [DOI] [PubMed] [Google Scholar]
- Katayama K, Wada K, Nakajima A, Mizuguchi H, Hayakawa T, Nakagawa S, Kadowaki T, Nagai R, Kamisaki Y, Blumberg RS, Mayumi T. A novel ppar gamma gene therapy to control inflammation associated with inflammatory bowel disease in a murine model. Gastroenterology. 2003;124(5):1315–24. doi: 10.1016/s0016-5085(03)00262-2. [DOI] [PubMed] [Google Scholar]
- Lang R, Rutschman RL, Greaves DR, Murray PJ. Autocrine deactivation of macrophages in transgenic mice constitutively overexpressing il-10 under control of the human cd68 promoter. J Immunol. 2002;168(7):3402–11. doi: 10.4049/jimmunol.168.7.3402. [DOI] [PubMed] [Google Scholar]
- Lytle C, Tod TJ, Vo KT, Lee JW, Atkinson RD, Straus DS. The peroxisome proliferator-activated receptor gamma ligand rosiglitazone delays the onset of inflammatory bowel disease in mice with interleukin 10 deficiency. Inflamm Bowel Dis. 2005;11(3):231–43. doi: 10.1097/01.mib.0000160805.46235.eb. [DOI] [PubMed] [Google Scholar]
- Mansen A, Guardiola-Diaz H, Rafter J, Branting C, Gustafsson JA. Expression of the peroxisome proliferator-activated receptor (ppar) in the mouse colonic mucosa. Biochem Biophys Res Commun. 1996;222(3):844–51. doi: 10.1006/bbrc.1996.0832. [DOI] [PubMed] [Google Scholar]
- Marzo AL, Klonowski KD, Le Bon A, Borrow P, Tough DF, Lefrancois L. Initial t cell frequency dictates memory cd8+ t cell lineage commitment. Nat Immunol. 2005;6(8):793–9. doi: 10.1038/ni1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohr E, Serre K, Manz R, Cunningham A, Khan M, Hardie D, Bird R, MacLennan C. Dendritic cells and monocyte/macropahges that create the il-6/april-rich lymph node microenvironments where plasmabasts mature. Journal of Immunology. 2009 February;182:2113–2123. doi: 10.4049/jimmunol.0802771. [DOI] [PubMed] [Google Scholar]
- Mokdad AH, Ford ES, Bowman BA, Nelson DE, Engelgau MM, Vinicor F, Marks JS. The continuing increase of diabetes in the us. Diabetes Care. 2001;24(2):412. doi: 10.2337/diacare.24.2.412. [DOI] [PubMed] [Google Scholar]
- Nesto RW, Bell D, Bonow RO, Fonseca V, Grundy SM, Horton ES, Le Winter M, Porte D, Semenkovich CF, Smith S, Young LH, Kahn R. Thiazolidinedione use, fluid retention, and congestive heart failure: a consensus statement from the american heart association and american diabetes association. Circulation. 2003 october 7;108(23):2941–8. doi: 10.1161/01.CIR.0000103683.99399.7E. 2003. [DOI] [PubMed] [Google Scholar]
- Odegaard JI, Ricardo-Gonzalez RR, Goforth MH, Morel CR, Subramanian V, Mukundan L, Red Eagle A, Vats D, Brombacher F, Ferrante AW, Chawla A. Macrophage-specific ppargamma controls alternative activation and improves insulin resistance. Nature. 2007;447(7148):1116–20. doi: 10.1038/nature05894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odegaard JI, Ricardo-Gonzalez RR, Red Eagle A, Vats D, Morel CR, Goforth MH, Subramanian V, Mukundan L, Ferrante AW, Chawla A. Alternative m2 activation of kupffer cells by ppardelta ameliorates obesity-induced insulin resistance. Cell Metab. 2008;7(6):496–507. doi: 10.1016/j.cmet.2008.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onishi Y, Fehervari Z, Yamaguchi T, Sakaguchi S. Foxp3(+) natural regulatory t cells preferentially form aggregates on dendritic cells in vitro and actively inhibit their maturation. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(29):10113–10118. doi: 10.1073/pnas.0711106105. 330BB Times Cited:23 Cited References Count:39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ott SJ, Musfeldt M, Wenderoth DF, Hampe J, Brant O, Folsch UR, Timmis KN, Schreiber S. Reduction in diversity of the colonic mucosa associated bacterial microflora in patients with active inflammatory bowel disease. Gut. 2004;53(5):685–93. doi: 10.1136/gut.2003.025403. [DOI] [PMC free article] [PubMed] [Google Scholar]; Ott SJ, Musfeldt M, Wenderoth DF, Hampe J, Brant O, Folsch UR, Timmis KN, Schreiber S. Research Support, Non-U.S. Gov’t England Gut. Gut. 2004 May;53(5):685–93. doi: 10.1136/gut.2003.025403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powrie F, Leach MW, Mauze S, Caddle LB, Coffman RL. Phenotypically distinct subsets of cd4+ t cells induce or protect from chronic intestinal inflammation in c. b-17 scid mice. Int Immunol. 1993;5(11):1461–71. doi: 10.1093/intimm/5.11.1461. [DOI] [PubMed] [Google Scholar]
- Reder C. Metabolic control theory: a structural approach. J Theor Biol. 1988;135(2):175–201. doi: 10.1016/s0022-5193(88)80073-0. [DOI] [PubMed] [Google Scholar]
- Riley JL, June CH, Blazar BR. Human t regulatory cell therapy: take a billion or so and call me in the morning. Immunity. 2009;30(5):656–65. doi: 10.1016/j.immuni.2009.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutgeerts P, Vermeire S, Van Assche G. Biological therapies for inflammatory bowel diseases. Gastroenterology. 2009;136(4):1182–97. doi: 10.1053/j.gastro.2009.02.001. [DOI] [PubMed] [Google Scholar]
- Sallusto F, Geginat J, Lanzavecchia A. Central memory and effector memory t cell subsets: function, generation, and maintenance. Annu Rev Immunol. 2004;22:745–63. doi: 10.1146/annurev.immunol.22.012703.104702. [DOI] [PubMed] [Google Scholar]
- Shevach EM. Cd4+ cd25+ suppressor t cells: more questions than answers. Nat Rev Immunol. 2002;2(6):389–400. doi: 10.1038/nri821. [DOI] [PubMed] [Google Scholar]
- Spiegelman BM. Ppargamma in monocytes: less pain, any gain? Cell. 1998;93(2):153–5. doi: 10.1016/s0092-8674(00)81567-6. [DOI] [PubMed] [Google Scholar]
- Stenson WF. Interleukin-4 hyporesponsiveness in inflammatory bowel disease: immune defect or physiological response? Gastroenterology. 1995;108(1):284–6. doi: 10.1016/0016-5085(95)90034-9. [DOI] [PubMed] [Google Scholar]
- Strober W, Fuss IJ, Blumberg RS. The immunology of mucosal models of inflammation. Annu Rev Immunol. 2002;20:495–549. doi: 10.1146/annurev.immunol.20.100301.064816. [DOI] [PubMed] [Google Scholar]
- Sugawara K, Olson TS, Moskaluk CA, Stevens BK, Hoang S, Kozaiwa K, Cominelli F, Ley KF, McDuffie M. Linkage to peroxisome proliferator-activated receptor-gamma in samp1/yitfc mice and in human crohn’s disease. Gastroenterology. 2005;128(2):351–60. doi: 10.1053/j.gastro.2004.11.001. [DOI] [PubMed] [Google Scholar]
- Swidsinski A, Ladhoff A, Pernthaler A, Swidsinski S, Loening-Baucke V, Ortner M, Weber J, Hoffmann U, Schreiber S, Dietel M, Lochs H. Mucosal flora in inflammatory bowel disease. Gastroenterology. 2002;122(1):44–54. doi: 10.1053/gast.2002.30294. [DOI] [PubMed] [Google Scholar]; Swidsinski Alexander, Ladhoff Axel, Pernthaler Annelie, Swidsinski Sonja, Loening-Baucke Vera, Ortner Marianne, Weber Jutta, Hoffmann Uwe, Schreiber Stefan, Dietel Manfred, Lochs Herbert. United States Gastroenterology. Gastroenterology. 2002 Jan;122(1):44–54. doi: 10.1053/gast.2002.30294. [DOI] [PubMed] [Google Scholar]
- Uhlig HH, Coombes J, Mottet C, Izcue A, Thompson C, Fanger A, Tannapfel A, Fontenot JD, Ramsdell F, Powrie F. Characterization of foxp3(+)cd4(+)cd25(+) and il-10-secreting cd4(+)cd25(+) t cells during cure of colitis. Journal of Immunology. 2006;177(9):5852–5860. doi: 10.4049/jimmunol.177.9.5852. 097VN Times Cited:81 Cited References Count:45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker LS, Chodos A, Eggena M, Dooms H, Abbas AK. Antigen-dependent proliferation of cd4+ cd25+ regulatory t cells in vivo. J Exp Med. 2003;198(2):249–58. doi: 10.1084/jem.20030315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wigginton JE, Kirschner D. A model to predict cell-mediated immune regulatory mechanisms during human infection with mycobacterium tuberculosis. J Immunol. 2001;166(3):1951–67. doi: 10.4049/jimmunol.166.3.1951. [DOI] [PubMed] [Google Scholar]
- Wohlfert EA, Nichols FC, Nevius E, Clark RB. Peroxisome proliferator-activated receptor gamma (ppargamma) and immunoregulation: enhancement of regulatory t cells through ppargamma-dependent and -independent mechanisms. J Immunol. 2007;178(7):4129–35. doi: 10.4049/jimmunol.178.7.4129. [DOI] [PubMed] [Google Scholar]
- Yang R, Han X, Uchiyama T, Watkins SK, Yaguchi A, Delude RL, Fink MP. Il-6 is essential for development of gut barrier dysfunction after hemorrhagic shock and resuscitation in mice. Am J Physiol Gastrointest Liver Physiol. 2003;285(3):G621–9. doi: 10.1152/ajpgi.00177.2003. [DOI] [PubMed] [Google Scholar]
- Yona S, Gordon S. Inflammation: glucocorticoids turn the monocyte switch. Immunol Cell Biol. 2007;85(2):81–2. doi: 10.1038/sj.icb.7100034. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.