Abstract
The glaucomas are a group of relatively common optic neuropathies, in which the pathological loss of retinal ganglion cells causes a progressive loss of sight and associated alterations in the retinal nerve fiber layer and optic nerve head. The diagnosis and management of glaucoma are often dependent on methods of clinical testing that either, 1) identify and quantify patterns of functional visual abnormality, or 2) quantify structural abnormality in the retinal nerve fiber layer, both of which are caused by loss of retinal ganglion cells. Although it is evident that the abnormalities in structure and function should be correlated, propositions to link losses in structure and function in glaucoma have been formulated only recently. The present report describes an attempt to build a model of these linking propositions using data from investigations of the relationships between losses of visual sensitivity and thinning of retinal nerve fiber layer over progressive stages of glaucoma severity. A foundation for the model was laid through the pointwise relationships between visual sensitivities (behavioral perimetry in monkeys with experimental glaucoma) and histological analyses of retinal ganglion cell densities in corresponding retinal locations. The subsequent blocks of the model were constructed from clinical studies of aging in normal human subjects and of clinical glaucoma in patients to provide a direct comparison of the results from standard clinical perimetry and optical coherence tomography. The final formulation is a nonlinear structure-function model that was evaluated by the accuracy and precision of translating visual sensitivities in a region of the visual field to produce a predicted thickness of the retinal nerve fiber layer in the peripapillary sector that corresponded to the region of reduced visual sensitivity. The model was tested on two independent patient populations, with results that confirmed the predictive relationship between the retinal nerve fiber layer thickness and visual sensitivities from clinical perimetry. Thus, the proposed model for linking structure and function in glaucoma has provided information that is important in understanding the results of standard clinical testing and the neuronal losses caused by glaucoma, which may have clinical application for inter-test comparisons of the stage of disease.
Keywords: glaucoma, optical coherence tomography, perimetry, retinal ganglion cells, retinal nerve fiber layer, structure-function
1. Introduction
The glaucomas are a class of optic neuropathies with manifest visual defects, abnormal thinning of the retinal nerve fiber layer (RNFL), and non-physiological cupping of the optic nerve head (ONH), all of which are related to pathological losses of the somas and axons of the retinal ganglion cells (RGCs) (Epstein, 1993; Kwon, et al., 2009; Quigley, 1993; Weinreb, 2004). Both the diagnosis and assessment of progression of glaucoma are often based on a method of ophthalmic testing to identify and quantify the pattern of visual defects (i.e., functional defects) or the thinning of the RNFL (i.e., structural defects) (Greve, 2004; Weinreb and Kaufman, 2009). Because of the unitary cause, structural and functional events should be correlated to the loss of RGCs (Tate, 1985; Anderson and Knighton, 1988; Bartz-Schmidt and Weber, 1993), and several methods of quantifying the amount of RGC loss represented by the loss of axons or visual sensitivity have been proposed (Quigley, et al.,1989; Harwerth, et al., 1999; 2002; 2004; 2007; Kerrigan-Baumrind, et al., 2000; Garway-Heath, et al., 2000; Swanson, et al., 2004; Harwerth and Quigley, 2006; Hood, 2007; Hood and Kardon, 2007; Hood, et al., 2007a, 2007b; Harwerth and Wheat, 2008; Harwerth, et al., 2008), but without consensus on the details. A unified structure-function model would have considerable clinical utilization for inter-test confirmation of standard clinical measures used in the diagnosis and assessment of progression of glaucoma, or permit substitution of one test for another when one of the procedures is not feasible. Specifically, the formalized models could quantify the RGC losses represented by clinical measures and, thereby, establish a relationship to determine whether the amount of structural damage is consistent with measurements of visual function, or vice versa (Weinreb and Kaufman, 2009).
In addition to the obvious clinical application, the derivation of quantitative relationships that link structure and function for normal eyes or eyes with glaucomatous neuropathy is also important for understanding the basic disease process. Specifically, a structure-function linking proposition may provide information bearing on several fundamental questions, such as: 1) What is the nature of tissue remodeling in the RNFL during axonal loss following normal aging or glaucomatous disease? (Varela and Hernandez, 1997; Wang, et al., 2002; Morgan, et al., 2006; Grieshaber, et al., 2007; Hernandez, et al., 2008) 2) Are there separate structure-function links for the various function-specific clinical tests, such as short-wavelength automated perimetry (SWAP), frequency doubling technology (FDT), or flicker defined form (FDF) perimetry, compared to standard automated perimetry (SAP) using less specific white-on-white contrast stimuli? (Maddess, and Henry, 1992; Johnson and Demirel, 1997; Burnstein, et al., 2000; Sample, et al., 2000; Quaid and Flanagan, 2005; Sharma, et al., 2008) 3) Are there structural changes that precede functional changes (i.e., “pre-perimetric glaucoma” that is not a result of the ability to detect subtle loss of function)? (Sommer, et al.,1991; Bowd, et al., 2001; Wollstein, et al., 2005; Bagga, et al., 2006). 4) Can measureable loss of function precede loss of structure changes (i.e., dysfunctional RGCs)? (Swanson, et al., 2004; Weber and Harman, 2005; Gardiner, et al., 2006; Ventura, et al., 2006). 5) Does clinical cupping of the ONH precede changes that can be detected by SAP or optical coherence tomography (OCT) measurement of the axons and other tissues in the RNFL? (Broadway, et al., 1999; Motoiko and Drance, 1999; Burgoyne, et al., 2005; Yang, et al., 2007).
Several general models have been proposed to link the visual losses and neural losses caused by glaucoma. The majority of these models have attempted to relate measures of visual sensitivity by SAP to the underlying RGC densities (Bartz-Schmidt and Weber, 1993; Harwerth, et al., 1999; 2002; 2004; Garway-Heath, et al., 2000; Swanson, et al., 2004). More recently, the development of the technology for high resolution imaging has led to models that use data from optical imaging of RNFL thickness (Harwerth, et al., 2007; Hood and Kardon, 2007; Hood, 2007a; 2007b; Harwerth and Wheat, 2008; Harwerth, et al., 2008) or ONH parameters to quantify structural changes (Chauhan, et al., 2000; Bowd, et al., 2006; Bathijia, et al., 1998; See, Nicolela and Chauhan, 2009; Reddy, et al., 2009). For either approach, the model must be built on an assumption about the relationship between visual perception and the substrate of retinal neurons, i.e., RGC somas or axons, which should be supported by empirical data.
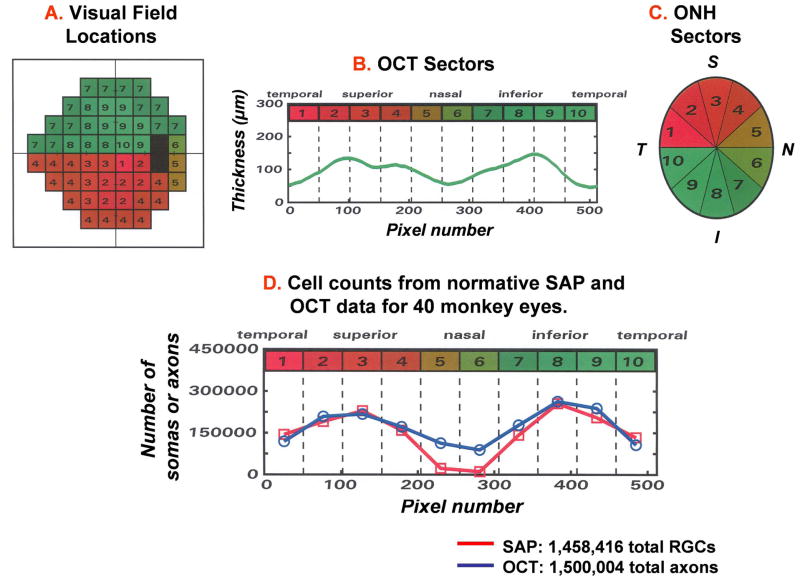
The present report addresses these issues and summarizes a series of investigations that were undertaken to develop a model of the relationship between losses of visual sensitivity and thinning of RNFL over progressive stages of glaucoma. The investigations leading to an empirical model for clinical glaucoma were an evolutionary process (Harwerth, 2008), in which each study suggested specific adaptations to account for normal variations or pathological alterations in anatomy and physiology, such as eccentricity effects for perimetry, or normal aging and stage-of-disease effects for RNFL thickness. The initial studies utilized the primate model of experimental glaucoma as a proof-of-principle of a relationship between visual sensitivities, from behavioral perimetry (Harwerth, et al., 1993A; 1997), and RGC densities determined by histological analysis in corresponding retinal locations (Harwerth, et al., 1999; 2002; 2004). Subsequent investigations involved OCT measures of RNFL thinning from experimental glaucoma (Harwerth, et al., 2007), followed by clinical studies of normal aging (Harwerth and Wheat, 2008; Harwerth, et al., 2008) and clinical glaucoma in humans (Wheat, JL et al., IOVS 2007; 48: E-Abstract 491) to produce a final formalization that was intended to provide a direct comparison of SAP and OCT data. The nonlinear structure-function model was applied to use the visual sensitivities in a region of the visual field to a predicted thickness in a correlated region of peripapillary RNFL and produce a TSNIT function from SAP measures of visual sensitivity (Harwerth RS, et al., IOVS 2009; 50: E-Abstract 3517), n.b., the acronym “TSNIT” is a description of the graphical presentation of OCT measurements of RNFL thickness (e.g., see Fig. 6).
Figure 6.
A plan for mapping SAP 24-2 visual field locations and RNFL thickness measures onto the ONH, in order to correlate structural and functional measures of glaucomatous neuropathy. The SAP 24-2 visual field locations were divided into 10 equal areas (A), with each representing 51 samples of the standard (512 point) OCT scan of the RNFL (B) or a 36 deg sector of the ONH (C). The curve of RNFL thickness plotted in panel B is referred to by the acronym “TSNIT” from the relationship between the pixel number (lower scale) in the OCT scan and the RNFL location of the scan (upper labels). The RNFL thickness measures start (pixel 1) at a retinal location that is Temporal to the ONH, the measurement progresses sequentially to the Superior, Nasal, Inferior, and back to the Temporal starting location (pixel 512) for a TSNIT representation of RNFL thickness. (D) Analogous TSNIT functions for the predicted numbers of somas and axons in the RNFL based on the structure-function model (see text, functions 1– 5). The functions represent the normative data from control eyes of monkeys to compare the number of RGC somas derived from the perimetry measurements (squares) and the number of RGC axons derived from OCT measurements of RNFL thickness (circles) for each of the 10 sectors of the optic nerve head (Adapted from Harwerth, et al., 2007).
2. The neural basis for glaucomatous visual field defects
The most common assessment of visual function in glaucoma utilizes perimetric measurements of visual sensitivity. The clinical version of perimetry, SAP, employs threshold measures for small, white-light test stimuli superimposed on a white background, with test locations spaced throughout the central 48 or 60 degrees of the visual field (Anderson, 1987; Johnson, 1996; Heijl, and Patella, 2002). The validity of this pointwise measure of visual function to gauge glaucomatous neuropathy requires a systematic relationship between the neural loss in a region of the retina and the resulting loss of sensitivity in the corresponding location in the visual field. Although, in the most elementary sense, there must be a causal relationship between RGC densities and the functions of the visual pathways in which the RGCs are involved, the quantitative structure-function linking relationship is neither theoretically nor empirically straightforward. The difficulty in defining the relationship was illustrated clearly by the initial study of post-mortem retinas of glaucoma patients that compared RGC densities to static perimetry thresholds (Quigley, et al., 1989). The point-by-point relationship between the logarithmic loss of visual sensitivity, with respect to mean normal values, expressed in decibels (dB) and the percent of RGC loss, with respect to mean normal values, showed that, on average, statistically significant abnormalities of visual sensitivity required neural losses of 20 – 50 %, depending on the retinal eccentricity, and for any given level of neural loss there was a very large range of visual defects. A later study with a larger number of glaucoma patients (Kerrigan-Baumrind, et al., 2000) also reported a low pointwise correlation between visual sensitivity and RGC losses, but the relationship was improved if global measures of sensitivity, such as average sensitivity loss or mean deviation (MD), were used to assess vision loss.
The variability in the relationship is smaller in studies of monkeys with laser-induced, experimental glaucoma (Harwerth, 2009). Monkeys that are trained to perform behavioural perimetry provide very reliable SAP data (Harwerth, et al., 1993a; 1997) and the timing of collection and processing of retinal tissue can be controlled (Harwerth, et al., 1999; 2002; 2004). The first report on experimental glaucoma (Harwerth, et al., 1999) assumed the log-linear relationship between visual sensitivity and RGC density that had been applied in the studies of retinas from human patients (Quigley, et al., 1989; Kerrigan-Baumrind, et al., 2000). The animal work confirmed the results of the studies of human tissue that the structure–function relationship was systematic, but it was not linear in the log-linear coordinate space (Harwerth, et al., 1999). The general relationship suggested that, when the RGC losses were less than about 50%, there were small reductions in visual sensitivity, but the functional losses were not proportional to the structural losses. With greater degrees of neuropathy, the structure-function relation was more systematic, although with considerable variability. Thus, these results suggested other factors need to be included in the translation of ganglion cell losses to visual field sensitivity, specifically, 1) more appropriate measurement scales for sensitivity and neural losses, and 2) retinal eccentricity as an independent parameter (Harwerth, et al., 2004). First, the quantification of visual loss on a decibel (dB) scale and the neural loss as a percentage, though intuitive, does not provide an accurate predictive relationship. As alternatives, linear and logarithmic transformations have been advocated, but a log-log coordinate system has a stronger theoretical basis for predicting the relationship between neural mechanisms for visual perception, i.e., the statistical description of probability summation for the detection of a stimulus that is imaged on a retinal area with multiple detectors (Pirenne, 1943; Nachmias, 1981; Robson, and Graham, 1981; Tolhurst, et al., 1983; Meese and Williams, 2000). The fundamental principle of probability summation is that an observer will detect a stimulus whenever at least one, or a small ensemble, of the potential detectors in the population actually detects the stimulus (Pirenne, 1943). By this principle, visual thresholds are not determined by linearly summed responses of all of the detectors in the total population, but rather by nonlinear pooling among neural detectors.
The general relationship between sensory events and neural substrates derived from probability summation is an exponential function of the number of detectors and the probability of detection for each of the available mechanisms (Robson, and Graham, 1981; Tolhurst, et al., 1983). To obtain a linear quantitative model of the structure–function relationship for clinical perimetry, the exponential function for visual sensitivity versus retinal ganglion cell density becomes linear via logarithmic transforms on both variables (Robson, and Graham, 1981). The logarithmic transforms are an expression of visual sensitivity in dB, from the threshold value at a given test location and RGC density in dB, from 10-times the logarithm of the histological density of RGCs at the corresponding retinal location. It is obvious that the use of probability summation to model the relationship cannot be exact because it would require a homogeneous population of neural detectors. Homogeneity is unlikely for retinal mechanisms involved in image processing of the white-light perimetry stimulus, especially with glaucomatous neuropathy, but a linear neural-sensitivity relationship with logarithmic coordinates has been shown for clinical SAP (Harwerth, et al., 2004).
The other source of variability in the psycho-physiological links between SAP and RGC density is retinal eccentricity. An eccentricity parameter was not considered in the initial studies of experimental glaucoma, although both visual sensitivity (Heijl, et al., 1987; 1988; Harwerth, et al., 1999) and RGC density (Rolls and Cowey, 1970; Drasdo, 1989; Curcio and Allen, 1990; Wassle, et al., 1990) vary as a function of eccentricity. For example, for the untreated, control eyes of rhesus monkeys (Harwerth, et al., 1999) the perimetric sensitivity is highest near the fovea and falls by fivefold in the mid-periphery and inter-subject variability of sensitivity also varies, being lowest in the central field with systematic increases across the peripheral visual field (see Table 1). Similarly, in normal monkey eyes the RGC density is dependent on retinal eccentricity with the highest concentrations of cells in the macular area and a 10-fold reduction in cell density in the mid-periphery.
Table 1.
Data from control and laser-treated eyes of monkeys that were used to derive an empirical structure-function relationship for glaucoma and the dynamic range of measurement for clinical perimetry.
| Eccentricity | |||||
|---|---|---|---|---|---|
| 4.2 deg | 12.8 deg | 21.2 deg | 24.0 deg | ||
| 1 | Normal density (cells/mm2) | 48,982 ± 4,906 | 11,188 ± 1,290 | 4,986 ± 1,016 | 4,458 ± 898 |
| 2 | Normal density (dB) | 46.9 ± 0.4 | 40.2 ± 0.6 | 36.9 ± 0.9 | 36.4 ± 0.9 |
| 3 | Normal threshold (asb) | 3.7 ± 1.4 | 5.4 ± 1.4 | 8.9 ± 3.5 | 14.9 ± 11.5 |
| 4 | Normal sensitivity (dB) | 34.6 ± 1.4 | 32.8 ± 2.1 | 29.9 ± 3.0 | 29.4 ± 3.2 |
| 5 | # Function slope (dB/dB) | 1.25 | 1.47 | 2.1 | 2.3 |
| 6 | # Function intercept (dB) | −25.2 | −32.3 | −46.2 | −55.7 |
| 7 | Single detector threshold (asb) | 3.3 * 106 | 1.7 * 107 | 4.2 * 108 | 3.7 * 109 |
| 8 | Cell density @ 2 SD loss (cells/mm2) | 39,355 | 7,727 | 2,624 | 2.203 |
| 9 | 2 SD cell-loss (%) | 20 | 26 | 50 | 51 |
| 10 | 2 SD cell-loss (dB) | 0.9 | 1.6 | 3.0 | 3.1 |
| 11 | Cell density @ 0 dB sensitivity (cells/mm2) | 100 | 160 | 170 | 250 |
| 12 | Cell density @ 0 dB sensitivity (dB) | 20.0 | 22.0 | 22.2 | 24.0 |
| 13 | Percent normal density @ 0 dB sensitivity | 0.2 | 1.4 | 3.4 | 5.6 |
| 14 | Dynamic range of SAP measurement (dB) | 25.9 | 16.9 | 11.9 | 9.4 |
Abbreviations: dB – decibels, defined as 10-times the common logarithm. asb – unit of light intensity for perimetry stimuli, defined as the brightness of a perfectly diffusing surface reflecting or emitting one lumen per square meter.
The data for the slopes and intercepts were calculated by equations 1 and 2, respectively.
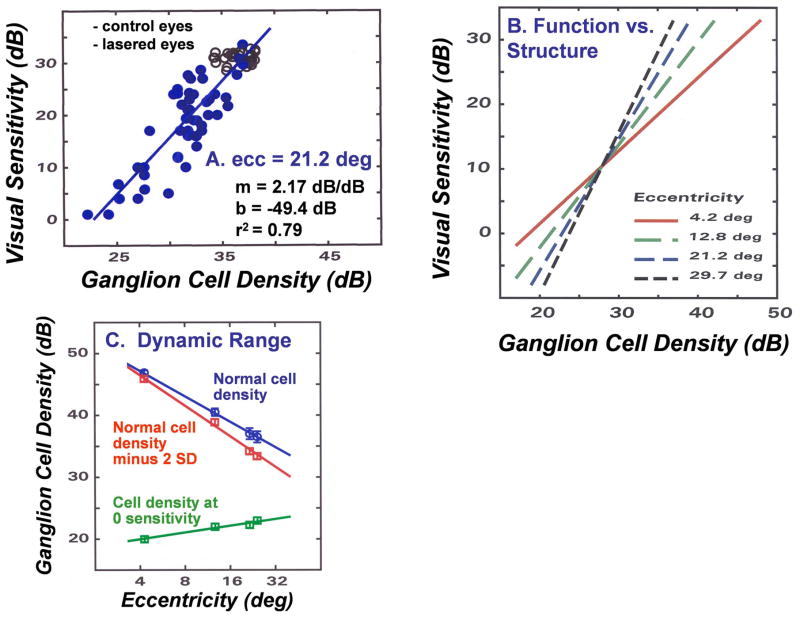
In order to derive an empirical model of the neural-sensitivity relationship, the data for behavioral SAP measurements and histological RGC densities as a function of retinal eccentricity were analyzed by linear regression in log-log coordinate space, with ganglion cell density as the independent variable (Harwerth, et al, 2002; 2004; 2005). An example of the regression analysis of the sensitivity and neural data for a retinal eccentricity of 21.2 deg, i.e., a perimetric test field location of 15 × 15 deg, is presented in Fig. 1A. The data represent the control (open symbols) and experimental (filled symbols) eyes from 16 monkeys with laser-induced glaucoma. The parameters of the linear function are presented in the inset along with the coefficient of determination (R2) showing that the linear function accounts for 79% of the variance. An analysis of data for 3 additional retinal eccentricities confirmed that the goodness-of-fit was similar at other eccentricities, but the parameters of the linear functions varied systematically with the retinal eccentricity. The histological and SAP data at the four eccentricities analyzed are presented in Table 1 in both linear units (cells/mm2 for cell counts and apostilb (asb) for threshold intensity), and in logarithmic (dB) units. Examples of the eccentricity-dependent functions are illustrated in Fig. 1B and with the slope and intercept values for the linear functions in log-log coordinates at four eccentricities are presented in Table 1. An additional regression analysis of the slope and intercept data showed that they are each also linear functions of eccentricity (deg) and, accordingly, provide a method to determine the slope and intercept parameters for the structure-function relationship at any given eccentricity. These linear regressions define the relationship between visual sensitivity and RGC density, but for clinical application the computation must be the opposite way, i.e., the quantification of RGC densities from SAP data. However, because the R2 values are high the functions presented in Fig. 1 were used to derive RGC densities from SAP measures and the non-linear, structure-function model for SAP was based on three functions. One function to derive the slope (dB sensitivity/dB RGC density) and another to derive the y-intercept (dB sensitivity) of the linear functions in log-log coordinates. The third function is the relationship between RGC density (in dB units) as a function of SAP sensitivity based on the slope and intercept parameters derived from the eccentricity-dependent functions. The specific functions developed for experimental glaucoma in monkeys are:
| 1 |
| 2 |
| 3 |
Figure 1.
A structure-function relationship between SAP visual sensitivity and histologically defined RGC density in monkeys with experimental glaucoma. (A) An example of the relationship for SAP visual sensitivity as a function of RGC density when both parameters are transformed to a logarithmic scale. Data for the control eyes are presented as open symbols and data for the lasered eyes are presented as filled symbols. The data for linear regression analysis on the data are presented in the inset (Adapted from Harwerth, et al., 2005). (B) The relationships between SAP visual sensitivity and RGC density for four retinal eccentricities, using the model described by equations 1 – 3. (C) The dynamic range of measurements by SAP based on the underlying RGC densities. The data for the normal RGC density as a function of eccentricity are based on the normal visual sensitivity at each eccentricity. The normal cell density decreased by 2 SD units represents the smallest loss of RGC density that would cause a statistically significant visual field defect. The cell density at zero sensitivity represents the RGC density at which SAP measurements fail and the RGC density cannot be assessed by clinical SAP. The distance between the lines for the cell densities minus 2 SD units and the cell densities at zero sensitivity represents the dynamic range of measurement.
Where m and b are the slope and y-intercept, respectively, for the function at retinal eccentricity ec, s is the SAP visual sensitivity, in dB units, and gl is the RGC density (somas/mm2), in dB units.
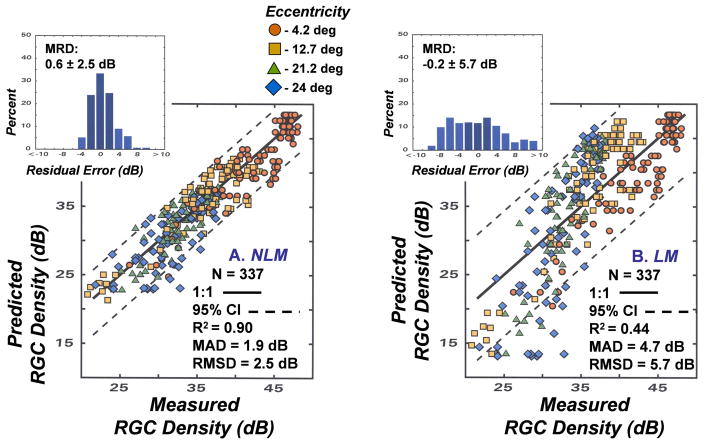
The model developed with SAP and RGC histology has implicit validity for quantifying the RGC density in an area of the retina from the corresponding SAP measurement, but it must be ascertained whether it is more accurate and precise than alternative models based on a linear translation of SAP data to the underlying RGC populations (Garway-Heath, et al., 2000; Swanson, et al., 2004; Hood and Kardon, 2007). The most appropriate neural-sensitivity relationship is fundamental to the psycho-physiological linking proposition for glaucoma and the differences in nonlinear models (NLM) and linear models (LM) should be evaluated for a common set of data (Harwerth, et al., 2005). Therefore, both algorithms were applied to data from monkeys with experimental glaucoma using SAP sensitivity measurements at a given test location and the histological counts of RGCs from the corresponding retinal area. The perimetry data were used to derive the predicted RGC densities and plotted as a function of the histologic counts. For the NLM (Fig. 2A) the predicted RGC densities were determined by functions 1 – 3, above. The predicted RGC densities for the LM (Fig. 2B) were based on the simple assumption of a reciprocal relationship between visual sensitivity and RGC density and, therefore, the SAP sensitivity, in dB, was converted to an inverse linear light intensity and then scaled to equate the models for RGC densities for the control eyes at the most central SAP test location (i.e., 4.2 deg eccentricity). The specific methods are as follows:
| 4 |
| 5 |
Figure 2.
A comparison of the relationships between the modeled and measured RGC densities. (A) Application of the NLM described by equations 1 – 3 and (B) application of the LM described by equations 4 and 5 for the translation between SAP visual sensitivity and RGC density that were used to obtain the predicted RGC densities. Symbols for data for each of the 4 eccentricities are indicated by the symbol legend. For each method of relating visual sensitivity to neuron density, the 1:1 relationship is illustrated by the solid line and the 95% limits of agreement are illustrated by the dashed lines. The upper inset histograms present the residual errors between modeled and measured data, with the mean residual deviation (MRD) and the standard deviation (SD) of the distribution shown on the graph. Other statistical goodness-of-fit indices that are inset to the graph represent the coefficient of determination (R2), the mean absolute deviation (MAD), and root mean squared deviation (RMSD)
Where: s_loss is the reciprocal of the SAP stimulus intensity, s is the SAP sensitivity in dB units, k is a constant of proportionality (175,534) to scale the data for a linear relationship at a 4.2 deg eccentricity to the data for a logarithmic relationship, and gc is the predicted RGC density (dB).
The results of the nonlinear and linear model predictions of RGC densities with respect to measured RGC densities (Fig. 2) were compared by several goodness-of-fit metrics that are presented as graph insets. First, the results can be visually compared to the perfect unity relationship, represented by the solid line, and by the coefficient of determination for the 1:1 relationship. The second metric, the accuracy of each model, is represented by the mean residual deviation (MRD) between the predicted and measured RGC densities, with the errors negative when the predicted values are greater than measured values, or the errors positive when the measured values are larger than the predicted values. Statistical indices for the precision of each model were based on three analytical methods; 1) the distributions of residual errors are presented as insets with the MRD ± standard deviation (SD) shown. The 95% limits of agreement, represented by the dashed lines on the main graphs, were determined by 1.96 times the SD of the error distribution., 2) the mean absolute deviation (MAD), which represents the average unsigned error with respect to the unity relationship, and 3) the root mean squared deviation (RMSD) as a measure of the variance with respect to the unity relationship that is influenced more by large deviations than small deviations, because large errors are especially important in evaluating the strength of the relationship.
In comparing the two models, it is interesting that their accuracies are very similar, with MRDs of less than 1 dB, but the distribution of residual errors is broader and, consequently, the 95% limits of agreement are larger for the LM compared to the NLM. The R2, MAD, and RMSD, all indicate a greater degree of precision for the NLM than the LM. Therefore, for purposes of assessing population data the accuracies of the NLM and LM are similar, but for individual subjects the NLM provides a higher probability of an accurate prediction of RGC densities from SAP measurements (Harwerth, et al., 2005).
Based on the analysis of the accuracy and precision, it is appropriate to apply the NLM to provide important descriptions of the neural mechanisms underlying perimetric visual field defects and the interpretation of stage of glaucoma from SAP measurements. For example, an interesting aspect of relating visual sensitivity to neural mechanisms is the sensitivity of the individual detection mechanisms. Because the structure-function relationship defines visual sensitivity as a function of the RGC density, the y-intercept represents the visual sensitivity (threshold) of a single detecting mechanism (Robson and Graham, 1981), or in this case, a single mechanism per mm2 of retinal area. The y-intercept values, which also have been converted to light intensities in row 7 of Table 1, are 2.5 to 5.5 orders of magnitude brighter than the maximum intensity of the standard clinical instrument (104 asb) and, therefore, the dynamic range of measurement cannot assess the full range of RGC losses (Bengtsson, and Heijl, 2003). On the other hand, the general characteristics of the neural detectors, i.e., an increasing threshold with retinal eccentricity, are in agreement with retinal anatomy, i.e., a decrease in packing density of cone photoreceptors (Curcio, et al., 1990; Jonas, et al., 1992) and a lower efficiency of shorter outer segments (Rodieck, 1998) with increasing eccentricity, which provides facial credibility to the form of structure-function relationship developed from the empirical data.
The single mechanism detection thresholds also suggest that the dynamic range of measurement varies with eccentricity (see Fig. 1C). At the high end of visual sensitivity, a certain amount of neural loss must occur in early glaucoma before a significant abnormality of visual sensitivity can be identified statistically. The minimum sensitivity loss at a given location in the visual field that is generally considered to be clinically significant is a loss greater than the lower 95% confidence interval (CI). The reductions in the normal RGC densities (row 1, Table 1) caused by a decrease in normal SAP sensitivity by 2 SD units (row 4, Table 1) are presented in row 8 of Table 1, with the RGC losses expressed as percent loss or dB loss in rows 9 and 10, respectively. The calculated losses of RGC density caused by reductions of 2 SD in visual sensitivity, which are also illustrated graphically in Fig. 1C, demonstrate that the 2 SD-loss in the absolute number of RGCs is considerably larger for eccentricities near the fovea, but because the normal densities are higher, the proportion of loss either as a percent, or in dB units, is much smaller for locations near fixation than for more eccentric locations.
With advanced stages of glaucomatous neuropathy, the visual sensitivity becomes too low to obtain a measurement and SAP fails to accurately define the neural losses. As was illustrated by the single detector threshold, the failure point that is indicated by a measurement of zero dB sensitivity occurs with a non-zero population of RGCs. The calculated RGC densities at zero dB sensitivity at each of four eccentricities are presented in linear units in row 11, in dB units in row 12, and as a percent of the normal population in row 13 of Table 1. These data also are presented graphically in Fig. 1C to illustrate that the RGC density that is insufficient to produce a visual sensation during the SAP measurement, is smallest near fixation (0.2% of the normal population) and increases systematically with eccentricity and is up to 5.6% of the normal density at an eccentricity of 24 deg.
The range of neural loss between the RGC density at the initial statistically significant loss (95% CI) and the density at which SAP fails as a measurement of RGC function provides the dynamic range of measurement (see row 14, Table 1 and Fig. 1C). The eccentricity dependent function shows a variation in the dynamic range from about 26 dB near the center of the visual field to just over 9 dB at the 24 deg eccentricity. It should be noted that the data used for this example, although based on data from experimental glaucoma, can be considered representative of young-adult humans (i.e., 25 – 30 years of age), but the normal cell density decreases with age (Blanks, et al., 1996; Harman, et al., 2000; Kerrigan-Baumrind, et al., 2000; and see section 5) and, thus, the dynamic range is also age-dependent. For example, the upper limit of the dynamic range of measurement for a normal 65 year-old patient would be about 1.2 dB lower than illustrated in Fig. 1C (Harwerth, et al., 2008).
Taken altogether, these data from an application of the structure-function model that was developed to relate visual sensitivity and neuronal populations are useful for explaining some of the typical characteristics of visual field defects caused by the neuropathy of primary open-angle glaucoma (Anderson, 1987; Epstein, 1993; Quigley, 1993). For example, because of the probabilistic nature of visual sensitivity, it would be expected that perimetric defects would occur in the peripheral visual field before the central field. At locations in the retinal periphery the structure-function relationship is steeper and, thus, a given loss of neurons will cause a greater loss of visual sensitivity, compared to more central locations with shallow structure-function relationships. Conversely, vision in the central field will be preserved until late stages because of the shallow slope of the relationship and because the initial RGC density is high. It is also important for the clinical interpretation of SAP data that the loss of retinal neurons associated with a given loss of visual sensitivity is dependent on retinal eccentricity. As an example, a 3 dB loss in the central field represents a much greater loss of RGCs than the same loss of sensitivity in the peripheral field, and the central defect would be significant at the p <0.05 level, while the peripheral defect would not.
3. Structure-Function for Non-Standard Perimetry: Spatial Contrast Sensitivity Defects from Experimental Glaucoma
The analyses of data from behavioral perimetry and histologic measures of RGC densities have provided a quantification of the neuronal basis for SAP measurements of visual sensitivity, but it is not certain that these findings will necessarily generalize to other methods of perimetry. On the one hand, the relationship between visual sensitivity and RGC density may be the same for any type of stimulus, while on the other hand, there may be separate structure-function links for the various clinical tests that have been designed to isolate specific visual functions such as, a single photoreceptor type with short-wavelength automated perimetry (SWAP), flicker or motion detectors with frequency-doubling technology (FDT), or mechanisms for a second-order flicker-defined form (FDF) perimetry (Maddess, and Henry, 1992; Johnson and Demirel, 1997; Burnstein, et al., 2000; Sample, et al., 2000; Quaid and Flanagan, 2005; Sharma, et al., 2008), compared to the achromatic contrast detection of white-on-white stimuli with SAP, which may activate multiple retinal mechanisms (Harwerth, et al., 1993b). Assuming the validity of the neural-sensitivity relationships defined for SAP (described above), the issues of alternative stimuli can be addressed by comparing visual field defects measured by SAP to the visual field defects measured by an alternate stimulus.
Several alternatives to SAP have been proposed that utilize sine-wave stimuli, which were designed to be more specific for a subset of RGCs, for diagnosis of glaucoma at an earlier stage (Lundh and Gottvall, 1995; Harwerth and Smith, 1997; Bodis-Wollner, and Brannan, 2000; Ansari, et al., 2002; Hawkins, et al., 2003; Tochel, et al., 2005; Hot, et al., 2008; Battista, et al., 2009). If the testing methods are based on statistical criteria that are similar to SAP, then earlier detection requires methods with either reduce inter-subject variability or involve a different underlying structure-function relationship. The latter idea of different structure-function relationships for different perimetry stimuli was investigated through studies of the spatial contrast sensitivity defects caused by experimental glaucoma (Harwerth, RS, et al., IOVS 2005; 46: E-Abstract 4667).
Spatial contrast sensitivity functions (CSFs), which are defined by contrast detection thresholds as a function of spatial frequency, provide a relatively complete description of a patient’s functional spatial vision (Campell and Green, 1965). Studies of changes in CSFs as a result of developmental disorders (e.g., amblyopia; Harwerth, et al., 1990), or acquired neuropathies (e.g., glaucoma and other optic neuropathies; Bodis-Wollner, et al., 1993) have revealed reduced sensitivities at low and intermediate spatial frequencies, as well as reduced sensitivities for the high spatial frequencies that underlie Snellen acuity. The early investigations also suggested that the contrast sensitivity losses that are associated with specific ocular disorders could be applied for early diagnosis as, for example, in distinguishing between early glaucoma and ocular hypertension.
Selective spatial frequency defects from primary open-angle glaucoma should initially develop in the mid-peripheral visual field, in the locations of initial visual defects by standard clinical perimetry, but the spatial frequency dependency of contrast sensitivity defects in areas of reduced visual sensitivity from glaucoma needed to be determined. A number of studies have suggested that a relative loss of spatial contrast sensitivity is an early sign of glaucomatous optic neuropathy, using contrast sensitivity data from multiple spatial frequencies for central vision or a single spatial frequency throughout the peripheral visual field (e.g., Hot, et al., 2008). The latter strategy has been implemented for clinical applications of contrast sensitivity perimetry that use either a low spatial frequency (0.25 c/deg) for perimetry using frequency-doubling technology (Brusini and Busatto, 1998; Cello, et al., 2000) or a higher spatial frequency (1.0 c/deg) for the newer Matrix perimeter (Anderson, et al., 2005; Patel, et al., 2006). The higher spatial frequency and smaller overall size for stimuli with the Matrix perimeter improves the detection of localized visual field defects, but a clearer understanding of the depth of glaucomatous visual field defects as a function of spatial frequency and overall size of the test stimulus is needed. Therefore, to determine whether there are spatial frequency dependent alterations in vision function that are caused by the loss of retinal ganglion cells, studies were undertaken to investigate spatial contrast sensitivity functions in areas of the visual field with depressed sensitivity from experimental glaucoma.
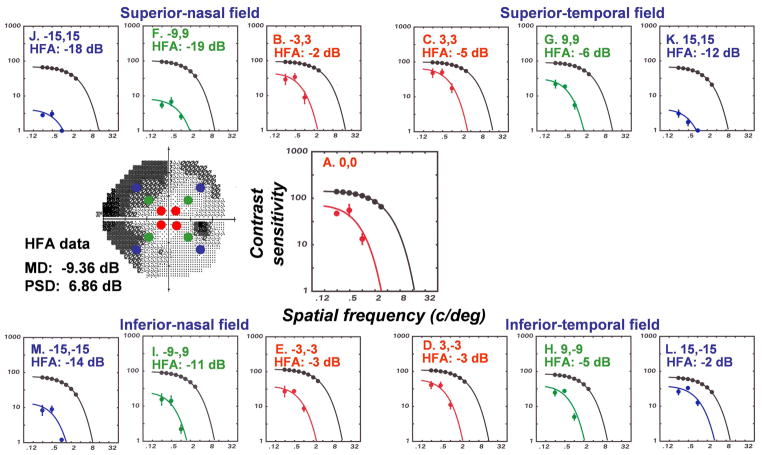
The data for the study were collected by behavioral measurements for SAP (Harwerth, et al., 1993) and of local spatial contrast sensitivities (Harwerth and Smith, 1997) in rhesus monkeys with unilateral experimental glaucoma. The contrast sensitivity stimuli were Gabor patches, constructed of horizontally oriented carrier gratings with spatial frequencies of 0.25 – 2.8 c/deg in cosine phase with the Gaussian spatial envelope (1.0 octave bandpass) and brief (140 msec) presentation times. The contrast sensitivity data were fitted by an exponential low-pass filter to determine the height (peak contrast sensitivity) and location (high spatial frequency cut-off) of each function. CSFs were obtained for central vision and three locations (3×3 deg, 9×9 deg, and 15×15 deg from fixation) along the oblique meridians in each visual field quadrant (indicated by the filled symbols on the SAP grayscale plot in Fig. 3).
Figure 3.
SAP and contrast sensitivity perimetry for a monkey (OHT-46) with laser-induced experimental glaucoma. The gray-scale plot for SAP shows the peripheral locations for contrast sensitivity testing by the filled symbols. The contrast sensitivity functions at each location for OHT-46 are presented and, for comparison, the mean function for control eyes. The fitted functions are a two-parameter, low-pass model used to determine the height (peak contrast sensitivity) and location (cut-off spatial frequency) of the contrast sensitivity function. The total deviations from expected sensitivities for SAP of normal monkey eyes by behavioral testing with the Humphrey Field Analyzer (HFA) are inset on the graphs.
Examples of the effects of experimental glaucoma on spatial contrast sensitivity are illustrated for the central test location and each of the 9 eccentric locations in Fig. 3. The data for the experimental eye can be compared to the upper curve that represents mean CSF for control eyes at the same test location. In addition, the inset data for the plots are the total deviations for the SAP measurements at the test field locations. Simple inspections of the CSFs across field locations indicate that there is an ordinal relationship for the losses of spatial contrast sensitivity and SAP sensitivity, but with milder SAP losses (e.g., Figs. 3C and 3D) the reduction in peak sensitivity is less than the reduction in the cut-off spatial frequency, while for more advanced visual defects, both contrast sensitivity parameters are affected equally (c.f., Figs. 3J and 3K).
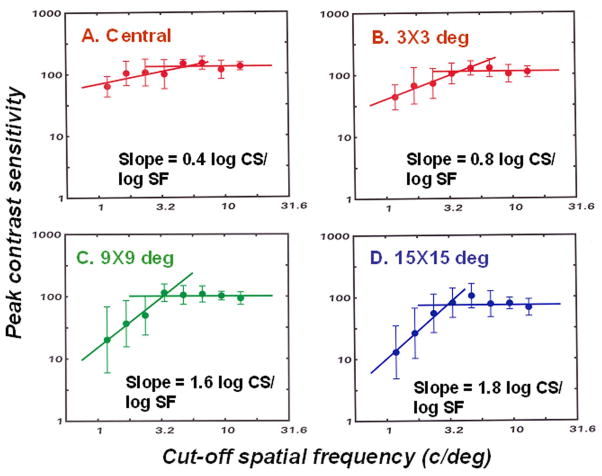
For the six monkeys, the glaucoma-induced losses in the peak and high frequency cut-off parameters of contrast sensitivity functions were well-described by two-line functions. Figure 4 presents the geometric mean and SD of the peak sensitivity as a function the cut-off spatial frequency for data grouped into 8 equal-width bins of log spatial frequency. These data present a clear picture of contrast sensitivity losses with two segments, with one segment representing early losses in cut-off spatial frequency without a reduction of peak contrast sensitivity, and a second segment for more advanced deficits with proportional reductions in cut-off spatial frequency and peak contrast sensitivity with slopes that vary with retinal eccentricity. Another abnormality of glaucomatous neuropathy was found in spatial summation - the peak contrast sensitivity increased with an increasing number of cycles of the carrier grating in the Gabor patch for control eyes, or eyes at a mild stage of experimental glaucoma, but the contrast sensitivity of eyes with advanced defects did not increase with the number of grating cycles (data not shown).
Figure 4.
The peak contrast sensitivity as a function of the cut-off spatial for monkeys with visual field defects from experimental glaucoma for central and peripheral visual field locations (A–D), shown in the graph labels. Data from six monkeys are included, with repeated measures as their visual field defects progressed. To present the main effects more clearly, the data for peak contrast sensitivities have been combined into 8 bins of spatial frequency with the mean ±SD plotted for each bin. The two-line functions were fitted to demonstrate a shift in the locations of the functions without a reduction in height, i.e., loss of contrast sensitivity. For the two-line function, with one segment was determined by linear regression over the four lowest spatial frequencies (slopes shown on the plot), and the other segment with a zero slope was placed at the mean contrast sensitivity for the three highest spatial frequencies.
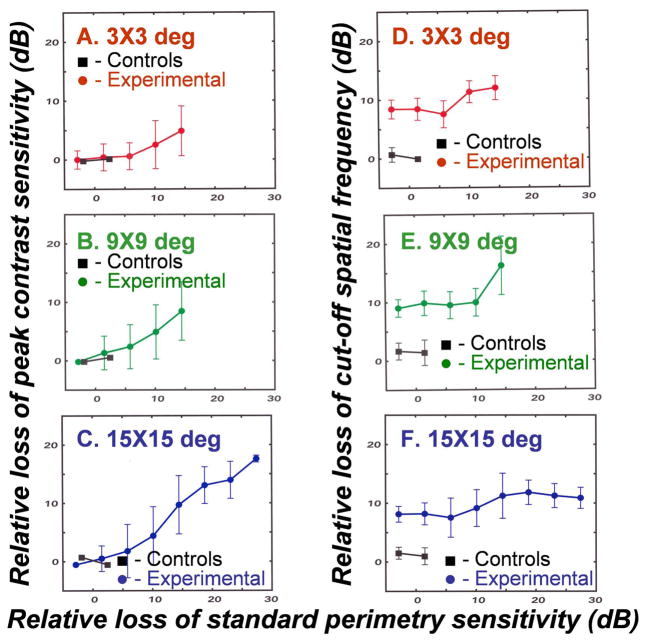
To determine whether there is evidence of a common neuronal basis for abnormalities in contrast sensitivity, the deficits in spatial contrast sensitivity and SAP sensitivity were compared. The results, presented in Fig. 5, demonstrate that the losses of peak contrast sensitivity are correlated with visual sensitivity deficits by SAP, while the losses in cut-off spatial frequency are not. The analysis of visual field defects with two different stimulus types required a transformation of data to similar scales by, 1) converting the contrast sensitivity data to decibel units (i.e., 10-times the log-values), 2) normalization of the data for both procedures as losses of sensitivity, in dB units with respect to expected normal values, and 3) for descriptive purposes, smoothing the data by taking means and SDs of contrast sensitivity data within small ranges (bins) of SAP losses. The principal result of the comparisons of visual field defects measured with Gabor patches and Goldmann III stimuli (Fig. 5) is that the losses of peak contrast sensitivity (Figs. 5A – C) are correlated to SAP data while the reductions in cut-off spatial frequency (Figs. 5D – E) are not. The functions for correlated losses in peak contrast sensitivity and SAP pass through the origin, indicating that abnormalities would be detected at a similar time in the course of glaucomatous field defects, but the relationships are not one-to-one, possibly because of differences in the definitions of contrast for the two types of stimuli. In distinction, there is no property of the broadband SAP stimuli that should reflect spatial vision or the spatial frequency cut-offs. Thus, the results comparing contrast sensitivity parameters and SAP sensitivity (Fig. 5) are consistent with the results from comparing the height and location parameters of contrast sensitivity functions (Fig. 3), which showed that contrast sensitivity losses at higher spatial frequencies precede losses at lower spatial frequencies and that the high spatial frequency losses may reduce the cut-off spatial frequency by several dB before they are reflected in losses of the height of the function or by SAP measurements.
Figure 5.
A comparison of visual defects measured by contrast sensitivity with Gabor patches versus SAP with Goldmann III stimuli for 3 peripheral visual field locations (A–F) shown in the graph labels. To compare the contrast sensitivity data to SAP data, the peak contrast sensitivities and cutoff frequencies were transformed to a dB scale by 10-times their logarithmic values. The losses of peak contrast sensitivity or cut-off spatial frequency represent the measured minus the expected values at each location, based on the data for normal eyes presented in Fig. 3. The relative loss of sensitivity by clinical perimetry represent the total deviations from expected sensitivities for SAP of normal monkey eyes by behavioral testing.
In sum, the early visual field defects from glaucoma represent selective spatial frequency effects where contrast sensitivity losses at high spatial frequencies precede losses at lower spatial frequencies. The pattern of contrast sensitivity losses represents a progressive filtering or blurring that may explain the often-reported complaints of poor vision by glaucoma patients with normal central fields and good visual acuity (Hawkins, et al., 2003). However, with respect to linking structure and function in glaucoma, contrast sensitivity perimetry will require a different model than SAP, and it is likely that other forms of function-specific perimetry will also require different models. Therefore, applications of the empirical nonlinear structure-function model that has been developed from SAP measurements and histological measurements should be restricted to linking structure to function via SAP measurements, such as the correlation of SAP visual field defects to the thinning of the retinal nerve fiber layer as will be described in the next section.
4. The neural basis for thinning of the RNFL in glaucoma
SAP measurements of visual fields have been the traditional clinical method for the diagnosis and assessment of the progression of glaucomatous neuropathy (Anderson, 1987; Johnson,1996), but more recently, high resolution imaging of retinal structure, such as OCT measurements of the RNFL thickness, also has become a standard examination procedure (Greenfield, 2002; Zangwill and Bowd, 2006). In most respects, the clinical evaluation of SAP and OCT data are similar in that both are based on a comparison of an individual patient’s data to an age equivalent normative database. With measurements of either visual sensitivity or RNFL thickness, abnormal findings are sufficient to identify RGC loss, but to understand the stage of disease and the underlying pathology it is important to understand the relationship between the functional and structural measurements. The structure-function model for perimetry (described above) has demonstrated that the degree of reduced visual sensitivity in an area of the visual field can quantify the loss of ganglion cells in the corresponding area of the retina. Similarly, the number of axons entering the optic nerve from an area of the retina also must be representative of the number of retinal ganglion cells and, therefore, also systematically related to the degree of reduced visual sensitivity. The formalization of methods to define the structure-function model for SAP and OCT through their common neural substrate of RGCs has been explored in investigations of experimental glaucoma in macaque monkeys (Harwerth, et al., 2007). In these investigations, data from normal eyes were used to relate specific areas of the visual field to regions of the ONH and for the conversion of RNFL thickness to numbers of axons. The numbers of axons in the RNFL were then compared to the numbers of RGCs derived from SAP data. Subsequently, the methods that were developed for normal eyes were used to study the optic neuropathy caused by experimental glaucoma.
The first step in defining the structure-function links for glaucomatous thinning of the RNFL was to estimate the number of retinal ganglion cells in a retinal location from the corresponding SAP measurements of visual sensitivity, as was described in the previous section. However, to account for the total number of ganglion cells in an area of the retina, the cell density derived from each perimetry measurement was considered to be uniform over an area of retina corresponding to an area of 6×6 degrees of visual space that separates test locations in SAP. In order to determine the total number of RGCs in a specific area represented by a visual field location, the antilog of the ganglion cell density from equation 3 was multiplied by 2.25 (based on a conversion factor of 1 mm retinal distance per 4 deg of visual angle for the monkey eye). Finally, to determine the number of axons entering a region of the optic nerve, the ganglion cell densities were summed across the visual field locations that mapped onto a given ONH sector, as will be described below.
The data used in these studies were obtained by time domain OCT (Stratus OCT), with measurements of RNFL thickness from 512 samples in a circle around the ONH to produce a thickness function that is called a “TSNIT” curve, as defined by Fig. 6. The numbers of RGC axons represented by TSNIT thickness measures were estimated from the area that was defined by the RNFL thickness (height) multiplied by scan length, which was then multiplied by an axon density (axons/μm2) to obtain the total number of axons (see Fig 3A). The calculations were based on the instrument’s nominal scan length values, without compensation for the shorter axial length of the eyes of monkeys. The OCT scan length for the standard scan (10.87 mm) was sampled in 512 pixels and, thus, each pixel represented a retinal distance of 21.2 μm. The scan height across pixels provided the total cross-section area occupied by RNFL axons in the optic nerve head. Because neither the axon density in the RNFL nor the proportion of RNFL that is neuronal tissue has been determined, a small range of axon densities that were compatible with published data were evaluated to obtain the best match between axon and RGC numbers for the normative data. Based on these calculations, a density of 1.71 axons/μm2 was set as the coefficient of proportionality for the number of axons per unit area of the OCT scan. For the measurements of normal monkey eyes, and omitting the 102 pixels of the nasal portion of the scan (see below), the total number of RGCs derived from OCT data was 1,494,444, compared to 1,537,621 derived from SAP measurements.
The final step for determining the relationship between nerve fiber and perimetry measurements was to develop an appropriate topographical mapping of the visual field onto the optic nerve head. Although several mapping relationships have been proposed, none produced a tenable relationship between the RGC and RNFL data, and, therefore, a modified plan was developed for the SAP-OCT relationship (Figs. 6A–C). With this scheme, the optic nerve head was divided into 10 equal sectors of 36 deg (Fig. 6C), each representing 51 pixels of the OCT scan (Fig. 6B). The number of visual field locations assigned to a sector varied from one SAP location near the fixation point that enters the ONH in sector 1 or 10, to 13 SAP locations for the arcuate locations of the visual field entering the ONH in sector 4 or 7 (Fig. 6A). The final RGC to RNFL relationship was derived by the sum of ganglion cells inputting to an ONH sector, as estimated from the perimetry sensitivities at each test field location in the sector, and the total number of RGC axons at the ONH that was estimated from the area of the nerve fiber layer for each sector multiplied by the density of RNFL axons.
The results of using these methods for deriving cell and axon numbers are presented in Fig. 6D as a TSNIT function. The data, based on the means of behavioral SAP and standard OCT measurements from separate groups of normal eyes, are represented by squares for the total number of ganglion cells and by circles for neuronal axons in each ONH sector, which are plotted at the center of the pixel range representing that sector. The agreement between the two estimates of neural elements is generally excellent. For example, the function indicates that the axons of nearly 150,000 ganglion cells from SAP test location 1 enter ONH sector 1 and, similarly, the OCT scan height across sector 1 converts to about 150,000 axons entering ONH sector 1. The agreement between the two estimates is consistent for all of the sectors except for sectors 5 and 6. The obvious SAP under-estimation of RGC axons entering these sectors is irresolvable because the HFA 24-2 protocol includes only two field locations nasal to the ONH, which is insufficient to determine the axon count into the nasal ONH and, consequently, these sectors were omitted from subsequent analyses of visual field and nerve fiber layer defects. For the other sectors, the estimates of the normal populations RGCs and axons were essentially equal, which provides an impetus for applying the procedures of deriving topographically related RGC populations from SAP and OCT measures to study the progressive neuropathy caused by experimental glaucoma.
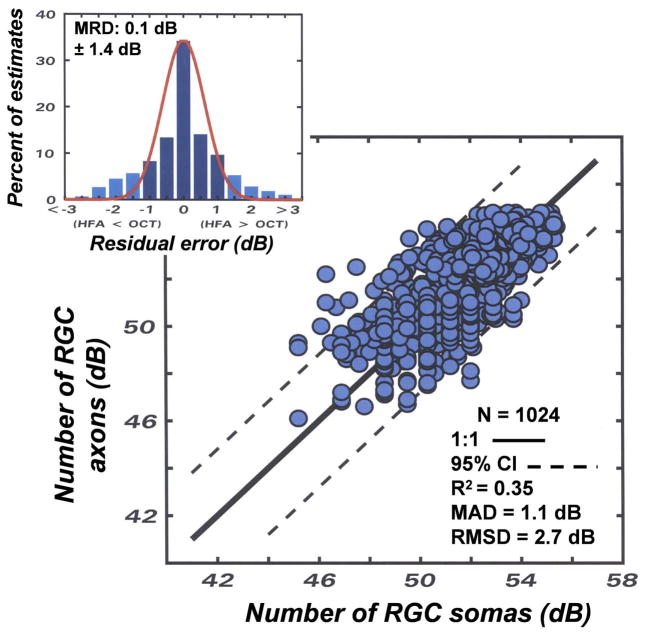
The results for experimental glaucoma are presented in Fig. 7 for the control and experimental eyes of seven monkeys with experimental glaucoma, with repeated measurements at three-week intervals (7 – 9 measurements per monkey). All of the experimental eyes had mild to moderate visual field damage and the data from both laser-treated and control eyes are included in the plot to compare the number of neurons predicted from SAP measurements of visual sensitivity to the number of axons predicted from OCT measurements of RNFL thickness. The accuracy and precision of the methods were evaluated by histograms of residual errors for each sector, with a sign convention of negative values for differences of an estimate of RGCs by SAP that was less than the estimate of axons by OCT, or positive values if the SAP estimate of neurons was larger than the OCT estimate. The MRD (−0.1 ±1.4 dB) was close to zero demonstrating excellent accuracy and precision of the model. In addition, the distribution of residual errors appears Gaussian, indicating that parametric statistics are appropriate for the evaluation of the goodness-of-fit for the modeled data. The goodness-of-fit and the limits of agreement of the modeled data are shown by the lower graph, with statistical data presented as an inset. Although the coefficient of determination was relatively modest (0.35), the MAD (1.1 dB) and RMSD (2.7 dB) statistical indices demonstrate an excellent precision for the estimation of neuronal populations.
Figure 7.
An application of the structure-function model for relating SAP visual sensitivity and OCT fiber layer thickness for control and laser-treated eyes of monkeys that is described in the text (equations 1 – 5). The number of RGC axons derived from RNFL data as a function of the number of RGC somas from visual field data for corresponding sectors of SAP and OCT measurements. The correspondence between the subjective and objective measurements was evaluated by the 1:1 relationship that is illustrated by the solid line and the 95% limits of agreement that are illustrated by the dashed lines. The upper inset histogram presents the residual differences between the estimated populations of neurons, with the mean residual deviation (MRD) and the standard deviation (SD) of the distribution shown on the graph. The line superimposed on the histogram is a Gaussian distribution with parameters based on the MRD and SD of the distribution of residuals. The other statistical goodness-of-fit indices shown in the inset of the graph represent the coefficient of determination (R2), the mean absolute deviation (MAD), and root mean squared deviation (RMSD) of the axon versus soma data.
The main outcome of the studies using non-human primates was the development of a structure-function model that produced a close agreement in the numbers of neurons derived from SAP and OCT data for both normal, control eyes and for the laser treated eyes with experimental glaucoma. The correlations from analyses of subjective and objective measurements provides support for the specific methods of translating the clinical measurements to neuronal populations and for the methods of dividing the visual field and TSNIT curve into sectors for comparison of spatial relationships (see Fig. 6). Therefore, the studies of experimental glaucoma in monkeys have produced a formalized model that provides the foundation for comparing glaucomatous neuropathy across measurements in patient populations.
5. Transitioning from experimental glaucoma to normal aging and clinical glaucoma in patients
The accuracy and precision of the model support the general methods for linking structure and function in normal eyes and for eyes with glaucoma, which might be extrapolated to clinical glaucoma. However, although experimental glaucoma is valid for the formalization of methods and the results provide a proof of principles that should generally hold for clinical glaucoma, there are obvious differences in monkeys and humans and in experimental and clinical glaucoma that must be considered prior to a generalization of these principles. For example, there are species differences with respect to: 1) the sizes of monkey eyes and human eyes, 2) the perimetry methods used with monkeys and patients, i.e., a full-threshold algorithm with an HFA I instrument versus the SITA strategy with an HFA II instrument, 3) age-related changes in patients that could not be evaluated in the homogeneous group of young-adult monkeys, 4) the relatively short timecourse of visual field defects for experimental glaucoma compared to the usually slow progression of disease in patients, and 5) the greater variability in measurements of visual sensitivity that is expected for SAP data from clinical patients compared to trained monkey subjects. These factors led to systematic investigations in which the basic model was applied and then modified to account for normal aging and the pathophysiology of glaucoma (Harwerth and Wheat, 2008; Harwerth, et al., 2008; Wheat, JL et al., IOVS 2007; 48: E-Abstract 491).
The preliminary clinical studies were undertaken to explore the potential for extending the structure-function model for experimental glaucoma to the clinical application of evaluating the stage of glaucomatous neuropathy in patients. These studies were designed, first, to differentiate between effects of normal aging versus glaucoma and, then, to relate structure and function in patients with primary open-angle glaucoma. The first studies of normal aging were necessary because, although the animal studies demonstrated that the measurements of visual sensitivities by SAP and RNFL thickness by OCT are both dependent on the underlying population of RGCs, the population of RGCs decreases with both aging and glaucoma. Consequently, an accurate interpretation of each measurement requires a differentiation between pathological losses from glaucoma and non-pathological, normal aging processes. The two causes of RGC loss must be considered separately because glaucoma patients are generally also elderly. Most clinical SAP and OCT instruments compensate for age-dependent effects by using normative data for the statistical comparison of an individual patient’s data. However, the comparison to normative data does not allow direct inter-instrument comparisons of measurements nor provide information about the amount of a patient’s neuronal loss from either aging or glaucoma.
Age-related losses of RGCs must be the primary cause of the age-related reduction in both visual sensitivity for SAP and thinning of the RNFL for OCT, but the rates are not equal (Harwerth and Wheat, 2008). The published data on aging indicates that the age-dependent rates of RGC loss is about 0.6%/year (Balazsi, et al., 1984; Mikelberg, et al., 1989; Jonas, et al., 1992; Blanks, et al., 1996; Harman, et al., 2000; Kerrigan-Baumrind, et al., 2000) compared to a RNFL thinning of 0.2%/year (Alamouti and Funk, 2003; Kanomori, et al., 2003; Ramakrishnan, et al., 2006; Hougaard, et al., 2006; Budenz, et al., 2007; Harwerth, et al., 2008; Sung, et al., 2009). The apparent methodology-dependence of measures of RGCs and axons should be reconcilable by adapting the structure-function model that had been developed in the animal studies. The initial adaptation of the model to account for the differences in the age-related functions was facilitated by analyzing the normative databases for SAP sensitivities and OCT measures of RNFL thickness. These normative data are based on large populations of normal observers and should provide well defined age-dependent functions for perimetry and imaging that can be used to establish the relationship between RGC somas and axons. The principal result of the analysis (Harwerth and Wheat, 2008) was that the apparent disagreement in age-dependent rates of losses of RGCs and axons in the RNFL can be reconciled by an age-dependent decrease in the proportion of the RNFL thickness that is comprised of axons. The assumption that the comparatively low rate of RNFL thinning is from an age-dependent remodeling in the RNFL was predicated on two findings, 1) the prior work on the relationship between SAP sensitivity and RGC sensitivity in both monkey (Harwerth, et al., 2004; 2005) and human subjects (Harwerth and Quigley, 2006) demonstrated a causal relationship while such relationships for OCT have not been established and, 2) in the analysis of the normative OCT data, calculations of the RNFL cross-sectional area that could be accounted for by axonal tissue decreased with age and produced systematic relationships between RGC numbers, RNFL thickness, and age (Harwerth and Wheat, 2008).
A similar analysis was conducted to compare the model of age-dependent soma and axon losses from normative data and was then tested on a group of normal control subjects, i.e., 55 subjects between the ages of 18 – 80 years with self-reported normal vision and SAP data classified as “within normal limits” by the Glaucoma Hemifield Test (GHT) (Harwerth, et al., 2008). The data for SAP were analyzed by methods that were similar to those described for relating the number of RNFL axons to SAP sensitivity described for experimental glaucoma, but with alterations to 1) account for the larger axial length of the human eye and 2) to compensate for the different decision rules for full-threshold and SITA thresholding strategies. Thus, equations 1 –3 (above) become:
| 6 |
| 7 |
| 8 |
| 9 |
Where the constant 1.32 in equations 6 and 7 is the ratio of human-monkey axial lengths to relate visual angles to retinal distances, gl is the number of RGCs (dB) in an area of the retina corresponding to a specific SAP test field location with a sensitivity of s. The constant −1 in equation 8 is a correction for the difference in full-threshold and SITA strategies (Bengston, et al., 1998, Artes, et al., 2002) and the constant 4.7 converts RGC density to total RGCs in the area of retina corresponding to a 6×6 deg area of the visual field (based on a conversion factor of 3.5 deg of visual angle per mm of retinal distance for the human eye). To obtain the total number of RGCs in a retinal area, gl, the numbers of RGCs are anti-logged and summed across the locations corresponding to that area. The results of the analysis for the total number of RGCs for the retinal areas sampled by the HFA 24-2 test (excluding sectors 5 and 6, see Fig. 6A) are represented by the circles in Fig. 8A. The rate of age-dependent reduction is 0.5%/year by the linear regression analysis, which is similar to published data (Blanks, et al., 1996; Harmon, et al., 2000; Kerrigan-Baumrind, et al., 2000).
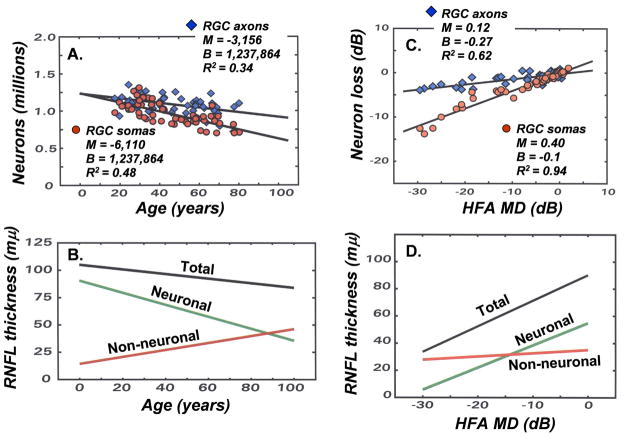
Figure 8.
Adapting the structure-function models for experimental glaucoma to human subjects by including age-dependent and stage-dependent variables for objective measures of RGC axons. (A) The decrease in the numbers of RGC somas as a function of age, using the modified relationships for the human eye (equations 6 – 9) is illustrated by the steeper linear function (parameters shown in the inset) and the decrease in RGC axons based on a constant density of axons in the RNFL is illustrated by the more shallow linear function (parameters shown in the inset). (B) To obtain agreement between the populations of RGC somas and axons, a model for the age-related thinning of the RNFL was proposed, in which the total RNFL thickness at each age represents the sum of two components of the total thickness, i.e., an age-dependent loss of neuronal tissue and a compensating increase of non-neuronal tissue, with the resulting axonal density in the RNFL and numbers of axons over a RNFL sector derived from equations 10 and 11 (figure adapted from Harwerth and Wheat, 2008). (C) The loss of neurons as a function of the perimetric index of disease severity (MD) based on the SAP visual sensitivities (steeper function, with parameters shown in the inset) or the OCT data with only compensation for the patient’s age (shallower slope, with parameters shown in the inset). (D) To obtain agreement between the populations of RGC somas and axons, a model for stage-dependent changes in RNFL thickness was proposed. The model is illustrated by data for 65 year-old patients, in which the total RNFL thickness at each stage of disease is determined by the sum of two components of the thickness, i.e., neuronal tissue thickness that decreases with the stage of disease and non-neuronal tissue that is relatively constant. The derived stage-dependent correction is described by equations 12 and 13.
The effects of aging on OCT measures, when based on an assumption that the axonal density is constant throughout life (diamonds, Fig. 8A), occur at a slower rate of 0.25%/year, which is consistent with recent studies of aging effects on RNFL thickness (Budenz, et al., 2007; Harwerth, et al., 2008; Sung, et al., 2009). Although there is overlap between the analyses of somas and axons, the trends represent an increasing divergence with age that is in agreement with the prior analysis of the normative databases. These differences in aging effects are most simply explained by a decrease in the proportion on axons in the total RNFL thickness that is illustrated diagrammatically in Fig. 8B by a model of the relative contributions of the neuronal and non-neuronal components to the total RNFL thickness. The model proposes that the number of neurons as a function of age is linear and the translation of RNFL thickness to numbers of axons is also linear. For patients with normal, age-dependent RNFL thickness by OCT, the number of RGC axons may be determined empirically by:
| 10 |
| 11 |
Where d is the density of axons (axons/μm2) for a patients of an age, ag, in years, a is the number of axons for a section of the RNFL scan with an mean height mh (μm) over px number of pixels, and 21.2 is the length per pixel (μm) for the standard 10.87 mm scan length.
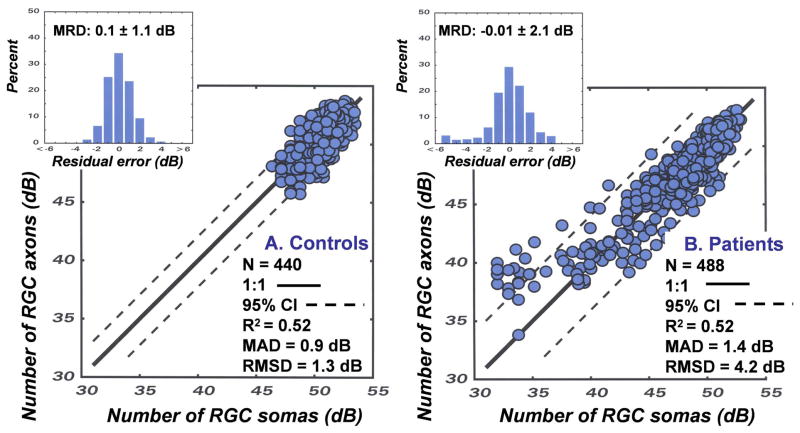
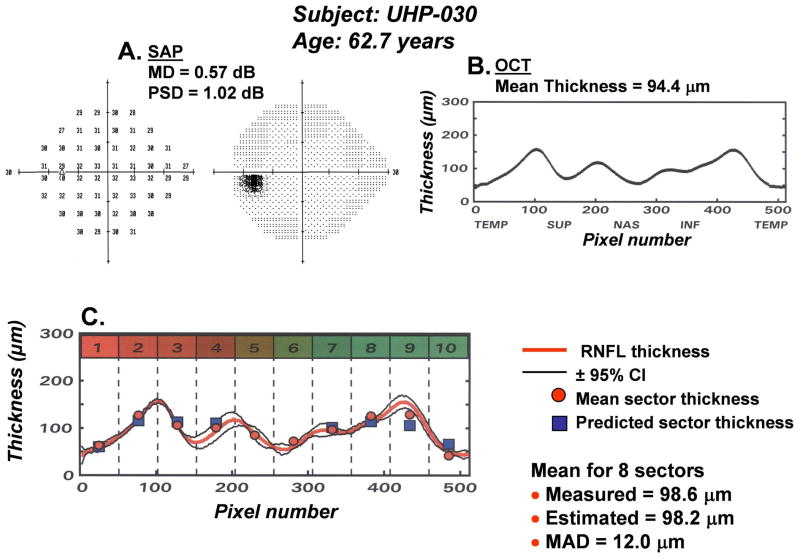
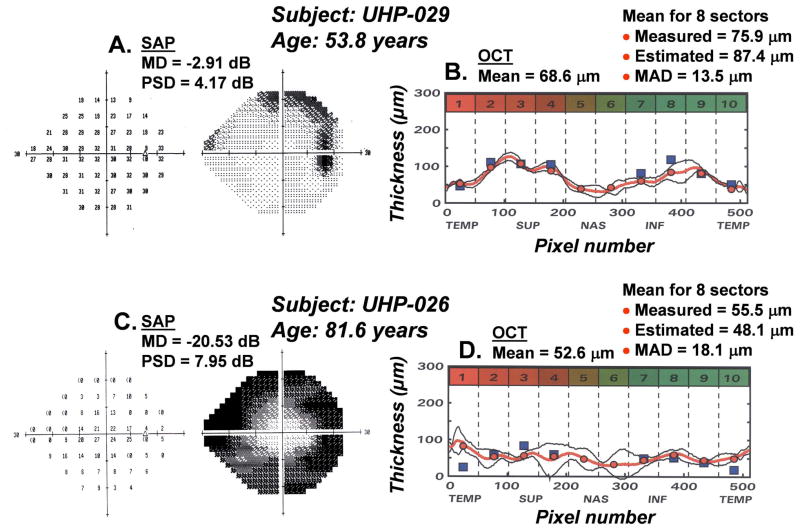
The results of an application of the model for predicting the number of RGC somas from SAP measurements and the number of RGC axons from OCT measurements are presented in Fig. 9A. The data represent the predicted RGC axons as a function of the predicted RGC somas for each of the 8 OCT scan sectors and SAP sectors for 55 subjects that vary in age from 18 to 80 years of age. It is apparent that the effects of aging are fully compensated and all of the data collapse to a single function with a total range of less than 10 dB of neurons per sector. The statistical indices for the goodness-of-fit of the modeled data indicate that it is accurate, (MRD = 0.1 ± 1.1 dB), precise (MAD = 0.9 dB and RMSD = 1.3 dB) and the model accounts for 52% of the variance of the data. These findings are evidence of a quantitative structure-function link for non-glaucomatous eyes and suggest that a similar application for glaucomatous eyes is worthwhile.
Figure 9.
Applications of the structure-function model to relate neuronal populations as measured by OCT and SAP. Data are presented for normal controls (A) and glaucoma suspects and patients with glaucoma (B). The details for the analyses and statistical indices for the goodness-of-fit are as described for Fig. 7.
The SAP and OCT data of 60 eyes of 32 patients (age = 62.5 years ± 15.5 years) with glaucoma, or suspected glaucoma (MD = −6.74 dB ± 8.66 dB, OCT = 77.1 μm ±19.4 μm) were analyzed by the same procedures described for normal eyes (Wheat, JL et al., IOVS 2007; 48: E-Abstract 491). The results revealed a discrepancy between the neuronal populations predicted by the two measures that increased with the stage of the disease. The systematic divergence between measures with severity of glaucoma is illustrated in Fig. 8C. The data represent the amount of loss of RGC somas and axons (in dB units), summed across the visual field or scan length (excluding sectors 5 and 6), as a function of the HFA mean deviation (MD) index for severity of visual field defects. In order to present neuronal losses in a way that is conceptually similar to MD, the data represent differences between the neuronal populations derived from a patient’s SAP or OCT data and the expected values for an age-equivalent normal subjects found in the study of normal aging effects. As shown by Fig. 8C, both functions represent decreased populations of neurons with decreased MD as expected, but with compensation for normal aging alone, the rate of loss of axons is not accurate. It is interesting that the function for SAP suggests that MD is a measure of the global loss of RGCs with a slope of 0.4 dB/dB, i.e., a 6 dB reduction on MD represents a 2.4 dB loss of RGCs, and, if the structure-function link is pure, then the decrease in axons should be equivalent.
The concordance of the measures of neural loss requires a model based on principles that are similar to the model for normal aging effects, i.e., remodeling of the RNFL axonal and non-axonal composition, which is presented diagrammatically in Fig. 8D. The functions for the example were based on calculations for 65 year-old patients. At an age of 65 years, the normal RNFL thickness is about 86 μm, while a patient with a glaucomatous loss of −30 dB MD would have a thickness of 43 μm. The corresponding loss of the neuronal component is from 60 μm to 5 μm and the increase in the non-neuronal component is from 26 μm to 38 μm. Thus, while the total loss of RNFL thickness is a sum of neuronal and non-neuronal components, the non-neuronal component changes little compared to the neuronal component and, after adjusting for normal aging, most of the thinning of the RNFL in glaucoma occurs from the loss of axons, which is consistent with clinical data and the SLM model proposed by Hood and Kardon (2007). For the present application, a term related to the stage of disease was introduced into the structure-function model to determine the correction for the non-neuronal component for individual patients with various stages of disease.
| 12 |
| 13 |
Where c (in dB units) is the correction factor for the stage of glaucoma denoted by the MD index, ax is the logarithmic value (in dB units) of the age-corrected population of axons, (the value for a is from equation 11) after adjustment for the stage of disease. However, the MD index is a global index that describes the average loss over the entire visual field, but there are regional variations in glaucomatous visual field defects that make it inappropriate to use the global MD for the stage-dependent correction in a sector-by-sector analysis. To derive a stage correction that is modified for localized areas, the MD-equivalent values for each sector of the 24-2 visual field (see Fig. 6) were calculated by comparing the individual patient’s data to the age-dependent expected values obtained from the normative database for the SITA strategy. The parameters for expected average SAP sensitivity for each sector (presented in Table 2) indicate that the age-related rates (slopes) of reduction in sensitivities are very similar for all of the sectors, while the intercepts reflect an expected eccentricity-dependent variation in SAP sensitivity. Thus, the MD modified for sectors (mean SAP sensitivity minus the expected mean sensitivity) is comparable to the global MD and is used for the calculation of a stage-dependent value for c, which is used in equation 13 to predict the number of axons in each sector of the TSNIT function.
Table 2.
Slope and intercept parameters for linear functions to determine the age-expected average of normal sensitivities across the test locations in a given sector of the HFA 24-2 perimetric field, which corresponds to a sector of the RNFL thickness scan, as presented in Fig. 6. The modified sector-MD is the average measured SAP sensitivity for a sector minus the expected average SAP sensitivity derived from the linear function with slope and intercept parameters listed in the table. The sector-MD is used in equation 12 to derive a stage-dependent correction, c.
| Sector number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Slope (dB/year) | −0.057 | −0.061 | −0.060 | −0.062 | −0.060 | −0.057 | −0.061 | −0.057 | −0.062 | −0.060 |
| Intercept (dB) | 34.68 | 33.60 | 33.32 | 31.68 | 32.43 | 31.68 | 31.19 | 33.46 | 33.01 | 34.45 |
The results of an application of the model to glaucoma patients and suspected patients, incorporating both normal aging and stage-dependent variables, are presented in Fig. 9B. The data are based on measurements from the 60 eyes of 32 patients and represent the predicted RGC axons as a function of the predicted RGC somas for each of the 8 OCT scan sectors and SAP sectors for each of the eyes. The data for the patients with glaucoma, along with the goodness-of-fit statistics, are presented in the same format as the data for normal subjects in Fig. 9A. Obviously, the range of data for the eyes of glaucoma patients is much larger, but in most respects the predictive value of the model is similar for glaucomatous and normal eyes. The overall accuracy (MRD = −0.01 ± 2.1 dB) and precision (MAD = 1.4 dB, RMSD = 4.2 dB, and R2 = 0.52) are comparable with the normal eyes, but there is a group of data from patients with advanced glaucoma that cluster at, or outside, of the 95% confidence limit. These data are from sectors with MDs less than −25 dB, which in the range where neural-sensitivity function approaches its intercept and fails to predict the density of RGCs with accuracy. On the other hand, the accuracy and precision of the relationship is high for global MDs greater than −20 dB, which is the range that is most important for the management of glaucoma (Bengtsson and Heijl, 2008).
As a whole, the analyses of the structure-function effects of normal aging and glaucoma have produced empirical methods for compensating for the non-neuronal components of the RNFL to find the numbers of RGC axons. The heuristic inclusion of specific functions for the effects of aging and disease severity is motivation for additional studies of structure-function modelling for direct comparisons of objective and subjective measurements and the assessment of the amount of a patient’s neuronal loss from aging and/or glaucoma. However, it is also important to apply the model to additional patient populations and to examine alternative models.
6. Applications to an independent population of patients and comparison to a linear structure-function model
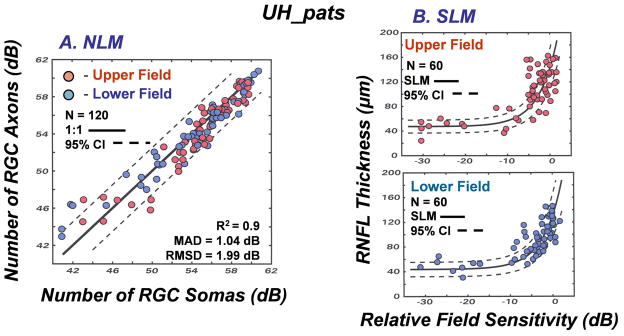
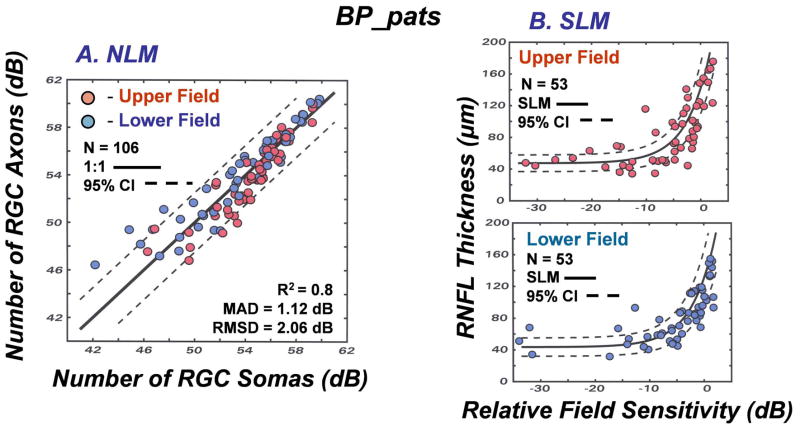
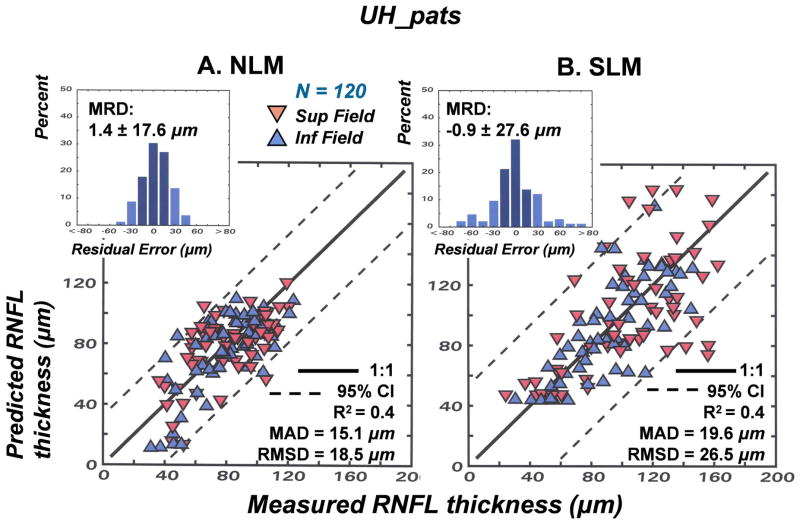
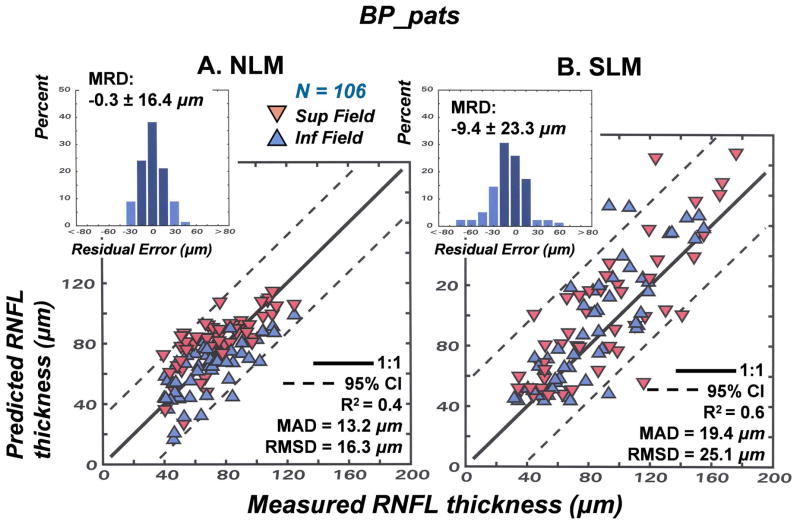
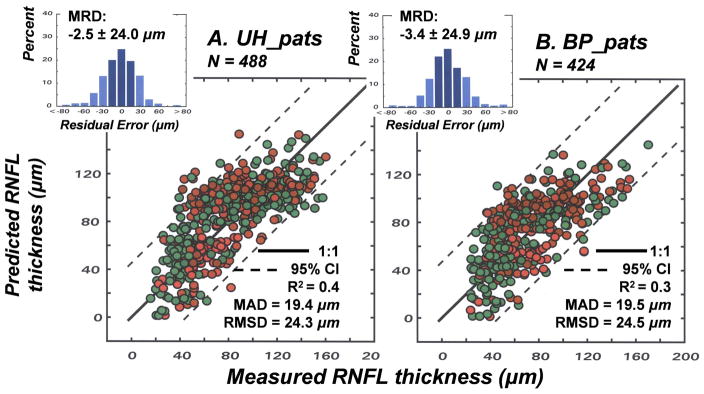
The results of the studies of normal aging and glaucomatous neuropathy support the application of the structure-function model to evaluate correspondence between subjective testing and objective measurements of neuronal losses in patients. However, it is an empiric model and, up to this point, the data used to develop the model were also used to test the model. Thus, although it seems obvious that different glaucoma patient populations will be very similar, the model needs to be applied to an independent population. Another issue that is important to consider is whether alternative models produce similar, or better, links between structure and function in glaucoma. The NLM model evolved through systematic modifications needed to account for normal aging and the severity of the disease, with all of the input data based on the individual patient’s data, rather than constants or free parameters. In each case during the development of the model, the approach was based on the authenticity of the SAP data, because of the histological evidence for a precise nonlinear relationship between visual sensitivity and RGC density that is independent of aging or stage of disease (Harwerth, et al., 2004; 2005; Harwerth and Quigley, 2006). However, other models based on different assumptions have been proposed and it is not clear whether the differences are substantive.
An alternative quantitative model has been proposed with an objective of correlating visual sensitivity from SAP measurements to the RNFL thickness derived from OCT measurements using essentially the same input data as described above (Hood, 2007; Hood and Kardon, 2007; Hood, et al., 2007a, 2007b). Although based on the same clinical measurements some of the assumptions of the two structure-function models are quite different, especially with respect to the translation of visual sensitivity to RGC populations, i.e., whether it is linear or nonlinear relationship. It is unknown, however, whether the differences in underlying assumptions will result in significant differences in the accuracy and precision of the predicted relationships between RNFL thickness and SAP sensitivity. For this reason, studies were undertaken to compare the accuracy and precision of linear versus nonlinear structure-function models of glaucomatous optic neuropathy for two patient populations, one from the University of Houston that has been described above and another group of patients from Bascom Palmer Eye Institute that has been described in other studies (e.g., Fredette, et al., 2008; Budenz, et al., 2008).
The linear model for structure-function relationships was based on analyses of RGC density and visual sensitivity that suggested a linear relationship when visual sensitivity was scaled as the reciprocal of light intensity and RGC density was adjusted for spatial summation (Garway-Heath, et al., 2000). Recently, a comprehensive form of the linear model, called the simple linear model (SLM), has been developed and tested on several forms of optic neuropathy, including glaucoma (Hood, et al., 2007a) and ischemic optic neuropathy (Hood, et al., 2007b). The model has been described in detail (Hood and Kardon, 2007), but in brief, the SLM assumes that the total RGC loss is proportional to the mean SAP total deviation over the superior or inferior locations in the arcuate bundles, using the map of visual field to optic disc proposed by Garway-Heath, et al., (2000). The structural component of the SLM proposes that RNFL thickness is proportional to the number of RGC axons plus a non-neuronal thickness that is constant across age and stage of disease. The formalization of the SLM can be expressed by four functions (Hood and Kardon, 2007).
| 14 |
| 15 |
| 16 |
| 17 |
Where rs is the relative sensitivity (in dB units) in either the superior or inferior arcuate region of the visual field, d is the SAP total deviation in dB units (i.e., the measured sensitivity minus the expected sensitivity for an age-matched normal patient) for a given test location in the visual field, and n is the number of SAP test locations in the arcuate region of the visual field. The RNFL thickness, R, is a function of the expected normal thickness, s0, for a patient with normal SAP data, T, the relative reduction in visual sensitivity and, b, the minimum residual thickness of the RNFL.
The comparison of the NLM (equations 6–13) and the SLM (equations 14–16) suggests that the most important differences between the NLM and SLM are: 1) The NLM is based on a logarithmic relationship between visual sensitivity and ganglion cell density, with a pointwise linear relationship when both visual sensitivity and ganglion cell density are in decibel units. The SLM proposes that the reduction in RGC density is proportional to the average age-adjusted difference between the expected and measured visual sensitivity, i.e., RGC loss is proportional to the antilog of SAP total deviation at each test location. 2) In the NLM the SAP sensitivity versus RGC density functions vary with eccentricity, but in the SLM the SAP sensitivity versus RGC density relationship is based on age-adjusted visual sensitivity at each eccentricity. 3) The third factor concerns the compensation for the amount of non-neuronal tissue contributing to the OCT measurement of total RNFL thickness. The SLM proposes that the non-neuronal component is constant for all ages of patients and stages of glaucoma while the NLM includes two variables, an age-dependent and a stage-dependent variable, to account for the difference between total thickness and the number of axons in the RNFL, but as illustrated by Fig. 8D the practical effects of a stage-dependent thickness versus a fixed residual thickness are relatively minor.
In order to evaluate the nonlinear and linear models directly, a study was designed to compare the models with respect to predicting RNFL thickness from SAP data. Both models are based on the correlation of a parameter related to RNFL thickness to a parameter derived from SAP measurements and, thus, for the present analysis, the SAP measurements were used to predict the RNFL thickness over a region of the OCT scan, which was compared to the measured thickness. For the NLM, two broad regions that corresponded to the superior (sections 7 – 10, Fig. 6) and the inferior (sections 1 – 4) of the OCT scan and visual field were analyzed. The methods for estimating the total number of RGCs for the sections of the visual field were described in equations 6 – 10. The total number of RGCs was substituted for the number of in axons in equation 13 and, using the age (d) and stage (c) corrections, the average RNFL thickness over the appropriate scan length was determined by equation 11. However, as was described in the previous section, because glaucomatous neuropathy is often asymmetrical between the hemifields, the global MD cannot be used as a measure of disease severity for these clinical investigations. Instead, a modified MD was derived separately for the superior and inferior hemifields by subtracting the expected mean sensitivity, derived from data from normal eyes (Harwerth, et al. 2008), from the average sensitivity for the hemifield locations.
The application of the SLM was straightforward using the methods described by Hood and Kardon (2007), in which the RNFL thickness derived from equation 15 or 16 was compared to the RNFL thickness from OCT measurements for the region of the scan that corresponds to the scan locations in the Garway-Heath, et al., (2000) map of the visual field onto the optic nerve head. For this application, the values for s0 and b for the superior and inferior fields were taken from the population averages provided by Hood and Kardon (2007).
Two independent populations of patients were used to compare the models; a group from the University of Houston Clinic (UH_pats) and a group from Bascom Palmer Eye Institute (BP_pats). The data for the BP_pats are unique in that the measurements for each test on each patient were repeated five times; otherwise the two populations are generally similar. As described above, the UH_pats data were SAP and OCT measurements from of 60 eyes of 32 patients (age = 62.5 years ± 15.5 years) with glaucoma or suspected glaucoma (MD = −6.74 dB ± 8.66 dB, OCT = 77.1 μm ±19.4 μm). The BP_pats data were the mean SAP and OCT measurements for 53 eyes of 50 glaucoma patients and 3 controls (age = 69.2 years ± 11.0 years, MD = −6.72 dB ± 7.06 dB, OCT = 68.9 μm ± 18.7 μm) based on five measurements that occurred within an 8 week period.
The applications of the two models, as they have been implemented previously, are presented separately for the UH_pats (Fig. 10) and the BP_pats (Fig. 11). The data for the NLM model (Figs. 10A &11A) represent the number of RNFL axons estimated from RNFL thickness as a function of the number of RGC somas predicted from perimetry, which is similar to Fig. 9 B except that the data are averaged over the superior or inferior hemifield instead of over the individual sectors. The data can be compared to the unity relation (solid line) and the 95% limits of agreement for the model predictions and measured thickness (dashed lines). It is important to note that the results of applying the NLM to two independent datasets are very similar (cf. Figs. 10A and 11A), both in terms of the accuracy and the precision. This comparison demonstrates that, although the empirical parameters of the model were derived from the data of one population of glaucoma patients, the model can be generalized to other patient populations with equal results.
Figure 10.
Structure versus function relationships in glaucoma analyzed by nonlinear and linear models for the patients from the University of Houston (UH_pats). (A) The NLM for relating the numbers of RGC axons and RGC somas that is described by equations 6 –13. The analysis was applied separately to SAP and OCT data representing the superior and inferior hemi-fields, with resulting statistical indices shown as graph insets. (B) The SLM for relating the RNFL thickness to the relative visual sensitivity from SAP measurements. The methods described by Hood and Kardon (2007) and reproduced by equations 14 – 17 were used to analyze data for the superior and inferior fields separately. The functions superimposed on the data were constructed using parameters from Hood and Kardon (2007).
Figure 11.
Structure versus function relationships in glaucoma analyzed by nonlinear and linear models for the patients from the Bascom Palmer Eye Institute (BP_pats). All of the other details are as described for Fig. 10.
The data from an application of the SLM are presented in Figs. 10B and 11B, by plots of the mean RNFL thickness as a function of relative sensitivity. The SLM was applied separately for data from the superior (upper plots) and inferior (lower plots) visual fields using the parameters published by Hood and Kardon (2007) for the model (solid line) and the 95% limits of agreement (dashed lines). By visual inspection, it is apparent that both models capture the major trends of the data, with the RNFL thickness changes in concert with reduced visual sensitivity, but in the separate forms it is difficult to compare their accuracy and precision. Therefore, the patient data were reanalyzed to compare predictions of RNFL thickness from measurements of visual sensitivity by SAP by common statistical indices of the goodness-of-fit between modeled and measured data.
The results of the analyses are presented in Fig. 12 for the UH_pats and in Fig. 13 for the BP_pats, with the NLM analysis in the right panels and the SLM in the left panels. In each case, the modeled RNFL thickness as a function of the measured RNFL thickness is presented in the main graph, with the 1:1 line and 95% confidence limits indicated by the solid and dashed lines, respectively. The accuracies of the models can be compared by the distributions of residual errors, with respect to the unity relationship, that are presented by the inset histograms, with the MRD values shown on the graph. The precision of the relationships can be assessed by the coefficient of determination (R2), the MAD, and the RMSD values presented as insets to the main graph.
Figure 12.
Applications of the NLM and SLM to predict RNFL thickness from SAP measures of visual sensitivity for the UH_pats. (A) To derive the relationship using the NLM, the total number of RGC somas for the superior and inferior fields, via equations 6 – 9, was substituted for the number of axons in equation 13 to back-solve for the mean thickness in equation 11. (B) The relationships for the SLM were derived from the thickness vs. sensitivity relations (equations 14 – 17) that are shown in Figs. 10 and 11 for the superior and inferior fields. The evaluations of the goodness-of-fit between the modeled and measured thicknesses for the NLM and SLM are the same as described for Fig. 7.
Figure 13.
Applications of the NLM and SLM to predict RNFL thickness from SAP measures of visual sensitivity for the BP_pats. All of the other details are as described for Fig. 12.
Interestingly, the accuracies are relatively similar across models and datasets, with only one instance where the difference between predicted and measured thickness was greater than approximately 1 μm, and in that case the SLM predicted an average RNFL thickness that was 9 μm greater than was measured by OCT (see Fig. 13B). The range of thickness values for the SLM is larger than for the NLM because the SLM analyzes a relatively narrow portion of the OCT scan near the two maxima of the TSNIT curve, while the NLM, as applied here, is based on a mean thickness of the scan corresponding to most of the superior or inferior visual field. The larger range of thickness values also is associated with a greater variance of the data for the thicker RNFLs, i.e., the data associated with early- to mid-stage glaucoma. The heteroscedasticity of the SLM is reflected in the statistical goodness-of-fit indices, with MAD and RMSD values, and the SD of the residual errors, that are 40 – 50% larger for the SLM compared to the NLM analyses. These comparative characteristics of the NLM and SLM are predictable from the comparison of the structure-function relationship for perimetry (see Fig. 1) that demonstrated that the linear relationship between SAP sensitivity and RGC density was less precise than the NLM (Harwerth, et al., 2005). It can, therefore, be concluded that the major difference between nonlinear and linear models lies in the translation of visual sensitivity to its neuronal substrate, rather than differences in the analysis of RNFL thickness. However, these parameters and methods of separating the contributions of neuronal and non-neuronal tissue to the total thickness are important to obtain quantitative agreement between the subjective and objective measures of glaucomatous neuropathy.
For both models, the mean RNFL thickness predicted for SAP measurement was within ±22 μm of the measured RNFL thicknesses approximately 75% of the time, indicating that they are equivalent in terms of the accuracy for describing group data. On the other hand, for application to individual patients, especially patients with early disease, the SLM will be less precise in providing inter-test confirmation of the presence of neural loss or the stage of neuropathy, as is illustrated by comparison of the 95% limits of agreement for the two models. The results were consistent for both patient databases, with the results of the applications of the models to the UH_pats and BP_pats essentially identical, indicating that the application does not depend on a specific patient population.
7. Mapping perimetric neural losses onto the TSNIT curve of nerve fiber layer thickness
An important component of the relationship between RNFL structure and SAP function in glaucoma is to define the spatial relationship between the thinning of the RNFL and the reduction of visual sensitivity. The basis for such spatial relationships has been suggested by investigations of the relations between regions of the OCT scan and visual field locations, which have suggested that the areas of neural loss identified by a reduction of visual sensitivity should be correlated to thinning in specific regions of the RNFL (Gardiner, et al., 2005; Harwerth, et al., 2007; Kanamori, et al., 2008; Ferreras, et al., 2008; Sato, et al., 2008; Horn, et al., 2009). These descriptions of correlated relationships between visual field defects and peripapillary RNFL thickness have led to several different proposals for mapping the visual field onto the ONH (Harwerth, et al., 2007; Kanamori, et al., 2008; Ferreras, et al. 2008), but few have reported systematic relationships between the visual sensitivity and the RNFL thickness (Harwerth, et al., 2007; Hood and Kardon, 2007). However, a complete structure-function model would include a spatial correlation of SAP and OCT measurements, with scaling to provide a quantitative correlation of the neuronal losses from RNFL thinning and visual field defects over the length of the TSNIT curve of RNFL thickness. Therefore, to complete the studies of the links between structure and function in glaucoma, further analyses of the data from the UH_pats and BP_pats were undertaken to determine whether the neural losses that are predicted by perimetric visual field defects can be directly correlated in magnitude and the location of RNFL thinning. The investigation involved an application of the structure-function model to translate SAP sensitivities to RNFL thicknesses (see Figs. 12A and 13A), which were mapped onto the TSNIT curve of RNFL thickness using the relationships described in Fig. 6 (Harwerth, RS et al., IOVS 2009; 50: E-Abstract 3517).
Examples of the results of the function-to-structure mapping for one of the UH_pats (UHP-030) are presented in Fig. 14. The patient was identified as a “glaucoma suspect” because of a suspicious ONH, but she was not being treated and the visual field (Fig. 14A) and nerve fiber layer (Fig. 14B) measurements were within the age-expected normal range. The representation of the function-to-structure analysis are presented in Fig. 14C, in which the mean TNSIT data are re-plotted as the heavy solid line and the ±95% CIs as a function of pixel location are plotted as thin lines. The 95% CIs were based on 2 SD units for the three scans and smoothed by the sum of 50% of the nominal pixel height plus 25% of each of the two adjacent pixels.
Figure 14.
An example of a method for mapping perimetric neural losses onto the TSNIT curve of RNFL thickness. The plan for mapping SAP areas onto sectors of the OCT scan described in Fig. 6, was used to derive an estimate of RNFL thickness from SAP measurements (A) and compared to the measured thickness from OCT measurements (B). The results for a glaucoma suspect with normal SAP and OCT are presented (C), with the RNFL scan shown by the thick solid line and the 95% CIs, based on three repeated measures, as the thin lines. The mean RNFL thicknesses from the OCT measurements are indicated by the solid circle at the mid-point of each sector and the RNFL thicknesses that were predicted from the corresponding SAP measurements are presented as the solid square symbols.
The individual sectors of RNFL thickness are marked by the dashed lines, with the mean thickness per sector shown by the circle symbols at the mid-point of each sector. The square symbols in the TSNIT sectors represent the RNFL thickness of the axonal representation from the groups of corresponding visual field locations, as described in Fig. 6. The structure-function model was applied to derive the mean RNFL thickness from the visual sensitivities associated with the SAP field locations corresponding to each TSNIT sector. The RNFL thickness calculations were made for only 8 of the 10 sectors because, as is apparent from the SAP data (Fig. 14A), there is very little of the retinal area nasal to the ONH that is sampled by perimetry, and the under-sampling negates the derivation of thickness from SAP data. For the 8 sectors with sufficient sampling, the degree of agreement between the measured and predicted thickness values can be judged visually by the size of the square symbols, which are scaled to 20 μm in height.
In this example, the agreements between the measured and modeled thicknesses for UHP-30 are excellent in most sectors, with only sectors 9 and 10 having differences greater than 20 μm. The MAD across the eight sectors is12 μm, but the difference between the mean measured and modeled thicknesses is less than 1.0 μm.
To demonstrate the results for glaucoma patients, representative data are presented in Fig. 15 for a patient with early glaucoma (UHP-29) and a patient with an advanced stage (UHP-26) of disease. The results are presented in the same form as for the glaucoma suspect, with the SAP data used to derive thickness values presented in Figs. 15A&C and OCT thickness data, along with the function-to-structure data presented in Figs. 15B&D. For both patients the degree of agreement between the measured and modeled data is very good, with only a few points falling outside the 20 μm symbol size. By visual inspection, for UHP-29 there is one TNSIT sector, sector 8, which represents part of the arcuate bundle from the superior visual field, where the visual sensitivity predicts a thicker RNFL than was measured. However, on average the agreement is reasonable; with a MAD across all eight sectors of 13.5 μm and a comparable difference between the mean measured and modeled thicknesses of 11.5 μm. Similarly, the data for UHP-26, a patient with advanced glaucomatous losses, are consistent across SAP and OCT measurements. The degree of variability of the OCT scans is noticeably larger in the nasal portion of the circumpapillary scan circle, but there are only two sectors where the difference between predicted and estimated values are about 50 μm, sectors 1 and 10 the primary SAP locations with RGC axons forming the papillomacular bundle and the SAP sensitivities are lower than would be predicted from the TSNIT thickness in the corresponding RNFL sections. The MAD across all eight sectors of 18.1 μm and a difference between the mean measured and modeled thicknesses of 7.4 μm demonstrates agreement between the functional and structural measurements.
Figure 15.
Examples of mapping perimetric neural losses onto the TSNIT curve of RNFL thickness for a patient with early glaucoma (A,B) and a patient with advanced glaucoma (C,D). The details of comparing the subjective and objective data are as described for Fig. 14.
The results for all of the patients are presented in Fig. 16A for the UH_pats and in Fig 16B for the BP_pats. The format of the data presentation is the same as Fig. 13, i.e., the main plots represent the relationship between the modeled and measured thicknesses for each of the 8 SAP and OCT sectors for all of the patients and the insets present the distribution of residual errors between the modeled and measured data. All of the statistical indices for the goodness-of-fit are remarkably similar for the two patient populations, with MRDs and 95% limits of agreement that reflect an accurate and precise relationship. Overall, the MRDs were small (2 – 3 μm), but the RMSDs were about, 24 μm. When applied to individual patients, about 26% of the time the modeled data was < 8 μm of the measured thickness, and for 65% of the patients the predicted thickness was within 22 μm of the measured thickness. On the other hand, the indices of variance between modeled and measured data are larger for this sector-by-sector analysis than for the prior analyses that were based on the means for hemifields (Figs. 12A and 13A). The differences are probably as result of reducing variability in sensitivity measures by averaging across more locations for the hemifield analysis and because the hemifield analysis does not require a strict relationship for mapping the visual field onto the ONH. For the sector-by-sector analysis, individual differences in the locations of the maxima of the TSNIT curve will introduce variability that is not present in the hemifield analysis.
Figure 16.
The relationship between the RNFL thicknesses predicted from SAP measurements as a function of thicknesses measured by OCT. Data from the UH_pats (A) and BP_pats (B) were analyzed separately. The symbols are shaded to indicate the SAP and RNFL sectors represented, as illustrated in Fig. 6. The statistical indices to evaluate the goodness-of-fit between the modeled and measured thicknesses for the UH_pats and BP_pats are the same as described for Fig. 7.
The examples for the individual patients were relatively representative of the full population of patients in that the residual errors are generally for single isolated sectors rather than systematic errors over a range of sectors. However, it is important to note that the patients enrolled in the studies were experienced with perimetry. Also, while doing the OCT scans special care was taken to get the best signal strength possible for each patient. These elements of the research datasets might have contributed to a stronger correlation than could be expected in a more general practice setting. However, even for this population, if there are cases where the residual errors were consistent in direction across sectors, then it is important to consider that the model might have failed. There were not any patients with consistent residual errors across the entire TSNIT curve, but there were a few with consistent errors over three sectors that represent most of a hemifield. The two primary conditions for this circumstance were; 1) a highly localized field defect that caused localized thinning of the measured RNFL thickness, but was not localized in the modeled RNFL thickness and 2) false-positive errors that did not exceed the reliability criterion but, nevertheless, caused a “trigger happy” result of a greater thickness for the modeled RNFL thickness than the measured thickness.
The overall results from these initial studies to map perimetric neural losses onto the TSNIT curve of RNFL thickness support the general validity of the approach. The methods may be improved by refining the system of dividing SAP test locations to specific portions of the OCT scan, perhaps by creating a method of adjusting the map on an individualized basis. On the other hand, the logarithmic scaling of visual stimuli during threshold measurements by SAP creates a degree of variability for scaling to a linear measure of RNFL thickness. However, even in this form, the method of presenting the results of functional testing as a direct comparison to the results from objective testing provides a visual analysis for confirmation of inter-test agreement, but it must be determined whether disagreements constitute evidence of structural defects preceding function losses, or vice versa. The basis for such an application of the concepts will require larger prospective studies.
8. Future directions and conclusions
This review was intended to describe processes and considerations that are important in defining the links between structure and function in glaucoma. It is a specific attempt to quantitatively relate the known pathophysiology of the disease with two common clinical measures used in the diagnosis and management of clinical patients. The general approach was to modify a model based on the relationships that had been found for visual sensitivity and corresponding RGC densities of monkeys with experimental glaucoma, in order to develop a clinical model for patients with glaucoma. The step-wise computations of structure and function relationships to relate both visual sensitivity and RNFL thickness to the population of RGCs includes factors to account for eccentricity variations, normal aging effects and the stage of glaucoma. The inclusion of three independent parameters raises a question of whether the goodness-of-fit justifies the complexity of the model. Overall, the trade-off seems balanced, because each component was based on normal physiology and the mechanisms of disease, and each parameter improved the goodness-of-fit substantially. Further, it was shown (cf., Figs. 12A and 13A) that the model does not over-fit the data because, although it was developed with data from one population (UH_pats), it was equally applicable to another population (BP_pats). The final formalization, as presented, produced a good overall accuracy of estimating RNFL from SAP data, but the precision was relatively low with respect to the dynamic range of measurements by OCT. The lack of precision is likely to be the result of, 1) deriving RNFL thickness on a linear scale from SAP data measured on a logarithmic scale and 2) inter-subject variations in the maxima of the TSNIT curve and variability in mapping the visual field onto the optic nerve head. This point is supported by the analysis of hemifields, rather than sectors, which reduced both the MRD and RMSD.
Another important application of the linking propositions suggested by the model is to provide a basis for the development and testing of hypotheses that may lead to a better understanding of the relationships between subjective and objective methods of determining the stage of optic neuropathy. In this respect, the formulation of relationships, described here as the NLM, must be considered as one approach among others. Specifically, alternative models based on a linear relationship between visual sensitivity and RGC density (SLM) also describe a systematic relationship between SAP and OCT measurements (Hood and Kardon, 2007). There are several aspects of the models that distinguish them, but the comparison of results based on the same patient populations indicated the most important difference is the modeled neural basis for visual thresholds, i.e., a linear or logarithmic relationship (Figs. 12 and 13). One other difference in the NLM to SLM comparison is that the NLM does not depend on a normative database - all of the input data are taken from the individual patient’s OCT and SAP measurements and the analysis covers the full area of retina assessed by the locations of the HFA 24-2 test grid, which provides data that can be mapped onto the TSNIT curve of RNFL thickness.
The methods developed to compare SAP sensitivity data and OCT thickness data on a common scale have suggested a remodeling of RNFL tissue in response to the loss of RGC axons from either aging or glaucoma. An increase in non-neuronal support tissue has been demonstrated histologically by increased glial cell density in human donor eyes with glaucoma and monkeys with experimental glaucoma, compared with control eyes (Varela and Hernandez, 1997; Wang, et al., 2002; Morgan, et al., 2006; Grieshaber, et al., 2007; Hernandez, et al., 2008). Preliminary data from confocal imaging of the RNFLs of monkeys with experimental glaucoma have demonstrated that, compared to the control eyes, the laser-treated eyes have a significant decrease in the proportion of actin staining elements, indicating a loss of RGCs, and an increase in the proportion of GFAP staining elements, indicating an increase in glial tissue (Wheat, JL et al., IOVS 2009; 50: E-Abstract 5826). However, additional data from these histologic analyses must be gathered to determine whether the relationships predicted by the structure-function model will be confirmed.
On the other hand, the empirical findings are sufficiently strong that the model does not hinge on precise definitions of remodeling mechanisms, but rather the accurate prediction of a patient’s functional status from objective measurements of RNFL thickness has considerable merit in itself. These empirical results provide motivation and guidance for future directions for research on both clinical and experimental glaucoma. For example, it is unknown whether there is application in clinical practice, in a situation where the patients are not selected to provide reliable visual fields and good quality RNFL scans. Even more importantly, the number of significant disagreements between modeled and measured thickness was too small to determine which result was invalid or how the disagreements could be used in the clinical management of glaucoma. Alternatively, the correlation of results may be tightened by modifications of the map of the visual field onto the ONH, or even developing methods to refine the mapping for individual patients. Thus, another area of future consideration is to determine whether the data from the subjective and objective measurements of optic neuropathy can be combined by a form of probability summation to decrease the level of visual or RNFL defect required for diagnosis or assessment of progression.
Several different aspects of linking structure and function in glaucoma have been explored, which are important in understanding subjective and objective measurements of glaucomatous neuropathy. Perhaps the most fundamental aspect was the relationship between RGC density and visual sensitivity for clinical SAP. The definitions of these structure-function links provided a method of determining RGC densities from SAP measures, which allowed quantification of the properties of SAP with respect to; 1) the dynamic ranges of measurements, 2) the numbers of remaining RGCs when the highest stimulus intensity is too low to elicit a positive response from the patient and, 3) an interesting theoretical calculation of the stimulus intensity at threshold for a single neural detector at each eccentricity. Subsequently, it was shown that the structure-function relationship that was defined for SAP is not directly transferrable to alternative procedures, such as contrast sensitivity perimetry. Therefore, the formulation and application of linking propositions was based on the standard white-on-white clinical perimetry, with an understanding that the relationships between visual sensitivity and RNFL thickness will probably need to be modified for other forms of perimetry such as SWAP, FDT, or FDF perimetry.
The nonlinear model that was developed through these studies produced closely correlated relationships between structure and function for normal eyes and eyes with various degrees of glaucoma, with the exception of very advanced stages. The relationships across the range of normal vision to early glaucoma did not suggest that either significant structural defects preceding functional defects, or functional defects preceding structural defects, could be detected by the clinical tests employed for the investigations. This result is in agreement with suggestions that the occurrence of non-concordant events is likely to be from the magnitude of change required to reach clinical significance with respect to the normal population variance (Harwerth, et al., 2004; 2007; Hood and Kardon, 2007). On the other hand, it may be that the model is insensitive to the early alterations in function from RGC injury that have been reported for electrophysiological measures by both pattern ERGs in clinical patients (Ventura, et al., 2006) and single-cell physiology in experimental glaucoma (Weber and Harman, 2005; Weber, et al., 2008).
It also seems likely that the sensitivity for detecting losses of RGCs by either SAP or OCT is less than the sensitivity of detecting clinical cupping of the optic nerve head. Recent studies of experimental glaucoma in monkeys found that the clinical signs of ONH cupping occurred with axonal losses of only 16 – 30% (Yang, et al., 2007), which are levels not likely to be detected by standard clinical SAP or OCT measures. Thus, a final future direction will be to collect HRT data, along with SAP and OCT data, to determine the relative time courses of defects as assessed by these clinical procedures.
In conclusion, the investigations of the links between structure and function in glaucoma have resulted in a model that, in its final form, produced a reasonable accuracy and precision for predicting structural changes from functional measures. However, in the light of new technology, the broader application of the present functions of formalization of linking propositions must be reconsidered for the newer instruments. All of the data for RNFL thickness were acquired by time domain OCT (TD OCT) but, more recently, higher resolution has been achieved by spectral domain OCT (SD OCT), which uses different algorithms to produce thickness data (Costa, et al., 2006). The differences between Stratus TD OCT and the various SD OCT instruments seem to vary and, thus, the specific details may be instrument-specific (Hood, et al., 2009; González-García, et al., 2009; Vizzeri, et al., 2009, Song, et al., 2009; Knight, et al., 2009; Sehi, et al., 2009)). It is, therefore, likely that the model may require modifications of the axon density calculation (equation 10) but, otherwise the general principles should hold. In the present form, the model provides an insight into the disease process that is important in understanding the results of clinical testing and the neuronal losses caused by glaucoma, but whether the formalization of methods for the inter-test comparisons has direct clinical relevance must be decided by the additional development that has been described as future directions for the research.
Acknowledgments
The research at the University of Houston (RSH & JLW) was supported in part by NIH/NEI grants R01 EY01139, T32 EY07024, P30 EY07751, and K23 EY018329 and by a John and Rebecca Moores Professorship. Research at the Bascom Palmer Eye Institute (MJF and DRA) was supported in part by NIH/NEI grant P30 EY014801, a fellowship from Laval University, Quebec City, Quebec, an unrestricted donation from Zeiss-Meditec-Humphrey, Dublin, California, an unrestricted donation from Allergan, Inc., Irvine, California, an investigator-initiated grant from Pfizer, Inc., and an unrestricted grant from Research to Prevent Blindness, Inc., New York, New York.
Footnotes
Disclosure: R.S. Harwerth, None; J.L. Wheat, None; M.J. Fredette, None; D. R. Anderson is a consultant for Carl Zeiss Meditec, Inc., Dublin, California, USA.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alamouti B, Funk J. Retinal thickness decreases with age: an OCT study. Br J Ophthalmol. 2003;87:899–901. doi: 10.1136/bjo.87.7.899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson AJ, Johnson CA, Fingeret M, et al. Characteristics of the normative database for the Humphrey matrix perimeter. Invest Ophthalmol Vis Sci. 2005;46:1540–1548. doi: 10.1167/iovs.04-0968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson DR. Perimetry, With and Without Automation. 2. St. Louis: C.V. Mosby, Co; 1987. [Google Scholar]
- Anderson DR, Knighton RW. Perimetry and acuity perimetry. In: Shields MB, Pollack IP, Kolker AE, editors. Perspectives in Glaucoma. Thorofare, NJ: Slack, Inc; 1988. pp. 59–70. [Google Scholar]
- Ansari EA, Morgan JE, Snowden RJ. Psychophysical characteristics of early functional loss in glaucoma and ocular hypertension. Br J Ophthalmol. 2002;86:1131–1135. doi: 10.1136/bjo.86.10.1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artes PH, Iwase A, Ohno Y, et al. Properties of perimetric threshold estimates from full threshold, SITA standard, and SITA fast strategies. Invest Ophthalmol Vis Sci. 2002;43:2654–2659. [PubMed] [Google Scholar]
- Bagga H, Feuer WJ, Greenfield DS. Detection of psychophysical and structural injury in eyes with glaucomatous optic neuropathy and normal standard automated perimetry. Arch Ophthalmol. 2006;124:169–176. doi: 10.1001/archopht.124.2.169. [DOI] [PubMed] [Google Scholar]
- Balazsi AG, Rootman J, Drance SM, et al. The effect of age on the nerve fiber population of the human optic nerve. Am J Ophthalmol. 1984;97:760–766. doi: 10.1016/0002-9394(84)90509-9. [DOI] [PubMed] [Google Scholar]
- Bathija R, Zangwill L, Berry CC, et al. Detection of early glaucomatous structural damage with confocal scanning laser tomography. J Glau. 1998;7:121–127. [PubMed] [Google Scholar]
- Battista J, Badcock D, McKendrick AM. Spatial summation properties for magnocellular and parvocellular pathways in glaucoma. Invest Ophthalmol Vis Sci. 2009;50:1221–1226. doi: 10.1167/iovs.08-2517. [DOI] [PubMed] [Google Scholar]
- Bartz-Schmidt KU, Weber J. Comparison of spatial thresholds and intensity thresholds in glaucoma. Internat Ophthalmol. 1993;17:171–178. doi: 10.1007/BF01007736. [DOI] [PubMed] [Google Scholar]
- Bengtsson B, Heijl A. Normal intersubject threshold variability and normal limits of the SITA SWAP and full threshold SWAP perimetric programs. Invest Ophthalmol Vis Sci. 2003;44:5029–5034. doi: 10.1167/iovs.02-1220. [DOI] [PubMed] [Google Scholar]
- Bengtsson B, Heijl A. A visual field index for calculation of glaucoma rate of progression. Am J Ophthalmol. 2008;145:343–353. doi: 10.1016/j.ajo.2007.09.038. [DOI] [PubMed] [Google Scholar]
- Bengtsson B, Heijl A, Olsson J. Evaluation of a new threshold visual field strategy, SITA, in normal observers. Swedish Interactive Thresholding Algorithm. Acta Ophthalmol Scand. 1998;76:165–169. doi: 10.1034/j.1600-0420.1998.760208.x. [DOI] [PubMed] [Google Scholar]
- Blanks JC, Torigoe Y, Hinton DR, et al. Retinal pathology in Alzheimer’s disease. I. Ganglion cell loss in the foveal/parafoveal retina. Neurobiol Aging. 1996;17:377–384. doi: 10.1016/0197-4580(96)00010-3. [DOI] [PubMed] [Google Scholar]
- Bodis-Wollner I, Brannan JR. Psychophysical examination of paracentral defects in glaucoma. Curr Opin Ophthalmol. 2000;11:140–144. doi: 10.1097/00055735-200004000-00013. [DOI] [PubMed] [Google Scholar]
- Bodis-Wollner I, Tagliati M, Peppe A, et al. Visual and visual perceptual disorders in neurodegenerative diseases. Baillieres Clin Neurol. 1993;2:461–491. [PubMed] [Google Scholar]
- Bowd C, Zangwill LM, Berry CC, et al. Detecting early glaucoma by assessment of retinal nerve fiber layer thickness and visual function. Invest Ophthalmol Vis Sci. 2001;42:1993–2003. [PubMed] [Google Scholar]
- Bowd C, Zangwill LM, Medeiros FA, et al. Structure-function relationships using confocal scanning laser ophthalmoscopy, optical coherence tomography, and scanning laser polarimetry. Invest Ophthalmol Vis Sci. 2006;47:2889–2695. doi: 10.1167/iovs.05-1489. [DOI] [PubMed] [Google Scholar]
- Broadway DC, Nicolela MT, Drance SM. Optic disk appearances in primary open-angle glaucoma. Surv Ophthalmol. 1999;43:S223–S243. doi: 10.1016/s0039-6257(99)00007-7. [DOI] [PubMed] [Google Scholar]
- Brusini P, Busatto P. Frequency doubling perimetry in glaucoma early diagnosis. Acta Ophthalmol Scand Suppl. 1998;227:23–4. doi: 10.1111/j.1600-0420.1998.tb00869.x. [DOI] [PubMed] [Google Scholar]
- Budenz DL, Anderson DR, Varma R, et al. Determinants of normal retinal nerve fiber layer thickness by Stratus OCT. Ophtahalmo. 2007;1114:1046–1052. doi: 10.1016/j.ophtha.2006.08.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budenz DL, Fredette MJ, Feuer WJ, et al. Reproducibility of peripalillary retinal nerve fiber thickness measurements with stratus OCT in glaucomatous eyes. Ophthalmol. 2008;37:661–666. doi: 10.1016/j.ophtha.2007.05.035. [DOI] [PubMed] [Google Scholar]
- Burgoyne CF, Downs JC, Bellezza AJ, et al. The optic nerve head as a biomechanical structure: a new paradigm for understanding the role of IOP-related stress and strain in the pathophysiology of glaucomatous optic nerve head damage. Prog Ret Eye Res. 2005;24:39–73. doi: 10.1016/j.preteyeres.2004.06.001. [DOI] [PubMed] [Google Scholar]
- Burnstein Y, Ellish NJ, Magbalon M, et al. Comparison of frequency doubling perimetry with humphrey visual field analysis in a glaucoma practice. Am J Ophthalmol. 2000;128:328–333. doi: 10.1016/s0002-9394(99)00364-5. [DOI] [PubMed] [Google Scholar]
- Campbell FW, Green DG. Optical and retinal factors affecting visual resolution. J Physiol. 1965;18:576–583. doi: 10.1113/jphysiol.1965.sp007784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cello KE, Nelson-Quigg JM, Johnson CA. Frequency doubling technology perimetry for detection of glaucomatous visual field loss. Am J Ophthalmol. 2000;129:314–322. doi: 10.1016/s0002-9394(99)00414-6. [DOI] [PubMed] [Google Scholar]
- Chauhan BC, Blanchard JW, Hamilton DC, et al. Techniques for detecting serial topographic changes in the optic disc and peripapillary retina using scanning laser tomography. Invest Ophthalmol Vis Sci. 2000;41:775–782. [PubMed] [Google Scholar]
- Costa RA, Skaf M, Melo LAS, et al. Retinal assessment using optical coherence tomography. Prog Ret Eye Res. 2006;25:325–353. doi: 10.1016/j.preteyeres.2006.03.001. [DOI] [PubMed] [Google Scholar]
- Curcio CA, Allen KA. Topography of ganglion cells in human retina. J Comp Neurol. 1990;300:5–25. doi: 10.1002/cne.903000103. [DOI] [PubMed] [Google Scholar]
- Curcio CA, Sloan KR, Kalina RE, et al. Normal photoreceptor topography. J Comp Neurol. 1990;292:497–523. doi: 10.1002/cne.902920402. [DOI] [PubMed] [Google Scholar]
- Drasdo N. Receptive field densities of the ganglion cells of the human retina. Vision Res. 1989;29:985–988. doi: 10.1016/0042-6989(89)90113-2. [DOI] [PubMed] [Google Scholar]
- Epstein DL. Primary open angle glaucoma. In: Epstein DL, Allingham RR, Schuman JS, editors. Chandler and Grant’s Glaucoma. 4. Baltimore: Williams & Wilkins; 1993. pp. 183–198. [Google Scholar]
- Ferreras A, Pablo L, Garway-Heath DF, et al. Mapping standard automated perimetry to the peripapillary retinal nerve fiber in glaucoma. Invest Ophthalmol Vis Sci. 2008;49:3018–3025. doi: 10.1167/iovs.08-1775. [DOI] [PubMed] [Google Scholar]
- Fredette MJ, Anderson DR, Porciatti V, et al. Reproducibility of pattern electroretinogram in glaucoma patients with a range of severity of disease with the new glaucoma paradigm. Ophthalmol. 2008;115:957–963. doi: 10.1016/j.ophtha.2007.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardiner SK, Demirel S, Johnson CA. Modeling the sensitivity to variability relationship in perimetry. Vision Res. 2006;46:1732–1745. doi: 10.1016/j.visres.2005.11.019. [DOI] [PubMed] [Google Scholar]
- Gardiner SK, Johnson CA, Cioffi GA. Evaluation of the structure-function relationship in glaucoma. Invest Ophthalmol Vis Sci. 2005;46:3712–3717. doi: 10.1167/iovs.05-0266. [DOI] [PubMed] [Google Scholar]
- Garway-Heath DF, Caprioloi J, Fitzke FW, et al. Scaling the hill of vision: the physiological relationship between light sensitivity and ganglion cell numbers. Invest Ophthalmol Vis Sci. 2000;41:1774–1782. [PubMed] [Google Scholar]
- Garway-Heath DF, Poinoosawmy D, Fitzke FW, et al. Mapping the visual field to the optic disc in normal tension glaucoma eyes. Ophthalmol. 2000;107:1809–1815. doi: 10.1016/s0161-6420(00)00284-0. [DOI] [PubMed] [Google Scholar]
- González-García AO, Vizzeri G, Bowd C, et al. Reproducibility of RTVue Retinal Nerve Fiber Layer Thickness and Optic Disc Measurements and Agreement with Stratus Optical Coherence Tomography Measurements. Am J Ophthalmol. 2009;147:1067–1074. doi: 10.1016/j.ajo.2008.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenfield DS. Optic nerve and retinal nerve fiber analyzers in glaucoma. Curr Opin Ophthalmol. 2002;13:68–76. doi: 10.1097/00055735-200204000-00003. [DOI] [PubMed] [Google Scholar]
- Greve EL, Weinreb RN. Glaucoma Diagnosis: Structure and Function. The Hague, The Netherlands: 2004. [Google Scholar]
- Grieshaber MC, Orgul S, Schoetzau A, et al. Relationship between retinal glial cell activation in glaucoma and vasacular dysregulation. J Glau. 2007;16:215–219. doi: 10.1097/IJG.0b013e31802d045a. [DOI] [PubMed] [Google Scholar]
- Harman A, Abrahams B, Moore S, et al. Neuronal density in the human retinal ganglion cell layer from 16 – 77 years. Anatom Rec. 2000;260:124–131. doi: 10.1002/1097-0185(20001001)260:2<124::AID-AR20>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Harwerth RS. The Charles F. Prentice Award Lecture 2006: A neuron doctrine for glaucoma. Optom Vis Sci. 2008;85:436–444. doi: 10.1097/OPX.0b013e31817841b5. [DOI] [PubMed] [Google Scholar]
- Harwerth RS. Glaucoma Models: Primate. In: Pang IH, Clark A, editors. Animal Models for Retinal Disease. New Jersey: Humana Press; 2009. in press. [Google Scholar]
- Harwerth RS, Carter-Dawson L, Shen F, et al. Ganglion cell losses underlying visual field defects from glaucoma. Invest Ophthalmol Vis Sci. 1999;40:2242–2250. [PubMed] [Google Scholar]
- Harwerth RS, Carter-Dawson L, Smith EL, et al. Neural losses correlated with visual losses in clinical perimetry. Invest Ophthalmol Vis Sci. 2004;45:3152–3160. doi: 10.1167/iovs.04-0227. [DOI] [PubMed] [Google Scholar]
- Harwerth RS, Carter-Dawson L, Smith EL, et al. Scaling the structure-function relationship for clinical perimetry. Acta Ophthalmol Scand. 2005;83:448–455. doi: 10.1111/j.1395-3907.2005.00494.x. [DOI] [PubMed] [Google Scholar]
- Harwerth RS, Crawford MLJ, Frishman LJ, et al. Visual field defects and neural losses from experimental glaucoma. Prog Ret Eye Res. 2002;21:91–125. doi: 10.1016/s1350-9462(01)00022-2. [DOI] [PubMed] [Google Scholar]
- Harwerth RS, Quigley HA. Visual field defects and retinal ganglion cell losses in patients with glaucoma. Arch Ophthalmol. 2006;124:853–859. doi: 10.1001/archopht.124.6.853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harwerth RS, Smith EL. Contrast sensitivity perimetry in experimental glaucoma: Investigations with degenerate gratings. In: Wall M, Heijl A, editors. Perimetry Update 1996/1997. Amsterdam: Kugler Publications; 1997. pp. 3–12. [Google Scholar]
- Harwerth RS, Smith EL, Crawford MLJ, et al. Behavioral studies of the sensitive periods of development of visual functions in monkeys. Behav Brain Res. 1990;41:179–198. doi: 10.1016/0166-4328(90)90107-p. [DOI] [PubMed] [Google Scholar]
- Harwerth RS, Smith EL, DeSantis L. Behavioral perimetry in monkeys. Invest Ophthalmol Vis Sci. 1993a;34:31–40. [PubMed] [Google Scholar]
- Harwerth RS, Smith EL, DeSantis L. Mechanisms mediating visual detection in static perimetry. Invest Ophthalmol Vis Sci. 1993b;34:3011–3023. [PubMed] [Google Scholar]
- Harwerth RS, Smith EL, DeSantis L. Experimental glaucoma: perimetric field defects and intraocular pressure. J Glau. 1997;6:390–401. [PubMed] [Google Scholar]
- Harwerth RS, Vilupuru AS, Rangaswamy NV, et al. The relationship between nerve fiber layer and perimetry measurements. Invest Ophthalmol Vis Sci. 2007;48:763–773. doi: 10.1167/iovs.06-0688. [DOI] [PubMed] [Google Scholar]
- Harwerth RS, Wheat JL. Modeling the effects of aging on retinal ganglion cell density and nerve fiber layer thickness. Graefes Arch Clin Exp Ophthalmol. 2008;246:305–314. doi: 10.1007/s00417-007-0691-5. [DOI] [PubMed] [Google Scholar]
- Harwerth RS, Wheat JL, Rangaswamy NV. Age-related losses of retinal ganglion cells and axons. Invest Ophthalmol Vis Sci. 2008;49:4437–4443. doi: 10.1167/iovs.08-1753. [DOI] [PubMed] [Google Scholar]
- Hawkins AS, Szlyk JP, Ardickas Z, et al. Comparison of contrast sensitivity, visual acuity, and Humphrey visual field testing in patients with glaucoma. J Glauc. 2003;12:134–138. [PubMed] [Google Scholar]
- Heijl A, Lindgren G, Olsson J. Normal variability of static perimetric threshold values across the central visual field. Arch Ophthalmol. 1987;105:1544–1549. doi: 10.1001/archopht.1987.01060110090039. [DOI] [PubMed] [Google Scholar]
- Heijl A, Lindgren G, Olsson J. Perimetric threshold variability and age. Arch Ophthalmol. 1988;106:450–452. doi: 10.1001/archopht.1988.01060130492014. [DOI] [PubMed] [Google Scholar]
- Heijl A, Patella VM. Essential Perimetry: The Field Analyzer Primer. 3. Dublin: Carl Zeiss Meditec, Inc; 2002. [Google Scholar]
- Hernandez MR, Miao H, Lukas T. Astrocytes in glaucomatous neuropathy. Prog Brain Res. 2008;173:353–373. doi: 10.1016/S0079-6123(08)01125-4. [DOI] [PubMed] [Google Scholar]
- Hood DC. Relating retinal nerve fiber thickness to behavioral sensitivity in patients with glaucoma: application of a linear model. J Opt Soc Am A Opt Image Sci Vis. 2007;24:1426–1430. doi: 10.1364/josaa.24.001426. [DOI] [PubMed] [Google Scholar]
- Hood DC, Anderson SC, Wall M, et al. Structure versus function in glaucoma: an application of a linear model. Invest Ophthalmol Vis Sci. 2007a;48:3662–3668. doi: 10.1167/iovs.06-1401. [DOI] [PubMed] [Google Scholar]
- Hood DC, Anderson S, Rouleau J, et al. Retinal nerve fiber structure versus visual field function in patients with ischemic optic neuropathy. A test of a linear model. Ophthalmol. 2007b;115:904–910. doi: 10.1016/j.ophtha.2007.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hood DC, Kardon RH. A framework for comparing structural and functional measures of glaucomatous damage. Prog Ret Eye Res. 2007;26:688–710. doi: 10.1016/j.preteyeres.2007.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hood DC, Raza AS, Kay KY, et al. A comparison of retinal nerve fiber layer (RNFL) thickness obtained with frequency and time domain optical coherence tomography (OCT) Optics Express. 2009;17:3997–4003. doi: 10.1364/oe.17.003997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn FK, Mardin CY, Lacemmer R, et al. Correlation between local glaucomatous visual field defects and loss of nerve fiber layer thickness measured with scanning laser polarimetry and spectral domain optical coherence tomography. Invest Ophthalmol Vis Sci. 2009;50:1971–1977. doi: 10.1167/iovs.08-2405. [DOI] [PubMed] [Google Scholar]
- Hot A, Dul MW, Swanson WH. Development and evaluation of a contrast sensitivity perimetry test for patients with glaucoma. Invest Ophthalmol Vis Sci. 2008;49:3049–3057. doi: 10.1167/iovs.07-1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hougaard JL, Ostenfeld C, Heijl A, et al. Modelling the normal retinal nerve fiber layer thickness as measured by Stratus optical coherence tomography. Graefe’s Arch Clin Exp Ophthalmol. 2006;244:1607–1614. doi: 10.1007/s00417-006-0372-9. [DOI] [PubMed] [Google Scholar]
- Johnson CA. Standardizing the measurement of visual fields for clinical research. Ophthalmol. 1996;103:186–189. doi: 10.1016/s0161-6420(96)30740-9. [DOI] [PubMed] [Google Scholar]
- Johnson CA, Demirel S. The role of spatial and temporal factors in frequency-doubling perimetry. In: Wall M, Heijl A, editors. Perimetry Update. New York: Kugler Publications; 1997. pp. 13–19. [Google Scholar]
- Jonas JB, Schmidt AM, Muller-Bergh JA, et al. Human optic nerve fiber count and optic disc size. Invest Ophthalmol Vis Sci. 1992;33:2012–2018. [PubMed] [Google Scholar]
- Jonas JB, Schneider U, Naumann GO. Count and density of human retinal receptors. Graefes Arch Clin Exp Ophthalmol. 1992;230:505–510. doi: 10.1007/BF00181769. [DOI] [PubMed] [Google Scholar]
- Kanamori A, Escano MTF, Eno A, et al. Evaluation of the effect of aging on retinal nerve fiber thickness measured by optical coherence tomography. Ophthalmologica. 2003;217:273–278. doi: 10.1159/000070634. [DOI] [PubMed] [Google Scholar]
- Kanamori A, Naka M, Nagai-Kushhara A, et al. Regional relationship between retinal nerve fiber layer thickness and corresponding visual field sensitivity in glaucomatous eyes. Arch Ophthalmol. 2008;126:1500–1506. doi: 10.1001/archopht.126.11.1500. [DOI] [PubMed] [Google Scholar]
- Kerrigan-Baumrind LA, Quigley HA, Pease ME, et al. Number of ganglion cells in glaucoma eyes compared with threshold visual field tests in the same persons. Invest Ophthalmol Vis Sci. 2000;41:741–748. [PubMed] [Google Scholar]
- Knight OJ, Chang RT, Feuer WJ, et al. Comparison of retinal nerve fiber measurements using time domain and spectral domain optical coherent tomography. Ophthalmol. 2009;116:1271–1277. doi: 10.1016/j.ophtha.2008.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwon YH, Fingert JH, Kuehn MH, Alward WLM. Primary open-angle glaucoma. N Eng J Med. 2009;360:1133–1113. doi: 10.1056/NEJMra0804630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundh BL, Gottvall E. Peripheral contrast sensitivity for static and dynamic sinusoidal gratings in glaucoma. Acta Ophthalmol Scand. 1995;73:202–206. doi: 10.1111/j.1600-0420.1995.tb00269.x. [DOI] [PubMed] [Google Scholar]
- Maddess T, Henry GH. Preformance of nonlinear units in ocular hypertension and glaucoma. Clin Vis Sci. 1992;7:371–383. [Google Scholar]
- Meese TS, Williams CB. Probability summation for multiple patches of luminance modulation. Vision Res. 2000;40:2101–2113. doi: 10.1016/s0042-6989(00)00074-2. [DOI] [PubMed] [Google Scholar]
- Mikelberg FS, Drance SM, Schulzer M, et al. The normal human optic nerve. Axon count and axon diameter distribution. Ophthalmol. 1998;96:1325–1328. doi: 10.1016/s0161-6420(89)32718-7. [DOI] [PubMed] [Google Scholar]
- Morgan JE, Datta AV, Erichsen JT, et al. Retinal ganglion cell remodeling in experimental glaucoma. Adv Exp Med Biol. 2006;572:397–402. doi: 10.1007/0-387-32442-9_56. [DOI] [PubMed] [Google Scholar]
- Motoiko M, Drance SM. Features in the optic disc in preglaucomatous eyes. Arch Ophthalmol. 1999;99:1992–1994. doi: 10.1001/archopht.1981.03930020868010. [DOI] [PubMed] [Google Scholar]
- Nachmias J. On the psychometric function for contrast detection. Vision Res. 1981;21:215–223. doi: 10.1016/0042-6989(81)90115-2. [DOI] [PubMed] [Google Scholar]
- Patel A, Wollstein G, Ishikawa H, et al. Comparison of visual field defects using matrix perimetry and standard achromatic perimetry. Ophthalmol. 2006;114:480–487. doi: 10.1016/j.ophtha.2006.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pirenne MH. Binocular and monocular thresholds for vision. Nature. 1943;153:698–699. [Google Scholar]
- Quaid PT, Flanagan JG. Defining the limits of flicker defined form: effect of stimulus size, eccentricity, and number of random dots. Vision Res. 2005;45:1073–1084. doi: 10.1016/j.visres.2004.10.013. [DOI] [PubMed] [Google Scholar]
- Quigley HA. Open-angle glaucoma. N Eng J Med. 1993;328:1097–1106. doi: 10.1056/NEJM199304153281507. [DOI] [PubMed] [Google Scholar]
- Quigley HA, Dunkelberger GR, Green WR. Retinal ganglion cell atrophy correlated with automated perimetry in human eyes with glaucoma. Am J Ophthalmol. 1989;107:453–464. doi: 10.1016/0002-9394(89)90488-1. [DOI] [PubMed] [Google Scholar]
- Ramakrishnan R, Mittal S, Sonal A, et al. Retinal nerve fibre layer thickness measurements in normal Indian population by optical coherence tomography. Indian J Ophthalmol. 2006;54:11–15. doi: 10.4103/0301-4738.21608. [DOI] [PubMed] [Google Scholar]
- Reddy S, Xing D, Arthur SN, et al. HRT III glaucoma probability score and Moorfields regression scores across the glaucoma spectrum. J Glau. 2009;18:368–272. doi: 10.1097/IJG.0b013e31818c6edd. [DOI] [PubMed] [Google Scholar]
- Robson JG, Graham N. Probability summation and regional variation in contrast sensitivity across the visual field. Vision Res. 1981;21:409–418. doi: 10.1016/0042-6989(81)90169-3. [DOI] [PubMed] [Google Scholar]
- Rodieck RW. The First Steps in Seeing. Sunderland: Sinauer Associates, Inc; 1998. Chapter 4, The rain of photons onto cones. [Google Scholar]
- Rolls ET, Cowey A. Topography of the retina and striate cortex and its relationship to visual acuity in rhesus monkeys and squirrel monkeys. Exp Brain Res. 1970;10:298–310. doi: 10.1007/BF00235053. [DOI] [PubMed] [Google Scholar]
- Sample PA, Bosworth CF, Blumenthal EZ, et al. Visual function-specific perimetry for indirect comparison of different ganglion cell populations in glaucoma. Invest Ophthalmol Vis Sci. 2000;41:1783–1790. [PubMed] [Google Scholar]
- Sato S, Hirooka K, Baba T, et al. Correlation between retinal nerve fibre layer thickness and retinal sensitivity. Acta Ophthalmol. 2008;86:609–613. doi: 10.1111/j.1600-0420.2007.01108.x. [DOI] [PubMed] [Google Scholar]
- See JL, Nicolela MT, Chauhan BC. Rates of neuroretinal rim and peripapillary atrophy area change: a comparative study of glaucoma patients and normal controls. Ophthalmol. 2009;116:840–847. doi: 10.1016/j.ophtha.2008.12.005. [DOI] [PubMed] [Google Scholar]
- Sehi M, Grewal DS, Sheets CW, et al. Diagnostic ability of Fourier-domain vs time-domain optical coherence tomography for glaucoma detection. Am J Ophthalmol. 2009 doi: 10.1016/j.ajo.2009.05.030. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma P, Sample PA, Zangwill LM, et al. Diagnostic tools for glaucoma detection and management. Surv Ophthalmol. 2008;53:S17–S32. doi: 10.1016/j.survophthal.2008.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sommer A, Katz J, Quigley HA. Clinically detectable nerve fiber layer atrophy precedes the onset of glaucomatous field loss. Arch Ophthalmol. 1991;199:77–81. doi: 10.1001/archopht.1991.01080010079037. [DOI] [PubMed] [Google Scholar]
- Song KR, Kim DY, Park SB, et al. Comparison of retinal nerve fiber layer thickness measured by Cirrus HD and Stratus optical coherence tomography. Ophthalmol. 2009;116:1264–1270. doi: 10.1016/j.ophtha.2008.12.045. [DOI] [PubMed] [Google Scholar]
- Sung KR, Wollstein G, Bilonic RA, et al. Effects of age on optical coherence tomography measurements of healthy retinal nerve fiber layer, macula, and optic nerve head. Ophthalmol. 2009;116:1119–1124. doi: 10.1016/j.ophtha.2009.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson WH, Felius J, Pan F. Perimetric defects and ganglion cell damage: interpreting linear relations using a two-stage neural model. Invest Ophthalmol Vis Sci. 2004;45:466–472. doi: 10.1167/iovs.03-0374. [DOI] [PubMed] [Google Scholar]
- Tate GW. The physiological basis for perimetry. In: Drance SM, Anderson DR, editors. Automatic Perimetry in Glaucoma. A Practical Guide. Orlando: Grune & Stratton, Inc; 1985. pp. 1–28. [Google Scholar]
- Tochel CM, Morton JS, Jay JL, et al. Relationship between visual field loss and contrast threshold elevation in glaucoma. BMC Ophthalmol. 2005;5:22. doi: 10.1186/1471-2415-5-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolhurst DJ, Movshon JA, Dean AM. The statistical reliability of signals in single neurons in cat and monkey visual cortex. Vision Res. 1983;23:775–785. doi: 10.1016/0042-6989(83)90200-6. [DOI] [PubMed] [Google Scholar]
- Varela HJ, Hernandez MR. Astrocyte responses in human optic nerve hrad with primary open-angle glaucoma. J Glauc. 1997;6:303–313. [PubMed] [Google Scholar]
- Ventura LM, Sorokac N, De Los Santos R, et al. The relationship between retinal ganglion cell function and retinal nerve fiber layer thickness in early glaucoma. Invest Ophthalmol Vis Sci. 2006;47:3904–3911. doi: 10.1167/iovs.06-0161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vizzeri G, Weinreb RN, Gonzalez-Garcia AO, et al. Agreement between spectral-domain and time-domain OCT for measuring RNFL thickness. Br J Ophthalmol. 2009;93:775–781. doi: 10.1136/bjo.2008.150698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Cioffi GA, Cull G, et al. Immunohistologic evidence for retinal glial cell changes in human glaucoma. Invest Ophthalmol Vis Sci. 2002;43:1088–1094. [PubMed] [Google Scholar]
- Wassle H, Grunert U, Rohrenbeck J, et al. Retinal ganglion cell density and cortical magnification factor in the primate. Vision Res. 1990;30:1897–1911. doi: 10.1016/0042-6989(90)90166-i. [DOI] [PubMed] [Google Scholar]
- Weber AJ, Harman CD. Structure-function relations of parasol cells in the normal and glaucomatous primate retina. Invest Ophthalmol Vis Sci. 2005;46:13197–3207. doi: 10.1167/iovs.04-0834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber AJ, Harman CD, Viswanathan S. Effects of optic nerve injury, glaucoma, and neuroprotection on the survival, structure, and function of ganglion cells in the mammalian retina. J Physiol. 2008;586:4393–4400. doi: 10.1113/jphysiol.2008.156729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinreb RN. Primary open-angle glaucoma. The Lancet. 2004;363:1711–1720. doi: 10.1016/S0140-6736(04)16257-0. [DOI] [PubMed] [Google Scholar]
- Weinreb RN, Kaufman PL. The glaucoma research community and FDA look to the future: A report from the NEI/FDA CDER glaucoma clinical trial design and endpoints symposium. Invest Ophthalmol Vis Sci. 2009;50:1497–1505. doi: 10.1167/iovs.08-2843. [DOI] [PubMed] [Google Scholar]
- Wollstein G, Schuman JS, Price LL, et al. Optical coherence tomography longitudinal evaluation of retinal nerve fiber layer thickness in glaucoma. Arch Ophthalmol. 2005;123:464–470. doi: 10.1001/archopht.123.4.464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H, Downs JC, Bellezza A, et al. 3-D histomorphometry of the normal and early glaucomatous optic nerve head: prelaminar neural tissues and cupping. Invest Ophthalmol Vis Sci. 2007;48:5068–5084. doi: 10.1167/iovs.07-0790. [DOI] [PubMed] [Google Scholar]
- Zangwill LM, Bowd C. Retinal nerve fiber layer analysis in the diagnosis of glaucoma. Curr Opin Ophthalmol. 2006;17:120–131. doi: 10.1097/01.icu.0000193079.55240.18. [DOI] [PubMed] [Google Scholar]