Empirical Evidence on Occupation and Industry Specific Human Capital

Abstract

This paper presents instrumental variables estimates of the effects of firm tenure, occupation specific work experience, industry specific work experience, and general work experience on wages using data from the 1979 Cohort of the National Longitudinal Survey of Youth. The estimates indicate that both occupation and industry specific human capital are key determinants of wages, and the importance of various types of human capital varies widely across one-digit occupations. Human capital is primarily occupation specific in occupations such as craftsmen, where workers realize a 14% increase in wages after five years of occupation specific experience but do not realize wage gains from industry specific experience. In contrast, human capital is primarily industry specific in other occupations such as managerial employment where workers realize a 23% wage increase after five years of industry specific work experience. In other occupations, such as professional employment, both occupation and industry specific human capital are key determinants of wages.

1. Introduction

A large literature has examined the sources of wage growth over the lifecycle, with considerable attention devoted to determining the relative importance of employer tenure and overall labor market experience in determining wages. According to this view of the human capital accumulation process skills are either firm specific or transferable across all jobs, but skills are not occupation or industry specific.² A different view of the human capital accumulation process is presented by Neal (1995) and Parent (2000), who both find that industry specific human capital is a key determinant of wages, while firm specific human capital contributes little to wage growth. More recently, Kambourov and Manovskii (2009) have challenged the view that human capital is primarily industry specific, finding that after controlling for occupation tenure both industry and firm tenure have little importance in determining wages.³ Their results suggest that previous estimates of large returns to industry experience were driven primarily by the omission of occupation specific work experience from wage regressions, a variable that is highly correlated with industry experience.

This paper presents new evidence on the specificity of human capital by estimating the returns to firm, occupation and industry specific work experience using data from the 1979 Cohort of the National Longitudinal Survey of Youth (NLSY). These explanatory variables are endogenous, so the wage equation is estimated using the instrumental variables approach developed by Altonji and Shakotko (1987). The empirical results demonstrate that the conclusions drawn about the specificity of human capital hinge on the treatment of within-firm occupational mobility. When within-firm occupational mobility is ruled out, the estimates confirm Kambourov and Manovskii’s (2009) finding that human capital is primarily occupation specific. However, this paper presents new empirical evidence on the validity of within-firm occupation changes by exploiting a change in the NLSY occupation coding scheme that was designed to more accurately detect within-firm occupation changes. Beginning in 1994 the NLSY occupation coding scheme changed so that within-firm occupation changes were allowed to occur only if workers directly reported a change in the type of work done on their job. In contrast, before 1994 NLSY respondents re-reported their occupation for all jobs, and were not directly asked whether or not they had switched occupations within their current firm. A comparison of pre and post 1994 data suggests that within-firm occupation changes do in fact reflect true changes in occupation, and are not simply the result of measurement error. When these within-firm occupational transitions are allowed, the empirical results point to a role for both industry and occupation specific human capital in determining wages.⁴

This paper also expands on the existing literature by allowing the returns to human capital to vary across occupations, departing from previous work which has constrained the parameters of the wage equation to be the same for all occupations. This is a key extension of existing research because there is no reason to believe that the technology of skill production is the same across all occupations. In fact, the results show that the specificity of skills accumulated at a job varies widely across one-digit occupations. For example, craftsmen accumulate skills that are primarily occupation specific, experiencing a wage gain of 14% after five years of occupation experience. On the other hand, human capital is primarily industry specific for managers, who experience a wage increase of 23% after five years of industry experience. In contrast, professionals accumulate skills that are both occupation and industry specific, as they realize wage increases of 22% after five years of occupation experience and 14% after five years of industry experience. Finally, sales workers do not experience wage gains from either occupation or industry experience, but they realize large wage gains as they accumulate general work experience. The differences in the returns to human capital across occupations are large and statistically significant. Restricting these effects to be equal across occupations leads to misleading estimates of the effects of occupation and industry specific human capital on wages.

Whether wage growth over the career is due to the accumulation of skills that are specific to firms, occupations, industries, or completely general and transferable between all jobs is a fundamental question about the wage determination process. In addition, the finding that human capital is both occupation and industry specific has implications for a number of areas of current research. For example, it suggests that studies of career choice and career mobility should define careers using both occupation and industry codes since workers acquire skills that are specific to both occupations and industries.⁵ The specificity of human capital is also relevant for macroeconomic studies of wage inequality and aggregate productivity. For example, Kambourov and Manovskii (2009a) develop a theoretical model which shows that rising occupational mobility can explain a large fraction of the observed increase in wage inequality if human capital is largely occupation specific.

The specificity of human capital is also relevant when studying the impact of job displacement, a topic which has been the subject of a large amount of research by economists as well as a considerable amount of policy discussion. The value of firm, occupation, and industry specific skills relative to the value of general skills is an important determinant of the cost of displacement since the transferability of a worker’s skills to a new job is a key determinant of the wage loss accompanying job displacement.⁶

2. Data

The National Longitudinal Survey of Youth (NLSY) is a panel dataset that contains detailed information about the employment and educational experiences of a nationally representative sample of young men and women who were between the ages of 14 and 21 when first interviewed in 1979. This study uses NLSY data ranging from 1979–2000. The employment data contain a weekly employment record that provides information about the durations of employment spells along with the wages, hours, and three-digit 1970 U.S Census occupation and industry codes for each job. One important feature of the data is that in 1994 the NLSY switched from annual to biennial interviews. This change does not directly impact the availability of the variables used in this analysis, but it may impact the quality of the data since the recall period for the data increases from one year to two years.⁷

This analysis uses only white men ages 18 or older from the nationally representative core sample of the NLSY. Individuals who ever report serving in the military, working as farmers, or being self-employed are excluded from the sample. These sample restrictions closely follow those imposed in the related literature, see Parent (2000) for an example.

The NLSY work history files are used to construct a monthly history of each individual’s primary employment using the weekly employment records. This analysis considers only full time employment, which is defined as a job where the weekly hours worked are at least 20. The intent of this analysis is to follow workers from the time they make a permanent transition to the labor market and start their career. This is no clear best way to identify this transition to the labor market, so this analysis follows people from the month they reach age 18 or stop attending school, whichever occurs later. Individuals are followed until the year 2000, or until they exit from the sample due to missing data.

The weekly labor force record is aggregated into a monthly employment record based on the number of weeks each full time job is worked at during each month. An individual’s primary job for each month is defined as the one in which the most weeks were spent during that month. Transitions between firms are identified using the NLSY variables that differentiate between employers within years and allow employers to be linked across survey years. The monthly employment record is used to create a running tally of firm tenure for each worker. Occupation and industry experience are also computed using the monthly labor force record. Occupation (industry) experience in each month is simply the total amount of experience that a worker has accumulated in the current occupation (industry). Total work experience is also computed in this manner, so this study uses actual work experience, as opposed to the potential experience variable used in many studies.

The NLSY work history files provide information about weekly employment status, but wages are recorded at the yearly level. For example, suppose that a person works in the same job during all twelve months of a year. The constructed employer tenure variable will increase by one in each month, but the wage will remain constant over the entire year. If the job continues into the next year, a new wage will be observed. Given this feature of the data, only months that include a new wage observation for jobs are used in the wage regressions. Summary statistics for the data are presented in Table 1. There are 1,932 individuals in the sample who contribute a total of 26,841 observations to the sample. The one-digit occupation and industry classifications used throughout the paper are described in detail in Appendix A.

Table 1.

Descriptive Statistics

	Mean
Real Hourly Wage	$7.72
Firm Tenure (in years)	1.95
Occupation Experience	2.53
Industry Experience	3.35
Total Experience	5.44
Years of Schooling	12.9
Age	27.50
Number of Observations	26,841
Number of Individuals	1,932
Fraction of Firm Spells with a Within-firm Occupation Switch	.185
Fraction of Firm Spells with a Within-firm Industry Switch	.103

2.1 Occupation and Industry Codes

The occupation and industry codes for each job are used to create a series of occupation and industry experience variables for each person in the sample. The bottom section of Table 1 summarizes the levels of within-firm mobility between occupations and industries found in the data used in this study. The table shows that 18.5% of firm spells include a within-firm occupation switch, and 10.3% of firm spells include a within-firm industry switch. A key issue when constructing these variables is the method used to identify transitions between occupations and industries. The most common approach used to identify transitions between occupations and industries is to consider an occupation or industry switch to be genuine only if it coincides with a switch of employer. Neal (1999) proposes this solution after noting that in the NLSY industry and occupation codes frequently vary over the course of an employment spell at a firm. Neal advocates constraining industry codes to be constant during each spell of employment at a firm because he argues that there is likely to be little scope for mobility between industries within a typical firm since a typical firm only operates in one industry. Parent (2000) adopts this approach when constructing industry experience variables using the NLSY.

Kambourov and Manovskii (2009) perform a detailed analysis of different methods of identifying true occupation switches using the Panel Survey of Income Dynamics (PSID). The strength of the PSID for this type of analysis is that it provides retrospectively coded occupation and industry codes created by coders who have access to a person’s sequence of job descriptions over their entire career, as opposed to the NLSY in which coders only have access to descriptions for a single year. Giving coders access to each respondent’s complete sequence of job description will reduce errors introduced into occupation data when job descriptions are translated into occupation codes. However, one would still expect measurement error to be present in the re-coded occupation data because of measurement error in respondent’s job descriptions. The re-coded occupation and industry codes in the PSID are available from 1968–1980. Unfortunately, Kambourov and Manovskii report that reliable employer tenure is not available until 1981 in the PSID, so the re-coded occupation and industry codes can be used to evaluate different methods of identifying occupation and industry switches, but the re-coded data does not span the years used in estimation (1981–1992).⁸

Section 4.1a-4.1b of this paper provides evidence regarding whether within-firm occupational transitions reflect actual changes in occupation by exploiting the fact that the NLSY occupation coding scheme changed in 1994 in a way designed to more reliably detect within-firm occupation switches. After examining this issue, the sensitivity of estimates of the returns to occupation and industry specific human capital to the treatment of within-firm changes in occupation and industry is addressed.

3. The Econometric Model of Wages

The baseline econometric model consists of the following log-wage equation for worker i employed at firm j in occupation q in industry d at time t,

$$\begin{array}{cc}\text{ln}(w_{\mathit{\text{ijqdt}}})=\hfill & {\beta }_1{\mathit{\text{Firm\_Ten}}}_{\mathit{\text{ijt}}}+{\beta }_2{\mathit{\text{Occ\_Exp}}}_{\mathit{\text{iqt}}}+{\beta }_3{\mathit{\text{Indus\_Exp}}}_{\mathit{\text{idt}}}\hfill \\ \hfill & +{\beta }_4{\mathit{\text{Old\_Firm}}}_{\mathit{\text{ijt}}}+{\beta }_5{\mathit{\text{Old\_Occ}}}_{\mathit{\text{iqt}}}{\beta }_6{\mathit{\text{Old\_Indus}}}_{\mathit{\text{idt}}}\hfill \\ \hfill & +\gamma X_{\mathit{\text{it}}}+{\psi }_{\mathit{\text{ij}}}+{\mu }_{\mathit{\text{iq}}}+{\lambda }_{\mathit{\text{id}}}+{\epsilon }_{\mathit{\text{ijqdt}}},\hfill \end{array}$$ (1)

where Firm_Ten_ijt represents firm tenure, and Occ_Exp_iqt and Indus_Exp_idt represent experience in the current occupation and industry. Quadratic terms in tenure and experience are also included in the regressions, but they are omitted here for ease of exposition. The dummy variable Old_Firm_ijt is equal to one if Firm_Ten_ijt>1 and equal to zero otherwise. The variables Old_Occ_iqt and Old_Indus_idt are the analogous dummy variables for occupation and industry spells. These variables are included so that the response to the first year of tenure or experience is not restricted to the quadratic specification.⁹ The vector X_it includes explanatory variables such as total labor market experience, education, industry and occupation dummy variables, year dummies, and age dummies.¹⁰

Wages are also affected by the value of the match between a worker and a firm, ψ_ij, and a worker’s innate skills in each occupation and industry, μ_iq and λ_id. These match values are unobserved by the econometrician but are observed by workers when they make employment choices. This model of wage determination implies that workers will self select into industries and occupations based on their innate ability. Random variation in wages that is independent across time is captured by ε_jqdt.

The presence of unobserved firm specific match values and occupation and industry specific match values implies that the tenure, and occupation and industry experience variables included in equation (1) are correlated with the error term in the wage equation. For example, workers with a high match value at a firm are likely to accumulate high amounts of tenure at that firm and also to have high wages. More precisely, the instrumental variables approach presented in this paper is designed to deal with correlations between Firm_Ten_ijt and ψ_ij, Occ_Exp_iqt and μ_iq, and Indus_Exp_idt and λ_id. Ordinary least squares (OLS) estimation of equation (1) provides biased and inconsistent parameter estimates in the presence of this type of correlation.

This work deals with endogeneity by employing the instrumental variables technique developed by Altonji and Shakotko (1987).¹¹ This procedure instruments for current firm tenure with deviations of current tenure from mean tenure on the current job. For example, let ${\overline{\mathit{\text{Firm\_Ten}}}}_{\mathit{\text{ij}}}$ represent the mean tenure for person i during his employment spell in job j. The instrument for firm tenure is ${\mathit{\text{Firm\_Indust}}}_{\mathit{\text{ijt}}}={\mathit{\text{Firm\_Ten}}}_{\mathit{\text{ijt}}}-{\overline{\mathit{\text{Firm\_Ten}}}}_{\mathit{\text{ij}}}$. This variable is uncorrelated with the firm specific match value by construction, and is highly correlated with firm tenure. Instruments are also constructed in this manner for occupation experience and industry experience using deviations of these variables from their occupation and industry spell means. Also, the dummy variables Old_Firm_ijt, Old_Occ_iqt, and Old_Indus_idt are instrumented with deviations from spell means. The exact equations used to construct each instrument are presented in Appendix C. Standard errors for the IV and OLS parameter estimates are corrected for clustering at the level of individuals, firms, occupations, and industries.

The Altonji and Shakotko instrumental variables approach does not eliminate all of the potential biases created by correlations between tenure and experience variables and the error terms in the wage equation. This approach is based on the assumption that the firm, occupation, and industry match values are constant over time, although random variation in wages is present due to due to ε_ijqdt. In addition, while the instrument for occupation experience is uncorrelated with the occupation match value (μ_iq) by construction, it may be correlated with the other unobserved match components of the wage equation. Similar correlations may exist for the industry experience and firm tenure instruments. This limitation of the IV estimation approach is acknowledged by Kambourov and Manovskii (2009) and Zangelidis (2008), although the literature has yet to develop a completely satisfactory solution.

Fortunately, most of these correlations are unlikely to lead to an overstatement of the importance of occupation and industry specific work experience in determining wages. For example, if firm tenure is positively correlated with the occupation (μ_iq) or industry (λ_id) match values, then the return to firm experience will be biased upward, and the returns to occupation (or industry) experience will be biased downward. Sources of endogeneity that are particularly worthy of attention include correlations between the firm match value and occupation or industry specific work experience. If these correlations are present, then the IV estimates would overstate the importance of occupation or industry specific experience in determining wages. Based on this concern, Section 5.3 discusses this issue in depth. In addition, Section 5.2 of this paper provides additional evidence about occupation and industry experience effects using an alternative empirical approach that should be less sensitive to the endogeneity problem. These results provide strong support for the IV result that both occupation and industry specific work experience are important determinants of wages.

4. Estimates of the Effects of Occupation and Industry Experience

This section discusses the instrumental variables estimates of the model of wage determination presented in the previous section, evaluates the impact of alternative assumptions about within-firm occupational mobility, and investigates whether within-firm occupation switches represent actual occupation switches.

4.1a Within-firm Occupational Mobility in the NLSY

This section presents information about the prevalence of within-firm occupational mobility in the NLSY. Jobs in the NLSY are assigned 1970 Census occupation codes based on individuals’ descriptions of the type of work done on each job. From 1979–1993, all individuals working in jobs continued from the previous interview were asked to provide a new description of their job, and these descriptions were translated into new occupation codes independently of the previous occupational code and description. The concern is that measurement error resulting from the coding of verbatim job descriptions into occupation codes will result in false within-firm occupation switches. In the 1994–2000 interviews the NLSY made a major change in how occupations were coded during employment spells at firms. Instead of asking all workers in continuation jobs to re-report their occupation, beginning in 1994 the NLSY first asked respondents if the type of work done on their job had changed. Only those people who responded that the type of work done on their job had changed were asked to re-report their occupation. One would expect this coding change to decrease the number of false within-firm occupation switches found in the NLSY data.

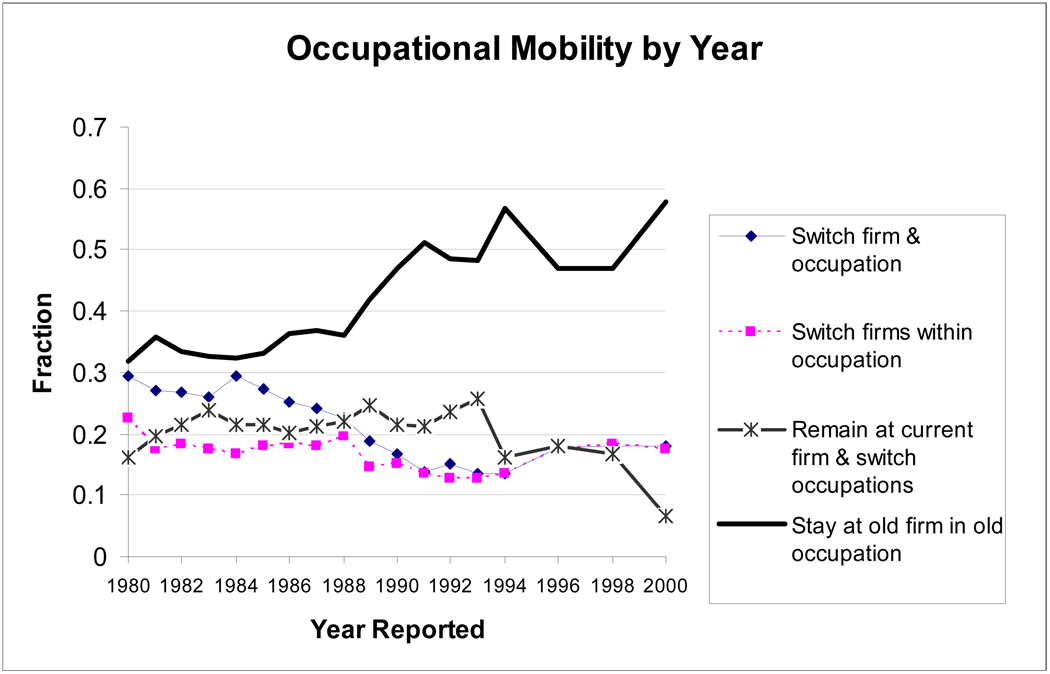
Figure 1 plots several different measures of occupational mobility by survey year. This figure plots annual mobility rates. The data shown in this figure is obtained by aggregating the weekly NLSY employment data into a yearly employment record.¹² The fraction of employed individuals reporting within-firm occupation switch, which is labeled as “remain at current firm & switch occupations” averages .21 between the 1980 and 1993 survey years. Within-firm occupational mobility peaks in 1993 at .25, the year before the occupation coding scheme changed. From 1994 to 1998 within-firm occupational mobility declines to approximately .17, before taking a large drop to .07 in the year 2000 survey. Note that the coding of within-firm occupation switches changed in 1994 and remained unchanged through the year 2000, so the sharp drop in this type of mobility in 2000 is not caused by changes in occupation coding. Given this feature of the data, in the following analysis the time period 1994–1998 is considered the relevant comparison group for examining the effect of the coding change on within-firm occupational mobility.

Figure 1.

When interpreting Figure 1, it is important to keep in mind that if within-firm occupational mobility is primarily made up of false transitions created by measurement error then one would expect a large drop in this type of mobility beginning in 1994 when individuals were directly questioned about within-firm occupational switches. Also, the decrease in within-firm occupational mobility should be accompanied by an equal increase in the fraction of respondents who report staying at their old firm in their old occupation, because the other two outcomes which involve switching firms should not be affected by the coding change. The decline in within-firm occupational mobility in 1994 is in fact matched by a corresponding increase in the fraction of respondents who report staying at their old firm in their old occupation. However, in the next interview (1996) the fraction of respondents reporting that they remain at their old firm in their old occupation returns to its pre-coding change (1993) level. The decrease in the fraction of people staying at their old firm and occupation is accompanied by an increase in the fraction of people who switch firms and occupations and switch firms within their old occupation. These patterns suggest that mobility rates are actually changing during this time period, so it is not simply a matter of the coding change re-classifying people from the “remain at current firm & switch occupations” category to the “stay at old firm in old occupation” category.

Given that the changes in mobility around the time of the coding change do not exactly correspond to what one would expect if the coding change was the only factor driving the observed changes in mobility, some caution must be used when interpreting the empirical evidence. However, the simplest comparison shows that average within-firm occupational mobility rates drop by .04 from 1980–1993 to 1994–1998, and drop by .08 from 1993 to 1994–1998. These numbers provide informal evidence on the impact of measurement error on within-firm occupational switches, but they do suggest that the vast majority of within-firm occupational transitions reflect true changes in occupation. Comparing within-firm occupation switches from 1980–1993 to 1994–1998 suggests a rough estimate of 81% of within-firm occupation switches being true occupation switches. Although this is only a rough estimate, it does suggest that treating all within-firm occupation switches as false transitions created by measurement error (as is commonly done) is inappropriate.

4.1b An Analysis of Within-firm Occupational Mobility

This section provides further evidence regarding whether within-firm occupational transitions are primarily real occupational transitions or simply false transitions created by misclassification of occupations. Consider a simple model of mobility between firms and occupations where a worker has the following four options in each time period: 1) switch firms and occupations, 2) switch firms within the current occupation, 3) switch occupations within the current firm, 4) remain at the current firm in the current occupation.¹³

Estimating a multinomial logit model (MNL) of employment transitions using these four outcomes provides information about the relationship between mobility and observable worker characteristics such as education and firm tenure.¹⁴ One limitation of simply examining the time trends in within-firm occupational mobility is that this simple analysis fails to control for the effects of observable variables on within-firm occupational mobility. The MNL model addresses this shortcoming by including a dummy variable for the 1994 to 1998 time period along with controls for other observable variables.

The parameter estimates for the multinomial logit model of mobility are presented in Table 2. This analysis uses NLSY data from 1980–2000. All coefficients are measured relative to the base choice of remaining at the current firm without switching occupations. The parameter estimate for the 1994 to 1998 dummy variable for outcome three (remain at current firm and switch occupations) is small and negative, but is not statistically significant at any conventional significance level. The marginal effect of the 1994 to 1998 dummy variable for outcome three is small and positive, but again is not statistically different from zero at the 5% level. These estimates imply that after controlling for the relevant observable variables, there is little evidence that the coding change caused a large drop in within-firm occupational mobility. The fact that the 1994 coding change does not appear to have greatly reduced within-firm occupation switches provides evidence against the strong assumption that within-firm occupation switches should be ruled out because they are solely the result of classification error.

Table 2.

Multinomial Logit Model of Mobility Between Firms and Occupations Outcomes

	1. Switch Firms and Occupations		2. Switch Firms within Current Occupation		3. Remain at Current Firm and Switch Occupations
Variable	Coefficient	Marginal effect	Coefficient	Marginal effect	Coefficient	Marginal effect
Constant	.8581* (.3185)	---	.2553 (.3382)	---	−1.6738* (.3507)	---
Years of education	−.0357 (.0215)	−.0067* (.0029)	−.0096 (.0220)	−.0018 (.0027)	.0505* (.0214)	.0093* (.0031)
High school diploma	−.0995 (.0794)	−.0093 (.0106)	−.1737* (.0820)	−.0201* (.0101)	−.0108 (.0821)	.0071 (.0116)
College diploma	−.1536 (.0987)	−.0219 (.0135)	.0506* (.1005)	.0133 (.0126)	−.0680 (.0947)	−.0067 (.0136)
Firm tenure	−.1977* (.0111)	−.0257* (.0015)	−.2136* (.0096)	−.0252* (.0012)	.0750* (.0079)	.0248* (.0014)
Occupation experience	−.1980* (.0112)	−.0144* (.0015)	.0534* (.0095)	.0208* (.0013)	−.2604* (.0104)	−.0350* (.0013)
Total experience	.0092 (.0091)	.0006 (.0012)	−.0360* (.0102)	−.0067* (.0019)	.0537* (.0097)	.0091* (.0014)
1994 ≤ Year ≤ 1998	−.7559* (.1918)	−.0795* (.0249)	−1.0989* (.2002)	−.1250* (.0240)	−.0250 (.2226)	.0558 (.0312)
Professional	−.9643* (.0910)	−.1388* (.0125)	−.3477 (.0891)	−.0236* (.0112)	.1612 (.0952)	.0689* (.0139)
Managers	−.5339* (.0807)	−.0697* (.0111)	−.6388* (.0909)	−.0783* (.0114)	.2587* (.0921)	.0779* (.0134)
Sales	−.2707* (.0953)	−.0498* (.0129)	−.2781* (.1052)	−.0451* (.0131)	.5103* (.1064)	.0966* (.0152)
Clerical	.0366 (.0884)	−.0155 (.0118)	−.5975* (.1149)	−.1152* (.0143)	1.108* (.0962)	.1879* (.0136)
Craftsmen	−.502* (.0733)	−.0830* (.0099)	−.1734* (.0776)	−.0206* (.0096)	.3891* (.0877)	.0827* (.0126)
Operatives	−.1949* (.0739)	−.0450* (.0099)	−.0183 (.0796)	−.0114 (.0098)	.4798* (.0893)	.0813* (.0128)
Laborers	.3625* (.0826)	.0140 (.0107)	−.0328 (.0963)	−.0509* (.0116)	1.178* (.0964)	.1702* (.0134)
Service	---	---	---	---	---	---
Observations	24,938
Mean of dependant variables	0.213		0.168		0.201

Notes: The omitted outcome is remaining at the current firm in the current occupation. Occupation dummies, industry dummies, age dummies, and year dummies are also included as explanatory variables. Tenure and experience are measured in years. Marginal effects are calculated at the means of the independent variables.

^*Denotes statistical significance at the 5% level.

The parameter estimates from this model of mobility also provide further evidence that within-firm occupational switches are true occupational transitions. Suppose that within-firm occupational transitions are caused exclusively by classification error and that this classification error is independent of observable worker characteristics. In this case one would not expect to find statistically or economically significant relationships between observable variables and the probability of observing an occupational switch within a spell of employment at a firm. The marginal effects in Table 2 show that large, statistically significant relationships exist between accumulated years of occupation and firm tenure and mobility between firms and occupations. Across all outcomes the signs of these effects are consistent with a model of worker behavior where job matching and/or human capital accumulation occurs at the level of both firms and occupations. For example, consider the relationship between mobility and firm tenure. A five year increase in firm tenure is associated with a 13 percentage point decrease in the probability of switching firms and occupations, a 13 percentage point decrease in the probability of switching firms within an occupation, and a 12 percentage point increase in the probability of switching occupations within a firm. The strength of these relationships is hard to reconcile with the view that within-firm occupational transitions are solely false transitions generated by classification error in occupation codes.

4.2 Wage Equation Estimates: Baseline Model

Table 3 presents ordinary least squares (OLS) and instrumental variables (IV) estimates of a log wage equation that incorporates various combinations of occupation and industry experience variables. This specification of the regression follows the related literature in imposing the restriction that the effects of firm, occupation, and industry experience are constant across occupations. To provide some sensitivity analysis the estimates are presented for specifications of the model that allow within-firm occupation and industry switches, and also for specifications that rule out mobility between occupations and industries within a firm.

Table 3.

Log Wage Equation Estimates

Independent Variable	(1a) OLS	(1b) IV	(2a) IV: no Industry Switches within Firms	(2b) IV: Industry Switches within Firms	(3a) IV: no Occupation Switches within Firms	(3b) IV: Occupation Switches within Firms	(4a) IV: no Occupation or Industry Switches within Firms	(4b) IV: Occupation Switches within Firms	(4c) IV: Occupation and Industry Switches within Firms
Firm tenure	.03816* (.00584)	.00206 (0.00393)	.00117 (.00510)	−.00448 (.00438)	−.00907 (.00494)	−.00243 (.00401)	−.00914 (.00562)	−.00239 (.00508)	−.00547 (.00438)
Firm tenure2/100	−.00155* (.00033)	−.00031 (.00024)	−.00011 (.00027)	−0.00003 (.00024)	.00012 (.00027)	−.00024 (.00024)	.00024 (.00030)	−.00005 .00027	.00001 (.00024)
Occupation experience	.02366* (.00509)	…	…	…	.02448* (.00679)	.01726* (.00569)	.02504* (.00684)	.01647* (.00578)	.01551* (.00579)
Occ. exp.2/100	−.00093* (.00033)	…	…	…	−.00086* (.00033)	−.00065* (.00030)	−.00081* (.00033)	−.00059* (.00030)	−.00058* (.00030)
Industry exp.	.00595 (.00593)	…	.00826 (.00698)	.01323* (.00647)	…	…	.00302 (.00711)	.00541 (.00705)	0.00988 (.00659)
Indus. exp.2/100	−.00004 (.00032)	…	−.00056 (.00035)	−.00076* (.00032)	…	…	−.00037 (.00035)	−.00050 (.00034)	−.00065* (.00032)
Total experience	.02816* (.00559)	.07448* (.00488)	.06384* (.00641)	.06354* (.00599)	.05806* (.00625)	.06458* (.00568)	.05298* (.00712)	.05768* (.00678)	.05783* (.00645)
Total exp. 2/100	−.00072* (.00025)	−.00178* (.00022)	−.00131* (.00030)	−.00136* (.00027)	−.00124* (.00028)	−.00152* (.00024)	−.00098* (.00033)	−.00116* (.00031)	−.00120* (.00029)
Old firm	.03031* (.01304)	.02518* (.00762)	−.00953 (.01056)	.00641 (.00910)	−.00464 (.00980)	.01425 (.00810)	−.02083 (.01113)	−.01384 (.01072)	.00440 (.00925)
Old occupation	.01316 (.01047)	…	…	…	.04998* (.01101)	.01521 (.01002)	.03213* (.01183)	0.00361 (.01026)	.00584 (.01026)
Old industry	.07108* (.01330)	…	.05782* (.01170)	.03552* (.01080)	…	…	.04487* (.01268)	.05208* (.01206)	.03374* (.01099)
Individuals	1,932
Observations	26,841

Notes: Robust standard errors adjusted for clustering at the level of individuals, firms, occupations, and industries are in parentheses. Column (1a) estimated using ordinary least squares (OLS), remaining columns estimated using instrumental variables (IV).

^*Denotes statistical significance at the 5% level.

The dependent variable is the log of the real hourly wage. Tenure and experience are measured in years. The other explanatory variables included in the regression are completed high school and college, college, graduate school, and high school graduation dummies, occupation dummies, industry dummies, year dummies, and age. Old firm, occupation, and industry dummy variables are equal to one after the first year of tenure in a firm, occupation, or industry.

Column 1a of Table 3 presents OLS estimates of a wage equation that includes firm tenure and industry and occupation specific work experience. Note that these OLS parameter estimates are likely to be biased because of the endogeneity problems discussed in Section 3 of this paper, but they provide a useful baseline for comparison with the IV estimates. According to the OLS estimates, wages increase by 17% after five years of firm tenure, 10% after five years of occupation experience, and 9.9% after five years of industry experience. Note also that the return to each year of industry experience in the quadratic specification is not statistically different from zero at the 5% level, but there is a large and statistically significant first year industry experience effect of 7%.

Column 1b of Table 3 presents IV estimates of a wage equation that includes firm tenure and total experience as explanatory variables but omits both industry and occupation experience. These estimates suggest that the first year of firm tenure increases wages by 2.5%, but the effect of additional years of firm tenure is small and statistically insignificant. This parameter estimate falls within the range of previous estimates of the firm tenure effect obtained using the Altonji and Shakotko IV estimator, which generally range from small negative effects to small positive effects. In addition, small firm tenure effects are found across a range of studies that use different methodologies.¹⁵

The specification of the wage equation reported in column 2a of Table 3 includes industry experience as an explanatory variable and restricts industry codes to be constant during the course of a worker’s employment spell at a firm. This specification is similar to the one used by Parent (2000), who does not include occupation experience as an explanatory variable. These estimates indicate that 5 years of industry experience increase wages by 9.9%. In the absence of occupation experience, industry experience appears to be an important determinant of wages. Note that similar to the OLS estimates, the IV estimates suggest that the majority of the wage increase from industry-specific experience is attributed to the first year effect (.058 out of a total increase of .099). The large effect of the first year of industry experience is quite robust across the six specifications of the wage regression that include industry experience. Column 2b repeats this regression, but allows workers to switch industries within a firm. This change increases the effect of five years of industry experience very slightly to 10%. As a basis for comparison, in another study using the Altonji and Shakotko IV estimator and restricting industry codes to be constant during employment spells, Parent (2000) finds that 5 years of industry experience increase wages by 9.5%, so the results from the two studies are extremely close.¹⁶

The estimates reported in columns 3a and 3b of Table 3 show that when occupation experience is included as an explanatory variable in place of industry experience there are substantial estimated returns to occupation experience. These estimates indicate that five years of occupation experience increases wages by 17.2% when occupation codes are restricted to be constant over the duration of an employment spell at a firm. However, the return to five years of occupation experience falls to only 10% when within-firm occupational mobility is allowed. Estimates of the returns to occupation experience appear to be quite sensitive to assumptions about within-firm occupational mobility. In contrast, the estimates of industry experience effects are very robust to allowing or ruling out within-firm industry switches.

The estimates presented in Table 3 show that the estimated return to occupation experience decreases by approximately 40% when within-firm occupation switches are allowed. The evidence presented in Section 4.1 suggests that these within-firm occupation switches represent actual changes in occupation, so it is important to consider why ignoring this type of mobility results in such a large overstatement of the effect of occupation experience on wages. The explanation is that workers frequently experience wage gains from moving to higher paying occupations within their firm. When occupation codes are constrained to be constant over the course of employment spells at firms the wage gains from moving to higher paying occupations within the firm are falsely attributed to gains from occupation experience. The net result is an overstatement of the importance of occupation experience in determining wages caused by ignoring within-firm occupational mobility.

The previously discussed wage equation estimates suggest returns to industry experience in the absence of occupation experience similar in magnitude to those found by Parent (2000). Columns 4a-4c of Table 3 show how the results change when both occupation and industry experience are included as explanatory variables. These regression results are summarized in Table 4, which shows the returns to occupation and industry experience under various assumptions about the possibility of within-firm occupation and industry switches. First, consider the IV estimates summarized in sections 2–4 of Table 4. When occupation and industry codes are not allowed to change during an employment spell at a firm, the estimates indicate that five years of occupation experience increases wages by 13.3%. Under this specification five years of industry experience increases wages by only 4.9%, while five years of total experience increases wages by 23.5%. These estimates suggest that human capital accumulates primarily at the level of occupations, rather than industries. In addition, general skills as measured by total work experience play a large role in determining the growth of wages over time.¹⁷ Kambourov and Manovskii (2009) also find that occupation experience is a more important determinant of wages than industry experience when they use employer switches to identify occupation and industry switches. Using this approach, they find that five years of industry experience increases wages by 4.6%, and five years of occupation experience increases increase wages by 8.0%.

Table 4.

Cumulative Returns to Occupation and Industry Experience

			2 years	5 years
1) OLS estimates (specification 1a)
Firm tenure			.0992 (.0103)	.1747 (.0160)
Occupation experience			.0560 (.0080)	.1036 (.0131)
Industry experience			.0828 (.0113)	.0997 (.0178)
Total experience			.0528 (.0102)	.1190 (.0219)
2) IV: no occupation or industry switches within firms (specification 4a)
Firm tenure			−.0379 (.0099)	−.0594 (.0175)
Occupation experience			.0783 (.01358)	.1330 (.0245)
Industry experience			.0491 (.0142)	.0489 (.0253)
Total experience			.1013 (.0129)	.2355 (.0280)
3) IV: occupation switches within firms, no industry switches within firms (specification 4b)
Firm tenure			−.0188 (.0085)	−.0272 (.0144)
Occupation experience			.0337 (.0114)	.0684 (.0203)
Industry experience			.0605 (.0140)	.0640 (.0253)
Total experience			.1098 (.0123)	.2535 (.0267)
4) IV: occupation and industry switches within firms (specification 4c)
Firm tenure			−.0065 (.0072)	−.0227 (.0123)
Occupation experience			.0341 (.0114)	.0661 (.0205)
Industry experience			.0504 (.0124)	.0635 (.0232)
Total experience			.1099 (.0118)	.2531 (.0256)
	Tests of null hypothesis: five-year returns are equal between specifications 4a and 4b
Type of experience	Firm tenure	Occupation experience	Industry experience	Total experience
χ2 Test statistic	10.69*	9.29*	4.65*	4.83*

Entries are changes in log wages. The 5% critical value for the hypothesis test is ${\chi }_{.95}^2(1)=3.84$

^*denotes null hypothesis is rejected at the 5% level.

The previously discussed results suggest that occupation specific capital is a far more important determinant of wages than industry specific capital when within-firm occupational switches are ruled out. However, the results presented in Table 4 show that this result is quite sensitive to assumptions about within-firm occupational mobility. When within-firm occupation switches are allowed, the return to 5 years of occupation experience falls from 13.3% to 6.8% while the return to 5 years of industry experience rises from 4.9% to 6.4%. Based on these results, one would conclude that industry and occupation specific human capital are of approximately equal importance in determining wages.

One important consideration is whether or not the alternative assumptions about within-firm occupational mobility lead to a statistically significant change in the estimated parameters. A type of Hausman test can be used to test whether or not the alternative estimators have the same probability limit. Let θ(1) represent the estimated effect of occupation-specific work experience on wages under the assumption that occupations do not change within firm spells, and let θ(2) represent the estimated effect of occupation-specific work experience under the assumption that occupations can change during firm spells. The hypothesis of interest is

$$\begin{array}{c}{H}_{0:}p\text{lim}(\theta (1)-\theta (2))=0\hfill \\ H_{A:}p\text{lim}(\theta (1)-\theta (2))\ne 0,\hfill \end{array}$$

and the test statistic is

$$H=\frac{{(\theta (1)-\theta (2))}^2}{\text{var}(\theta (1)-\theta (2))}.$$

The only practical difficulty in performing this test is that the variance of θ (1) – θ (2), which is needed to compute the test statistic, is not an immediate output of the regressions. The simplest solution to this problem, which is employed here, is to obtain a bootstrap estimate of the covariance between the two estimators.¹⁸ The null hypothesis is rejected at the 5% level if the test statistic is greater than ${\chi }_{.95}^2(1)=3.84$. The bottom section of Table 4 shows the test statistics for the equality of the returns to firm tenure, occupation experience, industry experience, and total experience between the regressions which restrict occupation codes to be constant within firm spells (specification 4a), and allow occupation codes to change within firm spells (specification 4b). The null hypothesis that the probability limits of each of the five-year experience effects are equal is rejected at the 5% level when these hypotheses are tested separately.

The final three rows of Table 4 show that these results are extremely robust to assumptions about within-firm mobility between industries. When within-firm industry switches are allowed in addition to within-firm occupation switches the return to 5 years of occupation experience falls very slightly by .2 percentage points to 6.6%, while the return to 5 years of industry experience falls by only .05 percentage points to 6%. The most directly comparable results reported in Kambourov and Manovskii (2009) are those on their “uncontrolled” PSID data which treats all observed occupation and industry changes as true transitions. They report returns to five years of occupation and industry tenure of 2.84% and 1.81%, effects that are approximately one-third of those shown in the final section of Table 4. One important difference between the PSID and NLSY data that may partially account for this difference is that the PSID requires using self-reported employer tenure variables to infer employer switches, while the NLSY provides direct information about transitions between employers. It is generally believed that the NLSY approach leads to less measurement error in identifying transitions between employers. To the extent that this is the case, the PSID experience data may be noisier than the NLSY data, which could lead to downward bias in the estimated parameters. Another important difference between the PSID and NLSY data is that the NLSY focuses on the first part of workers’ careers whereas the PSID contains information about the entire career. The differences in the sample members’ ages could account for some of the differences in the results between the two datasets.

Overall, the results of the baseline specification of the wage regression suggest that both occupation and industry specific human capital play important roles in determining wages. The next section examines whether or not this result is robust to allowing the parameters of the wage equation to vary across occupations.

4.3 Variation in Occupation and Industry Experience Effects Across Occupations

The preceding analysis of occupation and industry experience effects restricts the parameters of the wage equation to be the same for all jobs. This approach is the one adopted in virtually all of the literature on estimating the returns to occupation and industry specific human capital.¹⁹ The preferred estimates of this specification of the wage equation indicate that five years of occupation experience increases wages by 6.8%, while five years of industry experience increases wages by 6.4%. These results indicate that skills have components that are both occupation and industry specific, but it appears that general skills that are transferable across all jobs (as measured by total experience) are a far more important determinant of wages.

Restricting the effects of all variables to be constant across jobs is a strong assumption about the wage determination process. There are a number of reasons to suspect that the monetary return to different types of experience and tenure could vary across jobs. The simplest possible explanation is that there is variation across jobs in the type of skills required to earn high wages, and that the extent to which these skills are firm-specific, occupation-specific, industry-specific, or completely general in nature varies across jobs. For example, a highly skilled manager may be rewarded for acquiring firm-specific knowledge about the workers that he is managing, or may require substantial knowledge of how competitors in the same industry operate. For this manager, switching firms or industries would result in lost human capital. In contrast, a low skilled worker who sweeps floors probably doesn’t acquire any skills that are truly industry or firm-specific. A more formal theoretical framework that contains some of these ideas is developed by Shaw (1987), who presents a model in which the technology of skill production, the monetary return to occupation specific skills, and the intensity of skill investment varies across occupations. When a wage equation based on this type of model is estimated, it is inappropriate to constrain the effects of human capital variables to be constant across occupations.

The most general way of allowing for heterogeneity in the model presented in this paper is to estimate the wage equation separately for each combination of the eight occupation classifications and twelve industry classifications found in the data. However, since there are only 1,932 individuals in the NLSY79 data used in this paper, estimating ninety-six separate wage equations is not feasible. As a result, the wage equation is estimated separately for different occupations, which allows for heterogeneity across occupations in the effect of the tenure and experience variables on wages. For example, the factors determining wages for professionals may be different from the factors determining the wages of service workers. However, it does not provide information about variation in returns across occupation and industry pairs.²⁰ One way to interpret the occupation-specific wage regressions is that they provide information about the specificity of different types of human capital across occupations. If general experience is very valuable in a particular occupation, then there is a high degree of transferability of skills into that occupation. Similarly, variation in the occupation and industry experience effects across occupations provides information about the importance of occupation and industry specific skills in determining wages in different occupations.

Table 5 shows estimates of tenure effects obtained from a regression that allows all the parameters of the wage equation to vary across occupations by estimating the wage equations separately for each one-digit occupation. This is the preferred specification of the regression equation because there is no reason to believe that the parameters of the wage equation are constant across occupations. These regressions are estimated using the Altonji and Shakotko IV approach under specification (4b) from Table 3. The results indicate that the importance of occupation and industry experience as well as total experience in determining wages varies widely across occupations. Restricting these effects to be constant across occupations obscures substantial variation in the specificity of skills that workers accumulate at jobs in different occupations. For example, in the professional occupation five years of occupation specific experience increases wages by 22.3%, while five years of industry specific experience increases wages by 14.3%. Five years of total experience increases professional wages by only 4.6%, which is the lowest five-year total experience effect found in any occupation. In addition, this general experience effect is not statistically different from zero at the 5% level. These results suggest that professional workers accumulate skills that are to a large extent both occupation and industry specific. General skills, as measured by total experience, are of relatively little value in the professional occupation compared to the other occupations. As a basis for comparison, Zangelidis (2008) reports that occupation specific experience is an important determinant of wages for British workers.

Table 5.

Returns to Occupation, Industry, and Total Experience by Occupation

	Firm tenure		Occupation experience		Industry experience		Total experience
	2 years	5 years	2 years	5 years	2 years	5 years	2 years	5 years
Professionals	−.0262 (.0241)	−.0802 (.0404)	.0769 (.0324)	.2230 (.0669)	.0485 (.0359)	.1434 (.0667)	.0224 (.0371)	.0467 (.0796)
Managers	.0094 (.0223)	−.0004 (.0358)	−.0168 (.0247)	−.0952 (.0478)	.0691 (.0333)	.2339 (.0671)	.0757 (.0319)	.1708 (.0678)
Sales	−.0207 (.0583)	−.0461 (.0816)	.0035 (.0563)	−.0097 (.1015)	−.0169 (.0695)	.0827 (.1120)	.1664 (.0485)	.3689 (.1043)
Clerical	−.0573 (.0522)	−.0500 (.0820)	.0347 (.0404)	.0545 (.0715)	.0329 (.0562)	.0708 (.1048)	.1452 (.0380)	.3522 (.0836)
Craftsmen	−.0063 (.0208)	−.0189 (.0317)	.0443 (.0219)	.1374 (.0443)	−.0014 (.0271)	.0259 (.0521)	.0704 (.0219)	.1710 (.0475)
Operatives	.0312 (.0232)	.0010 (.0348)	−.0119 (.0296)	−.0319 (.0492)	−.0079 (.0263)	.0255 (.0538)	.1502 (.0223)	.3576 (.0483)
Laborers	−.0605 (.0345)	−.0853 (.0604)	−.0622 (.0356)	−.1022 (.0665)	.0405 (.0446)	.0798 (.0867)	.1417 (.0278)	.3266 (.0577)
Service	.0140 (.0381)	.0474 (.0564)	.0711 (.0380)	.1684 (.0789)	−.0720 (.0488)	−.0221 (.0887)	.1317 (.0391)	.3200 (.0837)
Hypothesis tests	H0: Returns to firm tenure equal across occupations		H0: Returns to occupation exper. equal across occupations		H0: Returns to industry exper. equal across occupations		H0: Returns to total exper. equal across occupations
Test statistic:	19.30		48.83		46.58		23.75
χ2 critical value	χ2 (21,.05) = 32.67		χ2 (21,.05) = 32.67		χ2 (21,.05) = 32.67		χ2 (14,.05) = 23.68

Notes: Returns to tenure and experience are expressed as changes in log wages. Returns are computed using regression specification (4b) from Table 3 by running the IV regression separately for each occupation. Standard errors in parentheses. Hypothesis tests test the null hypothesis that the returns to the different human capital variables are the same across occupations. For example, H₀ for firm tenure is that the coefficients on firm tenure, firm tenure squared, and the “oldfirm” dummy variable are constant across the 8 occupations.

In contrast to professional workers, sales workers do not experience a statistically significant wage gain from occupation or industry specific work experience, but they experience a 36.9% wage increase after five years of total experience, which is the largest general experience effect accruing to workers in any occupation. The types of skills required to earn high wages as a sales worker appear to be highly transferable across occupations, and it does not appear that sales workers gain from investing in occupation or industry specific skills. This finding is consistent with those reported in British data by Zangelidis (2008), who finds that general experience is a very important determinant of sales worker wages. Turning to the managerial occupation, the results show that managers realize a 23% wage increase after five years of experience in an industry, which is the largest effect of industry specific human capital found in any occupation. This result indicates that managers accumulate valuable industry-specific knowledge and skills that cause wages to increase. Apparently, being a successful manager requires knowledge of a particular industry, and does not rely solely on accumulating managerial skills that apply across all industries. Interestingly, the results show that after controlling for this industry-specific experience, managerial wages do not increase due to the accumulation of experience as a manager.

Variation in the specificity of skills is also found in blue-collar occupations, especially in regard to the relative importance of industry specific skills and general skills. Craftsmen accumulate occupation specific skills that increase wages by 13.7% after five years of experience, but do not experience wage gains from industry specific experience. In terms of the type of work done on the job craftsmen are somewhat similar to operatives, except for the important difference that craftsmen are more skilled. For example, Shaw (1987) reports that craftsmen are ranked behind only professionals and managerial workers in terms of intensity of skill investment, while in contrast operatives are ranked among the lowest occupations in intensity of skill investment. There are substantial differences in the roles played by occupation specific skills and general experience between the two seemingly closely related occupations. General experience is approximately twice as valuable for operatives compared to craftsmen, with five-year total experience effects of 35.7% and 17.1%. Additionally, occupation experience has a large and statistically significant effect on wages for craftsmen, but not for operatives. The differences between the craftsmen and operatives wage equations indicate that relatively highly skilled occupations such as craftsmen reward the accumulation of occupation-specific skills, while lower skilled occupations such as operatives reward more general skills that are transferable across different types of work.

The final two occupations listed in Table 5 are the relatively low paid laborers and service occupations. Workers in both of these occupations experience wage gains of roughly 32% after five years of total experience. However, a key difference between these two occupations is that service workers realize a large wage gain of 16.8% after five years of occupation specific experience, but there is no evidence that occupation specific skills are valuable for laborers. These estimates are consistent with the view that laborers are low skill workers who have little opportunity to increase their wages by investing in occupation or industry specific skills.

The first column of Table 5 shows the estimated effects of firm tenure on wages in each occupation. The point estimate of the effect of five years of tenure on wages is negative in six out of the eight one-digit occupations, but these effects are not statistically different from zero at the 5% level in seven out of the eight occupations.

The bottom section of Table 5 presents the results of hypothesis tests of the equality of the returns to different types of human capital across occupations. For example, the hypothesis test for the firm tenure effects is a joint test of the null hypothesis that the coefficients on Firm_Ten_ijt, (Firm_Ten_ijt)², and Old_Firm_ijt are equal across the eight occupations. The alternative hypothesis is that at least one of these coefficients differs across occupations. Analogous tests are performed for the occupation, industry, and total experience effects. The results of these hypothesis tests show that the null hypothesis that the occupation experience effects are the same across occupations is rejected at the 5% level. The null hypothesis that the returns to industry specific experience are the same across occupations is also rejected at the 5% level. In contrast, the null hypothesis of the equality of the firm tenure effects across occupations is not rejected at the 5% level. This is not surprising, given that the firm tenure effects are generally small and not statistically different from zero. Overall, the large differences in the value of different types of human capital across occupations combined with the statistical significance of these differences suggests that heterogeneity in the returns to different types of human capital is an important feature of the wage determination process.

As discussed earlier in this paper, it is likely that measurement error is present in occupation and industry codes. In general, one would expect measurement error in occupation codes to lead to an understatement of the heterogeneity in returns to human capital across occupations. For example, suppose that each occupation has a different return to occupation-specific experience. If misclassification is present in occupation codes, the estimates should tend to understate the extent of heterogeneity in the return to occupation-specific human capital across occupations.

From the point of view of understanding the wage determination process, the results shown in Table 5 suggest substantial variation in the specificity of skills accumulated at jobs in different occupations. Occupation specific skills are highly valued in some occupations (craftsmen and service), and industry specific skills are highly valued in other occupations (managers). For professionals, human capital has large industry and occupation specific components. General human capital is the key factor determining wage growth in some occupations (sales and clerical), while it is much less important in other occupations (professionals). These conclusions about the process of wage determination are quite different from the ones reached in previous research, which has found that skills are either occupation or industry specific, and has restricted the specificity of human capital to be the same across occupations.

5. Further Analysis of Occupation and Industry Experience Effects

The NLSY provides the U.S Census occupation and industry codes for each job. Interviewers question respondents about the occupation and industry of each job held during the year with the following three questions. What kind of work do you do? That is, what is your occupation? What kind of business/industry is it [the job]? Coders use these descriptions to classify each job using the three-digit Census occupation and industry coding scheme. The potential for measurement error in occupation and industry classifications certainly exists. Evidence on this issue is provided by Mellow and Sider (1983), who perform a validation study of occupation and industry codes using occupation codes found in the CPS matched with employer reports of their employee’s occupation and industry. They find agreement rates for industry codes of 84% at the three-digit level and 92% at the one digit level. The agreement rates for occupation codes at the three and one digit level are 58% and 81%. This evidence indicates that industry codes are significantly less noisy than occupation codes, and raises serious doubts about whether or not it is appropriate to use three-digit occupation codes in empirical work. As one would expect, there appears to be less measurement error in the fairly broadly defined one-digit classifications compared to the more narrowly defined three digit groupings.²¹

The occupation and industry codes are used to create the occupation and industry experience variables used in the wage regressions, so classification error in the codes creates measurement error in the experience variables used in the wage regression. It is well known that the presence of measurement error in highly correlated regressors such as occupation and industry experience variables may bias parameter estimates. Evidence on the impact of measurement error in occupation codes on estimates of occupation-specific wage equations is provided by Sullivan (2009). This paper accounts for measurement in occupation codes by estimating an occupational choice model that incorporates a parametric model of occupational misclassification. Comparing parameter estimates from the model that corrects for classification error to one that ignores it provides information about the effects of misclassification. The estimates show that, averaged across one digit occupations, the effect of occupation-specific work experience on wages in that occupation is overstated by 6% on average when misclassification is ignored. However, in many cases the changes in the occupation-specific experience coefficients are very small relative to the standard error of the parameter. The largest biases from ignoring classification error are found in estimates of the transferability of occupation-specific human capital across occupations, and this paper does not attempt to estimate the extent of transferability of experience across occupations. The model estimated by Sullivan (2009) is very different from the one estimated in this paper because the papers have very different goals, but the estimates do provide information about the approximate magnitude of the bias from ignoring classification error.²²

5.1 Evaluating the Performance of OLS and IV in Predicting Wage Changes

At this point it is useful to compare the OLS and IV estimates of the effects of the different human capital variables on wages. The OLS estimates are biased by endogeneity, while the IV estimates should not be. A comparison of the OLS and IV (specification 4b) estimates shows that the five year firm tenure effect has a very large upward bias of .20 log wage points, while the five year occupation and industry experience effects are biased upwards by .035 and .055 log wage points. These results suggest that endogeneity causes a much larger upward bias in the firm tenure coefficient compared to the occupation and industry coefficients.

One possible concern regarding the IV results is that the decreases in the tenure and experience coefficients between the OLS and IV estimates may be driven to some degree by measurement error in tenure and experience variables. The concern is that the firm, occupation, or industry experience effects could be biased downward due to measurement error in the highly correlated tenure, occupation experience, industry experience variables, and the associated instruments. A natural test of the performance of the IV and OLS estimates is to compare their performance in predicting wage changes for workers who do not switch firms, industries, or occupations.²³ If the IV tenure and experience coefficients are correct, then the predicted wage changes based on the OLS parameter estimates for workers who do not switch firms, occupations, or industries should be greater than the wage changes observed in the data. If the IV estimates of the tenure and experience coefficients are unbiased, then the IV wage change predictions should be more accurate than the OLS predictions.

Table 6 shows the average within-person change in the log wage based on predicted wages obtained from both the OLS and IV wage equations along with the mean actual log wage change found in the NLSY data. The first column of Table 6 shows that for workers who do not switch firms, occupations, or industries (stayers), the average change in the log wage found in the NLSY data is .033. The predicted wage change for stayers based on the OLS equation is .069, so the OLS prediction error is .036 log-wage points. The IV equation overstates the average wage change for stayers by only .008, so the IV equation provides a much more accurate prediction of wage growth for workers who remain at the same firm, occupation, and industry. In other words, OLS overstates within-job wage growth by over 100% because the firm tenure, occupation experience, and industry experience effects are biased upward by endogeneity. These results suggest that OLS produces upward biased estimates of the effects of firm tenure, occupation experience, and industry experience relative to the IV estimates.

Table 6.

Comparison of Actual Log Wage Changes to OLS and IV Predicted Log Wage Changes

	Mean of actual Δw, (NLSY data)	Mean of predicted Δŵ, OLS	Mean of predicted Δŵ, IV
No switch: remain at old firm, in old occupation and old industry (stayers)	.033	.069	.041

Notes: The actual wage change is the average within-person log wage change, Δw = ln(w_it)-ln(w_it-1) from the NLSY data, averaged over all person-time observations. Predicted wages are computed using predicted values from the OLS and IV regressions found in columns (1a) and (4b) of Table 3.

5.2 An Alternative Test of the Importance of Occupation and Industry Specific Human Capital

Another way to examine the validity of the IV parameter estimates is to replicate the experiment performed by Neal (1995) in his study of displaced workers. He demonstrates the importance of industry specific capital by showing that when post-displacement wages are regressed on pre-displacement firm tenure, the coefficient is three times as large for workers who stay in the same industry compared to those who switch industries. This result suggests that workers accumulate skills that are industry specific. One way of extending this methodology to examine the importance of occupation and industry specific capital is to divide the sample of all workers who switch employers into the following four groups: 1) switch firms but not occupation or industry, 2) switch firms and occupations but not industry, 3) switch firms and industry but not occupation, 4) switch firms, industry, and occupation. Regressing the change in wages accompanying the move between firms on pre-switch firm tenure separately for each of the four groups provides information about the transferability of skills between occupations and industries. The advantage of this approach is that random misclassification of occupation codes will cause these regressions to understate the importance of occupation specific experience if the true effect of occupation experience on wages is positive.

Table 7 presents estimates of the effect of pre-switch firm tenure on changes in the log wage for each of the four types of mobility. These regressions allow within-firm occupation switches in the data. These estimates provide clear support for the IV regression results which indicate that occupation and industry-specific experience have large effects on wages, while firm tenure effects are negligible. The first column of Table 7 shows that there is no statistically significant relationship between pre-switch firm tenure and the change in the log wage for workers who switch firms within their current occupation and industry. When workers switch firms but do not switch industry or occupation, there are no truly firm specific skills that are not transferable to their new job. This result is consistent with the IV regression results which show that firm-specific skills contribute little to wage growth. The estimate in the second column of Table 7 shows that when a worker switches firms and occupations, the wage change decreases by .0187 with each year of pre-switch firm tenure. This estimate shows that when workers switch occupations but remain in the same industry they incur wage losses because their occupation-specific skills are lost when they switch occupations. Similarly, the third column of Table 7 shows that when a worker switches firms and industries but remains in the same occupation the wage change decreases by −.0163 with each year of pre-switch firm tenure. This indicates that industry-specific skills are lost when a worker switches industries. The final column of Table 7 shows that the relationship between pre-switch firm tenure and wage changes is even stronger for workers who switch occupations and industries compared to those who only switch occupation or industry. The decrease in wages associated with each year of pre-switch firm tenure is approximately twice as large as corresponding wage change for occupations switchers, and is 2.5 times as large as the corresponding wage change for industry switchers.²⁴

Table 7.

OLS Estimates of the Effect of Pre-switch firm Tenure on the Change in Log Wages Accompanying a Firm Switch

	Type of Switch
	Switch Firm Only, Remain in Old Occupation and Industry	Switch Firm and Occupation, Remain in Old Industry	Switch Firm and Industry, Remain in Old Occupation	Switch Firm, Industry, and Occupation
Pre-switch firm tenure	−.0063 (.0046)	−.0187 (.0065)	−.0163 (.0074)	−.0391 (.0063)
Mean of dependant variable: change in log wage	.045	.027	.041	.042
Number of observations	2,323	1,470	1,792	3,578

Notes: Robust standard errors are in parentheses.

The dependent variable is change in the log of the real hourly wage. Tenure is measured in years. The other explanatory variables included in the regression are education, occupation dummies, industry dummies, age, and total experience.

While it is reassuring that these results provide support for the general conclusion that industry and occupation-specific human capital are each key determinants of wages, it is also interesting to note that they also support the conclusion drawn from the IV estimates about the relative magnitudes of these two effects. Both the IV and wage change estimates show that after averaging across occupations, both industry and occupation specific skills are of approximately equal importance in determining wages. Setting aside selection effects, these results suggest that when workers switch either occupations or industries some skills are not transferable to their new job. These results are consistent with the IV estimates which suggest that truly firm-specific factors contribute little to within-job wage growth.

5.3 Endogeneity

As discussed in Section 3 of this paper, applying the Altonji and Shakotko instrumental variables approach to estimating the return to occupation and industry specific human capital does not eliminate all of the possible sources of correlation between the explanatory variables and the error terms in the regression. Given that the most important results presented in this paper concern the positive effects of occupation and industry specific experience on wages, it is important to consider possible sources of endogeneity that would create upward bias in these particular parameter estimates.

In particular, a positive correlation between the firm match value (ψ_ij) and the occupation specific experience variable would create an upward bias in the estimated effect of occupation specific human capital on wages. This could occur if workers frequently move to higher paying firms while remaining in the same occupation. The intuition behind the upward bias is that if this type of within-occupation mobility occurs frequently, some of the wage gains from mobility between firms will be falsely attributed to gains from occupation specific experience. A similar upward bias could occur in the estimated effect of industry specific experience if individuals frequently move to higher paying firms within industries.

Although it has been documented that many workers search across occupations for a suitable career and then search for a suitable firm match within a particular occupation, this does not necessarily imply that the estimated IV returns to occupation specific human capital are upward biased. Many transitions between firms are caused by layoffs, and it is also likely that non-wage considerations play an important role in determining mobility. The top half of Table 8 shows the average wage changes observed within occupation spells for workers who remain at the same firm and switch firms. Workers who switch firms while remaining in the same occupation experience an average wage increase of 0.061, while workers who remain in an occupation without switching firms experience an average wage increase of 0.070. The fact that within-occupation mobility between firms is associated with lower wage gains than remaining at the same firm casts some doubt on the idea that this type of mobility leads to a serious upward bias in the estimated effects of occupation specific experience on wages. The bottom half of Table 8 shows that the same pattern holds for the wage gains within industry spells.²⁵

Table 8.

Mean Log Wage Changes within Occupation and Industry Spells

	Mean wage change (NLSY data)
Stay in occupation, switch firms	0.061 (0.457)
Stay in occupation, no firm switch	0.070 (.340)
Stay in industry, switch firms	0.057 (0.439)
Stay in industry, no firm switch	0.074 (.338)

Notes: The actual wage change is the average within-person log wage change, Δw = ln(w_it)-ln(w_it-1) from the NLSY data, averaged over all person-time observations. Standard deviations in parentheses.

6. Conclusion

This paper presents instrumental variables estimates of the effects of firm tenure, occupation experience, industry experience, and general work experience on wages for a sample of young men from the NLSY. Multiple specifications of the wage equation are estimated, and the results show that estimates of occupation and industry experience effects are quite sensitive to the treatment of within-firm occupational mobility. When within-firm occupation switches are ruled out, it appears that human capital is primarily occupation specific. However, this paper provides new evidence on the validity of within-firm occupation switches by exploiting a change in the NLSY occupation coding scheme designed to increase the reliability of reported within-firm occupation switches. This new data, combined with empirical evidence from a simple model of worker mobility suggests that workers make actual occupation switches within firms. When within-firm occupation switches are allowed, the IV wage equation estimates show that wages increase with both occupation and industry experience.

Additional evidence supporting the industry and occupation specificity of human capital is provided by an analysis of the relationship between firm tenure and wage changes accompanying mobility between firms. High tenure workers who switch occupation or industry when switching firms experience larger wage losses than those who do not switch occupation or industry, which suggests that workers accumulate skills that are both occupation and industry specific. In addition, the IV specification of the wage equation consistently outperforms the OLS specification in predicting wage changes for all combinations of mobility across firms, occupations, and industries. This suggests that OLS provides upward biased estimates of the effects of firm tenure, occupation experience, and industry experience on wages.

The results presented in this paper show that workers accumulate skills that are specific to both occupations and industries, while truly firm specific skills contribute little to the growth of wages over the career. A key feature of the human capital accumulation process is that the value of occupation experience, industry experience, and general work experience varies substantially across occupations. Constraining the effects of human capital on wages to be the same across occupations leads to misleading estimates of the effects of occupation and industry specific human capital on wages. Skills are primarily occupation specific in some occupations (craftsmen and service), industry specific in others (managers), and both occupation and industry specific in others (professional). On the other hand, general skills are the primary determinant of wage growth in other occupations (sales and clerical). These conclusions about the importance of both occupation and industry experience are quite different from those reached in the recent literature, which has found that either occupation or industry experience affects wages, but not both types of experience.

Appendix A: Occupation Industry Classifications

Description of Occupations
One-Digit Occupation	Three-Digit 1970 Census Codes	Example Three-Digit Occupations
Professional, technical & kindred workers	001–195	Accountants, chemical engineers, physicians, social scientists
Managers & administrators	201–245	Bank officers, office managers, school administrators
Sales workers	260–280	Advertising salesmen, real estate agents, stock and bond salesmen, salesmen and sales clerks
Clerical & unskilled workers	301–395	Bank tellers, cashiers, receptionists, secretaries
Craftsmen & kindred workers	401–580	Carpenters, electricians, machinists, brickmasons and stonemasons, mechanics
Operatives	601–726	Dry wall installers, butchers, drill press operatives, truck drivers
Laborers	740–785	Garbage collectors, groundskeepers, freight handlers, vehicle washers
Service workers	901–965	Janitors, child care workers, waiters, guards and watchmen

Description of Industries
One-Digit Industry	Three-Digit 1970 Census Codes	Example Three-Digit Industries
Agriculture, forestry, & fishing	17–28	Forestry, fisheries, horticultural services
Mining	47–57	Metal mining, coal mining, nonmetallic mining
Construction	67–77	General building contractors, special trade contractors
Manufacturing	107–398	Furniture, office machines, motor vehicles, aircraft
Transportation & communications	407–479	Taxicab service, trucking service, gas utility
Wholesale & retail trade	507–698	Motor vehicles, electrical goods, grocery stores
Finance, insurance, & real estate	707–718	Banking, insurance, real estate
Business & repair services	727–759	Advertising, computer programming, electrical repair
Personal services	769–798	Hotels and motels, barber shops, garment services
Entertainment & recreation services	807–809	Theaters and motion pictures, bowling alleys
Professional & related services	828–898	Offices of physicians, legal services, colleges and universities
Public Administration	907–937	Postal service, state public administration, local public administration

Appendix B: The Switch to Biennial Interviews

The NLSY conducted annual interviews until 1994. These interviews required the respondents to provide information about events that occurred during the past year. In 1994, the NLSY switched to biennial interviews, which doubled the length of the time period covered by the questions. Dugoni, Lee, and Tourangeau (1997) investigate the impact of the switch to biennial interviews on the quality of the NLSY data. They compare the responses given by individuals to questions about the number of jobs held, gaps between jobs, and receipt of unemployment, Food Stamps, and AFDC over a one and two-year recall period.

Overall, they find that the switch to the two-year recall period had little impact on the means of these variables for the entire sample. However, they note that a closer examination of the data reveals that there is a tendency for individuals with complicated labor force histories to report fewer jobs under the two-year recall period. For example, the one-year recall group reports holding an average of 1.24 jobs in the preceding year, while the two-year recall group reports 1.01 jobs over the same time period. Based on these results, it is possible that the data used in this study tends to understate job mobility in the years after 1994. However, the data used in this paper aggregates the weekly NLSY data to a monthly labor force record. As a result, jobs with very short durations are unlikely to show up in the aggregated monthly data. As a result, aggregating the data to the monthly level will tend to lessen the impact of the two-year recall period because some of the jobs that are mistakenly not reported do not last long enough to show up in the aggregated monthly data.

Appendix C: Instrumental Variables

This appendix presents the equations used to construct the instrumental variables. Spell means are denoted with a “bar” superscript (ex. ${\overline{\mathit{\text{Firm\_Ten}}}}_{\mathit{\text{ij}}}$ refers to mean firm tenure on firm spell j). Spells refer to firm spells for the firm tenure instruments, occupation spells for occupation experience instruments, and industry spells for industry experience instruments.

1. Instruments for firm tenure, firm tenure squared, and the “old firm” dummy:

   $$\begin{array}{c}({\mathit{\text{Firm\_Inst}}}_{\mathit{\text{ijt}}})=({\mathit{\text{Firm\_Ten}}}_{\mathit{\text{ijt}}})-({\overline{\mathit{\text{Firm\_Ten}}}}_{\mathit{\text{ij}}})\hfill \\ {({\mathit{\text{Firm\_Inst}}}_{\mathit{\text{ijt}}})}^2={({\mathit{\text{Firm\_Ten}}}_{\mathit{\text{ijt}}})}^2-({\overline{\mathit{\text{Firm\_Ten}}}}^2)\hfill \\ {\mathit{\text{Old\_Firm\_Inst}}}_{\mathit{\text{tjt}}}={\mathit{\text{Old\_Firm}}}_{\mathit{\text{ijt}}}-{\overline{\mathit{\text{Old\_Firm}}}}_{\mathit{\text{ij}}}\hfill \end{array}$$
2. Instruments for occupation experience, occupation experience squared, and the “old occupation” dummy:

   $$\begin{array}{c}{\mathit{\text{Occ\_Inst}}}_{\mathit{\text{iqt}}}={\mathit{\text{Occ\_Exp}}}_{\mathit{\text{iqt}}}-{\overline{\mathit{\text{Occ\_Exp}}}}_{\mathit{\text{iq}}}\hfill \\ {({\mathit{\text{Occ\_Inst}}}_{\mathit{\text{iqt}}})}^2={({\mathit{\text{Occ\_Exp}}}_{\mathit{\text{iqt}}})}^2-({\overline{\mathit{\text{Occ\_Exp}}}}_{\mathit{\text{iq}}}^2)\hfill \\ {\mathit{\text{Old\_Occ\_Inst}}}_{\mathit{\text{iqt}}}={\mathit{\text{Old\_Occ}}}_{\mathit{\text{iqt}}}-{\overline{\mathit{\text{Old\_Occ}}}}_{\mathit{\text{iq}}}\hfill \end{array}$$
3. Instruments for industry experience, industry experience squared, and the “old industry” dummy:

   $$\begin{array}{c}{\mathit{\text{Indus\_Inst}}}_{\mathit{\text{idt}}}={\mathit{\text{Indus\_Exp}}}_{\mathit{\text{idt}}}-{\overline{\mathit{\text{Indus\_Exp}}}}_{\mathit{\text{id}}}\hfill \\ {({\mathit{\text{Indus\_Inst}}}_{\mathit{\text{idt}}})}^2={({\mathit{\text{Indus\_Exp}}}_{\mathit{\text{idt}}})}^2-({\overline{{\mathit{\text{Indus\_Exp}}}^2}}_{\mathit{\text{id}}})\hfill \\ {\mathit{\text{Old\_Indus\_Inst}}}_{\mathit{\text{idt}}}={\mathit{\text{Old\_Indus}}}_{\mathit{\text{idt}}}-{\overline{\mathit{\text{Old\_Indus}}}}_{\mathit{\text{id}}}\hfill \end{array}$$