Performance of the Cockcroft-Gault, MDRD, and New CKD-EPI Formulas in Relation to GFR, Age, and Body Size

Abstract

Background and objectives: We compared the estimations of Cockcroft-Gault, Modification of Diet in Renal Disease (MDRD), and Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equations to a gold standard GFR measurement using ¹²⁵I-iothalamate, within strata of GFR, gender, age, body weight, and body mass index (BMI).

Design, setting, participants, & measurements: For people who previously underwent a GFR measurement, bias, precision, and accuracies between measured and estimated kidney functions were calculated within strata of the variables. The relation between the absolute bias and the variables was tested with linear regression analysis.

Results: Overall (n = 271, 44% male, mean measured GFR 72.6 ml/min per 1.73 m² [SD 30.4 ml/min per 1.73 m²]), mean bias was smallest for MDRD (P < 0.01). CKD-EPI had highest accuracy (P < 0.01 compared with Cockcroft-Gault), which did not differ from MDRD (P = 0.14). The absolute bias of all formulas was related to age. For MDRD and CKD-EPI, absolute bias was also related to the GFR; for Cockcroft-Gault, it was related to body weight and BMI as well. In all extreme subgroups, MDRD and CKD-EPI provided highest accuracies.

Conclusions: The absolute bias of all formulas is influenced by age; CKD-EPI and MDRD are also influenced by GFR. Cockcroft-Gault is additionally influenced by body weight and BMI. In general, CKD-EPI gives the best estimation of GFR, although its accuracy is close to that of the MDRD.

With the increasing incidence of kidney dysfunction, the use of formulas to estimate kidney function is implemented more frequently in clinical practice (1). The most frequently used formulas are the Cockcroft-Gault and (abbreviated) Modification of Diet in Renal Disease (MDRD) equations (2). The Cockcroft-Gault equation estimates clearance of creatinine (3), whereas the MDRD estimates GFR (2). At present, for subgroups of people who are old, underweight, or overweight, no clear-cut advice exists regarding which formula is best used for optimal estimation of kidney function. Both Cockcroft-Gault and abbreviated MDRD have been compared in the same population against a gold standard method for estimating GFR (4–8). These studies show conflicting results because of different study populations, different gold standard GFR measurements, and differences in creatinine assay calibration (9). Furthermore, the recently developed Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) formula has not been validated yet, outside pf the original publication (10); therefore, a pragmatic study to evaluate the most often used formulas, in a study population in which a GFR measurement is requested, is needed. Furthermore, these formulas need to be compared with an excellent gold standard GFR measurement.

In our center, GFR is measured by a method that can be considered the gold standard in the absence of bladder catheterization, for clinical reasons with a continuous infusion of ¹²⁵I-iothalamate (11–13). ¹³¹I-hippuran is added to correct for inaccurate urine collections without using a bladder catheter to optimize GFR measurement further (13). The aim of this study was to assess the agreement between kidney function as estimated by the Cockcroft-Gault, MDRD, and CKD-EPI equations and the GFR as measured by a gold standard method using ¹²⁵I-iothalamate. To examine whether the agreement is influenced by the level of GFR, gender, age, body weight, and body mass index (BMI), we also analyzed the agreement within clinically relevant strata of these variables.

Materials and Methods

In this cross-sectional study, we used data from potential kidney donors and adult patients who underwent a GFR measurement with ¹²⁵I-iothalamate for clinical reasons between January 1, 2003, and January 1, 2007, at the Academic Medical Center in Amsterdam. To be included, the measured GFR had to be at least 15 ml/min, and body weight, height, and plasma creatinine level had to be available from the patients' record within 3 months of the GFR measurement. For patients with multiple GFR measurements, the last available measurement was used. The data collection was approved by the committee of medical ethics of the Academic Medical Center.

Measurements

GFR was measured with ¹²⁵I-iothalamate in patients in steady state, whereas the effective renal plasma flow was measured with ¹³¹I-hippuran simultaneously to correct for inaccurate urine collections. This procedure was described previously as the standard method by Donker et al. (12) and our group (13). The measurements started in the morning. After the patients were seated, a blood sample was drawn. Then they received a loading dose of ¹²⁵I-iothalamate and ¹³¹I-hippuran, followed by a continuous infusion of both tracers. The first 2 hours were used as an equilibration period; two clearance periods of 2 hours each followed. Patients drank at least 200 ml/h water during the measurements to maintain sufficient urine flow. At 2, 4, and 6 hours after the start of the infusion, urine samples were collected by spontaneous voiding and plasma samples were drawn. Plasma creatinine was determined with an isotope dilution mass spectrometry-validated enzymatic assay on an automated analyzer (Hitachi H911; Boehringer Mannheim, Mannheim, Germany).

For comparison with renal estimates of the formulas, the measured GFR was normalized to 1.73 m² of the body surface area (BSA) by multiplying the measured GFR by 1.73/BSA. The BSA was calculated according to Du Bois and Du Bois (14): BSA = (body weight^0.425 [in kg] × height^0.725 [in cm]) × 0.007184.

Prediction Formulas

The prediction of creatinine clearance (in ml/min) by the Cockcroft-Gault formula (3) was calculated as (140 − age) × body weight/plasma creatinine × 72 (× 0.85 if female). For comparison with the prediction of other formulas, the predicted creatinine clearance by Cockcroft-Gault was normalized per 1.73 m² of BSA using the formula of Du Bois and Du Bois (14) identical to the normalization of the GFR measurement.

The abbreviated MDRD estimate (2) of kidney function was calculated as 175 × plasma creatinine^−1.154 × age^−0.203 (× 0.742 if female; × 1.21 if black). The CKD-EPI estimate (10) of renal function was calculated as recommended: For women with a plasma creatinine ≤0.7, (plasma creatinine/0.7)^−0.329 × (0.993)^age (× 166 if black; × 144 if white or other); for women with a plasma creatinine >0.7, (plasma creatinine/0.7)^−1.209 × (0.993)^age (× 166 if black; × 144 if white or other); for men with a plasma creatinine ≤0.9; (plasma creatinine/0.9)^−0.411 × (0.993)^age (× 163 if black; × 141 if white or other); for men with a plasma creatinine >0.9, (plasma creatinine/0.9)^−1.209 × (0.993)^age (× 166 if black; × 144 if white or other).

The estimated renal functions using the (abbreviated) MDRD and the CKD-EPI equations are expressed as GFR in ml/min per 1.73 m². Age was expressed in years, body weight in kg, and plasma creatinine in mg/dl.

Statistical Analysis

Numbers are presented as means and SD. Relations between various parameters were tested using linear regression. Differences between genders were tested with the t test. All statistical analyses were performed in SPSS 16.0 for Windows (SPSS, Chicago, IL).

To compare the performance of the formulas, we calculated bias, precision, and accuracy as recommended (15). Bias was defined as the mean difference between estimated and measured kidney function, whereas precision was expressed as the SD of this difference. To define the best formula, we used the accuracy, because it is a combination of bias and precision. Accuracy was calculated as the percentage of patients who had an estimated kidney function within 30% limits of the measured GFR. Differences in bias and accuracy between the formulas were tested with a paired t test or McNemar test, respectively.

Bias, precision, and accuracies were also calculated within strata of measured GFR, gender, age, body weight, and BMI because these variables might influence the performance of the equations. Stratification of measured GFR was based on the stages of chronic kidney disease (CKD) (15). Clinical cutoffs were used for age (18 to 39, 40 to 59, and ≥60 years) and body weight (≤59, 60 to 79, 80 to 99, and ≥100 kg). BMI was calculated as body weight divided by the square of height, with body weight expressed in kg and height in meters. Stratification for BMI was performed according to World Health Organization guidelines (16,17): ≤18.5, 18.5 to 24.9, 25.0 to 29.9, or ≥30.0 kg/m².

Furthermore, we studied the relation between the GFR and measurement error by applying the method as proposed by Bland and Altman (18). We assessed the bias as well as the limits of agreement, which were calculated as the bias plus or minus two times the precision. Because our GFR measurements are far more likely to be closer to the real GFR than the predicted estimates by the formulas, we used the measured GFR on the x axes instead of the mean of both methods.

We tested the influence of the previously mentioned variables on the bias of the formulas by analyzing the relation between the variables and the magnitude of the absolute bias with univariate linear regression models. We used the absolute bias instead of the crude bias for this analysis because the crude bias can have positive and negative values, which complicates the interpretation of a linear regression on the crude bias.

Finally, patients were classified into stages of CKD according to level of measured GFR, as well as on the basis of the estimates of the Cockcroft-Gault, MDRD, and CKD-EPI formulas. Agreement between the measured GFR and the estimates of the formulas in their classification of patients into CKD stages was assessed by calculating Cohen's κ.

Results

In total, 685 GFR measurements were performed. After exclusion of measurements in children (n = 32); those without an available plasma creatinine level (n = 38), valid GFR (n = 2), body weight (n = 1), or height (n = 178); those with a GFR <15 ml/min (n = 4); and duplicate cases (n = 159), 271 patients remained eligible for inclusion. Patient characteristics are presented in Table 1.

Table 1.

Characteristics of study population

Characteristic	Value (N = 271)
Male gender (n [%])	118 (44)
Age (years; mean ± SD)	44.3 ± 14.5
Body weight (kg; mean ± SD)	75.8 ± 17.3
Height (cm; mean ± SD)	171.3 ± 9.4
BMI (kg/m2; mean ± SD)	25.8 ± 5.5
BSA (m2; mean ± SD)	1.9 ± 0.2
Black race (n [%])	28 (12)
Plasma creatinine (mg/dl; mean ± SD)	1.2 ± 0.6
Measured GFR (ml/min; mean ± SD)	78.2 ± 33.4
Measured GFR corrected for BSA (ml/min per 1.73 m2; mean ± SD)	72.6 ± 30.4

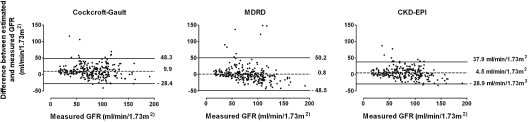
The overall mean bias was smallest for MDRD (P < 0.01; Figure 1). CKD-EPI had the highest accuracy (P < 0.01 compared with Cockcroft-Gault), although it was not statistically significantly different from MDRD (P = 0.14; Table 2).

Figure 1.

Bland-Altman figures of the estimated and measured kidney function. Bland-Altman plots—the difference between the estimated and measured renal function—is plotted against the measured GFR; therefore, a positive difference suggests an overestimation by the formula, whereas a negative difference suggests an underestimation. The dashed lines represent the mean difference between estimated and measured GFR; the solid lines represent the lines of agreement, calculated as mean difference plus or minus two times the SD of this difference.

Table 2.

Comparison of the estimation of the formulas to the gold standard GFR

Parameter	Mean Overall Bias	Overall Precision	Mean Absolute Bias	Absolute Precision	Accuracy within 30% (%)
Cockcroft-Gault	9.9	19.2	15.3	15.2	74.2
MDRD	0.8a	24.7	14.6	19.9	81.2
CKD-EPI	4.5	16.7	12.3a	12.1	84.5b

See the Materials and Methods section for definitions of (absolute) bias, precision, and accuracy.

^aP ≤ 0.01 versus both other formulas.

^bP < 0.01 versus Cockcroft-Gault, P = 0.14 versus MDRD.

Classification of patients according to measured and estimated kidney function for stages of CKD is presented in Table 3. Using Cockcroft-Gault, 63% of the patients were classified correctly. In 29%, Cockcroft-Gault underestimated kidney function, and in 8% it overestimated (Cohen's κ = 0.47). The MDRD equation classified 65% of the patients correctly, in 15% of the patients the GFR was underestimated, and in 20% it was overestimated (Cohen's κ = 0.51). CKD-EPI classified most patients correctly (69%). It underestimated GFR in 23% and overestimated GFR in 8% of the patients (Cohen's κ = 0.56).

Table 3.

Cohen's κ table, comparison of classification of patients in stages of CKD according to measured and estimated GFR by the formulas

Estimated GFR	Measured GFR (ml/min per 1.73 m2)
	≥90	60 to 89	30 to 59	15 to 29	Total
Cockcroft-Gault (ml/min per 1.73 m2; Cohen's κ = 0.47)
≥90	70	33	6	0	109
60 to 89	12	50	24	0	86
30 to 59	0	10	39	16	65
15 to 29	0	0	0	11	11
MDRD (ml/min per 1.73 m2; Cohen's κ = 0.51)
≥90	53	13	7	0	73
60 to 89	28	59	12	0	99
30 to 59	1	21	47	10	79
15 to 29	0	0	3	17	20
CKD-EPI (ml/min per 1.73 m2; Cohen's κ = 0.56)
≥90	73	30	6	0	109
60 to 89	9	50	17	0	76
30 to 59	0	13	45	9	67
15 to 29	0	0	1	18	19
Total	82	93	69	27	271

The bold numbers indicate the number of patients classified to the same CKD stage according to both compared methods.

Influence of GFR

Patients with a higher GFR were younger and had a lower body weight and a lower BMI. Each 1-ml/min per 1.73 m² higher GFR corresponded to a younger age of −0.20 years (95% confidence interval [CI] −0.25 to −0.15 years), to a lower body weight of −0.07 kg (95% CI −0.14 to −0.01 kg), and to a lower BMI of −0.03 kg/m² (95% CI −0.05 to −0.01 kg/m²).

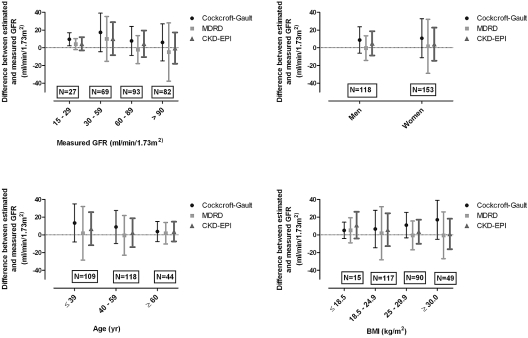
The absolute bias of MDRD and CKD-EPI was larger in patients with a higher GFR (Table 4). Mean bias and precision of the formulas in subgroups of GFR are presented in Figure 2. The CKD-EPI provided the highest accuracy in patients with a GFR in stage 1 CKD (92.7%); however, it did not differ statistically from the accuracy of Cockcroft-Gault (87.8%; P = 0.29) or MDRD (89.0%; P = 0.51). In the group with the lowest GFR, MDRD had the highest accuracy, although it was close to the accuracy of CKD-EPI (P = 0.63, compared with Cockcroft-Gault P = 0.04).

Table 4.

Influence of GFR, age, body weight, BMI, and gender on the absolute bias

Parameter	Cockcroft-Gault	MDRD	CKD-EPI
GFR (ml/min per 1.73 m2)	0.030 (−0.030 to 0.090)	0.150 (0.070 to 0.220)	0.050 (0.004 to 0.100)
Age (years)	−0.26 (−0.38 to −0.14)	−0.27 (−0.43 to −0.11)	−0.17 (−0.27 to −0.07)
Body weight (kg)	0.140 (0.040 to 0.25)	−0.130 (−0.270 to 0.004)	−0.090 (−0.170 to 0.003)
BMI (kg/m2)	0.55 (0.23 to 0.88)	−0.14 (−0.57 to 0.29)	−0.21 (−0.47 to 0.05)
Female gender	3.57 (−0.09 to 7.23)	7.77 (3.06 to 12.47)	2.19 (−0.72 to 5.10)

The numbers represent the change of the absolute bias in ml/min per 1.73 m² for an increase per unit of the given variables (β values) and their accompanying 95% CIs. One unit of GFR represents 1 ml/min per 1.73 m²; for age, one unit represents 1 year; for body weight, one unit represents 1 kg; for BMI, one unit represents 1 kg/m²; and for gender one unit represents being a woman compared with being a man.

Figure 2.

Comparison of the bias and precisions over subgroups. Mean bias and precision between estimated and measured GFR for to various strata of GFR, gender, age, and BMI. The mean bias was calculated as the mean of the differences between the estimated and measured GFR per subgroup, whereas the precision was the SD of this difference.

Influence of Gender

Compared with men, women had a lower body weight; men 83 kg (SD 14 kg), women 71 kg (SD 18 kg; P < 0.01). The absolute bias of MDRD was larger in woman than in men (Table 4). For both genders, mean bias and precision are presented in Figure 2. In men, the highest accuracy was reached by MDRD (86.4%), whereas in women, CKD-EPI had the highest accuracy (84.3%). These accuracies were higher than those of Cockcroft-Gault (men 76.3%, women 72.5%; P ≤ 0.01), but MDRD and CKD-EPI did not differ from each other (CKD-EPI in men 84.7% [P = 0.69]; MDRD in women 77.1% [P = 0.31]).

Influence of Age

Elderly patients had a lower GFR, a higher body weight, and a higher BMI. Each additional year of age corresponded to a lower GFR of −0.87 ml/min per 1.73 m² (95% CI −1.10 to −0.64 ml/min per 1.73 m²), a higher body weight of 0.18 kg (0.04 to 0.32 kg), and a higher BMI of 0.08 kg/m² (0.03 to 0.12 kg/m²).

All formulas had a smaller absolute bias in patients with a higher age (Table 4). Figure 2 presents mean bias and precision for subgroups of age. The accuracies of the MDRD and the CKD-EPI equations were similar in youngest and oldest subgroups (82.6% for the youngest and 81.8% for the oldest group). Both differed from the Cockcroft-Gault formula (69.7%; P ≤ 0.01) in the youngest group but not in the oldest group (75.0%; P = 0.45).

Influence of Body Weight and BMI

Furthermore, patients with a higher body weight had a lower GFR, were older, and had a higher BMI. Each 1-kg higher body weight corresponded to a −0.23-ml/min per 1.73 m² (95% CI −0.44 to −0.02 ml/min per 1.73 m²) lower GFR, a 0.13-year (0.03 to 0.23 year) older age, and a 0.28-kg/m² (0.26 to 0.30 kg/m²) higher BMI.

Patients with a higher BMI were older and had a higher body weight and a lower GFR. Each 1-kg/m² higher BMI corresponded to a 0.53-year (95% CI 0.23 to 0.84 year) older age, 2.71-kg (2.53 to 2.90 kg) higher body weight, and a −0.81-ml/min per 1.73 m² (−1.46 to −0.161 ml/min per 1.73 m²) lower GFR.

The absolute bias of Cockcroft-Gault was greater in patients with a higher body weight or BMI (Table 4). In the subgroup with lowest body weight, Cockcroft-Gault and CKD-EPI had a similar accuracy (71.4%), almost the same as that of MDRD (69.0%; P = 1.00). MDRD provided greatest accuracy (97.0%) in those with the highest body weight. This was different from the Cockcroft-Gault (57.1%; P = 0.02) but not from CKD-EPI (87.0%; P = 1.00).

The mean bias and precisions of the formulas per subgroup of BMI are presented in Figure 2. For patients who were underweight, Cockcroft-Gault had the greatest accuracy (80.0%). This was not statistically different from the accuracy of MDRD or CKD-EPI (66.7 and 60.0%, respectively; P ≥ 0.25). In the most overweight patients, accuracy was highest using CKD-EPI (85.7%), which differed from the accuracy of Cockcroft-Gault (57.1%; P < 0.01) but was close to that of MDRD (77.6%; P = 0.29).

Discussion

This pragmatic study comparing the Cockcroft-Gault, MDRD, and CKD-EPI formulas in a clinical setting showed that overall mean bias was smallest for MDRD. The highest accuracy, however, was reached with CKD-EPI and MDRD. As expected, CKD-EPI estimated GFR closest to the directly measured GFR in patients with a GFR of ≥90 ml/min per 1.73 m², whereas MDRD remained best when GFR ranged from 15 to 29 ml/min per 1.73 m². Differences in accuracy between MDRD and CKD-EPI, however, were small and not statistically significant. Our finding that the CKD-EPI formula gave the best overall accuracy and agreement after classification in subgroups of GFR is in line with the original publication on this formula (10). The present data add that the performance of the CKD-EPI formula is dependent on age and GFR.

The graphs show that the relation between mean biases of the formulas over subgroups of GFR was not linear. Mean bias was largest in those with a GFR in stage 3 CKD. Most studies showed a larger bias in stage 2 than in stage 3 CKD for Cockcroft-Gault or MDRD (6,7,19,20), which is in contrast to our findings. The relatively small number of patients in the subgroups in our study as well as in some of the aforementioned studies (7,19) could be an explanation for this difference; however, studying the accuracies over the subgroups, all formulas showed a pattern in which the accuracies became smaller per GFR subgroup, which is in line with others (6,20). Furthermore, the regression analysis that was based on the absolute bias per patient did show a linear relation between the GFR and the absolute bias.

In this study, we found no significant differences in accuracies between MDRD and CKD-EPI formulas within subgroups. It could be that the number of patients within subgroups was too small to detect these differences; however, most subgroups were large enough to measure a difference of the MDRD and CKD-EPI formulas to Cockcroft-Gault. This makes it more likely that the accuracy of MDRD and CKD-EPI are indeed highly in line with each other; however, in the elderly and in those with a low body weight or BMI, Cockcroft-Gault remains a good alternative. Our finding that the MDRD or the CKD-EPI formula seems to be the best option for young patients is in agreement with the results of Donadio et al. (5). Using these formulas in the elderly is also supported by others (8,21), although not by all (5,22). This difference might be caused by small differences in bias and precision between the formulas in the elderly, because all formulas had smaller absolute biases in these subjects. For Cockcroft-Gault, a relation between its bias and age has been shown before (5,8,22).

The influence of body composition on the performance of the formulas can be assessed by studying the influence of body mass or BMI. Our results showed that the absolute bias of Cockcroft-Gault was dependent on both of these parameters. For the CKD-EPI and MDRD formulas, this relation was not statistically significant; however, the regression analysis did show point estimates suggesting a smaller absolute bias in patients with a higher body weight or BMI. The relation of the absolute bias with body weight and BMI is surprising given their normalization for BSA. In line with our results, others also found the estimation of Cockcroft-Gault to be more dependent on body weight or BMI than MDRD (8,19,20). The influence of BMI on the bias of Cockcroft-Gault has been described before (5,23), although not all studies found this relationship (6,21).

This study has its limitations. Ideally, we would have measured the plasma creatinine on the same day the GFR measurement was performed in all patients. A plasma creatinine measurement on the same day as the GFR measurement was available for 48 (18%) patients, because of the retrospective data collection; however, a sensitivity analysis of patients with an available plasma creatinine value within 14 days of the GFR measurement (n = 204 [75%]) did not change our conclusions (data not shown). Furthermore, the stable state of the patients was judged by the clinician who requested the GFR measurement. For 144 (53%) subjects, a previous plasma creatinine value was available within 3 months of the GFR measurement (mean 1.24 mg/dl; SD 0.65 mg/dl). The difference between this plasma creatinine and the one used in our study was 0.002 mg/dl (SD 0.18 mg/dl). Given the small differences between the previous plasma creatinine and the used one, we conclude that indeed only stable patients were selected. Another limitation of this study is the relatively limited numbers of patients in the subgroups. This was mainly due to the absence of data on height. We needed this parameter for the normalization of Cockcroft-Gault and measured GFR for BSA to make a valid comparison, because MDRD and CKD-EPI are expressed that way; however, we were able to include a relevant number of patients, sufficient to allow stratification. Some of the studied parameters were correlated, such as age and GFR. We chose not to correct our findings for these influences because this describes clinical practice in which age and GFR are also correlated.

A strong feature of this study is that we were able to compare both the two most frequently used and the newest equations to estimate kidney function in one heterogeneous cohort against an excellent gold standard method to measure GFR (13). We were able to study the influence of measured GFR, gender, age, body weight, and BMI on the performance of the formulas by stratification on these parameters.

In conclusion, the absolute bias of all formulas is influenced by age. The CKD-EPI and MDRD formulas are also influenced by GFR, and the Cockcroft-Gault equation is additionally influenced by body weight and BMI. In general, CKD-EPI gives the best estimation of GFR, although the performance is close to that of MDRD.

Disclosures

None.