A novel P300-based brain-computer interface stimulus presentation paradigm: moving beyond rows and columns

Abstract

Objective

An electroencephalographic brain-computer interface (BCI) can provide a non-muscular means of communication for people with amyotrophic lateral sclerosis (ALS) or other neuromuscular disorders. We present a novel P300-based BCI stimulus presentation – the checkerboard paradigm (CBP). CBP performance is compared to that of the standard row/column paradigm (RCP) introduced by Farwell and Donchin (1988).

Methods

Using an 8×9 matrix of alphanumeric characters and keyboard commands, 18 participants used the CBP and RCP in counter-balanced fashion. With approximately 9 – 12 minutes of calibration data, we used a stepwise linear discriminant analysis for online classification of subsequent data.

Results

Mean online accuracy was significantly higher for the CBP, 92%, than for the RCP, 77%. Correcting for extra selections due to errors, mean bit rate was also significantly higher for the CBP, 23 bits/min, than for the RCP, 17 bits/min. Moreover, the two paradigms produced significantly different waveforms. Initial tests with three advanced ALS participants produced similar results. Furthermore, these individuals preferred the CBP to the RCP.

Conclusions

These results suggest that the CBP is markedly superior to the RCP in performance and user acceptability.

Significance

The CBP has the potential to provide a substantially more effective BCI than the RCP. This is especially important for people with severe neuromuscular disabilities.

1. Introduction

Brain-computer interfaces (BCIs) facilitate reestablishing communication and environmental control for people whose motor and communicative abilities have been impaired by severe neuromuscular disease (Wolpaw & Birbaumer, 2006). For example, although cognitive function is usually spared, the motoneuron death associated with amyotrophic lateral sclerosis (ALS) ultimately renders people physically incapacitated as they lose all voluntary muscle control. These people may become “locked-in” to their bodies, unable to communicate, and completely dependent upon caregivers to attend to their basic needs. Importantly, however, the use of a BCI can mitigate the isolation and dependence they experience by providing a mode of communication not contingent on neuromuscular activity.

BCIs translate volitional modulation of brain signals into computer commands, which can be recorded from the scalp using electroencephalography (EEG; e.g., Farwell & Donchin, 1988; Wolpaw & McFarland, 2004), from the dura mater or cortical surface using electrocorticography (ECoG; e.g., Leuthardt, et al., 2004), or from neurons within the cortex (e.g., Hochberg et al., 2006). A common signal for BCI is the P300 event-related potential (ERP). The P300 ERP is a positive deflection in the EEG over parietal cortex that occurs approximately 300ms after an “oddball” stimulus: a rare but meaningful stimulus among a series of frequently occurring stimuli. Because the P300 occurs amid other ongoing EEG activity, several P300 responses must usually be averaged for the response to be recognized (Fabiani et al., 1987; Polich, 2007; Pritchard, 1981).

Farwell and Donchin (1988) introduced the first P300-based BCI paradigm. In this paradigm, a computer presents a 6×6 matrix of letters and commands on-screen and participants attend to the item they wish to select. Groups of matrix items are flashed randomly. Only flashes of groups containing the attended item should elicit a P300. In this original implementation of a P300 BCI, and in most subsequent implementations, items are grouped for flashing as rows and columns; hence, the row-column paradigm, or RCP. The computer identifies the attended item as the intersection of the row and column that elicited the largest P300.

1.1. Improving the RCP

The RCP has been tested in various configurations to achieve efficient communication that is practical for in-home use. For example, researchers have explored various electrode montages (Krusienski et al., 2006), stimulus properties such as inter-stimulus interval (ISI) and matrix size (Sellers et al., 2006), and various signal processing methods (Kaper et al., 2004; Krusienski et al., 2006; Lenhardt et al., 2008; Serby et al., 2005).

Others have modified the RCP paradigm. For example, Martens et al. (2009) compared the RCP speller to an apparent motion paradigm where motion occurs in rows and columns. Similarly, Hong et al. (2009) compared the RCP to an apparent motion and color onset paradigm that also presents the color and motion stimuli in a row/column arrangement. Takano et al. (2009) recently investigated RCP accuracy using three different luminance and chromatic flash patterns: a white/grey pattern (luminance condition); a green/blue isoluminance pattern (chromatic condition); and a green/blue luminance pattern (luminance chromatic condition). The luminance chromatic condition produced online accuracy higher than the luminance or chromatic condition alone. Salvaris and Sepulveda (2009) compared changes to the background/foreground colors, item size, and distances between items. Their results demonstrated that, although no single paradigm was best for everybody, a white background produced the highest mean offline classification accuracy, and small symbol sizes produced the lowest mean classification accuracy. Finally, Guger et al. (2009) compared the RCP to a paradigm in which single items flash at random. They found that the RCP yielded higher accuracy and bit rate than the single item flash paradigm, even though the P300 responses were larger for the latter. In sum, none of these alternative paradigms substantially improves P300-based BCI performance.

Two additional studies have used stimuli that are not presented in a RCP format. Allison (2003) presented random groups of items in an arrangement referred to as a “splotch” presentation, somewhat similar to the method presented in this article. The splotch presentation reduced the number of flanking items that flash with the target, and participants reported that they preferred the method; however, no data with regard to BCI performance were reported. Hill et al. (2009) also tested a variation of a random stimulus presentation using an offline leave-one-out cross validation. Their results suggested that the random presentation did not perform as well as the standard RCP; however, no statistical analyses were performed to test the performance difference.

1.2. RCP and BCI errors

The RCP remains subject to errors that slow communication, cause frustration, and diminish attentional resources. Importantly, these errors appear to have two primary causes.

First, errors typically occur with the greatest frequency in locations adjacent to the attended item (i.e., the target item) and almost always in the same row or column (Fazel-Rezai, 2007). This inherent RCP error occurs because each time a target item flashes, a P300 is produced for every item in the row or column. However, only the intersection of the target row and column is unique to the target item. Errors arise when flashes of non-target rows or columns that are adjacent to the target, attract the participant’s attention, thereby producing P300 responses. We refer to these relatively systematic errors as “adjacency-distraction errors” (or the “adjacency-distraction problem”). This phenomenon is well documented in the spatial attention literature. For example, in a standard flanker task, response time significantly increases when nearby items belong to a response class different from the target class (e.g., Sanders & Lamers, 2002). In the RCP, when adjacency-distraction errors occur with sufficient frequency, the distractions cause one of the four adjacent items (or another item in the same row or column of the target) to be selected unintentionally.

Second, in order to conform to the oddball paradigm, sets of items must be intensified in random order. This allows target items to, at times, flash consecutively. That is, when a row flash is followed by a column flash (or vice versa), and the target item is at the intersection of that particular row and column, the target item flashes twice in immediate succession. Due to the rapid rate of intensification, double flashes can cause errors of two types. One, if the target item is involved in a double flash, the second flash may go unnoticed by the participant, so that it does not produce a P300 response. Two, even if the second flash is perceived, the P300 responses to the two flashes overlap temporally. This can reduce P300 amplitude or change its morphology (Martens et al., 2009; Woldorff, 1993). We refer to these errors as “double-flash errors” (or the “double-flash problem”).

1.3. Is there a better alternative to the RCP?

Further RCP research could possibly help severely disabled BCI users, who desire speed, accuracy, and ease of use. However, the kinds of errors that are inevitably associated with the RCP can still make it frustrating for users and burdensome for their caregivers (Vaughn et al., 2006). Moreover, with the RCP, some people are not able to achieve accuracy high enough for practical BCI use (Sellers & Donchin, 2006). In recognition of these issues, we sought to create an alternative stimulation paradigm that is faster, more accurate, and more reliable than the RCP.

To achieve this goal, we designed an alternative to the RCP that is called the checkerboard paradigm, or CBP. We used an 8×9 matrix containing 72 items. In the RCP, the eight columns and nine rows flash at random (Fig. 1A). In contrast, in the CBP, the standard 8×9 matrix is virtually superimposed on a checkerboard (Fig. 1B, left), which the participants never actually see. The items in white cells of the 8×9 matrix are segregated into a white 6×6 matrix and the items in the black cells are segregated into a black 6×6 matrix. Before each sequence of flashes, the items in Figure 1B (left) randomly populate the white or black matrix, respectively, as shown in Figure 1B (middle). The virtual checkerboard layout controls for adjacency-distraction errors, because adjacent items cannot be included in the same flash group. The end result is that the participants see random groups of six items flashing (as opposed to rows and columns) because the virtual rows and columns depicted in Figure 1 (middle) flash. For example, the top row of the white matrix includes the items: 2, Bs, Shift, H, Sp, EC. In this example, the participant is shown the standard 8×9 matrix Figure 1B (right) and the six items from the top row of Figure 1B (middle, top) flash. In other words, the standard matrix never changes; only the pattern of flashing items is changed. During one sequence, the six virtual rows in the white matrix (Fig. 1B, middle) flash in order from top to bottom followed by the six virtual rows in the black matrix. Then the six virtual columns in the white matrix flash in order from left to right followed by the six virtual columns in the black matrix.

Fig. 1.

A: The Row-Column paradigm (RCP) for the 8×9 matrix, with one row flashing. B: The Checkerboard paradigm (RCP) for the 8×9 matrix. On the left is the checkerboard pattern. In the middle are the two virtual 6×6 matrices derived from the checkerboard. On the right is the matrix as presented to the participant with the top row of the white 6×6 virtual matrix flashing. See text for details.

Due to the fact that the randomized virtual rows of each matrix flash first (12 flashes) and then the virtual columns of each matrix flash (12 flashes), any given matrix item cannot flash again for a minimum of six intervening flashes and a maximum of 18 intervening flashes. This eliminates the double-flash problem. After all rows and columns in both matrices have flashed (i.e., 24 flashes, comprising one complete sequence), the program re-randomizes the positions of the items in each virtual matrix and the next sequence of flashes begins. In addition, the CBP almost completely avoids overlapping target epochs because six intervening flashes correspond to 750 ms and we used classification epochs of 800 ms. Simply eliminating the double-flash problem does not ensure that enough time will be presented between target items to keep the target epochs from overlapping, and this has been shown to cause deleterious effects to the P300 (Squires, et al., 1976). By maximizing the time between successive flashes of the target item, the CBP should increase the amplitude of the P300 responses (Polich, et al., 1991) and should also improve BCI speed and accuracy.

1.4. The present study

In this study, our hypothesis is that the CBP will produce superior performance as compared to the RCP because it avoids the adjacency-distraction and double-flash errors to which the RCP is prone. In addition to comparing the two paradigms, we also sought to optimize the stepwise linear discriminant analysis (SWLDA; Draper & Smith, 1981) classifier to achieve the highest online speed and accuracy (i.e., bit rate) possible. Moreover, the expansion to an 8×9 matrix allows the inclusion of both alphanumeric keys and function keys, giving the participant more control and communication options. The larger matrix should also produce larger P300 amplitudes for the target items because the probability of the target stimulus occurring is reduced. This relationship is found in standard oddball experiments (e.g., Duncan-Johnson & Donchin, 1977) and also in BCI applications (Allison & Pineda, 2003; Sellers et al., 2006). Finally, while the larger matrix increases the time needed for each selection, it should increase the information transferred per selection.

2. Methods

2.1. Participants

Eighteen able-bodied adults (11 men, 7 women) were recruited from the East Tennessee State University undergraduate participant pool. All were naïve to BCI use. None had uncorrected visual impairments or any known cognitive deficit. The study was approved by the East Tennessee State University Institutional Review Board and each person gave informed consent.

In addition, three people with ALS (two women, one man) were recruited. They were all ventilator-dependent and were still able to move their eyes. Two were otherwise totally paralyzed (i.e., locked-in) while one retained a slight eyebrow twitch. The study was approved by the New York State Department of Health Institutional Review Board and each person gave informed consent.

2.2. Data acquisition, processing

Each participant sat in a comfortable chair approximately 1m from a computer monitor that displayed the 8×9 matrix. The EEG was recorded with a standard 32-channel electrode cap (with tin electrodes; Electro-Cap International, Inc.). All channels were referenced to the right mastoid and grounded to the left mastoid, and impedances were reduced below 10.0 kΩ before recording. The signals were amplified and digitized by two g.tec (Guger Technologies) 16-channel USB biosignal amplifiers (amplification to +/- 2V before ADC; high-pass and low-pass filters 0.5 Hz and 30 Hz, respectively; digitization rate 256 Hz). Only electrodes Fz, Cz, P3, Pz, P4, PO7, PO8, and Oz (Sharbrough et al., 1991) were used for BCI operation (Krusienski, et al., 2008). The general-purpose BCI software platform BCI2000 (Schalk, et al., 2004) controlled stimulus presentation, data collection, and online processing. Data acquisition and processing was identical for the ALS users with the exception that they used either a single 8-channel or 16-channel g.tec amplifier with the same characteristics described above, and they sat in their wheelchairs.

2.3. Experimental paradigm

Each participant completed two experimental sessions on separate days within a one-week period. Sessions were counter-balanced such that half of the participants began with the RCP session and the other half began with the CBP session. Each session consisted of a calibration phase and an online test phase. Classification coefficients were generated with data collected during the calibration phase and were subsequently applied during the online test phase. In each phase, participants were provided with strings of items to select. The string is displayed at the top of the monitor with the next item-to-spell (the target item) indicated in parentheses at the end of the string (Fig. 1A). For example, if the assigned string was “WADSWORTH,” it would appear at the beginning of the run as: WADSWORTH (W). The participant’s task was to attend to (or count) the number of times the item in parentheses flashed. After each target item was presented, a 3.5-sec pause ensued before the next target item appeared in parentheses (e.g. WADSWORTH (A)). This process repeated until the string of items was complete (one run). We used data from five such runs (four words and one numeric string) to train the feature weight classifier. For both the RCP and CBP, each set of items flashed for 62.5 ms, followed by a 62.5 ms inter-stimulus interval. Thus, a set flashed every 125 ms (i.e., 8 flashes/sec). For each of 38 item selections, five complete sequences (i.e., including 10 flashes of the target item) occurred. One RCP sequence included 17 flashes (8 columns; 9 rows), and one CBP sequence included 24 flashes (12 columns; 12 rows). As a result, each RCP selection took 10.63 sec, and each CBP selection took 15.00 sec. Thus, for each participant, 8 min, 53.25 sec of calibration data were collected for the RCP, while 11 min, 39.50 sec were collected for the CBP. However, the number of target items was the same for the two paradigms. Given that the goal is to classify after a minimal number of target presentations, we opted to present the same amount of targets per sequence rather than holding time constant and presenting additional targets in the RCP. Because the CBP presented more non-target stimuli, it is possible that it would produce a more efficient classifier than the RCP. Due to this discrepancy we conducted an analysis using only 2850 non-targets as input to the CBP classifier (the same amount used in the RCP), effectively controlling for the difference in presentation time.

The online test phase was identical to the calibration phase except for two differences. First, the number of sequences/selection was changed from five to a participant-specific number (described in Section 2.5.). Two, item selections were classified using SWLDA feature weights generated from the calibration data and visual feedback of the selections was provided to the participant directly below the item to be selected (in the grey area underneath the target string, Fig. 1A).

For the ALS users, the procedure was different in the following respects. First, in each session they used different numbers of character selections. User 1 was presented a variable number of characters in each session. Users 2 and 3 were each presented with 19 selections, although they were not the same selections. In addition, the users’ stimulus onset asynchrony (SOA) was different. SOA for User 1 and 2 was 250 ms (187.5-ms flash) and SOA for User 3 was 125 ms, (62.5-ms flash). Finally, the time between selections was increased from the 3.5 s used in the able-bodied participants to 4.75 s in Users 1 and 2 and 9 s in User 3.

2.4. Classification

As described in Krusienski et al. (2008), independent SWLDA classifiers were derived for the RCP and CBP (Draper & Smith, 1981). In the RCP calibration phase, each item selection included 85 flashes (i.e., 85 800-ms data segments from 10 target flashes and 75 non-target flashes). Thus, the RCP calibration phase consisting of 38 item selections, included data from 3230 flashes (380 targets and 2850 non-targets). In the CBP calibration phase, each of the 38 item selections included data from 4560 flashes (380 targets and 4180 non-targets). We used the SWLDA algorithm to determine the signal features that best discriminated between target and non-target flashes (MATLAB version 7.6 R2008a, stepwisefit function).

For online classification, epochs from each stimulus item were averaged before applying the SWLDA classification coefficients. In the RCP, the coefficients were applied to the spatiotemporal features of each row and column and then summed. The intersection of the row and column with the highest scores was selected and presented to the participant as feedback. In the CBP, the coefficients were applied to the specific spatiotemporal features of each of the 72 items and summed. The item with the highest score was selected and was presented to the participant as feedback.

For the ALS patients the procedure was the same; however given the differences in the amount of available data, more calibration data was used as input to the SWLDA analysis.

2.5. Determining the optimal number of sequences

Due to the P300 response’s relatively low signal-to-noise ratio, each item must be flashed multiple times and the results averaged (Cohen & Polich, 1997). During calibration, the number of target item flashes was constant across participants and presentation methods. Item sets were flashed in random sequences with two flashes of the target item per sequence, and thus 10 target item flashes in the five sequences used for each selection.

During the online testing phase, we optimized the number of sequences from each participant’s maximum written symbol rate (WSR, or symbols/min; Furdea et al., 2009). This metric represents the number of item selections a participant can correctly make in one minute, taking into account error correction. For practical purposes, people using the P300 speller need to correct errors. For a word processing application, this requires a backspace option. An error takes one extra item selection to erase it by using backspace and one more extra selection to choose the correct item. Assuming that the participant attempts to correct all errors, the WSR can be determined from the number of bits transmitted per trial (B; McFarland, et al., 2003). First, the Symbol Rate (SR) is determined from B:

$$\mathit{SR}=\frac{B}{{\log }_{2}N}$$

where N is the number of possible items used to calculate B. The WSR can then be determined as follows:

$$\mathit{WSR}=\{\begin{array}{cc}\frac{2\mathit{SR}-1}{T}& \mathit{SR}>0.5\\ 0& \mathit{SR}\le 0.5\end{array}$$

where T is the time to select one item. This metric only counts correctly selected items and excludes backspaces because they do not contribute to the final conveyed message. A WSR <0.5 indicates that a participant will, on average, make more errors than s/he is able to correct. Consequently, the final message will contain an abundance of uncorrected errors and will likely be indecipherable. Therefore, this range is assigned a WSR of zero. Importantly, the WSR provides a realistic (i.e., ecologically valid) measure of actual written communication rate that is useful for determining a suitable number of flashes for practical application of the P300 speller.

The time per selection and the classification accuracy both influence WSR. For each participant, the number of sequences that yields the highest WSR was determined. The SWLDA coefficients used online were derived from all 38 items. However, to determine the optimal number of sequences for a given participant, we generated two SWLDA classifiers; the first used the first 22 items of the calibration phase data as a training set and the last 16 items for a test set. The second classifier used the last 24 items of the calibration phase data as a training set and the first 14 items as a test set. We then determined the number of sequences that produces the highest WSR for each classifier, averaged the values, and rounded to the next highest sequence in the RCP and the next highest half sequence in the CBP. Fig. 2 shows for one participant the estimated accuracies and WSRs for 1, 2, 3, 4, and 5 sequences, using the CBP. For this example, the optimal number of sequences is two with an accuracy of 93% and a WSR of 7.5 selections/min. As accuracy increases with number of sequences, the WSR increases accordingly, until accuracy asymptotes at 100% (or some other value), and then the WSR steadily decreases as additional sequences are added. Thus, according to the present analysis, two sequences were optimal for this participant, and this number was used online. Given that more data were used to derive the classifier used online than for determining the optimal number of sequences, we expected that the optimal number of sequences would be overestimated. Thus, our estimate of WSR was a conservative one.

Fig. 2.

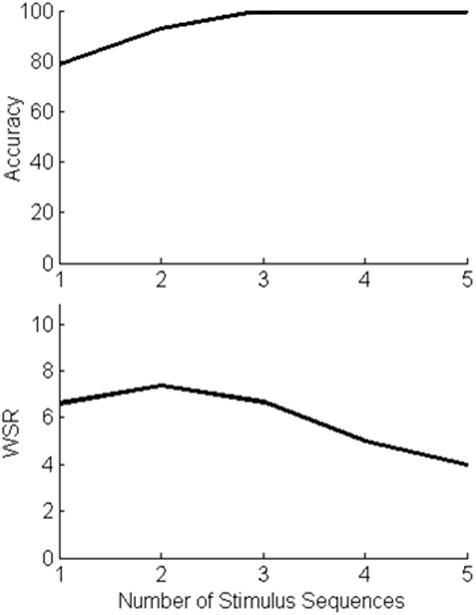
Optimizing the number of stimulus sequences. The top panel shows, for one participant, accuracy (the number of correct target selections) estimated after each of the five flash sequences. The bottom panel shows the corresponding written symbol rates (WSRs). For this participant, the optimal number of sequences is two, and this provides 7.5 selections/min, using the CBP.

2.6. Practical bit rate

Correcting an error requires a minimum of two additional selections (first a backspace, then a correct selection). Sellers et al. (2006) conducted a simulation (using 10,000 item selections) to determine how many selections would be necessary to complete a sequence of 10 correctly selected items with accuracy rates of 50 – 100%. With 51% accuracy, fully 500 selections were necessary to complete the 10-item sequence. Thus, while bit rate is an objective measure of information transfer rate, the importance of accuracy should not be overlooked (Sellers et al., 2006; Wolpaw, et al., 2000; Wolpaw, et al., 2002).

To investigate performance with error correction taken into account, we conducted an analysis of bit rates for the RCP and the CBP. To determine an ecologically valid metric of performance that each participant would likely achieve if correcting mistakes, we defined a formula for an error-corrected bit rate or “practical bit rate.” For every error made, a penalty of two additional selections would incur. However, if there is the same likelihood of making an error during the correcting process as in the original attempt (either while selecting the backspace or the replacement item) then additional corrections would be required. Assuming that the probability of making an error is “p” and the participant is attempting to communicate “N” correct selections, the total number of selections required to achieve success is given by the infinite series:

$$N+2(N)p+2(2(N)p)p+2(2(2(N)p)p)p+\dots =N\sum _{i=0}^{\infty }{(2p)}^i$$

This series converges to $\frac{N}{1-2p}$ provided that 2p < 1, which holds whenever p < 0.5.

Based on this formulation, we determined the expected number of total selections required by each participant in order to successfully complete all 38 selections in the test conducted, and calculated the practical bit rate from this result to determine the expected performance of each participant in a practical application where error correction is necessary. The value used for the probability of an error p was 1-accuracy.

3. Results

3.1. Online accuracy and bit rate

Table 1 shows the number of sequences, accuracy, selections/min, and bit rate for each participant with each paradigm. Online accuracy was significantly higher for the CBP, 91.52%, than for the RCP, 77.34%, t(17)=3.23, p=0.005. (An offline analysis matching the number of non-target stimuli for each paradigm produced similar results, i.e., CBP accuracy of 91.22% and RCP accuracy of 77.34%, and the p value for the t-test between the CBP and RCP was 0.005.) In addition, the number of sequences was significantly lower for the CB paradigm. However, it took longer to present one CBP sequence than one RCP sequence. Therefore, selections/min is a better indicator of performance than number of sequences. Importantly, despite the fact that each CBP selection took longer, selections/min was not significantly different for the two paradigms.

Table 1.

Online values for the number of sequences, accuracies, selections/min, and bit rates (bits/min) for the RC and CB paradigms in the online test phase of the experiment.

Participant	RC sequences	CB sequences	RC accuracy	CB accuracy	RC sel/min	CB sel/min	RC bit rate	CB bit rate
1	5.00	3.50	100.00	94.74	4.28	4.31	26.38	23.94
2	5.00	4.00	55.26	89.47	4.28	3.89	10.38	19.62
3	3.00	2.00	92.11	89.47	6.13	6.38	32.42	32.12
4	5.00	4.00	71.05	89.47	4.28	3.89	15.06	19.62
5	5.00	3.00	71.05	86.84	4.28	4.84	15.06	23.21
6	4.00	3.50	94.74	89.47	5.04	4.31	27.96	21.73
7	4.00	3.50	97.37	100.00	5.04	4.31	29.39	26.62
8	4.00	4.00	89.47	89.47	5.04	3.89	25.38	19.62
9	5.00	4.50	50.00	86.84	4.28	3.55	8.96	17.03
10	5.00	4.00	44.74	97.37	4.28	3.89	7.61	22.71
11	4.00	4.00	65.79	92.11	5.04	3.89	15.82	20.58
12	5.00	2.50	63.16	94.74	4.28	5.50	12.63	30.52
13	5.00	4.50	47.37	89.47	4.28	3.55	8.27	17.87
14	4.00	2.00	100.00	100.00	5.04	6.38	31.09	39.35
15	4.00	3.50	92.11	100.00	5.04	4.31	26.63	26.62
16	5.00	5.00	86.84	81.58	4.28	3.26	20.52	14.17
17	4.00	3.00	86.84	92.11	5.04	4.84	24.18	25.56
18	5.00	4.50	84.21	84.21	4.28	3.55	19.54	16.22
Mean	4.50	3.61	77.34	91.52	4.68	4.36	19.85	23.17

While online bit rate was not significantly different for the CBP, 23.17 bits/min and the RCP 19.85 bits/min, the difference did approach significance t(17)=1.93, p=0.071. The bit rate calculation in Table 1 includes the 3.5-sec pause between selections and thus shows the actual online bit rate. Many other studies have excluded such inter-selection time in calculating bit rate (e.g., Kaper et al., 2004; Meinicke et al., 2002; Serby et al., 2005). For comparison to such studies, Table 2 shows the selections/min and bit rates with the time between selections omitted.

Table 2.

Selections/min and bit rate (bits/min) for the RC and CB paradigms, excluding the 3.5-sec pause between selections.

Participant	RC sel/min	CB sel/min	RC bit rate	CB bit rate
1	5.65	5.71	34.84	31.71
2	5.65	5.00	13.70	25.19
3	9.41	10.00	49.75	50.37
4	5.65	5.00	19.89	25.19
5	5.65	6.67	19.89	31.99
6	7.06	5.71	39.17	28.78
7	7.06	5.71	41.17	35.26
8	7.06	5.00	35.56	25.19
9	5.65	4.44	11.83	21.33
10	5.65	5.00	10.05	29.16
11	7.06	5.00	22.16	26.43
12	5.65	8.00	16.69	44.39
13	5.65	4.44	10.93	22.39
14	7.06	10.00	43.55	61.70
15	7.06	5.71	37.31	35.26
16	5.65	4.00	27.10	17.39
17	7.06	6.67	33.88	35.24
18	5.65	4.44	25.81	20.31
Mean	6.41	5.92	27.40	31.51

3.2. Practical bit rate and simulated error correction performance

The online bit rate was not significantly different between the two paradigms, and due to the use of the copy-spelling mode, participants did not correct errors. Thus, to simulate error correction we used the practical bit rate metric. The results of these analyses demonstrated that the selections/min and bit rate are reduced compared to the original values. However, the decrease in performance was larger for the RCP, 3.24 bits/min, than for the CBP, 0.58 bits/min. The estimated practical bit rate and selections/min are shown in Table 3. Most importantly, the CBP practical bit rate, 22.59 bits/min, was significantly higher than the RCP practical bit rate, 16.61 bits/min, t(17)=2.50, p=0.02.

Table 3.

Selections/min and practical bit rates (bits/min) for the RC and CB paradigms taking error correction into account.

Participant	RC sel/min	CB sel/min	RC bit rate	CB bit rate
1	4.28	3.86	26.38	23.80
2	0.45	3.07	2.76	18.94
3	5.16	5.02	31.82	31.00
4	1.79	3.07	11.07	18.94
5	1.79	3.56	11.07	21.94
6	4.50	3.40	27.79	20.98
7	4.77	4.31	29.44	26.62
8	3.97	3.07	24.50	18.94
9	0.00	2.61	0.00	16.11
10	0.00	3.69	0.00	22.75
11	1.58	3.28	9.77	20.21
12	1.12	4.92	6.91	30.34
13	0.00	2.80	0.00	17.27
14	5.04	6.38	31.09	39.35
15	4.24	4.31	26.15	26.62
16	3.15	2.05	19.40	12.68
17	3.71	4.07	22.86	25.10
18	2.92	2.42	18.01	14.95
Mean	2.69	3.66	16.61	22.59

3.3. Error analysis

We hypothesized that the CBP would improve performance by reducing the selection of items adjacent to the target item (adjacency-distraction errors). Fig. 3 (left panel) illustrates the topographical distribution of errors in relation to the target item for the RCP. All target items have been centered in the matrix; the numbers in the black cells represent the number of correct selections for each paradigm. The numbers in other cells correspond to the locations of errors relative to the target location. First-degree errors (dark grey) are those that occurred directly adjacent to the target item in the RCP, 40.65%, and second degree errors (light grey) are those that occurred anywhere else within the same row or column, 44.52%. Only 14.83% of the 155 RCP errors occurred outside of the target row or column. This result confirms Fazel-Rezai’s (2007) findings, albeit with a much larger data set.

Fig. 3.

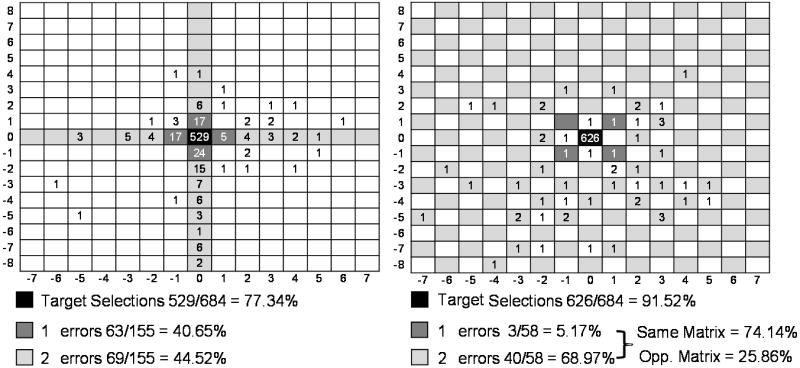
Error distributions for the RC paradigm (left) and CB paradigm (right). All target items have been centered in each matrix; the number in the black cell is the number of correct selections for each paradigm. Numbers listed in other cells represent the number of errors occurring in each cell relative to the target location.

In the CBP, we defined first-degree errors as the cells diagonal to the target item, since those items could flash with the target item. We defined second-degree errors as those that occurred in any location of the target’s virtual matrix. We were successful in reducing the number of first degree errors, only 5.17% of the errors were first-degree errors (dark grey; Fig. 3 right panel), and we reduced the overall error rate by 14.18%. However, in the CBP, adjacent cells can never flash together; therefore, only grey cells can flash with the target (in this illustration). Therefore, for the CBP, 35 of the 72 matrix items represent locations of possible second-degree errors as opposed to only 11 possible second-degree errors for the RCP. We found that the majority of CBP errors, 74.14%, were second-degree errors, as opposed to errors located in the opposite matrix, 25.85%. In other words, for the CBP, 43 of the 58 errors were items capable of flashing with the target. This result suggests that, for the CBP, temporal proximity to the target item is much more important than spatial proximity to the target item. In contrast, in the RCP, spatial proximity and temporal proximity occur together.

3.4. Waveform morphologies

The RCP and the CBP produced waveforms that differ in several respects. Our analyses focused on four electrodes, (Cz, Pz, Po7, and Po8), since these reliably capture most of the P300 energy in BCI applications (Kaper et al., 2004; Krusienski et al., 2008). Fig. 4 depicts the averaged waveforms for each of the 18 participants. We averaged these data across the 38 item selections of the calibration phase in order to keep the amount of data contributing to each average constant across all participants. Fig. 5 shows, for each of the four electrodes, target grand means (top row) and non-target grand means (bottom row). We examined amplitude and latency differences between targets and non-targets at each electrode location by paired t-test.

Fig. 4.

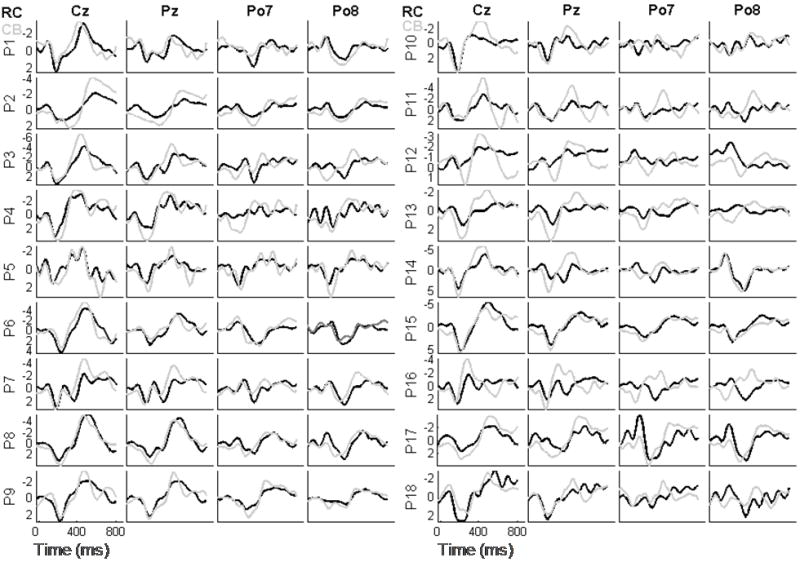
Target waveforms for electrode locations Cz, Pz, Po7, and Po8 for each of the 18 participants; RC paradigm data are presented in black and CB paradigm data are presented in grey. (Amplitude units are μV, scaling is participant specific.)

Fig. 5.

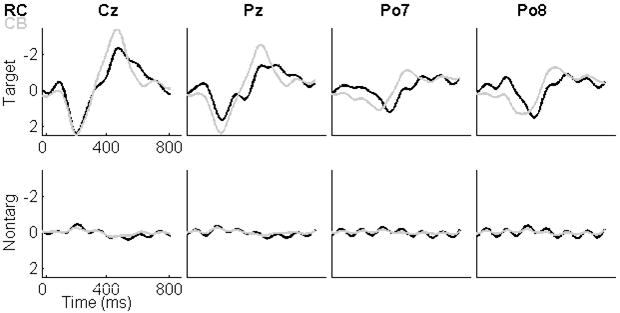
Grand mean waveforms for all 18 participants at electrode locations Cz, Pz, Po7, and Po8. (Amplitude units are μVs). The top row consists of target responses for both paradigms, and the bottom row consists of non-target responses for both paradigms. RC paradigm data are presented in black and CB paradigm data are presented in grey.

For the target responses located at electrode Cz, we found that the latency of the negative peak occurred significantly earlier for the CBP, 455 ms, than for the RCP, 486 ms, t(17)=3.36, p=0.004. In addition, we found that the amplitude of the negative peak was significantly larger for the CBP, -4.13 μV, than for the RCP, -2.86 μV, t(17)=4.65, p=0.0002. For the target responses located at electrode Pz, we found that the amplitude of the positive peak at approximately 200 ms was significantly larger for the CBP, 2.78 μV, than for the RCP, 2.00 μV, t(17)=3.16, p=0.006. We also found that the latency of the negative peak occurred significantly earlier for the CBP, 450 ms, than for the RCP, 499 ms, t(17)=3.25, p=0.005. In addition, the amplitude of the negative peak was significantly larger for the CBP, -3.09 μV, than for the RCP, -1.98 μV, t(17)=4.56, p=0.0003.

For the target responses at Po7 and Po8, the negative peaks at about 190 ms were larger for the RCP, -1.03 μV and -1.29 μV, than for the CBP, -0.46 μV and -0.52 μV, t(17)=2.40, p=0.03 and t(17)=3.91, p=0.001. The positive peak at electrode location Po7 and Po8 occurred earlier for the CBP, 286 ms and 272 ms, than for the RCP, 336 ms and 347 ms, t(17)=2.18, p=0.04 and t(17)=3.82, p=0.001. In addition, at Po8, the latency of the late negative peak occurred significantly earlier for the CBP, 484 ms than for the RCP, 551 ms, t(17)=5.02, p=0.0001. As at electrode locations Cz and Pz, at electrode locations Po7 and Po8 the late negative peaks were significantly larger for the CBP, -1.83μV and -1.80 μV, than for the RCP, -1.02μV and -1.11 μV, t(17)=4.22, p=0.0006 and t(17)=3.23, p=0.005.

Fig. 5(bottom) depicts the non-target responses for each of the four electrode locations. An 8-Hz oscillation is evident in both paradigms. This oscillation, which is at the frequency of the stimulus presentation, is a typical finding. (A comparable but less apparent oscillation is evident in the target responses, particularly for the RCP paradigm.) We compared the absolute maximum peak-to-peak values for the non-target responses over the 800-ms epoch for each electrode. The absolute amplitude was significantly less for the CBP at location Cz and Po8, 0.50 μV and 0.40 μV, than for the RCP, 0.64 μV and 0.63 μV, t(17)=3.22, p=0.005 and t(17)=2.84, p=0.01.

3.5. Data from BCI users with ALS

Given the success of the CBP as compared to the RCP in non-ALS participants, the logical next step was to test the method in people with ALS. Our initial users were three people (two women, one man) who had P300-based BCI systems in their homes. We tested one person severely disabled by ALS (remaining muscle movement limited to brow twitch and eye movements) on the RCP for 1 session, and we compared its accuracy to the CBP for the next 30 sessions, the person used the CBP and average accuracy was 89% (Fig. 6; User 1). The purpose of providing BCI’s to people with ALS is to give them the best communication option possible. Thus, upon finding that the CBP improved accuracy by 27% after a single session we did not conduct additional RCP sessions. Two additional people locked-in by ALS recently switched to the CBP from the RCP after extended experience (i.e., both over 2.5 years) with the RCP. We compared the CBP performance to an equal number of successive RCP sessions that were completed immediately prior to switching from the RCP to the CBP (Fig. 6; User 2 and User 3). For example, User 2 had completed 57 sessions of CBP; therefore, we compared the 57 preceding RCP sessions to the following 57 CBP sessions (similarly for User 3 with 39 CBP sessions). The results were quite dramatic. In the present study, non-disabled participants’ average performance increased by 14.18% for the CBP versus the RCP. In contrast, as shown in Fig. 6, the three people with ALS using home BCIs obtained an average performance increase of 24.60% with the CBP. To adopt a more conservative measure by removing User 1 (because only one RCP session was performed), the mean increase in accuracy was still approximately 23% (31% for User 2 and 15% for User 3). The p-values in Figure 6 are based on paired t-tests for the 57 (User 2) and 39 (User 3) sessions pre- and post-switch from RCP to CBP sessions. The practical bit rate with the CBP for Users 1, 2, and 3 was 13.49, 3.27, and 10.0, respectively. The practical bit rate was not computed for the RCP sessions because stimulus presentation parameters (i.e., SOAs and numbers of sequences) were manipulated continually to optimize performance. However, the CBP used the same number of sequences as the optimized RCP, thus each CBP character selection required additional time. In the non-ALS group, the mean number of sequences was 0.9 less in the CBP; thus, the accuracy values for the ALS group may be slightly inflated as compared to the non-ALS group in the current study.

Fig. 6.

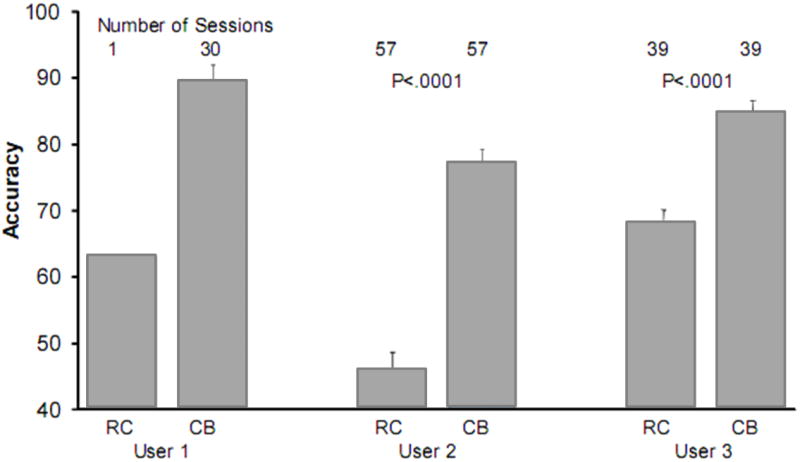
Preliminary data from three people severely disabled by ALS. The data were collected in each user’s home and the BCI system was operated by a caregiver. The three users began with the RC paradigm and switched to the CB paradigm (User 1 only completed 1 RC session). For Users 2 and 3, mean accuracy was compared for equal numbers of session before and after the switch from the RCP to the CBP.

4. Discussion

The primary goal of this study was to test a new presentation method for a P300-based BCI, the checkerboard paradigm (CBP), and compare it to the standard row/column (RCP) P300-based paradigm. Several general points bear mentioning. Foremost, both paradigms achieved relatively high accuracy and bit rates. With either paradigm, the P300-based BCI could be calibrated in approximately 10 min, similar to the results reported by Guger et al. (2009). The 8×9 matrix implemented here emulates most of the functions of a standard keyboard, which should provide disabled users more control of the tasks they wish to perform, and should thereby increase the usefulness of the BCI. The calculation of practical bit rate introduced here may be a worthwhile addition to other BCI performance measures because it should allow direct performance comparisons between studies. The WSR is a reasonable metric for BCI calibration. Using the WSR, a fixed number of stimuli are presented before classification. Others have used dynamic classifiers that stop when a classification criterion is met (e.g., Lenhardt et al., 2008; Serby et al., 2005); however, on average, the dynamic classifiers do not achieve online classification accuracy or practical bit rates as high as those reported here.

By disassociating the rows and columns, the CBP reduced error rates, presumably by eliminating adjacency-distraction errors. The CBP also increased the time between target flashes, thereby eliminating double-flash errors and nearly eliminating overlapping target epochs, which can be a substantial problem (Martens et al., 2009; Woldorff, 1993). Because we manipulated both of these factors concurrently, it is not clear which change was more important; however, the reduction in these two forms of errors appears to be responsible for the observed improvement in overall performance for the CBP over the RCP. Additional experimentation is required to determine the exact contribution of these paradigm changes (i.e., disassociating the rows and columns, or increasing the time between target flashes). An experiment that includes conditions manipulating the two factors independently and concurrently could determine the contribution of each factor to the increase in accuracy and bit rate. This is an important issue to clarify, which may allow further improvements of the system. Nonetheless, whether these factors are working separately or conjointly, the end result is an improved paradigm which was our primary goal when designing the CBP.

Additionally, informal polling of participants indicated that they found the CBP more appealing than the RCP, similar to the participants in the Allison (2003) “splotch” study. While the CBP vs. RCP performance difference may contribute to this preference, the preference has practical implications and is therefore important. Most participants also reported that they experienced less visual fatigue with the CBP because it was easier to focus attention on the target items. Finally, and most importantly, preliminary data suggested that people severely disabled by ALS perform significantly better using the CBP than the RCP.

4.1. Online accuracy and bit rate

Online accuracy should be the gold standard for evaluating BCI performance. Offline simulation and cross-validation can be extremely valuable techniques when developing and testing new algorithms. However, if the ultimate goal is to create a practical system for clinical use, online evaluation should be the standard evaluation method. An offline leave-one-out cross-validation evaluation is not sufficient because it does not test online performance. While the present study used cross-validation to calculate the WSR, it was then tested online.

In other words, only online performance can provide tangible evidence of any BCI system’s validity. Two primary reasons are responsible for this. One, leave-one-out cross-validation does not account for the temporal dependency necessary during online classification. That is, for online classification, only prior data can be used regardless of whether the data were collected one second or one year prior to the online classification. Two, offline analyses only estimate potential online performance; while they may show that a paradigm is likely to work, only online testing can establish that for certain (Klobassa et al., 2009).

In this study, online accuracy was significantly higher by 14.18% for the CBP compared to the RCP. While the difference in online bit rate did not reach statistical significance (CBP 23.17 bits/min; RCP 19.85 bits/min) this was largely due to the fact that the CBP takes about 30% longer to present one sequence of stimuli. Because bit rate is an objective measure of information transfer rate, this makes it an attractive option to be used for comparing BCI performance. However, in a BCI application, accuracy should be considered in addition to bit rate. For example, Meinicke et al. (2002) reported a maximum bit rate of 84.7 bits/min in a P300-based offline analysis. Their analysis, however, excluded the time between item selections and the accuracy level was less than 50%. This is not sufficient for BCI control, especially for any system intended for actual clinical use. Bit rate alone is not an adequate metric for BCI performance. An additional, more clinically relevant metric is needed.

4.2. Simulated error correction performance and online performance comparison

In an attempt to provide a realistic estimation of actual performance, we introduced a formula to estimate the practical bit rate. Practical bit rate takes error correction into account, whereas bit rate only takes accuracy into account. In a paper that focuses on the problem of using bit rate as the preferred or only performance metric, Dal Seno et al. (in press) have presented a general metric called “BCI Utility” and show that it predicts BCI performance better than bit rate (also see Bianchi et al., 2007).

In the current study, the practical bit rate calculation for the CBP was 22.59 bits/min. This value is only 0.58 bits/min less than the online bit rate (which does not take errors into account); the small reduction in bit rate was due to the high mean rate of accuracy, 91.52%. In contrast, the practical bit rate calculation for the RCP was 16.61 bits/min. This value is 3.24 bits/min less than the online bit rate because mean accuracy was only 77.34% in the RCP. Accuracy could be improved in the RCP by presenting more sequences of items. This may come with a cost of reducing bit rate because longer presentation times would reduce bit rate even though higher accuracy would increase bit rate. In this study, the number of selections per minute between the CBP and RCP were not significantly different. The number of sequences was limited to five per character presentation in both paradigms; accordingly, we cannot evaluate what the exact effects of including additional sequences would have been on the practical bit rates of the paradigms due to the non-linear relationship between bit rate and accuracy. Although, given the current data, the additional time needed to increase RCP accuracy would decrease the number of selections per minute, which should still result in a significantly higher practical bit rate for the CBP.

Although they did not correct for errors (similar to this study), Lenhardt et al. (2008) reported the highest P300 online accuracies and bit rates prior to this study. They recognized the need to present data accounting for the time between items. Thus, they used two metrics to calculate the time needed to complete 22 item selections using a 6×6 matrix. They defined “average theoretical time” as the time to complete the series of item selections with the time between item selections removed. This metric is not directly relevant to practical applications. In contrast, their “average real time” is relevant for applications, since it calculates the time to complete the series including the time between item selections. Therefore, a comparison of their average real time metric and online performance reported here is a valid comparison. Lenhardt et al. (2008) reported average real time in minutes to complete the 22 item sequence; we have converted their results to selections/min to correspond to our online selections/min (Table 1). In their fastest condition, 3.37 min were necessary to complete 22 item selections, which is a rate of 6.52 selections/min, and corresponds to a practical bit rate of 10.48 bits/min. However, mean accuracy was 65.53% in this condition; thus this level of accuracy is not sufficient for effective communication, as 70% is typically assumed to be required (Kűbler et al., 2001; Kűbler et al., 2009; Sellers et al., 2006). In their most accurate condition, 87.50%, 5.36 minutes were necessary to complete 22 item selections, which results in 4.10 selections/min, and corresponds to a practical bit rate of 15.92 bits/min. In comparison, CBP accuracy was 91.52% and produced 4.36 selections/min, which corresponds to a practical bit rate of 22.59 bits/min (using an 8×9 72-item matrix twice as large as their 6×6 36-item matrix).

4.3. Error analysis

The CBP should reduce errors for two primary reasons. First, the CBP should be less susceptible to adjacency-distraction errors than the RCP, since non-target items in scattered groups of items are less likely to attract attention than non-target items in entire rows or columns from the flanker effect (e.g., Sanders & Lamers, 2002), or from the Gestalt law of grouping (e.g., Prinzmetal, 1981). As expected, 85.17% of the errors in the RCP occurred in the same row or column as the target item (Fazel-Rezai, 2007).

Second, errors should be reduced because the CBP eliminates double-flash errors that result from overlapping stimulus epochs or when participants do not perceive the second target presentation, both of which generally serve to reduce the amplitude of the target response in the standard RCP (Martens et al., 2009; Woldorff, 1993). The combination of these two important effects of the paradigm change resulted in a significant reduction in error rate for the CBP as compared to the RCP. It also dissociated the errors from the rows and columns, which made errors appear random (Fig. 3). In the RCP, temporal and spatial relationships between the target item and non-target items occur together. Thus, as discussed above, the CBP eliminated one problematic effect of double-flash errors and reduced adjacency-distraction errors. With the CBP, errors were much more likely to come from the same virtual matrix than from the opposite virtual matrix. This result suggests that, in the CBP, the temporal relationship between the target item and non-target items is more significant than the spatial relationship between the target item and non-target items. The relationship between the temporal and spatial effects in the CBP and methods to minimize the errors that might result from the relationship between them requires further investigation.

4.4. Waveform morphologies

Fig. 4 shows target responses for each of the 18 participants’ at electrode locations Cz, Pz, Po7, and Po8. While some individual variation is evident, the individual participants’ averaged waveforms conform to the grand means shown in Fig. 5, which shows that both the target and non-target waveforms differ in several respects between the RCP and the CBP. Most notably for the target responses, the late negative peak is much larger in the CBP than in the RCP at electrode locations Cz and Pz, and electrode location Pz has a larger positive peak at about 200 ms. It is possible that the larger amplitude responses contributed to the higher accuracy of the CBP by increasing the signal-to-noise ratio. These results are also consistent with previous P300 research (including P300 BCI research) which shows that P300 amplitudes are higher when the probability of the target item is lower, as in the CBP (e.g., Duncan-Johnson & Donchin, 1977; Allison & Pineda, 2003; Sellers et al., 2006).

At electrode locations Po7 and Po8, a larger late negative peak is also apparent for the CBP paradigm and the main positive peak is earlier for the CBP, whereas the RCP has larger negative peaks at electrode locations Po7 and Po8 at about 200 ms, particularly at location Po8. This result is similar to those reported by Hong et al. (2009). While the locations we investigated are more occipital (relative to the P3 and P7 parietal electrodes they assessed), the amplitudes produced in the RCP are quite similar to theirs.

Regarding the non-target waveforms, the bottom panel of Fig. 5 shows an attenuated response at all electrode locations in the CBP; however, the amplitude differences were statistically lower than the RCP for only two electrodes, Cz and Po8. The non-target oscillating pattern corresponds to the stimulus presentation rate of 8 Hz. It is possible that the lower amplitude non-target responses contribute to higher classification accuracy rates in an analogous fashion to the higher amplitude target responses observed at electrode locations Cz and Pz.

4.5. Data from BCI users with ALS

Although the data from BCI users with ALS are only preliminary, they are encouraging. Figure 6 shows that average performance for the ALS group was much lower than the non-ALS group while using the RCP; however, upon switching to the CBP, ALS group performance was only slightly lower than the non-ALS group performance. Overall, these three users improved their classification accuracy rates by an average of 24.60% after switching from the RCP to the CBP. The data suggest that the CBP improvements may be more pronounced for ALS participants (or for those with lower performance for any reason) than for non-disabled participants, whose accuracy rates improved 14.18% in the current study. One of the users was already able to achieve accuracy sufficient for BCI control. For the two others, the improvement brought them into an accuracy range sufficient for effective BCI control; previously their accuracy was not consistently sufficient for effective control. Thus, the CBP is potentially of considerable practical importance for people severely disabled by ALS. It may help to restore their ability to communicate. For example, User 1 writes poetry with the BCI, for User 2 it is the only means of independent communication, and User 3 uses it for work and environmental control.

4.6. Conclusions

Brain-computer interfaces allow severely disabled people a mode of communication that does not rely on muscles. The CBP is the first P300-based BCI to demonstrate a significant increase in performance over the RCP. The online CBP performance presented here may be the highest online P300-based BCI performance to date. Online performance and “practical bit rate” as defined here are important measures to consider if the ultimate goal is to develop practical BCI systems for severely disabled people. Moreover, for BCI technology to be embraced on a large scale, researchers must develop useful and desired applications that can meet the needs of the disabled community (Vaughan et al., 2006). As the next logical step, the current results should be replicated in a study of a much larger group of people with ALS or other severe motor disabilities.