Coupling hemodynamics with vascular wall mechanics and mechanobiology to understand intracranial aneurysms

Abstract

Arteries exhibit a remarkable ability to adapt in response to sustained alterations in hemodynamic loading, to heal in response to injuries, and to compensate in response to diverse disease conditions. Nevertheless, such compensatory adaptations are limited and many vascular disorders, if untreated, lead to significant morbidity or mortality. Parallel advances in vascular biology, medical imaging, biomechanics, and computational methods promise to provide increased insight into many arterial diseases, including intracranial aneurysms. In particular, although it may be possible to identify useful clinical correlations between either the blood flow patterns within or the shape of aneurysms and their rupture-potential, our ultimate goal should be to couple studies of hemodynamics with those of wall mechanics and the underlying mechanobiology so that we can understand better the mechanisms by which aneurysms arise, enlarge, and rupture and thereby identify better methods of treatment. This paper presents one such approach to fluid-solid-growth (FSG) modeling of intracranial aneurysms.

1. Introduction

Intracranial aneurysms affect approximately two-to-five percent of the general population, often during the fifth and sixth decades of life, and represent one of the few vascular diseases that affects more women than men. These lesions arise as focal out-pouchings of the wall of a cerebral artery and they have either a saccular or a fusiform shape, though primarily the former. Ruptured intracranial aneurysms are the leading cause of non-traumatic subarachnoid hemorrhage and thus significant morbidity and mortality. There is, therefore, significant motivation to understand better the biomechanics of these lesions and to identify improved methods of treatment (Humphrey and Canham, 2000). The natural history of intracranial aneurysms consists of three phases: genesis, enlargement, and rupture. Although the pathogenesis remains controversial, it is generally agreed that fragmentation or degradation of intramural elastin, with associated loss of medial smooth muscle cells, is fundamental to initiating a lesion. Enlargement of intracranial aneurysms thus appears to depend primarily on the turnover of intramural fibrillar collagens, that is, a delicate balance between collagen synthesis and degradation that appears to be controlled largely by remnant fibroblasts in response to changing mechanical stimuli. Finally, rupture is a sudden event that occurs when wall stress exceeds wall strength, often near the fundus of the lesion. For more information on the histopathology, see Peters et al. (2001), Frosen et al. (2004), Pentimalli et al. (2004), Ruigrok et al. (2005), Kilic et al. (2005), Hashimoto et al. (2006), and references therein.

Given that each aspect of the natural history of intracranial aneurysms depends on cell-matrix processes within and stress-strain properties of the wall, one might ask what role computational fluid dynamics (CFD) should play in aneurysm research. The answer to this question is that knowledge of the hemodynamics is fundamental both to computing the stresses that govern the rupture-potential of the wall and to understanding the mechanobiology, that is, how the vascular cells respond to changes in their mechanical environment. The goals of this paper, therefore, are first to review the mechanobiology of vascular cells – primarily the endothelial cells that line the inner surface of all blood vessels, the smooth muscle cells that endow normal arteries with an ability to dilate or constrict to control local hemodynamics, the fibroblasts that regulate much of the overall strength of the wall, and finally circulating platelets and monocytes that often play important roles in cases of local disease and injury – and second to place this information within the context of the associated biofluid and biosolid mechanics. As it will be seen, the inherent complexity of intracranial aneurysms requires continued advances in biomechanics and vascular mechanobiology, but perhaps more importantly, a concerted effort to synthesize these often separate areas of research. It is suggested that a recently proposed fluid-solid-growth (FSG) approach to modeling offers promise in this regard (Humphrey and Taylor, 2008).

2. Vascular cell and matrix biology

2.1 Importance of mechanobiology

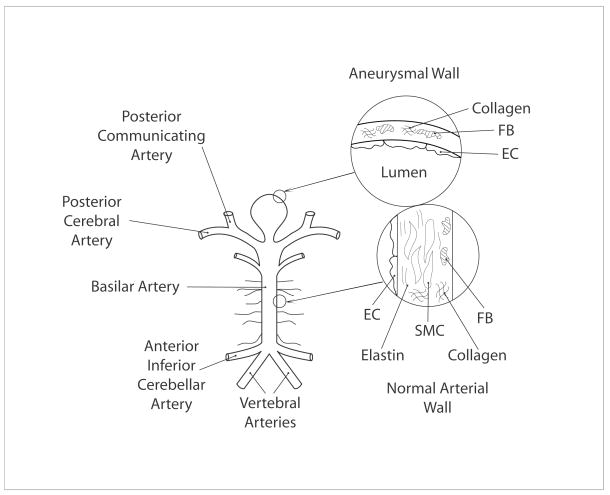
The normal cerebral arterial wall is a complex, layered, composite material (Lee, 1995). It consists of three primary layers: the innermost layer, or intima; the middle layer, or media; and the outermost layer, or adventitia. The intima consists of a monolayer of endothelial cells that rests on a basement membrane, which consists primarily of the extracellular matrix proteins type IV collagen and laminin. The media consists of layers of smooth muscle cells embedded within a matrix of sparse elastic fibers (which in turn consist of 90% elastin and 10% elastin-associated microfibrils, including the fibrillins and fibulins), various collagens (primarily types V, III, and I), and proteoglycans. The adventitia consists of fibroblasts embedded in a plexus of type I collagen fibers with small amounts of elastin and proteoglycans (Figure 1). Albeit simplified, basically, the smooth muscle endows an artery with an ability to constrict or dilate, the elastic fibers provide distensibility as well as elastic recoil, and the collagen fibers provide strength. Given that intracranial aneurysms arise, in large part, due to the loss of elastic fibers and smooth muscle (Yong-Zhong and van Alphen, 1990; Canham et al., 1999), these lesions tend to be very stiff and have little distensibility compared to the native artery (Scott et al., 1972; Seshaiyer et al., 2001). Because the loss of elastic fibers and smooth muscle cells also results in a much thinner wall, intracranial aneurysms can often be modeled mechanically as a membrane (Figure 1). Because of the relatively low wall mass and frequencies of loading, the inertial loads tend to be negligible, despite the inherent pulsatility, thus permitting quasi-static analyses of the wall mechanics (Shah and Humphrey, 1999).

Figure 1.

Schema of the posterior portion of the cerebral circulation and a basilar tip aneurysm. Shown, too, in exaggerated views are cross-sections of the normal wall (consisting of endothelial cells, smooth muscle cells, and fibroblasts as well as extracellular matrix constituents including elastin and collagen) and the aneurysmal wall (consisting primarily of endothelial cells and fibroblasts as well as fibrillar collagen).

To appreciate the main contributors to the mechanics of distended membranes, note that in the idealized case of quasi-static loading and axisymmetry, the two principal (in-plane wall) tensions T_i (i = 1,2) can be computed from equilibrium alone, namely (Humphrey, 2002)

$$T_1=\frac{P}{2{\kappa }_2},T_2=\frac{P}{{\kappa }_2}\left(1-\frac{{\kappa }_1}{2{\kappa }_2}\right),$$ (1)

where P is the transmural pressure and κ_i are principal curvatures. Moreover, in the very special case of a spherical membrane, κ_i ≡ 1/a, where a is luminal radius, and the two principal stresses reduce to σ_i = T_i/h = P a/2h (the classic Laplace relation), where h is wall thickness. When over-interpreted, this relation may suggest that larger radii lesions necessarily have higher stresses and thus should be more likely to rupture. Although many large lesions rupture, small lesions rupture as well. We are well advised to recall from equation (1), therefore, that it is actually shape (curvature), not size, that governs the stress distribution in pressurized membranes such as saccular aneurysms (cf. Kyriacou and Humphrey, 1996; Shah et al., 1997; Ma et al., 2007). The key role of geometry in determining intramural stresses emphasizes the importance of high resolution medical imaging (e.g., MRI) and explains the attempts by some to correlate lesion size/shape with rupture potential. Again, however, we must recall a fundamental principle – rupture occurs when stress exceeds strength. Whereas an aneurysm consisting of abundant, well cross-linked type I collagen can withstand hundreds of mmHg of distending pressure, local protease activity can weaken the wall significantly such that even lower than physiologic values of stress could cause rupture. There is, therefore, a need to understand not just the basic mechanics, but also the delicate balance between cell-mediated matrix production (synthesis) and removal (degradation); see, for example, Mimata et al. (1997) and Gaetani et al. (1998). This leads us to the mechanobiology.

2.2 Mechanobiology primer

From the perspective of biomechanics, one of the most important discoveries of modern biology is that many types of cells respond to changes in their mechanical environment. For example, cells can exhibit three basic types of responses to altered mechanical stimuli (Davies, 1995): an immediate response due to changes in ion channel activity (seconds), an intermediate response due to altered cytoskeletal structure and localization of transmembrane proteins as well as the initiation of second messenger signaling (minutes), and a delayed response consisting of altered gene expression, that is, changes in mRNA expression (hours) leading to altered protein synthesis. If sustained, these three different types of responses can contribute to long-term (days to months) changes in overall vascular geometry, structure, mechanical properties, and function (Langille, 1993, Chien et al., 1998; Lehoux et al., 2006). Of these responses, we focus primarily on changes in gene expression that likely dominate the long-term growth and remodeling of the arterial wall that results in an aneurysm (cf. Peters et al., 2001; Kilic et al., 2005).

Mechanobiology is the study of biological responses of cells to mechanical stimuli, independent of the basic governing equations of mechanics. Although cells cannot respond directly to mechanical stress, strain, or rates therein (Humphrey, 2001), these continuum metrics will remain fundamental in correlating molecular-level responses with tissue-level manifestations and thus will remain essential in both mechanobiology and clinical care. There are three basic processes in mechanobiology: transduction, transcription, and translation. Simply put, by transduction we mean the sensing and conversion of a mechanical stimulus into a biochemical signal. By transcription, we mean the copying of specific, small amounts of genetic information from DNA to create the desired (messenger) mRNA. By translation, we mean the use of this mRNA coding to synthesize a new protein. The production of a functional protein actually involves additional steps, including post-translational modifications both within and outside of the cell, but the reader is referred to Alberts et al. (2002) for further details. For structural proteins such as collagen, extracellular incorporation of newly produced molecules within extant matrix often requires enzyme mediated cleavage of propetide end groups and cross-linking (Kucharz, 1992). For purposes herein, however, the primary observation is that a mechanical stimulus sensed by a vascular cell can cause an increased production or removal of many different proteins that can affect myriad aspects of the overall wall biology in health and disease.

2.3 Endothelial cells

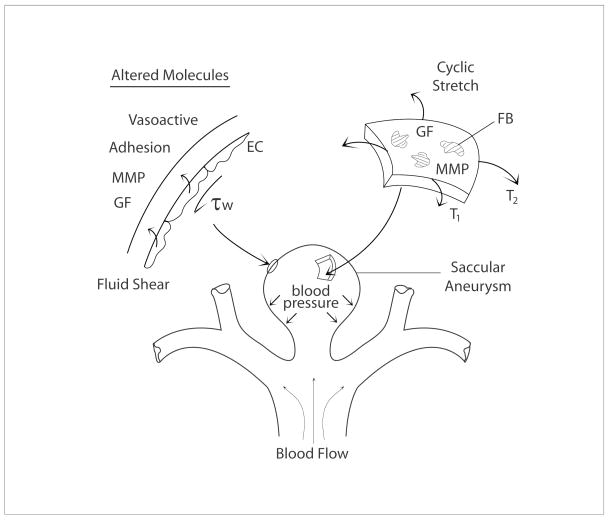
It was long thought that the endothelium served primarily as a selective non-thrombogenic barrier between the flowing blood and contents of the vascular wall. Since the mid-1970s, however, we have come to appreciate that the endothelium is biologically very active, capable of producing diverse molecules (e.g., vasoactive, growth regulatory, proteolytic, inflammatory, and blood clotting factors) that control overall vascular structure and function. In particular, endothelial production of many of these molecules is controlled by changes in flow-induced wall shear stress or pressure-induced cyclic stretch of the vascular wall to which they adhere (Davies 1995; Resnick and Gimbrone, 1995; Chien et al., 1998). For example, the endothelium increases its production of nitric oxide (a potent vasodilator and mild inhibitor of smooth muscle cell proliferation and synthesis of collagen) in response to increases in wall shear stress; conversely, it increases its production of endothelin-1 (a potent vasoconstrictor and promoter of smooth muscle cell proliferation and synthesis of collagen) in response to decreases in wall shear stress (Figure 2). In both cases, release of these vasoactive molecules normally affects smooth muscle contractility and thereby helps maintain the value of wall shear stress near its preferred (homeostatic) value (Valentin et al., 2009), which appears to be higher in the intracranial circulation than in the systemic/extracranial circulation. In addition, the endothelium upregulates diverse adhesion and chemotactic molecules in cases of very low wall shear stress, which promotes the recruitment of circulating monocytes to the vascular wall that can lead to or exacerbate diseases such as atherosclerosis or aneurysms, primarily via inflammatory mechanisms (cf. Kataoka et al., 1999; Libby and Ridker, 2006). The endothelium can also be damaged at very high wall shear stresses, which leads to the adhesion and aggregation of platelets that again can initiate or promote disease progression. See Table 1.

Figure 2.

Schema of mechanobiologic pathways involved in the enlargement and possible rupture of a saccular aneurysm. Shown are wall shear stress induced changes in endothelial cell (EC) production of vasoactive, adhesion, proteolytic (MMP – matrix metalloproteinase), and mitogenic (GF – growth factor) molecules. Shown too are intramural stress induced changes in proteolytic (MMP) and synthetic (GF) molecules by resident fibroblasts (FB). These mechanobiologic changes likely result in significant, regionally varying turnover (synthesis and degradation) of collagen.

TABLE 1.

Very Low Shear	Low Shear	Normal Shear	High Shear	Very High Shear
WBC Recruitment	Increased ET-1	Balanced NO/ET-1	Increased eNOS	Platelet Activation
M Φ Invasion			Increased PGI2	EC Damage

2.4 Vascular smooth muscle cells

Smooth muscle cells are the primary functional cells of the normal arterial wall; they usually reside in the middle (medial) layer of the wall and associate closely with many extracellular matrix proteins, including elastin, collagen V, and collagen III. Smooth muscle cells can exhibit two different phenotypes: a quiescent contractile phenotype, typical in maturity, and a proliferative, migratory, and synthetic phenotype typical in development as well as in cases of disease and injury. Phenotypic modulation is controlled in large part by chemo-mechanical stimuli. For example, platelet derived growth factor (PDGF) tends to promote a proliferative response, transforming growth factor-beta (TGF-β) tends to promote a synthetic response, and normal cyclic stretch due to blood pulsatility tends to promote a contractile phenotype. In addition, however, increased cyclic stretch or stress can increase smooth muscle cell production of PDGF and TGF-β as well as substances such as angiotensin-II (a vasoconstrictor and promoter of smooth muscle cell synthesis of collagen). Because loss of smooth muscle cells is a characteristic of intracranial aneurysms, we do not consider their mechanobiology further (cf. Lehoux et al., 2006). Rather, simply note that elastin not only endows the wall with the important mechanical properties of distensibility and elastic recoil, it also connects intimately to the vascular smooth muscle cells and thereby provides them with important biological cues (Karnik et al., 2003). Normal cross-linked elastin signals vascular smooth muscle cells to not proliferate or migrate; that is, elastin helps maintain the mature, quiescent, contractile phenotype (Brooke et al., 2003). Loss of elastin in intracranial aneurysms could promote early smooth muscle cell apoptosis (cf. Frosen et al., 2004) and hence the loss of wall contractility. This loss of smooth muscle function may be a key contributor to the early dilatation of the wall that perturbs the intramural stress from its homeostatic target (cf. Milewicz et al., 2008).

2.5 Adventitial fibroblasts

Fibroblasts are critical regulators of the extracellular matrix in most connective tissues. The mechanobiology of fibroblasts has been studied extensively within the context of both tissue engineering and wound healing (e.g., Grinnell, 2003). It is now becoming increasing evident that adventitial fibroblasts play a much more important role in vascular biology than previously thought (Strauss and Rabinovitch, 2000; McGrath et al., 2005). In healthy arteries, fibroblasts appear primarily to maintain the structural integrity of the collagenous adventitia and thereby contribute to tissue homeostasis; in disease or injury, these fibroblasts can modulate their phenotype (to myofibroblasts) and then proliferate, migrate, contract, and produce abundant extracellular matrix. Because of the loss of smooth muscle cells within intracranial aneurysms, the fibroblasts likely play the key role in maintaining structural integrity of the evolving wall. That is, intracranial aneurysms consist primarily of layers of fibrillar collagen having a transmural organization different from that of the normal artery (cf. Canham et al., 1996; Wicker et al., 2008), with significant deposition of new collagen in the inner portion of the evolving wall (Canham et al., 1999). There is a need, however, for more study of the mechanobiology of fibroblasts in aneurysms and possible effects of chemo-stimuli released by endothelial cells in response to changing wall shear stresses within the lesion.

2.6 Circulating cells

Many different types of cells circulate within the blood, notably red blood cells, diverse white blood cells, and platelets. Of these, consider the monocytes and platelets. Monocytes measure approximately 9 to 12 microns in diameter and normally constitute 3 to 8 percent of the circulating white blood cells. They spend only about a day and a half in the blood before they migrate into or across the vascular wall and become macrophages (Fawcett, 1986). The latter cells may survive in tissue for up to a month and play a vital role in tissue homeostasis by destroying bacteria, removing dead cells, or degrading matrix proteins. In particular, in addition to their phagocytotic activity, macrophages release matrix metalloproteinases (MMPs), which degrade select extracellular matrix proteins (e.g., MMP-12 degrades elastin). Monocytes/macrophages are recruited locally within arteries or aneurysms (cf. Kataoka et al., 1999) via the upregulation of endothelial adhesion molecules (e.g., ICAM-1) and they migrate into the wall in response to the upregulation of monocyte chemoattractant protein-1 (MCP-1). The expression of both ICAM-1 and MCP-1 is controlled, in part, by changes in local wall shear or intramural stress (Davies, 1995; Resnik and Gimbrone, 1995; Capers et al., 1997).

Platelets are flat, biconvex discs 2 to 3 microns in diameter; their normal life span within circulating blood is about 8 to 11 days (Fawcett, 1986). Platelets can patch small defects in the endothelium or limit hemorrhage by forming a blood clot; the latter function is particularly important immediately following the rupture of an aneurysm and can play an important role in the devastating sequlae leading to cerebral vasospasm (Baek et al., 2007a). Platelets must be activated, however, before they will adhere to a tissue surface or form aggregates among themselves. Platelets can be activated in regions of high shear stress within the blood or by contacting thrombogenic surfaces. Once activated, they can aggregate and release many different biologically active molecules, including growth factors (e.g., platelet derived growth factor) and vasoactive molecules (e.g., serotonin). Monocytes and platelets thus exhibit many complex interactions with the endothelium (Ley, 2006) that can be of importance to the development or rupture of aneurysms.

3. Towards integrated fluid-solid-growth modeling

3.1 Hemodynamics

It has been known since the early 1970s that hemodynamics plays important roles in vascular health and disease. For example, regions of disturbed flows tend to correlate with atherosclerosis (Malek et al., 1999; Libby, 2003). Solution of isothermal mass and linear momentum balance equations (e.g., the incompressible continuity and Navier-Stokes equations for Newtonian fluids, although non-Newtonian models of blood rheology may be important in particular cases) can provide important information on pressure and velocity fields within flowing blood, which in turn dictate tractions acting on the vascular wall. For example, with negligible gravitational effects, one must solve the classical linear momentum equation

$$\mathit{div}\mathbf{t}=\rho \mathbf{a},\mathbf{t}=-P\mathbf{I}+2\mu \mathbf{D},$$ (2)

where t is the Cauchy stress in the fluid, ρ the fluid mass density, a the acceleration, P the hydrostatic pressure (which enforces the incompressibility constraint trD = 0), I the identity tensor, μ the fluid viscosity, and D the stretching tensor (i.e., symmetric part of the velocity gradient tensor), subject to appropriate boundary and initial conditions. Advances in CFD have enabled hemodynamic simulations based on realistic, patient-specific geometries, which in turn have revealed different classes of flows within lesions having different shapes and locations within the cerebral circulation (e.g., Steinmann et al., 2003; Cebral et al., 2004, 2005; Shojima et al., 2004; 2005; Acevedo-Bolton et al., 2006; Chien et al., 2008; Jou et al., 2008; Sfora et al., 2009). Such information promises significantly increased clinical insight. Most attention has focused on wall shear stress within rigid models of the vasculature, however, not the intraluminal pressure. One reason for this situation is that the intraluminal pressure likely varies little between the parent vessel and the lesion (Shojima et al., 2005). Another reason for neglecting pressure is that there has been little interest in considering cyclic stretch- or stress-induced effects on fibroblast or endothelial biology and similarly little interest in considering actual mechanisms of enlargement and rupture of the aneurysmal wall (cf. Figure 1). Because of the aforementioned importance of the mechanobiology, however, there is clearly a need to model fluid-solid interactions and to compute accurately both the pressure and the velocity fields. Significant advances toward this end have been reported by Figueroa et al. (2006) and Vignon-Clementel et al. (2006), which have been incorporated within Figueroa et al. (2009) to study aneurysms as discussed further below.

3.2 Wall mechanics

Two longstanding hypotheses on aneurysmal enlargement and rupture implicated quasi-static and dynamic instabilities. For example, Simkins and Stehbens (1973) and Hung and Botwin (1975) suggested that aneurysms could be excited at their natural frequency and thus resonate; Akkas et al. (1990) and Austin et al. (1990) suggested that aneurysms could suffer limit point instabilities (i.e., bifurcations in their quasi-static equilibria) and thus expand rapidly at physiologic pressure. The former studies assumed linearized elasticity, however, and the latter studies assumed isotropic rubber-like elasticity. Like most soft tissues, intracranial aneurysms exhibit nonlinear, anisotropic mechanical behaviors over finite strains (Scott et al., 1972; Steiger et al., 1989; Seshayier et al., 2001). More appropriate analyses based on nonlinear wall mechanics suggest that it is unlikely that intracranial saccular aneurysms can suffer either limit point or dynamic instabilities (cf. Kyriacou and Humphrey, 1996; Shah and Humphrey, 1999). Indeed, nonlinear finite element analyses of idealized axisymmetric aneurysms further showed the importance of lesion shape, not size, in dictating stress levels; the potentially beneficial role of regional variations in anisotropy, that is collagen fiber orientations, in homogenizing and reducing wall stresses; the possibility that contact constraints due to interactions with other brain tissues could reduce stress levels locally; and that the propensity of the fundus to rupture, despite the neck often being thinner, can be explained in terms of the high levels of multiaxial stresses near the fundus (Shah et al., 1997; Seshayier and Humphrey, 2001). See also Ma et al. (2007), who initiated much needed nonlinear finite element analysis of saccular lesions based on patient-specific geometries, which is our ultimate goal. Notwithstanding these increased insights, the question remained: If not structural instabilities, why then do intracranial aneurysms enlarge and rupture?

Based on results from our nonlinear analyses of aneurysmal wall mechanics, we hypothesized that intracranial aneurysms enlarge in an attempt to return the multiaxial state of stress toward its homeostatic target (Ryan and Humphrey, 1999; Baek et al., 2005). That is, an initial insult that fragments or degrades elastin, with an associated loss of smooth muscle, should cause a slight bulging of the wall under normal pressures and thereby increase the intramural stresses well above normal because of the key role of local curvatures (cf. equation (1)). Given the mechanical homeostasis that appears to exist across multiple length and time scales within the vasculature (Humphrey, 2008), this change should set into motion ubiquitous cell-mediated growth and remodeling processes that attempt to return intramural stresses toward normal and similarly for wall shear stresses. Such an adaptive process in intracranial aneurysms could result primarily from the turnover of fibrillar collagen, with new pre-stressed collagen deposited interstitially but perhaps within the inner part of the wall (Canham et al., 1996; Canham et al., 1999). Interestingly, new collagen fibers in aneurysms appear to be deposited in alternating layers, much like an engineer would build a laminated composite (see Figure 8.11 in Humphrey, 2002), and regional variations in orientation could help return stresses toward normal (Shah et al., 1997; Ryan and Humphrey, 1999). Because of the low extensibility of collagen fibers, and yet the need to evolve a much different geometry to restore wall stresses (Ryan and Humphrey, 1999), such an adaptive process must involve balanced removal with deposition. It is well known that MMPs are upregulated in the aneurysmal wall (Bruno et al., 1998; Gaetani et al., 1998) and so too collagen synthesis (Mimata et al., 1997; Canham et al., 1999). We hypothesized further, therefore, that although intracranial aneurysms often enlarge to a mechanically and biologically stable state (note: mean rates of rupture are less than 0.1% per year), local imbalances between removal (MMP activity) and production (collagen synthesis) could render particular regions susceptible to either further enlargement (including the formation of blebs) or rupture during the otherwise adaptive enlargement process. In other words, initial enlargement may be more of a response to an insult rather than a pathologic process per se. Indeed, alterations in hemodynamics resulting from a changing lesion geometry could contribute further to both enlargement and rupture potential. Flow-induced localization of altered endothelial production of vasoactive and proteolytic molecules as well as recruitment of monocytes/macrophages likely contributes significantly to the local weakening and thus expansion of the wall. Finally, it is easy to imagine that an otherwise stabilized lesion, with near normal wall stresses, could be perturbed by longer term complications arising from disturbed hemodynamics, including local atherosclerosis or intraluminal thrombosis, both of which could establish a local inflammatory response that could lead to rupture (Kataoka et al., 1999; Hashimoto et al., 2006). See, too, Figure 8.28 in Humphrey (2002).

3.3 Growth and remodeling (G&R) mechanics

Motivated by the need to describe continuous turnover of cells and matrix within load-bearing soft tissues such as arteries and aneurysms, Humphrey and Rajagopal (2002) proposed a “constrained mixture theory” for biological growth and remodeling (G&R). By growth, we simply mean a change in mass; by remodeling, we mean a change in structure (Taber, 1995). Although some investigators consider growth and remodeling separately, we suggest that they are usually linked inextricably. For example, even for an overall unchanging mass and microstructure in normal arteries over long periods, tissue maintenance requires a slow but continual turnover of some constituents, which is to say production and removal of different constituents having different orientations. Briefly, therefore, it was suggested that full continuum mixture relations could be used to account for mass balance wherein individual constituents can turnover at different rates and to different extents. Because of the lack of information on potential momentum exchanges between evolving constituents and the difficulty of prescribing partial traction conditions in continuum mixtures, it was suggested that simple rule-of-mixture relations for the stress response could be used to satisfy the classical linear momentum balance equation, which similarly simplifies the enforcement of constitutive restrictions imposed by angular momentum balance and the entropy inequality. Linear momentum balance dictates the mechanical state in which cells and matrix turnover as well as the mechanical stimuli that drive such turnover. Conceptually, then, one must solve the classical balance equation of finite elasticity, namely

$$\mathit{div}\mathbf{t}=\rho \mathbf{a},\mathbf{t}=-p\mathbf{I}+2\mathbf{F}\frac{\partial W}{\partial \mathbf{C}}{\mathbf{F}}^T$$ (3)

where t is now the Cauchy stress in the solid (i.e., vascular wall), ρ the mass density of the wall, a the acceleration, p a Lagrange multiplier (not hydrostatic pressure) that enforces the incompressibility constraint (d eFt = 1) during transient motions, not G&R, I the identity tensor, W the energy stored elastically in the tissue upon deformation, and F the deformation gradient tensor, with C = F^T F the right Cauchy-Green tensor (which is properly invariant to rigid body motions), all subject to appropriate boundary and initial conditions. Conceptually, by the rule of mixtures W = Σφ^kW^k where φ^k are mass fractions for constituents k=1,2,…, n and W^k are associated stored energies. Note the absence of an active stress contribution because of the loss of smooth muscle in aneurysms.

Additional fundamental assumptions include the following: (a) individual structurally significant constituents (e.g., families of collagen fibers) are constrained to move together in current configurations despite having natural (stress-free) configurations that differ depending on the time they were incorporated within the extant matrix, and (b) newly synthesized constituents are deposited at a preferred (homeostatic) value of stretch or stress. The former hypothesis implies that individual deformation gradients can be computed via F^k = ∂x^k/∂X^k where x^k ≡ x because of the kinematic constraint, with X^k denoting individual natural configurations for each constituent. The latter hypothesis was originally argued heuristically, but increasing biological evidence suggests that cells stretch and orient extracellular matrix fibers that they secrete (Meshel et al., 2005; Wagenseil and Mecham, 2007). Cardamone et al. (2009) recently showed that accounting for individual “deposition stretches” within rule of mixtures models of the arterial wall enables one to predict many aspects of normal arterial behavior, including the existence of residual stress and axial prestress. Valentin and Humphrey (2009a) showed further, via numerical testing of multiple null hypotheses, that such deposition stretches can work synergistically with vasoactivity and stress-mediated turnover of matrix to endow arteries with the ability to adapt to normal changes in blood pressure and flow, thus providing further support for these hypotheses. Numerically tesing fundamental hypotheses is an important new aspect of model verification; it allows one to focus more on mechanisms rather than just the number of parameters. Nevertheless, parameter sensitivity studies can contribute further to model verification while guiding the experimental need (Valentin and Humphrey, 2009b).

To account for contributions of multiple structurally significant constituents that turnover at different rates and to different extents, and possess different natural configurations that evolve separately, we postulated the following rule-of-mixtures relation for the overall stored energy function (Baek et al., 2006)

$$W(s)=\sum _{k=1}^n\left(\frac{{\rho }^k(0)}{\rho (s)}{Q}^k(s){\widehat{W}}^k({\mathbf{C}}_{n(0)}^k(s))+{\int }_0^s\frac{m^k(\tau )}{\rho (s)}{q}^k(s,\tau ){\widehat{W}}^k({\mathbf{C}}_{n(\tau )}^k(s))d\tau \right)$$ (4)

where s is the G&R time, which spans days to months, and τ ∈ [0, s] the time at which a new constituent is deposited. Moreover, ρ(s) is the mass density of the mixture (i.e., wall), which appears to remain nearly constant throughout G&R, ρ^k (0) the apparent mass density of structurally significant constituents k = 1,2,…, n, Q^k (s) ∈ [0,1] a survival function that accounts for the percentage of material produced prior to G&R time 0 (e.g., time of the initial insult) that survives to current time s, and Ŵ^k (s;0) is the energy stored in constituent k at time s that was deposited at or before time 0 and thereby depends on the deformation at time s relative to its natural configuration defined at time 0 (i.e., ${\mathbf{C}}_{n(0)}^k(s)$). Similarly, m^k (τ) is the apparent mass density production rate for constituent k at its time of synthesis after G&R time 0, q^k (s, τ) ∈ [0,1] a survival function that accounts for the percentage of material produced at time τ that survives to time s, and Ŵ^k (s; τ) is the energy stored in constituent k at time s that was deposited at time τ and thereby depends on the deformation at time s relative to its natural configuration defined at time τ (i.e., ${\mathbf{C}}_{n(\tau )}^k(s)={({\mathbf{F}}_{n(\tau )}^k(s))}^T({\mathbf{F}}_{n(\tau )}^k(s))$ where ${\mathbf{F}}_{n(\tau )}^k(s)\equiv \partial \mathbf{x}(s)/\partial {\mathbf{X}}^k(\tau )$). One way to appreciate equation (4) is to consider the simple case prior to G&R, that is, at time s = 0. In this case, we have

$$W(0)=\sum _{k=1}^n\left(\frac{{\rho }^k(0)}{\rho (0)}{Q}^k(0){\widehat{W}}^k({\mathbf{C}}_{n(0)}^k(0))\right)=\sum _{k=1}^n\left({\phi }^k(0){\widehat{W}}^k({\mathbf{C}}_{n(0)}^k(0))\right)\equiv \sum _{k=1}^n\left({\phi }^k{\widehat{W}}^k\right)$$ (5)

which, as it should be, is a simple rule of mixtures without G&R (with φ^k = ρ^k/ρ a mass fraction and Q^k (0≡ 1) by definition). It can similarly be shown that one recovers a simple rule of mixtures in cases wherein balanced production and removal occur within an unchanging mechanical state, a process we call tissue maintenance (Valentin et al., 2009).

In summary, this constrained mixture theory emphasizes the importance of separate constitutive properties, rates of synthesis and removal, and natural configurations (as well as deposition stretches and orientations) for each structurally significant constituent, including multiple families of a single constituent such as type I collagen that are produced at different instants but otherwise occupy the same neighborhoods for some time. Vascular collagen has a normal half-life on the order of 70 days, but this can decrease by an order of magnitude in disease or injury states while production rates increase by as much as five-to-ten fold (Nissen et al., 1978; Strauss et al., 1996; Langille, 1996). One of the key challenges in implementing this constrained mixture theory, therefore, is identifying appropriate functional forms for the mass density production and survival functions. For example, vascular elastin is deposited and cross-linked primarily during the perinatal period and its normal half-life is on the order of many decades. Hence, under normal conditions in maturity, m^e (τ) ≡ 0 with Q^e (s) = 1. The latter can change tremendously in cases of disease and injury, however, for elastin can be degraded rapidly via heightened MMP-2,-9, or -12 activity. In such cases, a possible form is Q^e (s) ∝ e x −pK[^es], where the rate parameter K^e can depend on chemo-mechanical stimuli. For intracranial aneurysms, one could prescribe rapid degradation of elastic fibers and loss of smooth muscle cells as part of the yet poorly understood pathogenesis or one could simply prescribe an initial loss of both (cf. Watton et al., 2004; Baek et al., 2006). As an illustrative example for collagen production by normal smooth muscle within a thin-walled vessel, consider

$$m^k(\tau )=m_{\mathit{basal}}^k\left(1+K_{\sigma }^k\left(\frac{{\sigma }^k(\tau )-{\sigma }_h^k}{{\sigma }_h^k}\right)-K_{\tau }^k\left(\frac{{\tau }_w(\tau )-{\tau }_w^h}{{\tau }_w^h}\right)\right)$$ (6)

where $K_i^k$ are essentially rate parameters (gains) that control the degree of stress-mediated production, σ^k is a scalar metric of the intramural Cauchy stress for constituent k, and τ_w is wall shear stress; values with a super- or sub-script h denote homeostatic targets. Hence, if neither the intramural nor the wall shear stress deviates from homeostatic, one recovers basal production rates as we should. This form is motivated by the observation that increased cyclic stress/stretch promotes smooth muscle cell production of collagen (Li et al., 1998) whereas NO inhibits such production and ET-1 promotes such production (Rizvi et al., 1996; Rizvi and Myers, 1997). Recall, therefore, that increases in wall shear stress above normal increases endothelial production of NO whereas decreases in shear stress below normal increases endothelial production of ET-1 (Davies, 1995) – hence the negative sign preceding the shear stress related gain parameter. Note, too, that intramural stress is dictated largely by blood pressure (and lesion geometry) whereas wall shear stress is dictated largely by blood flow (and lesion geometry), thus emphasizing the importance of both hemodynamic and medical imaging information in this formulation of wall growth and remodeling. Finally, degradation appears to follow first order type kinetics (Nissen et al., 1978), hence the survival function can be written generally as

$$q^k(s,\tau )=exp\left(-{\int }_{\tau }^s{K}^h(\stackrel{\sim }{\tau };{\sigma }^k,{\tau }_w)d\stackrel{\sim }{\tau }\right)$$ (7)

where K^k is a rate-type parameter that may depend on changes in intramural stress or wall shear stress (similar to temperature-dependence of rate parameters in chemical kinetics). In the case of homeostatic values of stress, K^k becomes a constant (inverse the normal half-life) and one recovers a simple first order decay consistent with basic studies in the literature. For details on the implementation of these constrained mixture models, see Baek et al. (2005,2006,2007a) and Valentin et al. (2009).

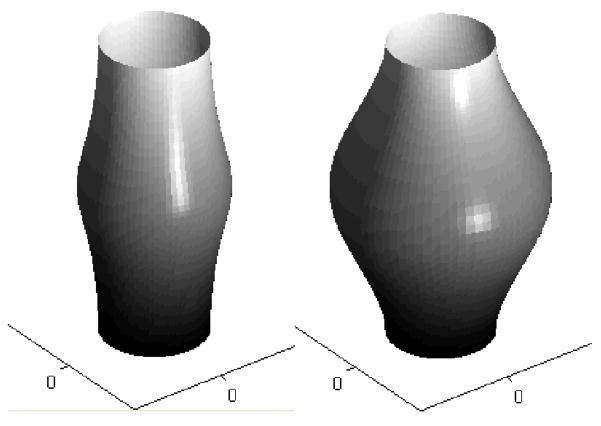
In particular, Baek et al. (2006) used this approach to simulate numerically the enlargement of an idealized axisymmetric fusiform aneurysm in the basilar artery based on changes in intramural stress alone, that is, without any wall shear stress regulation of turnover (Figure 3). Among other findings, it was shown that lesion enlargement was unbounded for an assumed basal turnover of collagen. In other words, stress-mediated production rates were essential to evolve a biologically stable lesion in the absence of vasoactivity and elastic recoil by elastin (cf. Valentin and Humphrey, 2009a), which appears to represent the majority of actual lesions. Similarly, it was shown that lesion enlargement was unbounded if the new collagen was oriented in the direction of maximum principal stress; in contrast, lesion enlargement could stabilize if the new collagen was deposited in the direction of the maximum principal stretch or the minimum principal stress. These and similar findings illustrate how numerical simulations can be used to compare the consequences of competing hypotheses and to guide histopathological examinations (cf. Canham et al., 1999). For other biosolid mechanics models of aneurysm growth and remodeling, see Kroon and Holzapfel (2007, 2008), Watton et al. (2004), and Watton and Hill (2008), each similarly based on the concept that enlargement is driven primarily by a collagen remodeling that requires turnover (cf. Humphrey, 1999).

Figure 3.

Simulations of the enlargement (from left to right, at two computational times) of an idealized fusiform aneurysm (based on results from Baek et al., 2006). The simulation was initiated via an abrupt degradation of intramural elastin, and associated loss of smooth muscle, which weakened the wall and perturbed the stresses from normal. This perturbation, in turn, initiated a G&R process characterized by an intramural stress-mediated turnover of fibrillar collagen within the wall, which was treated mechanically as a membrane. Depending on the assumptions used to drive the turnover, the computational lesion could stabilize (i.e., restore intramural stresses toward normal) or continue to enlarge without bound (until meeting a failure criterion). Note that symmetry was maintained along the long axis because of the assumed uniform intraluminal pressure. Figueroa et al. (2009) showed that this symmetry can be lost when one bases collagen turnover on changes in both intramural and wall shear stresses from homeostatic values. Intracranial aneurysms exhibit myriad shapes and sizes, of course, probably reflecting the evolving complex hemodynamic loading that stimulates the turnover and possibly complex perianeurysmal contact constraints that further affect regional stresses.

In addition to studying potentially bounded enlargement, there is a need to consider rupture potential. Recalling that rupture is expected to occur when stress exceeds strength, Steiger et al. (1989) reported yield stresses on the order of 0.5 MPa at the fundus and 1.2 MPa at the neck based on 1-D tensile tests on lesions from 7 patients. These values are similar to the 1.0 MPa assumed by Canham and Ferguson (1985), yet there remains a need for a multiaxial stress criterion. Moreover, it seems that this criterion should be based on intramural normal, not intramural shear, stresses (Kyriacou and Humphrey, 1996; Ryan and Humphrey, 1999); this would rule out the often considered von Mises failure criterion that was originally derived for metal plasticity. That is, in many lesions computed wall stresses tend to be nearly equibiaxial near the fundus where rupture tends to occur (cf. Shah et al., 1997; Ma et al., 2007), thus recall that maximum intramural shear stresses equal one-half the difference between the principal stresses in 2-D, and thus would be expected to be small near the fundus in many cases. An appropriate rupture criterion would be straightforward to incorporate within G&R codes, wherein potential rupture would be signified whenever the appropriate metric of stress exceeded the stated strength (at which point the computations would be terminated). There is a pressing need for increased attention to this important aspect of aneurysm mechanics. Finally, it is also noted that there is a need to account for additional G&R when a lesion contacts other brain tissues. Seshaiyer and Humphrey (2001) showed that such contact constraints could alter wall stresses, indeed in a protective manner in some cases, yet such changes in stress would be expected to affect subsequent G&R (cf. equation (6)). Such contact constraints have not be addressed yet in modeling, but they are attracting increased attention given advances in imaging capabilities (cf. Satoh et al., 2005; Ruiz et al., 2006).

3.4 Further modeling in mechanobiology

Equations (6) and (7), when used in equations (3) and (4), reveal one approach to incorporate information on stress or stretch mediated changes in cell-mediated production and removal of structurally significant constituents, primarily via gross correlations. Although such correlations reflect well our current understanding, and are computationally expedient, there is a need to pursue more complex “biochemomechanical” constitutive relations that account for actual increases or decreases in growth factors (promoters of production) and matrix metalloproteinases (promoters of removal). For example, we know that cyclic stretching of vascular smooth muscle cells increases the production of fibrillar collagen. We also know, however, that this production of collagen results from the local upregulation of ANG-II, which promotes the synthesis of latent TGF-β, which in turn stimulates collagen production both directly (via stress mediated activation of latent TGF-β) and indirectly via increased connective tissue growth factor (cf. Li et al., 1998). In other words, multiple biochemical signals can arise from the same mechanical stimuli (Humphrey, 2008). Once such effects are quantified, they can be accounted for simply within the proposed constrained mixture model by modifying the relations for the mass density production and survival (cf. equations (6) and (7)) to depend directly on the concentrations Cⁱ of these effector molecules (e.g., let m^k = f (σ^k,Cⁱ) for k = 1,2,…,n structurally significant constituents and i = 1,2,…,N-n non-structurally significant effector molecules). The stress-mediated production, consumption, and diffusion of these effector molecules can, in turn, be described simply via the aforementioned full mixture equations for mass balance, which via the usual assumptions yield standard reaction-diffusion equations in terms of the desired concentrations. As it should, therefore, this new theoretical framework is general enough to incorporate new data as they arise while highlighting needs for new experiments to quantify better the mechanobiology.

3.5 An integrative approach to modeling

Because of extreme differences in time-scales (cardiac cycles on the order of seconds versus long-term enlargement of lesions on the order of weeks or months), we have suggested that combined fluid-solid-growth (FSG) modeling of aneurysms can be accomplished via a loose coupling of fluid-solid interaction (FSI) computations of the hemodynamics over a cardiac cycle with G&R computations of wall mechanics over periods of days or weeks (Humphrey and Taylor, 2008). Although computationally involved, this formalism can be accomplished in a straightforward manner (Figueroa et al., 2009). For example, the theory of small deformations superimposed on large (Baek et al., 2007b) allows one to transfer information on evolving wall properties from a fully nonlinear G&R code (e.g., Baek et al., 2006) to a fully 3-D unsteady FSI code (e.g., Figueroa et al., 2006) that assumes linearized wall properties over a cardiac cycle. In other words, hemodynamic information from a FSI code can supply the requisite traction boundary conditions for a G&R code, which can then evolve the geometry and material properties over days to weeks. This information can, in turn, supply the requisite conditions to enable another FSI simulation to determine the evolving hemodynamics. Iterations can continue until the lesion either stabilizes biologically or ruptures (i.e., the stress exceeds locally the diminished strength), with the G&R code accounting for mechanobiological responses to altered wall shear stress and intramural stresses. A key advantage of this FSG approach is its ability to couple directly separate codes that are individually sophisticated and well-tested; a possible limitation is the potentially large number of iterations that will be needed to simulate long-term lesion enlargement, with each iteration effectively encompassing the solution of two separate nonlinear finite element codes based on patient-specific geometries. The computational cost will likely be considerable, yet there are no realistic alternatives at present to coupling the hemodynamics, wall mechanics, and mechanobiologically driven growth and remodeling. The basic concept of fluid-solid-growth modeling is reflected in the work of Chatziprodromou et al. (2006), yet they simply modeled the evolving lesion by decreasing locally the value of a single Young’s modulus to enable the wall to enlarge. As revealed by Scott et al. (1972) and others, however, the aneurysmal wall is actually stiffer than the native wall; what is different is a decreased mass fraction of elastin and smooth muscle and an increased mass fraction of collagen having different natural configurations. An advantage of basing the G&R step on a constrained mixture model is that such effects can be accounted for directly. Moreover, because many of the constitutive relations within the constrained mixture framework are structurally or biologically motivated, potential values of associated material parameters are often bounded over narrow ranges, which facilitates parameter sensitivity studies (Valentin and Humphrey, 2009b). Figueroa et al. (2009) extended the nonlinear constrained mixture model of G&R by Baek et al. (2006) to include effects of both intramural and wall shear stress on altered mass density productions of collagen (cf. equation 6). Results suggest that flow-induced effects can be dramatic and highly variable regionally, in contrast to pressure-induced effects since blood pressure does not vary much within a lesion. There is a pressing need, however, for additional mechanobiological data sufficient for the formulation of improved constitutive relations and for model validations.

4. Discussion

Intracranial aneurysms remain enigmatic: many lesions remain stable for years while others rupture suddenly and cause severe neurological deficits or death. There is, therefore, a need to understand better the natural history of these lesions and the conditions that render particular lesions susceptible to rupture. The underlying complex interplay between the hemodynamics, wall mechanics, and mechanobiology can be understood only via a synthesized computational framework (e.g., FSG) based on patient-specific geometries. Although much of the essential mechanobiological information remains wanting, continued advances in vascular biology, medical imaging, biomechanics, and computational methods promise to increase significantly our understanding of these potentially deadly lesions. In this paper, we have seen that hemodynamics is vital for it dictates in large part the mechanical stimuli experienced by key players in the genesis, enlargement, and rupture of aneurysms – that is, endothelial cells, smooth muscle cells, adventitial fibroblasts, monocytes/macrophages, and platelets. We have also seen that wall mechanics is vital for it is the wall that enlarges, with changes in geometry changing wall stress, and eventually ruptures when stress locally exceeds strength.

Much remains to be learned, however. The different phases of the natural history of these lesions may be governed by different biomechanics. For example, higher wall shear stresses may contribute to the genesis (Shojima et al., 2004), lower wall shear stresses may contribute more to enlargement (Shojima et al., 2004; Acevedo-Bolton et al., 2006), and higher wall shear stresses may contribute more to rupture (Chien et al., 2008), yet such a scenario remains speculative and has developed based solely on considerations of flow-induced local wall shear stress, not pressure-induced intramural stresses. Indeed, Jou et al. (2008) recently suggested that regions of low wall shear stress correlated better with rupture. Finally, the subsequent development of atherosclerosis or intraluminal thrombus may destabilize a previously developed and otherwise stable (i.e., quiescent) lesion; changes in pulse pressure may be more problematic than changes in mean arterial pressure in hypertension, an important risk factor for aneurysms; and short-lived changes in hemodynamics, as, for example, during exertion or emotional stress, could be benign unless this occurs during a short period of heightened local MMP activity that enables stress to rise above the failure strength. In other words, we must understand better the fundamental biological processes, yet we must also continue to advance our imaging, theoretical developments, and computational methods in anticipation of the type of biological information that will soon be available. Until then, we must build the best models possible based on the best data available, which alone should increase significantly our continuing understanding of intracranial aneurysms.