The alternating pattern of stereochemistry in the nonactin macrocycle is required for antibacterial activity and efficient ion binding

Abstract

Nonactin is a polyketide antibiotic produced by Streptomyces griseus ETH A7796. It is active against a range of Gram positive organisms, acting as an ionophore that has a high selectivity for K⁺ ions. Among the polyketides, nonactin has a unique structure. It is a 32-membered, cyclic tetraester generated from four monomers of nonactic acid, two of which are (+)-nonactic acid and two of which are (−)-nonactic acid. The monomers are arranged (+)-(−)-(+)-(−) in the macrocycle so that nonactin has S4 symmetry and is achiral. As the structure of nonactin is unique, so is the biosynthesis of the compound. There is much evidence that after an early achiral intermediate, there are two mirror image biosynthesis pathways, one for the synthesis of each enantiomer of nonactic acid. Emerging evidence suggests that the two pathways arose from gene duplication followed by divergent evolution. The central question, therefore, raised by both the structure and the biosynthesis of nonactin concerns the benefit, if any, to the producing organism in initially selecting for, and then maintaining, two independent pathways for nonactic acid synthesis and for generating only the achiral diastereoisomer of nonactin.

To understand why achiral nonactin is the naturally generated diastereoisomer we prepared through synthesis two alternate diastereoisomers of nonactin, one prepared solely from (+)-nonactic acid and one prepared solely from (−)-nonactic acid, referred to here as ‘all-(+)-nonactin’ and ‘all-(−)-nonactin’ respectively. Both all-(+)-nonactin and all-(−)-nonactin were more than 500-fold less active against Gram positive organisms than nonactin confirming that the biosynthesis of both nonactic acid enantiomers, and their incorporation into nonactin, is necessary for biological activity. To understand the lack of antibacterial activity we used isothermal calorimetry to measure the association constant K_a, ΔG, ΔH and ΔS of formation for the K⁺, Na⁺ and NH₄⁺ complexes of nonactin and all-(−)-nonactin. The natural diastereoisomer had a high selectivity for K⁺ to which it bound approximately 880-fold better than all-(−)-nonactin. We used a picrate partitioning assay to confirm that all-(−)-nonactin, unlike nonactin, could not partition K⁺ ions into organic solvent. To complement the thermodynamic data we used a simple experimental model to mimic ion transport. Using two concentric glass tubes we arranged for two aqueous samples to be separated by a CHCl₃ layer. By following the co-transport of picrate anion from one aqueous layer to the other, through the organic phase, we were able to measure the rates of K⁺ transport that were facilitated by the ionophores. Whereas nonactin allowed for efficient K⁺ transport, all-(−)-nonactin was completely ineffective. Modeling of the K⁺ complexes of nonactin and all-(−)-nonactin suggested that only in the case of the natural diastereoisomer, where the monomer stereochemistry is alternated around the macrocycle, can the hydrogen atoms at C3 and C6 of each monomer be on the inside of the cavity occupied by the ion. The latter conformation is unavailable to all-(−)-nonactin and so steric interactions prevent the closing of the macrocycle around the ion sufficiently to form optimum K–O bond lengths.

The data show conclusively that both enantiomers of nonactic acid are needed for the formation of an ionophore that has antibacterial activity, can selectively and strongly bind K⁺, can allow for the partitioning of K⁺ into an organic phase and that can support the transport of K⁺ across a membrane model. The requirement for both enantiomers of nonactic acid to be present in the nonactin structure for the latter to have activity is reflected in the fact that S. griseus has maintained two, mirror image biosynthesis pathways.

Introduction

Nonactin, 1 (Fig. 1), is a member of the macrotetrolides,^1–4 a class of ionophore antibiotic made by Streptomyces griseus ETH A7796. Nonactin has antibacterial and anticancer properties² and has also been shown to be an inhibitor of efflux pumps in multidrug resistant cancers.⁵ As nonactin shows selectivity for binding NH₄⁺ ions it has found widespread use in ammonia-selective electrodes.⁶ The antibacterial effects of nonactin depend upon its ability to form stable complexes with K⁺, Na⁺ or NH₄⁺ ions and for it to support the passive diffusion of these ions across cell membranes.

Figure 1.

Structures of nonactin and the naturally occurring macrotetrolides.

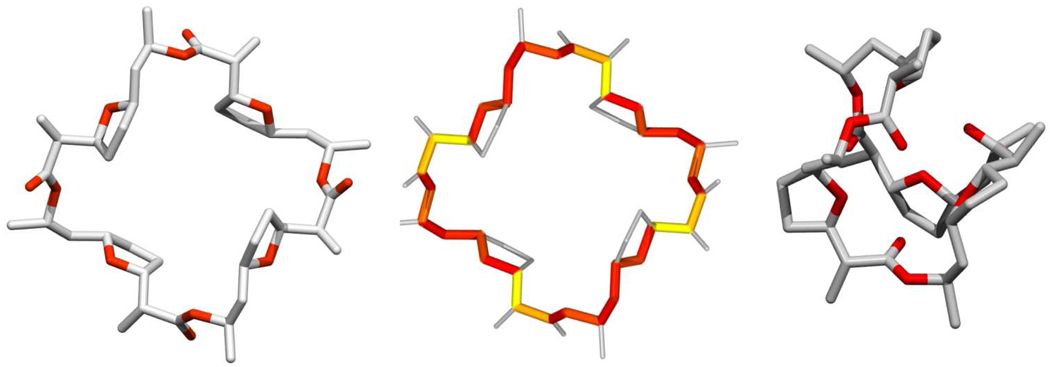
The structure of nonactin is highly unusual for a natural product.⁴ Nonactin is a cyclic tetraester assembled from nonactic acid. Both (+)-nonactic acid and (−)-nonactic acid are needed to construct the macrocycle and they are joined head-to-tail in an alternating (+)-(−)-(+)-(−) pattern. The overall structure has S4 symmetry in both the free and complexed forms and is achiral even though assembled from chiral precursors. Early crystallography studies of nonactin⁷ and its potassium complex⁸ delineated the major structural changes on ion binding. Nonactin assumes a flat doughnut-like structure in the absence of an ion that is approximately 17×17×8.5 Å (Fig. 2). During K⁺ binding there is a stepwise association of the carbonyl and tetrahydrofuran oxygen atoms of nonactin with the ion, together with the stripping of the water of hydration, that results in a more spherical complex approximately 15×15×12 Å in size. The eight coordinating oxygen atoms form a cubic geometry that completely shields the ion from solvent. Although the structural reorganization that occurs on ion binding appears substantial, the great majority of the change is accounted for by changes in the O16-C1-C2-C3 and C1-C2-C3-C4 torsion angles in each monomer (Fig. 2) which account for 67% of the total torsion angle changes. Further studies of nonactin, including the use of NMR^9,10 and Raman spectroscopy,¹¹ together with molecular dynamics simulation,¹² substantially confirmed the binding model.

Figure 2.

Structure of nonactin and the nonactin-K⁺ complex. Coordinates for the structures were taken from crystallography data. The left and center structures are those of nonactin without a coordinated metal ion. The main macrocycle ring of nonactin has been emphasized and color coded in the central structure to show the changes in torsion angle between nonactin and the nonactin-K⁺ complex – the color map runs from red (small change) to yellow (extensive change). The right structure is that of the nonactin-K⁺ complex with the ion omitted for clarity.

As the structure of nonactin is unique, so is the biosynthesis of the compound. Nonactin is a polyketide and is assembled from acetate, propionate and succinate. Much is known about the precursors of nonactin biosynthesis from labeling experiments,^13–15 the genetics of nonactin biosynthesis from analysis of the nonactin biosynthesis gene cluster^16,17 and the enzymology of nonactin biosynthesis.^18–20 These data show that after the formation of an early, achiral intermediate, the biosynthesis pathway for nonactin branches into two, mirror image pathways for the generation of (+)- and (−)-nonactic acid. The latter precursors are then stereoselectively assembled into nonactin. Emerging evidence suggests that the two pathways arose from gene duplication followed by divergent evolution. The central question raised, therefore, by both the structure and the biosynthesis of nonactin concerns the benefit, if any, to the producing organism in generating the natural, achiral diastereoisomer and for maintaining two independent pathways for the generation of nonactic acid.

To better understand the nonactin structure and biosynthesis we prepared two alternate diastereoisomers of nonactin, one prepared solely from (+)-nonactic acid and one prepared solely from (−)-nonactic acid, referred to herein as ‘all-(+)-nonactin’ and ‘all-(−)-nonactin’ respectively. These diastereoisomers are of interest as their stereochemical arrangement mimics that of valinomycin, another naturally occurring potassium ionophore.²¹ In all-(−)-nonactin the (2R,3R,5S,8S) pattern of (−)-nonactate is replicated four times around the macrocycle. Taking nonactate as the monomer, nonactin might be described as a syndiotactic polymer. In valinomycin the (R,S,S,S) pattern of D-valine-D-hydroxyvalerate-D-valine-L-lactate is replicated three times around the macrocycle. Taking the D-valine-D-hydroxyvalerate-D-valine-L-lactate structure as the repeating monomer of valinomycin, valinomycin and both all-(−)- and all-(+)-nonactin might be described as isotactic polymers. Our evaluation of the non-natural diastereoisomers with respect to their antibiotic activity, the thermodynamics of ion binding and their ability to partition ions into organic liquids and through bulk organic phase models of membranes confirm that the producing organism is required to use both enantiomers of nonactic acid in nonactin formation to achieve biological activity.

Results

Synthesis

Nonactic acid has been the target of many synthetic studies as it is a relatively small yet stereochemically complex molecule.^22,23 Fewer total syntheses of nonactin, on the other hand, have been reported as it is, at least in principle, straightforward to generate from nonactic acid.^24,25 The practical challenges in nonactin synthesis, however, lie in the need to prepare both enantiomers of nonactic acid and in the final reaction, the formation of a 32-membered macrocycle from a linear precursor; challenges for which excellent solutions are available.^24,25 We were fortunate that syntheses of non-natural diastereoisomers of nonactin could be patterned directly from known routes leaving the production of both enantiomers of nonactic acid as the main technological hurdle. As nonactin is readily available to us on a large scale we decided to use the natural product as a starting point rather than generate nonactic acid de novo. Methanolysis of nonactin^13,26 is a reliable procedure and we have used this in the past to generate tens of grams of methyl nonactate, 8, albeit as the racemate. Resolution of methyl nonactate was accomplished on a large scale using a Rhodococcus-mediated oxidation;²⁷ Rhodococcus cultures are effective in stereoselectively oxidizing methyl (−)-nonactate to methyl (−)-8-ketononactate leaving unreacted methyl (+)-nonactate, (+)-8. After biotransformation, separation of methyl (+)-nonactate and methyl (−)-8-ketononactate by flash chromatography is undemanding. Although (−)-8 can be obtained through reduction of methyl (−)-8-ketononactate in an anaerobic Rhodococcus culture²⁷ we chose to isolate (−)-nonactic acid directly from a culture of S. griseus ΔnonD, a mutant strain of the nonactin producing organism wherein the chromosomal copy of the cocaine esterase-like nonactin biosynthesis gene nonD had been disrupted. Overall, by degrading the natural product and by exploiting a mutant strain of the nonactin producing organism we had access to many grams of both enantiomers of 8.

The conversion of 8 into nonactin was predominantly an exercise in manipulating protecting groups. Thus, protection of the C-8 alcohol of 8 was achieved using TBSCl prior to saponification to generate the TBS-protected acid 9 (Scheme 1). Similarly, saponification of 8 prior to conversion to the corresponding benzyl ester lead to 11. Compounds 9 and 11 were the sole orthogonally protected nonactic acid monomers needed to complete the synthesis of all-(−)-nonactin, (−)-17. Coupling of 9 and 11 to afford the dimer 12 was accomplished using DCC (Scheme 1). Compound 12 was then deprotected by removing the silyl ether to afford benzyl protected alcohol 14 and by hydrogenolysis to afford protected acid 13. Following the guide of Fleming, 13 and 14 could be coupled to give a protected linear tetramer 15 using 2,4,6-trichlorobenzoyl chloride (Scheme 2).²⁴ Removal of the benzyl ester (hydrogenolysis) and the silyl ether (acidification) protecting groups from 15 was straightforward leading to the linear tetramer 16. At this point in the synthesis we had some concern that the macrocyclization reaction to form all-(−)-nonactin would prove problematic. It might be argued that the alternating (+)-(−)-(+)-(−) stereochemical pattern of nonactin may influence the manner in which a linear, tetrameric precursor might fold and therefore affect the cyclization reaction. The Yamaguchi coupling^24,28 to form all-(−)-nonactin from (−)-16, however, was quite straightforward. The simplicity of the cyclization reaction suggests that the ease of folding plays no role in the observed stereochemistry of the natural product, nonactin. After generating all-(−)-nonactin the entire synthetic sequence was repeated to generate all-(+)-nonactin with similar results. Comparison of the ¹H and ¹³C NMR spectra of the linear (+)-(−)-(+)-(−)-tetramer and nonactin, as demonstrated by Fleming,²⁴ revealed a significant simplification in the resonances assigned to the methyl groups at C-2 and C-8 of nonactic acid when the linear tetramer is converted into a cyclic form. The eight, resolved doublets in the linear tetramer collapse to two doublets showing that in nonactin there is S4 symmetry and that the four C-2 methyl groups and the four C-8 methyl groups are degenerate. Similar changes in the ¹H and ¹³C NMR spectra were observed upon formation of both all-(−)-nonactin and all-(+)-nonactin. These data show that there is C4 symmetry, and degeneracy of the methyl groups, in the non-natural diastereoisomers of nonactin.

Scheme 1.

Synthesis of orthogonally protected nonactic acid monomers and dimers.

Scheme 2.

Completion of the synthesis of all-(−)-nonactin.

We did two further experiments in addition to the spectroscopic and spectrometric characterization to confirm that we had prepared all-(−)-nonactin and all-(+)-nonactin. First, we subjected small samples of all-(−)-nonactin and all-(+)-nonactin to methanolysis to generate samples of methyl nonactate. The stereochemical purity of the methyl nonactate was confirmed by GC analysis using a chiral stationary phase. In each case the GC analysis demonstrated that only one enantiomer of 8, and also the expected enantiomer, was present after degradation thereby confirming that no inadvertent scrambling of synthetic samples had occurred during the synthesis. Second, conductivity measurements of methanol solutions of all-(−)-nonactin and all-(+)-nonactin confirmed that the synthetic samples did not contain any significant cations, the presence of which might confound later analysis.

Biological activity

We measured minimal inhibitory concentrations (MIC) for nonactin, all-(−)-nonactin and all-(+)-nonactin against a range of Gram positive and Gram negative bacteria (Table 1). As expected, nonactin showed significant potency against Gram positive organisms, including drug resistant forms of the pathogens Staphylococcus aureus and Enterococcus faecalis. Also, as expected, nonactin showed no activity against Gram negative organisms or against the pathogenic fungus Candida glabrata. In the latter cases, true MIC values could not be obtained as the solubility of nonactin became limiting. Regardless, it is reasonable that compounds that show MIC values in excess of 1 mM are classified as ‘inactive’ as such levels of potency have no practical application. The results for all-(−)-nonactin and all-(+)-nonactin were surprisingly clear cut. The latter compounds showed no significant antibiotic activity at concentrations up to their solubility limits.

Table 1.

Antimicrobial activity of nonactin, all-(+)-nonactin and all-(−)-nonactin against a range of microorganisms.

Organism	Minimum inhibitory concentration / µM
	Nonactin	All-(−)-nonactinb	All-(+)-nonactinb
Bacillus anthracis	2	> 500	> 500
Bacillus cereus	4	> 500	> 500
Bacillus subtilis	1	> 500	> 500
Enterococcus faecalis	2	> 500	> 500
E. faecalis – vancomycin resistant	2	> 500	> 500
Staphylococcus aureus	2	> 500	> 500
S. aureus – methicillin resistant	2	> 500	> 500
Escherichia coli	> 1000a	> 500	> 500
Pseudomonas aeruginosa	> 1000a	> 500	> 500
Candida glabrata	> 1000a	> 500	> 500

^a)MIC determinations are limited by the low solubility of nonactin.

^b)Solubility of all-(+)-nonactin and all-(−)-nonactin is lower than that of the natural product.

Ion binding − microcalorimetry

Having shown that all-(−)-nonactin and all-(+)-nonactin have no significant antibiotic activity we needed to understand why. Nonactin acts as an antibiotic as it is able to form stable complexes with alkali metal and NH₄⁺ ions catalyzing their passive diffusion down the electrochemical gradients that exist across bacterial cell membranes. The first question that we chose to address concerned, therefore, the ability of non-natural diastereoisomers to form complexes with metal ions. Microcalorimetry was the technique of choice as we would be able to extract much thermodynamic detail concerning ion binding. We chose to conduct these experiments in methanol. First, the solubility of nonactin in water is so low that conducting these experiments on aqueous samples was not practical.²⁹ Second, the comparison of binding data across the diastereoisomer series would be sufficient. The thermodynamic constants for metal ion binding were determined from titrations of KNCS, NaNCS or NH₄NCS into a solution of the appropriate nonactin diastereoisomer. The heat change observed during the titration series was used to compute association constants (K_a) and ΔH of binding from which ΔG and ΔS could then be derived (Table 2). We chose to use only all-(−)-nonactin to test the binding of non-natural diastereoisomers. This choice was reasonable as there can be no stereoselectivity involved in the binding reactions to achiral ions. Good data was obtained for nonactin with each of the ions tested which was in stark contrast to the situation for all-(−)-nonactin. In the latter case we were able to obtain reliable data only for K⁺ and Na+ binding. In the case of NH₄⁺, the signal derived from heat of dissolution of NH₄⁺ in methanol completely swamped out any signal due to NH₄⁺ binding that may, or may not, have been present. The negative entropy changes on ion binding to nonactin (Table 2) show that entropy loss from organization of the ionophore around the ion is greater than the entropy gain from the ion being stripped of solvent. The large and favorable enthalpy changes upon K⁺-nonactin formation derive from the coordination of the carbonyl and tetrahydrofuran oxygen atoms to the ion. The coordination effect is less favorable for Na⁺ than K⁺ as the cavity in nonactin is a better fit for K⁺. In the crystal structure of the nonactin-K⁺ complex the K–O distance is close to the sum of the ionic radii of K⁺ and O. The better fit for K⁺ to nonactin is reflected in the association constant for the nonactin-K⁺ complex which is approximately 200-fold larger than that of the nonactin-Na⁺ complex. The K⁺-all-(−)-nonactin complex, however, is approximately 900-fold less stable than the K⁺-nonactin complex. The low enthalpy change on formation of the K⁺-all-(−)-nonactin complex suggests that only one to two oxygen atoms likely coordinate to the K⁺. When combined with the low, positive entropy change on K⁺-all-(−)-nonactin complex formation, the data suggest a lack of a sequential binding pathway and that all-(−)-nonactin, unlike nonactin, cannot easily fold around the ion to allow for further coordination and the formation of a stable complex. The enthalpy change of Na⁺ binding to all-(−)-nonactin suggests that multiple coordinate bonds are formed to the Na+ although the association constant is still low. While the solution structure of all-(−)-nonactin remains to be determined it is quite clear from the data that the non-natural diastereoisomers of nonactin cannot effectively bind to monovalent cations and that the poor binding is directly related to their lack of biological activity.

Table 2.

Isothermal calorimetry data for the formation of ionophore-ion complexes in methanol at 298 K. The interactions between both Na⁺ and NH₄⁺ and all-(−)-nonactin could not be determined.

	Nonactin			All-(–)-nonactin
	K+	Na+	NH4+	K+	Na+
ΔG / kcal.mol−1	−6.24 ± 0.02	−3.08 ± 0.01	−6.40 ± 0.01	−2.24 ± 0.05	−2.20 ± 0.03
ΔH / kcal.mol−1	−12.9 ± 0.1	−6.3 ± 0.1	−17.8 ± 0.7	−2.1 ± 0.1	−13.5 ± 0.5
ΔS / cal.mol−1.K−1	−22.4 ± 0.3	−10.8 ± 0.3	−38 ± 2	0.45 ± 0.40	−38 ± 2
Ka / dm3.mol−1	38.6 ± 1.3 × 103	184 ± 4	51.9 ± 0.4 × 103	44 ± 4	42 ± 2

Partitioning assay

We regularly use a partitioning assay to quantify the amount of nonactin that is formed in fermentative cultures of S. griseus.³⁰ The assay relies upon the ability of the nonactin-K⁺ complex to partition into the organic phase of an organic-aqueous biphasic system. As the complex is formed and moves into the organic phase, a counter ion must follow to maintain electric neutrality. Commonly, the counter ion used is picrate which imparts a distinct yellow color to the organic layer (Fig. 3A). Conventionally, the assay is used to quantify nonactin concentrations as the amount of picrate found in the organic layer, quantified through UV spectroscopy, is proportional to the amount of nonactin present. We adapted the assay to obtain a standard curve for both nonactin and all-(−)-nonactin (Fig. 3). As our microcalorimetry data was obtained using methanol as a solvent, the partition experiment provides an alternative approach wherein the effects of water can be evaluated. Typical binding curves were obtained for both nonactin and all-(−)-nonactin. For equal concentrations of nonactin and all-(−)-nonactin, the amount of picrate present in the organic layer was minimally 100-fold less for all-(−)-nonactin than for nonactin. The data match well with the relative association constants for the two complexes that we obtained in methanol solution. The difference in ion binding and subsequent partitioning is demonstrated in the inset photograph in Fig. 3 where two vials are identically set up with the exception that one contains nonactin (3A) and one contains all-(−)-nonactin (3B). The lack of picrate color in the lower CHCl₃ phase is quite evident when all-(−)-nonactin is the ionophore.

Figure 3.

Determination of ionophore-K⁺ partition into an immiscible organic phase as a thermodynamic measure of ionophore ability. Differing amounts of ionophore were partitioned between equal volumes of CHCl₃ and an aqueous solution of potassium picrate solution. The amount of ionophore-K⁺ complex in the CHCl₃ phase was quantified by measuring the concentration of the picrate counter ion via its absorbance at 357 nm. This assay is a modification of the partition assay used to quantify tetranactin developed by Suzuki et al.³⁰ Inset picture: the picrate anion is quite visible in the lower, CHCl₃ layer when nonactin is used as the ionophore (A) and not present when all-(−)-nonactin is used (B).

Transport assay

At this point we have demonstrated that the lack of biological activity of the non-natural diastereoisomers of nonactin is most likely due to their inability to form complexes with monovalent cations. The data we have, however, is purely thermodynamic even though the data is consistent in both methanol and water-CHCl₃. To round out our data we sought to observe kinetic differences in the transport of monovalent ions by nonactin and its non-natural diastereoisomers. There is a substantial body of literature on the kinetics of nonactin-mediated ion transport through black lipid membranes, the latter being used as a surrogate for cell membranes.^31,32 For our purpose, however, there is a simpler experimental system that can mimic a cell membrane and ion transport. It has been demonstrated that ionophores can mediate the movement of K⁺ between two aqueous phases are separated by a common organic layer.^33–35 The K⁺-nonactin complex that forms in one aqueous phase can partition into the organic layer. Since the bulk organic solvent is being mechanically stirred there is a uniform concentration of K⁺-nonactin complex that can then partition into the second aqueous layer and dissociate. The free nonactin can move back through the organic phase to form further K⁺-nonactin complex in the first aqueous phase. Overall, the process results in the bulk transport of K⁺ from one aqueous phase to the other if they have different initial K⁺ concentrations. The transport process can be followed by monitoring co-transport of picrate as the counter ion. We used this approach to measure the relative rates of K⁺ transport that could be mediated by nonactin and all-(−)-nonactin (Fig. 4). The rate of K⁺ transport between the two aqueous phases is dependent upon the K⁺ concentration difference between them. Furthermore, as K⁺ is transported the concentration difference decreases; the process can be conveniently modeled by a 1^st order approach to an equilibrium. In this system, with all else other than the identity of the ionophore being equal, nonactin can support transport rates that are minimally 100-fold higher than those mediated by all-(−)-nonactin. It is noteworthy that the K⁺ transport rate with all-(−)-nonactin is not zero. Although the transport rate with all-(−)-nonactin is much lower than with nonactin, the end point, the equilibrium distribution of K⁺ and picrate, is the same. The difference between the equilibrium values of A₃₅₇ of 1.8 and 1.9 (Fig, 4) is a result of the large extrapolation needed to calculate the equilibrium value when the K⁺ transport rates are low in the case of all-(−)-nonactin.

Figure 4.

Determination of ionophore-K⁺ transport rates between two aqueous phases through an intermediate bulk organic solvent as a kinetic measure of ionophore ability and a simple model of passive membrane diffusion. The transport rate of K⁺ from the one aqueous phase to the other was measured by following the absorbance of the ‘receiving’ phase at 357 nm, that is, by measuring co-transport of the picrate anion. Fit lines were calculated by non-linear least squares regression to a simple rate equation modeling a first order approach to an equilibrium, A₃₅₇(t) = k₁.(1 − exp[−k₂t]). ● Nonactin as the ionophore; k₁ = 1.8, k₂ = 0.0009. ○ All-(−)-nonactin as the ionophore; k₁ = 1.9, k₂ = 0.100.

Molecular modeling

To gain insight into the structural differences between nonactin (1) and all-(−)-nonactin (17) in solution we used molecular dynamics to simulate their potassium complexes using an explicit water solvent model. Our work was guided by molecular dynamics studies of nonactin by Merz¹² and by our own previous studies of macrotetrolide selectivity.³⁶ Nonactin retains a tight, approximately cubic coordination to the K⁺ ion throughout the simulation. The K⁺-carbonyl oxygen distances (Fig. 5) are stable (2.90 ± 0.30 Å) as are the K⁺-tetrahydrofuran oxygen distances (3.60 ± 0.42 Å) for nonactin. The all-(−)-nonactin K⁺ complex has much less rigid structure. The K⁺-carbonyl oxygen distances (Fig. 5) (3.73 ± 0.86 Å) and the K⁺-tetrahydrofuran oxygen distances (3.50 ± 0.98 Å) show much more variation than similar distances in nonactin. Significantly, in the nonactin-K⁺ complex the hydrogen atoms at C3 and C6 of each monomer are on the inside of the structure "facing" the cation. In all-(−)-nonactin only the H-3 and H-6 hydrogen atoms of two, non-adjacent monomer units are inside the structure; the two other H-3 and H-6 sets face out towards solvent. The structure becomes distorted so that poor steric interactions between a tetrahydrofuran ring and a carbonyl group on the other edge of the closing macrocycle are avoided. The steric interaction prevents the macrocycle from closing to give sufficiently close contacts between the coordinating oxygen atoms and the central cation. Only if the stereochemistry of the monomer units alternates around the macrocycle, as is found in nonactin, can a conformation be accessed where all the H-3 and H-6 atoms are on the inside face of the macrocycle allowing for a tight complex to be formed.

Figure 5.

Representation of the nonactin and all-(−)-nonactin structures bound to potassium. 1, Distribution of K⁺-carbonyl oxygen distances for nonactin (blue) and all-(−)-nonactin (red) obtained from molecular dynamics simulation. 2, Representations of the poor steric interactions (A) that are avoided in all-(−)-nonactin by distorting the complex to a less favorable conformation for binding or that are absent (B) in the natural diastereoisomer, nonactin. For nonactin, H-3 and H-6 face inwards towards the cation; for all-(−)-nonactin H-3 and H-6 face outwards toward solvent. 3, Distribution of K⁺-tetrahydrofuran oxygen distances for nonactin (blue) and all-(−)-nonactin (red) obtained from molecular dynamics simulations.

Discussion

The stereochemistry of nonactin is unique among natural products in that the producing organism must generate both enantiomers of nonactic acid. It is clear from analysis of the nonactin biosynthesis gene cluster that there are separate, enantiocomplementary pathways to each enantiomer of nonactic acid and that there are parallel sets of biosynthesis enzymes. The stereochemical course of nonactin biosynthesis is complex, therefore, and this complexity has been maintained even against natural genetic drift. There is most likely a benefit to the producing organism in generating the achiral diastereoisomer of nonactin that outweighs the cost of running parallel biosynthesis pathways. At the outset we had two hypotheses. First, it would be quite conceivable that nonactin would be more active than all-(+)-nonactin or all-(−)-nonactin, however, the relative activity of the diastereoisomers was open to question. Second, we thought that during the late stages of nonactin biosynthesis there might be substantial differences in the manner in which (+)-(−)-(+)-(−) and (−)-(−)-(−)-(−) linear tetramers of nonactic acid could fold that might be reflected in the synthesis of the natural diastereoisomer being the more efficient process. The data that we obtained settles both of these questions.

The relative efficiency by which the folding of linear tetrameric species to form each of the nonactin diastereoisomers became apparent during the macrolactonization reactions that we used to form the latter. Each of the reactions was efficient and proceeded in high yield. Formation of the non-natural nonactin diastereoisomers was not noticeably slower than formation of nonactin. These data strongly suggest that the folding of precursor species plays no significant part in the observed stereochemistry of the natural product.

If the natural diastereoisomer of nonactin were more active than nonactin assembled from homochiral nonactic acid, how much more active would it be? We were surprised that the differences in biological activity of nonactin and its non-natural diastereoisomers was so clear (Table 1) as nonactin was minimally 100-fold more active. Should S. griseus derive a benefit from the antibiotic activity of nonactin then the large difference in activity between the natural and non-natural diastereoisomers can readily account for the evolution, and maintenance, of parallel biosynthesis pathways.

The antibacterial activity of nonactin derives from its ability to form stable complexes with K⁺, Na⁺ and NH₄⁺. Since all-(−)-nonactin and all-(+)-nonactin are not active against the set of Gram negative we tested it was a logical step to determine if they were able to form ion complexes; the microcalorimetry data was convincing that they could not to any appreciable degree. The association constant, K_a, for the K⁺-nonactin complex in methanol was found to be approximately 900-fold higher than that of the K⁺-all-(−)-nonactin complex (Table 2). Similarly, nonactin allowed for approximately 100-fold greater partitioning of potassium picrate into CHCl₃ than all-(−)-nonactin (Fig. 3). The data show a clear thermodynamic advantage for the natural product.

While the antibacterial activity and thermodynamic data show that the natural product is favored, we chose a simple transport assay to obtain comparative kinetic data. Again, the natural product was superior. Rates of K⁺ transport were over 100-fold higher when nonactin was used as the ionophore than when all-(−)-nonactin was used. No significant transport was observed without ionophore being present and it was noteworthy that transport rates, although very low (Fig. 4), were reliably measured for all-(−)-nonactin. Overall, the binding of K⁺ to all-(−)-nonactin is poor but sufficiently large so that transport rates can be measured, however, the extent of the binding and transport mediation are not sufficient to impart significant biological activity.

We used molecular dynamics to give us some structural insight into the structures of the all-(−)-nonactin and nonactin K⁺ complexes. Only in nonactin, with its alternating stereochemistry, can conformations where the H-3 and H-6 atoms of each tetrahydrofuran ring face the center of the complex. If two monomer units are inverted, as is the case with all-(−)-nonactin, two tetrahydrofuran rings have poor steric interactions with a carbonyl group (Fig. 5) on the other edge of the molecule preventing tight closure around the cation. Such modeling data allows us to account for the activity and affinity differences between nonactin and our non-natural diastereoisomers.

Summary

We have successfully prepared two non-natural diastereoisomers of nonactin, one assembled from (+)-nonactic acid and one from (−)-nonactic acid. We demonstrated that the latter diastereoisomers are significantly less potent as antibacterial agents than the natural product, nonactin. As nonactin is an ionophore we determined the ability of our analogs to bind to K⁺, Na⁺ and NH₄⁺. The microcalorimetry data showed that no significant binding to non-natural nonactin diastereoisomers could be achieved. In the case of K⁺ it is likely that only one to two carbonyl groups can complex with the ion but, unlike nonactin, this first association does not lead to a stepwise wrapping of the ionophore around the ion. To complement the microcalorimetry data we further demonstrated that all-(−)-nonactin was ineffective at partitioning K⁺ into an organic solvent and only poorly mediated K⁺ transport through a bulk organic phase. Modeling data suggest that the alternating stereochemistry of the monomer units in nonactin allows for the THF rings to adopt equivalent conformations where the macrocycle can close efficiently around the cation. Although the stereochemistry of nonactin biosynthesis is complex, and S. griseus has a unique system with enantiocomplementary biosynthesis pathways, our activity, thermodynamic and kinetic data all show that there is a likely benefit to S. griseus in having such a superbly complicated biosynthesis pathway.

Experimental Section

General procedures

Solvents were obtained from Fisher Scientific. All other chemicals, unless noted otherwise, were obtained from the Aldrich Chemical Company (Milwaukee, WI). The solvents MeOH (over Mg(OMe)₂), CH₂Cl₂ (over CaH₂), diethyl ether (over Na/K-benzophenone) and THF (over Na/K-benzophenone) were dried and distilled prior to use. MgSO₄ refers exclusively to anhydrous MgSO₄. Solutions were concentrated by evaporation in vacuo. All synthesis procedures, unless noted otherwise, were carried out under a slight positive pressure of argon gas at ambient temperature (21 °C – 25 °C). Column chromatography was performed using Merck Silica Gel 60. NMR spectra were acquired at 400 MHz (¹H) and 100 MHz (¹³C), were referenced to the residual solvent, and are reported as: chemical shift (δ / ppm), splitting pattern, coupling constant (J / Hz) and intensity. Nonactin was obtained from Promiliad Biopharma Inc. (Alberton, MT).

Methyl (±)-nonactate ((±)-8)

Methyl (±)-nonactate was obtained through methanolysis of nonactin as described by Ashworth et al.,¹³ adapted for a large scale as described by Dinges et al.²⁶

Methyl (+)-nonactate ((+)-8)

Methyl (+)-nonactate was obtained using a Rhodococcus-mediated resolution of racemic methyl nonactate in > 98 % ee as described by Nikodinovic et al.²⁷ and was shown to be identical to an authentic standard.

Methyl (−)-nonactate ((−)-8)

A four day, 10 L fermentation of Streptomyces griseus ΔnonD was clarified by centrifugation. The clarified broth was acidified to pH 2 by the addition of conc. aq. HCl. The broth was extracted twice with an equal volume of EtOAc. The combined EtOAc extracts were dried over MgSO₄, filtered and concentrated to yield a crude oil. (−)-Nonactic acid was isolated from the oil by chromatography on silica gel, eluting with EtOAc-hexanes-AcOH, as a colorless oil (3.1 g). The (−)-nonactic acid was converted into (−)-8 by Fisher esterification and was shown to be identical to an authentic standard (>98% ee by GC¹⁸).

(R)-2-((2R,5S)-5-((S)-2-(tert-Butyldimethylsiloxy)propyl)tetrahydrofuran-2-yl)propanoic acid ((+)-9)

Imidazole (1.3 g, 19.5 mmol) and TBSCl (1.5 g, 9.8 mmol) were added to a stirred solution of (−)-methyl nonactate (−)-8 (0.85 g, 3.9 mmol) in DMF (10 mL) and stirring continued at ambient temperature for 2 h. The reaction was quenched by pouring into water (50 mL); the resulting aqueous solution was then extracted with Et₂O (3 × 50 mL). The organic phases were combined, and concentrated to a crude oil. Chromatography on silica gel eluting with EtOAc/hexanes (1:9) gave an intermediate TBS-protected ester as a clear oil (1.24 g, 93%): [α]_D²⁵ +11 (c 0.90, CHCl₃); δ_H (400 MHz, CDCl₃) 0.03 (d, J = 2.2 Hz, 6H), 0.87 (s, 9H), 1.10 (d, J = 7 Hz, 3H), 1.11 (d, J = 5.9 Hz, 3H), 1.40–1.60 (m, 4H) 1.94 (m, 2H), 2.5 (m, 2H) 3.68 (s, 1H) and 3.84–4.00 (m, 3H); δ_C (100 MHz, CDCl₃) δ −4.95, −4.65, 13.44, 18.07, 24.61, 25.88, 28.71, 31.29, 45.53, 46.01, 51.52, 66.05, 76.16, 80.25, and 175.36. In a similar manner, TBS protection of (+)-8 (0.26 g, 1.2 mmol) gave the intermediate protected ester (0.36 g, 90%): [α]_D²⁵ −26° (c 0.52, CHCl₃). A solution of intermediate ester (1.1 g, 3.2 mmol) in THF (13 mL), MeOH (4.4 mL) and aqueous KOH (5 M, 4.4 mL) was stirred at ambient temperature for 16 h. The reaction was then concentrated; the resultant aqueous solution was further diluted with water (25 mL), acidified with 10% citric acid, and extracted with Et₂O (4 × 25 mL). The organic phases were combined and washed with water and brine, dried and then concentrated to give (+)-9 as a clear oil (0.95 g, 93% yield): [α]_D²⁵ +28° (c 0.75, CHCl₃); Analytical data was equivalent to the known compound.²⁴ In a similar manner, deprotection of the antipode (0.30 g, 0.9 mmol) gave (−)-9 (0.28 g, 96%); HRMS (ESI) m/z calcd. for C₁₆H₃₂NaO₄Si: 339.1968; found 339.1963 ([M+Na]⁺, Δppm 1.7).

(2R)-2-((2R,5S)-5-((2S)-2-hydroxypropyl)tetrahydrofuran-2-yl)propanoic acid; nonactic acid ((−)-10)

A solution of (−)-8 (0.85 g, 3.9 mmol, [α]_D²⁵ −31° (c 0.29, CHCl₃)) in MeOH (7.5 mL) and aqueous KOH (2 M, 15 mL) was stirred for 2 h at ambient temperature. The reaction was concentrated and diluted with water (75 mL), acidified with aqueous 1 M HCl and finally extracted with EtOAc (3 × 25 mL). The organic phases were combined, dried and concentrated to give (−)-nonactic acid (−)-10 as a colorless oil (0.49 g, 62% yield): analytical data was equivalent to the known compound.²⁴ In a similar manner, (+)-8 (0.30 g, 1.39 mmol, [α]_D²⁵ +30.6° (c 0.29, CHCl₃)) was used to prepare (+)-nonactic acid (+)-10 (0.25 g, 89%).

(R)-Benzyl 2-((2R, 5S)-6-((S)-2-hydroypropyl)tetrahydrofuran-2-yl)propanoate ((−)-11)

A solution of (−)-nonactic acid (−)-10 (0.49 g, 2.4 mmol) in dry DMF (30 mL) was treated with tert-BuOK and stirred at 60 °C for 30 min under an atmosphere of argon. Benzyl bromide (0.62 g, 3.6 mmol) was added to the stirred solution by syringe and the reaction held at 60 °C for 1.5 h. The reaction was quenched by pouring into water and the resulting aqueous solution was brought to pH 2 with 1 M HCl and extracted with Et₂O (4 × 20 mL). The organic layers were combined, dried and concentrated. The crude oil was purified by chromatography on silica gel eluting with EtOAc/hexanes (1:1) to give (−)-11 as a clear oil (0.51 g, 72%): [α]_D²⁵ −6.8° (c 1.10, CHCl₃); δ_H (400 MHz, CDCl₃) 1.14 (d, J = 7.0 Hz, 3H), 1.17 (d, J = 6.2 Hz, 3H), 1.52–1.72 (m, 4H), 1.97 (m, 2H), 2.59 (m, 1H), 2.71 (s, 1H), 3.93–4.16 (m, 3H), 5.14 (dd, J = 2.2 and 12.5 Hz, 2H) and 7.27–7.40 (m, 5H); δ_C (100 MHz, CDCl₃) 13.39, 23.23, 28.60, 30.60, 42.97, 45.30; 65.08, 66.12, 76.99, 80.78, 128.00, 128.06, 128.39, 135.99 and 174.50. In a similar manner, esterification of (+)-10 (0.21 g, 1.0 mmol) gave (+)-11 (0.256 g, 84%).

(R)-Benzyl 2-((2R, 5S)-((S)-2-((R)-2-((2R,5S)-5-((S)-2-(tert-butyldimethylsilyloxy)propyl) tetrahydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoate ((+)-12)

To a solution of acid (+)-9 (0.55 g, 1.8 mmol) and alcohol (−)-11 (0.51 g, 1.8 mmol) in dry CH₂Cl₂ (10 mL) was added DCC (0.38 g, 1.8 mmol) followed by DMAP (0.06 g, 0.5 mmol). The mixture was stirred under argon for 16 h and then concentrated prior to being resuspended in Et₂O, filtered and the filtrate then concentrated. The crude oil was purified by flash chromatography on silica gel on silica gel eluting with EtOAc/hexanes (1:9) to give (+)-12 as a clear oil (0.64 g, 64%): [α]_D²⁵ +9.8° (c 1.00, CHCl₃); δ_H (400 MHz, CDCl₃) 0.03 (s, 6H), 0.87 (s, 9H), 1.07 (d, J = 7.0, 3H), 1.11 (d, J = 5.9 Hz, 3H), 1.12 (d, J = 7.0 Hz, 3H), 1.21 (d, J = 6.6 Hz, 3H), 1.35–1.83 (m, 8H), 1.84–2.03 (m, 4H), 2.5 (q, J = 7.O Hz, 1H), 2.6 (q, J = 7.0 Hz, 1H), 3.82–4.06 (m, 5H), 4.96 (sextet, J = 6.2 Hz, 1H), 5.12 (d, J = 12.5 Hz, 1H), 5.16 (d, J = 12.5 Hz, 1H) and 7.27–7.39 (m, 5H); δ_C (100 MHz, CDCl₃) −4.86, −4.59, 13.15, 13.26, 18.04, 20.60, 24.63, 25.87, 28.33, 28.41, 31.34, 31.45, 42.42, 45.32, 45.40, 46.07, 66.08, 66.20, 69.18, 76.24, 76.60, 80.12, 80.25, 128.01, 128.44, 136.13, 174.30 and 174.62; IR (film-ATR): 2953, 2930, 2856, 1732, 1461, 1376, 1254, 1188, 1155, 1055 and 835 cm⁻¹; HRMS (ESI) m/z calcd. for C₃₃H₅₅O₇Si: 591.3717; found 591.3712 ([M+H]⁺, Δppm 0.9). In a similar manner, coupling of (+)-9 (0.24 g, 0.8 mmol) and (+)-11 (0.23 g, 0.8 mmol) gave (−)-12 (0.28 g, 62%): [α]_D²⁵ −22° (c 0.29, CHCl₃).

(R)-2-((2R,5S)-5-((S)-2-(R)-2-((2R,5S)-5-((S)-2-(tert-Butyldimethylsilyloxy)propyl)tetra hydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoic acid ((+)-13)

A mixture of (+)-12 (0.31 g, 0.53 mmol) and 10% Pd/C (0.03 g) in THF (10 mL) was stirred under 1 atm of hydrogen for 16 h. The mixture was filtered through Celite, washing with EtOAc, and the filtrate and washings concentrated to give (−)-13 as a clear oil (0.25 g, 93%): [α]_D²⁵ +20° (c 0.36, CHCl₃); δ_H (400 MHz, CDCl₃) 0.031 (s, 6H), 0.87 (s, 9H), 1.08 (d, J = 7.0 Hz, 3H), 1.11 (d, J = 6.2 Hz, 3H), 1.17 (d, J = 7.3 Hz, 3H), 1.25 (d, J = 6.2 Hz, 3H), 1.38–2.10 (m, 12H), 2.38–2.57 (m, 2H), 3.84–4.02 (m, 5H) and 5.00 (sextet, J = 6.2 Hz, 1H) ; δ_C (100 MHz, CDCl₃) δ −4.86, −4.57, 13.21, 13.27, 18.04, 20.45, 24.61, 25.87, 28.38, 29.02, 31.12, 31.42, 42.22, 44.82, 45.41, 46.08, 66.23, 68.78, 76.32, 80.14, 174.37 and 177.62; IR (film-ATR): 2956, 2934, 2857, 1732, 1711, 1054, 835, 774 and 540 cm⁻¹; HRMS (ESI) m/z calcd. for C₂₆H₄₉O₇Si: 501.3248; found 501.3242 ([M+H]⁺, Δppm 1.2). In a similar manner, hydrogenolysis of (+)-12 (0.13 g, 0.22 mmol) gave (+)-13 (0.10 g, 91%): [α]_D²⁵ −25° (c 0.42, CHCl₃); HRMS (ESI) m/z calcd. for C₂₆H₄₉O₇Si: 501.3248; found 501.3251 ([M+H]⁺, Δppm 0.6).

(R)-Benzyl 2-((2R,5S)-5-((S)-2-((R)-2-((2R,5S)-5-((S)-2-hydroxypropyl)tetrahydrofuran-2- yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoate ((−)-14)

A solution of dimer (+)-12 (0.32 g, 0.54 mmol) and p-TsOH monohydrate (0.02 g, 0.09 mmol) in acetic acid (2.5 mL) and water (0.27 mL) was stirred at ambient temperature for 30 min. The reaction was diluted with water (15 mL) and extracted with Et₂O (3 × 30 mL). The organic phases were combined and washed with aqueous sat. NaHCO₃, brine, and dried and then concentrated. The crude oil obtained was purified by chromatography on silica gel eluting with EtOAc/hexanes (1:1) to give (−)-14 as a clear oil (0.16 g, 62%): [α]_D²⁵ −3.4° (c 0.26, CHCl₃); δ_H (400 MHz, CDCl₃): δ 1.09 (d, J = 7.3 Hz, H), 1.11 (d, J = 7.3 Hz, 3H), 1.19 (d, J = 6.2 Hz, 3H), 1.21 (d, J = 6.2 Hz, 3H), 1.43–1.81 (m, 8H), 1.87–2.03 (m, 4H), 2.42–2.62 (m, 2H) 3.81, 4.16 (m, 5H), 4.98 (m, 1H), 5.12 (d, J = 12.5 Hz, 1H), 5.16 (d, J = 12.5 Hz, 1H) and 7.28–7.39 (m, 5H); δ_C (100 MHz, CDCl₃) δ 13.27, 13.36, 20.54, 23.17, 28.42, 28.70, 30.59, 31.32, 42.38, 42.76, 45.42, 45.49, 65.15, 66.11, 69.41, 76.41, 80.29, 81.11, 128.03, 128.44, 136.12, 174, 22 and 174.69; IR (ATR-film): 3403, 2973, 2936, 1730, 1457, 1378, 1188, 1165, 1087, 1056 and 540 cm⁻¹; HRMS (ESI) m/z calcd. for C₂₇H₄₁O₇: 477.2852; found 477.2863 ([M+H]⁺, Δppm 2.3). In a similar manner, deprotection of (−)-12 (0.14 g, 0.23 mmol) gave (+)-14 (0.083 g, 76%): [α]_D²⁵ +2.9° (c 0.41, CHCl₃).

(S)-Benzyl 2-((2R,5S)-5-((S)-2-((R)-2-((2R,5S)-5-((S)-2-((R)-2-((2R,5S)-5-((S)-2-(tert-butyldimethyl silyloxy)propyl)tetrahydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoate ((+)-15)

To a stirred solution of acid (+)-13 (0.16 g, 0.32 mmol), alcohol (−)-14 (0.16 g, 0.34 mmol) and DMAP (0.18 g, 1.44 mmol) in dry CH₂Cl₂ under argon, 2,4,6-trichlorobenzoyl chloride (0.16 g, 0.64 mmol) was added by syringe. The reaction was allowed to stir for 21 h and then concentrated to give a yellow semi-solid. The residue was dissolved in EtOAc and the organic phase washed with 10% citric acid, sat. NaHCO₃ and then brine, dried and then concentrated. The crude oil obtained was purified by chromatography on silica gel eluting with EtOAc/hexanes (1:3) to give (+)-15 as a clear oil (0.31 g, 99%): [α]_D²⁵ +8.0° (c 0.75, CHCl₃); δ_H (400 MHz, CDCl₃): 0.03 (s, 6H), 0.87 (s, 9H), 1.07 (d, J = 7.0 Hz, 9H), 1.11 (d, J = 6.2 Hz, 3H),1.12 (d, J = 7.0 Hz, 3H), 1.18–1.24 (m, 9H), 1.38–2.02 (m, 24H), 2.40–2.60 (m, 4H), 3.80–4.06 (m, 8H), 4.96 (m, 3H), 5.12 (d, J = 12.5 Hz, 1H), 5.16 (d, J = 12.5 Hz, 1H) and 7.28–7.38 (m, 5H); δ_C (100 MHz, CDCl₃) −4.86, −4.58, 12.92, 12.97, 13.14, 13.26, 20.57, 20.60, 20.63, 24.62, 25.87, 28.13, 28.34, 28.43, 31.31, 31.37, 31.40, 31.43, 42.37, 45.21, 45.26, 45.30, 45.42, 46.07, 66.07, 66.19, 69.21, 69.25, 69.28, 76.23, 76.44, 76.48, 76.57, 80.12, 80.22, 80.25, 127.98, 128.01, 128.44, 136.13, 174.20, 174.24, 174.27 and 174.64; IR (film-ATR): 2973, 2937, 2882, 1731, 1460, 1377, 1255, 1190, 1054 and 540 cm⁻¹; HRMS (APCI) m/z calcd. for C₅₃H₉₀NO₁₃Si: 976.6181; found 976.6158 ([M+NH₄]⁺, Δppm 2.4). In a similar manner, coupling of (−)-13 (0.06 g, 0.12 mmol) and (+)-14 (0.06 g, 0.13 mmol) gave (−)-15 (0.12 g, 99%): [α]_D²⁵ −21° (c 0.18, CHCl₃); HRMS (ESI) m/z calcd. for C₅₃H₈₆NaO₁₃Si: 981.5735; found 981.5737 ([M+Na]⁺, Δppm 0.2).

(S)-2-((2R,5S)-5-((S)-2-((R)-2-((2R,5S)-5-((S)-2-((R)-2-(2R,5S)-5-((S)-2-((R)-2-((2R,5S)-5-((S)-2-hydroxypropyl)tetrahydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoyloxy)propyl)tetrahydrofuran-2-yl)propanoic acid ((+)-16)

Ester (+)-15 (0.25 g, 0.26 mmol) was stirred with 10% Pd/C (0.025 g) in THF (5 mL) under 1 atm of hydrogen for 20 h. The reaction was filtered through Celite which was washed with EtOAc. The combined filtrates were concentrated to give the intermediate TBS-protected acid as a clear oil (0.23 g, 99%): [α]_D²⁵ +13° (c 0.73, CHCl₃); δ_H (400 MHz, CDCl₃) 0.03 (s, 6H), 0.86 (s, 9H), 1.05–1.09 (m, 9H), 1.11 (d, J = 6.2 Hz, 3H), 1.16 (d, J = 7.0 Hz, 3H), 1.23 (m, 9H), 1.38–2.08 (m, 25H), 2.41–2.55 (m, 4H), 3.81–4.03 (m, 9H) and 4.90–5.06 (m, 3H); δ_C (100 MHz, CDCl3) −4.85, −4.58, 12.99, 13.14, 13.17, 13.28, 18.05, 20.40, 20.64, 24.63, 25.87, 28.17, 28.34, 29.09, 31.09, 31.31, 31.38, 31.44, 42.23, 42.38, 42.45, 45.26, 45.31, 45.63, 46.07, 66.21, 68.79, 69.22, 69.30, 76.15, 76.27, 76.39, 80.12, 80.19, 80.25, 80.35, 174.23 and 174.32; ESI-MS m/z 891.2 ([M+Na]⁺). The intermediate TBS-protected acid (0.17 g, 0.19 mmol) and p-TsOH monohydrate (0.005 g, 0.13 mmol) were stirred in AcOH (1.3 mL) and water (0.14 mL) for 1 h at ambient temperature. The reaction was diluted with water (30 mL) and extracted with EtOAc (4 × 20 mL). The organic phases were combined, dried and concentrated. The crude oil obtained was purified by chromatography on silica gel eluting with EtOAc/MeOH (98:2) followed by EtOAc/MeOH/AcOH (95:4:1) to give (+)-16 as a clear oil (0.14 g, 95%): [α]_D²⁵ +3.0° (c 0.86, CHCl₃); δ_H (400 MHz, CDCl₃): 1.03–1.26 (m, 24H), 1.44–2.05 (m, 24H), 2.38–2.55 (m, 4H), 3.80–4.18 (m, 9H) and 4.90–5.05 (m, 3H); δ_C (100 MHz, CDCl₃) 13.03, 13.15, 13.18, 13.35, 20.39, 20.54, 20.59, 23.09, 28.20, 28.32, 28.67, 28.87, 30.55, 31.11, 31.28, 42.21, 42.32, 42.40, 42.77, 44.77, 45.31, 45.48, 45.59, 65.13, 68.92, 69.32, 69.40, 76.25, 76.37, 76.86, 76.90, 80.09, 80.30, 80.35, 81.10, 174.21 and 174.36; IR (ATR-film): 3406, 2974, 2936, 1728, 1460, 1377, 1192, 1054 and 539 cm⁻¹; HRMS (ESI) m/z calcd. for C₄₀H₆₆NaO₁₃: 777.4401; found 777.4389 ([M+Na]⁺, Δppm 1.5). In a similar manner, double-deprotection of (+)-15 (0.093 g, 0.13 mmol) gave (+)-16 (0.043 g, 60% overall for 2 steps): [α]_D²⁵ −6° (c 0.10, CHCl₃); HRMS (ESI) m/z calcd. for C₄₀H₆₇O₁₃: 755.4582; found 755.4595 ([M+H]⁺, Δppm 1.7).

All-(−)-nonactin ((−)-17)

To a stirred mixture of the hydroxyacid tetramer (+)-16 (0.067 g, 0.089 mmol), DMAP (0.044 g, 0.36 mmol) and 4 Å powdered molecular sieves (0.9 g) in dry CH₂Cl₂ (31 mL), 2,4,6-trichlorobenzoyl chloride (0.031 g, 0.125 mmol) was added by syringe. The reaction was allowed to stir for 20 h at ambient temperature. The reaction was then filtered, and the filtrate was washed with dilute HCl, sat. NaHCO₃ and brine. The filtrate was dried and concentrated to afford a crude oil which was purified by chromatography on silica gel eluting with EtOAc/hexanes (1:3) to give (−)-17 as a clear oil (0.045 g, 68%) : [α]_D²⁵ −8.8° (c 0.28, CHCl₃); δ_H (400 MHz, CDCl₃) 1.07 (d, J = 7.0 Hz, 12H), 1.25 (d, J = 6.2 Hz, 12H), 1.45–1.85 (m, 16H), 1.88–2.04 (m, 8H), 2.36–2.50 (m, 4H), 3.80–4.00 (m, 8H) and 4.90–5.02 (m, 4H); δ_C (100 MHz, CDCl₃) 13.61, 20.65, 28.66, 31.37, 42.46, 45.97, 69.64, 76.52, 80.75 and 174.18; HRMS (ESI) m/z calcd. for C₄₀H₆₅O₁₂: 737.4476; found 737.4475 ([M+H]⁺, Δppm 0.4). In a similar manner, cyclization of (+)-16 (0.042 g, 0.56 mmol) gave (+)-17 (0.034 g, 82%): [α]_D²⁵ +7.7° (c 0.36, CHCl₃); HRMS (ESI) m/z calcd. for C₄₀H₆₅O₁₂: 737.4476; found 737.4481 ([M+H]⁺, Δppm 0.7).

GC analyses

To a solution of (−)-17 (1 mg) in anhydrous MeOH (1 mL) in a sealable four dram vial was added conc. H₂SO₄ (50 µL). The vial was sealed and heated in a J-KEM reflux-reaction block (lower temperature, 65 °C; upper temperature 10 °C) for 48 h. After cooling to room temperature the reaction was quenched by the addition of water (0.25 mL), aq. NaOH (4 M, 0.25 mL) and aq. sat. NaHCO₃ (0.5 mL) followed, finally, by EtOAc (1.0 mL). The resulting mixture was shaken and allowed to separate; the upper EtOAc layer was analyzed by GC employing a chiral stationary phase. A Shimadzu GC-17A GC with flame ionization detection was used, fitted with a Supelco β-DEX 110 (30 m × 0.25 mm, d_f 0.25 µm) column. The chromatogram was obtained by injecting 1 isµL of the sample solution with a gas flow rate set at 1.5 mL/min and a split ratio of 30:1. The injector, oven and detector were set at 220 °C, 135 °C and 300 °C, respectively. The retention times under these conditions were: methyl (−)-nonactate, 49.5 min; methyl (+)-nonactate, 50.7 min. The sample of all-(−)-nonactin contained > 97% (−)-methyl nonactate.

Antibacterial / antifungal assays

Antibacterial and antifungal potency was measured in 96 well plate-based microbroth dilution assays. Test compounds were prepared as stock solutions in DMSO (50 mM) and stored at −20 °C until used. Each compound was diluted in a 2-fold dilution series and a small sample (1 µL) of each was added to wells in a test plate so that each column contained the dilution series for one compound. An inoculum (~ 1×10⁵ cfu) of a test organism in culture media (100 µL) was added to each well resulting in a dilution series running from 500 µM to 2 µM. Where necessary the measurements were repeated at lower concentrations of the test compound. After an incubation period determined from the strain-specific doubling time, Alamar blue (10 mL) was added and allowed to incubate; each well was scored for dye reduction.³⁷ The MIC value was taken as the lowest concentration of test compound that inhibits growth such that less than 1% reduction of the blue resazurin (λ_max 570 nm) component of the Alamar blue to the pink resorufin (λ_max 600 nm) was observed.

Isothermal calorimetry measurements and analysis

All experiments were performed using the VP-ITC system from Microcal, LLC. Macrolides and salt solutions (NaSCN, KSCN, and NH₄SCN) were prepared in dry MeOH and all samples were degassed with helium before performing each experiment. The ITC cell and syringe temperatures were set at 25 °C and for all experiments the metal thiocyanate solution was titrated into the macrolide solution. Controls were performed by titrating the metal thiocyanate solution into the cell containing only methanol. The reference cell for all experiments contained MeOH. For measurements with NaSCN an initial 3.0 µL injection was made prior to the standard series of 29 × 10.0 µL injections to attenuate the first titration point. Similarly for measurements with KSCN an initial 1.0 µL injection was followed by an additional 29 × 3.0 µL injections for each titration. Reliable ITC data was not forthcoming from measurements involving all-(−)-nonactin with NaSCN and NH₄SCN due to poor binding in the case of Na⁺ and both poor binding and a large heat of dissolution in the case of NH₄⁺.

Ionophore-mediated partitioning assay

As a measure of ion-ionophore binding we performed a partitioning assay described originally for tetranactin by Suzuki et al.³⁰ A set of two-phase mixtures were set up by mixing CHCl₃ (5 mL) and Tris buffer (5 mL, pH 8.0) containing Tris-HCl (100 mM), KCl (100 mM) and potassium picrate (0.17 mM). All-(−)-nonactin was added to the mixtures to obtain a range of ionophore concentrations from 0.1 to 0.01 mg/mL. Each test sample was thoroughly mixed and then the aqueous and organic layers left to separate. Where a K⁺-ionophore complex was formed, it was able to partition into the organic phase, bringing along the colored picrate anion to maintain neutrality. The concentration of K⁺-ionophore complex in the organic phase was estimated by measuring the concentration of picrate; the latter measurement relying upon the absorbance of the picrate anion at 357 nm (ε₃₅₇, 1,450 dm³.mol⁻¹.cm⁻¹). The experiment was repeated with nonactin for comparison. The wavelength of 357 nm is somewhat off the absorbance maximum for the picrate anion; this value was deliberately chosen to attenuate the large absorbance signal obtained at the picrate concentrations needed for this experiment.

Bulk transport through an organic phase as a simple mimic of kinetic transport through a membrane

To evaluate the relative rate at which all-(−)-nonactin and nonactin may likely allow for passive diffusion of ions across a membrane we adapted a bulk organic phase model.³⁵

The basic experimental consists of a system wherein two separate aqueous samples are in contact with one immiscible organic sample allowing for diffusion from one aqueous phase to the other via the organic phase. A relatively simple apparatus was assembled using a one-piece vacuum trap assembly (Chemglass, #CG-4510-03) with an outer diameter of 35 mm and an inner tube diameter of 16 mm. The lower part of the trap was filled with CHCl₃ (35 mL) so that the bottom of the inner trap tube was slightly below the surface of the organic layer. An aqueous Tris buffer (10 mL, 100 mM, pH 8.0) was placed in the outer tube. A solution of potassium picrate and KCl (2.5 mL, 0.25 mM potassium picrate, 100 mM KCl) in Tris buffer (100 mM, pH 8.0) was placed in the inner tube. The test ionophore, either nonactin or all-(−)-nonactin (0.5 mg in 1.0 mL of CHCl₃) was added to the lower organic phase by syringe. The organic phase was mechanically stirred at about 200 rpm using a magnetic stirrer bar. The stirring rate was carefully adjusted so that no ‘spilling’ between the two aqueous phases occurred. The transport of K⁺ from the inner tube to the outer tube, through the organic phase, mediated by the ionophore, was followed by measuring the concentration of the co-transported picrate anion via its absorption at 357 nm.

Molecular modeling

The nonactin structure was based on the X-ray crystal data for the KNCS complex⁸ and the all-(−)-nonactin structure was derived from it by direct manipulation. To obtain reasonable atomic charges we generated a low energy conformation of a cyclic nonactate dimer and obtained a minimum energy conformation at the HF/6–31G* level of theory using GAMESS (2005R2).³⁸ GAMESS was used again to calculate an electrostatic potential grid which was used as input to the RESP charge calculation of the AMBER-7 package.³⁹ Only partial charges on hydrogen atoms of methyl groups were averaged in the charge fitting. Dynamics calculations were done using the AMBER-7 suite of programs³⁹ together with the GAFF force field.⁴⁰ Calculations were performed on the K⁺ complexes, neutralized with one Cl⁻ ion together with 7920 water residues as an explicit solvent in a periodic box of 46.6 × 47.7 × 49.0 Å. A time step of 0.5 fs was used without application of the SHAKE procedure. After 100 ps of simulation at fixed temperature (300 K) and pressure (1 bar) to equilibrate the systems a further 20 ps of simulation was done to provide coordinate data for analysis.