Phenotypic plasticity in juvenile jellyfish medusae facilitates effective animal–fluid interaction

Abstract

Locomotion and feeding in marine animals are intimately linked to the flow dynamics created by specialized body parts. This interaction is of particular importance during ontogeny, when changes in behaviour and scale challenge the organism with shifts in fluid regimes and altered functionality. Previous studies have indicated that Scyphozoan jellyfish ontogeny accommodates the changes in fluid dynamics associated with increasing body dimensions and velocities during development. However, in addition to scale and behaviour that—to a certain degree—underlie the control of the animal, flow dynamics are also dependent on external factors such as temperature. Here, we show phenotypic plasticity in juvenile Aurelia aurita medusae, where morphogenesis is adapted to altered fluid regimes imposed by changes in ambient temperature. In particular, differential proportional growth was found to compensate for temperature-dependent changes in viscous effects, enabling the animal to use adhering water boundary layers as ‘paddles’—and thus economize tissue—at low temperatures, while switching to tissue-dominated propulsion at higher temperatures where the boundary layer thickness is insufficient to serve for paddling. This effect was predicted by a model of animal–fluid interaction and confirmed empirically by flow-field visualization and assays of propulsion efficiency.

1. Introduction

The swimming and feeding performance of marine animals depends on the interaction of fluid flow and body morphology. For example, an array of body appendages such as hairs, cilia or tissue lappets (figure 1a) can serve either as a paddle or as a sieve (Koehl et al. 2001), depending on the ratio of inertial versus viscous fluid forces as expressed by the Reynolds number:

1.1

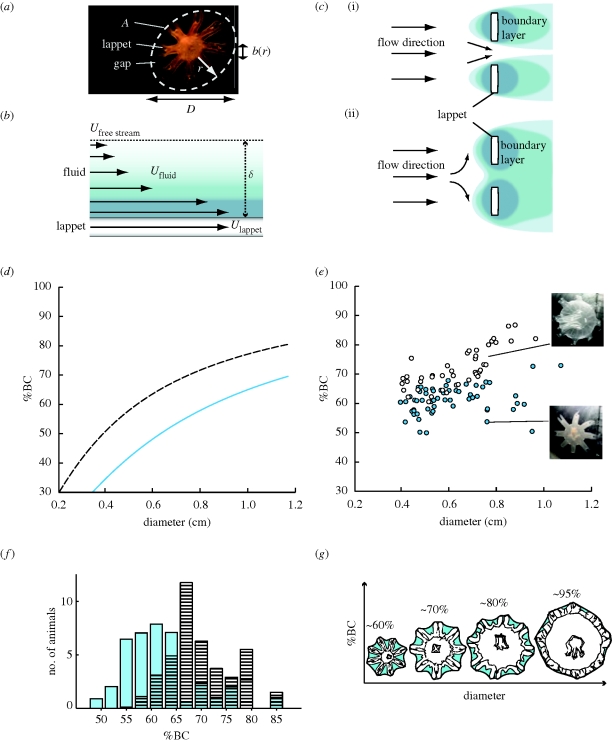
where ν is the kinematic viscosity of water, b is the appendage width and U is the velocity of appendage relative to water. As the appendage is set in motion, the surrounding fluid does not slip with respect to the surface of the appendage. Consequently, a velocity gradient, i.e. boundary layer, forms in the water between the appendage and the free-stream flow (figure 1b). The lower the Re, the thicker becomes this boundary layer of sheared fluid relative to the gaps of the appendage array, eventually overlapping between the neighbouring edges and conferring additional paddle surface. Conversely, at increasing Reynolds numbers, the boundary fluid layer retreats, turning the array into a grate useful for filtering (figure 1c). New functions may thereby arise from unchanged structures simply through a shift in velocity or scale (Koehl 2004), whereas continuous function may be achieved when changes in fluid dynamics owing to scaling effects are compensated by behavioural or morphological responses (Yen 2000). Furthermore, tuning morphogenesis to fluid dynamics may conserve resources as suggested by a recent study on ephyrae, i.e. juvenile scyphozoan medusae (Feitl et al. 2009). In particular, boundary layer overlap allows ephyrae to propel themselves through the water with a lean, star-like formation of lappets instead of employing a full bell. As the animals increase in size, the reduction in boundary layer thickness is balanced by gap-narrowing tissue growth, ensuring complete boundary layer overlap throughout the development. These results indicate that jellyfish ontogeny exploits viscous effects to minimize the costs of tissue maintenance without compromising momentum transfer essential for swimming and feeding.

Figure 1.

(a) Characteristic parameters of ephyra morphology. A, potential bell area; D, diameter; r, radial lappet position; b(r), lappet width at radial position r. (b) Model of boundary layer formation on solid surface. U, velocity. Arrows represent velocities relative to free stream flow. Thickness of boundary layer (δ) denotes distance from solid surface to the point where U_fluid = 0.99 × U_{free stream}. (c) Schematic illustration of the two operation modes of the lappet array with different flow Reynolds numbers: (i) filter mode with no boundary layer overlap (high Re); (ii) paddle mode with complete boundary layer overlap (low Re). Different shades of blue correspond to velocity gradient in boundary layer as in (b). (d) Stokes model of bell continuity (BC) as a function of diameter, with C = 0.8. Blue line, model for 13°C; black dashed line, model for 21°C. (e) Morphometric data of Aurelia aurita. BC is plotted against diameter. Blue circles, G₁₃ ephyrae; white circles, G₂₁ ephyrae. Right: two ephyrae from G₂₁ (top) and G₁₃ (bottom) are depicted to illustrate the differences in morphology. (f) Histogram of BC values of the two temperature groups (n = 41 for each group, equal distribution of diameters). Blue bars, G₁₃ ephyrae; black striped bars, G₂₁ ephyrae. (g) Model of continuous boundary layer overlap at all stages of bell development.

However, given that ephyral development is tuned to scale-dependent changes in Reynolds number, it raises the question as to whether it is capable of adapting to variation in other factors affecting Re, most notably water viscosity, which is strongly dependent on temperature. Such adaptive ‘phenotypic plasticity’, the environmentally sensitive production of alternative phenotypes by the given genotype (DeWitt & Scheiner 2004) would be beneficial for globally distributed scyphozoan jellyfish species like Aurelia aurita, which are subject to significant temperature (and thereby viscosity) variation.

Here, we extend the fluid-dynamical model of ephyral ontogeny proposed by Feitl et al. (2009), in conjunction with experimental measurements of ephyral morphology, fluid dynamics and swimming performance, in order to determine whether jellyfish morphogenesis is plastic in response to temperature conditions, and if so, whether the changes can be considered adaptive by facilitating economic and effective animal–fluid interaction.

2. Material and methods

(a). Animals

Experiments were performed with newly budded Scyphozoan medusae of the species A. aurita obtained from aquaculture (New England Aquarium, Boston, MA, USA). Animals were maintained in artificial sea water (Seachem's Marine Salt, Seachem Laboratories, Madison, GA, USA) gently stirred by aeration. At the onset of the study, the ephyrae were randomly distributed into two groups subsequently kept at water temperatures of 13°C and 21°C, a span that lies comfortably within the range encountered by A. aurita in the wild (Lucas 2001). The two groups will be referred to as G₁₃ and G₂₁ in the following. The animals were fed daily with freshly hatched Artemia salina.

(b). Morphometric analysis

Over the course of development, the eight-armed ephyra transforms into the circular adult medusa. An idealized adult silhouette can be superimposed onto the ephyral body plan by circumscribing the lappets with a circle of diameter D, enclosing the potential bell area A (figure 1a):

2.1

The progress of transformation from ephyral to adult shape was quantified using the so-called bell continuity (BC) index, defined as the percentage of potential bell area comprised of ephyral tissue:

2.2

where G is the total gap area, i.e. the sum of wedge-shaped spaces between adjacent lappets. A BC value close to 100 per cent thus corresponds to the approximate shape of an adult Aurelia medusa.

BC values were determined once every week by measuring diameters and gap areas (ImageJ software; National Institutes of Health, Bethesda, MD, USA). A two-tailed Wilcoxon rank sum test (equivalent to Mann–Whitney U-test) was used to compare median BC values in G₁₃ and G₂₁.

(c). Stokes model

A model of boundary layer formation around ephyral lappets was derived from Stokes' first problem, i.e. the flow over an abruptly started flat plate (Schlichting & Gersten 2000). The model was customized to ephyral morphology to assess the effect of temperature on morphogenesis under the constraint that complete boundary layer overlap be present at each stage of development (Feitl et al. 2009). Briefly, the fluid boundary layer thickness δ at radial position r along the lappet is estimated by,

2.3

where C is a constant of proportionality whose magnitude for flow past flat plates is approximately 1 (Schlichting & Gersten 2000). Re(r) is the lappet Reynolds number defined as:

2.4

with ν_T is the kinematic viscosity of sea water at temperature T; b, lappet width at radial position r; ω_T denotes angular speed of contraction at temperature T. Viscosities ν₁₃ = 1.25 × 10⁻⁶ and ν₂₁ = 1.05 × 10⁻⁶ m² s⁻¹ were determined empirically using a stress rheometer (AR 1000, TA Instruments, New Castle, Delaware, USA). Average angular speeds (swept angle divided by contraction time) were ω₁₃ = 14 and ω₂₁ = 18.5 rad s⁻¹ in both G₁₃ and G₂₁ animals. Note that from equation (2.4), we expect a 25 per cent greater value of δ(r) at 13°C when compared with 21°C, because of the temperature dependence of viscosity and angular speed.

The total boundary layer A_BL is approximately twice the area of the boundary layer integrated over each lappet edge:

2.5

with N = 8, number of lappets.

The constraint of complete boundary layer overlap demands that A_BL > G, and we can express the minimal BC value (equivalent to maximal gap area) fulfilling this condition as a function of diameter (see electronic supplementary materials for details), yielding a family of curves for different temperatures. The shift between the two model functions for T = 21°C and for T = 13°C predicts the difference in bell formation between animals raised at either temperature, under the constraint of complete boundary layer overlap (figure 1d).

(d). Boundary layer visualization

Fluorescein dye was used to visualize fluid boundary layers surrounding swimming ephyrae at different water temperatures (cf. electronic supplementary material). For this, dye/sea water solution was injected in the immediate proximity of a freely swimming animal and highlighted using side illumination.

(e). Swimming performance

Swimming performance was defined as the average distance travelled per full stroke (90° sweep), measured in units of body length/pulse. Measurements were obtained from movie recordings of freely swimming ephyrae at different ambient water temperatures (Sony HDR-SR12 Camcorder, 30 fps). Temperature changes were induced gradually (max. 0.2°C min⁻¹) to avoid shock responses. A two-tailed Wilcoxon rank sum test was used to compare median swimming performances in G₁₃ and G₂₁ animals.

3. Results

(a). Effects of temperature on morphogenesis and behaviour

BC values in G₁₃ jellyfish were significantly lower when compared with animals of equal diameter distribution grown at 21°C (G₁₃: median BC = 62, G₂₁: median BC = 70, Wilcoxon rank sum = 1232, n₁ = n₂ = 41, z-statistic = −4.3495, p = 1.4 × 10⁻⁵ two-tailed; figure 1f). G₁₃ ephyrae increased in body diameter at a two- to threefold lower rate than G₂₁ ephyrae. No obvious behavioural differences were observed in G₁₃ versus G₂₁ animals. In particular, pulsation frequencies as a measure of activity were comparable in both groups (ca 1.6 strokes s⁻¹).

(b). Fluid boundary layer overlap

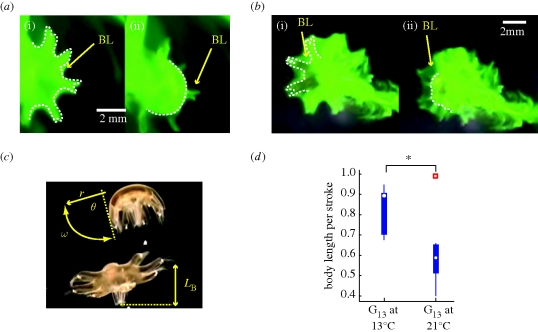
Consistent with Feitl et al. (2009), the relation of BC value to body diameter measured in G₁₃ and G₂₁ ephyrae approximately followed the shape of the Stokes model curves. Note that we do not expect quantitative agreement between experimental results and theoretical forecasts because of the free scaling parameter C; however, we do observe qualitative agreement. In particular, the distribution of (D, BC) measurements from G₂₁ ephyrae was shifted upward when compared with G₁₃ ephyrae, as predicted by the two model curves (figure 1d,e). This suggests that, as G₂₁ animals reduce gap sizes when compared with G₁₃ animals, they are able to compensate for the diminished boundary layer formation at 21°C and thereby avoid operating in the (propulsion-inefficient) sieving mode. Consistent with this assumption, G₁₃ animals swimming at 21°C indeed failed to develop fluid-webbing (figure 2a), whereas the same animals assayed at 13°C showed complete boundary layer overlap (figure 2b).

Figure 2.

Dye visualization of boundary layer during powerstroke. Dotted line indicates outline of animal body. BL, boundary layer. (a) Sieve-mode: G₁₃ ephyra swimming at 21°C water temperature. (i) Start of powerstroke, bell is fully relaxed, (ii) end of powerstroke, bell is fully contracted. Note that the thin boundary layer outlines the body but fails to connect between lappets. (b) Paddle-mode: G₁₃ ephyra swimming at 13°C water temperature. (i) Start of powerstroke, bell is fully relaxed, (ii) end of powerstroke, bell is fully contracted. Note the delay in boundary layer motion when compared with body motion, visualizing the velocity gradient at the fluid–solid interface. (c) Parameters of ephyra propulsion. r, Radial position along lappet; θ, swept angle; ω, angular velocity; L_B, body length. (d) Effect of ambient water temperature on propulsion efficiency of G₁₃ ephyrae. Box plots show body length travelled per stroke at 13°C (n = 7) and at 21°C (n = 7). White marks correspond to median, the edges of the box are 25th and 75th percentiles, whiskers indicate extreme data points not considered outliers. Outliers are plotted as individual squares. Asterisk represents significant difference in median values.

(c). Functional consequences

G₁₃ animals showed significantly higher stroke efficiency at 13°C than at 21°C water temperature (median performances of 0.88 versus 0.58 body lengths per stroke, Wilcoxon rank sum = 63, n₁ = n₂ = 7 (includes apparent outliers), p = 0.02 two-tailed; figure 2c,d). This result is consistent with the Stokes model and the dye visualization assay, suggesting a paddle mode of the G₁₃ morphology at a lower temperature when compared with a sieving or ‘water-treading’ action at the higher temperature (see electronic supplementary material for movies).

4. Discussion

Here we demonstrate that phenotypic plasticity in Scyphozoan ephyrae tunes ontogeny to temperature-dependent changes in fluid flow, facilitating efficient animal–fluid interactions and conserving resources during development. In particular, morphology was found to dynamically exploit viscous effects by recruiting adhering boundary fluid layers as additional paddles throughout development. Crucially, the animals do not depend on the presence of a particular boundary layer thickness but are able to compensate for temperature-dependent thinning of the fluid-webbing by tissue growth. Thereby, tissue formation is economized when possible, i.e. without compromising vital functions such as swimming performance. Such ‘smart’ economy can be crucial to survival in the ephyral stage, a bottleneck in jellyfish population dynamics (Haruto & Chiharu 2005) and may improve survivorship in jellyfish populations subjected to temperature variation as induced, for example, by climate and ocean circulation changes.

We acknowledge, however, that the correlation between temperature-dependent changes in morphology and Reynolds number need not be an evolutionary adaptation, even though the fluid dynamic effects we describe in the paper appear beneficial to the animal. Temperature affects many biological processes including development, and the differences in morphologies might be a side effect, not an adaptation specifically to changes in fluid regimes. Changing viscosity by chemical means does not seem to induce the phenotypic plasticity reported here, and further experiments are underway to confirm this finding (J. C. Nawroth & J. O. Dabiri 2010, unpublished data). This, however, does not rule out the possibility that temperature serves as a proxy for sensing boundary layer thickness during development, given that under natural conditions the animals would rarely encounter changes in viscosity and/or contraction speed brought upon by other means than temperature variation. Similarly, in addition to shedding light on fluid dynamic effects, the swimming performance assay might be sensitive to metabolic responses to the short-term temperature changes employed in this study. Along these lines, our next experiments will focus on isolating the acute physiological effects of temperature from its role on boundary layer thickness and animal–fluid interaction. In particular, we plan to investigate the propulsion efficiency of G₂₁ animals at 21°C water temperature when compared with G₁₃ animals in water of 21°C with artificially raised viscosity. Assuming that sufficient boundary layer thickness is the decisive factor in propulsion efficiency, and not exposure to a familiar ambient temperature, we expect both groups to show similar performances. In the long term, it would be interesting to elucidate the signalling pathways underlying the link between temperature, fluid forces and ontogenetic programmes, given the emerging role of gelatinous species as model systems for regeneration and development (e.g. Hoffmeister-Ullerich 2007).