Predicting the effects of temperature on food web connectance

Abstract

Few models concern how environmental variables such as temperature affect community structure. Here, we develop a model of how temperature affects food web connectance, a powerful driver of population dynamics and community structure. We use the Arrhenius equation to add temperature dependence of foraging traits to an existing model of food web structure. The model predicts potentially large temperature effects on connectance. Temperature-sensitive food webs exhibit slopes of up to 0.01 units of connectance per 1°C change in temperature. This corresponds to changes in diet breadth of one resource item per 2°C (assuming a food web containing 50 species). Less sensitive food webs exhibit slopes down to 0.0005, which corresponds to about one resource item per 40°C. Relative sizes of the activation energies of attack rate and handling time determine whether warming increases or decreases connectance. Differences in temperature sensitivity are explained by differences between empirical food webs in the body size distributions of organisms. We conclude that models of temperature effects on community structure and dynamics urgently require considerable development, and also more and better empirical data to parameterize and test them.

1. Introduction

A food web is a network of feeding interactions among the species in a community. If each species eats many other species, the food web contains many links and has high connectance. If each species eats few others, the food web has few links and low connectance. Whether food webs have many or few links (L), relative to the number of possible links (P), turns out to be very important. Connectance (L/P) appears to be one of the primary determinants of population stability and community structure.

MacArthur (1955) suggested that a generalist consumer, i.e. one with a large number of links to resources, would fluctuate in abundance less than a specialist. He reasoned that the multiple pathways for gaining energy available to a generalist make any one pathway less influential if lost. Organisms ranging from protists to woodpeckers provide support for this hypothesis (Koenig & Haydock 1999; Petchey 2000). High connectance may, however, contribute to instability of population dynamics (Gardner & Ashby 1970; May 1972). Dynamic models of food webs show that more connections between species lead to a lower chance of obtaining a feasible community (all populations with positive population size) and slower recovery from small perturbations (Saunders & Bazin 1975). The consequences of larger perturbations, such as extinction, also depend on the number of connections among species, with more connected species being less likely to remain stable after a deletion. The loss of stability following an extinction can lead to a cascade of secondary extinctions, the extent of which is greatly influenced by connectance (Pimm 1980; Borrvall et al. 2000; Dunne et al. 2002).

More recent work has demonstrated that food webs with random or uniform population traits (e.g. respiration, consumption, growth) are unstable, whereas food webs with a body-size structure and population traits that follow allometric scaling relationships are highly stable (Brose et al. 2006b; Brose 2008). This body-size structure is characterized by consumers that are at least 10 times larger than their resources and allometric degree distributions (i.e. the number of consumers and resources of a species decrease and increase, respectively, with its body mass) (Otto et al. 2007). Interestingly, accounting for this body-size structure yields a positive relationship between connectance and food web stability (Rall et al. 2008), thus matching earlier concepts (MacArthur 1955).

Connectance also plays a large role in determining the types of structures that real food webs display (Vermaat et al. 2009). Other properties of communities, such as food chain length, are strongly influenced by connectance. Indeed, some models of food webs use connectance (and species richness) as an input parameter (Cohen et al. 1990; Williams & Martinez 2000; Cattin et al. 2004; Stouffer et al. 2005). Its pivotal role for population dynamics and community structure has led researchers to argue for the importance of understanding the determinants of connectance, and how environmental variables affect connectance (Warren 1990, 1996).

Environmental temperature is one such variable. Observed and predicted changes in global and regional temperatures make understanding its effects on ecological communities a priority. Temperature difference may also contribute towards latitudinal and elevational changes in diversity and community structure. Reasonably widely accepted theories and empirical data link temperature and biological variables such as metabolic rate (Clarke 1991; Gillooly et al. 2001; Price & Sowers 2004; Savage et al. 2004; Apple et al. 2006), swimming speed (Olla & Studholme 1971; Winet 1976; Podolsky & Emlet 1993; Wilson et al. 2000; Wilson 2005), feeding rate (Bolton & Havenhand 1998; Yee & Murray 2004), growth rate (Savage et al. 2004; Rose & Caron 2007), developmental rate (Gillooly et al. 2002), body size (Atkinson et al. 2003) and phenology (Arft et al. 1999; Wagner & Benndorf 2007). The same is true for abundances (Rae & Vincent 1998; Strecker et al. 2004; Baulch et al. 2005), population dynamics (Yodzis & Innes 1992; Beisner et al. 1996; Vasseur & McCann 2005), ecosystem carbon flux and storage (Allen et al. 2005; Anderson et al. 2006) and ecosystem metabolism (Petchey et al. 1999; Baulch et al. 2005). Indeed, after accounting for size dependence, temperature explains the largest amount of variation in biological rates (Peters 1983) (though see for example, Makarieva et al. 2008; Johnson et al. 2009).

Less well researched are the effects of temperature on aspects of community structure, such as the distribution of biomass across trophic levels, the distribution of diversity across trophic levels, or the extent and distribution of specialism and generalism across species. There are exceptions: evidence and predictions exist of temperature effects on the strength of interspecific interactions (Sanford 1999; Vasseur & McCann 2005; Rall et al. in press), biomass and production (Petchey et al. 1999; Moss et al. 2003; Brown et al. 2004; Meehan 2006; Jennings et al. 2008) and food chain length (Arim et al. 2007). However, few models exist that are capable of making predictions about the effects of temperature on community structure, and we are unaware of models capable of predicting how connectance changes with temperature. Given the importance of connectance, this seems to be a serious gap in ecological theory.

This article has two aims: (i) to extend an existing model of food web structure to be capable of making predictions about the relationship between environmental temperature and connectance; (ii) to understand what in the model and data determine the predicted sensitivity of connectance to temperature change. A test of the predictions is left for when suitable data about food web structure across a temperature gradient are available.

2. Material and methods

(a). Modelling food web connectance

In order to make quantitative predictions about the effects of temperature on connectance we need (i) a quantitative model that can predict connectance and (ii) a route for temperature to drive the parameters and or variables of this model. We are aware of only one modelling framework that meets these two criteria: the diet breadth model (DBM) (Beckerman et al. 2006) and its size-based variant (the allometric diet breadth model, ADBM) (Petchey et al. 2008). The remainder of this section introduces the DBM and ADBM.

Connectance results from the determinants of the degree of specialism or generalism (i.e. diet breadth) of a consumer (Warren 1994). Diet breadth can be predicted by models of foraging behaviour, such as the contingency model of optimal foraging (Emlen 1996; MacArthur & Pianka 1996). In this model, diet breadth (specialism/generalism) is determined by the foraging behaviour of consumers (attack rates A_ij and handling times H_ij), the energetic value of resources (ɛ_i) and the density (N_i) of resource items in the environment. (Throughout i denotes the resource and j the consumer.) In the contingency model, foraging consumers spend their time either searching for resource items or consuming a resource item (Emlen 1966; MacArthur & Pianka 1966). Given this, a consumer's rate of energy intake depends on which of the available resource types it consumes, and there is a subset of the available resource types (species) that, if consumed, maximize the rate of energy intake (RoEI). This subset can be found for consumer j by ranking resource types by decreasing profitability (ɛ_i/H_ij) and finding the diet breadth (d) that maximizes the overall rate of energy intake (ORoEI).

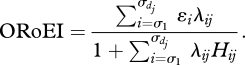2.1

Here, d_j is the number of resource items in the consumer's diet (i.e. diet breadth), σ is the permutation that orders the prey according to decreasing profitability, λ_ij is the encounter rate of consumer j on resource i, ɛ_i is the energetic value of resource i and H_ij is the handling time of resource i for consumer j. Encounter rate is the product of density and attack rate: λ_ij = A_ijN_i. The value of d_j that maximizes the value of this function is the predicted diet breadth of the species. Connectance is the sum of the diet breadths of all consumers ∑_j=1^S d_j divided by the number of possible links P. Here, we assume that all links, including cannibilistic ones, are possible, hence P = S², where S is the number of species in the food web.

Connectance in this model, therefore, results from diet breadth, which itself results from encounter rates and handling times. More specifically, diet breadth is determined (all else being equal) by the product of the mean handling time and mean encounter rate, calculated over all resources available to a consumer (hereafter 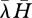) (Beckerman et al. 2006; figure 1). This prediction was known previously, for example see Begon et al. (1990, p. 307, 2nd edn). As they put it, ‘searchers should be generalists’ and ‘handlers should be specialists’. The term ‘searchers’ refers to consumers that spend little time handling and a long time searching (low 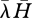). The term ‘handlers’ refers to consumers that spend much time handling and little time searching (high 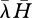). When parameterised with data about encounter rates and handling times gathered from 121 empirical studies, the model (abbreviated as DBM) predicts values of diet breadth and connectance that are not significantly different from those observed in some real food webs (Beckerman et al. 2006).

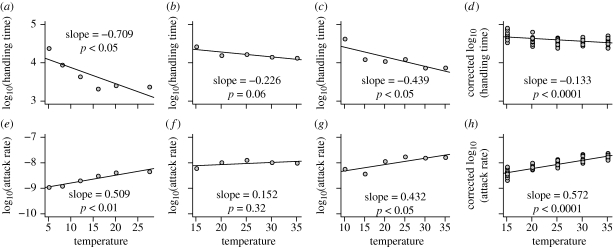
Figure 1.

(a–d) Empirical relationships between temperature and handling times and (e–h) attack rate and temperature from four published studies. The data are plotted on log₁₀ y-axis for clarity, while statistics and the slopes are calculated on natural log data with models equivalent to those in equations (2.2) and (2.4). (a,e) Thompson (1978), (b,f) Zhang et al. (1998), (c,g) Zhang et al. (1999) and (d,h) Xia et al. (2003). In (d,h) the y-axis variables are corrected to account for variation in prey and predator size among the data. In each plot the activation energy is given as the slope and the significance by the p-value.

Foraging traits such as encounter rates, handling times and energetic value can be related to body sizes of resources and consumers. For example, larger resources contain more energy, but take longer to consume and digest. Smaller resources are more abundant (higher encounter rate), but may be less visible and so attract lower attack rates (lower encounter rate) than larger resources. These size dependencies create covariances between the foraging traits, and these covariances can result in realistic predictions of the pattern of interactions among species. When coupled with the DBM, these allometries' results give what has been abbreviated as ADBM, which can correctly predict up to 65 per cent of the links in a real food web (Petchey et al. 2008).

(b). Temperature scaling of foraging traits

The Arrhenius equation is often used to describe the scaling of biological rates with temperature (Brown et al. 2004). Rates of biochemical reactions scale with temperature according e^{− E/kT} where E is the activation energy, k is the Boltzmann's constant (in units of electron Volts eV), and T is temperature in Kelvin. It is the activation energy that determines how metabolism scales with temperature, and values range from 0.47 to 0.74 eV (Gillooly et al. 2001; Vasseur & McCann 2005). Relationships between temperature and metabolic rate hold remarkably well across taxa including microbes, ectotherms, endotherms and plants (Gillooly et al. 2001).

The activation energy of foraging traits are required to predict how community-level properties, such as predator–prey dynamics or community structure, respond to temperature change (Brown et al. 2004; Vasseur & McCann 2005). There has been relatively little work, however, on the temperature dependence of these traits, and even less about the mechanistic bases for any dependencies. Rather than attempting to derive the activation energies from first principles, we examined empirical relationships in the literature. To a large extent therefore, we are using the Arrhenius equation as a phenomenological model, rather than for its clear mechanistic basis.

Brown et al. (2004) lists estimates of the activation energy of parasitism rate, attack rate, feeding rate and grazing rate (0.56–0.81 eV). Activation energies of ingestion rates can also be estimated from temperature dependence of digestion velocity, gastric evacuation and flow rates in burrows (0.46–0.77 eV) (Vasseur & McCann 2005). Aquatic capture rates are temperature dependent: e.g. a 34–67% reduction in polychaete ingestion rate has been observed, associated with a 10°C reduction in temperature (Bolton & Havenhand 1998, 2005; Loiterton et al. 2004). This corresponds approximately to an activation energy of 0.50. Similarly, grazing rate of a bacterivore increased twofold from 10–15°C (Delaney 2003), an activation energy of about 0.97 eV.

At least four published datasets contain empirical data suitable for estimating the activation energies of handling time and attack rates. Each comprises several functional responses, conducted over a range of temperatures and in one study, also with different sizes of predators and prey (figure 1). Thompson (1978) recorded functional responses of dragonfly larvae feeding on Daphnia at six temperatures, from 5–30°C. Zhang et al. (1998) recorded functional responses of large mites eating smaller mites at five temperatures, from 15 to 30°C. Zhang et al. (1999) recorded functional responses of large mites eating small mites at six temperatures, from 15 to 35°C. Xia et al. (2003) recorded functional responses of ladybird larvae feeding on aphids at six temperature (5–30°C), and also prey and predator sizes. We estimated the activation energies by fitting linearized versions of equations (2.2) and (2.4) (see below) to the attack rates and handling times of the functional responses. Activation energy of handling time varied from −0.13 (p < 0.0001) to −0.71 (p < 0.05), while that of the attack rate varied from 0.15 (n.s.) to 0.57 (p < 0.0001) (figure 1). Note that activation energies technically cannot be negative. Here, negative activation energies of handling times result from calculations based on times rather than rates. Though technically incorrect, we have chosen to retain this negative sign owing to the use of handling times in the standard formulation of the contingency model. This choice is entirely presentational and has no effect on any results.

(c). Adding temperature dependence to the ADBM

To extend the ADBM (Petchey et al. 2008) to include temperature dependence of foraging traits we added a Boltzmann factor to the size-scaling of attack rates and handling times. We assume that handling time is a power function of prey size and predator size, and that temperature dependence follows the Arrhenius equation

2.2

This type of relationship was termed a power handling time function (Petchey et al. 2008). The activation energy of handling times E_H determines how handling times scale with temperature. Mass scaling is determined by the exponents h_i and h_j. The parameters and variables of this and the following equations are described in table 1.

Table 1.

Parameters and variables in the handling time and attack rate scaling functions

parameter or variable	description
Hij	handling time for prey i and predator j (s)
hT0	normalization constant for handling time at temperature T0
mi	mass of a prey individual of type i (g)
hi	slope of prey mass dependence of handling time
mj	mass of a predator individual of type j (g)
hj	slope of predator mass dependence of handling time
EH	activation energy of handling time (eV)
b	critical mass ratio in ratio handling time function (equation 2.3)
T	environmental temperature (K)
T0	temperature offset (293.15 K) for regression
k	Boltzmann contant (eV)
Aij	attack rate or predator j on prey i (m2 s−1)
aT0	normalisation constant for attack rate at temperature T0
ai	slope of prey mass dependence of attack rate
aj	slope of predator mass dependence of attack rate
EA	activation energy of attack rate (eV)

Another handling time scaling relationship was termed the ratio handling time function, and was found to better predict food web structure via the ADBM (Petchey et al. 2008). Here handling time is based on a ratio of prey to predator mass:

2.3

Or if m_i/m_j ≥ b we set H_ij = ∞.

Attack rate is a function of prey size, predator size and temperature:

2.4

The activation energy of attack rates E_A determines how attack rates scale with temperature. Mass scaling is determined by the exponents a_i and a_j.

(d). Investigating the temperature–connectance relationship

We wish to know how the model parameters control the relationship between temperature and predicted food web connectance. Since analytical solutions of the model are not possible, we used exploration first of the importance of the two activation energies (one for handling time and one for attack rate). The activation energy of handling time was explored from −0.2 to −0.8 eV; values were negative so that handling times decreased as temperature increased. The activation energy of attack rates was explored from 0.2 to 0.8 eV; values were positive to make attack rates increase as temperature increases. Values of all other parameters were taken from Petchey et al. (2008) for the eight best predicted food webs (all greater than 40% links predicted correctly), including the use of body size to calculate density (N_i) and energy content (ɛ_i) of resources. This gave eight different combinations of parameters across which to explore the effects of activation energies. It soon became clear that parameters other than the two activation energies were important for the relationship between temperature and connectance. Consequently, we systematically explored effects of other parameters and variables on the temperature–connectance relationship. The details of this exploration should not be required to understand the generality of the results we found.

3. Results

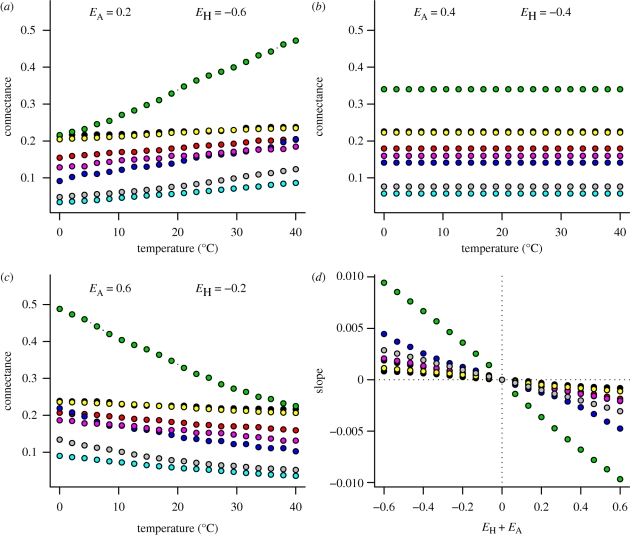
Whether temperature has a positive or negative relationship with connectance depends only on the relative size of the two activation energies (figures 2 and 3). When the activation energy of attack rate is lower (in magnitude) than the activation of handling time, warming causes increases in connectance (figures 2a and 3a). This occurs because in warmer environments consumers spend relatively more time searching and less time handling, and therefore generalism and connectance increases. If the two activation energies are equal in magnitude, warming has no effect on connectance (figures 2b and 3b). Here, the relative amount of time spent handling and searching is unaffected by temperature. Connectance decreases with warming if the activation energy of attack rate is larger in magnitude than that of handling time (figures 2c and 3c). This occurs because in warmer environments consumers spend relatively more time handling and less time searching, they specialize more and connectance is lower. The generality of this result is shown for many relative values of activation energies, for both the power and ratio handling time functions, and for all of the eight modelled food webs (figures 2d and 3d).

Figure 2.

Effects of temperature on food web connectance for different values of activation energies of attack rates (E_A) and handling times (E_H), using the power handling time function. Colours refer to different sets of parameter values that correspond to models fitted to eight food webs in Petchey et al. (2008). In (d) the x-axis represents the imbalance between effects of temperature on attack rates and handling times; the y-axis represents the slope of the temperature–connectance relationship. Black, Benguela Pelagic; red, Broadstone stream; green, Coachella; dark blue, EcoWEB41; light blue, Mill stream; pink, Sierra lakes; yellow, Small Reef; grey, Tuesday lake.

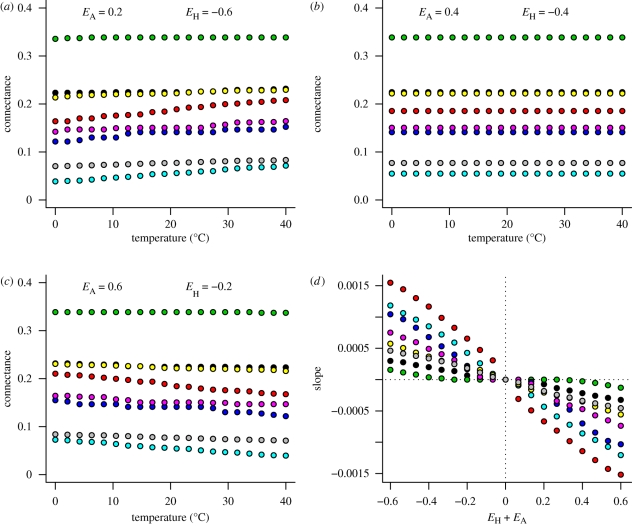
Figure 3.

Effects of temperature on food web connectance for different values of activation energies of attack rates (E_A) and handling times (E_H), using the ratio handling time function. Colours refer to different sets of parameter values that correspond to models fitted to eight food webs in Petchey et al. (2008). In (d) the x-axis represents the imbalance between effects of temperature on attack rates and handling times; the y-axis represents the slope of the temperature–connectance relationship. Black, Benguela Pelagic; red, Broadstone stream; green, Coachella; dark blue, EcoWEB41; light blue, Mill stream; pink, Sierra lakes; yellow, Small Reef; grey, Tuesday lake.

The sensitivity of connectance to temperature change for a particular food web was determined by the relative size of the two activation energies (figures 2d and 3d). Larger imbalances in activation energies (e.g. E_H = −0.2 and E_A = 0.8) resulted in greater sensitivity to temperature change; smaller imbalances (e.g. E_H = −0.3 and E_A = 0.4) resulted in lower sensitivity (figures 2 and 3). The relative magnitude of E_H and E_A controls sensitivity for the following reason, and recall that diet breadth and connectance are determined in large part by the product λH. When E_H = −0.2 and E_A = 0.8, the change in λH is about +1.5 log₁₀ units. When E_H = −0.8 and E_A = 0.2, the change in λH is about −1.5 log₁₀ units. Activation energies that are more similar in magnitude cause smaller changes in λH and, therefore, smaller changes in connectance. That is, the effect of temperature on λH is directly controlled by the relative difference between E_H and E_A (equations (2.2–2.4)).

Among the eight food webs the sensitivity of connectance to temperature change, measured as change in connectance per 1°C change in temperature, varies greatly (even when values of E_A and E_H are constant) (figure 2d). For example, the Coachella Valley model is sensitive (up to 0.01 connectance units per 1°C), whereas the Benguela pelagic model is insensitive (up to  0.001 connectance units per 1°C) (figure 2d). Furthermore, (i) the sensitivities predicted by the ratio ADBM (figure 3d) are generally lower than those predicted by the power ADBM (figure 2d) and (ii) the ranking of the eight food webs by sensitivity differs between the power and ratio ADBM (compare the vertical ordering of colours between figures 2d and 3d). For example, the Broadstone food web is predicted as the most sensitive by the ratio ADBM, but is one of the least sensitive according to the power ADBM.

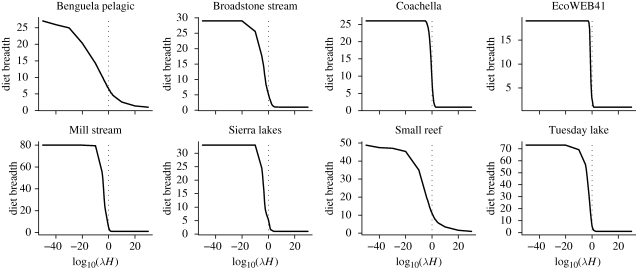
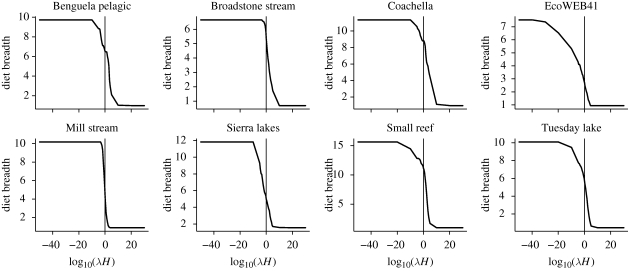
Within a model type (power or ratio) these differences in sensitivity are reflected in differences in the relationship between diet breadth and λH (figure 4). At 20°C (0 on the x-axis in figure 4) some webs have a very steep relationship between diet breadth and λH, whereas others show shallower slopes. The steepness of the slopes in figure 4 correspond with the sensitivities shown in figure 2d. That is, the models of different real webs exhibit different sensitivities to changes in handling times and encounter rates. The same is true of the ratio ADBM (compare figures 5 and 3d).

Figure 4.

Sensitivity of diet breadth in eight food webs to changes in the product of attack rates and handling times (power handling time function). The x-axis is an arbitrary multiplier applied to a_T0 to create variation in λH. The value of λH equivalent to 20°C is shown at x value of zero (vertical dotted line). The gradient of the solid line where it crosses the dotted line is the sensitivity of diet breadth to temperature change at 20°C. These gradients match the relative sensitivities shown in figure 2d.

Figure 5.

Sensitivity of diet breadth in eight food webs to changes in the product of attack rates and handling times (ratio handling time function). The x-axis is an arbitrary multiplier applied to a_T0 to create variation in λH. The value of λH equivalent to 20°C is shown at x value of zero (vertical dotted line). The gradient of the solid line where it crosses the dotted line is the sensitivity of diet breadth to temperature change at 20°C. These gradients match the relative sensitivities shown in figure 3d.

What causes these differences in sensitivity? First, recall that whether a consumer includes the ith most profitable resource in its diet depends on whether the profitability of this resource (P_i = ɛ_i/H_i) is larger or smaller than the overall profitability (P_{1 to i−1}) of including all of the i−1 most profitable resources (Emlen 1966; MacArthur & Pianka 1966; Begon et al. 1990). If P_i and P_{1 to i−1} are very similar to each other, it will take only small changes in attack rates or handling times to switch their relative values, with the result that the ith resources is in or out of the diet. Larger differences between P_i and P_{1 to i−1} mean that larger changes in attack rates of handling times are required to switch their relative size. In the ADBM, larger differences in resource mass translate directly into larger differences between P_i and P_{1 to i−1}.

For a simpler but less accurate explanation, consider a species that consumes (for some reason) resources that are larger than x grams and smaller than y grams. If the diet range changes (for some reason) to have an upper limit of z grams, the change in the number of resource items in the diet is altered by the number of items that are between y and z grams. Clearly it is the distribution of resource sizes that determines this number.

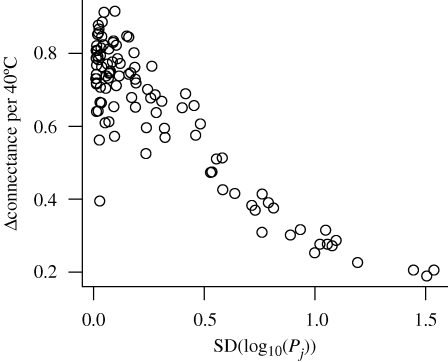
To confirm this reasoning, we manipulated the similarity between species' masses by drawing masses from log normal distributions with different standard deviation. Model food webs that were constructed from mass distributions that resulted in small differences between P_i and P_{1 to i−1} (mass distributions with a low standard deviation) were on average sensitive to changes in λH (figure 6). In contrast, mass distributions that resulted in larger differences between P_i and P_{1 to i−1} were relatively insensitive to changes in λH.

Figure 6.

Sensitivity of diet breadth depends on the magnitude of differences in profitability. Sensitivity is measured as change in connectance (Δconnectance) per 40°C. Differences in profitability are measured as the standard deviation of log₁₀ profitabilities.

4. Discussion

Temperature change could have large effects on connectance. We predicted temperature-sensitive food webs exhibiting slopes of up to 0.01 units of connectance per 1°C change in temperature. This corresponds to changes in diet breadth of one resource item per 2°C (assuming a food web containing 50 species). The less sensitive food webs exhibited slopes down to 0.0005, which corresponds to about one resource item per 40°C. Dynamical food web analyses suggest that these changes in connectance can cause substantial variation in population stability and species persistence depending on the body-size structure of the communities (Rall et al. 2008). The importance of connectance for ecological structure and dynamics makes improving and testing these predictions essential for developing a better understanding of how temperature change will affect populations, communities and ecosystems.

Whether warming increases or decreases connectance in our model depends only on the relative sizes of the activation energies of attack rate and handling times (figures 2 and 3). There is an enormous amount of available data regarding the scaling of metabolic and other vital rates with body size and temperature. However, there is a dearth of information about the temperature scaling of foraging traits, such as handling times, attack rates and maximum ingestion rates. We have no idea, for example, if activation energies of attack rates and handling times differ greatly between taxa. This is plausible, since attack rates and handling times have behavioural as well as biochemical components. This appears to represent a sizeable gap in ecological knowledge, one that limits progress about how temperature change will affect interspecific interactions. The limited empirical data make it difficult to give an empirically based prediction about even whether connectance will decrease or increase as a result of warming. Similarly, investigating how variation in activation energies among taxa affect model prediction would be very interesting: one could imagine that different taxa may become more or less connected. Such predictions would, however, at present have no guidance from empirical studies. Recent theoretical developments, including the one described above, urgently counsel for more and better empirical data to parameterize them, and require critical testing.

The sensitivity of connectance to temperature change differs greatly between our models of eight real food webs. This is a result of the differences between models in their sensitivity to changes in encounter rates and handling times (figures 4 and 5). These differences are largely determined by the mass distribution of the resource items (figure 6). More similar masses result in a more sensitive model food web, whereas greater differences between masses result in food webs less sensitive to changes in attack rates and handling times. This might imply that the structure of terrestrial food webs, in which species are more equally sized than in aquatic food webs (Brose et al. 2006a), could be more sensitive to environmental warming. This finding represents a link between the body size distributions of organisms and the sensitivity of food web structure to temperature change. Many types of environmental drivers (e.g. enrichment, habitat simplification, exploitation) can affect encounter rates and/or handling times, therefore this link may be used to make predictions about the sensitivity of the food web structure to other aspects of environmental change.

We know of no empirical data appropriate to test these predictions. Datasets of changes in diet breadth or connectance with changes in temperature would provide a first test. Such datasets could result from observation of ‘natural experiments’, for example, ecosystems that are in close proximity but that differ in temperature. Tests could also involve food web data across a latitudinal or elevational temperature gradient with few confounding factors (the eight food webs here are too distinct and environments too different for a meaningful analysis of this kind). If observations included individual diets collected by gut content analysis, as well as body sizes of consumers and their resources, one could look for differences in diet breadth and connectance across the temperature gradient. Attributing any observed relationships between temperature and diet breadth to a particular mechanism would require additional measurement and probably experimentation. Required would be measurements of activation energies of handling times and foraging traits, abundances of organisms in the environment and changes in body size along the temperature gradient. Manipulative experiments would be required to unambiguously attribute changes in diet breadth and connectance to changes in temperature, otherwise factors confounding the natural temperature gradient could not be ruled out.

Predictions here are made by modelling one general pathway of temperature effect on community structure: effects of temperature on connectance via changes in foraging rates. It seems likely that other pathways, such as effects of temperature on energy requirements, growth rates, death rates, dispersal and body sizes, will probably also be important. In addition, changes in vital and foraging rates could affect species' abundances, densities and dynamics (Vasseur & McCann 2005), as well as the trophic structure of communities (Arim et al. 2007). The contingency model makes no predictions about how changes in energy requirements of consumers will affect their diets. Changes in population density affect encounter rates, hence temperature effects on local population sizes are likely to have identical effects on connectance as the temperature effects on attack rates detailed above. Despite the importance of predicting the ecological consequences of temperature change, and with some noteable exceptions (Brown et al. 2004; Vasseur & McCann 2005; Meehan 2006; Arim et al. 2007; Rall et al. in press), a great remaining challenge for community ecology is to produce general models of mechanistic effects of temperature change on interspecific interactions. Only with these can we plan for how biological communities and ecosystems will respond to temperature change. The model presented above represents a new piece in the theoretical jigsaw of how temperature change can influence ecological communities.

5. Conclusions

The model presented in this article represents a first attempt at understanding how food web connectance might be expected to change as global and regional temperatures rise. It predicts that the nature of temperature effects will depend on the relative activation energies of attack rates and handling times. In addition, body size distributions play a critical role in determining the strength of predicted effects of temperature on connectance. The model remains untested, assumes a potentially implausible universal activation energy for foraging rates and does not include some mechanisms by which temperature could affect community structure. This is largely owing to the limited availability of empirical data about the temperature dependence of foraging rates. Model development and testing are essential, as are efforts to document and analyse how temperature affects foraging.