Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2010 Mar 17;277(1691):2185–2191. doi: 10.1098/rspb.2009.2344

Local community size mediates ecological drift and competition in metacommunities

John L Orrock 1,*, James I Watling 1
PMCID: PMC2880146  PMID: 20236983

Abstract

The outcome of competitive interactions is likely to be influenced by both competitive dominance (i.e. niche-based dynamics) and ecological drift (i.e. neutral dynamics governed by demographic stochasticity). However, spatial models of competition rarely consider the joint operation of these two processes. We develop a model based on the original competition-colonization trade-off model that incorporates niche and neutral processes and several realistic facets of ecological dynamics: it allows local competition (i.e. competition within a patch) to occur within communities of a finite size, it allows competitors to vary in the degree of competitive asymmetry, and it includes the role of local migration (i.e. propagule pressure). The model highlights the role of community size, i.e. the number of competitors in the local community, in mediating the relative importance of stochastic and deterministic forces. In metacommunities where local communities are small, ecological drift is substantial enough that strong competitors become effectively neutral, creating abrupt changes in the outcome of competition not predicted by the standard competition-colonization trade-off. Importantly, the model illustrates that, even when other aspects of species interactions (e.g. migration ability, competitive ability) are unchanged, local community size can alter the dynamics of metacommunity persistence. Our work demonstrates that activities which reduce the size of local communities, such as habitat destruction and degradation, effectively compound the extinction debt.

Keywords: community size, competition, metacommunity, neutral, niche, stochasticity

1. Introduction

In the metapopulation and metacommunity paradigm, competitive interactions occur within patches of habitat among members of the local community, and dispersal links the dynamics of habitat patches (Hanski & Gilpin 1997; Klausmeier & Tilman 2002; Amarasekare et al. 2004; Mouquet et al. 2005). Although the forces shaping the outcome of competitive interactions are unlikely to be entirely deterministic (Tilman 2004; Gravel et al. 2006; Adler et al. 2007; Cadotte 2007; Chase 2007; Adler & Drake 2008; Chase et al. 2009; Ellwood et al. 2009), models of spatial competition often treat the outcome of local competition in a deterministic way, assuming that a superior competitor always achieves victory within a local community, and that local communities are sufficiently large and the rate of competitive exclusion is sufficiently rapid that the effect of demographic stochasticity (i.e. ecological drift) can be ignored (reviewed in Klausmeier & Tilman 2002; Amarasekare et al. 2004; Mouquet et al. 2005). As such, introducing dynamics owing to ecological drift is important for developing a more robust theory of metacommunities, but also because metapopulation and metacommunity models form the basis of several important applied ecological problems, such as the potential for an extinction debt created by habitat destruction (Tilman et al. 1994).

We present a model that explicitly incorporates dynamics owing to ecological drift as well as deterministic dynamics mediated by competitive ability, placed within the context of competition in space. The model is a departure from other spatial models that incorporate stochasticity (Hurtt & Pacala 1995; Gravel et al. 2006; Ruokolainen et al. 2009) in which it focuses on the classic competition-colonization trade-off model and explicitly considers three key ecological parameters in light of niche and neutral processes: the number of individuals competing in a local community (i.e. community size; Hu et al. 2005; Orrock & Fletcher 2005; Gravel et al. 2006; Vellend & Orrock 2009), the rate of arrival of competitor propagules and competitive ability. In addition to providing a framework for understanding the relative importance of ecological drift and competitive ability in affecting a classic model of metacommunity dynamics, the model illustrates how local community size may alter dynamics throughout the entire metacommunity and presents a framework for modelling propagule pressure and the degree of competitive asymmetry among competitors. We also use the model to shed light on important, non-intuitive phenomena relevant to conservation by demonstrating how ecological drift can interact with habitat loss to exacerbate the extinction debt.

2. Material and methods

The competition-colonization trade-off is one of the most common theoretical mechanisms of spatial coexistence. The basic competition-colonization trade-off model is attributed to Levins & Culver (1971), Hastings (1980) and has been used by many other researchers in various forms (reviewed in Klausmeier & Tilman 2002; Amarasekare et al. 2004; Mouquet et al. 2005). In a two-species model, the dynamics of the superior competitor (species 1) is described by:

2. 2.1

where P1 is the proportion of local communities that contain the superior competitor, colonization rate is c1, and the rate at which local communities of species 1 experience extinction is e1. Inferior competitors occupy P2 of the local communities. The dynamics of the inferior competitor is described by:

2. 2.2

where c2 and e2 represent the colonization and extinction rates, respectively, of the inferior competitor. As the final term of these equations indicates, a single propagule of the superior competitor immediately displaces all individuals of the inferior competitor from the local community once the superior competitor arrives in a patch occupied by the inferior competitor. Hence, the model is often called one of hierarchical competition (Klausmeier & Tilman 2002) or dominance competition (Mouquet et al. 2005), where coexistence occurs as long as the inferior competitor has a colonization rate high enough to allow it to colonize patches, where the superior competitor does not exist.

Armstrong (1976) modified the competition-colonization trade-off model to relax the strict assumption of the competitive hierarchy, such that the successful local exclusion of an inferior competitor by colonizing superior competitors occurs with probability v, so the dynamics of the superior and inferior competitor become, respectively:

2. 2.3

and

2. 2.4

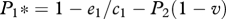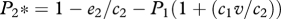At equilibrium, the proportion of patches occupied by the superior competitor, species 1, is Inline graphic and the proportion of patches occupied by the inferior competitor, species 2, is Inline graphic.

Although this approach has the intuitive advantage of not assuming that the superior competitor can always replace the inferior competitor, it simplifies dynamics by assuming that the probability of victory is arbitrarily determined. There is no change in the probability of victory as a function of local community size, because of the input of propagules of each competitor, or because of stochastic events during competition. Although empirical data suggest that both niche and neutral processes can occur within the competition-colonization trade-off (Cadotte 2007), the classic model has no mechanism for jointly considering the role of niche versus neutral processes.

To incorporate the effects of ecological drift, we extend Armstrong's (1976) model such that the probability of competitive exclusion (i.e. victory) in a local community becomes a function of the frequency of the invader, the competitive advantage of the invader and the likelihood that an invader will eventually obtain victory in a local community. The effect of these three components on the probability of victory can be simultaneously considered using the equation of Kimura (1962), which provides a mean-field approximation to the probability of fixation of a novel allele in a single-species population. This approximation is widely used in population genetics because it provides a robust method for incorporating stochastic genetic drift and deterministic selection to understand the likelihood that one allele will replace another, and it performs well under a wide array of situations (e.g. Otto & Whitlock 1997; Orrock 2005). Our implementation of Kimura's (1962) approximation assumes that the dynamics of competitive exclusion within a local community are rapid with regard to metacommunity dynamics between patches, an assumption we share with the classic competition-colonization trade-off as well as many other metacommunity models (reviewed in Klausmeier & Tilman 2002; Amarasekare et al. 2004; Mouquet et al. 2005). The robustness of this approach for modelling local competition has been demonstrated using simulations as well as comparisons of this approach dynamics using the classic Lotka–Volterra model (Orrock & Fletcher 2005); additional details regarding the use of genetic models for examining ecological competition can be found in Vellend & Orrock (2009).

In Kimura's equation, the probability of fixation of a novel allele in a single-species population is (1−exp(−2Nesp))/(1−exp(−2Nes)), where p is the frequency of the allele, s is its selective advantage and Ne is effective population size. If Je represents the effective size of each local community, i.e. the total number of individuals competing in each local patch (Hu et al. 2005; Orrock & Fletcher 2005; Gravel et al. 2006), the likelihood that the arriving propagules of a superior competitor will eventually exclude the resident inferior competitor is:

2. 2.5

where s is the competitive advantage of the superior competitor and fi represents the number of individuals of species i that enter a local community as a fraction of community size. If emigrants do not reduce the number of individuals in the communities they leave, i.e. surplus migrants (Amarasekare et al. 2004), as implied in the classic competition-colonization trade-off models (Levins & Culver 1971; Hastings 1980), the frequency of propagules of the superior competitor arriving in each local patch is equivalent to f1/(f1 + 1). This simplification is possible because the local abundance of the resident species will not be reduced by emigration and the resident species is assumed to completely occupy the local community (i.e. all individuals in the community are the resident species prior to colonization by the invader), such that f2 equals unity. For example, if Je = 100 and 10 propagules of the superior competitor colonize each local community that is filled with Je propagules of the inferior competitor, then f1 = 10/100 = 0.1 and f2 = 100/100 = 1, such that the relative frequency of species 1 propagules in the local community is 10/(10 + 100) = 0.1/(0.1 + 1), which is equivalent to f1/(f1 + 1) = 0.091. If zi represents the local relative frequency of species i, that is, z1 = f1/(f1 + 1), then s describes the change in the local relative frequency of the superior competitor with each time step t + 1, such that z1,t + 1 = z1,t(1 + s)/((z1,t(1 + s)) + z2,t), directly analogous to the change in the frequency of an allele with selective advantage s in a population. This formulation models competition in relative terms, such that the value of s is only represented for the superior competitor (i.e. the value of s for the inferior competitor is zero).

Combining equations (2.3) and (2.4) with equation (2.5) shows that the dynamics of the superior and inferior competitors become, respectively:

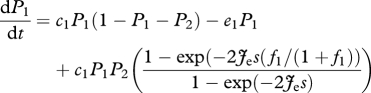2. 2.6

and

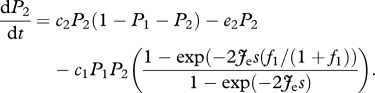2. 2.7

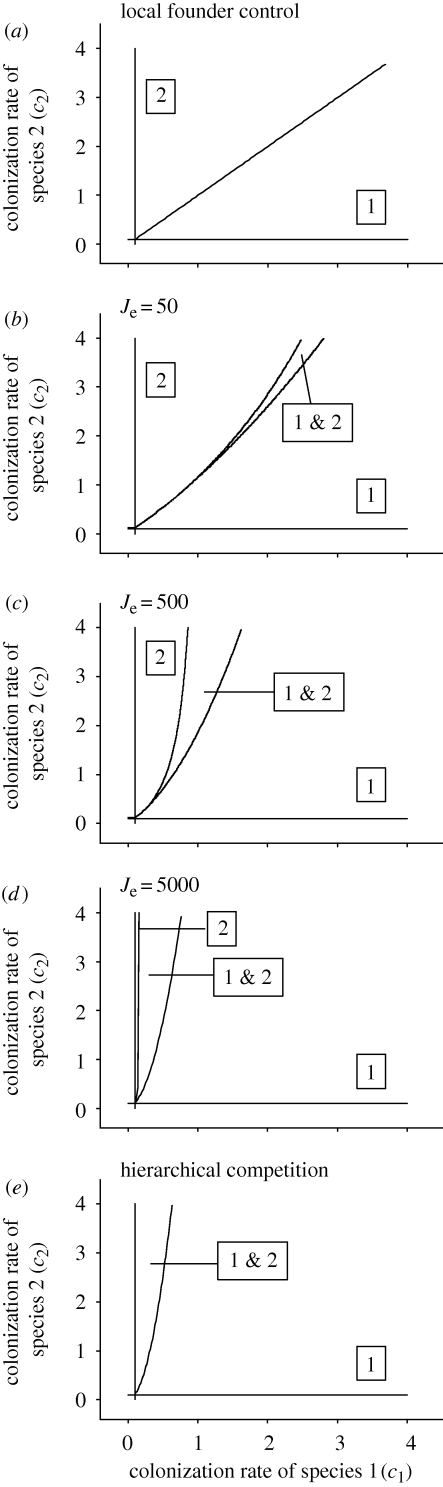
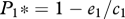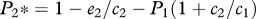As expected, when species 2 is not present or when the right-hand term in equations (2.6) and (2.7) approaches 1, the equilibrium for species 1 becomes equivalent to the solution of the competition-colonization trade-off with hierarchical competition, i.e. Inline graphic, and Inline graphic (figure 1). Similarly, when the right-hand term in equations (2.6) and (2.7) approaches 0, the model outcome converges on the dynamics of the model of local founder control (figure 1).

Figure 1.

Figure 1.

Open in a new tab

Comparing classic models of (a) local founder control and (e) a competitive hierarchy with the stochastic competition-colonization trade-off model where local community size, Je, is small (b, Je = 50), medium (c, Je = 500) or large (d, Je = 5000). Both species have the same extinction rates (e1 = e2 = 0.1); boxed numbers in each panel indicate the species are present at equilibrium in each region of state space. In panels (b)–(d), competitive ability of the superior competitor, s, is 0.01 and the frequency of the superior competitor, f1, is 0.01.

The model can be modified to examine the role of community size, propagule pressure and competitive ability in affecting the outcome of the ‘extinction debt’, an extension of the original competition-colonization trade-off model that illustrates how superior competitors are expected to go extinct with smaller amounts of habitat destruction because they are expected to have reduced colonization rates or greater mortality rates than inferior competitors (Tilman et al. 1994, 1997). If D represents the proportion of patches destroyed in the landscape, the proportion of empty and available patches represented by (1−P1−P2) in equation (2.3) becomes (1−D−P1−P2). At equilibrium, the occupancy of both species is reduced by habitat destruction, such that the new equilibria become:

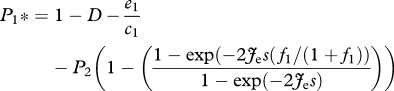2. 2.8

and

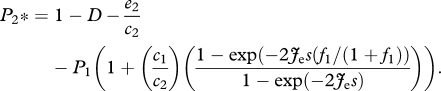2. 2.9

To determine the amount of habitat destruction required for the superior competitor to go extinct, we simplify notation of equations (2.8) and (2.9) by using v to represent the term for the probability of competitive exclusion (the inner-most right-hand term) and solve for D.

3. Results

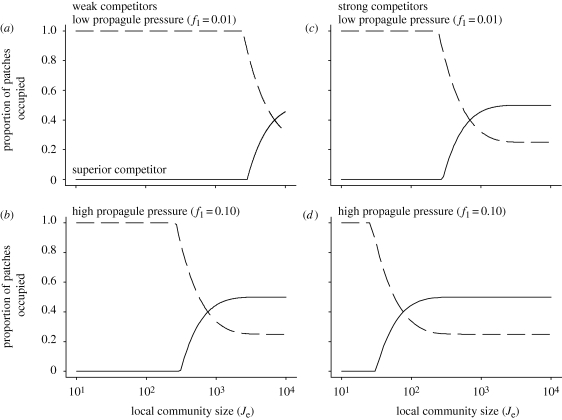
The model clearly demonstrates how local community size (Je), competitive ability (s) and propagule pressure (f) can act alone or in concert to determine the dynamics of metacommunity persistence and extinction. As local communities become larger, superior competitors are less likely to be lost owing to ecological drift when rare, and model dynamics increasingly resemble the original competition-colonization trade-off model with hierarchical competition (figure 1). However, when local community size is small, competitive superiority becomes less important, as small community sizes render competitors effectively neutral via the increased importance of ecological drift, creating abrupt thresholds in metacommunity dynamics where inferior competitors become increasingly represented and may readily exclude superior competitors (figures 1 and 2). Community size also alters the region in parameter space where coexistence is possible (figures 1 and 2). Competitive ability affects the proportion of patches occupied by each species at equilibrium: when competition is weak, inferior competitors are more likely to secure a fraction of the patches with superior competitors (figure 2). As the strength of competition increases, model outcomes increasingly resemble those of hierarchical competition. Increasing propagule pressure of a competitor species increases the likelihood of local victory for that species, and also increases metapopulation persistence (figure 2). Importantly, the model illustrates how community size, competitive ability and propagule pressure interact: even when the species are strong competitors and propagule pressure is high, small local communities can create competitive environments that are nonetheless largely structured by ecological drift. This favours the establishment of inferior competitors and can create changes in coexistence even when the intrinsic characteristics of the competitors themselves (e.g. competitive ability, movement ability) are unchanged.

Figure 2.

Figure 2.

Open in a new tab

The effect of competitive interactions and migrant frequency (i.e. propagule pressure) depend upon local community size. Each panel presents the proportion of patches occupied at equilibrium by superior competitors (solid line) and inferior competitors (dashed line); a species is extinct when its equilibrium is zero. (a,c) Low propagule pressure of the superior competitor corresponds to f1 = 0.01; (b,d) high propagule pressure corresponds to f1 = 0.1. (a,b) Weak competition is modelled as s = 0.01; (c,d) strong competition is modelled as s = 0.1. All other parameters are identical among panels (c1 = 0.2, c2 = 0.8, e1 = e2 = 0.1).

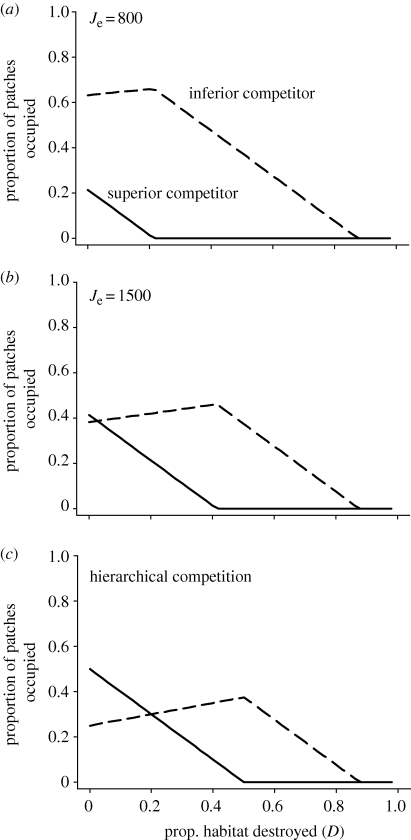
In terms of the extinction debt, the superior competitor is expected to go extinct at smaller values of D, because the inferior competitor is expected to have superior colonization abilities. This is illustrated by the solution to the original extinction debt model, such that extinction of the superior competitor occurs whenever D > 1−e1/c1 (Tilman et al. 1994). From equations (2.8) and (2.9), we find that D1 = 1−e1/c1−P2(1−v) for the amount of habitat destruction required to drive the superior species extinct, and D2 = 1−e2/c2−P1(1+ c1v/c2) for the amount of habitat destruction required for the inferior species to be driven extinct. This indicates that, as long as P2 > 0 and v < 1, the amount of destruction needed to ensure extinction of the superior competitor in this model will always be less than the amount of destruction required under the classic extinction debt model (figure 3). The amplification of the extinction debt increases whenever small community size, low propagule pressure or low competitive ability renders competitors effectively neutral. Under these conditions, the extinction of superior competitors is hastened because they suffer not only from reduced ability to locate local communities, but they are also less likely to exclude inferior competitors in local communities that they do colonize (figure 3).

Figure 3.

Figure 3.

Open in a new tab

The synergistic influence of habitat degradation (i.e. reducing local community size, Je) and habitat destruction (the proportion of patches destroyed, D) on coexistence. Panels (a, Je = 800) and (b, Je = 1500) illustrate the stochastic competition-colonization trade-off for different values of local community size. Panel (c) illustrates effect of habitat destruction under hierarchical competition used in the original extinction debt model (the outcome is analogous to the stochastic competition-colonization trade-off model with Je approaching infinity). Each panel presents the proportion of patches occupied at equilibrium by superior competitors (solid line) and inferior competitors (dashed line); a species is extinct when its equilibrium is zero. In panels (a) and (b), f1 = 0.01 and s = 0.05. In all panels, c1 = 0.2, c2 = 0.8 and e1 = e2 = 0.1.

4. Discussion

The outcome of competition is likely to be determined by the simultaneous operation of both competitive (niche-based) and stochastic (neutral) forces (e.g. Tilman 2004; Gravel et al. 2006; Leibold & McPeek 2006; Adler et al. 2007). Because competitive interactions occur along a continuum (sensu Gravel et al. 2006) between niche- and neutral processes, identifying characteristics that affect the position along the continuum is fundamental to understanding competitive dynamics. The key contribution of the model we develop is to demonstrate how a simple feature of ecological communities, i.e. community size, provides a mechanism capable of mediating the relative role of stochastic and deterministic processes and positioning an interaction along the continuum. We find that the role of chance is larger in smaller communities, which benefits weaker competitors (and stronger colonizers) over stronger competitors (and weaker colonizers). We further extend the model to incorporate other realistic elements of ecological interactions, such as differences in propagule supply and differences in competitive ability, into a single model framework.

(a). Coexistence and metacommunity dynamics

The model illustrates that inferior competitors may secure victory in a fraction of local communities solely because ecological drift removes superior competitors, i.e. even strong competitive asymmetries can be rendered nearly neutral by the considerable ecological drift present in small local communities (figure 2). This result has several important implications for metacommunity dynamics. First, it suggests that conditions for persistence can differ even when the intrinsic characteristics of competitors themselves do not change, because community size dictates whether competitive ability or ecological drift is more important for determining the outcome of local competition. Second, it suggests that species which are characterized by high colonization and poor competitive ability, i.e. fugitive species, would be especially likely to persist in situations where they encounter superior competitors in small local communities, highlighting a novel axis of coexistence: fugitive species need not be fugitives from all competitive interactions, they need only be fugitives from the deterministic exclusion that occurs in large local communities.

The model also demonstrates how community size, propagule pressure and differences in competitive ability can mediate the importance of particular metacommunity paradigms (Leibold et al. 2004) for characterizing community dynamics. For example, if local communities are large, metacommunity dynamics may be primarily governed by species sorting and patch dynamics, because any differences in competitive ability (s) among species will lead to deterministic exclusion of the inferior competitor in each local community (i.e. species sorting) and the persistence of the inferior competitor will rely entirely upon the colonization of competition-free local communities (i.e. patch dynamics). However, if community size is small, the same metacommunity may shift to being governed primarily by neutral dynamics (figure 2) because ecological drift in small communities effectively makes local competition neutral or nearly neutral (Orrock & Fletcher 2005).

The model illustrates how mass effects (Leibold et al. 2004) can also be important, as high rates of propagule input, f, can promote persistence of inferior competitors that would otherwise be eliminated (figure 2). Moreover, community size and propagule input may interact (figure 2) because the same absolute number of colonists will occupy a greater proportion of a small local community, increasing the likelihood of victory by increasing frequency within the local community (figure 2). This effect would be further exaggerated because small community size increases the role of drift, where the outcome of competition is more dependent upon frequency. As a result, phenomena that may simultaneously alter local community composition and competitor frequency, such as predators (Orrock et al. 2008; Chase et al. 2009), may have an important bearing on the outcome of competition.

(b). Applied implications: the extinction debt and biological invasions

An important implication of the competition-colonization trade-off model with hierarchical competition is that superior competitors may be more susceptible to habitat loss, leading to the ‘extinction debt’ (Tilman et al. 1994, 1997). However, habitat loss also creates smaller, often lower-quality patches of habitat, i.e. habitat loss is likely to also reduce the size of local communities by reducing the number of individuals a patch of habitat can support. Other anthropogenic impacts, such as climate change and overexploitation, are also likely to reduce the size of local communities. As the model demonstrates, this reduction in community size would be expected to reduce the number of local communities captured by superior competitors, effectively exacerbating the extinction debt for superior competitors (figure 3). This synergistic effect is expected to become greater with smaller local communities, decreased frequencies of the superior competitor and lower competitive asymmetries (figure 3). Importantly, habitat destruction, habitat degradation and a reduction in landscape connectivity are all likely to be underway in contemporary landscapes, and the model suggests that these changes are likely to interact, creating extinctions of superior competitors in excess of those predicted by the extinction debt alone (figure 3).

The model has implications for biological invasions via at least two mechanisms, and may interact with changes caused by habitat destruction and fragmentation. First, species that successfully invade are often characterized by high rates of propagule input (Lockwood et al. 2005). As our model demonstrates (figure 2), high rates of propagule input, especially when coupled with small local communities, provide a mechanism whereby inferior competitors might enter resident communities and potentially exclude residents; for a non-spatial case, see Vellend & Orrock (2009). Second, habitat degradation and fragmentation may promote the establishment of local invaders by reducing the size of local communities and/or reducing the input of resident species into local communities (f): even if they are inferior competitors relative to resident native species, inferior exotic organisms may be likely to succeed via ecological drift alone when local communities have been reduced in size and the frequency of resident propagules has been reduced. This mechanism of invasion may work in concert with other effects of habitat fragmentation that promote invasion (Didham et al. 2007). For example, habitat degradation and patch loss can interact to eliminate superior native competitors (figure 3), and release of exotic species from natural enemies in the introduced range could reduce the competitive asymmetry between native and exotic species, requiring smaller changes in local community size to render competitors nearly neutral (figure 2).

(c). Future directions

The model highlights how community size, propagule pressure and competitive asymmetries may play an important role in the dynamics of persistence. As with the majority of metacommunity models (Klausmeier & Tilman 2002; Amarasekare et al. 2004; Mouquet et al. 2005), our results are applicable to metacommunities where all patches are the same constant size and the dynamics of local competition occur more quickly than the dynamics of movement between local communities. In reality, the distribution of patch sizes is likely to vary, rates of competitive exclusion may not operate on such rapid time scales, and evolutionary processes may contribute to competitive dynamics (Urban & De Meester 2009). Moreover, competitive interactions may depend upon complex local interactions among colonizing and resident species, and understanding the relative importance of these interactions in light of community size effects is important. However, we emphasize that an interesting generality of the model is that the implications of local community size for ecological drift should extend to any model of local competition (e.g. resource competition), where stochastic forces are allowed to operate (see Orrock & Fletcher (2005) for an example using the Lotka–Volterra model of local competition). Although metacommunity models rarely consider the role of community assembly, both community composition and evolutionary dynamics may depend upon community size (Fukami 2004; Fukami et al. 2007), which can have overwhelming effects on the outcome of local competition (figure 2), especially in growing communities (Orrock & Fletcher 2005). Stochastic metacommunity models that incorporate temporal variation in species introduction and temporal changes in local community size, i.e. environmental stochasticity (Adler & Drake 2008), are also needed to more fully characterize the contribution of niche versus neutral processes to ecological interactions in space.

Acknowledgements

The manuscript was greatly improved by J. Chase, R. Fletcher, M. Vellend, M. Baskett, E. Damschen and two anonymous reviewers. Special thanks to M. Baskett for catalysing our further investigation of the extinction debt.

References

  1. Adler P. B., Drake J. M.2008Environmental variation, stochastic extinction, and competitive coexistence. Am. Nat. 172, E186–E195 (doi:10.1086/591678) [DOI] [PubMed] [Google Scholar]
  2. Adler P. B., HilleRisLambers J., Levine J. M.2007A niche for neutrality. Ecol. Lett. 10, 95–104 (doi:10.1111/j.1461-0248.2006.00996.x) [DOI] [PubMed] [Google Scholar]
  3. Amarasekare P., Hoopes M. F., Mouquet N., Holyoak M.2004Mechanisms of coexistence in competitive metacommunities. Am. Nat. 164, 310–326 (doi:10.1086/422858) [DOI] [PubMed] [Google Scholar]
  4. Armstrong R. A.1976Fugitive species: experiments with fungi and some theoretical considerations. Ecology 57, 953–963 (doi:10.2307/1941060) [Google Scholar]
  5. Cadotte M. W.2007Concurrent niche and neutral processes in the competition-colonization model of species coexistence. Proc. R. Soc. B 274, 2739–2744 (doi:10.1098/rspb.2007.0925) [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chase J. M.2007Drought mediates the importance of stochastic community assembly. Proc. Natl Acad. Sci. USA 104, 17 430–17 434 (doi:10.1073/pnas.0704350104) [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chase J. M., Biro B. G., Ryberg W. A., Smith K. G.2009Predators temper the relative importance of stochastic processes in assembly of prey communities. Ecol. Lett. 12, 1210–1218 (doi:10.1111/j.1461-0248.2009.01362.x) [DOI] [PubMed] [Google Scholar]
  8. Didham R. K., Tylianakis J. M., Gernmell N. J., Rand T. A., Ewers R. M.2007Interactive effects of habitat modification and species invasion on native species decline. Trends Ecol. Evol. 22, 489–496 (doi:10.1016/j.tree.2007.07.001) [DOI] [PubMed] [Google Scholar]
  9. Ellwood M. D. F., Manica A., Foster W. A.2009Stochastic and deterministic processes jointly structure tropical arthropod communities. Ecol. Lett. 12, 277–284 (doi:10.1111/j.1461-0248.2009.01284.x) [DOI] [PubMed] [Google Scholar]
  10. Fukami T.2004Assembly history interacts with ecosystem size to influence species diversity. Ecology 85, 3234–3242 (doi:10.1890/04-0340) [Google Scholar]
  11. Fukami T., Beaumont H. J. E., Zhang X., Rainey P. B.2007Immigration history controls diversification in experimental adaptive radiation. Nature 446, 436–439 (doi:10.1038/nature05629) [DOI] [PubMed] [Google Scholar]
  12. Gravel D., Canham C. D., Beaudet M., Messier C.2006Reconciling niche and neutrality: the continuum hypothesis. Ecol. Lett. 9, 399–409 (doi:10.1111/j.1461-0248.2006.00884.x) [DOI] [PubMed] [Google Scholar]
  13. Hanski I. A., Gilpin M. E.1997Metapopulation biology: ecology, genetics, and evolution San Diego, CA: Academic Press [Google Scholar]
  14. Hastings A.1980Disturbance, coexistence, history, and competition for space. Theor. Popul. Biol. 18, 363–373 (doi:10.1016/0040-5809(80)90059-3) [Google Scholar]
  15. Hu X. S., He F., Hubbell S. P.2005Neutral theory in macroecology and population genetics. Oikos 113, 548–556 (doi:10.1111/j.2006.0030-1299.14837.x) [Google Scholar]
  16. Hurtt G. C., Pacala S. W.1995The consequences of recruitment limitation: reconciling chance, history and competitive differences among plants. J. Theor. Biol. 176, 1–12 (doi:10.1006/jtbi.1995.0170) [Google Scholar]
  17. Kimura M.1962On the probability of fixation of mutant genes in a population. Genetics 47, 713–719 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Klausmeier C. A., Tilman D.2002Competition in spatial habitats. In Competition and coexistence (eds Sommer U., Worm B.), pp. 43–78 Berlin, Germany: Springer [Google Scholar]
  19. Leibold M., McPeek M.2006Coexistence of the niche and neutral perspectives in community ecology. Ecology 87, 1399–1410 (doi:10.1890/0012-9658(2006)87[1399:COTNAN]2.0.CO;2) [DOI] [PubMed] [Google Scholar]
  20. Leibold M. A., et al. 2004The metacommunity concept: a framework for multi-scale community ecology. Ecol. Lett. 7, 601–613 (doi:10.1111/j.1461-0248.2004.00608.x) [Google Scholar]
  21. Levins R., Culver D. C.1971Regional coexistence of species and competition between rare species. Proc. Natl Acad. Sci. USA 68, 1246–1248 (doi:10.1073/pnas.68.6.1246) [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lockwood J. L., Cassey P., Blackburn T. M.2005The role of propagule pressure in explaining species invasions. Trends Ecol. Evol. 20, 223–228 (doi:10.1016/j.tree.2005.02.004) [DOI] [PubMed] [Google Scholar]
  23. Mouquet N., Hoopes M. F., Amarasekare P.2005The world is patchy and heterogeneous! Trade-off and source-sink dynamics in competitive metacommunities. In Metacommunities: spatial dynamics and ecological communities (eds Holyoak M., Leibold M. A., Holt R. D.), pp. 237–262 Chicago, IL: University of Chicago Press [Google Scholar]
  24. Orrock J. L.2005Conservation corridors affect the fixation of new alleles. Conserv. Genet. 6, 623–630 (doi:10.1007/s10592-005-9016-6) [Google Scholar]
  25. Orrock J. L., Fletcher R. J.2005Changes in community size affect the outcome of competition. Am. Nat. 166, 107–111 (doi:10.1086/430641) [DOI] [PubMed] [Google Scholar]
  26. Orrock J. L., Grabowski J. H., Peacor S. D., Peckarsky B. L., Preisser E. L., Sih A., Werner E. E.2008Consumptive and non-consumptive effects of predators on metacommunities of competing prey. Ecology 89, 2426–2435 (doi:10.1890/07-1024.1) [DOI] [PubMed] [Google Scholar]
  27. Otto S. P., Whitlock M. C.1997The probability of fixation in populations of changing size. Genetics 146, 723–733 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ruokolainen K., Ranta E., Kaitala V., Fowler M. S.2009When can we distinguish between neutral and non-neutral processes in community dynamics under ecological drift? Ecol. Lett. 12, 909–919 (doi:10.1111/j.1461-0248.2009.01346.x) [DOI] [PubMed] [Google Scholar]
  29. Tilman D.2004Niche tradeoffs, neutrality, and community structure: a stochastic theory of resource competition, invasion, and community assembly. Proc. Natl Acad. Sci. USA 101, 10 854–10 861 (doi:10.1073/pnas.0403458101) [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Tilman D., May R. M., Lehman C. L., Nowak M. A.1994Habitat destruction and the extinction debt. Nature 371, 65–66 (doi:10.1038/371065a0) [Google Scholar]
  31. Tilman D., Lehman C. L., Yin C. J.1997Habitat destruction, dispersal, and deterministic extinction in competitive communities. Am. Nat. 149, 407–435 (doi:10.1086/285998) [Google Scholar]
  32. Urban M. C., De Meester L.2009Community monopolization: local adaptation enhances priority effects in an evolving metacommunity. Proc. R. Soc. B 276, 4129–4138 (doi:10.1098/rspb.2009.1382) [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Vellend M., Orrock J. L.2009Ecological and genetic models of diversity: lessons across disciplines. In The theory of island biogeography revisited (eds Losos J. B., Ricklefs R. E.), pp. 439–461 Princeton, NJ: Princeton University Press [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES