Dynamics and the Failure of Transition State Theory in Alkene Hydroboration

Abstract

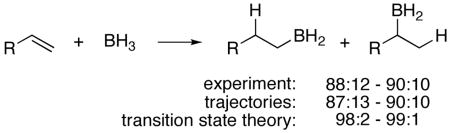
Transition state theory fails to accurately predict the selectivity in an example where it is ubiquitously invoked, hydroboration. The hydroboration of terminal alkenes with BH₃ is moderately regioselective, affording an 88:12 - 90:10 ratio of anti-Markovnikov:Markovnikov adducts. High-level ab initio calculations predict too large of an energy difference between anti-Markovnikov and Markovnikov transition structures to account for the observed product ratio, and the consideration of calculational error, solvent, tunneling, and entropy effects does not resolve the discrepancy. Trajectory studies, however, predict well the experimental selectivity. The decreased selectivity versus transition state theory arises from the excess energy generated as the BH₃ interacts with the alkene, and the observed selectivity is proposed to result from a combination of low selectivity in direct trajectories, moderate RRKM selectivity, and high selectivity after thermal equilibration.

The hydroboration of simple alkenes with BH₃ preferentially occurs in an “anti-Markovnikov”¹ fashion. The standard explanation for this preference in the literature,^1,2 reproduced in some form in all general textbooks of organic chemistry, is that the selectivity arises from a greater stability for the anti-Markovnikov transition state over the alternative “Markovnikov” transition state. We find here that transition state theory fails to accurately account for the regioselectivity of hydroboration. Instead, a consideration of dynamic trajectories allows understanding of the selectivity.

The addition of BH₃ to terminal alkenes is only moderately regioselective. With simple terminal alkenes such as 1-hexene, the ratio of primary to secondary alcohol products after hydroboration with BH₃ at 0 – 25 °C followed by oxidation is approximately 94:6.^1,3 This ratio as it has been observed is a composite of the regioselectivity in three separate steps – hydroboration by BH₃, hydroboration by RBH₂, and hydroboration by R₂BH. When unhindered, the intermediate alkylboranes are more reactive,⁴ but they are more regioselective as well, so the initial reaction of BH₃ is less selective than the composite ratio. Using the observed 1-hexanol/2-hexanol ratio of 97:3 for the reaction of n-butylborane with 1-hexene⁵ as a measure of the selectivity of the second and third steps of hydroboration, the regioselectivity for reaction of 1-hexene with BH₃ itself would be ≈88:12. In our hands, the hydroboration of propene-d₆ at 21 °C with 100 equiv of BH₃•THF (to minimize the contribution of hydroboration by alkylboranes) affords a 90.0:10.0 ratio of primary and secondary alcohols (based on direct analysis of the oxidized reaction mixture by ²H NMR). Assuming the applicability of transition state theory, the ΔΔG^‡ for the transition states leading to the two products would be 1.1 – 1.3 kcal/mol.

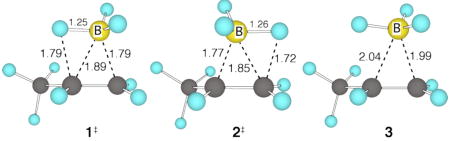
A variety of gas-phase computational approaches were explored in an attempt to predict this ΔΔG^‡.⁶ CCSD(T)/aug-cc-pvdz calculations were used to locate transition structures 1^‡ and 2^‡ for formation of the regioisomeric products from the precursor complex 3. The relative energetics of the anti-Markovnikov transition structure 1^‡ and the Markovnikov structure 2^‡ in high-level single-point calculations, as well as analogous structures optimized in other ways, are summarized in Table 1. All of the calculations, including particularly a converged series of CCSD(T) single-point energies employing very large basis sets, predict an energetic preference for 1^‡ that greatly exceeds that implied by the experimental selectivity. In other words, the experimental reaction is considerably less selective than the 98:2 – 99:1 expected from the calculations.

Table 1.

Calculated ΔΔE^‡ or ΔΔG^‡ for Transition Structures 1^‡ versus 2^‡ for the Hydroboration of Propene with BH₃.

Method/Basis Set	ΔΔE‡a or ΔΔG‡b (kcal/mol)
B3LYP/6-31G*	2.4b
G3	2.4b
CBS-QB3	2.3b
CCSD(T)/cc-pvtzc	2.4a
CCSD(T)/aug-cc-pvtzc	2.4a
CCSD(T)/cc-pvqzc	2.4a
CCSD(T)/aug-cc-pvqzc	2.4a
BD(TQ)/aug-cc-pvdzc	2.6a
CCSD(T)/extrapolated to infinitebasis + enthalpy correction – TΔS	2.5b,d
Experiment (assuming transition state theory)	1.1–1.3

^aΔΔE^‡ (as potential energy).

^bΔΔG^‡ at 25 °C including harmonic enthalpy and entropy estimates based on the unscaled frequencies.

^cSingle point calculations on the CCSD(T)/aug-cc-pvdz structures.

^dMP4/cc-pvdz frequencies were used in the enthalpy and entropy estimates.

We considered many possible reasons for this discrepancy. The simplest possibility, unadorned error in the calculated relative energies, seems doubtful based on the similarity of the structures being compared, the convergence of the results from various calculational methods, and the quality of the methods employed. A second possibility is that entropy strongly favors 2^‡ in a way that is missed by the often-erring harmonic entropy estimate. Treatment of the most-vulnerable methyl-group rotation as a hindered rotor based on CCSD(T)/cc-pvtz single points on the rotational second-order saddle points favors 2^‡, but by only 0.1 kcal/mol at 25 °C. On the other hand, inclusion of anharmonic corrections (B3LYP/6-31G*) increased the preference for 1^‡ by 0.1 kcal/mol. A third possibility is that tunneling favors the Markovnikov process since its barrier is higher. Experimentally, however, there was no apparent difference in the regioselectivity of the reaction of BH₃ versus BD₃ with 1-octene. A one-dimensional infinite-parabola tunneling estimate⁷ based on the curvature of the transition vectors (301i and 530i cm⁻¹ for 1^‡ and 2^‡, respectively) does favor 2^‡, but by only a rate-factor of 1.22.

A more complex possibility to consider is the role of solvent. We first consider the effect of solvent polarity. Experimentally, solvent polarity has no discernable effect on the regioselectivity.⁸ Theoretically, the SCF dipole moments (aug-cc-pvqz) for 1^‡ and 2^‡ are only 3.34 and 2.95 D, respectively, and because the dipole moment of 1^‡ is greater, solvent polarity should favor 1^‡, not 2^‡. In accord with this, solvent-model calculations (PCM, CPCM, SCIPCM) increase the preference for 1^‡ by 0.3–0.4 kcal/mol, further from experiment.

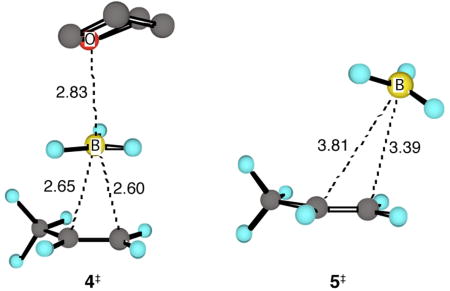
A second possible role for solvent is the mechanistic complication of a direct transfer of the BH₃ from the solvent as ligand. This is a debated issue (see the Supporting Information for a discussion). In calculations at various levels,⁶ loose transition structures for BH₃ transfer from THF to propene are readily located, e.g. 4^‡ (B3LYP/6-31G*,⁶ variationally optimized), but the product of these structures is complex 3, uncoordinated by THF. In such circumstances the 1^‡/2^‡ energy difference would still control the regioselectivity. Notably, the free-energy barrier associated with 4^‡ is predicted to be 2.3 kcal/mol above a dissociative pathway followed by variational transition structure 5^‡ (CCSD(T)/6-31+G**//B3LYP/6-31G*, after allowing for neat THF as its standard state).

Why does transition state theory fail to account for the product ratio? The formation of 3 from BH₃/propene is enthalpically barrierless (experimentally, 2 ± 3 kcal/mol with ethylene in the gas phase⁹) and downhill by 11.0 kcal/mol (CCSD(T)/aug-cc-pvqz + harmonic enthalpy estimate). Considerable excess energy is thus available from the formation of 3, and the barriers for formation of products from 3 are quite small – 1^‡ is only 0.8 kcal/mol above 3 in free energy. Under these circumstances, we considered that trajectories may pass directly to the products or afford the products faster than thermal equilibration with solvent, making transition state theory inappropriately applicable.¹⁰

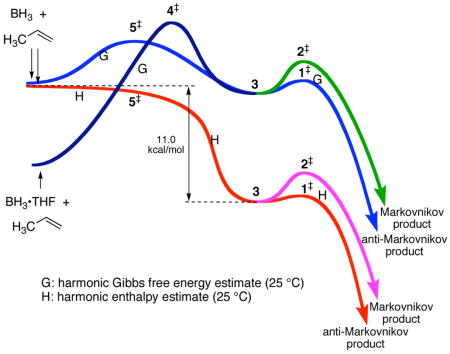
To explore this idea, a series of classical trajectory studies were performed by direct dynamics¹¹ (Table 2), including B3LYP/6-31G* trajectories started directly from 3, 4^‡, and 5^‡, and ONIOM (B3LYP/6-31G*:AM1) trajectories started from 4^‡ or 5^‡ in a bath of 18 THF molecules confined to a 14 Å cubic box after a 500 – 8500 fs equilibrations. Trajectories started from 3 statistically at 25 °C, i.e., with no excess energy, underwent addition with a half-life of ≈700 fs and afforded ≈1% of the Markovnikov product. This fits quite well with transition state theory, though not with experiment, and weighs against recrossing or unknown subtle classical entropy effects as the source of the discrepancy. In contrast, trajectories started from points before 3 on the reaction coordinate, thus having excess energy in the area of 3, afforded 10–12% of the Markovnikov product, fitting strikingly well with experiment.

Table 2.

Classical Trajectory Studies.

Starting point	anti- Markovnikov	Markovnikov	Unreactive in 5000 fs
3	875	10 (1%)	3
4‡	338	47 (12 %)	496a
5‡	739	110 (13%)	465
5‡ + 18 THF, equilibratedb	76	9 (11%)	17a
4‡ + 17 THF, equilibratedc	19	2 (10%)	3a

^aIncludes trajectories affording THF•BH₃

^b500 fs equilibrations before releasing a fixed B–C distance.

^c1000 –8500 fs equilibrations.

A more detailed understanding of the regioselectivity can be gleaned from considering the time-course of the selectivity for trajectories started from 5^‡. For the 25% of trajectories that afford product within 800 fs, the amount of Markovnikov product is particularly high (21%). The selectivity is higher for the 39% of trajectories that afford product in the 800 – 5000 fs range, with 7.5% Markovnikov addition. An RRKM calculation based on the energy difference between 5^‡ and 3 predicts 7.4%. From these observations, we envision the selectivity in solution as involving three stages: a ‘direct-trajectory’ stage, with low selectivity, an RRKM stage, with medium selectivity, and a thermally-equilibrated stage, developing over several picoseconds¹² as the excess energy is transferred to solvent. This last stage should be quite selective, as evidenced by the results with trajectories starting from 3, but by then the damage is done.

Some unusual experimental observations in hydroboration support the mechanistic picture here. In particular, hydroboration has long been recognized as “remarkably insensitive to major changes in the structure of the olefin”,¹³ a factor in its broad utility, and it exhibits an equally remarkable low intermolecular H/D isotope effect of 1.18.¹⁴ These observations were shoehorned into a conventional mechanistic picture, though in retrospect they clearly contradict it. A new unusual observation is that the regioselectivity is surprisingly temperature-insensitive – hydroboration of propene-d₆ at 21, 45 and 70 °C afforded 10.0, 10.6 and 11.2% Markovnikov addition, respectively. This corresponds to a ΔΔH^‡ of only 0.5 ± 0.2 kcal/mol.

In this most ‘textbook’ of reactions, transition state theory fails and the selectivity can only be understood by consideration of dynamic trajectories. We are unaware of any more striking example of the role of dynamics in an experimentally preeminent reaction.