A model of direction selectivity in the starburst amacrine cell network

Abstract

Displaced starburst amacrine cells (SACs) are retinal interneurons that exhibit GABA_A receptor-mediated and Cl ⁻ cotransporter-mediated, directionally selective (DS) light responses in the rabbit retina. They depolarize to stimuli that move centrifugally through the receptive field surround and hyperpolarize to stimuli that move centripetally through the surround (Gavrikov et al, PNAS 100(26):16047–16052, 2003, PNAS 103(49):18793–18798, 2006). They also play a key role in the activity of DS ganglion cells (DS GC; Amthor et al, Vis Neurosci 19:495–509 2002; Euler et al, Nature 418:845–852, 2002; Fried et al, Nature 420:411– 414, 2002; Gavrikov et al, PNAS 100(26):16047–16052, 2003, PNAS 103(49):18793–18798, 2006; Lee and Zhou, Neuron 51:787–799 2006; Yoshida et al, Neuron 30:771–780, 2001). In this paper we present a model of strong DS behavior of SACs which relies on the GABA-mediated communication within a tightly interconnected network of these cells and on the glutamate signal that the SACs receive from bipolar cells (a presynaptic cell that receives input from cones). We describe how a moving light stimulus can produce a large, sustained depolarization of the SAC dendritic tips that point in the direction that the stimulus moves (i.e., centrifugal motion), but produce a minimal depolarization of the dendritic tips that point in the opposite direction (i.e., centripetal motion). This DS behavior, which is quantified based on the relative size and duration of the depolarizations evoked by stimulus motion at dendritic tips pointing in opposite directions, is robust to changes of many different parameter values and consistent with experimental data. In addition, the DS behavior is strengthened under the assumptions that the Cl⁻ cotransporters Na⁺-K⁺-Cl⁻ and K⁺-Cl⁻ are located in different regions of the SAC dendritic tree (Gavrikov et al, PNAS 103(49):18793–18798, 2006) and that GABA evokes a long-lasting response (Gavrikov et al, PNAS 100(26):16047–16052, 2003, PNAS 103(49):18793–18798, 2006; Lee and Zhou, Neuron 51:787–799, 2006). A possible mechanism is discussed based on the generation of waves of local glutamate and GABA secretion, and their postsynaptic interplay as the waves travel between cell compartments.

Introduction

In the context of visual neuroscience, the term direction selectivity, a phenomenon first described in the vertebrate retina in the 1960’s (Barlow et al. 1964), refers to a neural pathway that relays information about the specific direction that an object is moving. A basic experiment in this context is the following. Suppose that the retina of an animal is stimulated directly on its surface using a small moving light source. By measuring the voltage response of a so-called directionally selective ganglion cell (DS GC) to the light signal, one finds that these cells generate a large number of action potentials in response to the moving light—but only when the light moves in a specific direction called the preferred direction (Fig. 1(a)). If the light moves in the opposite direction (known as the null direction), then few or no signals are recorded. Each On-Off DS GC in the rabbit, the species in which this light response has been studied most thoroughly, has one of four preferred directions, which are parallel to the directions in which the four rectus muscles move the eye (Oyster 1968). Also, the response doesn’t change significantly if one varies the general location of the light input within an area around the DS GC known as the receptive field.

Fig. 1.

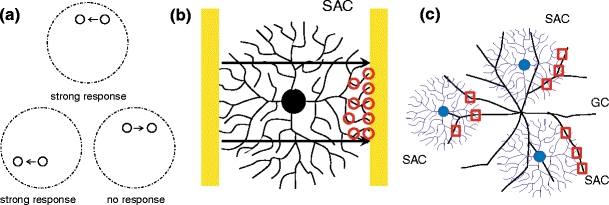
(a) Directionally selective ganglion cells (DS GC) respond strongly to light stimuli moving in a particular direction anywhere within their receptive field, but respond little or not at all to stimuli moving in the opposite direction. (b) Illustration of hypothesis (1). As a light signal moves, say, from left to right, only the right-most SAC dendritic tips depolarize (marked with circles). (c) Illustration of hypothesis (2). The SAC dendrites (shown in blue) connecting to a DS GC tend to point towards a single direction, in this case towards the right, which is the null direction of the DS GC. A stimulus that moves in the null direction of the DS GC (e.g., in this case toward the right) depolarizes the rightmost SAC dendritic tips, which then inhibit the DS GC (Cellular communication marked with squares)

An important problem in retinal neuroscience, which is still unresolved to a large extent, has been to uncover the mechanisms behind this simple behavior. How does the DS GC only fire in response to light signals moving in one direction, but not in another? Various potential mechanisms have been constructed; see for instance Masland (2004) for a review. A consensus is emerging in the literature that a special type of radially symmetric retinal interneuron, the starburst amacrine cell (SAC), might be implicated in an important way in this process.

The DS GC does not respond directly to light. Rather, a light moving over the retinal surface directly stimulates a sequence of cones that then signal a sequence of bipolar cells. The light responses of cones and bipolar cells are not directionally selective - they respond in the same way to light moving in any direction, and the bipolar cells relay this signal to both DS GCs and SACs. SACs signal DS GCs at the synaptic contacts between SAC distal dendritic tips and the dendrites of the DS GCs. Therefore, signaling between the bipolar cell, SAC, and DS GC constitutes a neural network that generates the DS light responses of the DS GC.

Two recently proposed hypotheses (Dmitriev, Gavrikov and Mangel, manuscript in preparation; Euler et al. 2002; Fried et al. 2002; Gavrikov et al. 2003, 2006) that, if both true, could explain the directionally selective behavior of the DS GC (see Fig. 1) are the following:

1. When a light signal moves across the receptive field of a SAC, the only dendritic tips of the SAC that become strongly depolarized are those pointing in the direction that the light is moving (Dmitriev, Gavrikov and Mangel, manuscript in preparation; Euler et al. 2002; Gavrikov et al. 2003, 2006).

2. All SAC dendrites that connect to a given DS GC are pointing in the null direction of the DS GC and inhibit the DS GC when they are depolarized (Dmitriev, Gavrikov and Mangel, manuscript in preparation; Fried et al. 2002; Gavrikov et al. 2003, 2006).

In this way, if a SAC has a dendrite that points in the null direction of a DS GC and connects to that DS GC, then by (1), a light signal moving across the SAC receptive field in that direction would depolarize the SAC dendrite, which would then inhibit the DS GC. More importantly, a light signal moving across the SAC receptive field in another direction would not strongly depolarize the dendrite (also by (1)), and this dendrite would therefore not signal the DS GC. The asymmetry necessary for the DS GC to signal only when light moves in its preferred direction is provided by the inhibition it receives from synaptically-connected SAC dendrites that point in its null direction (by 2).

Note that condition (1) can explain the experimental observation that the DS GC responds to a single direction of motion. Also, (1) implies that the radially symmetrical SACs have dendrites which behave to some extent independently of each other.

Evidence for (2) is given in Fried et al. (2002), where the voltage of a DS GC is measured using voltage clamp recording as it is stimulated by a light signal moving along its null direction. The authors show that the inhibition of the DS GC begins some time before the signal reaches the cell and ends immediately after the signal leaves it, suggesting the presence of a ‘lobe of inhibition’ immediately before the DS GC. This is consistent with the situation in Fig. 1(c), where the SACs which communicate with the DS GC are located on the left side. Additional evidence is given in that paper by demonstrating that depolarizing SACs with current provided through the recording electrode inhibited nearby DS GCs only if the SACs were on the null side of the GCs (i.e., the depolarized SAC dendrites were pointing in the null direction of the GCs).

In this paper, we provide a model of a network of SACs that satisfies the behavior in hypothesis (1), which can be thought of as a ‘directionally selective’ behavior for the SAC. There are several previous models of (1) in the literature for individual cells; for instance, see the recent work by Tukker et al. (2004), which uses a spatially explicit compartmental model of a SAC and measures different peak voltages to light signals moving centripetally or centrifugally (i.e., towards or away from the soma, respectively). Note that studying centrifugal and centripetal motion is in a sense equivalent to moving light across the receptive field of the cell and studying individual dendritic responses.

We construct a network of multiple interacting SACs, as opposed to a single SAC, in order to model the way in which neighboring SACs communicate with each other, and to address the role that this communication may have in direction selectivity. This work is closely related to the previous model of Dmitriev, Gavrikov and Mangel (manuscript in preparation), which studied the question of direction selectivity in a single SAC using sequential glutamate and GABA inputs. A simplified discrete network model was also proposed by Münch and Werblin, however using a very different set of assumptions (Münch and Werblin 2006).

As we will show below, our model of SACs presents a strong DS effect (in the sense of (1)), which is robust when a number of parameters are varied. The DS effect relies on the presence of multiple overlapping cells; for example, it breaks down when only one cell is used. It is also enhanced when the neurotransmitter GABA has a sustained postsynaptic effect after its release (Gavrikov et al. 2006; Lee and Zhou 2006). Finally, the DS effect is strengthened in the presence of a Cl⁻ potential gradient along the length of the SAC dendritic branches (Gavrikov et al. 2006).

GABA, glutamate, and Cl⁻ cotransporters

We now describe some of the basic biology and experimental findings that will be used in constructing our computational model.

The GABA and glutamate inputs

Each SAC may be either locally excited or inhibited depending on two different types of inputs. The first is the excitatory bipolar cell input resulting from a light signal stimulating that section of the retina at a given time. As mentioned above, SAC dendrites cannot sense light directly, but the cones located above them signal bipolar cells directly below, which release the neurotransmitter glutamate locally onto the SAC dendrites. The glutamate binds and opens ion channels in the SAC dendrite, which allows the cations Na⁺ and K⁺ to transverse the membrane, resulting in a strongly depolarizing net effect. In this paper, we refrain from modeling cones or bipolar cells directly. Rather, we consider the presence of glutamate as a proxy for a cone to bipolar cell to SAC signal.

The second input that a SAC receives in our model is a signal coming from other SACs, and it is mediated by the neurotransmitter GABA. Whenever a SAC dendritic tip becomes sufficiently depolarized, it is assumed to release GABA (Brecha et al. 1988; O’Malley et al. 1992; Vaney and Young 1988), which binds to GABA_A receptors (Brandstatter et al. 1995) and opens Cl⁻ channels in postsynaptic SAC dendrites. GABA is released from SAC dendritic tips through a vesicular mechanism (Famiglietti 1991; Lee and Zhou 2006), and it is assumed to open Cl⁻ channels along the length of the postsynaptic SAC, as long as they lie sufficiently close to where it was released.

The effect of opening a Cl⁻ channel nevertheless may be either excitatory or inhibitory, depending on the location of the Cl⁻ channel along the dendrite. This is due to the presence of so-called Cl ⁻ cotransporters along the SAC dendrites, which we describe now.

Cl⁻ cotransporters and the Cl⁻ potential gradient

The presence of two types of Cl⁻ cotransporters in SACs has been documented by Gavrikov et al. (2006), and it allows for different Cl⁻ reversal potentials to coexist in the same SAC. In particular, the reversal potential near the soma is more positive than the resting potential in this location. Also, the Cl⁻ reversal potential near the dendritic tips is more negative than the resting potential at this position. Thus, the effect of GABA is excitatory proximally and inhibitory distally. This is shown in the model to strengthen the directionally selective response of the SACs.

The gradient of the Cl⁻ reversal potential along SAC dendrites can be understood as follows. It was concluded in Gavrikov et al. (2006) that the Cl⁻ cotransporters known as K⁺-Cl⁻ and Na⁺-K⁺-Cl⁻ are present along SAC dendrites, and that they are preferentially located near the dendritic tips and the cell soma, respectively (Fig. 2). The cotransporter K⁺-Cl⁻ is known to transport pairs of ions, one K⁺ and one Cl⁻, together across the cell membrane (Payne et al. 2003). Because the concentration of K⁺ is higher inside the cell under physiological conditions, overall the K⁺-Cl⁻ pairs are transported outside. The net effect is that the concentration of Cl⁻ inside the cell becomes lower locally in that dendritic section; thus the Cl⁻ reversal potential is lowered where the K⁺-Cl⁻ cotransporter is present.

Fig. 2.

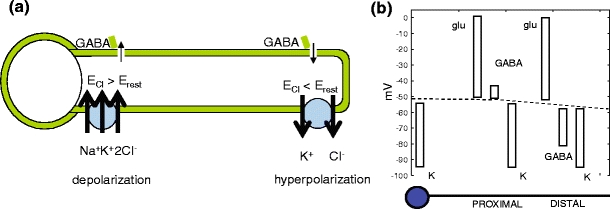
(a) The Cl⁻ reversal potential varies along the length of the dendrite due to the presence of one Cl⁻ cotransporter (Na⁺-K⁺-Cl⁻) in the proximal dendrite near the soma and a second type of Cl⁻ cotransporter (K⁺-Cl⁻) in the distal dendrite (Gavrikov et al. 2006). Therefore a GABA-evoked increase in Cl⁻ conductivity depolarizes the proximal dendrite and hyperpolarizes the distal dendritic tip. (b) GABA, glutamate, and K⁺ reversal potentials (as well as the resting potential-dotted line), as a function of SAC dendritic position. See Dmitriev, Gavrikov and Mangel (manuscript in preparation) for an experimental derivation of these reversal potentials

The effect of the Na⁺-K⁺-Cl⁻ cotransporter is opposite to that of K⁺-Cl⁻, thus effectively shifting the equilibrium potential of Cl⁻ to a value more positive than the resting potential in the section of dendrite where it is present. Given that the two ion cotransporters are located near the soma (Na⁺-K⁺-Cl⁻) and the dendritic tips (K⁺-Cl⁻), the Cl⁻ gradient forms as described.

Model description

For the sake of computational efficiency, each individual SAC is modeled as six straight ‘dendrites’ radiating from a central point. Each dendrite contains two compartments: one distal compartment at the tip and one proximal compartment halfway along the dendrite. There is also a somatic compartment at the center of the cell, for a total of 13 compartments per SAC, as shown in Fig. 3(a). We also consider in Fig. 8 below a similar model with three compartments per dendrite instead of two.

Fig. 3.

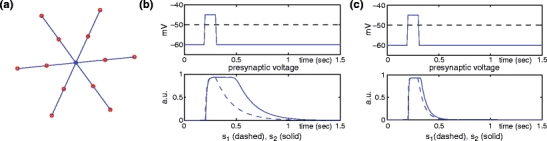
(a) Each SAC was modeled using a hexagonal array of six dendrites. Each dendrite had one proximal and one distal compartment. One additional compartment was used to represent the cell soma. Several cells were then synaptically linked together for the full model. (b) Response of the Cl⁻ gating variables (bottom) to a step increase in the presynaptic voltage signal (top). The dashed line corresponds to θ ₁. The variables s _c,1, s _c,2 are drawn using dashed and solid lines, respectively. (c) Same graph, but with a shortened delay produced by using the different parameter values α = 240, β = 18, θ ₂ = 0.6

Fig. 8.

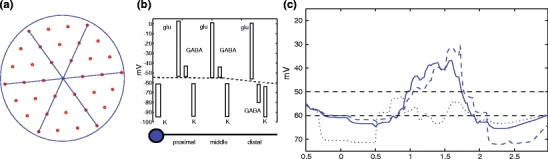
(a) A SAC with three compartments per dendrite, illustrating the number of somatic compartments within a dendrite length of the soma. Using this criterion, the cell has a coverage factor of around 36. Notice that the displayed somas that are not touching the cell are nevertheless part of cells with dendrites that co-localize and interact with the cell. (b) The voltage potentials for this three-compartment model. (c) A generalized simulation was implemented with a 4 × 12 array of such SACs, and the voltages shown were measured at the cell in row 4, column 8

We consider arrays of cells, in which each cell lies half a dendrite length away from its closest cell neighbor (or a third dendrite length away in the three compartment case). Because of the regular hexagonal configuration, several compartments from different cells may lie in the same spatial location, i.e., are co-localized. This is important for cell-to-cell communication (described below). Similarly, one can define adjacent compartments, which are two compartments within the same SAC that are directly linked (such as the somatic compartment and any proximal compartment, or a proximal compartment and its adjacent distal compartment).

Every compartment c in a given SAC contains three types of ion channels (in addition to the Cl⁻ cotransporters, which are not modeled explicitly). The conductance of two of these ion channels is increased by the light-evoked release of glutamate and GABA by presynaptic bipolar cells and other SACs, respectively. One is a cation channel sensitive to glutamate receptor binding, which increases its conductance g _glu to model the presence of a light signal. Another is a GABA-sensitive Cl⁻ channel, which increases its conductance g _Cl whenever co-localized dendritic tips of other SACs are sufficiently depolarized to release GABA. A third ion channel is a constitutive K⁺ channel, which has a standing conductance that is not altered by light or transmitter receptor binding.

The dynamics of the voltage v _c(t) at a given (non-somatic) compartment c is given by the equation

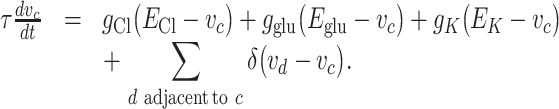1

Equilibrium potentials are represented by the letter E and conductances by the letter g. The letters τ and v represent a time constant and the voltage, respectively. The positive parameter δ represents the strength of the connection between adjacent compartments. Notice that two compartments are adjacent only when they are together in the same dendrite. In addition, there are no gap junctions coupling dendrites of two different cells. Figure 2(b) shows the values of the equilibrium potentials as a function of the distance from the soma. The equilibrium potentials E _K and E _glu are constant, but E _Cl varies depending on whether the compartment is proximal or distal. It is at this point that the presence of the Cl⁻ cotransporters is implicitly used.

The glutamate conductance can be defined as a continuously increasing function of the light signal strength, g _glu = σ(L(c,t)). Since we will only have two types of light signal stimulating the network in this paper (strong light or no light), the conductance is determined for convenience by the formula

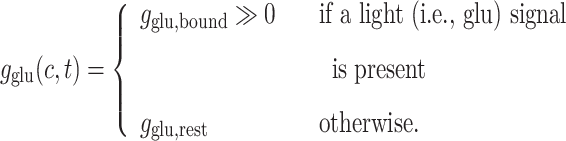The conductance g _K as well as the time-constant τ are fixed parameters of the system.

We now describe the equation for g _Cl = g _Cl(c,t). Define auxiliary gating variables s _c,1(t), s _c,2(t) by

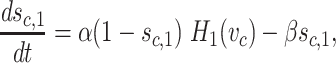2

where α ≫ β > 0 are fixed parameters, and 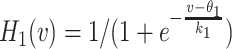is a sigmoidal threshold function similar to the Heaviside function and centered around θ ₁ = − 50 mV. The variable s _c,2(t) represents the level of GABA secretion by the distal compartment c and it is defined by the equation

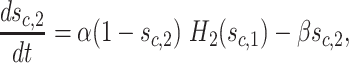3

for 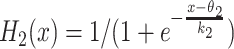. Finally, let

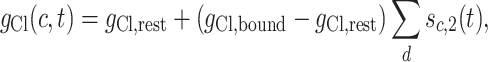where d varies over all distal compartments that are co-localized with c but different from c.

The constants g _Cl,rest and g _Cl,bound describe the Cl⁻ conductance under no GABA input and maximal GABA input, respectively. The purpose of the auxiliary gating variable s _c,1 is to introduce a long-lasting GABA-evoked postsynaptic Cl⁻ conductance after the presynaptic release of GABA. This incorporates in the model the finding that the GABA-evoked responses of SACs are several times longer than their glutamate counterparts (Dmitriev, Gavrikov and Mangel, manuscript in preparation; Gavrikov et al. 2006; Lee and Zhou 2006). Notice that in choosing the parameter values, we define α to be several times larger than β.

Once a presynaptic voltage crosses to above the threshold value θ ₁, the variables s _c,1 and s _c,2 rise rapidly to 1. However, when the presynaptic voltage crosses to below the threshold, s _c,1 begins to decay slowly to 0; the second synaptic variable s _c,2 must wait until s _c,1 crosses the threshold θ ₂ before it begins to decay. This is shown in Fig. 3(b), where we plot the response of the gating variables in response to a step increase in the presynaptic voltage signal.

In the case of the somatic compartment c, there are only K⁺ ion channels assumed to be involved, and the somatic voltage is determined by these channels together with the effect of adjacent compartments:

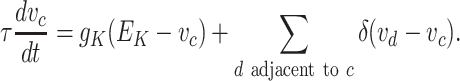Refer to Table 1 for the parameter values used in this model.

Table 1.

The baseline parameter values used in this system

E glu:	0 mV	g glu,rest:	1/60 (GΩ) − 1
E Cl,proximal:	−45 mV	g glu,bound:	1/6 (GΩ) − 1
E Cl,distal:	−80 mV	g Cl,rest:	1/72 (GΩ) − 1
E K:	−94.7 mV	g Cl,bound:	1/2.4 (GΩ) − 1
		g K:	1/40 (GΩ) − 1
θ 1:	−50 mV	k 1	0.2 mV − 1
θ 2:	0.3	k 2	0.02
τ:	0.03 s	SAC diameter:	0.4 mm
δ:	1/3;	glu signal speed:	0.5 mm s − 1
α:	80 s − 1	glu signal width:	0.2 mm
β:	6 s − 1	integration interval:	(−0.5 s, 2.4 s)

For a derivation of reversal potentials and conductance values, refer to Dmitriev, Gavrikov and Mangel (manuscript in preparation)

Results

Consider a 2D array of SACs in five rows, each cell separated by a half dendritic length (0.1 mm) from its neighbors, as in Fig. 4. The soma of each dendrite has a specific position on a hexagonal array, shared with compartments of neighboring cells. This system is stimulated by a glutamate signal of width 0.2 mm (i.e., one dendritic length), moving from left to right with a speed of 0.5 mm s^− 1. The center of the moving bar passes through the left edge of the array at time t = 0, and the system is modeled starting at time t = − 0.5 s.

Fig. 4.

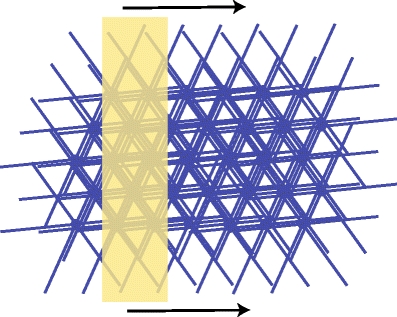
A 2D array of five rows of SACs with 6–7 cells/row was stimulated with a glutamate signal of width 0.2 mm moving at a speed of 0.5 mm s^− 1 (SAC diameter = 0.4 mm). Each cell is rotated and slightly displaced in this figure for visualization purposes

Although the voltage at the SAC soma can be experimentally measured, it is not possible to record the voltage at the dendritic tips of SACs using microelectrodes. Figure 5(a) represents the somatic voltage over time of the fifth cell, third row (solid line), for a simulation containing a long GABA reabsorption delay as in Fig. 3(b) and a Cl− potential gradient along the SAC dendrites from −45 mV proximally to −80 mV distally. Figure 5(b) shows an experimental patch-clamp recording of the somatic response to a light stimulus of the same width and speed. Although not every feature of the somatic experimental voltage is reproduced by the model, several qualitative features of the experimental measurements are captured (e.g., the amplitude and time course of the depolarization).

Fig. 5.

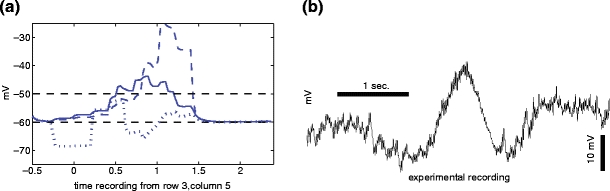
(a) Dendritic voltages of the right (dashed) and left (dotted) dendritic tips of the fifth cell, third row. Note the stronger depolarization of the right, compared to the left, dendritic tip to the moving glutamate stimulus. The somatic voltage over time is shown as a solid line. (b) An experimental measurement of the somatic voltage of a SAC to a moving light stimulus of the same width and speed

However, because the dendritic tips of SACs are thought to be the sites from which SACs release transmitter onto DS GCs and onto other SACs (Famiglietti 1991), the more interesting behavior of the model takes place at the dendritic tips of the cells. We concentrate on the fifth cell from left to right, third row, for display purposes (which receives input from multiple neighboring distal compartments). Nevertheless a similar behavior is observed along all neighboring cells (i.e., as long as sufficiently many cells remain on the left to produce the necessary network effects). In Fig. 5(a) we also display the voltage of the left and right dendritic tips of the same cell over time (dotted and dashed, respectively). Note that the highest voltage reached by the right dendritic tip is much higher than that at the left dendritic tip—this would allow the cell to send a signal downstream to the DS GC only from dendritic tips pointing in the direction of the light motion, as described in the previous sections. This asymmetric response constitutes the essential directionally selective behavior produced in this model.

Model analysis

Parameter sensitivity

In order to better understand the mechanisms underlying direction selectivity, we have analyzed how solutions of the model depend on changes in a number of parameters from the original parameter set. In the simulations shown in Fig. 6, we eliminate or change two important features of the model: the delay in GABA channel closing and the gradient of intracellular chloride along the length of the dendrite. In Fig. 6(a), we present the full model using the parameter set in Table 1, including a gradient in the Cl⁻ equilibrium potential and a full GABA channel delay. In Fig. 6(b), the GABA channel open time in response to a voltage increase is substantially reduced by dividing τ _GABA and multiplying α, β by a factor of 3. Next, as described in Fig. 2, a constant Cl⁻ reversal potential of −55 mV, which equals the resting membrane potential, corresponds to the condition in which there are no active Cl⁻ cotransporters on the dendrites. In this case, activation of GABA_A receptors opens Cl⁻ channels, but does not produce a potential change, although it can decrease the amplitude of concomitant glutamate-evoked depolarizations due to shunting inhibition. In contrast, a constant Cl⁻ reversal potential of −80 mV corresponds to the condition in which the K⁺-Cl⁻ cotransporter is located along the entire length of the SAC dendrites and the Na⁺-K⁺-Cl⁻ cotransporter is absent. In this case, GABA_A receptor activation hyperpolarizes the cells and decreases the amplitude of glutamate-evoked depolarizations to a greater extent. Fig. 6(c) and (d) shows that the DS effect is reduced in the absence of active cotransporters, but preserved, although somewhat diminished (see below), in the presence of a constant inhibitory Cl⁻ gradient, respectively.

Fig. 6.

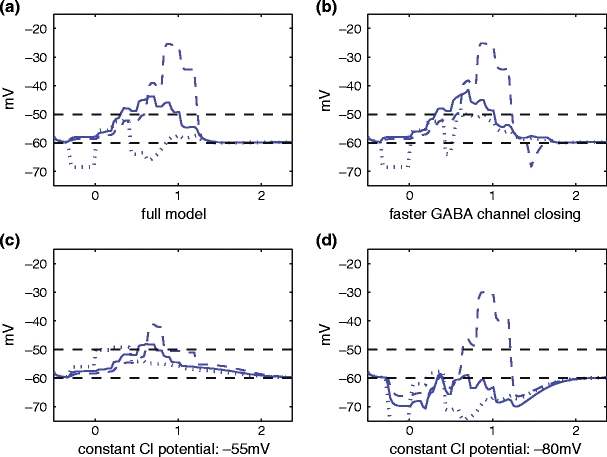
The performance of the model is examined by changing the parameter values in several ways. Once again, the solid, dashed, and dotted lines represent the voltages over time at the soma, right tip and left tip, respectively. (a) The full model used the parameter values in Table 1. (b) The delay in GABA channel closing time is reduced, by multiplying α, β by 3 and doubling θ ₂ (i.e., the postsynaptic Cl⁻ conductance closely reflects the presynaptic voltage). The Cl⁻ gradient along the SAC dendrites is as in case (a)) and Table 1. The DS effect is preserved almost intact in this case. (c, d) the GABA (Cl⁻) reversal potential gradient from Fig. 2(b) is eliminated, and it is replaced by a constant reversal potential of −55 mV, corresponding to the absence of active the Cl⁻ cotransporters (c) or −80 mV, corresponding to the presence of the K⁺-Cl⁻ cotransporter located along the entire length of the dendrites (d). A DS effect is preserved in the inhibitory case (d), but not in the shunting case (c). In cases (c) and (d), the delay in GABA channel closing is as in case (a) and Table 1

In Table 2, we provide two quantitative measures of the graphs in Figs. 6 and 7, by calculating for each case the direction selectivity index (DSI) and the area, A, under the right voltage curve that is bounded from below by the firing threshold line. The definition of DSI is given in the table caption. Computation of the area A is a useful additional measure of the degree of direction selectivity because this area is larger when there is a strong maximum depolarization (which is what DSI measures), but also when the depolarization is sustained over a longer period of time. Because larger values of the area A indicate increased neurotransmitter secretion, the area A is a useful complementary measure of the degree of direction selectivity. Although the graphs in Fig. 6(b)–(d) all have a DSI that is similar to that of the full model in Fig. 6(a), they all show a smaller area (see Table 2, lines 2–4, rightmost column) compared to the full model (see Table 2, line 1, rightmost column), suggesting that the full model produces the strongest overall DS behavior due to the sustained depolarization exhibited at the right dendritic tip. Moreover, the more than ten-fold smaller area produced by a constant Cl⁻ potential = − 55 mV (i.e., absence of active Cl⁻ cotransporters on SAC dendrites), compared to the full model, further suggests that DS is dependent on Cl⁻ cotransporter activity.

Table 2.

A quantification of the DS response for the different parameter sets

Parameter set	DSI	A
Original parameters	0.6282	9.9714
Fast GABA channel closing: α = 240 s − 1, β = 18 s − 1, θ 2 = 0.6	0.5241	7.1710
Constant CL− potential: E Cl = − 55 mV	0.5218	0.7899
Constant CL− potential: E Cl = − 80 mV	1.0437	3.9245
Fast GABA channel closing and E Cl = − 80 mV	0.6172	4.3129
Slower signal speed: 0.166 mm s − 1	0.4009	31.2267
Faster signal speed: 1.5 mm s − 1	0.6262	3.3144
Weaker compartmental connection: δ = 1/9	0.7674	12.8596
Stronger compartmental connection: δ = 1	0.2376	0
Lower firing threshold: v threshold = − 55 mV	0.8430	3.8467
Higher firing threshold: v threshold = − 45 mV	0.6253	6.9536
Cell voltage, row 2 column 6	0.6356	10.7029
Cell voltage, row 3 column 1	0.0366	13.1888
Three compartments per dendrite	0.679	6.5

Let m ₁ and m ₂ be the maximum voltage over time at the left and right dentritic tips respectively (fifth array cell unless noted). Let r be the average resting potential. Then DSI: = [(m ₂ − r) − (m ₁ − r)]/[(m ₂ − r) + (m ₁ − r)]. The second column corresponds to the area A bounded by the right dendritic voltage above the upper threshold line

Fig. 7.

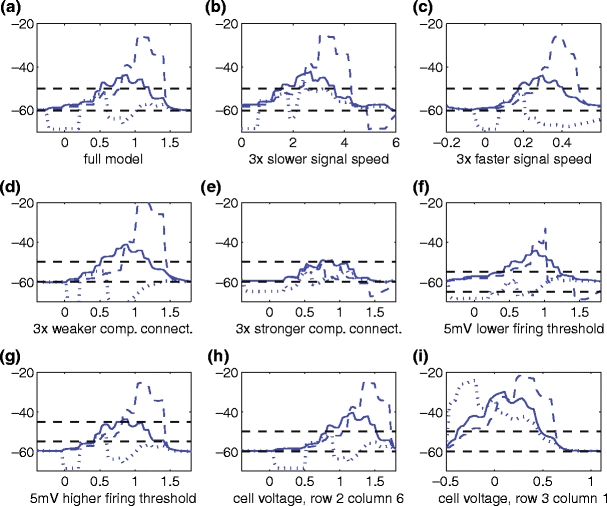
Sensitivity of the full model (a) to various other parameter changes—the horizontal and vertical axes correspond to time and membrane potential, respectively. (b, c) A 3-fold decrease and increase of the glutamate stimulus speed. (d, e) A 3-fold decrease and increase of the connection parameter δ. (f, g) A 5-mV decrease and increase of the parameter θ ₁. (h, i) The voltage is recorded (using the standard parameter set) from a different cell in the array: row 2, column 6 (h), and row 3, column 1 (i); notice that the voltage behavior in (h) is very similar to (a), but that DS completely breaks down in (i)

We also consider in Fig. 7 parameter changes that alter the speed of the moving glutamate stimuli, the strength of the compartmental connection, and the voltage threshold for GABA signaling. The system was robust under these changes, with the exception of the compartmental connection parameter which, if strengthened by a factor of 3, greatly reduced the DS effect. We also illustrate how a nearby cell in the array presents the same DS response as the baseline cell (row 3, column 5); however a cell located near the left edge has a substantially reduced DS (Fig. 7(i)). This suggests that sufficiently many cells need to be modeled on the left side of the recorded cell to provide sufficient inhibitory input. Recording the voltages in a cell on the right half of the array seems to produce very similar results as in Fig. 5(a) (see Fig. 7(h)).

Finally, we generalize our simulations to SACs which have three compartments per dendrite instead of two. Each compartment is modeled identically as in the two compartment case, and only the tip of each dendrite is assumed to release GABA. The distance between two neighboring cells is now one third of a dendritic length instead of one half. The Cl⁻ reversal potentials are assumed to be ( − 45, − 45, − 80) mV along the proximal, middle and distal dendritic compartments, respectively, of each dendrite, see Fig. 8(b). Otherwise the same parameters are used as in the original two compartment model (Figs. 6(a) and 7(a)). Figure 8(c) shows that the directionally selective effect is still present in this case; in fact, in the right half of the array, all cells behave in a similar way as in Fig. 8(c) (see Table 2 for the DSI and the area index). This shows also that the DS behavior is robust to models with a closer spacing between cells, allowing for a higher coverage factor. In addition, notice that the increase in dendritic overlap results in a somatic voltage response that includes hyperpolarizations immediately before and after the depolarization, a somatic response that more closely approximates the somatic voltage response that has been experimentally-measured with patch-clamp recording (Gavrikov et al. 2006).

GABA and glutamatergic waves

Let us take a closer look at the presence of glutamate and GABA signals along the cells in this network. The presence of glutamate represents the input signal as described above. A measure of the presence of GABA is the conductance level of the GABA ion channels, as given by the variable s ₂(t) ∈ [0, 1] at any given compartment. Given a region R in space and a time t, one can add the variable s ₁(t) over all compartments in R to obtain a quantitative proxy for the presence of GABA in that region. Given that the spatial location of the left and right dendritic tips of the fifth array cell are (3, 0) and (7, 0) respectively, this is done along the time axis in Fig. 9 for the regions R = {(x, y) | 2.5 ≤ x ≤ 3.5 } and R = {(x, y) | 6.5 ≤ x ≤ 7.5 }, to measure the presence of GABA around these two compartments, respectively. The region marked by the vertical bars represents the presence of a glutamate signal at each compartment over time.

Fig. 9.

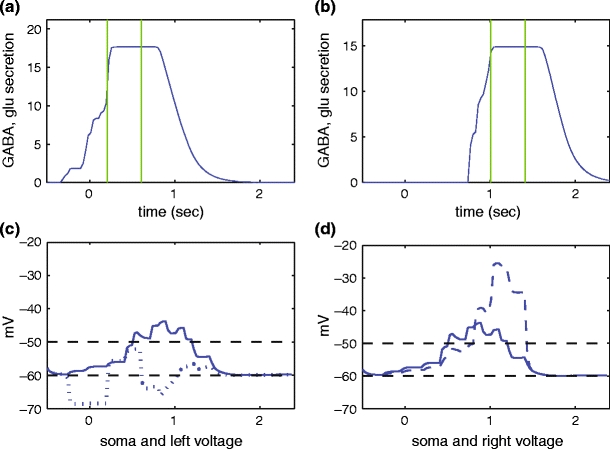
GABA and glutamate waves around the location of the left (a) and right (b) dendritic tips of the fifth cell in the array. The vertical lines mark the time intervals when a glutamate signal is present over the compartment. For every time t, the curves in (a) and (b) represent the sum of the variables s ₁ along all compartments in R = {(x, y) | 2.5 ≤ x ≤ 3.5 } (a) and R = {(x, y) | 6.5 ≤ x ≤ 7.5 } (b), respectively. The voltages of each compartment over time are displayed in (c) and (d) for comparison

Figure 9(a) and (b) shows how a GABA wave is generated in this system, as GABA is signaled by the different SACs in the network. Note that this wave both precedes and succeeds the glutamate wave: as each cell’s leftmost dendrites are depolarized, the depolarization spreads along the dendrites and through the cell soma, ensuring that some GABA is released even before the glutamate wave reaches a given location. Also recall that the extracellular GABA concentration remains high for a delayed period of time after it has been released. (The form of the final GABA wave ideally should be independent of the location of the region R along the x-axis—nevertheless the function in Fig. 9(b) is not exactly a translation of that in Fig. 9(a), since around x = 5 the system has not yet converged to its final wave-like form.)

The waves shown in Fig. 9(a) and (b) help to explain the voltage dynamics at the two dendritic tips, which are displayed for comparison in Fig. 9(c) and (d). Note, for instance, that the voltage at the left dendritic tip changes around t = − 0.2 s and that it is an inhibitory response to the appearance of the GABA wave in Fig. 9(a). Then around t = 0.1, the curve depolarizes for a time interval coinciding with the presence of the glutamate signal, up to about t = 0.5. The strongest depolarization of the right dendritic tip also coincides with the secretion of glutamate in that position (Fig. 9(b, d)).

But if the voltage at both tips was only a response to the local GABA and glutamate waves, then the maximum voltages should be similar, since there is no substantial difference between the waves at both compartments. An ultimate explanation of the DS effect must, therefore, come from elsewhere. Notice that between t = 0.5 s and t = 1.0 s, the right dendritic tip experiences a depolarization which does not have a counterpart in the voltage at the left dendritic tip. This depolarition is due to the spread of voltage from other compartments inside the same cell, especially the proximal compartments which contain Na⁺-K⁺-Cl⁻ and are thus depolarized by GABA.

This effect of the spread of voltage along adjacent dendritic compartments is analogous to that described in Tukker et al. (2004). In that paper, the authors describe a wave, which seems to originate at the soma and then spreads through the dendrites. See also the earlier work by Borg-Graham and Grzywacz (1992), where they also find such an effect in the spread of voltage between adjacent SAC dendritic compartments. This inter-compartmental behavior takes place in our model as well: as each compartment changes its voltage due to local stimuli, it affects neighboring compartments, including eventually the soma. From the soma this change reaches other compartments. The effect is much more noticeable at the right dendritic tip than at the left. This is because the left compartment is still being hyperpolarized by GABA due to the delayed closing of the GABA channels: indeed, when the GABA channels close more quickly in Fig. 6(b), this depolarization also appears at the left dendritic tip.

Even when this intercompartmental voltage spread, which is produced primarily by GABA at the Na⁺-K⁺-Cl⁻-containing proximal dendritic compartments, reaches both the left and right dendritic tips, its timing with respect to the glutamate wave provides another asymmetry: the glutamate-induced depolarization at the left tip takes place early on, before the voltage spread has yet occurred; therefore, the inter-compartmental voltage spread causes a second activation of the left tip at a later time. However, the spread reaches the right dendritic tip before the glutamate wave, producing a longer, more sustained depolarization at the right dendritic tip, when GABA depolarizes the proximal compartments and hyperpolarizes the distal compartments (Fig. 6(a)), compared to when GABA hyperpolarizes both the proximal and distal compartments (Fig. 6(d)). This double depolarization of glutamate and GABA also provides for a higher maximum voltage at the right tip. These effects ultimately explain the DS response in this model.

Discussion

The results of our model suggest that several factors are essential in the generation of a robust DS light response difference at the left and right dendritic tips of SACs. First, we found a strong DS response difference when our model incorporated a 2D network of overlapping SACs. In contrast, the DS response difference was greatly reduced when the amount of input from other SACs was low, as occurred for SACs on the left edge of the 2D array.

Second, although a typical antagonistic, center-surround receptive field organization, in which the Cl⁻ potential was −80 mV along the entire SAC dendritic tree and GABA response duration was relatively short (see Table 2, line 5, rightmost column), produced a DS response difference at the left and right dendritic tips, our model also shows, when one considers both the amplitude and duration of the depolarization at the right dendritic tip (see the indices in Table 2, especially the index in the rightmost column), that a Cl⁻ gradient along the dendrites and the delayed closure of GABA channels on SAC dendrites both increase the DS effect. When the Cl⁻ potential was equal to −55 mV throughout (i.e., Cl⁻ cotransporter activity was absent), the left dendritic tip was not substantially inhibited and the right dendritic tip was not substantially depolarized during the glu wave, and the area A was reduced ten-fold, compared to the full model. If on the contrary the Cl⁻ potential was set to −80 mV throughout, the voltage spread between adjacent dendritic compartments was weakened, and the depolarization at the right tip, though strong, was short lived compared to the full model. These latter two findings suggest that direction selectivity is dependent on the presence of K⁺-Cl⁻ cotransporter activity (i.e., a hyperpolarizing surround) and not simply that GABA evokes a shunting inhibition (but see Borg-Graham and Grzywacz 1992). In addition, as shown in Table 2 (rightmost column), if GABA hyperpolarizes SAC dendrites along their entire length due to K⁺-Cl⁻ cotransporter activity along the length of the dendrites, the depolarization at the right dendritic tip is of large amplitude, but short-lived compared to the full model in which the Na⁺-K⁺-Cl⁻ and K⁺-Cl⁻ cotransporters are located in the proximal and distal compartments, respectively, of SAC dendrites. The prolonged depolarization at the right dendritic tip due to the GABA-evoked depolarization of the proximal, Na⁺-K⁺-Cl⁻ containing compartments would produce a prolonged release of GABA from the right dendritic tips, resulting in a more effective shunting inhibition of bipolar cell-evoked glutamate depolarizations of ON-OFF DS GCs.

Our model suggests the following mechanism for direction selectivity of SACs: as the light moves across the network of cells, two fronts or ‘waves’ of neurotransmitter secretion develop, a narrow glu wave and a broader GABA wave. These neurotransmitter waves induce a special inter-compartmental voltage spread, especially a depolarization of the dendritic sections which are close to the soma. At the dendritic tips pointing in the direction of the stimulus motion, this intercompartmental voltage spread protects against GABA inhibition and acts together with the glutamate wave to create a strong and sustained depolarization. At the opposite dendritic tips the glutamate depolarization takes place under sustained GABA inhibition, before the spread of voltage between dendritic compartments occurs.