A Novel Method Combining Linkage Disequilibrium Information and Imputed Functional Knowledge for tagSNP Selection

Abstract

Analyses of high-density SNPs in genetic studies have the potential problems of prohibitive genotyping costs and inflated false discovery rates. Current methods select subsets of representative SNPs (tagSNPs) using information either on potential biologic functionality of the SNPs or on the underlying linkage disequilibrium (LD) structure, but not both. Combining the two types of information may lead to more effective tagSNP selection. The proposed method combines both functional and LD information using a weighted factor analysis (WFA) model. The WFA was applied to the dense SNP collection from 129 genes sequenced by the SeattleSNPs Program for Genomic Application. TagSNPs selected by WFA were compared with those selected by an LD-based method. WFA allowed prioritization of SNPs that would otherwise share equivalent ranking due to underlying LD structure alone. Furthermore, WFA consistently included SNPs not selected by function or by LD alone. A literature review of a subset of genes revealed that SNPs selected by WFA were more likely represented in published reports.

Introduction

Single nucleotide polymorphisms (SNPs) occur at a frequency of 2 to 10 millions across the human genome and constitute the most common form of genetic variation [1]. As genetic markers, SNPs also have lower mutation rates than microsatellites [2]. These qualities make SNPs ideal markers in genetic association studies, which typically involve genotyping thousands of SNPs [3,4,5]. However, the application of high-density SNPs to genetic association studies also introduces potential problems of expensive genotyping costs and more false positive findings.

Inflated rates of false positive findings (type I errors) result from testing thousands of SNP markers repeatedly for association with the same traits or phenotypes in the same sample (i.e. ‘multiple testing’). Spurious positive results occur merely due to chance. If the number of tests is moderate compared with the number of observations, a body of statistical literature addresses concerns of ‘multiple testing’ and offers standard procedures (e.g. Bonferroni correction) for adjusting significance levels. In the case of association studies that use highly dense SNPs, the number of tests is overwhelmingly large and it becomes extremely difficult to achieve proper adjustment of p values due to the overly conservative assumption of independence between SNPs. Therefore, it is desirable to reduce the total number of tests by selecting only a subset of ‘informative’ SNPs, loosely referred to as ‘tagSNPs’. Appropriate selection of a representative panel of SNPs may reduce the number of tests to a level where proper corrections of type I errors can be achieved.

Existing methods for tagSNP selection assume two distinctive approaches to reducing dimensionality in SNP data. One approach is to focus on the biological property inherent to each SNP and to select only those likely to bear relevant functionality [6, 7]. This approach, which is limited to those SNPs with known or suspected functions (such as those SNPs in coding and promoter regions), has been applied in many association studies. However, it ignores the linkage disequilibrium (LD) structure among SNPs, which measures informational redundancy present in the SNPs. The other approach uses this LD structure to remove information redundancy among the SNPs and select a subset that can explain the genotypic variations observed in the data [8, 9]. Although this approach neglects the biologic significance of SNPs, it can be widely applied to all SNPs in panels of any size. The HapMap project, with the goal to determine genome-wide tagSNPs in four world populations, is based on an LD-determined selection process [10].

The purpose of the present study is to investigate ways of combining functional information with LD data to further extend the reductive nature of LD-based tagSNP selection. A scoring method [11] is extended to derive weights reflective of potential functionality of each SNP. In the algorithm presented, greater weights are assigned to SNPs residing in regions conserved across species and included in a consensus sequence for transcription factor binding. The LD structure among SNPs is analyzed using a pairwise LD matrix similar to that of SNPSpD [9]. A weighted factor analysis (WFA) method using oblique rotation is then applied to combine the two sources of information for selection of the most informative SNPs. A suite of computer programs is developed to automate the process to query online genomic databases, generate weight matrices, perform weighted factor analysis, and finally, to select a list of tagSNPs. The panel of tagSNPs selected by the proposed method was applied to 129 genes sequenced by the SeattleSNPs Program for Genomic Applications (PGA, http://pga.gs.washington.edu) and compared to those tagSNPs selected by methods based solely on LD.

Methods

Impute and Use SNP Functionality

The selection of functionally important SNPs has traditionally been performed in an ad hocmanner by simply examining whether a SNP resides in a region with potential functionality (i.e., promoter regions, coding regions, intron/exon splice sites, etc.). A newer method now exists for assessing potential functional importance of promoter SNP by examining cross-species conservation and transcription factor binding capability of sequences flanking the SNP [PromoLign, see [7]]. This method has been extended to impute allele-specific functional scores for SNPs residing anywhere in a candidate gene (region) and has been demonstrated to enhance the power to detect important genetic associations in a hypertension candidate gene study [11].

The premise of the imputed functional score (IFS) method is that functionally important SNPs may also exist in regions outside of traditional promoter and coding sequences. Highly conserved regions of DNA, such as those found to contain transcription factor binding sites (TFBS), are more likely to be of biological importance due to their retention across species through evolution. SNPs within these TFBS are of interest due to their potentially significant effect on the regulation of gene expression. This assumption is supported by findings in recent studies that have identified alterations to TFBS sequences in intronic and 3′ untranslated regions that alter mRNA expression and/or stability [12, 13]. Therefore, the current method provides a more meaningful tagSNP selection by combining existing LD-based methods with a method of identifying variants with plausible biologic importance.

Remove Redundant LD Information

The LD-based methods of SNP selection seek to reduce redundancy by selecting a subset of SNPs representative of the group through LD. Principal component analysis (PCA) and other latent factor analysis methods are often used for dimension reduction. The matrix of pairwise LD is analyzed to identify a smaller subset of factors retaining most of the original LD structure. The number of factors extracted is dependent upon the desired proportion of variance explained.

After factors are derived from the LD matrix, tagSNP selection is based on an interpretation of the so-called ‘factor pattern’ (or loadings of each SNP on the derived factors). Existing methods, such as SNPSpD [9] and eigen2htSNP [14]), use orthogonal (Varimax) factor rotation for this purpose. Varimax rotation, the most common form of orthogonal factor rotation, focuses on maximizing the loadings of individual variables (SNPs) on each of the retained factors while minimizing their inter-factor correlations [15]. For example, SNPSpD simply selects one SNP with the largest factor loading from each factor; and the eigen2htSNP selects representative SNPs that have the largest loading averages in the leading factors. While the orthogonal rotation is computationally efficient, it focuses exclusively on LD information.

Combine IFS and LD to Enhance SNP Selection

The current method enhances tagSNP selection by combining information from two sources by weighted factor analysis (WFA) using oblique rotations. This is achieved by: (1) extending the IFS method [11] by developing an algorithm and computer programs to perform automated queries of online databases to collect relevant transcriptional factor binding site and conservation information; (2) constructing a weight matrix based on the imputed functional importance of the selected SNPs; and (3) using the weight matrix to perform oblique rotations on factors derived from pair-wise LD data. This algorithm is designed to select tagSNPs with the greatest functional potential while still maximizing LD information content.

Algorithm and Implementation

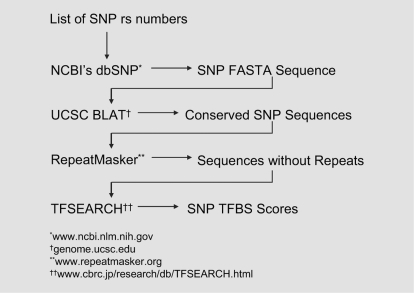
The major components of the proposed extended IFS algorithm are shown in figure 1. The first steps of the algorithm are to retrieve the sequence flanking the SNP (20 bp both upstream and downstream), to mask repetitive and low complexity elements, and to assess for conservation across species. Using TRANSFAC [16], a web-based program designed to query sequence fragments against transcription factor binding site databases, it is determined whether the resulting sequence contains consensus sequences which may be indicative of transcription factor binding (i.e., a transcription factor binding site [TFBS]). Unlike the method by [9] where an allele-based IFS was estimated for each allele of a SNP for the purpose of association analyses, the current method defines a composite, site-based IFS for both alleles of a SNP since the factor analysis operates on pairwise LD data that is calculated between SNPs and not their respective allelic variants. The site-based IFS is calculated by equation 1, where TFBS_i^SNP is the i-th TFBS score for a given SNP, m is the number of TFBSs associated with the given SNP (as determined from the database built by the IFS algorithm), and n is the total number of SNPs in consideration. The value of IFS is normalized (maximum of 1) and reflects the relative potential functional importance of the SNP.

$$IFS\left(SNP\right)=\frac{{\displaystyle \sum _{i=1}^{m}TFB{S}_i^{SNP}}}{{\displaystyle \sum _{j=1}^n{\displaystyle \sum _{i=1}^{m}TFB{S}_i^{SN{P}_j}}}}$$ (1)

Fig. 1.

Flowchart of IFS calculation by extending the PromoLign algorithm. Imputed functional score (IFS) of a SNP was estimated by processing formation gathered from a list of public databases for sequences flanking the SNP, cross-species conservation, and transcription factor binding capability of the sequences.

A target factor pattern reflecting the imputed functional information of the SNPs is then constructed based on the IFS values. This involves assigning the IFS for each SNP to specific factors in a target matrix. In optimizing the algorithm, two slightly different methods of constructing pattern matrices were tested. One construction mimics the SNP LD factor pattern by placing the IFS associated with each SNP on the same factor in the target pattern that also had the greatest loading for the SNP in the LD factor patterns. The alternative construction builds a target factor pattern by grouping SNPs with similar weights, as determined by the IFS algorithm, within the same factor (see pseudo-code below). In each case, the number of factors in the target factor pattern is determined by the number required to explain a prespecified proportion of the variance [17]. As the latter method yields target patterns that are more reflective of the functional importance of each SNP given its IFS value, this construction method was used to generate the results presented henceforth.

1. Given a list of SNPs {SNP₁ … SNP_N} and a list of IFSs {IFS₁ … IFS_N}, the target pattern T is an N×k matrix where k is the minimum number of required factors, as specified by Cheverud [17].

2. For any given SNP_m and 1 ≤ n ≤ k, the value of T_m,n is equal to IFS_m if n = k – [IFS_m*k] + 1 (where ‘[x]’ denotes the smallest integer ≥ x); or an assigned value of 0.001 otherwise.

To retrieve the WFA factor pattern, a Procrustes rotation is applied on the derived factors using the pattern discussed above as a target. Procrustes rotation is an oblique rotation method where preference is given to a partially specified target pattern [15]. It allows the user to specify a ‘target pattern’ matrix, which provides a means for incorporating prior knowledge of the hidden structure of interest. This target pattern was used to incorporate imputed functional information of SNPs into the selection of tagSNP. The outcome of the Procrustes rotation usually does not result in an exact match of the target matrix, but rather a new factor pattern that reflects the underlying importance of the original attributes assigned in the target pattern. Since Procrustes rotation is an oblique method, eigenvalues of the resulting factors are not directly linked to the proportion of the LD explained by the factors. Therefore, the SNP selection is derived from all factors resulting from the rotation. The new algorithm selects only the SNPs with the largest loading from each of the factors. The number of factors considered in the rotated factor pattern, k, is calculated by the total number of factors required to represent a fixed proportion of the variance in the original SNP LD data [17]. A set of Perl scripts and SAS routines were coded to perform all database queries and calculations in an automated fashion.

The proposed WFA method was applied to a set of 129 genes directly sequenced by the SeattleSNPs PGA for the purpose of SNP discovery; this genotype data has been made available on their project website. DNA samples from two ethnic samples (African-descent and European-descent subjects) were studied. The African-descent sample consists of 24 African-American individuals and the European-descent sample consists of 23 CEPH Parents, both from the Coriell Cell Repository (http://locus.umdnj.edu/nigms/). Only true biallelic SNPs (triallelic SNPs and insertion/deletions excluded) were considered to allow estimation of LD among all SNPs. Analyses were performed separately in each race group in order to minimize the effect of potential differences in SNP allele frequencies and haplotype structures across different populations. To evaluate performance of WFA, we considered 3 LD-based methods: SNPSpD by Nyholt et al. [9], eigen2htSNP by Lin et al. [14], and ldSelect by Carlson et al. [8]. The ldSelect identifies ‘bins’ of SNPs with pairwise LD exceeding a threshold level measured by r², and designate all SNPs in a bin that meet the criterion as tagSNPs (even though only one tagSNP is needed per bin). Therefore, the ldSelect is not directly comparable to WFA which removes such apparent redundancy by factor analysis. The eigen2htSNP and SNPSpD both use PCA to determine ‘effective’ number of tagSNPs, and can be overly conservative (selecting more tagSNPs than minimal) when there are higher order LD (very strong LD among >2 SNPs). The eigen2htSNP is much more conservative and in our analyses almost always select more SNPs than SNPSpD (many times selected almost all SNPs with MAF >10%). Therefore, we present below only comparisons of the new method to SNPSpD.

Results

WFA Yields More Focused SNP Selection

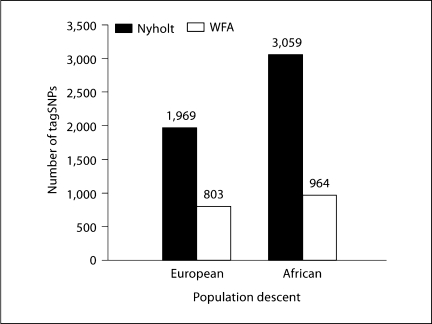
The total number of tagSNPs selected to represent all 129 genes was approximately a 2- to 3-fold fewer using the WFA method compared to the strictly LD-based approach (data is presented for each race group, fig. 2).

Fig. 2.

Comparison of total number of tagSNPs selected by WFA and SNPSpD. SNP selections of tagSNP were compared for the 129 genes sequenced by the SeattleSNPs PGA in both European- and African-descent populations. The WFA method selected fewer SNPs than SNPSpD in both populations, suggesting that the WFA approach resulted in more focused selection of tagSNPs sets.

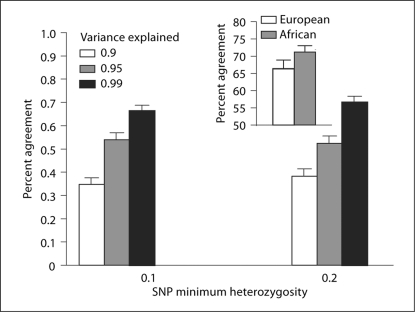
However, in both race groups, the sets of tagSNPs selected by the WFA method overlapped substantially with that selected by the SNPSpD method. For any particular gene, the percent agreement was defined as the proportion of SNPs selected by WFA that were also selected by SNPSpD. The percent agreement observed between the methods suggests that a core set of SNPs is selected largely due to underlying LD structure; however, the remaining SNPs selected by WFA were due to their imputed functional importance. The average percent agreement using two lower bounds of SNP heterozygosity (0.1 and 0.2) is shown in figure 3.

Fig. 3.

Proportion of SNPs selected by WFA that were also selected by SNPSpD. Percent agreement between the two methods (WFA and SNPSpD) was shown for varying levels of minimum SNP heterozygosity and the amount of variance explained by the selected SNPs. It was clear that the latter had greater effect on the agreement. On average, percent agreement of WFA to SNPSpD was greater in the African- than in the European-descent population (insert).

Greater percent agreement was found for tagSNP selection in the African-descent sample than in the European-descent sample (fig. 3, insert), probably a reflection of relatively smaller haplotype blocks in that population. However, including more rare SNPs (with lower heterozygosity) led to slightly less agreement of the two methods in both races.

WFA Is More Useful in Larger Genes

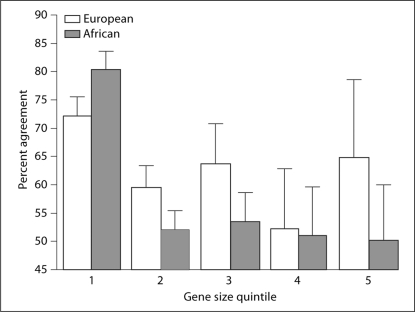
Empirical and simulation studies have shown that the average size of haplotype blocks (defined by regions of high LD) is about 16 kb [1, 18, 19]. As such, smaller genes are likely to have better-defined LD structures and can often be well-represented by fewer LD blocks. Therefore, the agreement between the two methods is expected to be lower in larger genes compared to smaller genes due to the greater complexity of the underlying LD block structure found in the larger genes. The 129 genes were divided into quintiles based on the number of SNPs discovered (correlated with the gene size) in each gene and the percent agreement within each quintile was determined (fig. 4 and table 1).

Fig. 4.

More diverse selections by WFA and SNPSpD in larger genes. Percent agreement of WFA to SNPSpD is shown as a function of quintile of gene sizes (1 for smallest genes and 5 for largest genes). The gene size quintile had a significantly negative effect on the percent agreement in both populations (p = 0.047 for European-descent and p<0.001 for African-descent) suggesting that the WFA selections contained a greater proportion of unique SNPs (i.e., not selected by SNPSpD) in larger genes.

Table 1.

WFA resulted in more focused tagSNPs selection

Genesize quintile	Number of genes	SNPSpD a	WFAa	Agreementb
African-American
1	45	486 (10.8)	145 (3.2)	0.80
2	41	931 (22.7)	272 (6.6)	0.52
3	22	763 (34.7)	210 (9.5)	0.53
4	12	475 (39.6)	152 (12.7)	0.51
5	9	404 (44.9)	185 (20.6)	0.50
Total	129	3,059 (23.7)	964 (7.5)	0.62
Caucasian
1	58	466 (8.0)	161 (2.8)	0.72
2	43	703 (16.3)	284 (6.6)	0.59
3	14	352 (25.1)	161 (11.5)	0.64
4	11	348 (31.6)	141 (12.8)	0.52
5	3	100 (33.3)	56 (17.7)	0.64
Total	129	1,969 (15.3)	803 (6.2)	0.62

^aTotal number of SNPs selected as tagSNPs by SNPSpD and WFA for all genes in quintile (average SNPs per gene in quin-tile).

^bThe proportion of SNPs selected by WFA also selected by SNPSpD.

The average number of SNPs selected per gene is shown according to gene size is also shown in table 1. In both races, linear regression models found significant negative effect of the size of the genes (represented by total number of SNPs discovered in each gene) on the percent agreement between the two methods (p = 0.047 for European-descent and p < 0.001 for African-descent samples), suggesting that the proposed WFA approach may be particularly useful in larger genes where LD blocks structure is more complex.

Selection with More Functional SNPs

To understand how WFA may offer an advantage over the solely LD-based SNPSpD, a literature review was performed to identify English-language peer-reviewed original manuscripts of association studies (single SNPs or haplotypes) in humans in a subset of 24 candidate genes using PubMed (http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?DB=pubmed). A total of 53 SNPs were identified in the literature search of these 24 genes. Among these 24 genes, WFA selected 119 tagSNPs whereas SNPSpD selected 281 SNPs (table 2). The tagSNPs found by the literature review were grouped as follows: (1) ‘Perfect Match’ when the specific SNP discussed in the manuscript was itself a tagSNP; (2) ‘LD = 1’, and (3) ‘1 > LD > 0.5’ where the literature SNP was in either perfect or meritorious LD with a tagSNP, respectively. Five tagSNPs from both selection methods were found in the literature, three of which were common to both methods. For each method, the proportion of literature SNPs captured in the tagSNP sets (i.e., sum of columns 3, 4, and 5 to the total number of tagSNPs in column 2, value shown in column 6) reflects each method's ability to identify SNPs with potential functional importance. Among the WFA tagSNPs, a greater proportion overlapped with the literature SNPs, suggesting that WFA may identify a greater number of SNPs with functional importance from a more parsimonious tagSNP panel. This was true independent of the size of the genes. For example, table 3 shows the results of four genes of variable sizes randomly selected from the list, where WFA always tended to select a higher proportion of tagSNPs that were either found in functional studies in the literature or in strong LD with such a SNP.

Table 2.

WFA selects a greater proportion of SNPs represented in review of literature^a

	Number of tagSNPs	Perfect match	LD = 1 b	1 > LD > 0.5 b	Literature SNPs captured
SNPSpD	281	5	10	29	15.6%
WFA	119	5	18	7	25.2%

^aBy literature review of 24 genes using PubMed.

^bMaximum LD between SNP represented in the literature and any tagSNP selected by each method.

Table 3.

Examples of literature review of tagSNPs in candidate genes

Candidate gene	SNPsin literature (totalSNPs)	European-descenta		African-descent a
		WFA	SNPSpD	WFA	SNPSpD
ADRB1	2 (67)	3 (5)	6 (10)	3 (8)	3 (13)
APOH	5 (129)	2 (6)	2 (18)	2 (12)	4 (24)
CSF2	4 (30)	2 (4)	2 (5)	2 (7)	3 (11)
CYP4F2	1 (144)	3 (6)	3 (20)	2 (8)	1 (25)

^aSNPs either identical or in high LD with literature SNPs (total number tagSNPs selected for the gene).

Discussion

Optimal selection of tagSNPs is an important, yet challenging task in genetic association studies and is pertinent in both candidate gene and whole-genome studies. In studies of complex diseases, where the number of candidate genes is expected to be large, this problem is even more apparent. Early SNP association studies predominantly focused on a relatively few number of non-synonymous (coding) SNP resulting in amino acid changes; however this strategy ignores variants leading to changes in gene expression or mRNA stability. TagSNPs selected based on underlying linkage disequilibrium (LD) structure provides the basis for the HapMap project [1], which strives to identify informative SNPs at the whole-genome level and in multiple populations. Several recent studies used LD information to select tagSNPs in local regions of interest [8, 9, 14, 20]. However, there is currently no method to integrate multiple sources of information for optimal selection of informative tagSNPs in studies using high-density SNPs.

In a previous study, we developed a method of imputed functional score (IFS) for SNP association analysis, and applied IFS to analyzing association of hypertension-related traits and SNPs in AGT (angiotensinogen) in a large study (n = 1,426) where power was much enhanced by modeling IFS of SNPs [9]. The findings encouraged us to further incorporate functional information in SNPs in selecting tagSNPs. The current study presents a new method that applies a weighted factor analysis (WFA) approach to combine LD information with SNP-based imputed functional scores (IFS) for tagSNP selection. Pair-wise LD information was analyzed in a manner similar to previously described methods to generate tagSNPs that capture a specified proportion of the total variation of the LD structure [9]. The potential functional importance of SNPs was imputed by extending an existing algorithm developed by our group [7, 11]. The imputed functional score (IFS) was then used to construct a factor pattern to generate a target matrix for Procrustes (oblique) factor rotation analysis. Application of the new method to SNPs in candidate genes resulted in selections of fewer tagSNPs compared with other LD-based methods. This was likely partially due to the oblique rotation that is known to be more suitable for handling higher order LD in SNPs in candidate genes [21]. Further studies are underway to investigate how much of the reduction was due to oblique rotation alone and, more importantly, how to achieve optimal reduction without eliminating key representative SNPs under oblique rotation.

The SNP functional importance was imputed using SNP sequence information from the National Center for Biotechnology Information (NCBI) database, conservation information from the University of California Santa Clara (UCSC) mouse BLAST-like alignment tool (BLAT), and TFBS information from the TFSEARCH database. Recent bioinformatics studies of promoter SNPs [23] and empirical functional studies of non-coding sequences [12, 13] indicate that the information of conservation and TF binding capacity in flanking sequences can indeed be extended to assess functional potential of variants across the genome in general. However, we are aware that functional information exists beyond these two types, and the method presented is by no means complete. There are many ways to extend the proposed IFS algorithm to be more inclusive and therefore more informative. For example, one may consider using degree of conservation of the flanking sequences of SNPs across more distant species, weight on locations of SNPs (promoter regions, CpG islands, 5′UTRs, translation start/stop sites, splice sites, coding exons, etc.), or model secondary and tertiary structure implication of flanking sequences. As more databases resources become available [22], better tagSNPs selection may be possible by integrating such information with LD structure as we have done by WFA.

As expected, the integration of the imputed SNP function into the process of tagSNP selection helped resolve the ambiguity problem where multiple SNPs may appear equally important based on LD information alone. The results from applying the proposed WFA method to SNPs in 129 candidate genes sequenced by the SeattleSNPs PGA were shown. For a wide-range of SNP characteristics, including minor allele frequency, candidate gene size, and explained proportion of variation of LD, selections by the WFA approach were generally more focused on SNPs more likely to have functional importance. Because existing selection programs do not discriminate SNPs known or suspected to have functional significance in a systematic way, this new method provides a utility to allow prioritization of SNPs for genotyping and analysis. This will help studies where highly dense SNPs in candidate regions are likely to yield large pockets of SNPs in perfect LD.

It remains to be seen how the WFA algorithm will perform when applied to very large sets of SNPs (e.g., at the whole-genome level). One of the practical difficulties will be the size of the resulting factor pattern. The genotype data used in the present study consists of an overwhelmingly large number of SNPs in a relatively small number of subjects, which inevitably results in less stable LD estimates in pockets across the genome. This added variability in LD structure may affect the resulting factor rotations. However, the general utility of the new method remains. For example, future strategies could include combining the WFA selection with other methods that assess the genome-wide robustness of LD estimates [23] or means of multi-level selections. Because the target matrix used in the Procrustes rotation is representative of the information associated with each SNP, independent of the LD structure, there are many ways to incorporate this information into the selection process by constructing different factor patterns. As more information is obtained about the functional potential of SNPs, extension of this new WFA approach may lead to more optimal selection of tagSNPs, and consequently more efficient genetic association studies.