Abstract
It is widely recognized that the mixed linear model is an important tool for parameter estimation in the analysis of complex pedigrees, which includes both pedigree and genomic information, and where mutually dependent genetic factors are often assumed to follow multivariate normal distributions of high dimension. We have developed a Bayesian statistical method based on the decomposition of the multivariate normal prior distribution into products of conditional univariate distributions. This procedure permits computationally demanding genetic evaluations of complex pedigrees, within the user-friendly computer package WinBUGS. To demonstrate and evaluate the flexibility of the method, we analyzed two example pedigrees: a large noninbred pedigree of Scots pine (Pinus sylvestris L.) that includes additive and dominance polygenic relationships and a simulated pedigree where genomic relationships have been calculated on the basis of a dense marker map. The analysis showed that our method was fast and provided accurate estimates and that it should therefore be a helpful tool for estimating genetic parameters of complex pedigrees quickly and reliably.
MUCH effort in genetics has been devoted to revealing the underlying genetic architecture of quantitative or complex traits. Traditionally, the polygenic model has been used extensively to estimate genetic variances and breeding values of natural and breeding populations, where an infinite number of genes is assumed to code for the trait of interest (Bulmer 1971; Falconer and Mackay 1996). The genetic variance of a quantitative trait can be decomposed into an additive part that corresponds to the effects of individual alleles and a part that is nonadditive because of interactions between alleles. Attention has generally been focused on the estimation of additive genetic variance (and heritability), since additive variation is directly proportional to the response of selection via the breeder's equation (Falconer and Mackay 1996, Chap. 11). However, to estimate additive genetic variation and heritability accurately, it can be important to identify potential nonadditive sources in genetic evaluations (Misztal 1997; Ovaskainen et al. 2008; Waldmann et al. 2008), especially if the pedigree being analyzed contains a large proportion of full-sibs and clones, as these in particular give rise to nonadditive genetic relationships (Lynch and Walsh 1998, pp. 145). The polygenic model using pedigree and phenotypic information, i.e., the animal model (Henderson 1984), has been the model of choice for estimating genetic parameters in breeding and natural populations (Abney et al. 2000; Sorensen and Gianola 2002; O′Hara et al. 2008).
Recent breakthroughs in molecular techniques have made it possible to create genome-wide, single nucleotide polymorphism (SNP) maps. These maps have helped to uncover a vast amount of new loci responsible for trait expression and have provided general insights into the genetic architecture of quantitative traits (e.g., Valdar et al. 2006; Visscher 2008; Flint and Mackay 2009). These insights can help when calculating disease risks in humans, when attempting to increase the yield from breeding programs, and when estimating relatedness in conservation programs. High-density SNPs of many species of importance to science and agriculture can now be scored quickly and relatively cheaply, for example, in mice (Valdar et al. 2006), chickens (Muir et al. 2008), and dairy cattle (VanRaden et al. 2009).
In the analysis of populations of breeding stock, the inclusion of dense marker data has improved the predictive ability (i.e., reliability) of genetic evaluations compared to the traditional phenotype model, both in simulations (Meuwissen et al. 2001; Calus et al. 2008; Hayes et al. 2009) and when using real data (Legarra et al. 2008; VanRaden et al. 2009; González-Recio et al. 2009). Meuwissen et al. (2001) suggested that the effect of all markers should first be estimated, and then summed, to obtain genomic estimated breeding values (GEBVs). An alternative procedure, where all markers are used to compute the genomic relationship matrix (in place of the additive polygenic relationship matrix) has also been suggested (e.g., Villanueva et al. 2005; VanRaden 2008; Hayes et al. 2009); this matrix is then incorporated into the statistical analysis to estimate GEBVs. A comparison of both procedures (VanRaden 2008) yielded similar estimates of GEBVs in cases where the effect of an individual allele was small. In addition, if not all pedigree members have marker information, a combined relationship matrix derived from both genotyped and ungenotyped individuals could be computed; this has been shown to increase the accuracy of GEBVs (Legarra et al. 2009; Misztal et al. 2009). Another plausible option to incorporate marker information is to use low-density SNP panels within families and to trace the effect of SNPs from high-density genotyped ancestors, as suggested by Habier et al. (2009) and Weigel et al. (2009). However, fast and powerful computer algorithms, which can use the marker information as efficiently as possible in the analysis of quantitative traits, are needed to obtain accurate GEBVs from genome-wide marker data.
This study describes the development of an efficient Bayesian method for incorporating general relationships into the genetic evaluation procedure. The method is based on expressing the multivariate normal prior distribution as a product of one-dimensional normal distributions, each conditioned on the descending variables. When evaluating the genetic parameters of natural and breeding populations, high-dimensional distributions are often used as prior distributions of various genetic effects, such as the additive polygenic effect (Wang et al. 1993), multivariate additive polygenic effects (Van Tassell and Van Vleck 1996), and quantitative trait loci (QTL) effects via the identical-by-decent matrix (Yi and Xu 2000). A Bayesian framework is adopted to obtain posterior distributions of all unknown parameters, estimated by using Markov chain Monte Carlo (MCMC) sampling algorithms in the software package WinBUGS (Lunn et al. 2000, 2009). By performing prior calculations in the form of the factorized product of simple univariate conditional distributions, the computational time of the MCMC estimation procedure is reduced considerably. This feature permits rapid inference for both the polygenic model and the genomic relationship model. Moreover, the decomposition allows for inbreeding of varying degree, since the correct genetic covariance structure can be inferred into the analysis. In this article, we test the method on two previously published pedigree data sets: phenotype data from a large pedigree of Scots pine, incorporation of information on both additive and dominance genetic relationships (Waldmann et al. 2008); and genomic information obtained from a genome-wide scan of a simulated animal population (Lund et al. 2009).
METHODS
Statistical model:
Following Henderson (1984), we made use of the following linear mixed effect model under Gaussian assumptions,
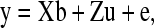 |
(1) |
where y is a vector of size n × 1 containing phenotypic records of a continuous trait for all members in the population; b is a vector of size p × 1 containing systematic environmental effects; u is a vector of size n × 1 containing genetic effects that follow a multivariate normal distribution with zero mean vector and covariance structure 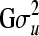 ; X and Z are known incidence matrices relating phenotypic records to respective location parameters included in (1); and e is a vector containing independent residual errors that follow a multivariate normal distribution with zero mean vector and covariance structure
; X and Z are known incidence matrices relating phenotypic records to respective location parameters included in (1); and e is a vector containing independent residual errors that follow a multivariate normal distribution with zero mean vector and covariance structure 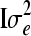 , where I is the identity matrix of order n. Note that records can be missing for some pedigree members (here, yi = NA if individual i has a missing record). Typically, u contains the additive polygenic effect, although nonadditive genetic effects such as dominance, or QTL effects estimated from marker data, could be included in the model. To make inferences in model (1), the mixed model equations can be formed, so that y is associated to
, where I is the identity matrix of order n. Note that records can be missing for some pedigree members (here, yi = NA if individual i has a missing record). Typically, u contains the additive polygenic effect, although nonadditive genetic effects such as dominance, or QTL effects estimated from marker data, could be included in the model. To make inferences in model (1), the mixed model equations can be formed, so that y is associated to 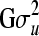 . A well-known, efficient Bayesian technique for the estimation of genetic parameters in the linear mixed effect model is MCMC methods (e.g., Wang et al. 1993; Sorensen and Gianola 2002; Bauer et al. 2009).
. A well-known, efficient Bayesian technique for the estimation of genetic parameters in the linear mixed effect model is MCMC methods (e.g., Wang et al. 1993; Sorensen and Gianola 2002; Bauer et al. 2009).
The most common distribution used for u in model (1) is the multivariate normal distribution (Lynch and Walsh 1998, pp. 194), since u contains n variables (u1, u2, … , un), that on their own are assumed to be normally distributed. The multivariate normal is, therefore, a natural choice of distribution for u. For example, the traditional polygenic model relies on normal distribution assumptions for the Mendelian inheritance of genes from parents to offspring (Bulmer 1971). In addition, when using Bayesian inference to estimate parameters in model (1), the choice of the multivariate normal distribution helps to form conditional distributions, which are of key importance in MCMC sampling (Sorensen and Gianola 2002; Rue and Held 2005). The hierarchical structure of model (1) can be usefully interpreted as a graphical model, which facilitates computations because this representation allows the joint distribution of genetic effects and other parameters to be broken down into products of local components (Lauritzen et al. 1990). In this article, genetic effects (u) are assumed to follow a Gaussian distribution with an imposed dependency structure given by the pedigree, estimated relatedness from markers, or both. The factorization of the dependency structure in the graph gives (1) a Markov property (Lauritzen et al. 1990), which can be successfully utilized in Bayesian MCMC methods. See Rue and Held (2005) for a comprehensive survey of this topic and see Steinsland and Jensen (2010) for how to use the Markov property for making inference in the classical animal model. In addition, the standard decomposition procedure of the additive polygenic effect (Thomas 1992; Lin 1999; Waldmann 2009) utilizes the Markov property of the animal model, where an offspring is conditioned on its parents in the analyzed pedigree.
Conditional expressions of multivariate normal distributions:
Drawing samples from multivariate normal distributions quickly becomes computationally demanding as the number of parameters becomes large, e.g., when performing genetic evaluations of complex pedigrees. A reasonable alternative, therefore, is to decompose the multivariate normal distribution into conditionally dependent parts. If we replace the multivariate normal prior, with the product of these (lower dimensional) distributions, both the mean and the variance are shifted, for each conditional distribution. Let us assume that we wish to decompose u into two subsets of column vectors, 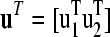 , where u1 and u2 are of length l and n – l, respectively. The mean and variance can be expressed as
, where u1 and u2 are of length l and n – l, respectively. The mean and variance can be expressed as
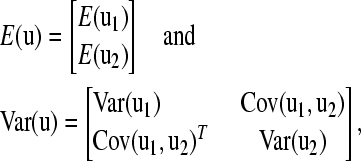 |
(2) |
where 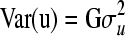 is believed to be a positive definite, symmetric matrix of order n. By decomposing the multivariate normal distribution (Jensen 1998), we obtain:
is believed to be a positive definite, symmetric matrix of order n. By decomposing the multivariate normal distribution (Jensen 1998), we obtain:
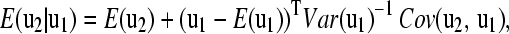 |
(3) |
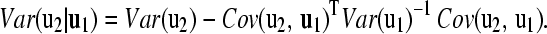 |
(4) |
Hence, the distribution of u2 conditional on u1 is multivariate normal according to
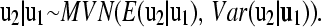 |
(5) |
More generally, for 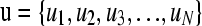 , where N is the number of partitions of u (typically the number of members in the pedigree, i.e., N = n), we have
, where N is the number of partitions of u (typically the number of members in the pedigree, i.e., N = n), we have
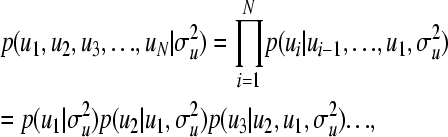 |
(6) |
where 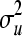 is the variance component of u. Our target is to generate u, which is a realization from a multivariate normal distribution with given mean (vector of zeros) and covariance structure
is the variance component of u. Our target is to generate u, which is a realization from a multivariate normal distribution with given mean (vector of zeros) and covariance structure 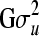 . The vector u is here generated by element-wise draws,
. The vector u is here generated by element-wise draws, 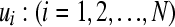 , from univariate (lower-dimensional) normal distributions conditioned on all the elements that have been drawn so far, i.e., from
, from univariate (lower-dimensional) normal distributions conditioned on all the elements that have been drawn so far, i.e., from 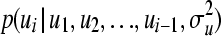 . It should be emphasized that this sequential strategy is exact and will lead to the correct vector u, drawn from the full multivariate normal distribution MVN(0,
. It should be emphasized that this sequential strategy is exact and will lead to the correct vector u, drawn from the full multivariate normal distribution MVN(0, 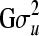 ). First, let us assume individual-wise partitions for u. Conditional expectation and conditional variance of
). First, let us assume individual-wise partitions for u. Conditional expectation and conditional variance of 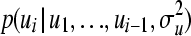 are thought of here as the weighted mean and the weighted variance for pedigree member i. To compute weights for the mean (for individual i), the following general expression can be used:
are thought of here as the weighted mean and the weighted variance for pedigree member i. To compute weights for the mean (for individual i), the following general expression can be used:
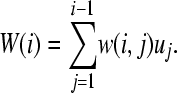 |
(7) |
The precalculated weights are then read into WinBUGS together with the data. The code for the weights in the model includes only one indexed univariate normal distribution with conditional mean (Equation 7) and variance (Equation 4) as a prior for ui. Hence, for every pedigree member i, we have one vector 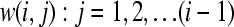 calculated for the mean where most of the terms are zero; this feature yields a sparse format that is suitable for storing the weights. The weights for the mean (w(i, j)) and variance, which specify the conditional prior distribution of each individual, need to be calculated only once and are thus computed outside the MCMC estimation (i.e., before compilation of the code). The order of the weights is important since the drawing of samples needs to follow the same unique order throughout the simulation process. Furthermore, it is also possible to use the same principle to update the parameters in blocks, sampling from multiple multivariate normal distributions, each of small dimension. When estimating the additive polygenic effect, the approach proposed here gives identical results to the standard decomposition suggested earlier (e.g., Thomas 1992; Lin 1999; Waldmann 2009) for noninbred pedigrees (nonrelated parents). Our proposed method could, however, incorporate nonzero covariances between parents, and inbreeding coefficients greater than zero, if complex relationships between relatives arising from dominance are neglected (e.g., Abney et al. 2000). Two small numerical examples for computing a realization of additive and dominance polygenic effects and illustrating the effect of inbreeding on the additive polygenic covariance structure are given in the Appendix.
calculated for the mean where most of the terms are zero; this feature yields a sparse format that is suitable for storing the weights. The weights for the mean (w(i, j)) and variance, which specify the conditional prior distribution of each individual, need to be calculated only once and are thus computed outside the MCMC estimation (i.e., before compilation of the code). The order of the weights is important since the drawing of samples needs to follow the same unique order throughout the simulation process. Furthermore, it is also possible to use the same principle to update the parameters in blocks, sampling from multiple multivariate normal distributions, each of small dimension. When estimating the additive polygenic effect, the approach proposed here gives identical results to the standard decomposition suggested earlier (e.g., Thomas 1992; Lin 1999; Waldmann 2009) for noninbred pedigrees (nonrelated parents). Our proposed method could, however, incorporate nonzero covariances between parents, and inbreeding coefficients greater than zero, if complex relationships between relatives arising from dominance are neglected (e.g., Abney et al. 2000). Two small numerical examples for computing a realization of additive and dominance polygenic effects and illustrating the effect of inbreeding on the additive polygenic covariance structure are given in the Appendix.
Bayesian inference of the factorized model:
Following Waldmann (2009), uniform distributions were assigned as priors to the standard deviations, since this prior distribution was shown to be a good and robust noninformative choice of prior for variance components (Gelman 2006). This prior corresponds to a truncated inverse-χ2 distribution with −1 degree of freedom, that is, 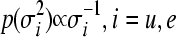 . To obtain an upper boundary for the uniform distributions, we performed a preliminary analysis in which uninformative inverse-gamma distributions were assigned as priors for the variance components, thereby obtaining estimates of standard deviations; these were then multiplied by 5 to obtain the upper bounds.The chosen upper bounds were considerably larger than the upper bounds of the 95% highest probability density (HPD; Box and Tiao 1973) regions obtained in the preliminary analysis. Note that this procedure is a pragmatic solution and should not be viewed as a strictly Bayesian solution. A flat, noninformative prior was assigned to the systematic environmental fixed effect in both examples, as bj ∼ N(0, 106) for systematic effect level j. For u, we used the common multivariate normal distribution as prior: u ∼ MVN(0,
. To obtain an upper boundary for the uniform distributions, we performed a preliminary analysis in which uninformative inverse-gamma distributions were assigned as priors for the variance components, thereby obtaining estimates of standard deviations; these were then multiplied by 5 to obtain the upper bounds.The chosen upper bounds were considerably larger than the upper bounds of the 95% highest probability density (HPD; Box and Tiao 1973) regions obtained in the preliminary analysis. Note that this procedure is a pragmatic solution and should not be viewed as a strictly Bayesian solution. A flat, noninformative prior was assigned to the systematic environmental fixed effect in both examples, as bj ∼ N(0, 106) for systematic effect level j. For u, we used the common multivariate normal distribution as prior: u ∼ MVN(0, 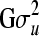 ) (Sorensen and Gianola 2002) and then used the decomposition of the multivariate normal distribution into univariate normal distributions, proposed here as
) (Sorensen and Gianola 2002) and then used the decomposition of the multivariate normal distribution into univariate normal distributions, proposed here as 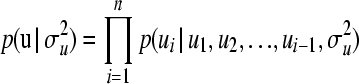 . The vector y is assumed to follow a Gaussian distribution; thus the likelihood function is given as
. The vector y is assumed to follow a Gaussian distribution; thus the likelihood function is given as
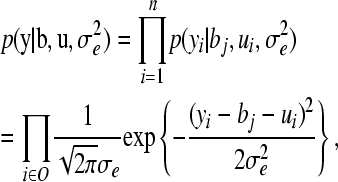 |
(8) |
where bj is the corresponding systematic effect level (covariate) of pedigree member i, connected through X, and O is the set of members in the pedigree for which phenotypic records are available. If conditioning on hyperparameters is neglected, and the location parameters are believed to be independent a priori, the joint distribution of all parameters conditional on the data is proportional to
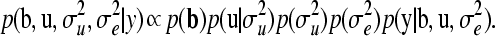 |
(9) |
The phenotype model (1) was run in the Bayesian software package WinBUGS (Lunn et al. 2000) version 1.4.3, which is freely available on http://www.mrc-bsu.cam.ac.uk/bugs/. WinBUGS exploits a graphical modeling technique to translate the supplied prior distributions of the parameters into corresponding full conditional distributions. The computation of the weights (7) using (3) and (4) was executed in ANSI C. The WinBUGS code is available in supporting information, File S1, while the computer code used for calculating weights is available in File S2. Because we place NA for phenotypes for individuals without a record, phenotype predictions for them are obtained as a by-product of the WinBUGS analysis. However, these predicted values do not influence the estimation of underlying model parameters. Therefore, random effects for those individuals are estimated on the basis of covariance structure only. To check mixing properties of our implementation in WinBUGS and compare the mixing to alternative implementations, we calculated the effective sample size (ESS) of the obtained MCMC chains (Kass et al. 1998; Waagepetersen et al. 2008). ESS can be seen as the number of independent samples from the estimated posterior that contain amounts of information equivalent to those of our dependent MCMC samples (i.e., exceed same-estimation accuracy). Low ESS values indicate poor mixing (i.e., high autocorrelation between consequtive samples) in the MCMC chain.
Polygenic example:
To verify our proposed decomposition method, data acquired from a 26-year-old field trial of Scots pine (Pinus sylvestris L.), previously published by Waldmann et al. (2008), Finley et al. (2009), Hallander and Waldmann (2009), and Waldmann (2009), were analyzed to obtain posterior distributions of additive and dominance polygenic effects for all trees in the pedigree. The pedigree consists of 52 parents crossed according to a partial diallel design resulting in mixed half-sib and full-sib families totaling 4970 surviving offspring. The parents were assumed to be nonrelated and noninbred. In total, 202 families were distributed over approximately 4 ha of forest. The field trial was subdivided into 70 square (or nearly square) blocks, which were used in the subsequent evaluations as a systematic environmental effect. Several traits of interest for breeding purposes were measured in 1997, although for the current study we chose to analyze only trunk diameter at breast height (DBH). The mean value of DBH was 114 mm. We made use of the following covariance structure in the mixed linear model: 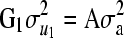 and
and 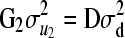 , where A is the additive relationship matrix;
, where A is the additive relationship matrix; 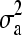 is the variance component of additive genetic effects; D is the dominance relationship matrix; and
is the variance component of additive genetic effects; D is the dominance relationship matrix; and 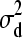 is the variance component of dominance genetic effects. A and D were calculated using standard equations (Lynch and Walsh 1998, pp. 763 and 768). Uniform densities were assigned as prior distributions for σa and σd as described in the previous section. See Waldmann et al. (2008), Finley et al. (2009), and Hallander and Waldmann (2009), for a more detailed analysis of the Scots pine pedigree.
is the variance component of dominance genetic effects. A and D were calculated using standard equations (Lynch and Walsh 1998, pp. 763 and 768). Uniform densities were assigned as prior distributions for σa and σd as described in the previous section. See Waldmann et al. (2008), Finley et al. (2009), and Hallander and Waldmann (2009), for a more detailed analysis of the Scots pine pedigree.
Genomic example:
This was a simulated data set, typical of the data acquired from an animal breeding protocol, consisting of 5865 pedigree members from seven generations. The data set is freely available from the QTLMAS XII workshop webpage, http://www.computationalgenetics.se/QTLMAS08/QTLMAS/DATA.html (Lund et al. 2009). Six thousand loci are evenly distributed over six chromosomes (1000 markers per chromosome), with 0.1 cM between markers. Forty-eight QTL, each of small effect, were assumed to code for the trait of interest. Pedigree and phenotype information were available from the first four generations of animals. The animals from generations five to seven had no given phenotype, but did have complete marker information. From each generation, 15 males and 150 females were randomly selected and mated according to a hierarchical mating design, resulting in a total of 1500 animals being born per generation. Interested readers are invited to consult Lund et al. (2009) for further details of the data set. The genomic relationship matrix (or realized relationship matrix) was computed using the second method proposed by VanRaden (2008), which follows G = ZDZ′. In this article, Z = M – P, where M is a matrix of size n × m containing genotypes at all m loci for all n members of the pedigree; P is a matrix of the same size containing allele frequencies that differ from 0.5 at all loci; and finally, D is a diagonal matrix of size m × m with diagonal elements 1/m[2pi(1−pi)], where pi is the allele frequency at locus i. We analyzed a subset of the complete pedigree consisting of the first four generations (1014 animals in total) to reduce computational time. See Table S1 for original identification numbers of pedigree members in the analyzed subpopulation.
RESULTS
Polygenic example:
To facilitate a comparison between the results obtained from our proposed method and the results reported by Waldmann et al. (2008), we performed the same procedure as Waldmann et al. (2008) when analyzing the Scots pine pedigree. One MCMC was run for a total of 225,000 iterations, from which the first 25,000 iterations were omitted (burn-in) from the analysis, and every 10th iteration was saved (thinned), resulting in an effective sample of 20,000 iterations. Table 1 shows the results of the analysis using our method, together with the results from Waldmann et al. (2008) for the trait DBH. Our posterior point estimates and their 95% HPD regions closely agree with those obtained by Waldmann et al. (2008), although slightly different degrees of freedom for the inverse-χ2 distributions used as prior to the variance components (−1 in our method while Waldmann et al. 2008 used −2 in theirs) could cause some differences in the respective posterior distributions. We believe, however, that the priors have little influence on the parameter estimates obtained from the analyzed data, mainly due to both the large size of the pedigree and the similar parameter estimates obtained by Waldmann et al. (2008) and Finley et al. (2009) using different priors.
TABLE 1.
Summary statistics including posterior estimates (mode, mean and median) and effective ESS obtained from the WinBUGS analysis in the polygenic model example for additive genetic variance (σa2), dominance genetic variance (σd2), residual variance (σe2), heritability (h2), and dominance proportion (d2)
| Mode |
Mean |
Median |
95% HPD region |
ESS |
REML |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | DEC | HYB | DEC | HYB | DEC | HYB | DEC | HYB | DEC | HYB | HYB |
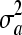 |
53.16 | 54.70 | 63.29 | 62.52 | 60.49 | 59.62 | [29.47, 103.1] | [27.67, 103.7] | 376.4 | 417.2 | 55.95 |
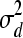 |
77.56 | 82.88 | 84.69 | 88.41 | 82.5 | 85.71 | [39.86, 136.9] | [39.70, 142.2] | 399.2 | 456.8 | 83.06 |
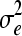 |
726.4 | 722.2 | 724.3 | 721.7 | 725.0 | 722.6 | [670.7, 778.3] | [665.3, 776.8] | 733.2 | 756.1 | 728.5 |
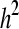 |
0.0617 | 0.0630 | 0.0724 | 0.0714 | 0.0694 | 0.0685 | [0.0340, 0.1158] | [0.0327, 0.1170 | 372.2 | 420.9 | 0.0645 |
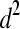 |
0.0894 | 0.0939 | 0.0970 | 0.1014 | 0.0946 | 0.0983 | [0.0463, 0.1567] | [0.0500, 0.1616] | 394.5 | 447.5 | 0.0957 |
The results of the decomposition approach are denoted DEC while the results of Waldmann et al. (2008) are denoted HYB including both MCMC estimates and restricted maximum likelihood (REML) estimates.
The additive and dominance covariance structures resulted in 9940 and 61,247 nonzero weights, respectively. For variance components and heritability, 95% HPD intervals were estimated using the R library, “boa” (Smith 2007). In WinBUGS, each scan of the MCMC took 0.4241 sec on an AMD Opteron Dual Core Processor (2.39 GHz) with 1 GB of RAM. The corresponding average time, for each MCMC scan, using the method in Waldmann et al. (2008) was 1.840 sec. In each iteration in the MCMC procedure, all nonzero weights for means need to be multiplied by the corresponding genetic parameter of the preceding pedigree members (a matrix–vector multiplication: see Equation 7). The actual number of nonzero weights depends on the covariance structure, as more nonzero relationships will result in a higher number of nonzero weights. For the Scots pine data, little computational time was needed to obtain reliable posterior estimates due to the sparseness of the additive and dominance polygenic relationship matrices. Consequently, the total computational time is greatly reduced in the current example because of the few nonzero weights. Hence, our proposed method seems to be very beneficial for analyzing polygenic data.
The slightly lower ESS (sample size adjusted for autocorrelation) obtained by our method reflects the fact that single-site Gibbs sampling is performed in WinBUGS, while the hybrid Gibbs sampler, proposed by Waldmann et al. (2008), also applies block updating of parameters, which is known to improve the mixing of the MCMC chain. In addition, the transformation of genetic covariance structures applied in Waldmann et al. (2008) improves the ESS further. However, in this case, the marginally lower ESS of the current method is well compensated for by the improved speed. Furthermore, we tested two additional updating options (block hybrid and conjugated multivariate) in OpenBUGS version 3.0.3 (Thomas et al. 2006), to see whether the ESS was improved. Only the ESS of dominance genetic effects was improved while the ESS of the other parameters was unaffected or even decreased (results not shown). On the other hand, the computing time increased markedly: we therefore believe that the standard updating (multivariate forward) option in WinBUGS/OpenBUGS gives acceptable mixing of the MCMC. Furthermore, we investigated whether changing the sequential order of conditioning would generate a different number of weights and, thereby, a difference in computational time. However, the number of weights remained the same, regardless of the sequence, and we therefore can conclude that the order is unimportant from a computational perspective.
Genomic example:
First, a purely additive polygenic model was used to obtain initial values of the variance components for all 225,000 iterations. A preliminary analysis was then conducted to estimate the standard deviations of the variance components, which were used to set the upper limit of the uniform prior distributions. The MCMC procedure was run for 45,000 scans in total, from which the first 35,000 scans were discarded to give 10,000 saved iterations. The heritability estimates obtained are shown in Table 2. The posterior point estimates from our analyzed subset agree closely with the true corresponding parameter values given in Lund et al. (2009), both for posterior mean and mode. However, the additive polygenic model resulted in heritability point estimate being too large, although with both models, true value is included within the estimated 95% HPD regions. In addition, in Table 2, it is important to note that the 95% HPD region obtained by a genomic model is clearly more narrow than the one given by a polygenic model, suggesting that the inclusion of the genomic relationship matrix improves the estimation accuracy of heritability. Similar conclusions have been drawn by, for example, Meuwissen et al. (2001), Villanueva et al. (2005) and Hayes et al. (2009). For a thorough explanation of improved accuracy, see Xu (2006).
TABLE 2.
Posterior estimates obtained from the WinBUGS analysis in the genomic model example for heritability (h2) using a model including genomic relationship matrix (Gσu2) and a model including additive polygenic relationship matrix (Aσa2)
| Model | Mode | Mean | Median | 95% HPD region |
|---|---|---|---|---|
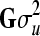 |
0.3053 | 0.3052 | 0.3052 | [0.2675, 0.3433] |
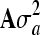 |
0.3376 | 0.3418 | 0.3397 | [0.2191, 0.4691] |
The true value of 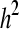 for the entire pedigree should be 0.3 (Lund et al. 2009).
for the entire pedigree should be 0.3 (Lund et al. 2009).
The computational effort in the genomic example was unfortunately massive, due to the large number of nonzero weights (in total, 513,591). On the same computer as that used for the polygenic example, each scan took 39.40 sec. Initially, we truncated small elements in the genomic relationship matrix to reduce the number of nonzero elements, but this modification effectively prevented convergence of the MCMC chain. Truncating small values in the resulting weight matrix, instead of the genomic matrix itself, might be a more suitable procedure because the individual weights for computing the variance of each genetic parameter (i.e., each normal distribution) are correctly calculated given the genomic covariance matrix, and only weights used for computing the mean of each normal distribution are affected. Conversely, if elements in the genomic covariance structure are truncated before the decomposition procedure, then weights for computing the means and the variances of the normal distributions of all parameters are affected. By truncating small elements in the weight matrix, the computational time could potentially be greatly reduced, although the accuracy of estimated posterior and 95% HPD regions would be negatively affected. However, some preliminary experiments on truncating weights have given promising results (i.e., the obtained posterior estimates were only slightly affected), although we chose to include the full-weight matrix when analyzing the simulated data (other results not shown).
DISCUSSION
Decomposition of high-dimensional multivariate normal distributions provides a very flexible Bayesian method that allows us to make inferences in linear mixed effect models with a large number of genetic parameters. For example, the proposed method can be used for the following: variance component-based linkage and association mapping methods for the estimation of QTL effects; estimating nonadditive genetic effects, such as dominance and epistasis; estimation of genomic breeding values; and estimation of maternal and permanent environmental effects, which are important in breeding evaluations. The approach was implemented in the user-friendly computer software WinBUGS and was shown to be fast and accurate on both real and simulated data. By using this approach, researchers will be able to perform advanced genetic evaluations of complex traits and pedigrees without possessing advanced knowledge in animal models and programming.
Recently, several studies have shown that the accuracy of genetic evaluations can be increased by incorporating the genomic relationship matrix (Villanueva et al. 2005; Hayes et al. 2009; Misztal et al. 2009). For large, complex pedigrees with a high number of polymorphic markers, the resulting genomic relationship matrix will probably be dense, i.e., most pedigree members will have nonzero, pairwise estimated relatedness. A general problem with this approach is that when making inferences in animal models, most currently available methods rely on either sparse solvers (e.g., Schaeffer and Kennedy 1986; Johnson and Thompson 1995; Waldmann et al. 2008) or efficient graph model techniques (Wilkinson and Yeung 2004; Rue and Held 2005; Steinsland and Jensen 2010). Compared to standard, nonsparse methods, these methods will not result in the same reduction in computational time when incorporating sparse covariance structures (i.e., when using pedigree information only). Unfortunately, even though our proposed method can handle dense genetic covariance structures, as demonstrated in the genomic example, the computational time required is massive. One way to overcome this hurdle would be to truncate small elements in the weight matrix obtained by our approach, thereby obtaining a good approximation of the genetic covariance matrix. An alternative method would be to apply transformation on the covariance matrix to facilitate the inference of parameter estimation as, for example, suggested by Mrode and Thompson (1989), Wilkinson and Yeung (2004), and Waldmann et al. (2008). As a result, estimating parameters using the linear mixed model does not depend on the sparsity of the genetic covariance structure.
A good mixing property of the MCMC method is very important in Bayesian analysis to obtain reliable posterior estimates, especially if parameters are highly correlated in the model. In Gibbs sampling, the updater samples from the fully conditional posterior distribution, which is proportional to the likelihood function and the prior distribution through Bayes theorem. Our proposed method samples from the multivariate normal distribution for the prior, but samples from the likelihood function are taken for one parameter at a time, which introduces dependencies to the posterior (i.e., introduces higher correlation between parameters in the posterior as these are drawn elementwise). Thus, the mixing property of our algorithm does not match the mixing properties achieved with block updating of parameters, where sampling from both prior distribution and the likelihood are performed in a block (García-Cortés and Sorensen 1996; Roberts and Sahu 1997). On the other hand, for elementwise or single-site updating (without decomposition), sampling from both likelihood and prior are made for each parameter, which introduces heavy dependencies to the posterior distribution, resulting in poor mixing properties of the MCMC chain (Sorensen and Gianola 2002). Hence, our method should result in better mixing than single-site updating but should result in less effective mixing than block updating of parameters. This insight is confirmed, to some extent, empirically when the mixing property in our approach was compared to the mixing property of the standard single-site sampler (Sorensen and Gianola 2002) implemented in C (results not shown). However, this comparison should be interpreted while bearing in mind that WinBUGS uses an expert system that attempts to utilize the most appropriate sampling scheme for each stochastic node (Lunn et al. 2000, pp. 328).
If a better mixing property is warranted, one plausible alternative might be to combine our suggested decomposition approach with block updating of parameters into a hybrid sampler. A similar approach (i.e., combining single-site and block sampling) was implemented by Waldmann et al. (2008), which resulted in better mixing of the MCMC chain than was obtained in pure single-site updating. However, it would not be possible to implement the combined sampling approach in WinBUGS, as the block updating requires a large equation system to be solved during each iteration in the MCMC procedure. If only single-site sampling is possible (due to computational limitations), the parameters can be randomly updated in each MCMC step and not in the same sequential order, as suggested by Levine and Casella (2006). An additional alternative to improve mixing is to apply transformation of the location parameters in the model (Vines et al. 1996; Waldmann et al. 2008).
The lack of freely available computer packages designed for the genetic evaluation of complex pedigrees using a Bayesian framework has, unfortunately, prevented more regular use of these models. The graphical model representation within the Bayesian software package WinBUGS is very well suited for decomposition of joint distributions into products of local components, i.e., parent and offspring nodes in a directed acyclical graph (Lunn et al. 2000, 2009). WinBUGS also applies an intelligent, automatic approach to the choice of updaters needed in the implementation of the MCMC procedure. Both Damgaard (2007) and Waldmann (2009) successfully executed the animal model in WinBUGS and produced results that show how evaluating the genetics of complex pedigrees can be performed smoothly without the need of expensive hardware and software. As an extension to these studies, we have shown how general relationship structures can be decomposed and hence can be efficiently implemented in WinBUGS.
One important improvement offered by our proposed method, compared to the standard factorization method of additive polygenic effects (e.g., Thomas 1992; Lin 1999; Waldmann 2009), is the ability to obtain realizations from the correct additive covariance structure of inbred populations. If such populations are analyzed with the standard factorization model, additive variance, and consequently heritability, can be overestimated, depending on the level of inbreeding and the size of the pedigree. Problems with handling inbred pedigrees arise with the standard model because the covariances between parents are assumed to be zero. Since it is not uncommon to have some degree of inbreeding in both breeding and natural populations of animals and plants, the standard factorization of additive polygenic relationships can be erroneous. Differences in the estimated posterior of the polygenic variance components, obtained by the standard factorization model and our approach, need further verification in extensive computer simulations. It should be noted that the nonadditive genetic relationships, introduced by inbreeding, can have a considerable influence on the genetic variances (Harris 1964; Abney et al. 2000).
We have, in this study, demonstrated the benefit of decomposing the multivariate normal distribution, often used as prior for genetic effects in the standard, linear mixed effect model. To our knowledge, this procedure of decomposing the prior distribution has not been utilized before, in the context of parameter estimation in genetics. The decomposion approach was put forward and excecuted successfully in WinBUGS by Vines et al. (1996); they utilized a random effect model to analyze clinical data in the context of epidemiology. However, they did not include covariance between random effects, which makes the decomposition procedure more complex. In general, there also exist alternative procedures for efficiently implementing the prior distribution, which deserves more attention. One such alternative, which is likely to be equally as efficient as the approach presented here, is obtained by multiplying vector of univariate normal distributed variables by a Cholesky factor (square root) of the original covariance matrix (Golub and Van Loan 1996). As in our approach, (Cholesky) weights can be calculated once, prior to the WinBUGS analysis. Both procedures involves one matrix–vector multiplication each iteration in the MCMC process and are, therefore, likely to be computational equally time consuming for analysis of large pedigrees.
Acknowledgments
We thank the associate editor and three anonymous reviewers for comments that improved the manuscript.This work was supported by funding from the Research School of Tree Breeding and Forest Genetics for J.H. and P.W.; Föreningen svensk skogsträdsförädling for C.W. and P.W.; and research grants from the Academy of Finland and the University of Helsinki's Research Funds for M.J.S. In addition, the Scots pine data used in the polygenic example were provided by the Forestry Research Institute of Sweden, Skogforsk.
APPENDIX: CALCULATION OF WEIGHTS FOR DOMINANCE RELATIONSHIPS
We calculate conditional prior distributions for dominance genetic effects from the pedigree given in Table 3. The corresponding dominance polygenic relationship matrix, D, can be obtained as described in, for example, Waldmann et al. (2008) as
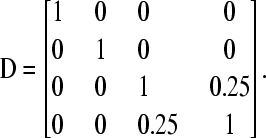 |
For individual 1: E(d1 |
 ) = 0, Var(d1) =
) = 0, Var(d1) =  , and d1 |
, and d1 | 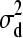 ∼ N(0,
∼ N(0, 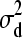 ).
).For individual 2:
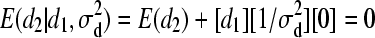 ,
, 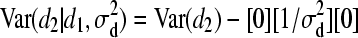 and d2 | d1,
and d2 | d1, 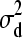 ∼ N(0,
∼ N(0, 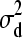 ).
).- For individual 3:
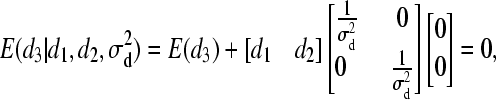
and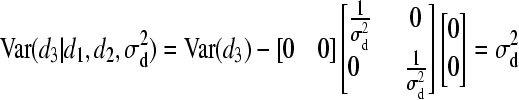
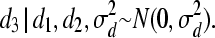
- Finally, for individual 4:
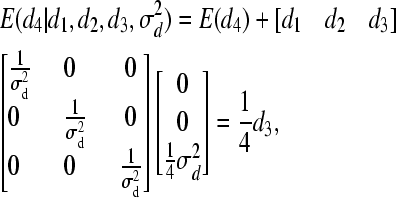
and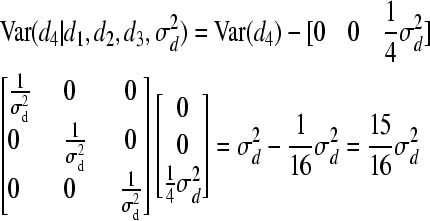
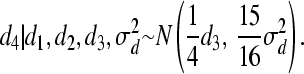
TABLE 3.
Example pedigree for sampling of dominance polygenic effects where a 0 indicates that an individual has an unknown father or mother
| Individual | Father | Mother |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 1 | 2 |
| 4 | 1 | 2 |
For individual 4, both mean and variance are shifted (reduced) because individuals 3 and 4 are full sibs. The following weights for reduction in mean are, consequently, obtained for individual 4: w(4, 1) = 0, w(4, 2) = 0, and w(4, 3) = 0.25. Using Equation 7, we obtain W(4) = 0.25d3. Hence, instead of drawing d from MVN(0, 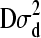 ), we make use of the following univariate normal distributions:
), we make use of the following univariate normal distributions: 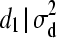 ∼ N(0,
∼ N(0, 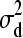 ), d2 | d1,
), d2 | d1, 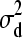 ∼ N(0,
∼ N(0, 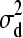 ), d3 | d1, d2,
), d3 | d1, d2, 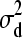 ∼ N(0,
∼ N(0, 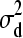 ) and
) and 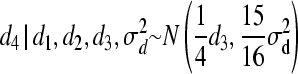 .
.
Inbreeding affects calculation of additive weights as follows. In Table 4, an example pedigree that includes a loop is shown; this will cause pedigree member 6 to be inbred. The corresponding additive relationship matrix is
 |
TABLE 4.
Example pedigree for sampling of additive polygenic effects where a 0 indicates that an individual has an unknown father or mother
| Individual | Father | Mother |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 1 | 2 |
| 5 | 3 | 2 |
| 6 | 4 | 5 |
When obtaining realization from additive polygenic effects of pedigree members 1 to 5, our proposed method and the standard factorization method (e.g., Lin 1999) give exactly the same mean and variance used in the normal univariate distributions as a1, a2, a3 ∼ N(0, 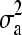 ),
),
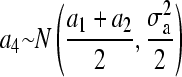 |
and
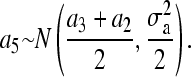 |
However, for pedigree member 6, the standard factorization method yields
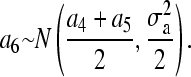 |
Our proposed method, on the other hand, gives
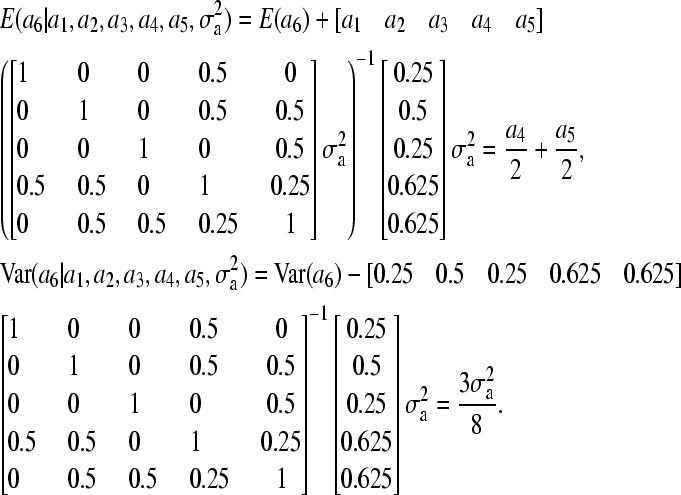 |
Using our proposed method, for individual 6, we make use of the following normal univariate distribution:
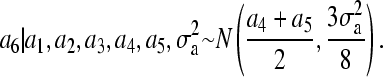 |
Consequently, the weight for the variance component differs between our method (3/8) and the standard method (1/2); this will cause a6 to be sampled from an incorrect distribution if the standard method is applied to the current pedigree.
Supporting information available online at http://www.genetics.org/cgi/content/full/genetics.110.114249/DC1.
References
- Abney, M., M. S. McPeek and C. Ober, 2000. Estimation of variance components of quantitative traits in inbred populations. Am. J. Hum. Genet. 66 629–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer, A. M., T. C. Reetz, F. Hoti, W.-D. Schuh, J. Léon et al., 2009. Bayesian prediction of breeding values by accounting for genotype-by-environment interaction in self-pollinating crops. Genet. Res. 91 193–207. [DOI] [PubMed] [Google Scholar]
- Box, G. E. P., and G. C. Tiao, 1973. Bayesian Inference in Statistical Analysis. Wiley, New York.
- Bulmer, M. G., 1971. Effect of selection on genetic variability. Am. Nat. 105 201–210. [Google Scholar]
- Calus, M. P. L., T. H. E. Meuwissen, A. P. W. de Roos and R. F. Veerkamp, 2008. Accuracy of genomic selection using different methods to define haplotypes. Genetics 178 553–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damgaard, L. H., 2007. How to use Winbugs to draw inferences in animal models. J. Anim. Sci. 85 1363–1368. [DOI] [PubMed] [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1996. Introduction to Quantitative Genetics. Longman, New York.
- Finley, A. O., S. Banerjee, P. Waldmann and T. Ericsson, 2009. Hierarchical spatial modeling of additive and dominance genetic variance for large spatial trial datasets. Biometrics 65 441–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint, J., and T. F. C. Mackay, 2009. Genetic architectures of quantitative traits in flies, mice and human. Genome Res. 19 723–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Cortés, L. A., and D. Sorensen, 1996. On a multivariate implementation of the Gibbs sampler. Genet. Sel. Evol. 28 121–126. [Google Scholar]
- Gelman, A., 2006. Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 1 515–534. [Google Scholar]
- Golub, G. H., and C. F. Van Loan, 1996. Matrix Computations, Ed. 3. Johns Hopkins University Press, Baltimore.
- González-Recio, O., D. Gianola, G. J. Rosa, K. A. Weigel and A. Kranis, 2009. Genome-assisted prediction of a quantitative trait measured in parents and progeny: application to food conversion rate in chickens. Genet. Sel. Evol. 41 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habier, D., R. L. Fernando and J. C. M. Dekkers, 2009. Genomic selection using low-density marker panels. Genetics 182 343–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallander, J., and P. Waldmann, 2009. Optimum contribution selection in large general tree breeding populations with an application to Scots pine. Theor. Appl. Genet. 118 1133–1142. [DOI] [PubMed] [Google Scholar]
- Harris, D. L., 1964. Genotypic covariances between inbred relatives. Genetics 50 1319–1348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes, B. J., P. M. Vissher and M. E. Goddard, 2009. Increased accuracy of artificial selection by using the realized relationship matrix. Genet. Res. 91 47–60. [DOI] [PubMed] [Google Scholar]
- Henderson, C. R., 1984. Applications of Linear Models in Animal Breeding. University of Guelph, Guelph, ON, Canada.
- Jensen, D. R., 1998. Multivariate normal distribution, pp. 2906–2911 in Encyclopedia of Biostatistics, edited by P. Armitage and T. Colton. Wiley, Chichester, UK.
- Johnson, D. L., and R. Thompson, 1995. Restricted maximum likelihood estimation of variance components for univariate animal models using sparse matrix techniques and average information. J. Dairy Sci. 87 449–456. [Google Scholar]
- Kass, R. E., B. P. Carlin, A. Gelman and R. Neal, 1998. Markov chain Monte Carlo in practice: a roundtable discussion. Am. Stat. 52 93–100. [Google Scholar]
- Lauritzen, S. L., A. P. Dawid, B. N. Larsen and H.-G. Leimer, 1990. Independence properties of directed Markov fields. Networks 20 491–505. [Google Scholar]
- Legarra, A., C. Robert-Granie, E. Manfredi and J. M. Elsen, 2008. Performance of genomic selection in mice. Genetics 180 611–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legarra, A., I. Aguilar and I. Misztal, 2009. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 92 4656–4663. [DOI] [PubMed] [Google Scholar]
- Levine, R. A., and G. Casella, 2006. Optimizing random scan Gibbs samplers. J. Mult. Anal. 97 2071–2100. [Google Scholar]
- Lin, S., 1999. Monte Carlo Bayesian methods for quantitative traits. Comp. Stat. Data Anal. 31 89–108. [Google Scholar]
- Lund, M. S., G. Sahana, D. J. de Koning, G. Su and Ö. Carlborg, 2009. Comparison of analyses of the QTLMAS XII common dataset. I. Genomic selection. BMC Proc. 3 S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunn, D. J., A. Thomas, N. Best and D. Spiegelhalter, 2000. WinBUGS—a Bayesian modelling framework: concepts, structure, and extensibility. Stat. Comp. 10 325–337. [Google Scholar]
- Lunn, D. J., D. Spiegelhalter, A. Thomas and N. Best, 2009. The BUGS project: evolution, critique and future directions. Stat. Med. 28 3049–3067. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and B. Walsh, 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA.
- Meuwissen, T. H. E., B. J. Hayes and M. E. Goddard, 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics 157 1819–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misztal, I., 1997. Estimation of variance components with large-scale dominance models. J. Dairy Sci. 80 965–974. [Google Scholar]
- Misztal, I., A. Legarra and I. Aguilar, 2009. Computing procedures for genetic evaluation including phenotypic, full pedigree, and genomic information. J. Dairy Sci. 92 4648–4655. [DOI] [PubMed] [Google Scholar]
- Mrode, R., and R. Thompson, 1989. An alternative algorithm for incorporating the relationships between animals in estimating variance components. J. Anim. Breed. Genet. 106 89–95. [Google Scholar]
- Muir, W. M., K. S. G. Wong, Y. Zhang, J. Wang, M. A. M. Groenen et al., 2008. Genome-wide assessment of worldwide chicken SNP genetic diversity indicates significant absence of rare alleles in commercial breeds. Proc. Natl. Acad. Sci. USA 105 17312–17317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Hara R. B., J. M. Cano, O. Ovaskainen, C. Teplitsky, and J. S. Alho, 2008. Bayesian approaches in evolutionary quantitative genetics. J. Evol. Biol. 21 949–957. [DOI] [PubMed] [Google Scholar]
- Ovaskainen, O., J. M. Cano and J. Merilä, 2008. A Bayesian framework for comparative quantitative genetics. Proc. R. Soc. Lond., B, Biol. Sci. 275 669–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts, G. O., and S. K. Sahu, 1997. Updating schemes, correlation structure, blocking and parameterization for the Gibbs sampler. J. R. Stat. Soc. Series B, Stat. Methodol. 59 291–317. [Google Scholar]
- Rue, H., and L. Held, 2005. Gaussian Markov Random Fields: Theory and Applications. Chapman & Hall, London.
- Schaeffer, L. R., and B. W. Kennedy, 1986. Computing solutions to mixed model equations. J. Dairy Sci. 69 575–579. [Google Scholar]
- Smith, B. J., 2007. boa: an R package for MCMC output convergence assessment and posterior inference. J. Stat. Soft. 21 1–37. [Google Scholar]
- Sorensen, D., and D. Gianola, 2002. Likelihood, Bayesian and MCMC Methods in Quantitative Genetics. Springer-Verlag, New York.
- Steinsland, I., and H. Jensen, 2010. Utilising Gaussian Markov random field properties of Bayesian animal models. Biometrics (in press). [DOI] [PubMed]
- Thomas, A., R. B. O'Hara, U. Ligges and S. Sturtz, 2006. Making BUGS open. R. News 6 12–17. [Google Scholar]
- Thomas, D. C., 1992. Fitting genetic data using Gibbs sampling: an application to nevus counts in 38 Utah kindreds. Cytogenet. Cell Genet. 59 228–230. [DOI] [PubMed] [Google Scholar]
- Valdar, W., L. C. Solberg, D. Gauguier, S. Burnett, P. Klenerman et al., 2006. Genome-wide genetic association of complex traits in heterogeneous stock mice. Nat. Genet. 38 879–887. [DOI] [PubMed] [Google Scholar]
- VanRaden, P. M., 2008. Efficient methods to compute genomic predictions. J. Dairy Sci. 91 4414–4423. [DOI] [PubMed] [Google Scholar]
- VanRaden, P. M., C. P. Van Tassell, G. R. Wiggans, T. S. Sonstegard, R. D. Schnabel et al., 2009. Reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 92 16–24. [DOI] [PubMed] [Google Scholar]
- Van Tassell, C. P., and L. D. Van Vleck, 1996. Multiple-trait Gibbs sampler for animal models: flexible programs for Bayesian and likelihood-based (covariance) component inference. J. Anim. Sci. 74 2586–2597. [PubMed] [Google Scholar]
- Villanueva, B., R. Pong-Wong, J. Fernández and M. A. Toro, 2005. Benefits from marker-assisted selection under an additive polygenic genetic model. J. Anim. Sci. 83 1747–1752. [DOI] [PubMed] [Google Scholar]
- Vines, S. K., W. R. Gilks and P. Wild, 1996. Fitting Bayesian multiple random effects models. Stat. Comp. 6 337–346. [Google Scholar]
- Visscher, P. M., 2008. Sizing up human height variation. Nat. Genet. 40 489–490. [DOI] [PubMed] [Google Scholar]
- Waagepetersen, R., N. Ibánêz-Escriche and D. Sorensen, 2008. A comparison of strategies for Markov chain Monte Carlo computation in quantitative genetics. Genet. Sel. Evol. 40 161–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waldmann, P., 2009. Easy and flexible Bayesian inference of quantitative genetic parameters. Evolution 63 1640–1643. [DOI] [PubMed] [Google Scholar]
- Waldmann, P., J. Hallander, F. Hoti and M. J. Sillanpää, 2008. Efficient Markov chain Monte Carlo implementation of Bayesian inference of additive and dominance genetic variances in non-inbred pedigrees. Genetics 179 1101–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, C. S., J. J. Rutledge and D. Gianola, 1993. Marginal inference about variance components in a mixed linear model using Gibbs sampling. Genet. Sel. Evol. 21 41–62. [Google Scholar]
- Weigel, K. A., G. de los Campos, O. González-Recio, H. Naya, X. L. Wu et al., 2009. Predictive ability of direct genomic values for lifetime net merit of Holstein sires using selected subsets of single nucleotide polymorphism markers. J. Dairy Sci. 92 5248–5257. [DOI] [PubMed] [Google Scholar]
- Wilkinson, D. J., and S. K. H. Yeung, 2004. A sparse matrix approach to Bayesian computation in large linear models. Comp. Stat. Data Anal. 44 493–516. [Google Scholar]
- Xu, S., 2006. Separating nurture from nature in estimating heritability. Heredity 97 256–257. [DOI] [PubMed] [Google Scholar]
- Yi, N., and S. Xu, 2000. Bayesian mapping of quantitative trait loci under the identity-by-descent-based variance component model. Genetics 156 411–422. [DOI] [PMC free article] [PubMed] [Google Scholar]


