Skip to main content
NCBI home page
Genetics logoLink to Genetics
. 2010 Jun;185(2):685–693. doi: 10.1534/genetics.110.115766

The Evolutionary Dynamics of Operon Distributions in Eukaryote Genomes

Asher D Cutter *,†,1, Aneil F Agrawal *
PMCID: PMC2881147  PMID: 20382830

Abstract

Genes in nematode and ascidian genomes frequently occur in operons—multiple genes sharing a common promoter to generate a polycistronic primary transcript—and such genes comprise 15–20% of the coding genome for Caenorhabditis elegans and Ciona intestinalis. Recent work in nematodes has demonstrated that the identity of genes within operons is highly conserved among species and that the unifying feature of genes within operons is that they are expressed in germline tissue. However, it is generally unknown what processes are responsible for generating the distribution of operon sizes across the genome, which are composed of up to eight genes per operon. Here we investigate several models for operon evolution to better understand their abundance, distribution of sizes, and evolutionary dynamics over time. We find that birth–death models of operon evolution reasonably describe the relative abundance of operons of different sizes in the C. elegans and Ciona genomes and generate predictions about the number of monocistronic, nonoperon genes that likely participate in the birth–death process. This theory, and applications to C. elegans and Ciona, motivates several new and testable hypotheses about eukaryote operon evolution.

THE genomes of nematodes, ascidians, and trypanosomes are unusual among most eukaryotes in that they contain many operons—runs of two or more genes that are transcribed into a single, polycistronic primary transcript. Approximately 15% of genes in the genome of the nematode model organism Caenorhabditis elegans occur in operons (Zorio et al. 1994; Blumenthal et al. 2002), with operons being prevalent among nematodes inside and outside this genus as well (Evans et al. 1997; Lee and Sommer 2003; Stein et al. 2003; Guiliano and Blaxter 2006; Qian and Zhang 2008). The ascidian Ciona intestinalis also harbors ∼20% of its genes in operon structures (Satou et al. 2006, 2008). Trypanosome genomes, like Leishmania major, appear to be transcribed in long polycistronic blocks tens of kilobases long that contain scores of genes (Donelson et al. 1999). Polycistronic transcription also has been described in other eukaryotes, including flatworms, algae, Drosophila, and humans (Lynch 2007; Michalak 2008). Despite extensive empirical work, little theory has been developed to explain the abundance and distribution of genes in operons within eukaryote genomes. Here we describe several alternative models of operon dynamics and compare them to observed patterns in the genomes of C. elegans and Ciona intestinalis.

In C. elegans, cooperonic genes share a single promoter, but prior to translation, the polycistronic pre-mRNA is spliced into multiple mature mRNAs that each comprise a single gene (Blumenthal and Gleason 2003). The presence of internal promoters in some operons (Huang et al. 2007) and RNA processing leads to imperfect covariation in expression among the members of an operon (Blumenthal and Gleason 2003; Lercher et al. 2003), in contrast to bacterial operons. Impressive efforts in C. elegans have enabled determination of the molecular basis of operon transcriptional mechanisms (Spieth et al. 1993; Blumenthal and Gleason 2003) and the identification, through experimental and computational means, of the extent of the genome that is cloistered into operons (Blumenthal et al. 2002). This body of work has demonstrated that in C. elegans, ∼1200 operons each contain two to eight closely spaced genes, but that the members of an operon share little functional similarity besides tending to be expressed in “female” germline tissue (Blumenthal 2004; Cutter et al. 2009; Reinke and Cutter 2009). Furthermore, 96% of C. elegans operons appear to be conserved in the genomes of related species (Stein et al. 2003; Qian and Zhang 2008), although recent work suggests greater turnover in operon composition among Caenorhabditis species than appreciated previously (J. Zhang, personal communication).

The first attempt to model nematode operon dynamics (Qian and Zhang 2008) considered the rate of change in operon abundance over time as

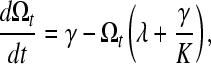graphic file with name M1.gif (1)

with Ωt being the number of operons in the genome at time t, K the maximum possible number of operons in the genome, γ the rate of operon gain, and λ the rate of operon loss. K also can be defined as f · G · ī−1, where f is the fraction of genes in the genome that could possibly reside in an operon, G is the number of genes in the genome, and ī is the average number of genes per operon (Qian and Zhang 2008). As shown by Qian and Zhang (2008), this formulation (model 0) implies that the equilibrium number of operons will be

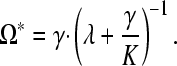graphic file with name M2.gif (2)

Of course, if Ω* = K, then this approach is problematic; more generally, it is unfortunate that it is not obvious how to estimate empirically K or f in this framework.

As an alternative simple model (model 1), we can consider the separate rates of addition (v) and subtraction (u) of genes from operons. In this analogy to a standard forward-and-reverse mutation population genetic model (Cutter et al. 2009), the equilibrium fraction of genes in the genome that will be present in operons is simply

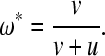graphic file with name M3.gif (3)

Consequently, the ratio of rates of operon gene gain and loss is v/u = ω*/(1 − ω*). If we assume that the observed fraction of C. elegans genes in operons is at equilibrium (ω* ∼ 15%) (Blumenthal et al. 2002), then we would infer that v/u = 0.176 or that the rate of removal of genes from operons is about six times greater than the rate of addition of genes to operons (given ω* ∼ 20% for Ciona, v/u = 0.25). Note that model 1 focuses on the evolution of the number of genes within operons without regard to operon size or abundance, whereas model 0 focuses on the evolution of the number of operons assuming a constant number of genes per operon.

However, neither of the above approaches provides a framework for predicting the size distribution of operons; i.e., What fraction of operons should contain two, three, or four or more genes? The evolution of genomic features like introns, gene duplicates, gene-family size, and transposable element abundance has been modeled in a birth–death framework (Charlesworth and Langley 1989; Lynch 2002; Lynch and Conery 2003), and this approach also can apply to operon evolution. In general, birth–death models predict a convexly curved size distribution in a log–log plot, unlike the linear relation predicted for a power law distribution (Lynch 2007); the operon distributions for C. elegans and Ciona intestinalis are visibly convex, suggesting that birth–death models likely are appropriate. Here, we consider the birth and death of operons of size i (i.e., containing i genes) from movement of genes into and out of operons of that size class. We find that this approach successfully recapitulates the size distribution of operons in the C. elegans and Ciona intestinalis genomes, permits estimation of biologically pertinent parameters, and generates testable predictions about operon evolution.

MATERIALS AND METHODS

Here we develop two sets of predictions (models 2 and 3) that differ on the basis of alternative conceptions of the biology of gene movement into and out of operons. In model 2, we assume that the probability that an operon loses or gains a gene is independent of the number of genes in that operon. This might occur if gene movement is constrained to a particular position within operons; i.e., only the last gene in an operon can successfully leave an operon and a gene can successfully enter an operon only by adding itself to the end of an existing operon (e.g., paths b and e in Figure 1). In Model 3, we treat the gene as the unit of action so that the probability that an operon loses or gains a gene increases with the number of genes in that operon. Longer operons are more likely to lose genes because they have more genes that could leave; longer operons also are more likely to gain a gene because they are bigger targets for insertion.

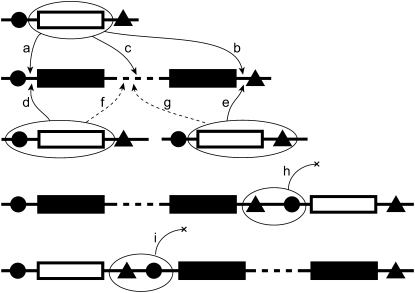
Figure 1.—

Figure 1.—

Open in a new tab

A simple conception of mutational events leading to increased size of operons (solid rectangles represent genes within an operon). Translocation of monocistrons (open rectangles; a–g) or fusion via deletion of transcription termination and promoter elements (triangles and circles, respectively; h and i) between adjacent genes on the same strand could create or increase the size of an operon. Solid horizontal line represents noncoding DNA. For simplicity, we diagram only two genes in an operon; events of type a, b, d, e, or h involving only monocistrons would lead to the creation of a polycistronic operon. A dashed line represents DNA sequence between the first and last gene in an operon, in which additional gene members of the operon might reside. Also for simplicity, we diagram the enlargement of operons, although translocations f and g would result in the operon retaining the same number of genes or possibly decreasing in size. Conceivably, monocistrons in the diagram could be replaced by operons to increase operon size by more than one gene at a time; segmental duplication of operons also could generate changes in the abundance of an operon size class. Models 2 and 3 do not formally distinguish among these alternative mutational ways in which operon size could change. However, the models assume either that a single gene moves per time step or that genes move independently of one another. Consequently, these models do not capture fission–fusion events (paths h and i).

We emphasize that both of the models described below represent neutral birth–death processes. The models do not allow for any selective advantage or disadvantage to individuals with more or larger operons. As described below, the models implicitly assume very strong selection against gene loss (i.e., when genes move, they must successfully reinsert elsewhere), but the other aspects of operon state are assumed to be selectively neutral. The goal is to ask whether these types of neutral models can accurately reflect observed distributions. To the extent observed patterns deviate from predicted patterns, it is worth considering alternatives including alternate modes of operon mutation and, of course, selection.

Model 2—operon dynamics independent of operon size:

Let Oi[t] be the number of operons containing i genes at time t; O1[t] is the number of individual genes not currently in operons but that could be (i.e., monocistronic “operons”). If f is the fraction of genes in the genome that could possibly reside in an operon, then

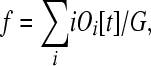graphic file with name M4.gif (4)

where G is the total number of genes in the genome. We expect that f < 1, because many genes in the genome likely have regulatory requirements that either preclude or facilitate their ability to persist in operons, such as predominantly promoter-dependent spatio-temporal regulation of sperm genes vs. 3′-UTR regulation of female germline genes (Merritt et al. 2008; Reinke and Cutter 2009).

Let pout be the probability that a gene leaves an operon in a given time step. This interval of time, τ1, which represents a fraction of a generation, is taken to be sufficiently short that pout is very small. Following this excision step (denoted by the prime), we have

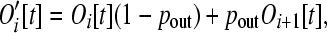graphic file with name M5.gif (5)

as a result of those operons of size i that lose genes, decreasing the number of operons of size i, while the simultaneous loss of genes from operons of size i + 1 increases the number of operons of size i. During this brief time interval there are 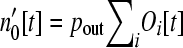Inline graphic genes that are “loose” in the nucleus that must reinsert into the genome.

With probability b, a loose gene will incorporate itself into one of the existing operons; there are a total of 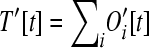Inline graphic possible operons where this can happen. With probability 1 − b, the gene successfully inserts itself into the genome as an independent gene, i.e., a monocistronic operon. We assume that gene loss is strongly disadvantageous so that the loose genes must successfully be reincorporated somewhere. (It is not necessary to account for the probability of gene loss because the lineages where this occurs will not persist. Thus, the probability b should be interpreted as being conditional on a successful insertion occurring.)

Following one complete time step of excision and reinsertion, the number of potential operon genes that exist as monocistronic operons is

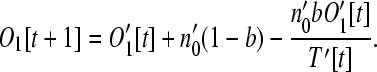graphic file with name M8.gif (6)

The first term is the number of monocistronic operons prior to reinsertion. The second term represents new monocistronic operons formed by loose genes reinserting into the genome outside of any existing operons. The third term represents the conversion of monocistronic operons to dicistronic operons when a loose gene adds itself to an existing monocistronic operon.

The number of operons of larger size classes (i > 1) is

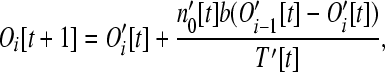graphic file with name M9.gif (7)

as a consequence of the number of operons of size i increasing from the addition of loose genes into operons of size i − 1, yet decreasing from the addition of loose genes into operons of size i. The recursions here assume that no more than one gene leaves or enters a given operon during any one time step. These assumptions are reasonable provided that pout is small.

By setting Oi[t + 1] = Oi[t] for all i and assuming pout and b are small (i.e., pout, b << 1), we obtain the following analytical approximation for the equilibrium frequency of operonic genes in operons of size class i (including “potentially operonic” monocistrons with i = 1):

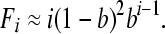graphic file with name M10.gif (8)

Simulations that do not rely on the assumptions of pout, b << 1 are described in supporting information, File S1.

Model 3—operon dynamics based on operon size:

In this model, longer operons are more likely to lose genes and more likely to gain them than are short operons. Following the excision phase, the number of operons of size class i is given by

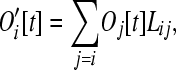graphic file with name M11.gif (9)

where Lij is the probability that (j – i) genes are excised out of an operon of size j. In other words, Lij represents the probability that an operon of size j is converted to size i. Because we assume genes move independently of one another, Lij follows a binomial form,

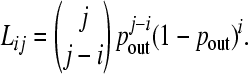graphic file with name M12.gif (10)

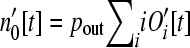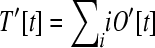The number of genes that are loose is Inline graphic. Because longer operons represent larger insertional targets, the effective total target size is Inline graphic.

Assuming no more than one gene inserts into a given operon in any one time step, the number of monocistronic operon genes (i = 1) is

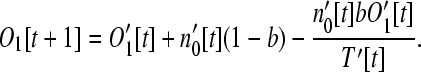graphic file with name M15.gif (11)

This equation has the same form as Equation 6 and can be interpreted in the same way. For larger size classes (i > 1), the number of operons is

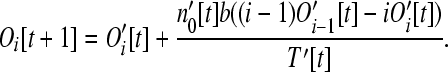graphic file with name M16.gif (12)

This equation has a similar form to Equation 7 and the interpretation is similar. However, Equations 7 and 12 are not identical because in Equation 12 we account for the increased target size of larger operons.

Again assuming pout, b << 1, the equilibrium frequency of operonic (or potentially operonic) genes in operons of size class i is given by

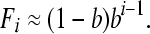graphic file with name M17.gif (13)

Equation 13 is formally equivalent to that given by a geometric distribution (i.e., the discrete analog to the exponential distribution). An exact model that does not rely on the assumption b << 1 is described in File S1.

Comparison of models with data:

We obtained from WormBase WS190 (http://www.wormbase.org) the total number of protein-coding genes (20,222) and the abundances of operon sizes for the 1150 operons annotated in the C. elegans genome. We used the abundances of different operon sizes in the Ciona intestinalis genome, as well as total number of genes in its genome, from Satou et al. (2008). For each of the two models described above, we applied a likelihood-based procedure to find model parameters that best fit each of the two data sets, C. elegans and Ciona. This was done by minimizing the goodness-of-fit statistic G for frequency distributions using the optim procedure in R (R Development Core Team 2009). For each of the two models, we used both the analytical approximations given above and the more exact simulations described in the File S1. In addition, we performed a similar analysis for power law distributions, which are commonly applied to abundance distributions, with

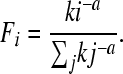graphic file with name M18.gif (14)

In all cases of model fitting, we considered only the genes in operons of size ≥2. Many monocistronic genes are unlikely to be able to exist in operons given the strongly nonrandom distribution of genes found in operons (i.e., a disproportionate abundance of genes in operons are expressed in female germline tissue in C. elegans) (Reinke and Cutter 2009). By estimating our parameters on the basis of the genes in operons of size ≥2, we can then use these parameters to predict how many monocistronic genes could potentially move into operons.

RESULTS AND DISCUSSION

We developed two new models of operon evolution to describe the “birth” and “death” of operons as a consequence of gene movements into and out of operons. In this framework, an operon death or the loss of genes from an operon does not imply their deletion from the genome, but simply that the gene composition of an operon has changed due to individual gene translocations. The first model (model 2) considers the operon as the unit of action, such that the size of an operon is independent of the probability of gain or loss of genes. This size-independent model could apply if genes could enter or leave an operon only from particular positions within the operon, such as at the 3′ end of the operon (Figure 1). Alternatively, model 3 treats genes as the unit of action, such that longer operons are more likely both to lose genes and to gain them by translocation events. This size dependence arises as a consequence of longer operons being a source of more genes that could move elsewhere and also presenting bigger targets for gene insertion.

Application to C. elegans operons:

Both of our models of operon gene dynamics (models 2 and 3) fit well the observed genomic distribution of operon sizes, assuming that the operon size distribution in the C. elegans genome is at equilibrium (Table 1, Figure 2). For both models, the exact solution fits the data significantly better than does the analytical approximation (the log-likelihood statistic G differs by >2 units), despite the very similar estimates of the gene-movement parameter b within each model (Table 1). The approximations assume b << 1 and are expected to become less accurate descriptions of reality when this is violated. We can see that the estimates of b are quite large. This means that there is a small but nonnegligible probability that multiple loose genes enter the same operon simultaneously. Because we have neglected this possibility in the approximations, they are somewhat less realistic than the simulations. Details of the derivation and simulation for the exact solutions are given in File S1.

TABLE 1.

Model fits to C. elegans and Ciona intestinalis operon size abundance distribution

Organism Model Ga Model parameter (b) Monocistrons (fraction of operons) Polycistrons (fraction of operons)
C. elegans Observed — — — (—) 1,150 (—)
C. elegans Model 2 (approximation) 34.833 0.340 2,224 (0.435) 1,146 (0.563)
C. elegans Model 2 (exact) 30.440 0.342 2,207 (0.434) 1,145 (0.566)
C. elegans Model 3 (approximation) 38.677 0.452 3,491 (0.548) 1,155 (0.451)
C. elegans Model 3 (exact) 28.156 0.456 3,434 (0.544) 1,153 (0.455)
C. elegans Power law 190.009 2.712b 11,159 (0.795) 1,161 (0.203)
Ciona Observed — — — (—) 1,310 (—)
Ciona Model 2 (approximation) 9.998 0.183 5,835 (0.667) 1,308 (0.332)
Ciona Model 2 (exact) 9.964 0.183 5,834 (0.667) 1,308 (0.333)
Ciona Model 3 (approximation) 7.458 0.258 8,370 (0.742) 1,310 (0.258)
Ciona Model 3 (exact) 7.342 0.258 8,366 (0.742) 1,310 (0.258)
Ciona Power law 102.910 4.094b 38,377 (0.930) 1,313 (0.070)
Open in a new tab
a

Log-likelihood G-statistic values are directly comparable within species.

b

Model parameter for the power law model is the exponent a.

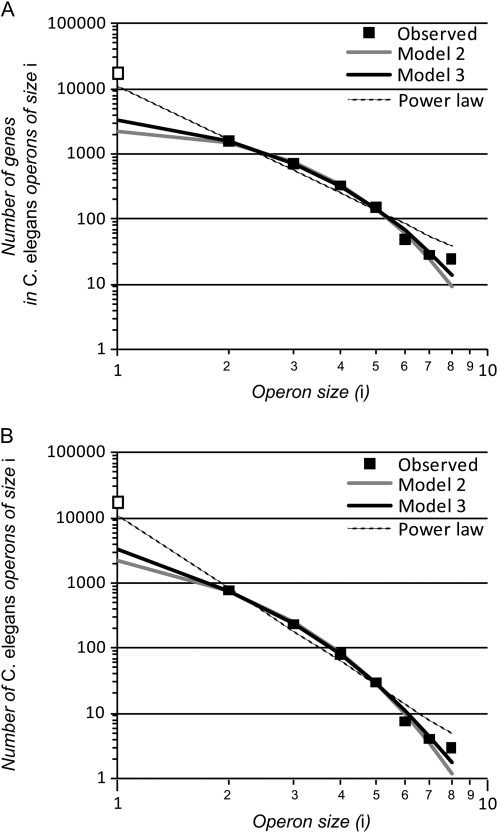
Figure 2.—

Figure 2.—

Open in a new tab

Model fits to C. elegans' operon size distribution in terms of the number of genes in a given operon size class (A) and for the number of operons of a given size (B). The “exact” solutions for models 2 and 3 were used in model fitting, although curves for approximate fits are indistinguishable by eye. Only operons containing two or more genes (solid squares) were used in model fitting.

Model 3, which assumes that genes are more likely to move into and out of longer operons than shorter operons, provides a significantly better fit to the observed operon size distribution than does model 2 (which assumes size independence; Table 1). A power law distribution, by contrast, poorly describes the distribution of operon sizes in the C. elegans genome (Table 1, Figure 2). We do not discount the possibility that alternative models might also recapitulate the genomic operon size distribution, either neutral models based on different mutational dynamics (e.g., fission–fusion) or models that explicitly consider natural selection. Future development of such models would be valuable to help determine whether the dynamics assumed in models 2 and 3 capture the true biology of operon evolution.

When fit to C. elegans operon size distribution, the size-dependent model 3 converges on an operon-insertion parameter b of ∼0.45, implying that nearly half of translocated genes with the potential to successfully enter into a polycistronic operon will do so (Table 1). As a result, this model predicts that a total of only ∼6317 current or potential operon genes in the genome contribute to the operon birth–death process, of which ∼3434 currently are monocistrons (i.e., the i = 1 class). By contrast, the size-independent model 2 predicts that a smaller fraction (b ∼ 34%) of genes will insert into an operon of ≥2 genes, resulting in a smaller overall pool of “potential” operon genes in the genome (Tables 1 and 2). Given the significantly better fit of the size-dependent model (model 3), as well as its more intuitive biological rationale, we focus further discussion on this model.

TABLE 2.

Observed and predicted operon size distributions for model 3

Operon size (i) No. of C. elegans operons (genes)
 No. of Ciona operons (genes)
Observed Model 3 “exact” predictiona Observed Model 3 “exact” predictiona
1 — (17,339) 3,434.0 (3,434.0) — (12,345) 8,366.0 (8,366.0)
2 773 (1,546) 784.4 (1,568.9) 1,079 (2,158) 1,079.3 (2,158.5)
3 243 (729) 238.9 (716.8) 185 (555) 185.6 (556.9)
4 87 (348) 81.9 (327.4) 36 (144) 35.9 (143.7)
5 32 (160) 29.9 (149.6) 8 (40) 7.4 (37.0)
6 8 (48) 11.4 (68.3) 2 (12) 1.6 (9.6)
7 4 (28) 4.5 (31.2)
8 3 (24) 1.8 (14.3)
Total 1,150 (20,222) 4,586.7 (6,317.0) 1,310 (15,254) 9,676.4 (11,275.6)
Open in a new tab
a

The model predicts <1 operon being present of size i > 8 for C. elegans or i > 6 for Ciona.

The very longest operon class appears slightly more abundant in the C. elegans genome than expected (Figure 2). Why might this be the case? The seeming excess of very long operons could simply reflect sampling, as the C. elegans genome is just a single realization of the historical process of operon evolution. Future determination of an excess of very long operons for operon size distributions in related taxa could refute this explanation. Alternatively, natural selection might favor disproportionately the retention of very long operons. If so, we would expect the gene content of very long operons to be preserved over evolutionary time to a greater extent than shorter operons. Again, this could be tested with comparisons of orthologous operons in related taxa. Weaker negative selection against gene addition to long operons also could potentially generate an excess of long operons. Under such a scenario, we might expect species with smaller effective population sizes to accrue more and longer operons (by genetic drift) than species with larger effective sizes. Note that this contrasts with Lynch's (2007) prediction that smaller effective population sizes should generally lead to operon elimination. Comparisons of operon size-abundance distributions between obligately outbreeding and highly inbreeding species of Caenorhabditis provide one possible test of this idea due to their drastically different effective sizes (Cutter et al. 2009). Two complications for testing for an influence of effective population size in Caenorhabditis are that inbreeding hermaphroditism might have evolved too recently to see an effect (Cutter et al. 2008, 2010) and that the evolution of operons might be confounded by the evolution of breeding system—operon genes are expressed disproportionately in the germline and alterations to germline development were key features in the evolution of selfing hermaphroditism (reviewed in Haag 2009). Finally, the nonrandom clustering of operons along chromosomes might facilitate fusion of neighboring operons in a way that deviates from the mutational dynamics assumed in our models. Specifically, the clustered arrangement of operons in C. elegans (Reinke and Cutter 2009) could conceivably enable this process, so that operon fusion (via a process like paths h and i in Figure 1) contributes relatively more to operon size dynamics for long operons compared to gene translocation. This possibility could be tested comparatively by examining operon sizes in syntenic chromosomal regions that contain operon clusters, once operon structures in species other than C. elegans are determined empirically.

It also would be valuable to explore the genomic distributions describing the number of neighboring genes oriented in the same direction with respect to operon proximity, as appropriate orientation should be a precursor for fission–fusion mechanisms of operon size change. Further analyses of operon evolution, in terms of gene identity and location, will help elucidate the relative roles of fission–fusion of neighboring genes vs. translocation in operon dynamics. Translocation within chromosomes is widespread in comparisons of Caenorhabditis genomes (Stein et al. 2003; Hillier et al. 2007), but extant operons in C. elegans also tend to be clustered (Reinke and Cutter 2009). Thus, it is difficult to discern a predominant role for either translocation or fission–fusion over the long term.

To contrast with the birth–death approach taken above, we also considered a model to describe the operon abundance distribution in the C. elegans genome that is relatively free of biological motivation. Specifically, a power law distribution also roughly captures the C. elegans operon size distribution (Figure 2), albeit much worse than the birth–death models. The power law distribution also poorly describes Ciona operons (Table 1; Figure 3). The literature is rife with fitting of empirical distributions to power law functions, although the biological interpretation of the parameters in the operon case is not intuitive. It is encouraging that biologically motivated models (models 2 and 3) perform much better.

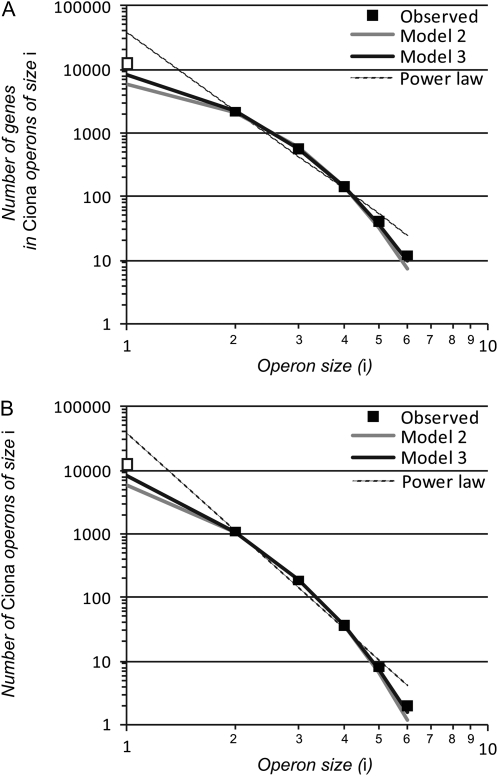
Figure 3.—

Figure 3.—

Open in a new tab

Model fits to Ciona intestinalis' operon size distribution in terms of the number of genes in a given operon size class (A) and for the number of operons of a given size (B). The “exact” solutions for models 2 and 3 were used in model fitting, although curves for approximate fits are indistinguishable by eye. Only operons containing two or more genes (solid squares) were used in model fitting.

If the size-dependent model 3 accurately predicts the abundance of potential operon genes in the genome, then this should represent the number of genes with characteristics conducive to entering a polycistronic operon. The uniting characteristic of operon genes in C. elegans is expression in the female germline: as many as ∼95% of genes in operons exhibit germline expression as assayed by microarray or in situ hybridization (Reinke and Cutter 2009). Microarray experiments have identified ∼2800 genes with enriched expression in the germline (excluding spermatogenesis-enriched genes), ∼1750 of which do not reside in operons (Reinke et al. 2004; Reinke and Cutter 2009). We speculate that these ∼1750 loci, plus another ∼1700 unknown loci, represent good candidates for the pool of ∼3434 monocistronic genes predicted to participate in the operon birth–death process. Empirical identification of operon compositions in other Caenorhabditis species would permit testing of the hypothesis that operon genes present in other species, but not in C. elegans, would include disproportionate representation of orthologs for these ∼1750 germline-expressed, monocistronic C. elegans genes.

Reinke and Cutter (2009) demonstrated that nearly all genes within operons are expressed in the female germline, a tissue in which post-transcriptional regulation of RNA is known to play a particularly critical role (Kimble and Crittenden 2007). Moreover, sperm-related genes, whose expression patterns are controlled primarily by promoter-based regulation (Merritt et al. 2008), are nearly absent from operons (Reinke and Cutter 2009). Reinke and Cutter (2009) consequently proposed that it is the RNA regulation of oocyte- and female germline-associated genes (via 3′-UTRs) that facilitates their successful entry and evolutionary persistence in polycistronic operons. However, it is not entirely clear why post-transcriptional regulation would disproportionately affect female germline-associated genes. Kimble and Crittenden (2007) suggest that post-transcriptional regulation might facilitate reversibility of transient states of differentiation for germ cells, which is necessary for the transition from gamete cells to developing embryo—a plausible hypothesis. With the emerging importance of small RNA-mediated regulation at the post-transcriptional level in germline tissues (Ruby et al. 2006; Batista et al. 2008; Das et al. 2008; Wang and Reinke 2008), there must be much more to learn about how these various pieces of biology fit together.

Application to Ciona's operons:

The genome of the ascidian Ciona intestinalis also contains a large complement of operons, which include ∼20% of the genes in its genome (Satou et al. 2008). Assuming that the size distribution is at equilibrium, we applied our birth–death models to the distribution of operon sizes for Ciona and observed similarly good agreement to that for C. elegans. The size-dependent model 3 again provided a significantly better fit than size-independent model 2, but the approximate and exact formulations of the models performed equivalently (Table 1). Operon gene dynamics in Ciona, however, appear quite distinct from those in C. elegans, with an estimate lower by nearly half for the probability of successful entry into an operon (b ∼ 0.26 for model 3; Table 1, Figure 3). The model also predicts a greater total abundance of monocistrons involved in the operon birth–death process (∼8366; Table 2), so that the total number of genes currently or potentially residing in operons makes up a much greater fraction of the Ciona genome (11,275/15,254 = 73.9% vs. 31.2% for C. elegans). To our knowledge, it is unknown what characteristics, if any, are shared among operon genes in Ciona. If it is a propensity for post-transcriptional regulation that predisposes genes to persist successfully within eukaryotic operons, rather than germline expression per se (Reinke and Cutter 2009), then we hypothesize that genes encoded within Ciona operons would tend to exhibit RNA-dependent rather than promoter-dependent regulation.

Presence and absence of operons among eukaryote genomes:

Why do nematode and ascidian genomes contain so many operons, when few other eukaryotes do? Lynch (2007) proposed that the typically smaller effective population size (Ne) of eukaryotes is responsible for the loss, by drift, of operon structures in most lineages from their common ancestors with operon-rich prokaryotes. Species of Ciona, however, have exceptionally large Ne (Dehal et al. 2002; Vinson et al. 2005; Small et al. 2007). Although the present-day effective size of C. elegans is small, it is probably a result of a relatively recent origin of highly self-fertilizing reproduction, and related species with the ancestrally outbreeding mode of reproduction appear to have very high Ne (reviewed in Cutter et al. 2009). Note that a recently small Ne for C. elegans means that the operon distribution in its genome will reflect primarily the evolutionary processes in its large Ne ancestor. If this attribute of very large Ne is common to the deep ancestors of these groups, then the persistence of operons in nematodes and ascidians would be consistent with Lynch's view.

Notably, parasitic nematode species also appear to have operons (Guiliano and Blaxter 2006), and those that lack a free-living stage are thought to have experienced for a long time much smaller effective population sizes than free-living nematodes (Cutter et al. 2006). Moreover, the parasitic nematodes Strongyloides ratti, Brugia malayi, and Ascaris suum appear to use only one main mechanism of trans-splicing of operon genes (with spliced leader SL1) in contrast to other species like C. elegans that use both SL1- and SL2-like spliced leaders (Spieth et al. 1993; Lee and Sommer 2003; Guiliano and Blaxter 2006). It has been proposed that SL2-like spliced leaders evolved after the origin of SL1 and operons in nematodes and are restricted to the Rhabditina clade as an adaptation for more efficient trans-splicing of downstream genes within operons (Spieth et al. 1993; Guiliano and Blaxter 2006). However, it will be important to assess whether SL2-like mechanisms are present in free-living members of nonrhabditine nematodes, because it could be that long-term small Ne of the parasitic lineages allowed the evolutionary loss by drift of SL2-like trans-splicing capacity from an ancestor that harbored both SL1- and SL2-like spliced leaders, much akin to how Lynch (2007) proposes that most eukaryotes lost the ability to utilize operons. Spliced leader-mediated trans-splicing, which is a necessary precursor for proper eukaryotic operon transcript maturity, occurs in a wide diversity of eukaryotes (reviewed in Pettitt et al. 2008). It may prove fruitful to test for operons in the genomes of species that have very large effective population sizes within these groups to better understand the evolutionary loss of polycistronic transcription.

Conclusions:

The polycistronic transcription of genes—operons—in eukaryotes is common in nematodes and ascidians, although these genomic features differ substantially from their bacterial counterparts. Despite well-described molecular biology in C. elegans, generalities about the function and evolution of genes encoded in operons have proved more elusive. Here we derived birth–death models to describe the genomic distribution of operon sizes and find that they largely recapitulate the empirical distributions for C. elegans and Ciona intestinalis. A size-dependent model of operon dynamics better fits the genomic distributions of operon abundances than does a size-independent model of gene turnover in operons. These models also predict that ∼17% of C. elegans' coding genes and ∼55% of Ciona's coding genes are made up of single, monocistronic loci that contribute to the operon birth–death process and could potentially enter successfully into an operon over the course of evolution. Comparative analysis among Caenorhabditis species, in particular, holds great promise for testing hypotheses about operon dynamics made explicit by this theory of operon evolution.

Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.110.115766/DC1.

References

  1. Batista, P. J., J. G. Ruby, J. M. Claycomb, R. Chiang, N. Fahlgren et al., 2008. PRG-1 and 21U-RNAs interact to form the piRNA complex required for fertility in C. elegans. Mol. Cell 31 67–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Blumenthal, T., 2004. Operons in eukaryotes. Brief. Funct. Genomic. Proteomic. 3 199–211. [DOI] [PubMed] [Google Scholar]
  3. Blumenthal, T., and K. S. Gleason, 2003. Caenorhabditis elegans operons: form and function. Nat. Rev. Genet. 4 112–120. [DOI] [PubMed] [Google Scholar]
  4. Blumenthal, T., D. Evans, C. D. Link, A. Guffanti, D. Lawson et al., 2002. A global analysis of Caenorhabditis elegans operons. Nature 417 851–854. [DOI] [PubMed] [Google Scholar]
  5. Charlesworth, B., and C. H. Langley, 1989. The population-genetics of Drosophila transposable elements. Annu. Rev. Genet. 23 251–287. [DOI] [PubMed] [Google Scholar]
  6. Cutter, A. D., J. D. Wasmuth and M. L. Blaxter, 2006. The evolution of biased codon and amino acid usage in nematode genomes. Mol. Biol. Evol. 23 2303–2315. [DOI] [PubMed] [Google Scholar]
  7. Cutter, A. D., J. D. Wasmuth and N. L. Washington, 2008. Patterns of molecular evolution in Caenorhabditis preclude ancient origins of selfing. Genetics 178 2093–2104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cutter, A. D., A. Dey and R. L. Murray, 2009. Evolution of the Caenorhabditis elegans genome. Mol. Biol. Evol. 26 1199–1234. [DOI] [PubMed] [Google Scholar]
  9. Cutter, A. D., W. Yan, N. Tsvetkov, S. Sunil and M. A. Felix, 2010. Molecular population genetics and phenotypic sensitivity to ethanol for a globally diverse sample of the nematode Caenorhabditis briggsae. Mol. Ecol. 19 798–809. [DOI] [PubMed] [Google Scholar]
  10. Das, P. P., M. P. Bagijn, L. D. Goldstein, J. R. Woolford, N. J. Lehrbach et al., 2008. Piwi and piRNAs act upstream of an endogenous siRNA pathway to suppress Tc3 transposon mobility in the Caenorhabditis elegans germline. Mol. Cell 31 79–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dehal, P., Y. Satou, R. K. Campbell, J. Chapman, B. Degnan et al., 2002. The draft genome of Ciona intestinalis: insights into chordate and vertebrate origins. Science 298 2157–2167. [DOI] [PubMed] [Google Scholar]
  12. Donelson, J. E., M. J. Gardner and N. M. El-Sayed, 1999. More surprises from Kinetoplastida. Proc. Natl. Acad. Sci. USA 96 2579–2581. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Evans, D., D. Zorio, M. MacMorris, C. E. Winter, K. Lea et al., 1997. Operons and SL2 trans-splicing exist in nematodes outside the genus Caenorhabditis. Proc. Natl. Acad. Sci. USA 94 9751–9756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Guiliano, D. B., and M. L. Blaxter, 2006. Operon conservation and the evolution of trans-splicing in the phylum Nematoda. PLoS Genet. 2 e198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Haag, E. S., 2009. Caenorhabditis nematodes as a model for the adaptive evolution of germ cells. Curr. Top. Dev. Biol. 86 43–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hillier, L. W., R. D. Miller, S. E. Baird, A. Chinwalla, L. A. Fulton et al., 2007. Comparison of C. elegans and C. briggsae genome sequences reveals extensive conservation of chromosome organization and synteny. PLoS Biol. 5 e167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Huang, P., E. D. Pleasance, J. S. Maydan, R. Hunt-Newbury, N. J. O'Neil et al., 2007. Identification and analysis of internal promoters in Caenorhabditis elegans operons. Genome Res. 17 1478–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kimble, J., and S. L. Crittenden, 2007. Controls of germline stem cells, entry into meiosis, and the sperm/oocyte decision in Caenorhabditis elegans. Annu. Rev. Cell Dev. Biol. 23 405–433. [DOI] [PubMed] [Google Scholar]
  19. Lee, K. Z., and R. J. Sommer, 2003. Operon structure and trans-splicing in the nematode Pristionchus pacificus. Mol. Biol. Evol. 20 2097–2103. [DOI] [PubMed] [Google Scholar]
  20. Lercher, M. J., T. Blumenthal and L. D. Hurst, 2003. Coexpression of neighboring genes in Caenorhabditis elegans is mostly due to operons and duplicate genes. Genome Res. 13 238–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lynch, M., 2002. Intron evolution as a population-genetic process. Proc. Natl. Acad. Sci. USA 99 6118–6123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lynch, M., 2007. The Origins of Genome Architecture. Sinauer Associates, Sunderland, MA.
  23. Lynch, M., and J. S. Conery, 2003. The evolutionary demography of duplicate genes. J. Struct. Funct. Genomics 3 35–44. [PubMed] [Google Scholar]
  24. Merritt, C., D. Rasoloson, D. Ko and G. Seydoux, 2008. 3′ UTRs are the primary regulators of gene expression in the C. elegans germline. Curr. Biol. 18 1476–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Michalak, P., 2008. Coexpression, coregulation, and cofunctionality of neighboring genes in eukaryotic genomes. Genomics 91 243–248. [DOI] [PubMed] [Google Scholar]
  26. Pettitt, J., B. Müller, I. Stansfield and B. Connolly, 2008. Spliced leader trans-splicing in the nematode Trichinella spiralis uses highly polymorphic, noncanonical spliced leaders. RNA 14 760–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Qian, W., and J. Zhang, 2008. Evolutionary dynamics of nematode operons: easy come, slow go. Genome Res. 18 412–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. R Development Core Team, 2009. R: A Language and Environment for Statistical Computing, Reference Index Version 2.10.1. Foundation for Statistical Computing, Vienna.
  29. Reinke, V., and A. D. Cutter, 2009. Germline expression influences operon organization in the Caenorhabditis elegans genome. Genetics 181 1219–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Reinke, V., I. S. Gil, S. Ward and K. Kazmer, 2004. Genome-wide germline-enriched and sex-biased expression profiles in Caenorhabditis elegans. Development 131 311–323. [DOI] [PubMed] [Google Scholar]
  31. Ruby, J. G., C. Jan, C. Player, M. J. Axtell, W. Lee et al., 2006. Large-scale sequencing reveals 21U-RNAs and additional microRNAs and endogenous siRNAs in C. elegans. Cell 127 1193–1207. [DOI] [PubMed] [Google Scholar]
  32. Satou, Y., M. Hamaguchi, K. Takeuchi, K. E. M. Hastings and N. Satoh, 2006. Genomic overview of mRNA 5′-leader trans-splicing in the ascidian Ciona intestinalis. Nucleic Acids Res. 34 3378–3388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Satou, Y., K. Mineta, M. Ogasawara, Y. Sasakura, E. Shoguchi et al., 2008. Improved genome assembly and evidence-based global gene model set for the chordate Ciona intestinalis: new insight into intron and operon populations. Genome Biol. 9 R152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Small, K. S., M. Brudno, M. M. Hill and A. Sidow, 2007. Extreme genomic variation in a natural population. Proc. Natl. Acad. Sci. USA 104 5698–5703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Spieth, J., G. Brooke, S. Kuersten, K. Lea and T. Blumenthal, 1993. Operons in C. elegans: polycistronic mRNA precursors are processed by trans-splicing of SL2 to downstream coding regions. Cell 73 521–532. [DOI] [PubMed] [Google Scholar]
  36. Stein, L. D., Z. Bao, D. Blasiar, T. Blumenthal, M. R. Brent et al., 2003. The genome sequence of Caenorhabditis briggsae: a platform for comparative genomics. PLoS Biol. 1 166–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Vinson, J. P., D. B. Jaffe, K. O'Neill, E. K. Karlsson, N. Stange-Thomann et al., 2005. Assembly of polymorphic genomes: algorithms and application to Ciona savignyi. Genome Res. 15 1127–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wang, G., and V. Reinke, 2008. A C. elegans Piwi, PRG-1, regulates 21U-RNAs during spermatogenesis. Curr. Biol. 18 861–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zorio, D. A., N. N. Cheng, T. Blumenthal and J. Spieth, 1994. Operons as a common form of chromosomal organization in C. elegans. Nature 372 270–272. [DOI] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES