Interactions between Declarative and Procedural-Learning Categorization Systems

Abstract

Two experiments tested whether declarative and procedural memory systems operate independently or inhibit each other during perceptual categorization. Both experiments used a hybrid category-learning task in which perfect accuracy could be achieved if a declarative strategy is used on some trials and a procedural strategy is used on others. In the two experiments, only 2 of 53 participants learned a strategy of this type. In Experiment 1, most participants appeared to use simple explicit rules, even though control participants reliably learned the procedural component of the hybrid task. In Experiment 2, participants pre-trained either with the declarative or procedural component and then transferred to the hybrid categories. Despite this extra training, no participants in either group learned to categorize the hybrid stimuli with a strategy of the optimal type. These results are inconsistent with the most prominent single-and multiple-system accounts of category learning. They also cannot be explained by knowledge partitioning, or by the hypothesis that the failure to learn was due to high switch costs. Instead, these results support the hypothesis that declarative and procedural memory systems interact during category learning.

Introduction

There is now much evidence that humans have multiple memory systems (Eichenbaum & Cohen, 2001; Schacter, Wagner, & Buckner, 2000; Squire, 2004). In fact the existence of multiple memory systems is so widely accepted that some researchers have begun asking how these putative systems interact (Poldrack et al., 2001; Poldrack & Packard, 2003; Schroeder, Wingard, & Packard, 2002). As we will see, the available evidence suggests inhibition, or at least competition, between medial temporal lobe-based declarative memory and striatal-based procedural memory. Even so, this evidence all comes either from animal studies that used lesions or pharmacological intervention or else from human neuroimaging studies that reported negative correlations between medial temporal lobe and striatal activation in memory-dependent tasks. To our knowledge there is little or no human behavioral evidence of such interactions.

This article reports the results of two experiments that were designed to investigate this issue. Both experiments used a hybrid category-learning task in which perfect accuracy could be achieved if a declarative strategy is used on some trials and a procedural strategy is used on others. Of the 53 participants in the two experiments who tried to learn these categories, only 2 appeared to use a strategy of the optimal type. The responses of all other participants were consistent with the perseverative use of a single memory system throughout the experiment. These results run counter to the predictions of existing single-system theories of category learning and to the predictions of multiple systems theories that assume independent learning in the two systems. To our knowledge, they are the first human behavioral data to support the inhibition suggested by the previous neuroscience research.

For a variety of reasons, we chose a perceptual category-learning task for our behavioral paradigm. First, during the past decade or so, many studies have reported evidence that human categorization is mediated by a number of functionally distinct category-learning systems. The evidence suggests that these different systems are each best suited for learning different types of category structures, and are each mediated by different neural circuits (e.g., Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Erickson & Kruschke, 1998; Love, Medin, & Gureckis, 2004; Reber, Gitelman, Parrish, & Mesulam, 2003). Second, there is evidence that these different category-learning systems map directly onto the major memory systems that have been proposed (Ashby & O’Brien, 2005). Third, much of the neuroimaging data that supports inhibition between declarative and procedural memory systems used a category-learning paradigm. In particular, a number of fMRI studies have reported an antagonistic relationship between neural activation in the striatum and medial temporal lobes during category learning – that is, striatal activation tended to increase with category learning, whereas medial temporal lobe activation decreased (Moody, Bookheimer, & Knowlton, 2004; Nomura et al., 2007; Poldrack, Prabhakaran, Seger, & Gabrieli, 1999; Poldrack et al., 2001). Similar results have been reported within the more general memory systems literature. For example, several fMRI studies of skill learning have also reported negative correlations between medial temporal lobe and striatal activation (Dagher, Owen, Boecker, & Brooks, 2001; Jenkins, Brooks, Nixon, Frackowiak, & Passinghem, 1994; Poldrack & Gabrieli, 2001). In addition, a number of animal lesion studies have reported that medial temporal lobe lesions can improve performance in striatal-dependent habit-learning tasks, and conversely that striatal lesions can improve performance in medial temporal lobe-dependent spatial learning tasks (e.g., Mitchell & Hall, 1988; O’Keefe & Nadel, 1978; Schroeder et al., 2002). Together, all these results are consistent with the hypothesis that there is inhibition between declarative and procedural memory systems during category learning.

The specific categorization task used in this article depends strongly on prior research with rule-based and information-integration category-learning tasks. In rule-based tasks, the categories can be learned via some explicit reasoning process. Frequently, the rule that maximizes accuracy (i.e., the optimal strategy) is easy to describe verbally (Ashby et al., 1998). In the most common applications, only one stimulus dimension is relevant, and the subject’s task is to discover this relevant dimension and then to map the different dimensional values to the relevant categories. A variety of evidence suggests that success in rule-based tasks depends on declarative memory systems, and especially working memory and executive attention (Ashby et al., 1998; Maddox, Ashby, Ing, & Pickering, 2004; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006). For example, there is evidence that rule-based category learning is supported by a broad neural network that includes the prefrontal cortex, anterior cingulate, the head of the caudate nucleus, and medial temporal lobe structures (e.g., Brown & Marsden, 1988; Filoteo, Maddox, Ing, & Song, 2007; Muhammad, Wallis, & Miller, 2006; Seger & Cincotta, 2006).

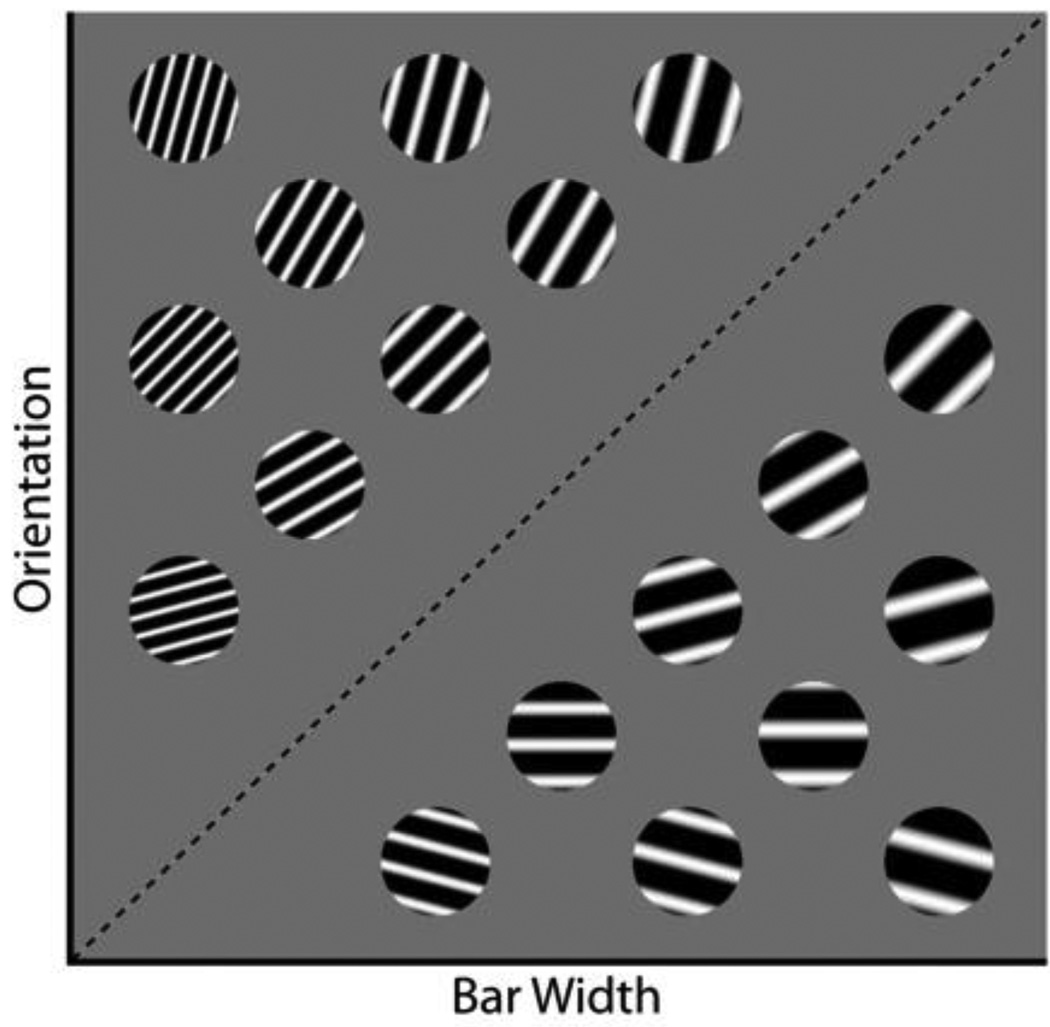
In information–integration category-learning tasks, accuracy is maximized only if information from two or more stimulus components (or dimensions) is integrated at some predecisional stage (Ashby & Gott, 1988). In many cases the optimal strategy is difficult or impossible to describe verbally (Ashby et al., 1998). An example of an information-integration task is shown in Figure 1 (and in the top panel of Figure 2). In this case the two categories are each composed of circular sine-wave gratings that vary in the width and orientation of the dark and light bars. The diagonal line denotes the category boundary. Note that no simple verbal rule correctly separates the disks into the two categories. Nevertheless, many studies have shown that people reliably learn such categories, provided they receive consistent and immediate feedback after each response (for a review, see Ashby & Maddox, 2005). Evidence suggests that success in information-integration tasks depends on procedural learning that is mediated largely within the striatum (Ashby & Ennis, 2006; Filoteo, Maddox, Salmon, & Song, 2005; Knowlton, Mangels, & Squire, 1996; Nomura et al., 2007). For example, switching the locations of the response keys has no effect on rule-based categorization, but as in more traditional procedural-learning tasks, switching response keys interferes with information-integration categorization (Ashby, Ell, & Waldron, 2003; Maddox, Bohil, & Ing, 2004; Spiering & Ashby, 2008).

Figure 1.

Some stimuli that might be used in an information-integration category learning experiment.

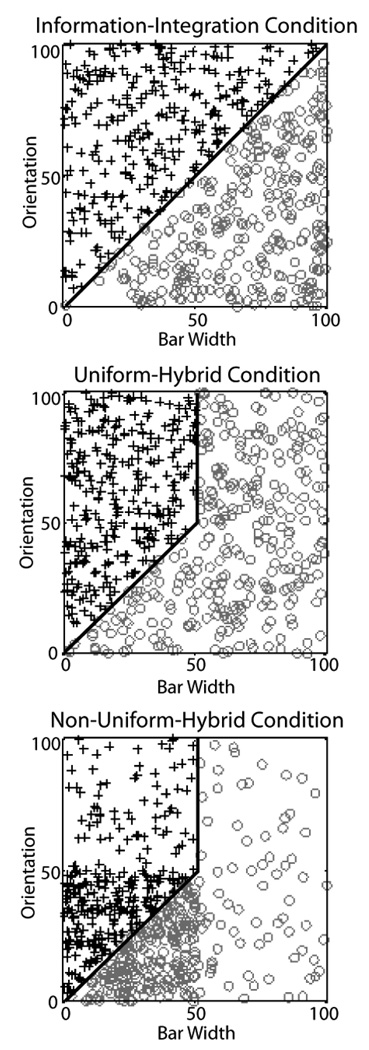
Figure 2.

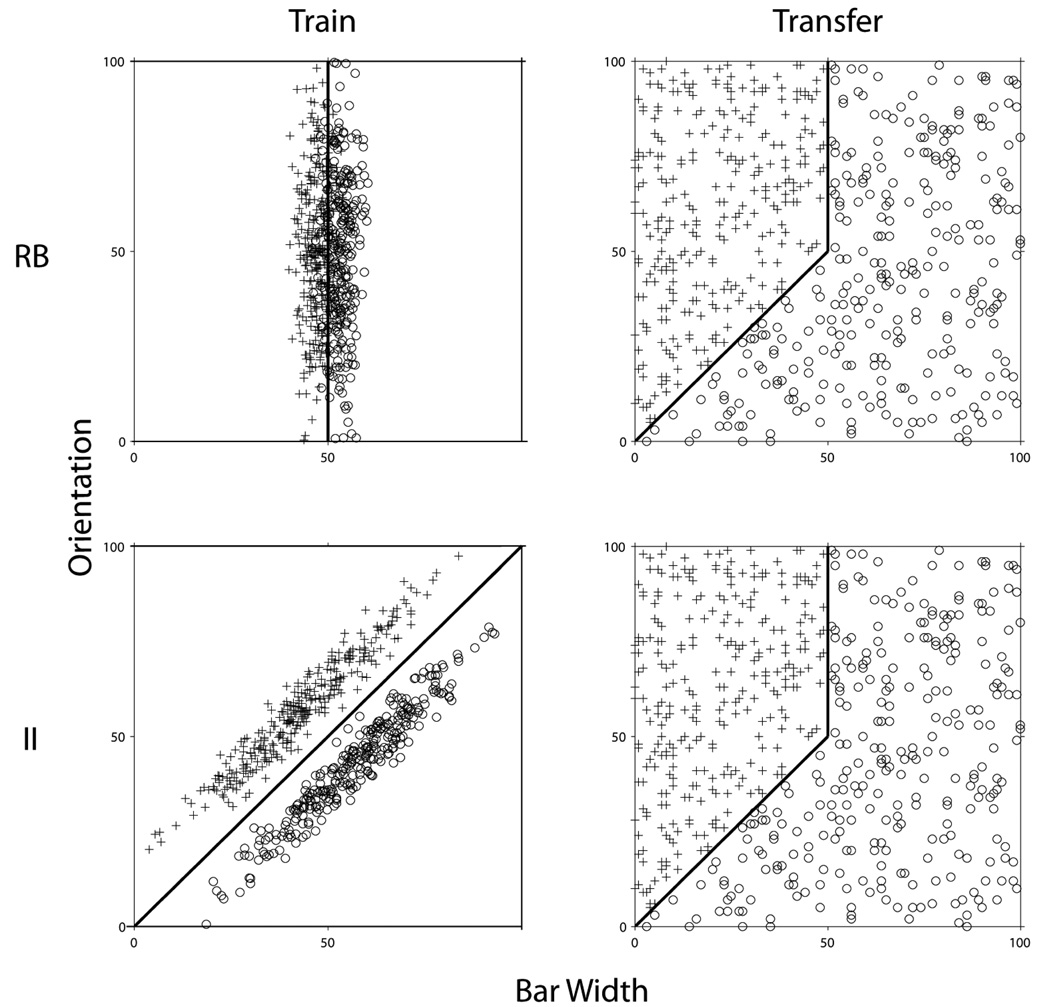
Abstract representation of the categories used in the three conditions of Experiment 1. Each plus denotes the bar width and orientation of an exemplar of Category A and each circle denotes the bar width and orientation of an exemplar of Category B. All stimuli were circular sine-wave gratings of the type shown in Figure 1.

Rule-based and information-integration tasks have been invaluable, both for providing evidence that category learning is mediated by multiple systems, and for providing insights into the unique properties of two of these systems. In real life however, difficult category-learning problems are probably not dominated by a single system, as seems the case for both rule-based and information-integration category learning. Instead, it seems likely that multiple systems contribute. For example, radiologists clearly gain much explicit knowledge (e.g., from lectures in medical school) about assigning x-rays to the categories “tumor” versus “nontumor”. True expertise, however, also requires extended hands-on experience, and it seems plausible that procedural learning mediates some of the improvements that occur during this kind of training.

To study how declarative and procedural-learning systems interact, it seems preferable to use a task in which both systems might be active. The problem with this approach however, is that in most such paradigms, it is impossible to tell which system is used on any given trial. The ideal task would be one in which both systems are heavily used but for which we could be reasonably confident as to which responses are controlled by the rule-learning systems and which are controlled by the procedural-learning system. Such an ideal is probably not possible, but a task that attempts to achieve this goal is described in the middle panel of Figure 2. Each plus describes an exemplar from category A and each circle describes an exemplar from category B. As in Figure 1, the stimuli are circular sine-wave gratings. When bar width and orientation are both low, the optimal strategy requires information integration, whereas when orientation is high, a simple rule-based strategy can be used. This hybrid categorization task will be used in Experiments 1 and 2 to study how declarative and procedural systems interact during category learning.

Many previous studies have shown that the rule-based component of the optimal bound in this hybrid task (i.e., the vertical line segment) is much easier for healthy young adults to learn than the diagonal component (for a review, see Ashby & Maddox, 2005). Thus, the hybrid categories have some stimuli that require a strategy that is easy to learn and some that require a strategy that is difficult to learn. In contrast, the information-integration categories shown in the top panel of Figure 2 only include stimuli that require a strategy that is difficult to learn. For this reason, if rule-based and procedural learning systems operate independently then the hybrid conditions should be no more difficult than the information-integration condition, and may actually be easier. The hybrid conditions should also be easier than the information-integration condition if the two systems somehow facilitate each other. On the other hand, if there is inhibition between the two systems, then the hybrid categories shown in Figure 2 should be especially difficult to learn.

Experiment 1

Experiment 1 included the three conditions shown in Figure 2. Every participant in all conditions received 1,200 trials of categorization training (with feedback) spread over two separate sessions. One group of participants learned the hybrid categories shown in the middle panel of Figure 2. As a control, a second group learned information-integration categories that were created from the same stimuli used in the hybrid condition (Figure 2, top panel). The only difference between the conditions was that in the information-integration condition the decision bound was the single diagonal line that extends the diagonal component of the hybrid bound. With the hybrid categories shown in the middle panel of Figure 2, a participant using a one-dimensional rule of the type: “Respond A if the bars are thin, and B if they are thick” could achieve an accuracy of nearly 90% correct. This could induce participants to adopt a strategy in which they sacrifice 10% accuracy in favor of a strategy that is simpler to learn. To control for this possibility we also included a second hybrid condition, shown in the bottom panel of Figure 2, in which more stimuli are presented from the lower left quadrant of the stimulus space. In this condition, the best one-dimensional rule only yields an accuracy of 74% correct, which is the same accuracy that the best one-dimensional rule can achieve in the information-integration control condition.

Method

Participants

There were 22 participants in the Information-Integration condition (top panel of Figure 2), 24 participants in the Uniform-Hybrid condition (middle panel of Figure 2), and 15 participants in the Non-Uniform-Hybrid condition (bottom panel of Figure 2). All participants were UCSB undergraduates who received course credit for completing the experiment.

Stimuli

Stimuli were gray-scale circular sine-wave gratings that only varied in spatial frequency (cycles per degree, CPD) and orientation (radians, rad). Each stimulus subtended approximately 5 degrees of visual angle and was displayed against a gray background using routines from Brainard’s (1997) Psychophysics toolbox.

To create stimuli for the Uniform-Hybrid condition we first drew 300 random samples from a uniform distribution defined over the A region illustrated in the middle panel of Figure 2. We then drew another 300 random samples from the uniform distribution defined over the B region illustrated in the middle panel of Figure 2. The result of this process was 600 ordered pairs of numbers (x,y), with each value ranging between 0 and 100. These (x,y) pairs were then converted to stimuli with spatial frequency and orientation (f,o) via the following linear transformations:

$$\begin{array}{c}f=x/30+0.25\\ o=(\mathrm{\pi }/200)y\end{array}$$

Spatial frequency units were cycles per degree and orientation units were radians. These linear transformations were selected in an attempt to equate the salience of spatial frequency and orientation dimensions.

To create stimuli for the Non-Uniform-Hybrid condition we first drew 450 random samples from the uniform distribution defined over the region in the lower left quadrant illustrated in the bottom panel of Figure 2. Each (x,y) pair in this region was given a category label according to the following rules: if x < y, then the stimulus is in category A, otherwise the stimulus is in category B. We then drew 75 random samples from the uniform distribution defined over the region in the upper left quadrant illustrated in the bottom panel of Figure 2. Each (x,y) pair in this region was assigned to category A. Finally, we drew 75 random samples from the region in the upper right and lower right quadrants illustrated in the bottom panel of Figure 2. Each of these stimuli was assigned to category B. The (x,y) pairs were then converted to stimuli with spatial frequency and orientation (f,o) via the same linear transformation used for the Uniform-Hybrid stimuli.

To create stimuli for the Information-Integration condition that is illustrated in the top panel of Figure 2, we first drew 600 random samples from the uniform distribution defined over the entire 0 to 100 space. Each (x,y) pair was given a category label according to the following rules: if x <y, then the stimulus is in category A, otherwise the stimulus is in category B. The (x,y) pairs were then converted to stimuli with spatial frequency and orientation (f,o) via the same linear transformation used for the Uniform-Hybrid stimuli.

Procedure

The experiment took place in a dimly lit room over the course of two 60-minute sessions that occurred within 48 hours of each other. On day 1, participants were informed that they would be learning to classify novel stimuli into an A category or a B category according to a hidden, experimenter-defined structure. They were told that the stimuli would be circles with stripes that could only vary in stripe thickness and stripe angle. On day 2 they were told that they would be doing exactly the same experiment that they did on day 1.

Each trial of the experiment began with a fixation cross that was followed by stimulus onset 1 second later. The stimulus was cleared from the screen immediately after a response was made. Subjects received a visual and auditory warning if they failed to respond within 3 seconds of stimulus onset. Each trial was completed with auditory feedback indicating whether the response was correct or incorrect. Feedback following a correct response was a 0.73 second sine wave tone at 500 Hz and feedback following an incorrect response was a 1.22 second sine wave tone at 300 Hz. There was an intertrial interval of 2 seconds between feedback offset and the next stimulus onset, although the fixation cross was visible immediately after feedback termination. Participants used two keys on a standard keyboard labeled “A” and “B” to make their responses.

The same 600 stimuli were used on both days. The order of stimulus presentation was randomized across participants and across days so that every session used the same stimuli in a different order.

Results

Accuracy-Based Analyses

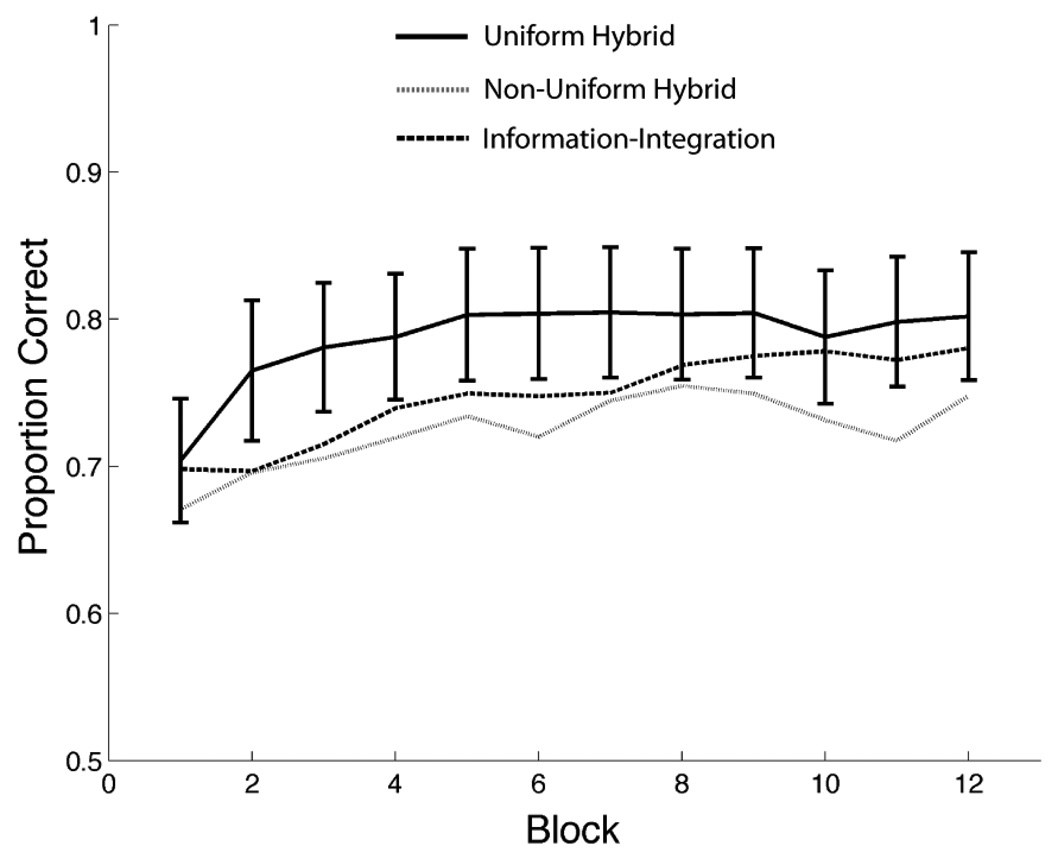
Figure 3 shows the mean accuracy in each 100-trial block for all three conditions across both days of the experiment. To aid visual presentation, error bars are shown only for the Uniform-Hybrid condition. The error bars for the other conditions were of similar magnitude. Note that mean accuracy in the Uniform-Hybrid condition was greater than mean accuracy in either other condition on every block of the experiment. Both of these differences are significant by a sign test [12/12, p < 0.001]. Even so, a 3 × 12 mixed ANOVA [3 conditions (Uniform-Hybrid versus Non-Uniform-Hybrid versus Information-Integration) × 12 blocks] revealed no main effect of condition [F(2,58) = 1.75, p = 0.18] and no interaction [Greenhouse-Geisser corrected F(22,638) = 0.79, p = 0.61], although the main effect of block was significant [Greenhouse-Geisser corrected F(11,638) = 9.71, p <0.001].

Figure 3.

Mean accuracy for each 100-trial block in Experiment 1. Error bars, which were similar in all conditions, are only shown for the Uniform Hybrid condition.

Model-Based Analyses

The accuracy-based analyses suggest that performance in the Uniform-Hybrid condition may have been slightly better than in either other condition. Before drawing any strong conclusions from this result, however, it is important to know what decision strategies participants used in these three conditions. In particular, it is critical to know whether hybrid participants eventually adopted a hybrid decision strategy. To answer this question, we fit four different types of decision bound models (e.g., Maddox & Ashby, 1993) to the data from each individual participant: pure-guessing, rule-based, hybrid, and information-integration models (see the Appendix for details).

As their name implies, the pure-guessing models assumed participants guessed at random on each trial. The rule-based models assumed either a single vertical or horizontal bound, or that participants used a conjunction rule of the type: Respond A if the bar width is narrow and the orientation is steep; otherwise respond B. The hybrid models assumed participants used a hybrid strategy, but allowed for suboptimalities in the slope and intercept of the diagonal piece of this bound (i.e., see Figure 2) and in the x-intercept of the vertical component of the bound. The information-integration models assumed that the decision bound was a single line of arbitrary slope or intercept. We did not fit models that assumed a quadratic decision bound (e.g., as in Maddox & Ashby, 1993, or Ashby, Waldron, Lee, & Berkman, 2001). If participants approximated the optimal bound with a quadratic curve, then a hybrid model would fit better than an information-integration model that assumes a linear bound. For this reason, note that there is an asymmetry in the strength of the conclusions we can draw from this model fitting exercise. If a linear-bound information-integration model fits better than a hybrid model, then we have strong evidence that participants did not use a strategy of the optimal type. In contrast, if a hybrid model fits best, our conclusions must be weaker. Either participants used a strategy of the optimal type, or they did a reasonably good job of approximating the optimal strategy. All four types of models were fit separately to the data from the last 100 trials of days 1 and 2 of each individual participant.

Table 1 shows the number of participants in the three conditions whose data were best fit by a model of each of these four types. Note that in the Information-Integration condition, an information-integration model (i.e., which assumes a strategy of the optimal type) fit best for about 2/3 of the participants on both days of the experiment. However, in each Hybrid condition, no data sets were best fit by a hybrid model on the first day, and only one participant’s responses in each condition were best fit by a hybrid model on the second day. These differences are significant – that is, the percentage of participants whose data were best fit by a model assuming a strategy of the optimal type was significantly greater in the Information-Integration condition than in the Uniform-Hybrid condition [t(46) = 4.81, p < 0.001] or in the Non-Uniform-Hybrid condition [t(37) = 9.10, p < 0.001]. Table 1 also indicates that the main effect of adding more stimuli to the lower left quadrant in the Hybrid conditions was to increase the percentage of participants who data were best fit by a model that assumed a linear information-integration strategy from 17% in the Uniform-Hybrid condition to 47% in the Non-Uniform-Hybrid condition (i.e., on Day 2). Clearly however, this manipulation did not increase the number of participants who were best fit by a hybrid strategy.

Table 1.

Number of Experiment 1 participants best fit by each model type.

	Guessing		Rule-Based		Information- Integration		Hybrid
	Day 1	Day 2	Day 1	Day 2	Day 1	Day 2	Day 1	Day 2
Information-Integration	0	0	7	6	15	16	0	0
Uniform Hybrid	0	1	20	18	4	4	0	1
Non-Uniform Hybrid	1	1	9	6	5	7	0	1

The hybrid model has one more free parameter than the information-integration model (i.e., the GLC; see the Appendix). Thus, one concern is that the hybrid model might actually be the better model but that it loses during model comparison because its extra parameter incurs a higher penalty in the goodness-of-fit statistic that was used (i.e., BIC). To address this question, we reran the model comparisons using the AIC fit statistic, which reduces the penalty difference between the hybrid and GLC models, relative to the BIC statistic (i.e., given the sample sizes we used). Although there were some minor changes, the most important result was that the number of participants whose responses were best fit by the hybrid model was unchanged. In particular, when the winning model is determined by AIC, only one participant in the Uniform-Hybrid condition and only one participant in the Non-Uniform-Hybrid condition produced responses that were best fit by the hybrid model. Thus, the apparent lack of hybrid responding in Experiment 1 was not due to the use of an especially punitive goodness-of-fit statistic.

Note that the modeling results also showed that the responses of more participants were best fit by a model that assumed a strategy of the optimal type in the Information-Integration condition than in the Hybrid conditions. Given this, it may seem strange that overall accuracy was highest in the Uniform-Hybrid condition (i.e., see Figure 3). In this condition, four participants were best fit by an information-integration model on each day, but the responses of more than 80% of the participants were best described by a rule-based model. Most of these models assumed a one-dimensional rule, with only four participants on day 1 and one participant on day 2 best fit by a model that assumed a conjunction rule.

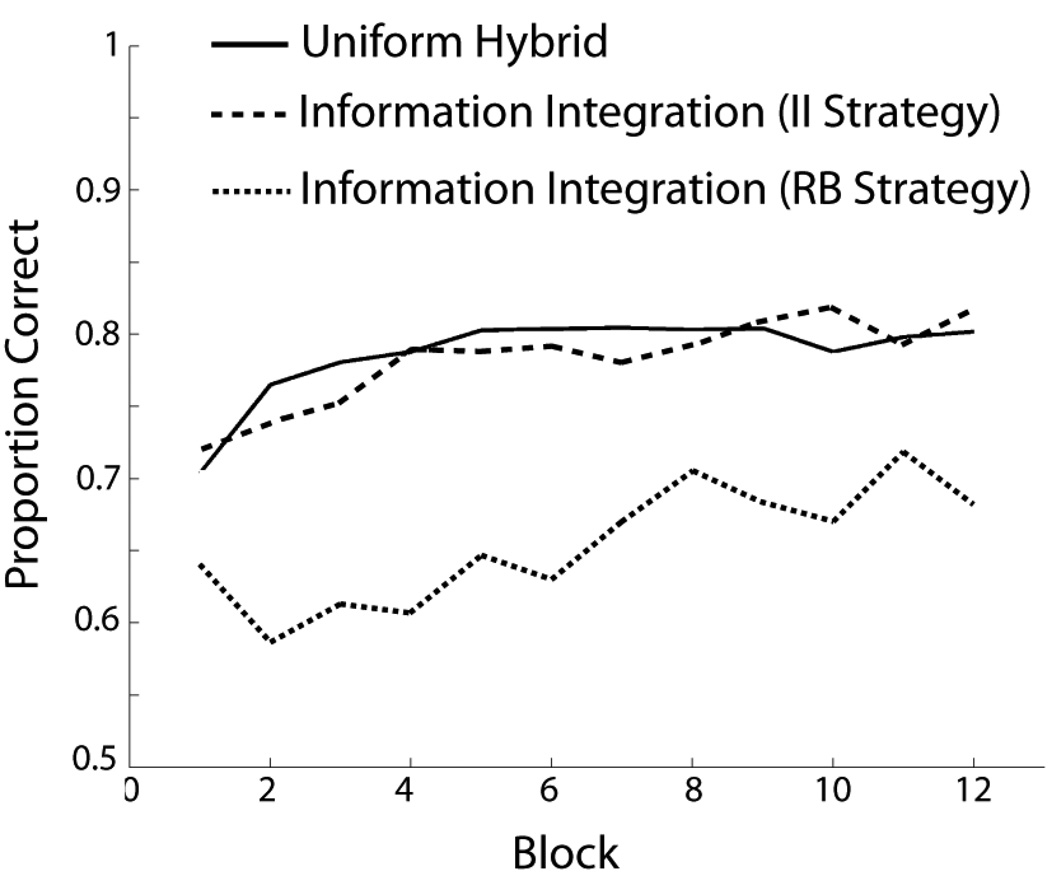
A comparison of the top two panels of Figure 2 suggests that a vertical line decision bound will achieve higher accuracy in the Uniform Hybrid condition than in the Information-Integration condition. In fact, as mentioned above, a vertical bound can achieve accuracy as high as 90%. This raises the possibility that the higher overall accuracy of participants in the Uniform Hybrid condition (see Figure 3) may be because one-dimensional rules were more successful in this condition, rather than because Uniform-Hybrid participants learned more. To answer this question, we separated participants in the Information-Integration condition according to the type of model that best fit their data. Figure 4 shows the learning curves following this partitioning. Note that, as predicted, the accuracy difference in Figure 3 is driven solely by the poor performance of the Information-Integration participants whose response were best fit by a model that assumed a one-dimensional rule.

Figure 4.

Experiment 1 accuracy where Information-Integration condition participants are separated by the strategy that best described their responses (II = Information Integration, RB = Rule Based).

Discussion

Perfect accuracy is possible with the hybrid categories if a simple one-dimensional rule is used on some trials and a more complex information-integration strategy is used on the other trials. Many previous studies have shown that healthy young adults can readily learn to use either type of strategy (e.g., Ashby & Maddox, 2005). In addition, near perfect performance could be achieved with a quadratic bound that approximates the piecewise linear bound of the hybrid strategy, and many previous studies have shown that people are adept at learning a wide variety of quadratic decision boundaries (e.g., Ashby & Maddox, 1992). These quadratic bounds are at least as complex as the hybrid bound, so it would be difficult to argue that the failure of our participants to adopt a hybrid strategy was because the hybrid strategy was too complex.

The hypothesis that participants could be satisficing – that is, sacrificing perfect accuracy for a simpler strategy – is also problematic. In the Non-Uniform Hybrid condition, use of a one-dimensional rule only yields 74% correct. Yet even in this condition only 2 of 39 Hybrid participants produced data that was consistent with a hybrid strategy. Furthermore, 74% correct is also the accuracy of the best one-dimensional rule in the Information-Integration control condition. If participants in the Hybrid conditions were satisficing then the control participants should have resisted an information-integration strategy by the same overwhelming percentage. Instead, the responses of 16 of 22 Information-Integration participants were best fit by an information-integration model. Thus, our participants were far more successful at learning the information-integration strategy required in the Information-Integration condition than at learning the hybrid strategy required in the Hybrid conditions.

Experiment 2

The results of Experiment 1 suggest that people failed to learn the hybrid categories. The results of the Experiment 1 Information-Integration condition indicated that about 1/3 of those participants failed to learn the information-integration categories, despite two days of training. One possible reason for the poor performance of the Hybrid participants, therefore, could be that they mostly failed on the information-integration component of the hybrid bound (i.e., the diagonal component). The results from the Information-Integration condition suggest that this component is difficult to learn even when every trial can be used for practice. With the hybrid categories, only some trials require information-integration, so an optimal Hybrid participant might have less overall practice at information-integration.

Experiment 2 tests this hypothesis by pre-training participants on either the information-integration component of the hybrid bound or on the rule-based component. The design is illustrated in Figure 5. If the Experiment 1 Hybrid participants performed poorly because they did not have enough practice at the more difficult information-integration component of the hybrid bound, then pre-training with this component should lead to much better performance on the hybrid categories than pre-training on the simpler rule-based component.

Figure 5.

Stimuli and optimal category boundaries used in the training and transfer conditions of Experiment 2 (RB = Rule-Based Training condition; II = Information-Integration Training condition).

In the Information-Integration Training condition of Experiment 2, participants trained for 600 trials on the information-integration component of the hybrid bound, and then transferred to the hybrid categories on the second day. In the Rule-Based Training condition, participants trained for 600 trials on the rule-based component of the hybrid bound, and then transferred to the hybrid categories on the second day. In the hybrid categories, the stimuli were uniformly distributed over each response region (i.e., see Figure 5). If we had used similar uniform distributions for the pre-training categories, then because one-dimensional rules are so easy for people to learn, the Rule-Based Training participants would have achieved much higher accuracy than the Information-Integration Training participants by the end of the pre-training session. To avoid this confound, we trained participants on categories that were defined by bivariate normal distributions – that is, the exemplars in each pre-training category were random samples from a bivariate normal distribution (see Figure 5). Bivariate normal distributions were chosen because by changing the category means and variances, we could easily change the category separation, and therefore categorization difficulty. In fact, we set the category overlap during rule-based training to be higher than during information-integration training in an attempt to control difficulty. As we will see, these efforts were reasonably effective. It is important to note, however, that despite the different category distributions used in training and transfer, the optimal decision bounds agreed exactly – that is the optimal rule-based training bound was identical to the vertical line component of the hybrid bound, and the optimal information-integration training bound was identical to the diagonal component of the hybrid bound (except the training bounds extended across the entire stimulus space).

Method

Participants

There were 14 participants in the Rule-Based Training condition and 14 in the Information-Integration Training condition. All participants were UCSB undergraduates who received course credit for completing the experiment.

Stimuli

The rule-based and information-integration categories used for training were created using the randomization technique developed by Ashby and Gott (1988). Specifically, the A and B categories were defined as bivariate normal distributions using the parameters defined in Table 2. Stimuli were generated by drawing 300 random samples (x,y) from each category distribution. The (x,y) values obtained from this process were transformed so that the sample statistics equaled the population parameter values reported in Table 2. Next, to control for statistical outliers, all (x,y) pairs more than three standard deviations away from the mean (i.e., Mahalanobis distance > 3; e.g., Fukunaga, 1972) were discarded and new samples were drawn to replace them. Finally, (x,y) pairs were converted to (f,o) pairs using the linear transformations:

$$\begin{array}{c}f=x/30+0.25(\text{CPD})\\ o=(\mathrm{\pi }/200)y+\mathrm{\pi }/9(\text{rad}).\end{array}$$

Table 2.

Parameters used to generate the training categories used in Experiment 2

	Category A					Category B
	μx	μy	σx	σy	cov	μx	μy	σx	σy	cov
Rule-Based	55	50	10	300	0	47	50	10	300	0
Information-Integration	43	57	209	209	201	57	43	209	209	201

Hybrid stimuli used for transfer were created by adding π/9 radians to every stimulus used in the Hybrid condition of Experiment 1. This was done so that the diagonal bound of the hybrid categories matched the diagonal bound of the information-integration training categories.

Procedure

The procedure on day 1 was identical to the procedure used in Experiment 1. On day 2 participants were told that the first 100 trials would be from the same category structures as on day 1, but that during the following 600 trials, the categories might change. Each trial consisted of the same events as in Experiment 1.

In the Information-Integration Training condition, all stimuli on day 1 and the first 100 stimuli on day 2 were from the information-integration categories. In the Rule-Based Training condition, all stimuli on day 1 and the first 100 stimuli on day 2 were from the rule-based categories. In both conditions, the last 600 stimuli on day 2 were from the hybrid categories. The order of stimulus presentation was randomized between participants.

Results

Accuracy-Based Analyses

Participants were excluded from all accuracy-based analyses (but not from model-based analyses) if 1) the model that best accounted for their last 100 responses during the Day 1 training session assumed random guessing, and 2) accuracy on these 100 trials was less than 65% correct. One participant failed to meet this criterion in the Rule-Based Training condition, and four participants failed in the Information-Integration Training condition.

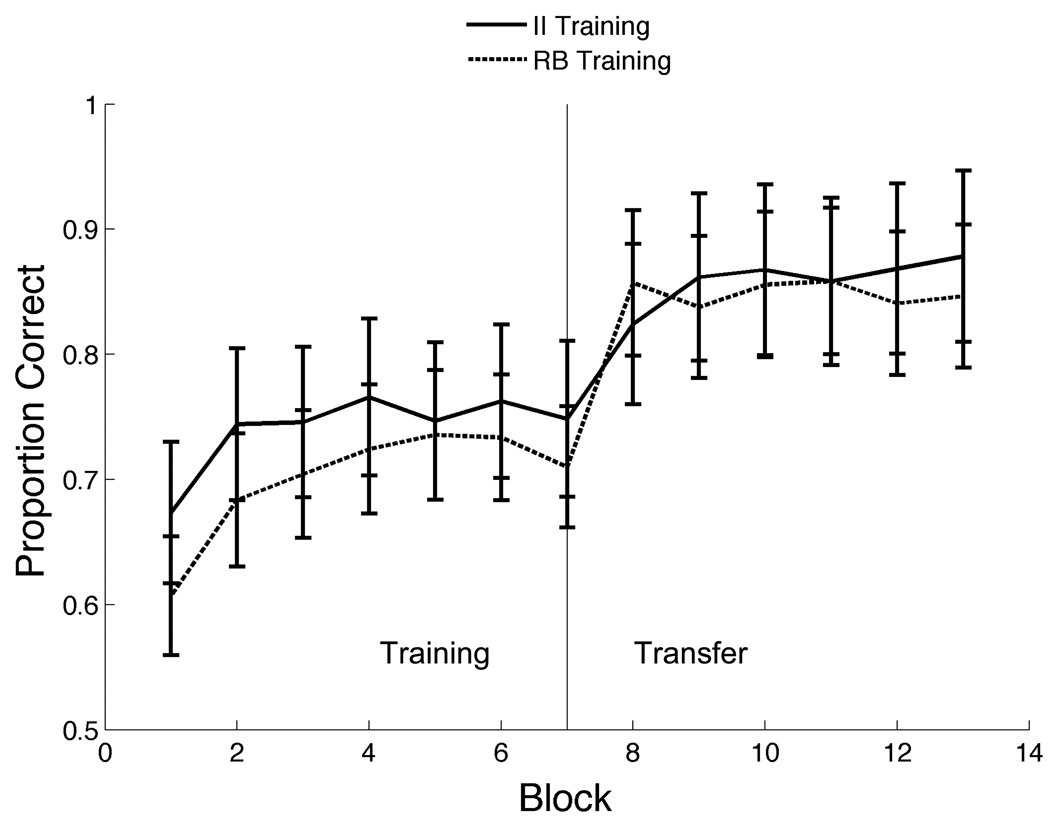
Figure 6 shows the average learning curves for both conditions across both days in Experiment 2. Recall that the category overlaps in the two training conditions were set differently in an attempt to control difficulty. Specifically, the rule-based training categories overlapped more than the information-integration training categories. Figure 6 shows that this effort was mostly successful, in the sense that the performance of the participants in the two training conditions was not too different. Although there was a trend for higher accuracy in the Information-Integration Training condition, a 2 conditions (rule-based versus information-integration) × 7 blocks repeated measures ANOVA failed to find a significant effect of condition [F(1,24) = 3.94, p = 0.59] or a significant interaction [Greenhouse-Giesser corrected F(6,144) = 0.54, p = 0.72]. The effect of block was significant, however, indicating that performance improved with training [Greenhouse-Geisser corrected F(6,144) = 8.73, p < 0.01].

Figure 6.

Mean accuracy for each 100-trial block during training and transfer in both conditions of Experiment 2 (II Training = Information-Integration Training condition, RB Training = Rule-Based Training condition).

Note that accuracy jumps in both conditions during transfer to the hybrid categories. This is to be expected regardless of whether participants switched to a hybrid strategy because the training categories had more stimuli that were difficult to categorize than the hybrid categories (i.e., more stimuli near the category bound) and fewer stimuli that were easy to categorize (i.e., fewer stimuli far from the category bound). This is easily seen in Figure 6. More important, however, Figure 6 indicates that during transfer, performance on the hybrid categories was about the same in the two conditions. A 2 conditions × 6 blocks repeated measures ANOVA confirmed this conclusion. Specifically, the main effect of condition was not significant [F(1,24) = 0.97, p = 0.33], nor was the interaction [Greenhouse-Geisser corrected F(5,120) = 2.68, p = 0.025]. Importantly, the main effect of block was also not significant [Greenhouse-Geisser corrected F(5,120) = 1.25, p = 0.29], which suggests no significant learning by either group during the 600 trials of training with the hybrid categories.

Model-Based Analyses

As in Experiment 1, we fit hybrid, rule-based, information-integration, and random guessing models to the last 100 trials of each participant’s training and transfer data. The numbers of participants best fit by each model type are shown in Table 3.

Table 3.

Number of Experiment 2 participants best fit by each model type.

	Guessing		Rule-Based		Information- Integration		Hybrid
	Training	Transfer	Training	Transfer	Training	Transfer	Training	Transfer
RB Training	1	0	13	10	1	5	0	0
II Training	4	0	2	10	10	6	0	0

First note that none of the participants in either condition produced responses that were best fit by a model that assumed a hybrid decision strategy, either during training or transfer. Thus, pre-training on the information-integration component of the hybrid bound did not appear to facilitate the learning of hybrid strategies. Second, note that during training, a model that assumed a bound of the optimal type fit best for the majority of participants in both groups. Thus, the training was effective. Third, note that the responses of most participants in the Rule-Based Training condition continued to be best fit by models that assumed an explicit rule. In the Information-Integration Training condition, the data of 10 of 16 participants were best fit by a rule-based model during transfer. Included in this group were 5 participants whose responses were best fit by an information-integration model during training. Thus, these 5 participants learned the information-integration component of the hybrid bound during training, but then apparently switched away from this to an explicit rule when they encountered the hybrid categories.

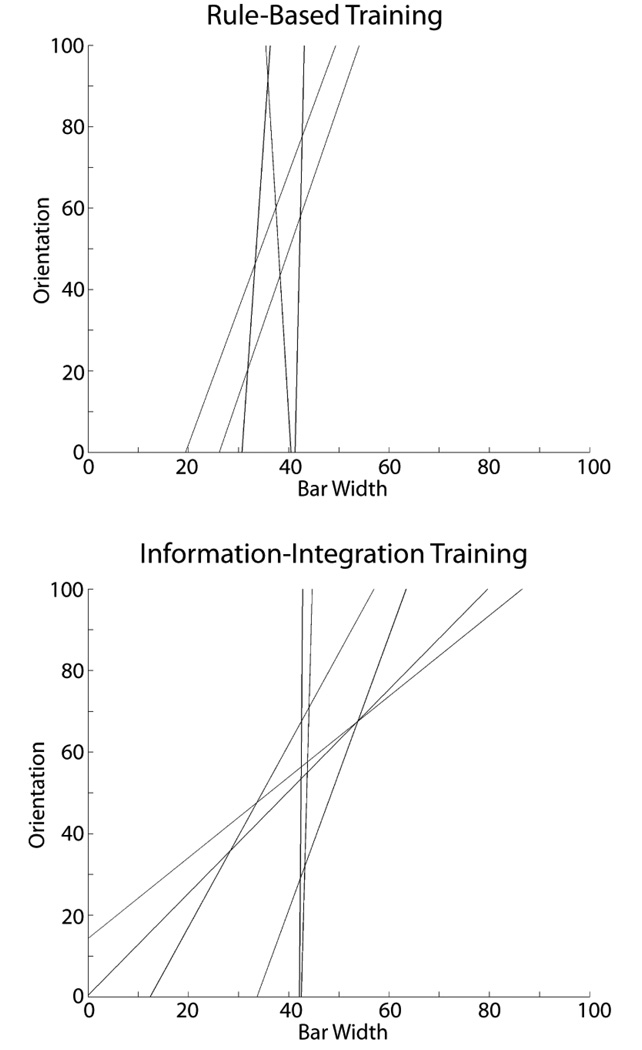
Table 3 also indicates that the last 100 transfer trials of 5 participants in the Rule-Based Training condition and 6 in the Information-Integration Training condition were best fit by an information-integration model. The best-fitting bounds for these participants are shown in Figure 7. Note that in the Rule-Based Training condition, these bounds are essentially vertical for 3 participants and just off vertical for 2, suggesting that these participants allocated almost all attention to the bar-width dimension. In the Information-Integration Training condition there were 3 subgroups of 2 participants each. For 2 participants the best-fitting bound was almost vertical, 2 participants appeared to perseverate with essentially the same bound they used during training (the two shallowest lines in Figure 7), and the bounds for 2 participants were of an intermediate slope.

Figure 7.

Decision bounds that provided the best fit to the last 100 trials of the transfer (i.e., hybrid) session of Experiment 2 for those participants whose responses were best fit by a model that assumed a linear information-integration strategy.

Discussion

No Experiment 2 participants learned the hybrid categories, even though almost all of them mastered a component of the hybrid strategy during a pre-training period. The model fits suggested that participants who first learned the rule-based component of the hybrid strategy almost all perseverated with a simple rule throughout the 600 trials with the hybrid categories. Similarly, these analyses suggest that the participants who were trained on the more difficult information-integration component of the hybrid strategy either persisted with a linear information-integration strategy on hybrid trials, or else switched to a pure rule-based strategy.

General Discussion

In two experiments, a total of 53 participants received feedback training with the hybrid categories. Some participants received 1200 trials of practice with the hybrid categories, and others received extensive pre-training with the most difficult component of the hybrid strategy. Yet in this large group, we found evidence that only two participants successfully adopted a strategy of the optimal type. As we will show in the next few sections, these results are inconsistent with almost all current accounts of category learning.

Single System Accounts

The most popular single-system accounts of category learning, including exemplar theory and the striatal pattern classifier (Ashby & Waldron, 1999), predict that participants should readily adopt a strategy of the optimal type when faced with the hybrid categories. For example, consider exemplar theory. The key result is that exemplar theory predicts that participants will eventually become nearly optimal in every categorization task, so long as some attention is allocated to all relevant perceptual dimensions (Ashby & Alfonso-Reese, 1995). Furthermore, exemplar theory predicts that people learn to allocate attention optimally (i.e., the attention optimization hypothesis; Nosofsky, 1986, Nosofsky & Johansen, 2000), and in the hybrid task the optimal strategy is to allocate some attention to both dimensions. Thus, exemplar theory predicts that participants will learn to respond optimally in the hybrid task. In addition, exemplar theory predicts no difficulty difference between the hybrid and information-integration conditions of Experiment 1. Neither of these predictions was supported by our data.

Previous empirical results from the category-learning literature also would cause one to predict near optimal performance in the hybrid task. This is because the optimal hybrid strategy can be closely approximated by a quadratic bound, and many previous studies have shown that participants can readily learn a wide variety of quadratic bounds, including parabolas, circles, ellipses (e.g., Ashby & Maddox, 1992; Ashby & Waldron, 1999; Filoteo & Maddox, 2004; Filoteo, Maddox, & Davis, 2001), and hyperbolas (e.g., Maddox & Bohil, 1998; Maddox & Ing, 2005). In many of these studies, the optimal bound that participants were trying to learn had more curvature than the hybrid bound shown in Figure 2. Thus, previous experiments with nonlinearly separable categories would cause one to predict that participants should have little trouble learning the hybrid categories. In other words, many previous studies have shown that under different conditions, participants have no particular problem learning categories that are at least as complex as the hybrid categories. Thus, a simple complexity argument does not account for our results.

A natural question to ask therefore, is what feature of the hybrid categories makes them so difficult to learn? Although our experiments do not speak directly to this question, an obvious candidate is the vertical line component of the optimal bound. According to this hypothesis, the vertical line component induces explicit rule use, and if the declarative memory systems that subserve rule-based responding inhibit the use of procedural memory-based strategies, then this would prevent procedural memory from adopting a nonlinear bound that approximates the optimal hybrid bound.

Multiple System Accounts

To our knowledge, all existing theories that postulate multiple category-learning systems assume that those systems learn independently and compete only to control the observable categorization response. By independently, we mean that each system learns and performs just as effectively regardless of whether the other system is also in operation, and that each system has unfettered access to the response. It is important to note, however, that even under these conditions, there must be some competition between the systems. If two separate systems are each suggesting a response, but the environment allows the participant to emit only one response, then the two systems will be in conflict any time they suggest competing responses. By unfettered access to the response, we therefore mean that the system capable of learning the categories is not prevented by the other system from expressing this knowledge.

Included in the list of multiple systems models that assume independence are ATRIUM (Erickson & Kruschke, 1998) and COVIS (Ashby et al., 1998). Both models assume that one system is rule based and one is similarity based. ATRIUM assumes the similarity-based system is a standard exemplar model, whereas COVIS assumes it is mathematically equivalent to a multiple prototype model. In ATRIUM the response competition is resolved by blending the outputs of the two systems and in COVIS the competition is resolved by allowing the more confident of the two systems to respond.

ATRIUM and COVIS both predict near optimal performance with the hybrid categories. The similarity-based components in both models are sophisticated enough to easily learn the hybrid categories by themselves. Thus, one possibility is that these components would come to dominate performance and the models would essentially reduce to single-system models. Another possibility is that the similarity-based component would come to control performance for stimuli with shallow orientations and the rule-based component would control performance for stimuli with steep orientations. For example, in ATRIUM “each module learns to classify those stimuli for which it is best suited” (Erickson & Kruschke, 1998, p. 119). In COVIS, the system that is most confident controls the response. For stimuli with steep orientations, the two systems would have similar levels of confidence, but the model is biased towards the rule-based system, so presumably the rule-based system would control responding for these stimuli. For most stimuli with shallow orientations, the rule-based system would have low confidence, so responding would be controlled by the similarity-based system.

Knowledge Partitioning

Knowledge partitioning is the phenomenon in which people break down a task into subtasks, and apply a unique strategy in each subtask that is not influenced by the strategies used in the other subtasks (Lewandowsky & Kirsner, 2000; Yang & Lewandowsky, 2004). In most knowledge partitioning experiments, one or more cues signal the participant where to make the partition. The subtasks in most knowledge partitioning experiments access the same memory system (usually declarative), but Erickson (2008) reported the results of a knowledge partitioning experiment in which participants successfully switched between rule-based and information-integration categorization strategies on a trial-by-trial basis. Thus, Erickson’s (2008) data suggest that people can switch trial-by-trial between declarative and procedural memory systems. In the Erickson (2008) experiments, however, three cues signaled participants which strategy to apply. First, the stimuli requiring an information-integration strategy were perceptually distinct from the stimuli requiring a rule-based strategy (i.e., unlike our experiments, there was a large gap between stimuli in the two clusters). Second, stimuli requiring an information-integration strategy were presented in one color, whereas stimuli requiring a rule-based strategy were presented in a different color. Third, the information-integration categories required different responses from the rule-based categories (i.e., A and B versus C and D). Especially because of the different responses that were required, it seems plausible that participants in the Erickson (2008) experiments were aware of which memory system they should use on each trial.

The present experiments had none of these features, and we found no evidence of knowledge partitioning. Our results taken together with Erickson’s (2008), therefore suggest that trial-by-trial switching between declarative and procedural category-learning systems is possible if enough cues are provided to signal the participant which system should be used on each trial. In the absence of such unambiguous cues however, our results suggest that such switching does not occur automatically. Instead, participants perseverate with one system.

Switch Costs

Given that system switching failed in our experiments, a natural question to ask is why? Before concluding that switching failed because of inhibition between memory systems, it is important to rule out motivational hypotheses. For example, perhaps switch costs were too high. In the task-switching literature, it is well known that there is a cost for switching between two tasks (Meyer & Kieras, 1997; Rogers & Monsell, 1995). If the cost is too high, participants might avoid task switching and persist instead with a suboptimal strategy. Most task-switching studies have investigated the ability of participants to switch among tasks that depend on executive function (e.g., rule-based tasks). Perhaps switching between rule-based and information-integration tasks incurs a higher switch cost, which our participants chose not to pay. The problem with this account is that Erickson (2008) reported that under conditions that favor knowledge partitioning, participants readily switched between rule-based and information-integration strategies. Thus, under very similar task conditions participants readily switched between systems. In our experiments they did not. It seems unlikely that any of the extra cues that Erickson (2008) added to facilitate switching should affect the effort or cost of a system switch. If not, then Erickson’s results suggest that, in general, the cost of switching between rule-based and information-integration tasks is not prohibitive. As a result, it seems unlikely that our participants failed to adopt a hybrid strategy because of high switch costs.

Null Results

Finally it is important to note that our findings are not null results. A null result is a failure to find significance. We fit a variety of models to each participant’s data and in almost every case we found clear statistical evidence that one model fit better than the others. The important result was that in almost every case the best-fitting model assumed a suboptimal decision strategy. Thus, our findings are not null results, rather they are evidence of a fundamental suboptimality in human category learning.

Interactions between Multiple Systems

In summary, the results of Experiments 1 and 2 are inconsistent with the most prominent single- and multiple-system accounts of category learning. The existing data also suggest that the cost of switching between rule-based and information-integration strategies is low enough that the failure of participants to adopt a hybrid strategy cannot be attributed to high switch costs. What hypotheses then could account for our results? One possibility is that there are multiple systems, but unlike ATRIUM and COVIS, the use of one system either inhibits learning in the other, or denies access of the other system to control of the response. Our results do not allow us to test between these two possibilities, but there is data supporting the latter of these two hypotheses – that is, that the inhibition is at the output stage, and that the use of one system does not necessarily inhibit learning in the other. First, Packard and McGaugh (1996) reported that animals displaying hippocampal-dependent (place-learning) behavior immediately exhibited behavior that showed prior striatal-dependent (response) learning following inactivation of the hippocampus. Similarly, animals displaying striatal-dependent behavior immediately exhibited hippocampal-dependent behavior following inactivation of the striatum. Second, using fMRI, Foerde, Knowlton, and Poldrack (2006) reported that the introduction of a secondary task shifted the brain region that correlated with learning from the hippocampus to the striatum, but that the overall level of striatal activation was equal in the two conditions. Furthermore, Foerde, Poldrack, and Knowlton (2007) reported evidence that this striatal activation had a behavioral effect. In particular, they showed that a dual task that impaired learning in declarative memory systems in probabilistic classification did not prevent implicit learning of the correct cue–response associations. These results are consistent with the hypothesis that the use of strategies that depend on declarative memory systems does not prevent simultaneous striatal-mediated procedural learning, but it does restrict access of that procedural learning to motor output systems.

What brain mechanisms could be mediating this type of output inhibition? One intriguing but speculative hypothesis is that frontal cortex and the subthalamic nucleus control system interactions via the hyperdirect pathway through the basal ganglia. The hyperdirect pathway begins with direct excitatory glutamate projections from frontal cortex to the subthalamic nucleus. The subthalamic nucleus then sends excitatory glutamate projections directly to the internal segment of the globus pallidus (GPi; Joel & Weiner, 1997; Parent & Hazrati, 1995). This extra excitatory input to the GPi tends to offset inhibitory input from the striatum, making it more difficult for striatal activity to affect cortex. Hence, the hyperdirect pathway could permit (by reducing subthalamic activity), or prevent (by increasing subthalamic activity) signals coming from the striatum from influencing cortex.

Assuming the cortical input to the subthalmic nucleus is under prefrontal control, this hypothesis could account for the differences between our results and Erickson’s (2008). The extra cues presented by Erickson could be sufficient to inform the participant when to turn this signal on and off. In addition, note that this model is consistent with the neuroscience data suggesting that the inhibition between systems is at the output stage. The hyperdirect pathway has no direct effect on processing within the striatum, which has frequently been identified as a key site of procedural learning. Thus, this hyperdirect pathway hypothesis predicts that when declarative memory systems control behavior, procedural learning and memory operates normally but is blocked from (cortical) motor output systems.

Note that this hypothesis also accounts for the asymmetries we found in these inhibitory influences – that is, our results suggest that use of an explicit strategy prevents access to procedural knowledge, but we failed to find evidence of the opposite influence. For example, note that in Experiment 2, there was no evidence that participants who pretrained with the information-integration strategy perseverated with this strategy during transfer. Ten of the 15 participants who pretrained with the rule-based component of the hybrid bound used rules during transfer to the hybrid categories, and 10 of the 16 participants who pretrained with the information-integration component switched to rules during transfer. The hyperdirect pathway through the basal ganglia provides a mechanism via which the prefrontal cortex can inhibit a response selected by the striatum, but it does not allow the striatum to inhibit a response selected by the prefrontal cortex (i.e., there are direct projections from prefrontal cortex to premotor areas of cortex, but all striatal projections to cortex pass through the GPi or its analogue in the substantia nigra).

Evidence in support of this model comes from studies using the so called stop-signal task. On a typical stop-signal trial, participants are required to initiate a motor response as quickly as possible when a cue is presented. On some trials, however, a second cue is presented soon after the first and in these cases participants are required to inhibit their response. A variety of evidence implicates the subthalamic nucleus in this task (Mostofsky & Simmonds, 2008; Aron et al, 2007; Aron & Poldrack, 2006). A popular model is that the second cue generates a “stop signal” in cortex that is rapidly transmitted though the hyperdirect pathway to the GP_i, where it cancels out the “go signal” being sent through the striatum. We hypothesize that when declarative memory is controlling behavior a similar stop signal may be used to inhibit a potentially competing response signal generated by the procedural memory system. Obviously, much more work is needed to test this model.

Conclusions

Humans are very good at categorization. This has been demonstrated in the many previous studies that have reported optimal or nearly optimal categorization behavior with a wide variety of stimuli and category structures. Discovering how good people are at categorization has been theoretically beneficial, but we often learn the most about complex systems when we observe them fail. The failure of participants to learn the hybrid category structures in Experiments 1 and 2 represents a novel suboptimality that is not predicted by current cognitive theory and to our knowledge, has not been previously demonstrated.

Our results are consistent with the hypothesis that humans have at least two separate category-learning systems, and that the use of one system either inhibits learning in the other, or denies access of the other system to control of the response. No one or two cognitive experiments, however, will definitively answer the question of how the various category-learning systems interact, just as no one experiment conclusively proved that humans have multiple category-learning systems. Thus, although our results support inhibition between systems, much more work on this question is clearly needed.

Appendix

Three different rule-based decision bound models were fit to each participant’s data (2 one-dimensional models and a model that assumed a conjunction rule). We also fit one model that assumed an information-integration strategy, one model that assumed a hybrid strategy, and two different random guessing models. For more details, see Ashby (1992) or Maddox and Ashby (1993).

Rule-Based Models

The One-Dimensional Classifier

This model assumes that participants set a decision criterion on a single stimulus dimension. For example, a participant might base his or her categorization decision on the following rule: “Respond A if the bar width is small, otherwise respond B”. Two versions of the model were fit to the data. One version assumed a decision based on bar width, and the other version assumed a decision based on orientation. These models have two parameters: a decision criterion along the relevant perceptual dimension, and a perceptual noise variance.

The General Conjunctive Classifier (GCC)

This model assumes that the rule used by participants is a conjunction of two one-dimensional classifiers: “Respond A if the bar width is small AND the orientation is steep, otherwise respond B.” The GCC has 3 parameters: one for the single decision criterion placed along each stimulus dimension (one for orientation and one for bar width), and a perceptual noise variance.

Information-Integration Models

The General Linear Classifier (GLC)

The GLC assumes that participants divide the stimulus space using a linear decision bound. Categorization decisions are then based upon which region each stimulus is perceived to fall in. These decision bounds require linear integration of both stimulus dimensions, thereby producing an information-integration decision strategy. The GLC has 3 parameters: the slope and intercept of the linear decision bound, and a perceptual noise variance.

Hybrid Model

The hybrid model uses two linear bounds – one with arbitrary slope and intercept and one that is constrained to be vertical. The model responds A to any stimulus perceived to fall above the diagonal bound AND to the left of the vertical bound, and it responds B to all other stimuli. The hybrid model has 4 free parameters – a slope and intercept for the diagonal bound, an x-intercept for the vertical bound, and a noise variance.

Random Guessing Models

Fixed Random Guessing Model

This model assumed that the participant responded randomly, essentially flipping an unbiased coin on each trial to determine the response. Thus, the predicted probability of responding “A” (and “B”) was .5 for each stimulus. This model has no free parameters.

General Random Guessing Model

This model assumed that the participant responded randomly, essentially flipping a biased coin on each trial to determine the response. Thus, the predicted probability of responding “A” was a free parameter in the model that could take on any value between 0 and 1. This model is useful for identifying participants who are biased towards pressing one response key.

Goodness-of-Fit Measure

Model parameters were estimated using the method of maximum likelihood, and the statistic used for model selection was the Bayesian Information Criterion (BIC; Schwarz, 1978), which is defined as:

$$\text{BIC}=r\text{ln}N-2\text{ln}L,$$

where r is the number of free parameters, N is the sample size, and L is the likelihood of the model given the data. The BIC statistic penalizes models for extra free parameters. To determine the best fitting model within a group of competing models, the BIC statistic is computed for each model, and the model with the smallest BIC value is the winning model.