Micromechanical Models of Helical Superstructures in Ligament and Tendon Fibers Predict Large Poisson’s Ratios

Abstract

Experimental measurements of the Poisson’s ratio in tendon and ligament tissue greatly exceed the isotropic limit of 0.5. This is indicative of volume loss during tensile loading. The microstructural origin of the large Poisson’s ratios is unknown. It was hypothesized that a helical organization of fibrils within a fiber would result in a large Poisson’s ratio in ligaments and tendons, and that this helical organization would be compatible with the crimped nature of these tissues, thus modeling their classic nonlinear stress strain behavior. Micromechanical finite element models were constructed to represent crimped fibers with a super helical organization, composed of fibrils embedded within a matrix material. A homogenization procedure was performed to determine both the effective Poisson’s ratio and the Poisson function. The results showed that helical fibril organization within a crimped fiber was capable of simultaneously predicting large Poisson’s ratios and the nonlinear stress strain behavior seen experimentally. Parametric studies revealed that the predicted Poisson’s ratio was strongly dependent on the helical pitch, crimp angle and the material coefficients. The results indicated that, for physiologically relevant parameters, the models were capable of predicting the large Poisson’s ratios seen experimentally. It was concluded that helical organization within a crimped fiber can produce both the characteristic nonlinear stress strain behavior and large Poisson’s ratios, while fiber crimp alone could only account for the nonlinear stress-strain behavior.

Introduction

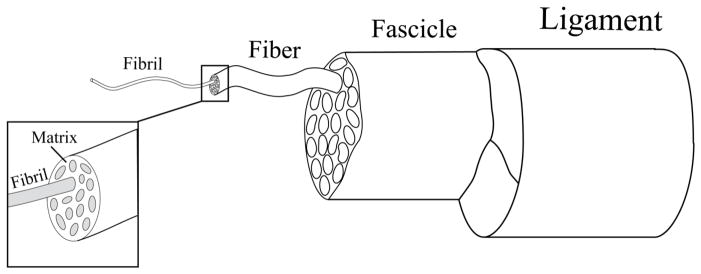
Tendons and ligaments are fibrous, load bearing tissues that are characterized by a hierarchical organization of collagen microstructures. A basic structural component of ligaments and tendons is the collagen fibril. Fibrils are closely packed within an extrafibrillar proteoglycan rich matrix to form a fiber. Individual fibers are encased in the endotendinous sheath and packed into fasicular units, which then become the constituents of the whole tendon or ligament complex (Kastelic, Galeski et al. 1978; Kannus 2000) (Fig 1).

Figure 1.

Schematic of tendon and ligament microstructure, adapted from Kastelic et al.

Although there is a wealth of literature on the elastic and viscoelastic behavior of ligaments and tendons, most studies have focused on uniaxial stress strain behavior and largely ignore volumetric behavior (e.g. Poisson’s ratio). In the biphasic theory, the compressibility of the solid phase is governed by the volumetric material coefficients in the constitutive model (Mow, Kuei et al. 1980). For uniaxial tensile loading in linear elasticity, the Poisson’s ratio is a measure of volume change and describes the lateral contraction in response to an axial strain. The Poisson’s ratio is strictly a kinematic measure, and can be defined both for the kinematically linear and nonlinear cases (generally referred to as the Poisson function in nonlinear theory), and applies to both isotropic and anisotropic materials. In the latter case, more than one Poisson’s ratio must be defined.

The reported Poisson’s ratios for tendon and ligament subjected to tensile loading along the fiber direction have ranged from 0.8 ± 0.3 in rat tail tendon fascicles (Screen and Cheng 2007), to 2.0 ± 1.9 in capsular ligament (Hewitt, Guilak et al. 2001) and 2.98 ± 2.59 in bovine flexor tendon (Lynch, Johannessen et al. 2003). Under tensile loading, these large Poisson’s ratios are indicative of volume loss, which may result in fluid exudation (Adeeb, Ali et al. 2004; Wellen, Helmer et al. 2004).

The magnitude of volume loss and thus the quantity of fluid exuded during deformation may play an important role in the mechanics and function of these tissues. It has been suggested that biphasic theory may explain some if not all of the viscoelastic behavior of ligament and tendon (Atkinson, Haut et al. 1997; Yin and Elliott 2004). Furthermore, fluid transport resulting from mechanical forces may aid in nutrient delivery within these tissues. Finally, shear forces and or cell membrane deformation resulting from pressure driven fluid flux may be an important mechanotransduction signal for tenocytes and fibroblasts (Butler, Kohles et al. 1997; Chen, Malkus et al. 1998; Lavagnino, Arnoczky et al. 2008). In light of this information, the volumetric behavior, and thus Poisson’s ratio, is of fundamental importance in understanding healthy and diseased ligament and tendon tissue.

A number of studies have examined structure-function relationships between the fibrillar microstructure and macroscopic behavior of the “toe region” of ligaments and tendons under tensile loading (Diamant, Keller et al. 1972; Lanir 1978; Ault and Hoffman 1992; Hurschler 1997; Freed and Doehring 2005; Grytz and Meschke 2009). However, there are no models in the literature that predict or explain the large Poisson’s ratio of these tissues. A review of the literature on fiber based composites reveals that at least two microstructural fiber geometries are capable of generating large Poisson’s ratios. One possibility is multiple fiber families crossing at non-orthogonal angles (Peel 2007), but histological studies suggest that fibrils and fibers in most ligaments and tendons are predominantly aligned in a parallel fashion (Provenzano and Vanderby 2006). The other possibility is the helical arrangement of a fiber family (Marklund 2007).

Several studies have reported the presence of helical structures within fibers and fascicles of ligament and tendon. Yahia et al. presented histological evidence that suggests the presence of a super-helical organization of fibrils in canine patellofemoral tendon and ACL. An organizational scheme was suggested in which a helical twist was superimposed on top of crimp structures. The scale of this twist was suggested as being an order of magnitude larger than that of the crimp (Yahia and Drouin 1989). Studies by Vidal et al. have also presented histological evidence suggesting a super helical arrangement of fibrils (Vidal Bde 1995; Vidal 2003; Vidal Bde and Mello 2009). It was suggested that this helical arrangement is difficult to see in standard preparations, which may account for their absence in past histological studies.

It was hypothesized that a micromechanical model with super helical fibril organization in the presence of crimp would predict the large Poisson’s ratios seen experimentally while simultaneously predicting the nonlinear stress strain behavior of these tissues. The objective of this study was to use homogenization methods and finite element micromechanical models to test this hypothesis, as well as to assess the influence of material coefficients and geometric characteristics of the micromechanical model on the predicted Poisson’s ratio.

Methods

Fiber Geometry and Unit Cell

It was assumed that a fiber is the fundamental repeating structural unit within a tendon and ligament. For the purposes of homogenization, a single fiber unit was considered to be a periodic unit cell. Unit cells were modeled by embedding discrete fibrils within a more compliant matrix material and were assumed to be hexagonally packed within the fiber (Chen, Malkus et al. 1998). It was assumed that the matrix material modeled both the inter-fibrillar and inter-fiber space The number of fibrils embedded within the fiber was varied as part of the study, with models featuring 7 to 91 discrete fibrils (Fig 2). The fibril diameter was set to 100 nm, based on values reported in the literature for ligament and tendon (Baek, Carlin et al. 1998). The inter-fibrillar spacing was set to 25 nm (Baek, Carlin et al. 1998), which generated a fibril volume fraction of 57%. The baseline model contained 37 fibrils (based on a convergence study described later in the text), had a diameter of 0.769 μm and a height of 8.0 μm. Transformations were applied to the baseline model in order to generate models with planar crimp, helical twisting and planar crimp models with a super helical twist (Fig 3).

Figure 2.

Separate models were constructed with 7, 19, 37, 61 and 91 discrete fibrils. Model C, which had 37 fibrils, was considered to be the base model and was used for most simulations.

Figure 3.

A - Untransformed model; B - Planar crimp model; C - Helically transformed model; D - Helically transformed model combined with planar crimp. The top models show the full mesh while bottom models show just the fibrils with the matrix material removed.

Sinusoidal and Helical Transformation of Unit Cells

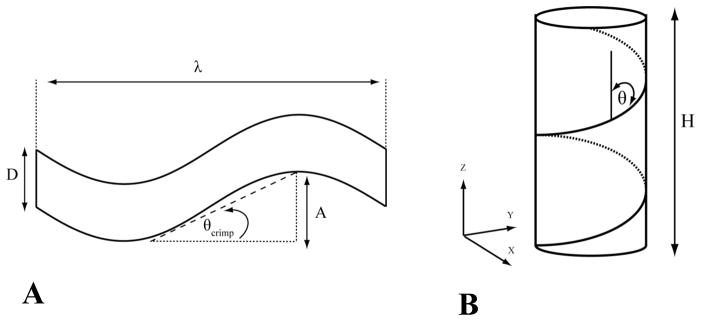
The most accepted geometric model of fiber crimp is planar crimp, in which the crimp plane is constant throughout the fiber and fascicle (Rowe 1985; Gathercole and Keller 1991; Hansen, Weiss et al. 2002). Planar crimp models were generated by applying a sinusoidal transformation of the following form along the fiber axis:

$$y^{\prime }=y+A_{\theta }sin\left(2\pi \frac{z}{\lambda }\right);A_{\theta }=\frac{\lambda }{4}tan\left({\theta }_{\mathit{crimp}}\right),$$ (1)

where λ is the crimp period and θ_crimp is the crimp angle (Fig 4A). To accurately represent the crimp structures observed in histological studies (Hansen, Weiss et al. 2002; Hurschler, Provenzano et al. 2003; Jarvinen, Jarvinen et al. 2004), the models were scaled such that the ratio of the crimp period to fiber diameter was similar to that seen experimentally:

$$\frac{{\lambda }_{\mathit{experiment}}}{D_{\mathit{experiment}}}=\frac{{\lambda }_{\mathit{model}}}{D_{\mathit{model}}},$$ (2)

where λ_experiment and D_experiment are the experimentally measured crimp period and fiber diameter and λ_model and D_model are the model crimp period and model fiber diameter. Histologically measured values for the crimp period and fiber diameter vary between tendons and ligaments, as well as between studies. Table 1 provides values from the literature for rat tail tendon, rat MCL, human Achilles tendon and for the baseline model used in this study (Gathercole and Keller 1991; Hansen, Weiss et al. 2002; Hurschler, Provenzano et al. 2003; Jarvinen, Jarvinen et al. 2004; Franchi, Fini et al. 2007).

Figure 4.

A - A sinusoidally crimped fiber was defined by its diameter D, crimp angle θ_crimp, crimp amplitude A and crimp period λ. B - The helical pitch angle was defined as the angle between the vertical (z) axis and the fibrils. All models shared the same coordinate system. The fiber axis was aligned with the z axis and the x-y plane was transverse to the fiber.

Table 1.

Experimentally measured values of crimp period and fiber diameter for rat tail tendon, rat MCL and human Achilles tendon as compared to the values used in this study.

	λ	D	λ/D
Rat Tail Tendon	150 μm	25 μm	6.00
Rat MCL	50 μm	20 μm	2.50
Human Achilles Tendon	230 μm	289 μm	0.80
37 Fiber model	2 μm	0.736 μm	2.72

Helical models were generated with a mean fibril pitch (averaged over all fibrils) ranging from 0 to 60° (Fig 4B). To generate the helical models, the mesh nodes were rotated an angle θ about the fiber axis such that a complete rotation was generated. Since the diameter of a given fiber model was constant, the helical pitch was altered by changing the height of the model such that:

$${\theta }_{\mathit{pitch}}=\frac{2\pi r}{H}.$$ (3)

These models were then modified to include planar crimp superimposed with helical twist. The scaling of the models required that the length was a multiple of the crimp period, which restricted the possible model lengths and thus the helical pitch.

Constitutive Model

Both the fibrils and matrix were modeled using an isotropic, compressible neo-Hookean hyperelastic constitutive model. This model was chosen because it is rotationally invariant and, in the limit of infinitesimal strains, the material coefficients can be cast in terms of the familiar linear material coefficients, namely the Young’s modulus E and Poisson’s ratio ν. The fibrils were assigned a Young’s modulus of E_f = 1 GPa, which is consistent with experimental values in the literature (Wenger, Bozec et al. 2007). Although published values are not available for the modulus of the matrix material E_m, Ault et al. estimated a value of 0.25 MPa using analytic micromechanical models (Ault and Hoffman 1992). With this guidance, a value of E_m = 1.0 MPa was assigned for the baseline models. Experimental values for the Poisson’s ratios of the fibril and matrix have not been reported, so a value of ν_f = ν_m = 0.3 was assigned to the baseline model. The effect of the Young’s modulus and Poisson’s ratio were explored as part of a parametric study.

Discretization of Unit Cell

Unit cells were constructed of fibrils embedded within a hexagonally shaped fiber using trilinear hexahedral elements and transformed according to equations (1) and (3). A mesh convergence study was performed to determine the optimal mesh density. Since a large number of elements was needed to discretize the domain, a tradeoff was made between model accuracy and model size. Model size was limited by practical constraints such as memory and computation time, while accuracy was affected by the mesh density. The convergence study revealed that the final meshes used in the study (111,000 elements and 144,635 nodes for the largest 37 fibril model) resulted in errors of less than 12% as compared to more refined meshes.

Homogenization Procedure and FE Analysis

To obtain effective material properties, periodic boundary conditions were applied to the transformed unit cells. Briefly, periodic boundary conditions require that opposing faces deform identically and that boundary tractions are anti-periodic. The so called master node approach was used to enforce the kinematic requirement of identically deforming faces (Garnich and Karami 2004; Pahr DH 2006; Xia, Zhou et al. 2006; Pahr and Zysset 2008). It was not necessary to enforce the requirement for anti-periodic tractions directly, as previous work has shown that for displacement based FEM solvers this constraint is automatically satisfied when the kinematic constraints are met (Xia, Zhou et al. 2006). Additional boundary conditions were also applied to the models in order to prevent rigid body translation and rotation. To prevent translation, the center node on the top and bottom face were constrained in the x-y plane. To prevent rotation, an appropriate edge node on the top face was constrained in the x-direction and an appropriate edge node on the bottom face was constrained in the y direction. Tensile loading was simulated by applying prescribed displacements in the axial direction to the master nodes on the top and bottom faces of the model. All finite element analysis was conducted using the nonlinear FE solver FEBio (http://mrl.sci.utah.edu/software.php). The periodic boundary conditions were implemented as linear constraint equations and enforced using an augmented Lagrangian method.

The untransformed models (straight fiber unit cells) and the sinusoidally transformed models (crimped fiber unit cells) were perfectly periodic. After helical transformation, the models lose their perfect periodicity. However, opposing faces can still be constrained to deform identically if the linear constraint equations are transformed into a helical coordinate system. With the loss of perfect periodicity, the effective material properties become approximate. The small error introduced by this approximation will be addressed in the discussion.

Effective Poisson’s Ratio

This study focused primarily on obtaining the effective Poisson’s ratio (the Poisson function computed near a reference configuration, λ_a = 1). However, the Poisson function was also obtained for a number of models over a large range of finite strains. The Poisson function ν(λ_a) (Beatty and Stalnaker 1986) is given by

$$\nu ({\lambda }_a)=-\frac{{\epsilon }_t({\lambda }_a)}{{\epsilon }_a({\lambda }_a)}=\frac{1-{\lambda }_t}{{\lambda }_a-1},$$ (4)

where ε_a and λ_a are the engineering strain and stretch ratio in the fiber direction and ε_t and λ_t are the engineering strain and stretch ratio transverse to the fiber direction. This reduces to the Poisson’s ratio ν₀ at small strains:

$${\nu }_0=\underset{{\lambda }_a\to 1}{\text{limit}\nu ({\lambda }_a)}.$$ (5)

ν(λ_a) and ν₀ were determined by subjecting the unit cell to simulated tensile loading. To obtain ν₀, an axial strain of 0.5% was applied. Note that the small strain allows for the linear coefficient, the Poisson’s ratio, to be obtained. However, the use of the nonlinear constitutive model for the fibril and matrix made these models intrinsically nonlinear. To obtain ν(λ_a), strains of up to 8% were applied.

λ_a was computed from the prescribed axial displacements, and λ_t was computed from the nodal displacements of the master nodes for each face. For the crimped models, the presence of a crimping plane transformed the models from transverse isotropy (caused by the presence of the fibrils) to orthotropy. This lead to the presence of two different Poisson’s ratios, ν_xz and ν_yz. Pilot testing revealed that this additional anisotropy within the helically twisted crimp models was relatively small, with the ratio of ν_xz/ν_yz typically close to unity. Therefore ν₀ and ν(λ_a) were computed to be the average of the two, making the effective properties those of transverse isotropy.

Parametric Studies

Parametric studies were performed to determine the effects of θ_pitch, θ_crimp, E_m, ν_m, ν_f and fibril number. θ_pitch was varied between 0° and 60°. E_m was varied such that the ratio of the fiber to matrix modulus (denoted as the modulus ratio M_r=E_f/E_m) spanned five orders of magnitude, while the ratio of the fiber to matrix Poisson’s ratio (denoted as the compressibility ratio, C_r = ν_f/ν_m) was varied between 1.0 and 30.0. The number of fibrils was also varied from 7 to 91 in order to determine the validity of extrapolating the results from the baseline model with 37 fibrils to real fibers, which typically contain many thousands of fibrils.

Results

Nonlinear Stress Strain Behavior

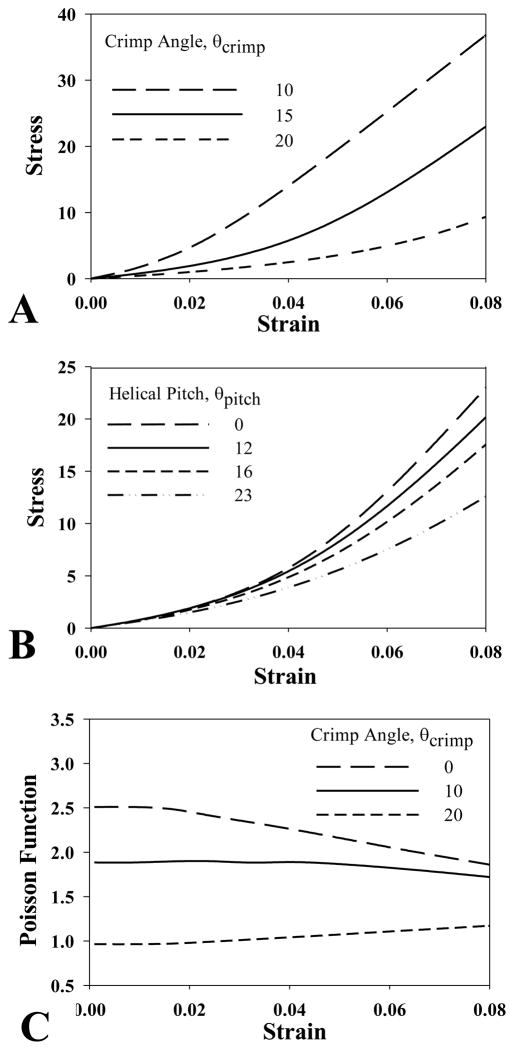
Fig 5A shows stress strain curves for the baseline model featuring crimp angles of 10, 15 and 20 degrees. A classic “uncrimping” behavior was predicted, with an initial nonlinear toe region changing to a linear region at the so-called transition strain. Increasing θ_crimp increased the length of the toe region and the magnitude of the transition strain. Adding a super helical organization to the crimped models did not affect the length of the toe region, but did change the slope of the linear region (Fig 5B).

Figure 5.

A - Plot of the stress vs. strain for models with θ_crimp =10, 15 and 20 degrees. B - Plot of the stress vs. strain for crimped models (θ_crimp=15 degrees) with a helical pitch of θ_pitch = 0, 12, 16 and 23 degrees. C - The Poisson function plotted vs. strain for models with crimp angles of θ_crimp = 0, 10 and 20 degrees.

Poisson Function

The Poisson function ν(λ_a)for the baseline model (θ_pitch = 23°) is shown in Fig 5C for three different crimp angles. In helical models with no crimp (θ_crimp = 0), ν(λ_a) decreased with increasing strain. This is a result of the fibrils progressively compressing until they are almost in contact. In models with moderate crimp (θ_crimp = 10), ν(λ_a) was nearly constant until about 6% strain, at which point it also decreased. In models with large crimp (θ_crimp = 20), ν(λ_a) increased with increasing strain and then leveled off in the linear region.

Effect of Helical Pitch and Crimp Angle on effective Poisson’s Ratio

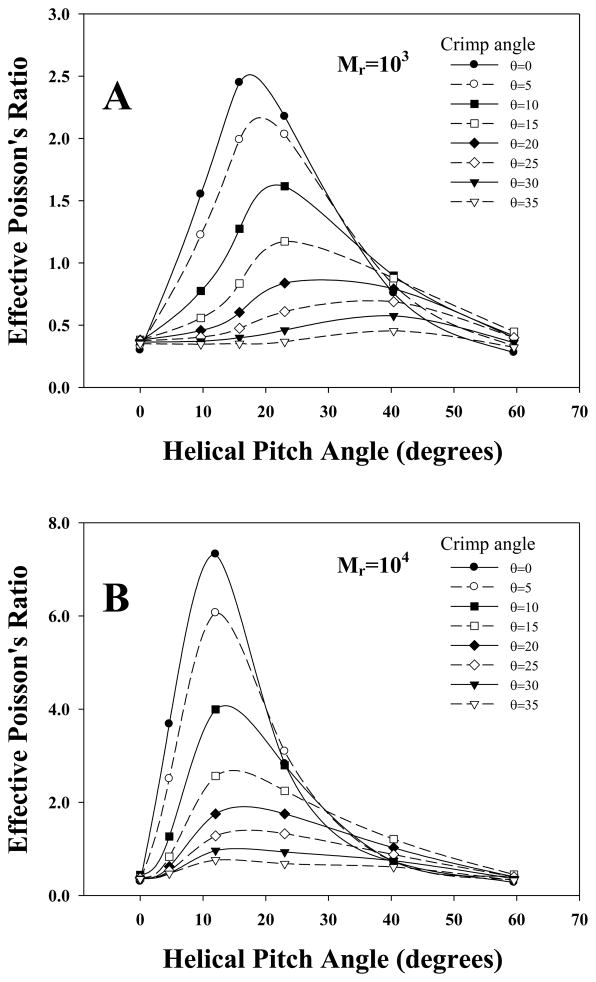
There was a nonlinear relationship between the effective Poisson’s ratio ν₀ and the mean helical pitch angle θ_pitch. At θ_pitch = 0 (straight fibers), ν₀ was the volume average of the matrix and fibril Poisson’s ratio (ν₀ = 0.3). As θ_pitch increased, ν₀ increased until a transition angle was reached, at which point ν_a again decreased until the so called “neutral angle” was attained and the volume averaged Poisson’s ratio was once again observed. This is seen in the top curve of Fig 6A, which represents the results for a helical model with θ_crimp = 0° (no crimp). For the baseline model with 37 fibrils and a modulus ratio of M_r =10³, a maximum value of ν₀ = 2.5 was obtained at θ_pitch = 17.5°. Poisson’s ratios exceeding the isotropic limit of 0.5 were obtained for angles greater than 1.7°.

Figure 6.

A - The effective Poisson’s ratio plotted as a function of mean helical pitch for models with a modulus ratio of M_r=10³. B - The effective Poisson’s ratio as a function of mean helical pitch for models with a modulus ratio of M_r =10⁴. The top curve in both plots corresponds to a helical crimp of 0°, with successive curves featuring an increase in crimp angle by 5° until an angle of 35° is reached at the bottom.

As the crimp angle θ_crimp was increased from 0°, the maximum effective Poisson’s ratio decreased and the optimal pitch angle increased. For a θ_crimp = 5°, a maximum ν₀ of 2.2 occurred at an optimal pitch angle of θ_pitch = 19°, while θ_crimp = 10° resulted in a maximum ν₀ of 1.6 at an optimal pitch of θ_pitch = 21°. This trend continued for crimp angles of 15°, 20°, 25°, 30° and 35°, which had maximum Poisson’s ratios of 1.6, 0.9, 0.7, 0.6 and 0.45 for optimal angles of 23°, 29°, 36°, 39° and 40° (Fig 6A). All crimp angles except for the 35° crimp were capable of generating Poisson’s ratios larger then the isotropic limit.

Parametric Studies

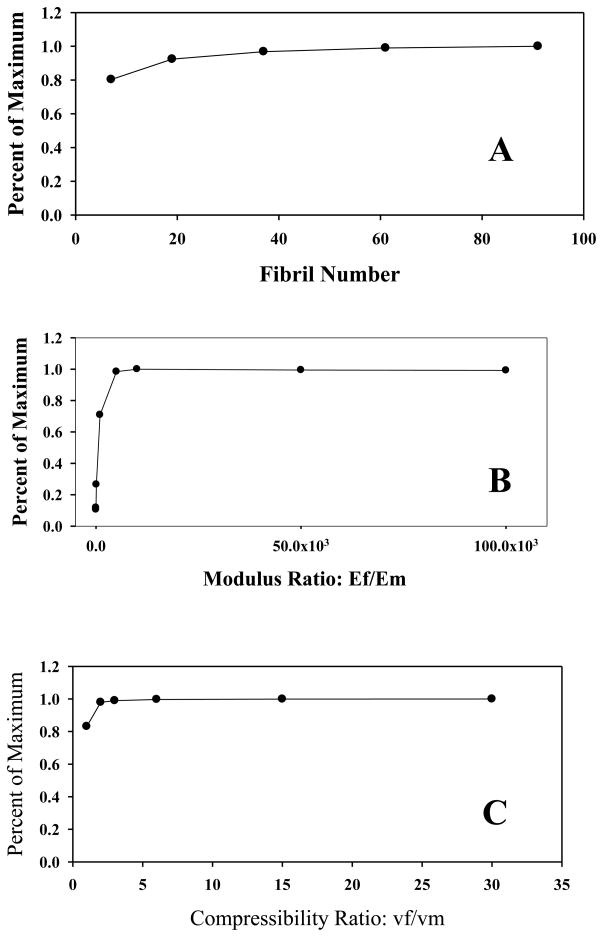
Real tendon and ligament fibers contain many hundreds if not thousands of fibrils. To determine the applicability of the baseline RVE fiber model with 37 fibrils to real fibers, a convergence study was performed on the fibril number. As shown in Fig 7A, the effective Poisson’s ratio asymptoted as the number of fibrils was increased (θ_pitch held constant for all models). This important result indicates that large aggregates of fibrils can be modeled with a smaller number of fibrils as long as θ_pitch is kept constant. The increase in Poisson’s ratio with increasing number of fibrils likely resulted from two model artifacts. The first artifact is the center fibril, which is straight and thus does not contribute to the transverse compressive forces that generate the large Poisson’s ratios. The other source of artifact is the model edges, which contain only matrix material. As the number of fibrils is increased, the effects of these artifacts become negligible.

Figure 7.

A - The percent of the maximum Poisson’s ratio plotted as a function of the total number of fibrils. The mean pitch for all models was 15° and the modulus ratio was 10⁴. B - Sensitivity of the effective Poisson’s ratio to changes in the modulus ratio. Mean pitch = 23° and compressibility ratio C_r= 1. (C) Sensitivity of the effective Poisson’s ratio to changes in the compressibility ratio. Mean pitch = 23° and modulus ratio M_r =10⁴.

The effective Poisson’s ratio was also sensitive to the modulus ratio M_r (Figs. 6A, 6B) As M_r was increased, the maximum ν_a also increased until a value of M_r = 5000 was reached, at which point it asymptoted (Fig 7B). The results in Fig 7B are for a helical model with no crimp, but increasing M_r in the crimped models had a similar effect. In addition to increasing the maximum ν₀, M_r also affected the transition pitch angle and the shape of the Poisson’s ratio vs. pitch curve (Fig 6B). Interestingly, as M_r was increased, not only did the transition angle shift left, but the maximum ν₀ at that angle also increased. For M_r = 10⁴ values for ν₀ were as large as 7.3 at the optimal angle of 12°.

The effective Poisson’s ratio ν₀ was also sensitive to the compressibility ratio, C_r (Fig. 7C). Varying C_r had the same effect as varying M_r in that a quick increase was seen, followed by asymptotic behavior. Unlike M_r, however, the magnitude of this effect was considerably less.

Discussion

Micromechanical models were capable of reproducing the classic “uncrimping” stress-strain behavior of tendon and ligament tissue while simultaneously generating Poisson’s ratios that were in agreement with experimental data. The length of the toe region was affected by the crimp angle, which is consistent with the results from a previous micromechanical model (Ault and Hoffman 1992). The Poisson function also depended on the crimp angle. Although little experimental data on the Poisson function for tendon and ligament tissue are available, it was noted by Lynch et al. (2003) that the Poisson’s ratio for sheep flexor tendon was constant. The model with a 10 degree crimp angle was capable of generating a curve with a nearly constant Poisson’s ratio (Fig 5C).

The largest determining factors for the magnitude of the effective Poisson’s ratio in the helical models were the mean helical pitch and the ratio of the fiber modulus to the matrix modulus. The dependence on the mean helical pitch qualitatively agrees with results for center filled, helically wound cylindrical tubes (Marklund 2007). The largest Poisson’s ratios were generated for a pitch angle between 12 to 18 degrees. However, Poisson’s ratios greater than the isotropic limit were predicted even for small pitch angles.

The value of the matrix modulus was explored in sensitivity studies, as no direct measurements were available. It has been suggested that the matrix modulus may be many orders of magnitude smaller than the fiber modulus (Ault and Hoffman 1992).. Ault et al. estimated the matrix modulus to be 0.25 MPa and the fiber modulus to be 2 GPa by using an analytic micromechanical model that coupled crimped fibrils to the matrix material, which provides a modulus ratio of 8,000. Although not a direct measurement of matrix modulus, the compressive modulus for MCL ligament as computed from published data provided a modulus of 0.05 MPa, while the modulus in the fiber direction for MCL has been measured as approximately 300 MPa (Weiss 2000; Gardiner and Weiss 2003). This provides an approximate modulus ratio of 6000. Based on this information, it seems reasonable to assume that the modulus ratio is large enough to be in the asymptotic region (M_r>5,000) (Fig 7B).

The planar crimp models predicted lower effective Poisson’s ratios than the helical models. This can be interpreted in light of the fact that the uncrimping of the fiber will tend to decrease the tensile stress within the helically wound fibrils. This leads to a decrease in the compressive forces, which then leads to a decrease in the Poisson’s ratios. In a study on the homogenization of crimped composite structures by Garnich et al., the average Poisson’s ratio never exceeded the isotropic limit, showing that planar crimp alone is not capable of generating large Poisson’s ratios (Garnich and Karami 2004). This was confirmed in the present study.

Although the predicted Poisson’s ratio was sensitive to the modulus ratio, pitch angle and crimp angle, physiologically relevant parameters predicted large Poisson’s ratios. Models of both crimped and uncrimped unit cells were capable of predicting Poisson’s ratios within the range of those seen experimentally, but they were strongly dependent on the crimp angle. Reported values for the crimp angle vary greatly across the literature, ranging from 10° to 60°, depending on the tissue and study (Gathercole and Keller 1991; Hansen, Weiss et al. 2002; Hurschler, Provenzano et al. 2003; Jarvinen, Jarvinen et al. 2004; Franchi, Fini et al. 2007). The models in present study will only predict large Poisson’s ratios if the crimp angle is in the low end of this range. It is interesting to note that previous micromechanical studies all required smaller crimp angles (10–20 degrees) to match experimental data (Ault and Hoffman 1992; Grytz and Meschke 2009).

In this study, the helical transformation of the unit cell models resulted in a loss of perfect periodicity. To determine the magnitude of error introduced by this approximation, a verification study was performed in which the helically transformed unit cell models were compared to perfectly periodic unit cells with embedded helical fibrils. The latter models were constructed by embedding a cylindrical mesh of helically twisted fibrils into a mesh of a hexagonal unit cell with a cylindrical hole. The two meshes were nonconforming, therefore tied surface constraints were used to connect the two meshes. Results of this study indicated that the maximum error for the helically transformed models was 8%, with the errors for most models being much less. The addition of a tied surface constraint required meshes with higher resolutions and thus considerably longer solution time. Furthermore, the tied surface constraint introduced another possible source of discretization error.

The current study assumed that the material symmetry of the individual collagen fibrils was isotropic, but it has been suggested that individual collagen fibrils may be anisotropic (Wenger, Bozec et al. 2007). It is also possible that a helical organization exists at a hierarchical level above that of the fiber. It was noted by Screen et al. that when individual rat tail tendon fascicles were subjected to tension in the fiber direction a non-negligible amount of rotation was present (Screen, Bader et al. 2004). This suggests that fibers themselves may be helically oriented within the fascicle. Finally, it is possible that other mechanisms, namely fiber crossing, interweaving or linking may contribute to the large Poisson’s ratios.

In conclusion, this study demonstrated that microstructural models of ligaments and tendons with a super-helical organization of fibrils within a crimped fiber are capable of predicting the large Poisson’s ratios measured experimentally. Furthermore, these models were capable of reproducing the nonlinear stress strain behavior seen experimentally. Although the results of this study lend credibility to the hypothesis that helical organization of fibrils may provide a structure-function relationship between tissue microstructure and large Poison’s ratios, experimental validation is necessary to confirm or refute this. Furthermore, the novel methodology developed for this study may provide a useful starting point for modeling helical microstructures in other biological tissues and composites.