Integrating quantitative proteomics and metabolomics with a genome-scale metabolic network model

Abstract

Motivation: The availability of modern sequencing techniques has led to a rapid increase in the amount of reconstructed metabolic networks. Using these models as a platform for the analysis of high throughput transcriptomic, proteomic and metabolomic data can provide valuable insight into conditional changes in the metabolic activity of an organism. While transcriptomics and proteomics provide important insights into the hierarchical regulation of metabolic flux, metabolomics shed light on the actual enzyme activity through metabolic regulation and mass action effects. Here we introduce a new method, termed integrative omics-metabolic analysis (IOMA) that quantitatively integrates proteomic and metabolomic data with genome-scale metabolic models, to more accurately predict metabolic flux distributions. The method is formulated as a quadratic programming (QP) problem that seeks a steady-state flux distribution in which flux through reactions with measured proteomic and metabolomic data, is as consistent as possible with kinetically derived flux estimations.

Results: IOMA is shown to successfully predict the metabolic state of human erythrocytes (compared to kinetic model simulations), showing a significant advantage over the commonly used methods flux balance analysis and minimization of metabolic adjustment. Thereafter, IOMA is shown to correctly predict metabolic fluxes in Escherichia coli under different gene knockouts for which both metabolomic and proteomic data is available, achieving higher prediction accuracy over the extant methods. Considering the lack of high-throughput flux measurements, while high-throughput metabolomic and proteomic data are becoming readily available, we expect IOMA to significantly contribute to future research of cellular metabolism.

Contacts: kerenyiz@post.tau.ac.il; tomersh@cs.technion.ac.il

1 INTRODUCTION

Modern genome-sequencing capabilities have led to the generation of genome-scale metabolic network reconstructions for many microorganisms, giving rise to more than 50 highly curated metabolic reconstructions that have been published to date (Duarte et al., 2004; Feist and Palsson, 2008). A metabolic network reconstruction is composed of a set of biochemical reactions, and the associations between these reactions and their enzyme-coding genes. The constraint-based modeling (CBM) computational framework serves to analyze the functionality of these genome scale models, enabling the prediction of various metabolic phenotypes in microorganism such as growth rates, nutrient uptake rates, by-product secretions and gene essentiality (Price et al., 2004). CBM has been used for a variety of applications including the comparative metabolic analyses over multiple organisms (Blank et al., 2005; Lee et al., 2009), drug discovery (Gordana et al., 2005), metabolic flux analysis (Rantanen et al., 2008), studies of network evolution (Fong et al., 2005) and metabolic engineering tasks (Pharkya et al., 2004).

Using metabolic models as scaffolds for the analysis of high throughput data such as transcriptomics, proteomics and metabolomics suggests the possibility of inferring condition-dependent changes in the metabolic activity of an organism. Developing computational methods capable of predicting metabolic flux by integrating these data sources with a metabolic network is hence a major challenge of metabolic network modeling. Previous investigations have already utilized CBM to integrate high-throughput molecular datasets with a metabolic network in a qualitative manner: The methods developed by Åkesson et al. (2004) and Becker and Palsson (2008) use gene expression data to identify genes that are absent or likely to be absent in certain contexts. They then search for metabolic states that prevent (or minimize) the flux through the associated metabolic reactions. A recent method by Shlomi et al. (2008) considers data on both lowly and highly expressed genes in a given context, as cues for the likelihood that their associated reactions carry metabolic flux and employs CBM to accumulate these cues into a global, consistent prediction of the metabolic state. The lack of dependency on a cellular objective is a marked advantage of this approach as the latter is difficult to define for multi-cellular organisms.

While transcriptomics and proteomics data provides important insight into hierarchical regulation of metabolic flux (representing the control over the maximum activity of enzymes—i.e. vmax), metabolomics may provide information on an additional level of regulation called, metabolic regulation (Rossell et al., 2006). The latter denotes the effect of metabolite concentrations on actual enzyme activity through mass action, kinetic and allosteric effects. A previous CBM method for integrating metabolomic data with a metabolic network model, thermodynamic-based metabolic flux analysis (TMFA) (Henry et al., 2007), derives constraints on reaction directionality from metabolite concentration data based on thermodynamic principles. Another method by Cakir et al. (2006) integrates quantitative metabolome data with genome-scale models to identify reporter reactions, defined as the set of reactions that respond to genetic or environmental perturbations through coordinated variations in the levels of surrounding metabolites. Currently, however, there is no CBM method that enables the integration of quantitative metabolomic data with a metabolic network model to directly infer the metabolic fluxes themselves.

In this article we introduce a novel CBM method, integrative omics-metabolic analysis (IOMA), for integrating quantitative proteomic and metabolomic data with genome-scale metabolic network models to predict metabolic flux. This is achieved primarily by considering a mechanistic model of reaction rates. The method is formulated as a quadratic programming (QP) problem (Nocedal and Wright, 2006) geared to find a feasible, steady-state flux distribution, such that: (i) a set of stoichiometric mass-balance and enzymatic directionality constraints are satisfied; (ii) the flux through a core set of reactions for which measured proteomic and metabolomic data exists is as consistent as possible with flux estimations derived via Michaelis Menten-like kinetic rate equations for these reactions. The latter involves the estimation of missing enzyme kinetic constants, by searching for optimal parameters as part of the optimization problem, as described below. To examine the predictive performance of IOMA, we applied it to predict metabolic flux for red blood cells (RBC) for which a detailed kinetic model is available for validation (utilizing it to simulate metabolic flux changes following gene knockouts based on artificially generated proteomic data). As a further validation, we applied IOMA to predict metabolic flux for Escherichia coli under different gene knockouts, utilizing available metabolomic and proteomic data as input, and available experimental fluxes for validation (Ishii, 2007). A comparison of IOMA's performance to that of the commonly used methods of flux balance analysis (FBA) (Fell and Small, 1986; Kauffman et al., 2003; Varma and Palsson, 1994) and minimization of metabolic adjustment (MOMA) (Segre et al., 2002) shows the significant advantage of IOMA in both validation tests.

2 METHODS

2.1 CBM of metabolic network

A metabolic network consisting of n metabolites and m reactions can be represented by a stoichiometric matrix, denoted by N, where the entry n_ij represents the stoichiometric coefficient of metabolite i in reaction j (Price et al., 2004). A CBM model imposes mass balance, directionality and flux capacity constraints on the space of possible fluxes in the metabolic network's reactions through the set of linear equations:

(1)

(2)

where stands for the flux vector for all of the reactions in the model (i.e. the flux distribution). The exchange of metabolites with the environment is represented as a set of exchange reactions, enabling for a pre-defined set of metabolites to be either taken up or secreted from the growth media. The steady-state assumption represented in Equation (1) constrains the production rate of each metabolite to be equal to its consumption rate. Enzymatic directionality and flux capacity constraints define lower and upper bounds on the fluxes and are embedded in Equation (2). In the following, flux vectors satisfying these conditions will be referred to as feasible stead-state flux distributions.

2.2 The IOMA method

To associate quantitative measurements of protein and metabolite levels with metabolic fluxes, we used the following Michaelis Menten-like rate equation to estimate the flux in a reaction transforming a set of substrates S to a set of products P:

(3)

where S_i and P_i denote the concentrations for the i-th substrate and i-th product, respectively, and e denotes the enzyme concentration. k_m, s_i and k_m, p_i denote the dissociation constants for the i-th substrate and i-th product, respectively. Enzyme turnover rates in the forward and backward directions are denoted by k_cat⁺ and k_cat⁻, respectively. Given the substrate and product metabolites' concentration and their dissociation constants, the following saturation values for the enzyme in the forward and backward directions can be computed as following:

Given the above definitions, the rate Equation (3) takes the following form:

(4)

To account for proteomics data that reflect relative protein levels compared to some reference state (rather than absolute protein concentrations), Equation (4) can be rewritten as following:

(5)

where e^ref denotes the enzyme concentration in the reference state, and v_max⁺ and v_max⁻ are equal to the corresponding enzyme turnover rates multiplied by e^ref. Hence, in order to predict the metabolic flux through a certain enzyme given relative concentration level and saturation coefficients (computed given absolute metabolite levels and metabolite dissociation constants), the corresponding v_max value of the enzyme is also required.

We describe a new CBM method that addresses the problem of predicting genome-scale metabolic flux distributions, 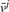, for a set of k growth conditions (j =1,…, k), given (Fig. 1): (i) relative enzyme concentrations for a core set of enzymes (denoted E), under the various conditions, e_i^j/e_i^ref, where (j=1,…, k) and i∈E; (ii) absolute substrate and product metabolite concentrations for enzymes in E; (iii) metabolite dissociation constants. Concentrations and dissociation constants together enable us to compute enzyme saturation values, a_i^j+ and a_i^j− where j=1,…, k, and i∈E. The method is formulated as a QP problem that searches for k flux distributions, such that: (i) each flux distribution satisfies stoichiometric mass-balance and reaction directionality constraints, (ii) the fluxes through the core reactions (for which proteomic and metabolomic data is given) are as consistent as possible with the estimated rates calculated via Equation (5). The latter is facilitated by searching for the v_max,i⁺ and v_max,i⁻ parameters for all enzymes i∈E as part of the QP optimization. IOMA's QP problem is formulated as following:

(6)

(7)

(8)

where Equation (6) represents mass-balance constraint for the k-th flux distributions, Equation (7) represents reaction directionality and flux capacity constraints, and Equation (8) represents the estimated fluxes for the core reactions based on the proteomic and metabolomic data. To account for missing concentration levels of substrate and product metabolites for some enzymes, the presence of noise in both the proteomic and metabolomic data, and the simplifying assumptions employed in the rate equation formalism, the error ε_i^j variables were added to Equation (8), guaranteeing a feasible solution for the QP problem. The optimization is hence formulated to minimize the total sum of variance in the error variables for each enzyme across the k conditions. We chose to minimize the variance of the error variables (and not their total sum) to account for potential metabolic regulation mechanisms that are not explicitly incorporated in the model (e.g. allosteric regulation) and may systematically affect the metabolic flux.

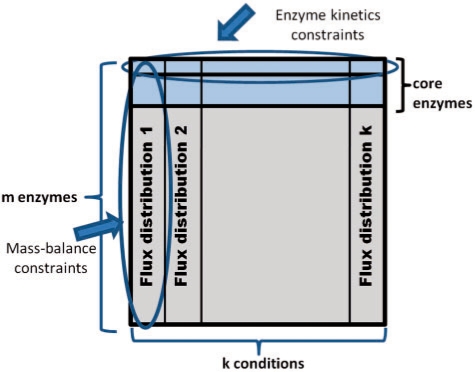
Fig. 1.

The figure illustrates the associations between variables in IOMA's optimization problem imposed by the various constraints. Rows represent enzymes and columns represent growth conditions—i.e. the j-th column representing the flux distribution for the j-th condition (denoted by . Mass-balance [Equation (6)] and reaction directionality [Equation (7)] create dependencies between fluxes through different enzymes in one condition, irrespectively of all others conditions (i.e. associating fluxes in one column). The enzyme-kinetic constraint [Equation (8)] associates between fluxes through one enzyme in different growth conditions (via the enzyme's parameters v_max⁺ and v_max⁻, which are condition-invariant), irrespectively of all other enzymes (i.e. associating fluxes in one row). The latter constraint is defined only for a core set of enzymes for which metabolomic and proteomic data is available (marked in blue). The union of both types of row and column constraints in IOMA's optimization indirectly associates between many additional fluxes through various enzymes in different conditions.

The application of IOMA in this article considers additional constraints by utilizing additional datasets given as input for each knockout condition: first, for a knockout condition j of an enzyme-coding gene that is not backed up by isozymes in the model, the flux through the corresponding reactions was constrained to zero via the following constraint:

Second, the organism's growth rate (denoted v_GR) in a knockout condition j is given and is used to constrain the biomass yield rate:

Third, experimentally measured exchange fluxes (uptake and secretion rates for several metabolites) were further used to constrain the predicted flux distributions via a two-step procedure: (i) we applied QP for each condition j (j=1,…, k) in order to find a feasible steady-state flux distribution for which the Euclidean distance to the given exchange fluxes is minimized; (ii) we added the following constraints to IOMA's optimization problem, so that the exchange fluxes are fixed at the values predicted in (i):

The commercial CPLEX solver was used for solving QP problems, on 64-bit machines running Linux.

Matlab implementation of IOMA can be found at www.cs.technion.ac.il/~tomersh/tools.

3 RESULTS

3.1 Predicting gene knockout effects in the red blood cell model

As a first validation of IOMA, we applied it to predict metabolic fluxes in human erythrocytes. For this metabolic system, a detailed kinetic model (Jamshidi, 2001) is readily available for validation, by simulating the steady-state metabolic flux after gene knockouts. This model consists of four basic pathways: glycolysis, pentose-phosphate pathway (PPP), adenosine nucleotide metabolism, and the Rapoport-Leubering shunt, accounting for 48 metabolites, 39 internal reactions and nine exchange reactions. The set of differential equations in the model, describing the dynamics of metabolite concentration, were solved via the ‘ode15s’ solver in Matlab (The Mathworks, Inc.). To generate synthetic proteomic and metaoblomic data that can be used as input to IOMA, and the corresponding flux data for validation, we utilized the RBC kinetic model in the following way: a gene knockout was modeled by restricting the flux through its corresponding reaction to zero. Random protein levels were drawn from a uniform distribution, reflecting up to 5-fold increase or decrease in concentration compared to the wild-type condition. These protein levels were then used to determine the values in the kinetic model.

To apply IOMA to predict metabolic fluxes for all gene knockouts given a CBM model of RBC metabolism, we provide it with the randomly generated proteomic data and the corresponding steady-state metabolomic data (identified by the RBC kinetic model) for a core set of 10 reactions whose rate equations (in the kinetic model) are based on Michaelis Menten-like kinetics. The performance of IOMA is evaluated in terms of predicting significant changes in flux between the wild-type strain and each of the knockouts, considering a threshold of 0.001 to define a significant increase or decrease in flux. Repeating the analysis 50 times with random proteomic data provided an average precision of 0.95, recall of 0.93, and an overall accuracy of 0.91 (where accuracy is the rate of true predictions) (Fig. 2a). Similar results were obtained assuming a normal distribution for protein levels with an average precision of 0.96, recall of 0.94, and an overall accuracy of 0.92. IOMA's prediction accuracy is insensitive to the specific choice of threshold, with thresholds in the range 0.0001–0.1 yielding <2.5% change in the prediction accuracy. Notably, applying other flux prediction methods such as FBA and MOMA in this setup, given only metabolomic and proteomic data is problematic: FBA depends on a definition of a cellular objective function (commonly assumed to be the maximization of biomass yield rate in microbes), which is not available in the RBC model. MOMA depends on data regarding the wild-type flux distribution, which in this test scenario was not given as input. Utilizing a sampling technique (Becker et al., 2007) to predict a set of 100 feasible flux distributions for the wild-type strain and applying MOMA to predict the knockout effects starting from each of them resulted in a markedly lower average accuracy of 0.45 (Fig. 2a).

Fig. 2.

Precision, recall and accuracy of predicted changes in fluxes between the wild-type and knockout strains in the RBC model, obtained by IOMA (blue) and MOMA (red). The average and standard deviation of the precision, recall and accuracy are shown across the 50 simulation runs in two scenarios. (a) No flux data is given as input for MOMA and IOMA, hence MOMA relies on random sampling of possible wild-type flux distributions to predict knockout effects. (b) Exchange fluxes are given as input to both methods, and are used by MOMA to obtain a more reliable prediction of the wild-type flux distribution. In both test scenarios, IOMA's predictions are significantly more accurate.

To enable further comparison with MOMA, we considered a second test scenario in which the fluxes through exchange reactions (representing the uptake and secretion of metabolites from the growth environment; which are easier to measure experimentally) as identified by the kinetic model, are also given as input to IOMA and MOMA. The flux distribution of the wild-type strain is computed via QP, by searching for a feasible flux vector, satisfying mass-balance and reaction directionality constraints, minimizing the Euclidian distance between the predicted exchange fluxes and those given as input. MOMA was applied starting from this predicted wild-type flux distribution, utilizing also the given flux rates through the exchange reactions for all knockout conditions (via additional constraints in MOMA's QP formulation). The additional flux data through exchange reactions is also utilized in a similar manner by IOMA as described in the ‘Methods’ section. The results show that while MOMA's performance significantly improves in this test scenario, reaching an average accuracy of 0.82, IOMA still achieves a statistically significant higher accuracy of 0.91 (Fig. 2b) (Wilcoxon P-value = 1.61 × 10⁻⁵).

To test the robustness of IOMA to noise in the proteomic and metabolomic data, we repeated the first test scenario (the more challenging one, without using metabolite uptake and secretion rates as input), while adding random noise to both data sources given as input to IOMA. The noise was drawn from a normal distribution with mean zero and SD = 10–50% of the true proteomic and metabolomic levels (as obtained from the kinetic simulations). The results show that IOMA still achieves a high accuracy of 0.95 and 0.84, for SD levels of 10–50%, respectively, testifying for IOMA's robustness to noisy measurements.

3.2 Predicting metabolic fluxes in E.coli via the integration of experimental metabolomic and proteomic data

As a second validation of IOMA, we applied it to the genome-scale E.coli metabolic network model of Feist et al. (2007) accounting for 1260 metabolic genes, 2382 reactions and 1668 metabolites, to predict metabolic flux distributions for wild-type E.coli K-12 and 23 single-gene knockouts, which cover most viable glycolysis and PPPs knockouts, grown in glucose minimal medium. As input we utilized experimentally measured absolute protein (mg-protein/g-dry cell weight) and metabolite (mM) concentrations for a core set of 11 reactions, uptake and secretion rates for nine metabolites, and measured growth rates, all taken from the E.coli multi-omics database (Ishii, 2007). Metabolites' dissociation constants (k_m) were obtained from the BRENDA database (Bennett et al., 2009). To validate the predicted flux distributions, we utilized experimentally measured fluxes in these knockout strains for 26 reactions in E.coli's central metabolism, also taken from the multi-omics database.

To assess the accuracy of IOMA versus that of MOMA and FBA, we compared their predictions of significant increase or decrease in flux for the 26 measured reactions between the wild-type and knockout strains (considering the same threshold of 0.001 to define significant changes in flux as done above). As shown in Figure 3, IOMA achieves a prediction accuracy of 0.54 which is markedly higher than that achieved by FBA and MOMA (0.44 and 0.38, respectively). The prediction accuracy is significantly high compared to random predictions, with a hypergeometric P-value of 1.26 × 10⁻⁴ and 5.12 × 10⁻⁸ for the prediction of increased and decreased fluxes compared to the wild-type strain, respectively. Notably, IOMA's prediction accuracy is insensitive to the specific choice of threshold (with thresholds in the range of 0.0001–0.1 yielding <5% change in the prediction accuracy of the various methods).

Fig. 3.

Precision, recall and accuracy of predicted changes in flux between wild-type and following gene knockouts in the E.coli model, obtained by IOMA (blue), FBA (green) and MOMA (red).

An example flux distribution predicted by IOMA following the knockout of an enzyme in the non-oxidative branch of the PPP, talB (Transaldolase B), is shown in Figure 4. The figure shows that IOMA correctly predicts an increase in flux through most of the enzymes in glycolysis and a decreased flux through enzymes in PPP following the knockout of talB. FBA is only partially correct, predicting an increased flux through both glycolysis and PPP, while MOMA falsely predicts both the increased glycolysis and decreased PPP fluxes.

Fig. 4.

An example flux distribution predicted by IOMA following the knockout of talB (Transaldolase B). The network shows E.coli's glycolysis and PPP. Green (red) edges represent a measured increase (decrease) of flux between the wild-type and knockout strains. The letters F, M and I, represent predictions made by FBA, MOMA and IOMA, respectively, with green (red), representing a predicted increase (decrease) in flux. Predictions of no significant change in flux are not shown. As evident, IOMA correctly predicts the measured pattern of increased flux throughout glycolysis and decreased flux throughout the PPP pathways, with only two mismatches, while FBA and MOMA perform significantly worse.

To demonstrate the added value of utilizing both proteomics and metabolomics to infer metabolic flux, we compared IOMA's performance when given both proteomics and metabolomics, to its performance when only one of the sources is given as input. To utilize IOMA only with proteomic data, we considered zero saturation coefficients (a⁺ and a⁻) for all enzymes, while for utilizing it only with metabolomic data, we considered a constant expression level for each enzyme across the various conditions (e/e^ref = 1). We find that, quite expectedly, when only a single data source is used, the accuracy achieved is lower than that obtained when using both data sources together, with the prediction accuracy obtained when using only proteomic or metabolomic down to 0.45 and 0.42, respectively. Notably, using either data source alone still improves the prediction accuracy upon FBA and MOMA. Gene expression is significantly easier to measure than proteomics and was previously shown to significantly correlate with protein levels (Lee et al., 2000; Tuller et al., 2007). Here, we find an average correlation of 0.65 (with 19 knockouts yielding a significant P-value <0.05) between measured gene and protein expression levels across all gene knockouts in the employed dataset (Ishii, 2007). Considering this high correlation, we further explored the predictive performance of IOMA's given gene expression data instead of proteomic data. The analysis shows that IOMA obtains an accuracy of 0.49 when utilizing gene expression and metabolomics with a hypergeometric P-value of 3.15 × 10⁻⁴ and 8.63 × 10⁻⁸ for the prediction of increased and decreased fluxes compared to the wild-type strain, respectively (higher than the accuracy obtained with FBA and MOMA as reported above).

4 DISCUSSION

This study presents a novel approach for integrating quantitative proteomic and metabolomic data with a genome-scale metabolic network model to predict flux alterations under different perturbations, based on a mechanistic model for determining reaction rate. The method predicts feasible flux distributions while accounting for missing concentration levels of substrate and product metabolites for some enzymes, for potential noise in both the proteomic and metabolomic data, and for the simplifying rate equation formalism used. IOMA is shown to successfully predict changes in fluxes both in E.coli's central metabolism under various genetic perturbations and in a simulated RBC kinetic model, displaying a significant improvement versus the commonly used FBA and MOMA methods.

Metabolic fluxes are the most informative and direct indices of the metabolic and physiological state of cells/tissues, and hence, inferring their state in different biological contexts is probably the holy grail of metabolic modeling. However, in a somewhat spiteful way, while we are facing an ever increasing availability of numerous pertaining high-throughput ‘omics’ data including transcriptomic, proteomic and metabolomic measurements, the measurement of fluxes is still very challenging and limited to a small fraction of the reactions present in cells. Hence, there is an emerging need to continue and develop new computational methods for robustly inferring the flux state, while capitalizing on these other available ‘omics’ measurements. In this context, IOMA presents an important step forward in this direction, which hopefully will be followed upon by others. IOMA profits from the absolute quantification of metabolites levels (in contrast to fold changes), that are becoming available, while absolute quantification of proteins is not necessary. Apart from the specific kind of reaction rate laws utilized in this work, IOMA can be used with a variety of rate laws including different types of regulation or enzyme saturation. The only restriction is that the rate laws can be represented in the form of Equation (5), where estimates of the terms a⁺ and a⁻ can be recomputed based on available data. Future work for improving flux predictions, could possibly utilize existing information on the thermodynamic constants of reactions to further constraint the model's solution space, following Henry et al. (2007).

Another potential application of IOMA is the prediction of metabolic flux alterations associated with human metabolic disorders (as means for predicting potential clinical biomarkers). Encouragingly, genome-scale human metabolic models have already shown their value in this highly important clinical task [e.g. in the case of inborn errors of metabolism (Shlomi and Cabili, 2009)], but as the methods used up until now have been simple and straightforward, there is certainly much room for improvement ahead, to which methods like IOMA are bound to serve as solid starting points.

Funding: Grant from the Israel Science Foundation (ISF) to T.S.; European Commission [BaSysBio, grant number LSHG-CT-2006-037469] to W.L.; Fellowship from the Edmond J. Safra Bioinformatics program at Tel-Aviv University.

Conflict of Interest: none declared.