Assessing the functional coherence of gene sets with metrics based on the Gene Ontology graph

Abstract

Motivation: The results of initial analyses for many high-throughput technologies commonly take the form of gene or protein sets, and one of the ensuing tasks is to evaluate the functional coherence of these sets. The study of gene set function most commonly makes use of controlled vocabulary in the form of ontology annotations. For a given gene set, the statistical significance of observing these annotations or ‘enrichment’ may be tested using a number of methods. Instead of testing for significance of individual terms, this study is concerned with the task of assessing the global functional coherence of gene sets, for which novel metrics and statistical methods have been devised.

Results: The metrics of this study are based on the topological properties of graphs comprised of genes and their Gene Ontology annotations. A novel aspect of these methods is that both the enrichment of annotations and the relationships among annotations are considered when determining the significance of functional coherence. We applied our methods to perform analyses on an existing database and on microarray experimental results. Here, we demonstrated that our approach is highly discriminative in terms of differentiating coherent gene sets from random ones and that it provides biologically sensible evaluations in microarray analysis. We further used examples to show the utility of graph visualization as a tool for studying the functional coherence of gene sets.

Availability: The implementation is provided as a freely accessible web application at: http://projects.dbbe.musc.edu/gosteiner. Additionally, the source code written in the Python programming language, is available under the General Public License of the Free Software Foundation.

Contact: lux@musc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

For a gene set, the functional coherence is a measure of the strength of the relatedness of the functions associated with the genes, which can be used to differentiate a set of genes performing coherently related functions from ones consisting of randomly grouped genes. It is commonly evaluated by analyzing the genes' functional annotations, which are almost invariably in the form of the controlled vocabulary from the Gene Ontology (GO; Ashburner et al., 2000; Brown et al., 2000; Huang et al., 2009; Khatri and Drălghici, 2005; Mateos et al., 2002). The vocabulary terms are organized as a graph, with concepts ranging from very general to very specific. They are used to annotate gene products by a variety of methods, including human curation, based on evidence from the literature. The annotations capture what is known about the biology. Functional coherence can be reflected in two aspects. First, whether genes share similar functions or whether they participate in the same biological processes. For example, if a sufficient number of genes from a set are annotated with a common GO term, the annotation is considered to be ‘enriched’ and, therefore, the genes are deemed functionally coherent. Second, whether the distinct functions are related. The relationship between functional annotations can be either semantic or biological in nature. For example, if a gene is annotated with the term regulation of apoptosis and another one is labeled with the term induction of apoptosis, their functions can be considered coherent because the terms are semantically alike. Alternatively, annotations can be semantically distinct, e.g. apoptosis and electron transport chain, yet their co-occurrence in a gene set can be biologically meaningful if many genes in the set participate in both processes. Ideally, a measure of functional coherence should take the above aspects into account during evaluation. To date, a method unifying the enrichment and relatedness aspects of functional coherence remains to be developed.

The first aspect of functional coherence, evaluating GO term enrichment, is usually performed by various count-based methods that evaluate the probability of observing a GO term in a set by random chance—to determine if an individual term is over-represented in a gene set. The widely used count-based methods are based on the hypergeometric distribution or other similar probabilistic models (Cho et al., 2001; Huang et al., 2009; Khatri and Drăghici, 2005; Man et al., 2000). The merits and limitations of this family of methods are well documented (Khatri and Drăghici, 2005; Zheng and Lu, 2007). Since the objective of count-based methods is focused on individual terms, directly utilizing their results, e.g. P-values, to assess overall coherence encounters the following difficulties: (i) schemes (ad hoc or sophisticated) need to be devised in order to combine the results of individual tests into a unified measure; (ii) the relationships among the terms are ignored by treating each annotation independently; and (iii) multiple testing potentially leads to false positives results, thus a less reliable unified measure.

The second aspect, evaluating the relatedness among distinct annotations, has been investigated in several studies that utilized the directed acyclic graph (DAG) representation of the GO. A number of studies have used the ontology graph structure in the context of functional analyses; however, the specific purpose or information used often differs from the methods proposed in this study, making a direct comparison between methods less meaningful. One theme is to find the representative summary term(s) utilizing the graph structure. For example, the lowest common ancestor terms have been used to find summarizing GO terms (Lee et al., 2004). Making use of the topology of the GO graph, Alexa et al. (2006) devised several algorithms to identify the representative GO terms and further to reweight the scores of the terms. Another theme utilizing the GO graph structure is to quantify the semantic relationships among the GO terms and derive statistics to assess their similarity. For example, the average of pairwise shortest paths between the annotated terms has been used to develop both pairwise and group-level measures of gene set similarity (Ruths et al., 2009; Wang et al., 2007). Other authors have used semantic similarity to summarize the results of enrichment analyses (Xu et al., 2009). Another measure of similarity, the total ancestry measure, was developed by Yu and co-workers (Yu et al., 2007) to summarize the functional similarity of GO terms from a gene set. Furthermore, GO graph-based studies have been carried out to evaluate the functional coherence of gene sets via the integration of multiple data sources. Several methods make use of microarray expression data (Goeman and Mansmann, 2008; Kong et al., 2006), while others use the biomedical literature associated with genes (Raychaudhuri and Altman, 2003; Zheng and Lu, 2007). However, none of these methods have considered both aspects of functional coherence, nor have they explicitly considered the relationships among GO terms co-annotating genes, which provide additional biological information.

In this study, we introduce a novel approach to assess the functional coherence of gene sets by taking into account both the enrichment of GO terms and their relationships among terms, of which a conceptual overview is illustrated in Figure 1. Our methods offer three novel aspects. First, the genes and their annotations are represented with a subgraph derived from the GO graph, in which genes and GO terms are represented as nodes, and their relationships are represented as quantifiable edges (gene-to-term and term-to-term). By studying the topological properties of the graph with methods from graph theory (Barabási and Oltvai, 2004; Newman, 2003), we have identified a set of metrics that reflect both the enrichment of GO terms and the relationships among them, which makes possible the differentiation of known coherent gene sets from randomly grouped ones. Second, we utilized the information of co-annotation of genes by a pair GO terms, a source of information ignored by most of contemporary methods, to further enhance the discriminative power of the graph-based metrics. Finally, we have developed a principled framework by employing simulation and non-parametric statistical methods, which enables us to directly test the null hypothesis that a gene set consists of random grouped genes. When applied to the gene sets from the Kyoto Encyclopedia of Genes and Genomes (KEGG) database (Kanehisa et al., 2006), the metrics were shown to be highly discriminative in terms of differentiating known coherent gene sets from random ones; when tested on gene sets derived from microarray analysis, the metrics provided biologically sensible assessments.

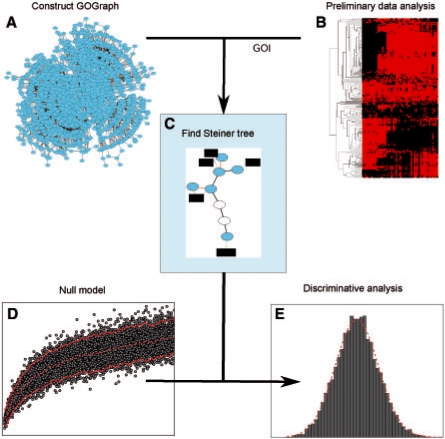
Fig. 1.

Conceptual overview of graph-based functional coherence evaluation. (A) A graph representation of the GO is constructed and referred to as a GOGeneGraph, in which a node is a GO term or a gene, and an edge reflects the semantic relationship between a pair of GO terms or gene-term relationship. (B) A GOI is produced by high-throughput technology or other methods. (C) A GO Steiner tree is extracted and several types of network statistics of the GO Steiner tree are collected. (D) Through simulation experiments, the distributions of the network statistics from randomly grouped gene sets are estimated. (E) The hypothesis that the GOI belongs to the population of the random gene sets is tested and a P-value is returned. In addition, users may choose from several visualization tools to discover more about the functional relationships between the GOI.

2 METHODS

2.1 Constructing GO-based graphs

For each organism considered in the study (Saccharomyces cerevisiae, Mus musculus and Homo sapiens), a specific gene–GO association file was downloaded from the website of the GO Annotation project of the European Bioinformatics Institute (August 13, 2009) from http://www.geneontology.org/GO.current.annotations.shtml. Additionally, on the same day an ontology file was downloaded from http://archive.geneontology.org/latest-termdb/go_daily-termdb.obo-xml.gz. The definition file was also downloaded from the GO website and it was used to construct a DAG in the biological process subspace. We have developed a Python library with a set of application programming interfaces for building different GO-related graphs and performing various queries (Muller et al., 2009). This library is based on the Python package NetworkX (Hagberg et al., 2008). In a graph representation of the GO, referred to as GOGraph, each node (vertex) represents a GO term and each directed edge corresponds to the IS_A relationship between a parent–child GO term pair. The directed edges between terms represent their semantic relationship such that the concept of a parent node subsumes those of its children nodes. Hence, the constructed GOGraph obeys the ‘true path rule’ or in other words the pathway from a child term to the most top-level parent is always true. Then, genes are added as another type of node to the GOGraph via an edge to its associated GO term(s) to create the GOGeneGraph. The GOGeneGraph is further modified by the addition of edges between terms that share the same gene annotations. Associating GO terms with the genes they annotate enables the calculation of semantic distance for edges from a GOGraph using the established methods, see Section 2.2 for details. After initialization of the edge distances, the graph is further transformed into a weighted, undirected graph, so that the functional coherence of list of GO terms can be reflected by connectivity and distances among the terms rather than the directionality. The algorithm for constructing a GOGeneGraph is detailed in Supplementary Algorithm 1.

2.2 Semantic distance

A commonly used method to measure the semantic distance between terms is based on information theory, in which differences in the information content (IC; Jiang and Conrath, 1998; Lord et al., 2003; Pesquita et al., 2009; Resnik, 1995) of semantic entities are employed as a measure of the semantic distance. Adopting the same principle, the IC of a GO term was calculated as follows:

(1)

where P(t) is the number of annotation instances for the term divided by total number of annotation instances from the annotation database. We can then define the semantic distance between a parent–child pair of GO terms as

(2)

Adding gene nodes into a GOGraph introduces new paths/connections between a pair of GO terms (through term-gene-term paths), if they share one or more genes. Thus, a GOGeneGraph not only provides information about the semantic relationship between terms according to the GO definitions, but also reveals the presence of biological relationships between terms according to biological annotation evidence. To quantify the strength of a biological relationship, a new term-to-term edge is added between a pair of terms sharing one or more genes. The distance for a given new edge is then set to the length of the semantic edge in the GOGraph G occupying the fifth percentile d_P5 divided by the number of genes shared by the pair

(3)

where d_G is the set of all edge distances in the GOGraph G and |g_i,j| is the number of genes providing biological connections between GO terms i and j. Equation 3 reflects the following reasonings: (i) co-annotation is relatively rare event and often biologically meaningful, thus its semantic distance should correspond to a significantly short distance for which we chose the fifth percentile of all edges; and (ii) the more genes that provide the connection between a pair of GO terms, the shorter the distance and the stronger the biological relationship between the terms.

2.3 Extracting a GO Steiner tree

Given a gene set, the GO terms associated with the genes, referred to as seed terms, are identified in the GOGeneGraph. To investigate the relationship among the seed terms, we extract a subgraph connecting the seed terms, including both inherited term–term and augmented term–term edges [see Equations (2) and (3)], such that the sum of all edge lengths for the subgraph is minimized for all possible subgraphs connecting the terms. The problem of finding such a subgraph is known as the Steiner-tree problem in computer science (Gilbert and Pollak, 1968). We refer to the Steiner tree subgraph of a GOGeneGraph as a GO Steiner tree (T_st). In this study, Kou's algorithm (Kou et al., 1981) is adopted to extract a GO Steiner tree from a GOGeneGraph. The heuristic algorithm for obtaining T_st is summarized in Supplementary Algorithm 2.

2.4 Graph-based functional coherence metrics

Three metrics were devised based on the topological properties of GO Steiner trees in order to reflect the functional coherence of a gene set. Building on the concept of enrichment, we define the number of genes associated with a seed term as seed degree (k_s) and the averaged seed degree of a tree, is denoted as 〈k_s〉, which reflects a global measure of enrichment for the GO terms in the gene set. To integrate the semantic relationships between terms, we define the sum of the lengths of all edges within a tree as the total length (l) of a GO Steiner tree, which reflects the overall relatedness of the functions. We also define 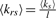as a measure of relative seed degree, which combines the above two aspects of functional coherence. The GO Steiner-tree metrics 〈k_s〉 and l are produced by summing a number of variables, in proportion to the size of a gene set n and with respect to a given n they tend to be Gaussian distributed, with estimable parameters μ_n and σ²_n.

2.5 Non-parametric regression

The distribution of the aforementioned metrics change as the size of the gene set (n) changes. In particular, the mean and variance may exhibit a distinct relationship with the get set size. To capture these relationships, we adopted a non-parametric regression method (Nadaraya, 1964) to estimate the means and variances, μ_n and σ²_n, of trees as nonlinear functions of n. Let y_n denote the value of a metric from a GO Steiner tree with size of n. We then define the following relationships:

(4)

(5)

(6)

The relationship between the gene set size n and the parameters governing the graph-based metrics y_n for the random gene sets was investigated by sampling a large number of randomly generated gene sets as training data, 𝒟 = {(y_i, n_i)}_i=1^|𝒟|, followed by estimation of the parameters μ_n and σ_n² for a n as follows:

(7)

(8)

(9)

where 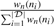is the Nadaraya–Watson weight for the i-th observation and w_n the Gaussian kernel function with bandwidth parameter p, which was set to 15 for all regressions in this study. All numerical analyses were carried out using the Python package Numpy (http://numpy.scipy.org) and the statistical language R (http://www.r-project.org).

The assumption that 〈k_s〉 and l are Gaussian distributed with respect to the size of a gene set n was tested using the Shapiro–Wilk (Shapiro and Wilk, 1965) test, as implemented in R, and the results (see Supplementary Methods) indicate that the P−value for observing a statistic from a tree with n genes can be calculated according to the Gaussian distribution function. Under certain assumptions, the distribution of the statistic 〈k_rs〉 can be represented using a Cauchy distribution. However, empirical results indicated that the majority of samples could be represented with Gaussian distributions , which also provided better discriminative performances. Hence, the P-values for 〈k_rs〉 were determined according to the Gaussian distribution. All tests for significance are one-sided. A value of 〈k_s〉 or 〈k_rs〉 is considered to be significant if it is higher than an upper critical value; while a value of l is significant when it is less than a lower critical value.

3 RESULTS

3.1 Capturing the functional relationships of genes with GO-based graphs

In this research, we studied the functional coherence of gene sets through the investigation of the relationships between constituent genes in GO graph space. To this end, we first constructed a GOGraph, which consists of only GO terms (nodes) and their ontology relationships (edges) as defined by the GO. Then, we added all annotated genes as nodes to the GOGraph, based on the instances specified in the GO database, leading to a graph consisting of both types of nodes, which is referred to as a GOGeneGraph. During the process, we further augmented the GOGeneGraph by adding edges between pairs of GO nodes that were used to co-annotate one or more genes. After augmentation, a GOGeneGraph was further transformed into a weighted, undirected graph, of which an edge's length was calculated according to the semantic distance between a pair of GO terms. More details about the graph construction are available in Section 2 and in a report on the utilized software package (Muller et al., 2009). The motivation for augmenting a GOGeneGraph is that co-annotation by a pair of GO terms, whether semantically close or remote, is generally biologically meaningful. Table 1 provides examples of co-annotation instances in yeast. For example, co-annotation of 25 genes by the two semantically remote terms, cell death and oxidation reduction, may be puzzling at first glance, but it is less surprising when one understands that many of the genes involved in oxidation reduction are also involved in the process of programmed cell death. On the other hand, co-annotation by the terms with closely related semantic meanings is understandable as the genes themselves are likely closely related in function. In both cases, taking co-annotation into account during functional coherence analysis will reflect the biological relationships between GO terms that are not explicitly considered in most previous GO-based function analysis methods.

Table 1.

Examples of term–term co-annotation in S.cerevisiae

	Term 1		Term 2		No. genes	Example genes
	GO:0051301	cell division	GO:0019953	sexual reproduction	37	SEC15, BEM1, BOI1
Semantically	GO:0008219	cell death	GO:0055114	oxidation reduction	25	CYT1, COX8, ATP3
dissimilar	GO:0000910	cytokinesis	GO:0000003	reproduction	23	BUD3, SEC15, SEC3
terms	GO:0019740	nitrogen utilization	GO:0015696	ammonium transport	6	MEP2, ADY2, ATO2
	GO:0042493	response to drug	GO:0007047	cell wall organization	6	ECM17, PHO85, FPS1
	GO:0006281	DNA repair	GO:0006974	response to DNA damage stimulus	35	MSH6, ELG1, RAD27
Semantically	GO:0016568	chromatin modification	GO:0016573	histone acetylation	17	SPT3, TAF9, YNG1
similar	GO:0034605	cellular response to heat	GO:0009266	response to temperature stimulus	12	TPS1, HSP104, ECM4
terms	GO:0015849	organic acid transport	GO:0015837	amine transport	12	GAP1, BAP3, LYP1
	GO:0051276	chromosome organization	GO:0006338	chromatin remodeling	6	ISW1, VPS71, SWC4

3.2 Comparing GO graphs across species

To assess if our approach can be broadly applied in different species, we first analyzed the properties of the GO graphs from different species to determine if their characteristics are comparable across species, because many GO terms and annotated genes are species-specific. Additionally, because the graphical representation of the GO represents the organization of biological concepts and the gene annotations reflect contemporary knowledge of the biology of genes, it is of interest to investigate how the concepts and genes are organized in the gene-concept space. We constructed and studied species-specific graphs, corresponding to the biological process domain of the GO, for three organisms: S.cerevisiae, M.musculus and H.sapiens, and we then investigated the topological properties of the graphs for comparison.

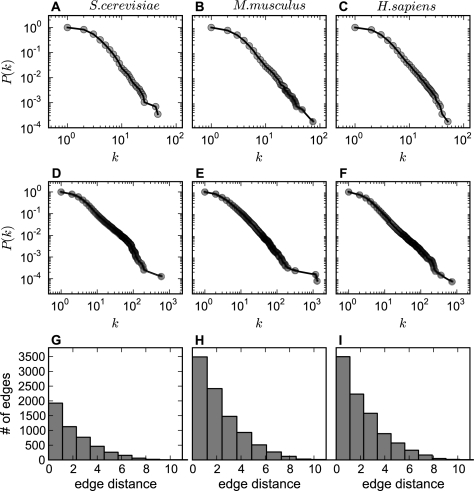
A common way to summarize the topology of a graph is to study the relationship between the node degree k (the number of edges connected to a node) and the cumulative degree distribution P(k) (the probability that a node has a degree greater than or equal to k) in logarithmic scales (Newman, 2003). Figure 2A–C shows that for the GOGraphs, despite differences in the number of annotations and genes between species-specific graphs, the relationship between k and P(k) can be fitted with a similar power–law curve for all three species. The similar degree distributions in Figure 2A–C suggest that biological concepts are organized in a similar fashion across the organisms. The nearly linear relationships in the panels indicate that the GOGraphs have the characteristics of scale-free graphs with a hub-spoke-like organization (Barabási and Oltvai, 2004; Newman, 2003). With respect to the GO, this means that some concepts are highly connected and play critical roles in connecting various concepts. Similarly, the GOGeneGraphs from the three species have comparable power–law exponents and are thus similar in architecture (Fig. 2D–F). These results indicate that some GO terms are used to annotate a large number of genes, and some genes are connected with multiple GO terms. In addition to degree, histograms of edge distances are shown (Fig. 2G–I) in order to quantitatively summarize the semantic relationships among the GO terms. The overall similarity of the plots for the three species indicates that the graph properties and, thus, functional coherence metrics based on these properties, are likely to be applicable to other species with similar annotation topologies.

Fig. 2.

Comparison of GOGraph network topology of different species. (A–C) The log–log plots for the cumulative term degree distributions of GOGraphs for S.cerevisiae, M.musculus and H.sapiens. The horizontal axis is node degree k, and the vertical axis is cumulative probability P(k), where k corresponds to the number edges connecting to a node, and P(k) is the probability that a node has k or more degree. (D–F) The cumulative degree distributions for GOGeneGraphs augmented by adding all annotated genes from the three species, respectively. (G–I) The distributions (histograms) of edge distances of GOGraphs for the species.

3.3 Metrics for capturing functional coherence

Given a set of genes, we extract a subgraph of GOGeneGraph, which connects the genes through their function annotations to reflect how genes are functionally related to each other. We further constrain the subgraph to have the shortest total semantic distance among all possible subgraphs connecting the genes, which leads to a subgraph commonly referred to as Steiner tree (see Section 2). In a GO Steiner tree, in addition to the GO terms directly associated to the genes, seed terms, more terms (nodes) may be included to provide connections among all seed terms. A GO Steiner tree not only reflects how genes are annotated but also represents how the functions of the genes are related to each other. Thus, the properties of a GO Steiner tree can be used to evaluate both aspects of functional coherence—the enrichment of functional annotations and the relatedness of the distinct annotations.

Three metrics were devised based on the topological properties of GO Steiner trees in order to reflect the functional coherence of a gene set: the sum of the lengths of all edges within the tree l, the averaged seed degree of a tree 〈k_s〉 and the combined metric 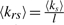. The values of the metrics can be interpreted as follows. A greater 〈k_s〉 than expected by random chance indicates a functionally coherent gene set, because many genes within the set share the same function annotations. A smaller l than expected by random chance represents a functionally coherent gene set, because the annotations of the genes are semantically or biologically related. Similarly, a greater 〈k_rs〉 than expected denotes a more coherent gene set, because in such a set either many genes share the same function annotations or the function of the genes are closely related to each other or both. The quantities measured with these metrics are collectively referred to as network statistics.

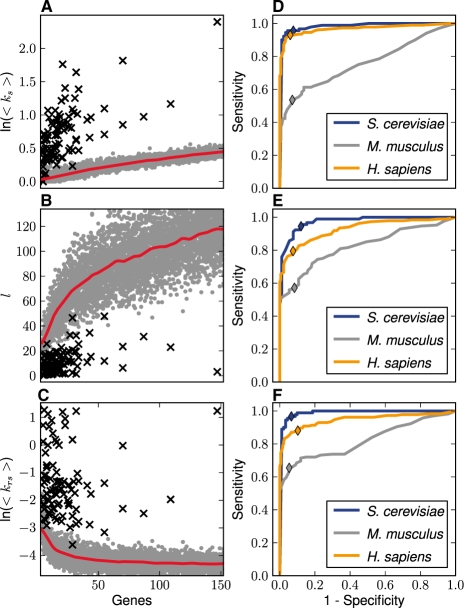
We further investigated if the network statistics were different between functionally coherent gene sets and randomly grouped ones. By sampling from all annotated genes in a genome, we produced a large number of randomly grouped gene sets of various sizes to serve as samples from a population of non-coherent gene sets. For comparison, we extracted the pathways from the KEGG database (Kawashima et al., 2003) and used the corresponding genes as samples of coherent gene sets. Each network statistic was plotted as a function of the size of the gene sets n, because the values of the metrics, in particular l, vary with the size of the gene sets. Figure 3A–C summarizes the results for the S.cerevisiae data in a scatter plot. In Figure 3A, <k_s> increases as a nonlinear function of n for random groups, and the data points from the KEGG pathways significantly deviate from the trend of the random sets. Indeed, most functionally coherent data are above the estimated means (see Section 2) of the random gene sets with similar sizes, indicating that the GO terms in the KEGG gene sets are more enriched. Figure 3B plots l as a function of group size n. While the data exhibit a monotonically increasing function for the random groups, the lengths (l) of the GO Steiner trees for the KEGG pathways are significantly shorter than those from the random sets, indicating that the GO terms from the KEGG gene sets are more closely related (semantically or biologically) than in randomly grouped gene sets. The results measured by the unified coherence metric <k_rs>, shown in Figure 3C, also suggest that the groups are separable.

Fig. 3.

Network statistics of random and coherent gene sets. (A–C) The network statistics corresponding to 8850 randomly sampled gene sets (gray dots) and 90 pathways (black crosses) from the KEGG database for S.cerevisiae are shown as functions of gene set size n for the three metrics, <k_s>, l and <k_rs>. The red lines in (A–C) are the means of the random gene sets as functions of n fitted with the Nadaraya–Watson method (see Section 2). (D–F) The ROC curves for the network statistics, where AUC values are shown in Table 2. (D–F) illustrate the discriminative performance for <k_s>, l and <k_rs>, respectively. The colors indicate the species and the colored diamonds show the sensitivity and false positive rates of the metrics when the P-value threshold is set at 0.05.

3.4 Statistical testing and discriminative analysis

We further evaluate the discriminative power of the metrics in terms of classification accuracy. Our approach was to train a model that employs a non-parametric regression method to capture the distributions of the network statistics from randomly sampled gene sets. Under the null hypothesis that any gene set belongs to the random gene set population, the trained model can determine the P-value for an arbitrary gene set—the probability that the set is comprised of randomly drawn genes. As for the hypothesis testing, the P-value returned by the model can also be used for discriminative analysis. In the latter case, the model can further classify a gene set into a coherent or non-coherent class based on a predefined threshold P-value. Under this setting, the discriminative power of a metric can be assessed with the receiver operating characteristics (ROCs) curve (Zweig and Campbell, 1993) analysis, in which the area under the ROC curve (AUC) is used as a measure of discriminative power. The closer an AUC value is to one, the stronger the discriminative ability.

We performed ROC analyses for each of the three selected metrics, <k_s>, l and <k_rs>, using the KEGG pathways as positive cases and randomly sampled gene sets with corresponding sizes as negative cases. The results for all three species are shown in Figure 3D–F. The AUC values are listed in Table 2 for all the species and for each metric. The results indicate that the graph-based metrics are highly discriminative, with AUC values >0.9 for S.cerevisiae and H.sapiens. The AUC values for M.musculus, although not as high as other two species, can also be considered excellent. To illustrate the effect of augmenting a GOGeneGraph with co-annotation edges, Table 2 also compares the AUC values obtained from GO Steiner trees with and without augmented edges. This empirically indicates that augmenting GOGeneGraph with co-annotation edges significantly enhances the discriminative power of our methods.

Table 2.

A comparison of AUC values with the addition of augmented edges and without. The differences between the methods are most noticeable in the M.musculus and H.sapiens organisms. The column of AUC values with the addition of co-annotation edges corresponds to the curves in Figure 3D–F.

Species	Metric	AUC with	AUC without
	<ks>	0.983	0.985
S.cerevisiae	l	0.974	0.883
	<krs>	0.988	0.968
	<ks>	0.759	0.757
M.musculus	l	0.824	0.689
	<krs>	0.823	0.614
	<ks>	0.967	0.967
H.sapiens	l	0.923	0.767
	<krs>	0.948	0.813

We noted that by testing against a null distribution of random sets, our statistical test served directly the goal of evaluating if a gene set consists of random-grouped genes. As such it transcends the conventional count-based approaches that concentrate on testing whether or not an observed GO term in a gene set is a random event, which is tangentially related to the original goal. As shown in Figure 3, a P-value of 0.05 from our test serves as an almost optimal decision threshold for all three metrics in all species. Thus, this conventional threshold (P<0.05) of statistical significance can be readily applied in our statistical test, whereas in the count-based methods one often needs to adjust the significance threshold to avoid false positive calls (Cho et al., 2001; Huang et al., 2009; Khatri and Drăghici, 2005; Man et al., 2000).

3.5 Robustness of the metrics

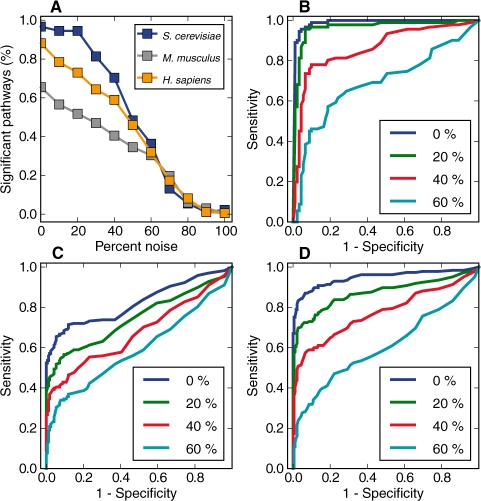
It is inevitable that results from high-throughput approaches contain noise of varying degrees. To evaluate the robustness of the metrics against noise, we performed a noise simulation experiment by replacing different percentages of the genes from KEGG pathways with randomly selected ones, followed by the evaluation of the metrics' discriminative power. As an example, we studied the discriminative power of the unified metric (<k_rs>) tested with contaminated data for all three species (Fig. 4). With a P-value threshold at 0.05, we examined the percent of KEGG pathways that were classified as coherent after introducing different degrees of noise. The results are plotted as a function of the percent of noise in Figure 4A. Our metric classified the majority of the lightly contaminated (noise <30%) KEGG gene sets as coherent and the heavily contaminated (noise >60%) ones as non-coherent. The ROC curves in the presence of different amounts of noise for S.cerevisiae, M.musculus and H.sapiens are shown in Figure 4B–D, respectively. Overall, the figure shows that <k_rs> retains a high degree of discriminative power, even with a relatively large amount of noise under these simulation conditions.

Fig. 4.

Testing for metric robustness. In a noise simulation experiment, P-values derived from the <k_rs> method were used to evaluate the robustness of the metrics in the presence of different amounts of simulated noise. (A) With the P≤0.05 as the threshold, the percent of KEGG pathways classified as coherent in the presence of noise was plotted against the percent of simulated noise. The line colors indicate the species. (B–D) The ROC curves using <k_rs> in presence of different degrees of noise are shown for S.cerevisiae, M.musculus and H.sapiens, respectively. Specifically, the AUCs for curves with 0–60% (increasing by 20%) are presented.

3.6 Application to microarray gene expression analysis

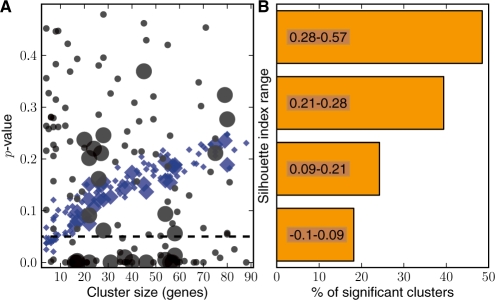
To evaluate the performance of the metrics at a systems level, we investigated the metrics developed in this study using a real world microarray dataset. We collected microarray data from yeast cells subjected to oxidative stress (see Supplementary Methods), and the k-means clustering algorithm (Tavazoie et al., 1999) was employed to partition the genes into 225 clusters, among which 132 clusters had a number of genes that fell between 5 and 300. These clusters were further investigated using our GO Steiner tree methods. We assess the performance of the methods in several ways (Fig. 5).

Fig. 5.

Application to microarray analysis. (A) The relationship between the P-values by the metrics and cluster size. The black circles correspond to results for clusters tested by the <k_rs> method and the blue diamonds indicate those of the count-based one. The points for each method have two sizes where the larger ones denote differentially expressed clusters that were statistically significant (≤0.05) as determined by a GSA method. (B) The relationship between significance calls by <k_rs> and silhouette index. According to their silhouette index ranks, the 132 clusters were divided into four evenly sized groups then the percent of clusters classified as significant within each group was plotted.

We investigated the relationship between the P-values produced by graph-based metrics and cluster size (Fig. 5A). As a comparison, we also calculated the enrichment P-values of each GO term within the clusters based on a hypergeometric assumption (Cho et al., 2001; Kong et al., 2006), and an averaged P-value of the cluster was determined and subsequently plotted in Figure 5A. The P-values from the GO term enrichment analysis are often sensitive to geneome size and the extent of annotation completeness (Khatri and Drăghici, 2005). Similarly, if these methods are extended to evaluate global functional coherence of a gene set as by simple averaging of P-values the results can be shown to be sensitive to the gene set sizes. The averaged P-values by the count-based metric showed a clear trend as a nearly linear function of the size of the clusters; in contrast, the P-values from the graph-based metric span a broader range, indicating cluster size has little if any impact on its coherence evaluation. The results confirm a well-known phenomenon that GO terms observed within a small cluster are more likely to be evaluated as ‘enriched’ due to the characteristics of hypergeometric distribution (Khatri and Drăghici, 2005; Zheng and Lu, 2007). The panel also shows that the clusters evaluated as significant by the graph-based metric tend to be rich with differentially expressed genes per a gene set analysis (GSA) method (Efron and Tibshirani, 2007).

To further investigate the results, we assessed how well the graph-based functional coherence evaluations agree with a metric commonly used to measure similarity of profiles within a cluster—the silhouette index (Rousseeuw, 1987). An underpinning assumption for many microarray analysis methods is that closely co-regulated genes, whose expression profiles are tightly clustered within a gene set (reflected as a high silhouette index) are likely to function coherently (Eisen et al., 1998). The results (Fig. 5B) indicate that, as the silhouette value increases, a cluster is more likely to be evaluated as significant by the graph-based metric.

Lastly, we assessed the functional coherence of the clusters by manually studying their annotations and their GO Steiner trees. We found that according to expert assessment, many biologically coherent clusters were correctly classified by the graph-based metric. For example, our graph-based evaluation correctly called a cluster of genes rich with ribosomal proteins as coherent gene set, thus conforming with well-documented knowledge that the expressions of these genes are significantly and coordinately repressed during various cellular stresses (Gasch and Werner-Washburne, 2002). Overall, the results demonstrate the ability of this method to filter through large amounts of potentially interesting gene sets in order to focus on those of relevant biological interest.

3.7 Visualization

Visualization provides another means to assess the functional coherence of a gene set beyond solely relying on P-values. Visualization allows for the generation of new hypotheses based on the functional groupings of genes and terms and the way they are connected, and equally important it may be used to confirm existing knowledge about the underlying biology. To this end, we have implemented a web application.

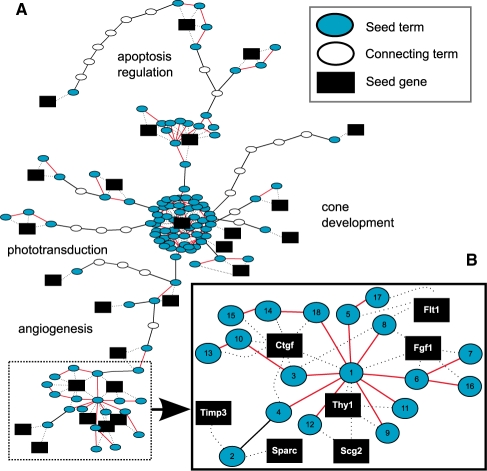
As an example to illustrate the utility of visualization, we explored the GO Steiner tree for a set of genes published in a study on retina degeneration (Rohrer et al., 2004) (Fig. 6). An evaluation with <k_rs> resulted in a significant P-value of 0.043, suggesting that the GO terms from the gene set are more coherent than random. Indeed, when inspecting the GO Steiner tree for the gene set, we found that there are two major clusters of nodes consisting of both genes and GO terms. One cluster consists of 99 GO terms associated with one gene, Drd2, while another is comprised of 7 genes and 18 highly connected GO terms. Visualization thus enabled, in this case of this cluster, the user to focus in immediately on the most biologically interesting part of the GO Steiner tree. Observing the clusters also helped to explain why the gene set was considered statistically significant, supporting the idea that exploring a GO Steiner tree is an efficient means to facilitates functional investigation.

Fig. 6.

Steiner tree visualization. (A) An example of GO Steiner tree visualization for a gene cluster involved in retinal degeneration. Oval nodes are GO term nodes, with cyan ovals representing the seed terms and open ovals denoting the GO terms needed to connect all seed terms. A black edge represents the semantic edge defined in the GOGraph and a red edge is an augmenting edge representing the connection between GO terms that co-annotate proteins. A gene is represented with a black box and the dashed edges denote gene-to-term relationship. Summarizing annotation descriptions are displayed as text. The whole gene expression cluster takes the form of several distinct groups. (B) One group (subgraph) of interest is examined more closely to highlight the characteristics of a more functionally coherent part of the overall GO Steiner tree. The GO terms labeled with a number are further explained in the Supplementary Results.

Visualization helped us derive the following biological thoughts and insights. The animal model analyzed here is the rd1 mouse (Farber, 1995), a very well-studied model for retinitis pigmentosa (RP), a disease resulting in rod photoreceptor degeneration. Many pathophysiological aspects of the disease model were correctly recognized by the GO terms phototransduction, ion transport, apoptosis regulation and cone development. Photoreceptor cell death in this model can be slowed down using dopaminergic agonists (regulation of dopamine), which provides the rationale for Drd2 (Ogilvie and Speck, 2002). It is known that the photoreceptor cell death leads to cytoskeleton reorganization and changes in protein localization both within the dying cell as well as in the remaining surviving cells. Visualization provides the user with a method to investigate functional subgraphs of a GO Steiner tree. For example, by visualizing the functional cluster subplot (Fig. 6B) it is easier to tease out the relationships between genes and terms than it is with a list of annotations alone. The subplot along with the annotation descriptions (see Supplemental Results) provide the genes associated with the cells surviving initial apoptotic events. These cells reorganize into a novel network due to migration and proliferation of certain cell types (Marc et al., 2007). Because, no links exist yet for Scg2 and Thy1 in photoreceptor degeneration, this leads to the generation of hypotheses that may be used to characterize their roles in the rd1 model and ultimately in RP. There are grounds for further investigation, because Scg2 is expressed in the retina (Liu et al., 2006) during development and Thy1 is crucial for retinal development (Simon et al., 1999).

4 DISCUSSION

The main goal of this study was to introduce functional coherence metrics with high levels of discriminative power, based on the currently available GO annotations. Moreover, the method was intentionally developed independent of data types that are used to generate the gene set of interest (GOI). Two graph-based metrics, <k_s> and l, were developed, where the former measures the enrichment of functional annotations, and the latter summarizes the relatedness of the annotations. Furthermore, <k_rs> was devised so that both aspects of functional coherence can be evaluated with a unified metric. In addition to quantitative evaluation, we have also provided tools to visualize GO Steiner trees as a means to further assess the results by inspecting how genes and annotations are organized, rather than solely relying on P-values. In the real world application, the metrics returned biologically sensible calls. The advantages of these metrics include but are not necessarily limited to the following: (i) by incorporating semantic and biological relationships in the evaluation, our methods treat genes annotated with semantically close GO terms as functionally similar; (ii) providing an global evaluation method for proteins/gene sets, rather than treating each function annotation of genes as independent; and (iii) addressing the multiple testing problem by reducing the number of tests. However, like all GO-based evaluation methods, the metrics are dependent on how well genes are annotated. Therefore, the utilities of the metrics are limited when considering species that have less comprehensive annotations, and the metrics may reflect potential annotation biases from the databases. This is likely to hold true for localized areas of the GOGraph as well.

The discriminative power of the graph-based metrics may be attributed to the following factors. First, the methods capture the key properties that differentiate coherent gene sets from random ones—GO terms in a functionally coherent gene set are more likely to be enriched and their functions are more closely related semantically and biologically. In addition to the semantic relationships considered, our metrics further take into account the relationships among GO terms that co-annotate genes, which leads to a better performance. Second, through a sampling approach, our method accurately estimates the distribution of network statistics of the randomly grouped gene sets, which is directly relevant to the task at hand—determining if an arbitrary gene set consists of randomly grouped genes.