Detection of DTI White Matter Abnormalities in Multiple Sclerosis Patients

Abstract

The emergence of new modalities such as Diffusion Tensor Imaging (DTI) is of great interest for the characterization and the temporal study of Multiple Sclerosis (MS). DTI indeed gives information on water diffusion within tissues and could therefore reveal alterations in white matter fibers before being visible in conventional MRI. However, recent studies generally rely on scalar measures derived from the tensors such as FA or MD instead of using the full tensor itself. Therefore, a certain amount of information is left unused.

In this article, we present a framework to study the benefits of using the whole diffusion tensor information to detect statistically significant differences between each individual MS patient and a database of control subjects. This framework, based on the comparison of the MS patient DTI and a mean DTI atlas built from the control subjects, allows us to look for differences both in normally appearing white matter but also in and around the lesions of each patient. We present a study on a database of 11 MS patients, showing the ability of the DTI to detect not only significant differences on the lesions but also in regions around them, enabling an early detection of an extension of the MS disease.

1 Introduction

Multiple sclerosis (MS) causes a demyelination of the white matter fibers. The origin and evolution of this disease are still not well understood, and numerous studies have been conducted to evaluate its evolution and its influence on neighboring brain structures. To this end, several methods have been proposed, mainly using conventional MR modalities like T1, FLAIR or T2 images to delineate lesions as in [1]. This task is challenging and crucial, as having access to the lesion load over time, coupled with measurements such as local brain atrophy, can bring a lot of information on the characterization of the disease.

The emergence of new modalities, and in particular diffusion tensor imaging (DTI) [2], is of great interest in MS. DTI gives information about water diffusion within tissues, and could therefore reveal alterations in normal appearing white matter fibers before being visible in conventional MRI. For this purpose, Filippi et al. [3] evaluated the differences in fractional anisotropy (FA) between MS patients and controls on normal appearing white matter regions. While this type of studies tend to show that diffusion MRI could be beneficial to detect more accurately MS lesions, they generally rely on scalar measures derived from the tensor such as FA or mean diffusivity, instead of using the full tensor itself. A certain amount of information is thus lost in the processing of this data. In parallel, other studies have shown the interest of using the whole tensor information. For example, [4] showed that it was possible to compare diffusion tensors of two populations using Log-Euclidean (LE) metrics [5], and that the comparison was more sensitive, i.e. could reveal more differences, than considering only a scalar parameter such as the FA.

In this work, we propose a framework that relies on the whole diffusion tensor information to detect statistically significant differences between MS patients and controls. Recent work proposed methods for the detection of group differences between two tensor populations such as [4] on diffusion tensors, or [6] on Jacobian tensors derived from deformation fields. However, in our context, these methods are not directly applicable as lesions are not spatially consistent. Consequently, it is necessary to compare each patient individually with the group of control subjects. This approach also raises the question of the construction of an unbiased reference frame from the controls.

To address those problems, we propose a framework to compute an unbiased atlas of diffusion tensors from a database of controls. Based on this atlas, we show how to compute statistical differences between a patient and the atlas using a z-score derived from the whole tensor.

This framework was evaluated on a database of 11 MS patients and 31 normal controls, showing significant differences between each individual patient and the controls in regions identified as lesions on the T1 and FLAIR images. Interestingly, our results shows that DTI can remain sensitive inside a thick ribbon surrounding the lesions, suggesting that DTI could be more sensitive than conventional MRI to detect MS lesions.

2 Materials and Methods

2.1 Construction of a Diffusion Tensor Atlas of Controls

In order to compare the DTI of normal controls with the patient DTI, we need to bring all the DTI into the same reference frame. Using any subject as a reference would introduce a bias due to the specific anatomy of this reference image. Therefore, we chose to build a geometrically unbiased atlas from the dataset of controls extending the work of [7], and use this atlas as the reference for the rest of the study.

Our algorithm basically iterates over two steps. In a first step, ail images I_k are non linearly registered onto an initial (randomly chosen) reference image R, using a block-matching based non linear registration method presented in [8]. These registrations produce the deformation fields T_k. A mean image M is built from all registered images by averaging them. In a second step, the deformation fields T_k are averaged to get a mean transformation T̄, which inverse is applied to M. This new mean image is then used as the new reference image for the next iteration, i.e. $R=M\circ {\stackrel{-}{T}}^{-1}$. Notice that we used the Log-Euclidean framework for diffeomorphisms [9] when averaging deformation fields to ensure the invertibility of T̄. Transformations are calculated based on T1 images and then applied on DTIs, the main reason being that DTI registration is still not a mature research topic.

When warping diffusion tensor images, special attention must be paid to the reorientation of tensors. Indeed, tensors are supposed to remain aligned with underlying tissues under any transform. We chose the finite strain reorientation strategy proposed in [10] to reorient the tensors with respect to the Jacobian of the deformation. Note that the principal direction of diffusion preserving method [11] could be used as well. Tensors are resampled and averaged using Log-Euclidean metrics as they provide a fast way to extend any interpolation method to tensors while preserving the positive-definite constraint, and without suffering from the swelling effect as this is the case of the Euclidean calculus.

In summary, a set of transformations T_k is obtained for each T1 image I_k along with a mean T1 image Ī. Each T_k is applied to its corresponding DTI. The DTI atlas is finally generated by averaging these images.

2.2 Evaluation of Statistical Differences between Atlas and Patient

In statistics, differences between a test data and a population are estimated through the Mahalanobis distance, or so-called z-score. This distance requires to know the covariance matrix of the population (of tensors in our case). We propose to detail its computation in a first step, and show in a second step how to extract a p-value from it to test for significance.

Covariance Matrix and Z-Scores

The covariance matrix is computed as follows. Tensor logarithms are turned into vectors by keeping only the 6 independent coefficients and multiplying off-diagonal elements by $\sqrt[]{2}$, so that the L₂ norm of tensors is compatible with the L₂ norm of vectors. We call this operation the Vec mapping. Then, the covariance matrix C of this 6-dimensional vector is calculated. Finally, the Mahalanobis distance between a tested tensor D̃ and the ensemble mean/covariance matrix of the atlas is given by:

$$z\left(\tilde{D}\right)={\left({\tilde{D}}_{\mathit{Log}}-{\stackrel{-}{D}}_{\mathit{Log}}\right)}^{\top }{C}^{-1}\left({\tilde{D}}_{\mathit{Log}}-{\stackrel{-}{D}}_{\mathit{Log}}\right)$$

where D̃_Log and D̄_Log are the Vec mappings of the tensor logarithms, i.e. D̃_Log = Vec (log(D̃)).

Computing the p-value associated to the z-score

In our case, the null hypothesis is that the diffusion tensor being tested belongs to the normal population. As in the scalar case, the p-value is given by P(X > I_c(z)), where I_c(z) is defined as the points x where r ≡ (x − D̄_Log)^⊤C⁻¹(x − D̄_Log) = z². In our specific context, the probability density function to be integrated is a 6D multivariate Gaussian, leading to the following formulation:

$$V\left(z\right)=1-P(X<I_c\left(z\right))=1-{\int }_{r<z^2}{G}_{{\stackrel{-}{D}}_{\mathit{Log}},C}\left(x\right)\mathit{dx}$$ (1)

where G is a multivariate Gaussian of mean D̄_Log and covariance matrix C. It can be shown that this integration is equivalent to the integration of a multivariate Gaussian of mean 0 and covariance Id for values of x such as x^⊤x < z². Using this simplification and a change of coordinates to spherical coordinates, we obtain the following expression for the p-value:

$$V\left(z\right)=e^{-\frac{z^2}{2}}\left(1+\frac{z^2}{2}+\frac{z^4}{8}\right)$$ (2)

Following the usual practice in voxel-based morphometry, mean p-values are computed over spatially coherent regions of interest R (for instance MS lesions). To this end, we have chosen to compute first a mean z-score over the voxels i in region R and then compute the p-value, i.e. ${\stackrel{-}{V}}_R=V\left(\frac{1}{N}{\Sigma }_{i\in R}z\left({\tilde{D}}_i\right)\right)$.

3 Results

3.1 Image Databases

Data

For this study, we used a dataset of 31 controls and 11 patients diagnosed with MS. For each control, a T1 image and a DTI were acquired. T1 images have a resolution of 256 × 256 × 176 and a voxel size of 1 × 1 × 1 mm³. DTI images were acquired with 12 gradients and have a resolution of 256 × 256 × 60 and a voxel size of 1 × 1 × 2.5 mm³.

For each patient, a T1 image (resolution 124 × 256 × 256, voxel size 1.3 × 1 × 1 mm³) and a DTI (12 gradients, resolution 256 × 256 × 60, voxel size 1 × 1 × 2.5 mm³) were also available, as well as T2 and FLAIR images.

Pre-processing

For each control and each patient, the image sequence (DTI, FLAIR, T2) was rigidly registered onto the T1 image. For the DTI, the B0 image was rigidly registered on the T1 image and the obtained transform was applied to the diffusion gradients. To correct for acquisition distortion in DTI, we applied a non rigid registration procedure between the B0 of the DTI acquisition and the T1 image using the B-Splines method of [12] with few control points (5 × 5 × 5). B0 to T1 registration results were visually validated by a radiologist. T1 and FLAIR images were finally used to manually delineate the MS lesions on each patient.

For each MS patient, non linear registration of the T1 image onto the atlas was done. Patient to atlas registration consists in two steps. First, a global affine transformation was computed between the T1 images. Then, non linear registration was performed to locally align the anatomies of the atlas and the patient. As intensities in voxels with lesions are different from those of the atlas, the transformation was interpolated inside a dilated mask of the patient's lesions following a method similar to [13]. Thus, abnormalities in lesions signal did not interfere during the registration process. The final transformations were then applied to the patient DTI as presented in Sec. 2.1. Finally, voxel-wise z-score and p-value calculation were done to obtain a map of statistical differences. Results are presented in the next section.

3.2 Diffusion Tensor Differences in MS Lesions

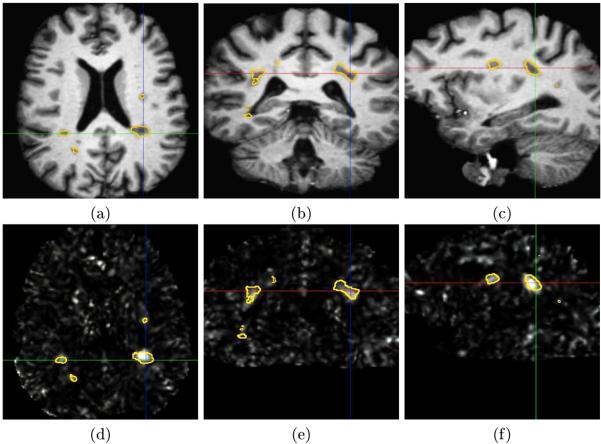
The initial evaluation consisted in looking at differences between patients and controls in the lesion regions. We present in Fig. 1 the maps of z-scores, with the manual delineations of the lesions superimposed, for one patient of the database.

Fig. 1. Voxel-wise z-scores for a given MS patient.

Illustration of the z-score maps obtained for a patient (images (d), (e), (f)) compared to the corresponding anatomy (axial (a), (d), coronal (b), (e) and sagittal slices (c), (f)). The contours correspond to the manual delineations of the MS lesions.

This figure shows that MRI regions with visible lesions have the highest z-scores. This indicates that the diffusion tensor is affected by MS and that lesions are highly likely to be significantly different with respect to an atlas of controls. We can also see on this figure (particularly on the sagittal slice) that, for some lesions, the manual delineation does not correspond exactly to the high z-score values. This is mainly caused by local errors in manual delineation, as shown in the sagittal view of Fig. 1 (c) at the position of the axes. More interestingly, the map of z-scores presents hyper-signals in regions not labeled as lesion by the expert. For instance, a possible extension of a lesion can be seen on the sagittal slice. There are indeed high z-score values around the large lesion on the right of this view that are not seen in the T1 image.

To verify and quantify the DTI signal difference between the patients and the control subjects, we computed the mean tensor-based p-value inside the manually delineated lesions. Results are presented in Table 1.

Table 1. Quantitative evaluation results on the MS lesions.

Mean p-values obtained on regions corresponding to the MS lesions for each patient.

Patient #	p-value	Patient #	p-value	Patient #	p-value
1	2.1 × 10−18	5	4.2 × 10−7	9	8.7 × 10−4
2	7.9 × 10−5	6	7.5 × 10−5	10	6.8 × 10−4
3	0.045	7	3.4 × 10−4	11	4.2 × 10−7
4	4.9 × 10−4	8	1.8 × 10−7

All p-values are below the critical value of 0.05, therefore rejecting for all patients the null hypothesis: tensors in lesions are not likely to belong to the normal variability represented by the atlas of controls. Interestingly, patient 3 is closer to 0.05 than the other patients.

3.3 Evaluation of Tensor Differences around Lesions

The previous section has shown the existence of significant tensor-based differences between patients and controls inside the lesions. To go beyond this sensitivity analysis, we looked at surrounding regions to check whether regions around the lesions exhibit large z-score values.

These ring-like regions around the lesions were obtained by subtracting the binary mask of the manually segmented lesions to its dilation. P-values were then computed withing those regions surrounding the lesions. These results are presented in Table 2.

Table 2. Quantitative evaluation results on regions around the MS lesions.

Mean p-values obtained on regions around the MS lesions for each patient (see text).

Patient #	p-value	Patient #	p-value	Patient #	p-value
1	8.1 × 10−7	5	0.009	9	1.9 × 10−3
2	0.059	6	1.8 × 10−3	10	0.028
3	0.101	7	0.079	11	0.019
4	0.066	8	0.016

Results show, for 7 patients out of 11, a p-value that is below the threshold of 0.05. Remaining p-values are also very low (the maximum value being 0.101). This may suggest that some patients exhibit an extension of the lesions that is not visible in conventional MRI, but is detectable in DTI using higher order statistical analysis. These results tend to prove that DTI may effectively be used as a complementary diagnostic imaging modality to study and understand the evolution of MS.

4 Conclusion

We have presented in this article a new framework for the detection of significant differences between DTI of patients and normal controls. This framework was applied to the study of multiple sclerosis and highlighted the great interest of DTI measurements made on the whole tensor for a better understanding and characterization of the disease. Results indeed indicated, qualitatively and quantitatively, that diffusion tensors were not only significantly different inside the lesion regions, but also for some patients in regions around the lesions. This suggests the existence of an extension of the disease invisible in conventional MRI, but revealed by DTI.

This comparison framework is however dependent on the choice of the registration method to build and register the statistical atlas. This choice may indeed bias the p-values results. The comparison of different registration methods will therefore be interesting to quantify this dependency. This evaluation will also include the use of registration methods taking into account the specificities of the DTI such as [14], allowing to register more precisely regions such as the white matter, which has a uniform intensity in conventional MRI.

Another way to cope with this bias and with possible preprocessing errors is the study of robust analysis methods, including more information on the local neighborhood of the tensors. An interesting solution could be for example the use of the STAPLE method [15] on each of the tensors components, allowing at the same time to compute a robust mean tensor image and the error parameters of the patient tensors.

This work also opens wide and important perspectives for the understanding of multiple sclerosis. One of them will be the temporal study of the evolution of the lesions and the comparison of the invisible extents found through DTI with the real evolution of the disease. This will allow us to see if these extents effectively evolve into lesions or if they are more related to a local edema. This framework will also be used for the evaluation of the influence of the disease on normal appearing white matter regions such as the corticospinal tracts.

In the future, we would also like to perform a quantitative comparison of all available imaging modalities to independently detect and quantify the lesion volume in the brain. Finally, as an extension to the present work, it will be interesting to propose a multi modal statistical framework to compute statistics on multivariate data (i.e. DTI, FLAIR, T1, T2) of higher dimensions. Indeed, this statistical study will also allow to do a sensitivity analysis of the contribution of each modality in the final detection performance.